2021广西大纲卷数学(文)高考真题下载

合集下载

2021版高考数学(文)大一轮人教A广西专用单元质检八立体几何(A)

单元质检八立体几何(A)(时间:45分钟满分:100分)单元质检卷第17页一、选择题(本大题共5小题,每小题7分,共35分)1.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则()A.直线a必垂直于平面βB.直线b必垂直于平面αC.直线a不一定垂直于平面βD.过a的平面与过b的平面垂直答案:C解析:α⊥β,a⊂α,b⊂β,a⊥b,当α∩β=a时,b⊥α;当α∩β=b时,a⊥β,其他情形则未必有b⊥α或a⊥β,所以选项A,B,D都错误,故选C.2.(2019云南曲靖沾益四中高三三模)如图,一个透明的球形装饰品内放置了两个共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,已知圆锥底面面积是这个球面,则较大圆锥与较小圆锥的体积之比为()面积的316A.2∶1B.3∶1C.4∶1D.5∶1答案:B解析:不妨设球的半径为4,则球的表面积为64π,圆锥的底面积为12π,所以圆锥的底面半径为2√3.由几何体的特征知球心到圆锥底面的距离、球的半径以及圆锥底面的半径三者可以构成一个直角三角形,由此可以求得球心到圆锥底面的距离是√42-(2√3)2=2,所以圆锥体积较小者的高为4-2=2,同理可得圆锥体积较大者的高为4+2=6.又这两个圆锥的底面相同,所以较大圆锥与较小圆锥的体积之比等于它们的高之比,即3∶1,故选B. 3.(2019广东潮州高三二模)一个几何体的三视图如图所示,该几何体外接球的表面积为()A.28πB.32πC.36πD.112π3答案:D解析:该几何体是一个底面为正方形的四棱锥,其中一个侧面为正三角形且与底面垂直,分别过正方形底面和正三角形侧面的中心作面的垂线,交点为外接球球心,由勾股定理求得球的半径为√283,表面积为112π3.4.我国古代数学名著《孙子算经》中有如下问题:“今有筑城,上广二丈,下广五丈四尺,高三丈八尺,长五千五百五十尺,秋程人功三百尺.问:须工几何?”意思是:“现要筑造底面为等腰梯形的直棱柱的城墙,其中底面等腰梯形的上底为2丈,下底为5.4丈,高为3.8丈,直棱柱的侧棱长为5 550 尺.如果一个秋天工期的单个人可以筑出300立方尺,问:一个秋天工期需要多少个人才能筑起这个城墙?”(注:一丈等于十尺)( ) A.24 642 B.26 011 C.52 022 D.78 033 答案:B解析:根据棱柱的体积公式,可得城墙所需土方为20+542×38×5550=7803300(立方尺),一个秋天工期所需人数为7803300300=26011,故选B .5.在空间四面体ABCD 中,平面ABD ⊥平面BCD ,且DA ⊥平面ABC ,则△ABC 的形状是( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定答案:B解析:作AE ⊥BD ,交BD 于E ,∵平面ABD ⊥平面BCD ,∴AE ⊥平面BCD ,BC ⊂平面BCD , ∴AE ⊥BC.而DA ⊥平面ABC ,BC ⊂平面ABC , ∴DA ⊥BC.又∵AE ∩AD=A ,∴BC ⊥平面ABD.而AB ⊂平面ABD ,∴BC ⊥AB , 即△ABC 为直角三角形.故选B .二、填空题(本大题共3小题,每小题7分,共21分)6.已知四棱锥P-ABCD 的三视图如图所示,则此四棱锥外接球的半径为 .答案:√5解析:因为三视图对应的几何体是四棱锥,顶点在底面的射影是底面矩形的长边的中点,底面边长分别为4,2,满足侧面PAD⊥底面ABCD,△PAD为等腰直角三角形,且高为2,如×√42+22=√5.图所示,可知外接球球心为底面对角线的交点,可求得球半径为127.已知PA垂直于平行四边形ABCD所在的平面,若PC⊥BD,则平行四边形ABCD的形状一定是.答案:菱形解析:因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.又PC⊥BD,且PC⊂平面PAC,PA⊂平面PAC,PC∩PA=P,所以BD⊥平面PAC.又AC⊂平面PAC,所以BD⊥AC.又四边形ABCD是平行四边形,所以四边形ABCD是菱形.8.已知A,B,C,D是球面上不共面的四点,AB=AC=√3,BD=CD=√2,BC=√6,平面ABC⊥平面BCD,则此球的体积为.π答案:8√23解析:如图所示,设球心坐标为O,连接OD,交BC于点E,连接AE,由题意可知OE2+AE2=OA2.设球的半径R=OD=OA=x,由题意,得(√22-x)2+(√62)2=x 2,解得x=√2,则此球的体积为V=43πR 3=8√23π. 三、解答题(本大题共3小题,共44分)9.(14分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在右面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连接BC',证明BC'∥平面EFG. 答案:(1)解如图:(2)解所求多面体体积V=V 长方体-V 正三棱锥=4×4×6-13×(12×2×2)×2=2843(cm 3).(3)证明在长方体ABCD-A'B'C'D'中,连接AD',则AD'∥BC'.因为E ,G 分别为AA',A'D'的中点, 所以AD'∥EG.从而EG ∥BC'.又BC'⊄平面EFG ,所以BC'∥平面EFG.10.(15分)(2019全国Ⅱ,文17)如图,长方体ABCD-A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.答案:(1)证明由已知得B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,故AE=AB=3,AA1=2AE=6.作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.所以,四棱锥E-BB1C1C的体积V=1×3×6×3=18.311.(15分)如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,AC⊥AB,AC=AB=AA1=2,∠AA1B1=60°,E,F分别为棱A1B1,BC的中点.(1)求三棱柱ABC-A1B1C1的体积;(2)在直线AA1上是否存在一点P,使得CP∥平面AEF?若存在,求出AP的长;若不存在,说明理由.解:(1)在三棱柱ABC-A1B1C1中,A1B1=AB.因为AB=AA 1=2,所以A 1B 1=AA 1=2.又因为∠AA 1B 1=60°,连接AB 1,所以△AA 1B 1是边长为2的正三角形. 因为E 是棱A 1B 1的中点,所以AE ⊥A 1B 1,且AE=√3. 又AB ∥A 1B 1,所以AE ⊥AB. 又侧面ABB 1A 1⊥底面ABC , 且侧面ABB 1A 1∩底面ABC=AB ,又AE ⊂侧面ABB 1A 1,所以AE ⊥底面ABC ,所以三棱柱ABC-A 1B 1C 1的体积为V=S △ABC ·AE=12AB ·AC ·AE=12×2×2×√3=2√3. (2)在直线AA 1上存在点P ,使得CP ∥平面AEF.理由如下:连接BE 并延长,与AA 1的延长线相交,交点为P.连接CP. 因为A 1B 1∥AB ,故PEPB =PA 1PA=A 1E AB.因为E 为棱A 1B 1的中点,AB=A 1B 1,所以A 1E AB =12,所以PE=EB.又F 为棱BC 的中点,所以EF 为△BCP 的中位线, 所以EF ∥CP.又EF ⊂平面AEF ,CP ⊄平面AEF , 所以CP ∥平面AEF.故在直线AA 1上存在点P ,使得CP ∥平面AEF. 此时,PA 1=AA 1=2,所以AP=2AA 1=4.快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。

广西2021届高三综合能力测试(CAT)(一)文科数学试题及答案

7π −6
1 2
ℎ
=
1 2
∴h
=
1 4
ab
=
4SinASinB
=
4SinASin（
2 3
π
−
A）
=
4SinASin(
2 3
πCosA
−
Cos
2 3
πSinA)
= 2 3SinACosA + 2Sin2A =
3Sin2A
+
1
−
Cos2A
=
2Sin（2A
−
π 6
）
+
1----------9
分
∵
A
∈
(0,
7.已知点 A(l, 0) , B(3, 0），若直线缸一少＋1=0上存在点P，满足曰·PB=O ，则是的取值范
围是（）
A. ［一一， OJ
B. [O ’一43 ］
C. ［一一43 ’ 一 !6 ］
D. （一oo, OJ
8.电表度’数的“ 度 ”用字母 “ KW-H “表示，比如用电 88度，就可用字母 88KW-H 表示．电动车的 “ 用电效率” 是指电动车每消耗I KW-H 所行驶的里程，右图描述了甲、乙、丙兰辆汽车在不同速度下
A.23
B.22
C .21
D.20
i 11.
若
J(:i.:）
的图象上两点关于原点对称，则称这两点是一对对偶点，若
f(x)=
[2.:i:+3α x>O
1.r.1 -.r,x,v
的图象上存在两对对偶点，则实数a的取值范围是（）
A. （一一，O)
B. (0, +oo)

2021年全国统一高考数学试卷(文科)(大纲版)

2021 年全国统一高考数学试卷（文科）（大纲版）一．选择题1．（5分）（2012•大纲版）已知集合A＝{x|x是平行四边形}，B＝{x|x是矩形}，C＝{x|x是正方形}，D＝{x|x 是菱形}，则（）A．A⊆B B．C⊆B C．D⊆C D．A⊆D2．（5分）（2012•大纲版）函数的反函数是（）A．y＝x2﹣1（x≥0）B．y＝x2﹣1（x≥1）C．y＝x2+1（x≥0）D．y＝x2+1（x≥1）3．（5分）（2012•大纲版）若函数是偶函数，则φ＝（）A．B．C．D．4．（5分）（2012•大纲版）已知α为第二象限角，，则sin2α＝（）A．B．C．D．5．（5分）（2012•大纲版）椭圆的中心在原点，焦距为4，一条准线为x＝﹣4，则该椭圆的方程为（）A．B．C．D．6．（5分）（2012•大纲版）已知数列{a n}的前n项和为S n，a1＝1，S n＝2a n+1，则当n＞1时，S n＝（）A．（）n﹣1B．2n﹣1C．（）n﹣1D．（﹣1）7．（5分）（2012•大纲版）6位选手依次演讲，其中选手甲不在第一个也不在最后一个演讲，则不同的演讲次序有（）A．240 种B．360 种C．480 种D．720 种8．（5分）（2012•大纲版）已知正四棱柱ABCD﹣A1B1C1D1中，AB＝2，CC1＝2，E为CC1 的中点，则直线AC1 与平面BED 的距离为（）A．2 B．C．D．19．（5分）（2012•大纲版）△ABC中，AB边的高为CD，若＝，＝，•＝0，||＝1，| |＝2，则＝（）A．B．C．D．10．（5分）（2012•大纲版）已知F1、F2为双曲线C：x2﹣y2＝2的左、右焦点，点P在C上，|PF1|＝2|PF2|，则cos∠F1PF2＝（）A．B．C．D．11．（5分）（2012•大纲版）已知x＝lnπ，y＝log52，，则（）A．x＜y＜z B．z＜x＜y C．z＜y＜x D．y＜z＜x12．（5分）（2012•大纲版）正方形ABCD的边长为1，点E在边AB上，点F在边BC上，．定点P 从E 出发沿直线向F 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为（）A．8 B．6 C．4 D．3二、填空题（共4 小题，每小题5 分，共20 分，在试卷上作答无效）13．（5分）（2012•大纲版）的展开式中x2的系数为．．5（2012•大纲版）若x，y满足约束条件则z＝3x﹣y的最小值为．15．（5分）（2012•大纲版）当函数y＝sin x﹣cos x（0≤x＜2π）取得最大值时，x＝．16．（5分）（2012•大纲版）已知正方体ABCD﹣A1B1C1D1中，E，F分别为BB1，CC1的中点，那么异面直线AE 与D1F 所成角的余弦值为．三、解答题：本大题共6 小题，共70 分．解答应写出文字说明、证明过程或演算步骤．在试卷上作答无效！17．（10分）（2012•大纲版）△ABC中，内角A，B，C成等差数列，其对边a，b，c满足2b2＝3ac，求A．18．（12分）（2012•大纲版）已知数列{a n}中，a1＝1，前n项和（1）求a2，a3；（2）求{a n}的通项公式．19．（12分）（2012•大纲版）如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA＝2，E 是PC 上的一点，PE＝2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C 为90°，求PD 与平面PBC 所成角的大小．20．（12分）（2012•大纲版）乒乓球比赛规则规定：一局比赛，对方比分在10平前，一方连续发球2 次后，对方再连续发球两次，依次轮换．每次发球，胜方得1 分，负方得0 分．设在甲、乙的比赛中，每次发球，发球方得1 分的概率为0.6，各次发球的胜负结果相互独立．甲、乙的一局比赛中，甲先发球．（1）求开始第4 次发球时，甲、乙的比分为1：2 的概率；（2）求开始第5 次发球时，甲领先得分的概率．21．（12分）（2012•大纲版）已知函数．（1）讨论f（x）的单调性；（2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x 轴的交点在曲线y＝f（x）上，求a 的值．22．（12分）（2012•大纲版）已知抛物线C：y＝（x+1）2与圆（r ＞0）有一个公共点A，且在 A 处两曲线的切线为同一直线l．（Ⅰ）求r；（Ⅱ）设m，n 是异于l 且与C 及M 都相切的两条直线，m，n 的交点为D，求D 到l 的距离．2012 年全国统一高考数学试卷（文科）（大纲版）参考答案与试题解析一．选择题1．（5分）（2012•大纲版）已知集合A＝{x|x是平行四边形}，B＝{x|x是矩形}，C＝{x|x是正方形}，D＝{x|x 是菱形}，则（）A．A⊆B B．C⊆B C．D⊆C D．A⊆D【分析】直接利用四边形的关系，判断选项即可．【解答】解：因为菱形是平行四边形的特殊情形，所以D⊂A，矩形与正方形是平行四边形的特殊情形，所以B⊂A，C⊂A，正方形是矩形，所以C⊆B．故选：B．【点评】本题考查集合的基本运算，几何图形之间的关系，基础题．2．（5分）（2012•大纲版）函数的反函数是（）A．y＝x2﹣1（x≥0）B．y＝x2﹣1（x≥1）C．y＝x2+1（x≥0）D．y＝x2+1（x≥1）【分析】直接利用反函数的求法求解即可．【解答】解：因为函数，解得x＝y2﹣1，所以函数的反函数是y＝x2﹣1（x≥0）．故选：A．【点评】本题考查函数的反函数的求法，考查计算能力．3．（5分）（2012•大纲版）若函数是偶函数，则φ＝（）A．B．C．D．【分析】直接利用函数是偶函数求出ϕ的表达式，然后求出ϕ的值．【解答】解：因为函数是偶函数，所以，k∈z，所以k＝0 时，ϕ＝∈[0，2π]．故选：C．【点评】本题考查正弦函数的奇偶性，三角函数的解析式的应用，考查计算能力．4．（5分）（2012•大纲版）已知α为第二象限角，，则sin2α＝（）A．B．C．D．【分析】直接利用同角三角函数的基本关系式，求出cosα，然后利用二倍角公式求解即可．【解答】解：因为α为第二象限角，，所以cosα＝﹣＝﹣．所以sin2α＝2sinαcosα＝＝．故选：A．【点评】本题考查二倍角的正弦，同角三角函数间的基本关系的应用，考查计算能力．5．（5分）（2012•大纲版）椭圆的中心在原点，焦距为4，一条准线为x＝﹣4，则该椭圆的方程为（）A．B．C．D．【分析】确定椭圆的焦点在x 轴上，根据焦距为4，一条准线为x＝﹣4，求出几何量，即可求得椭圆的方程．【解答】解：由题意，椭圆的焦点在x 轴上，且∴c＝2，a2＝8∴b2＝a2﹣c2＝4∴椭圆的方程为故选：C．【点评】本题考查椭圆的标准方程，考查椭圆的几何性质，属于基础题．6．（5分）（2012•大纲版）已知数列{a n}的前n项和为S n，a1＝1，S n＝2a n+1，则当n＞1时，S n＝（）A．（）n﹣1B．2n﹣1C．（）n﹣1D．（﹣1）【分析】利用递推关系与等比数列的通项公式即可得出．【解答】解：∵S n＝2a n+1，得S n＝2（S n+1﹣S n），即3S n＝2S n+1，由a1＝1，所以S n≠0．则＝．∴数列{S n}为以1 为首项，公比为的等比数列∴S n＝．故选：A．【点评】本题考查了递推关系与等比数列的通项公式，考查了推理能力与计算能力，属于中档题．7．（5分）（2012•大纲版）6位选手依次演讲，其中选手甲不在第一个也不在最后一个演讲，则不同的演讲次序有（）A．240 种B．360 种C．480 种D．720 种【分析】直接从中间的 4 个演讲的位置，选 1 个给甲，其余全排列即可．【解答】解：因为6 位选手依次演讲，其中选手甲不在第一个也不在最后一个演讲，甲先安排在除开始与结尾的位置还有个选择，剩余的元素与位置进行全排列有，所以甲只能在中间的4 个位置，所以不同的演讲次序有＝480 种．故选：C．【点评】本题考查排列、组合以及简单的计数原理的应用，考查计算能力．8．（5分）（2012•大纲版）已知正四棱柱ABCD﹣A1B1C1D1中，AB＝2，CC1＝2，E为CC1 的中点，则直线AC1 与平面BED 的距离为（）A．2 B．C．D．1【分析】先利用线面平行的判定定理证明直线C1A∥平面BDE，再将线面距离转化为点面距离，最后利用等体积法求点面距离即可【解答】解：如图：连接AC，交BD 于O，在三角形CC1A 中，易证OE∥C1A，从而C1A∥平面BDE，∴直线AC1 与平面BED 的距离即为点A 到平面BED 的距离，设为h，在三棱锥E﹣ABD 中，V E﹣ABD＝S△ABD×EC＝××2×2×＝在三棱锥A﹣BDE 中，BD＝2 ，BE＝，DE＝，∴S△EBD＝×2 ×＝2 ∴V A﹣BDE＝×S△EBD×h＝×2 ×h＝∴h＝1故选：D．【点评】本题主要考查了线面平行的判定，线面距离与点面距离的转化，三棱锥的体积计算方法，等体积法求点面距离的技巧，属基础题9．（5分）（2012•大纲版）△ABC中，AB边的高为CD，若＝，＝，•＝0，||＝1，| |＝2，则＝（）A．B．C．D．【分析】由题意可得，CA⊥CB，CD⊥AB，由射影定理可得，AC2＝AD•AB 可求AD，进而可求，从而可求与的关系，进而可求【解答】解：∵•＝0，∴CA⊥CB∵CD⊥AB∵| |＝1，| |＝2∴AB＝由射影定理可得，AC2＝AD•AB∴∴∴＝＝故选：D．【点评】本题主要考查了直角三角形的射影定理的应用，向量的基本运算的应用，向量的数量积的性质的应用．10．（5分）（2012•大纲版）已知F1、F2为双曲线C：x2﹣y2＝2的左、右焦点，点P在C 上，|PF1|＝2|PF2|，则cos∠F1PF2＝（）A．B．C．D．【分析】根据双曲线的定义，结合|PF1|＝2|PF2|，利用余弦定理，即可求cos∠F1PF2 的值．【解答】解：将双曲线方程x2﹣y2＝2 化为标准方程﹣＝1，则a＝，b＝，c＝2，设|PF1|＝2|PF2|＝2m，则根据双曲线的定义，|PF1|﹣|PF2|＝2a 可得m＝2，∴|PF1|＝4 ，|PF2|＝2 ，∵|F1F2|＝2c＝4，∴cos∠F1PF2＝＝＝＝．故选：C．【点评】本题考查双曲线的性质，考查双曲线的定义，考查余弦定理的运用，属于中档题．11．（5分）（2012•大纲版）已知x＝lnπ，y＝log52，，则（）A．x＜y＜z B．z＜x＜y C．z＜y＜x D．y＜z＜x【分析】利用x＝lnπ＞1，0＜y＝log52＜，1＞z＝＞，即可得到答案．【解答】解：∵x＝lnπ＞lne＝1，0＜log52＜log5＝，即y∈（0，）；1＝e0＞＝＞＝，即z∈（，1），∴y＜z＜x．故选：D．【点评】本题考查不等式比较大小，掌握对数函数与指数函数的性质是解决问题的关键，属于基础题．12．（5分）（2012•大纲版）正方形ABCD的边长为1，点E在边AB上，点F在边BC上，．定点P 从E 出发沿直线向F 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为（）A．8 B．6 C．4 D．3【分析】根据已知中的点E，F 的位置，可知入射角的正切值为，通过相似三角形，来确定反射后的点的位置，从而可得反射的次数．【解答】解：根据已知中的点E，F 的位置，可知入射角的正切值为，第一次碰撞点为F，在反射的过程中，直线是平行的，利用平行关系及三角形的相似可得第二次碰撞点为G，在DA，且DG＝，第三次碰撞点为H，在DC 上，且DH＝，第四次碰撞点为M，在CB 上，且CM＝，第五次碰撞点为N，在DA 上，且AN＝，第六次回到E 点，AE＝．故需要碰撞6 次即可．故选：B．：【点评】本题主要考查了反射原理与三角形相似知识的运用．通过相似三角形，来确定反射后的点的位置，从而可得反射的次数，属于难题二、填空题（共 4 小题，每小题 5 分，共 20 分，在试卷上作答无效） 13．（5 分）（2012•大纲版）的展开式中 x 2的系数为 7．【分析】直接利用二项式定理的通项公式，求出 x 2 的系数即可．【解答】解：因为的展开式的通项公式为＝，当 8﹣2r ＝2，即 r ＝3 时，的展开式中 x 2 的系数为：＝7．故答案为：7．【点评】本题考查二项式定理的应用，特定项的求法，考查计算能力．14．（5 分）（2012•大纲版）若 x ，y 满足约束条件则 z ＝3x ﹣y 的最小值为 ﹣1 ．【分析】作出不等式组表示的平面区域，由 z ＝3x ﹣y 可得 y ＝3x ﹣z ，则﹣z 表示直线 3x﹣y ﹣z ＝0 在 y 轴上的截距，截距越大 z 越小，结合图形可求【解答】解：作出不等式组表示的平面区域，如图所示由 z ＝3x ﹣y 可得 y ＝3x ﹣z ，则﹣z 表示直线 3x ﹣y ﹣z ＝0 在 y 轴上的截距，截距越大 z 越小结合图形可知，当直线 z ＝3x ﹣y 过点 C 时 z 最小由可得 C （0，1），此时 z ＝﹣1故答案为：﹣1【点评】本题主要考查了线性规划的简单应用，解题的关键是明确目标函数中z 的几何意义，属于基础试题15．（5分）（2012•大纲版）当函数y＝sin x﹣cos x（0≤x＜2π）取得最大值时，x＝．【分析】利用辅助角公式将y＝sin x﹣cos x化为y＝2sin（x﹣）（0≤x＜2π），即可求得y＝sin x﹣cos x（0≤x＜2π）取得最大值时x 的值．【解答】解：∵y＝sin x﹣cos x＝2（sin x﹣cos x）＝2sin（x﹣）．∵0≤x＜2π，∴﹣≤x﹣＜，∴y max＝2，此时x﹣＝，∴x＝．故答案为：．【点评】本题考查三角函数的最值两与角和与差的正弦函数，着重考查辅助角公式的应用与正弦函数的性质，将y＝sin x﹣cos x（0≤x＜2π）化为y＝2sin（x﹣）（0≤x＜2π）是关键，属于中档题．16．（5分）（2012•大纲版）已知正方体ABCD﹣A1B1C1D1中，E，F分别为BB1，CC1的中点，那么异面直线AE 与D1F 所成角的余弦值为．【分析】设正方体ABCD﹣A1B1C1D1 棱长为2，以DA 为x 轴，DC 为y 轴，DD1 为z 轴，建立空间直角坐标系，则，＝（0，2，﹣1），由此利用向量法能够求出异面直线AE 与D1F 所成角的余弦值．【解答】解：设正方体ABCD﹣A1B1C1D1 棱长为2，以DA 为x 轴，DC 为y 轴，DD1 为z 轴，建立空间直角坐标系，则A（2，0，0），E（2，2，1）D1（0，0，2），F（0，2，1）∴，＝（0，2，﹣1），设异面直线AE 与D1F 所成角为θ，则cosθ＝|cos＜，＞|＝| |＝．故答案为：．【点评】本题考查异面直线所成角的余弦值的求法，是基础题．解题时要认真审题，仔细解答，注意向量法的合理运用．三、解答题：本大题共6 小题，共70 分．解答应写出文字说明、证明过程或演算步骤．在试卷上作答无效！17．（10分）（2012•大纲版）△ABC中，内角A，B，C成等差数列，其对边a，b，c满足2b2＝3ac，求A．【分析】由题设条件，可先由A，B，C 成等差数列，及A+B+C＝π得到B＝，及A+C ＝，再由正弦定理将条件2b2＝3ac 转化为角的正弦的关系，结合cos（A+C）＝cos A cos C﹣sin A sin C 求得cos A cos C＝0，从而解出A【解答】解：由A，B，C 成等差数列，及A+B+C＝π得B＝，故有A+C＝由2b2＝3ac 得2sin2B＝3sin A sin C＝，所以sin A sin C＝所以cos（A+C）＝cos A cos C﹣sin A sin C＝cos A cos C﹣即cos A cos C﹣＝﹣，可得cos A cos C＝0所以cos A＝0 或cos C＝0，即A 是直角或C 是直角所以A 是直角，或A＝【点评】本题考查数列与三角函数的综合，涉及了三角形的内角和，两角和的余弦公式，正弦定理的作用边角互化，解题的关键是熟练掌握等差数列的性质及三角函数的相关公式，本题考查了转化的思想，有一定的探究性及综合性18．（12分）（2012•大纲版）已知数列{a n}中，a1＝1，前n项和（1）求a2，a3；（2）求{a n}的通项公式．【分析】（1）直接利用已知，求出a2，a3；（2）利用已知关系式，推出数列相邻两项的关系式，利用累积法，求出数列的通项公式即可．【解答】解：（1）数列{a n}中，a1＝1，前n项和，可知，得3（a1+a2）＝4a2，解得a2＝3a1＝3，由，得3（a1+a2+a3）＝5a3，解得a3＝＝6．（2）由题意知a1＝1，当n＞1 时，有a n＝s n﹣s n﹣1＝，整理得，于是a1＝1，a 2＝ a 1， a 3＝ a 2， …， a n ﹣1＝a n ﹣2，，将以上 n 个式子两端分别相乘，整理得：．综上{a n }的通项公式为【点评】本题考查数列的项的求法，累积法的应用，考查计算能力．19．（12 分）（2012•大纲版）如图，四棱锥 P ﹣ABCD 中，底面 ABCD 为菱形，PA ⊥底面 ABCD ，，PA ＝2，E 是 PC 上的一点，PE ＝2EC ．（Ⅰ）证明：PC ⊥平面 BED ；（Ⅱ）设二面角 A ﹣PB ﹣C 为 90°，求 PD 与平面 PBC 所成角的大小．【分析】（I ）先由已知建立空间直角坐标系，设 D （，b ，0），从而写出相关点和相关向量的坐标，利用向量垂直的充要条件，证明 PC ⊥BE ，PC ⊥DE ，从而利用线面垂直的判定定理证明结论即可；（II ）先求平面 PAB 的法向量，再求平面 PBC 的法向量，利用两平面垂直的性质，即可求得 b 的值，最后利用空间向量夹角公式即可求得线面角的正弦值，进而求得线面角【解答】解：（I ）以 A 为坐标原点，建立如图空间直角坐标系 A ﹣xyz ，设D（，b，0），则C（2，0，0），P（0，0，2），E（，0，），B（，﹣b，0）∴＝（2，0，﹣2），＝（，b，），＝（，﹣b，）∴•＝﹣＝0，•＝0∴PC⊥BE，PC⊥DE，BE∩DE＝E∴PC⊥平面BED（II）＝（0，0，2），＝（，﹣b，0）设平面PAB的法向量为＝（x，y，z），则取＝（b，，0）设平面PBC的法向量为＝（p，q，r），则取＝（1，﹣，）∵平面PAB⊥平面PBC，∴•＝b﹣＝0．故b＝∴＝（1，﹣1，），＝（﹣，﹣，2）∴cos＜，＞＝＝设PD 与平面PBC 所成角为θ，θ∈[0，]，则sinθ＝∴θ＝30°∴PD 与平面PBC 所成角的大小为30°【点评】本题主要考查了利用空间直角坐标系和空间向量解决立体几何问题的一般方法，线面垂直的判定定理，空间线面角的求法，有一定的运算量，属中档题20．（12分）（2012•大纲版）乒乓球比赛规则规定：一局比赛，对方比分在10平前，一方连续发球2 次后，对方再连续发球两次，依次轮换．每次发球，胜方得1 分，负方得0 分．设在甲、乙的比赛中，每次发球，发球方得1 分的概率为0.6，各次发球的胜负结果相互独立．甲、乙的一局比赛中，甲先发球．（1）求开始第4 次发球时，甲、乙的比分为1：2 的概率；（2）求开始第5 次发球时，甲领先得分的概率．【分析】（Ⅰ）记A i 表示事件：第1 次和第2 次这两次发球，甲共得i 分，i＝0，1，2，B i 表示事件：第3 次和第4 次这两次发球，甲共得i 分，i＝0，1，2，A 表示事件：第3次发球，甲得1 分，B 表示事件：开始第4 次发球时，甲、乙的比分为1 比2，C 表示事件：开始第5 次发球时，甲得分领先．B＝，由此能求出开始第4 次发球时，甲、乙的比分为1：2 的概率．（Ⅱ），P（B1）＝2×0.4×0.6＝0.48，，，由C＝A1•B2+A2•B1+A2•B2，能求出开始第5 次发球时，甲领先得分的概率．【解答】解：（Ⅰ）记A i表示事件：第1次和第2次这两次发球，甲共得i分，i＝0，1，2，B i 表示事件：第3 次和第4 次这两次发球，甲共得i 分，i＝0，1，2，A 表示事件：第3 次发球，甲得1 分，B 表示事件：开始第4 次发球时，甲、乙的比分为1 比2，C 表示事件：开始第5 次发球时，甲得分领先．∴B＝，P（A）＝0.4，P（A0）＝0.42＝0.16，P（A1）＝2×0.6×0.4＝0.48，P（B）＝＝P（A0•A）+P（）＝＝0.16×0.4+0.48×（1﹣0.4）＝0.352．答：开始第4 次发球时，甲、乙的比分为1：2 的概率是0.352．（Ⅱ），P（B1）＝2×0.4×0.6＝0.48，，，∵C＝A1•B2+A2•B1+A2•B2，∴P（C）＝P（A1•B2+A2B1+A2•B2）＝P（A1•B2）+P（A2•B1）+P（A2•B2）＝P（A1）P（B）+P（A2）P（B1）+P（A2）P（B2）＝0.48×0.16+0.36×0.48+0.36×0.16＝0.3072．答：开始第5 次发球时，甲领先得分的概率是0.3072．【点评】本题考查事件的概率的求法，解题时要认真审题，仔细解答，注意n 次独立重复试验的性质和公式的灵活运用．21．（12分）（2012•大纲版）已知函数．（1）讨论f（x）的单调性；（2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x 轴的交点在曲线y＝f（x）上，求a 的值．设l 与x 轴的交点为（x0，0）得x0＝，【分析】（1）先对函数进行求导，通过a 的取值，求出函数的根，然后通过导函数的值的符号，推出函数的单调性．（2）根据导函数的根，判断 a 的范围，进而解出直线l 的方程，利用l 与x 轴的交点为（x0，0），可解出a的值．【解答】解：（1）f′（x）＝x2+2x+a＝（x+1）2+a﹣1．①当a≥1 时，f′（x）≥0，且仅当a＝1，x＝﹣1 时，f′（x）＝0，所以f（x）是R 上的增函数；②当a＜1 时，f′（x）＝0，有两个根，x1＝﹣1﹣，x2＝﹣1+ ，当x∈时，f′（x）＞0，f（x）是增函数．当x∈时，f′（x）＜0，f（x）是减函数．当x∈时，f′（x）＞0，f（x）是增函数．（2）由题意x1，x2，是方程f′（x）＝0 的两个根，故有a＜1，，，因此＝＝＝＝，同理．因此直线l 的方程为：y＝．＝，由题设知，点（x0，0）在曲线y＝f（x）上，故f（x0）＝0，解得a＝0，或a＝或a＝【点评】本题主要考查函数在某点取得极值的条件，考查分类讨论，函数与方程的思想，考查计算能力．22．（12分）（2012•大纲版）已知抛物线C：y＝（x+1）2与圆（r ＞0）有一个公共点A，且在 A 处两曲线的切线为同一直线l．（Ⅰ）求r；（Ⅱ）设m，n 是异于l 且与C 及M 都相切的两条直线，m，n 的交点为D，求D 到l 的距离．【分析】（Ⅰ）设A（x0，（x0+1）2），根据y＝（x+1）2，求出l的斜率，圆心M（1，），求得MA 的斜率，利用l⊥MA 建立方程，求得A 的坐标，即可求得r 的值；（Ⅱ）设（t，（t+1）2）为C上一点，则在该点处的切线方程为y﹣（t+1）2＝2（t+1）（x ﹣t），即y＝2（t+1）x﹣t2+1，若该直线与圆M相切，则圆心M到该切线的距离为，建立方程，求得t 的值，求出相应的切线方程，可得D 的坐标，从而可求D 到l 的距离．【解答】解：（Ⅰ）设A（x0，（x0+1）2），∵y＝（x+1）2，y′＝2（x+1）∴l 的斜率为k＝2（x0+1）当x0＝1 时，不合题意，所以x0≠1圆心M（1，），MA的斜率．∵l⊥MA，∴2（x0+1）×＝﹣1∴x0＝0，∴A（0，1），∴r＝|MA|＝；（Ⅱ）设（t，（t+1）2）为C上一点，则在该点处的切线方程为y﹣（t+1）2＝2（t+1）（x ﹣t），即y＝2（t+1）x﹣t2+1若该直线与圆M 相切，则圆心M 到该切线的距离为∴∴t2（t2﹣4t﹣6）＝0∴t0＝0，或t1＝2+，t2＝2﹣抛物线C在点（t i，（t i+1）2）（i＝0，1，2）处的切线分别为l，m，n，其方程分别为y＝2x+1①，y＝2（t1+1）x﹣②，y＝2（t2+1）x﹣③②﹣③：x＝代入②可得：y＝﹣1∴D（2，﹣1），∴D 到l 的距离为【点评】本题考查圆与抛物线的综合，考查抛物线的切线方程，考查导数知识的运用，考查点到直线的距离公式的运用，关键是确定切线方程，求得交点坐标．。

2021届广西桂林市高三上学期第一次联合调研考试文科数学试题(解析版)

2021年高考桂林市第一次联合调研考试高三数学（文科）考生注意：1．本试卷满分150分，考试时间120分钟。

2．考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域．．．．．．书写的答案无效．．．．．．．，．在试题卷．．．．、．草稿纸上作答无效．．．．．．．．。

．3．做选考题时，考生须按照题目要求作答，并用2B 铅笔在答题卡上把所选题目的题号涂黑。

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}2340x x A x --<=，{}05B x x =<<，则AB =（） A ．{}01x x <<B ．{}14x x -<<C ．{}15x x -<<D ．{}04x x << 2．若()()32i 3i z =-+，则复数z 的实部与虚部之和为（） A ．12 B ．11 C ．10D ．6 3．曲线()e 21x x x f =++在点()0,0处的切线的方程为（）A ．y x =B ．3y x =C ．0y =D ．4y x =4．七巧板是中国古代劳动人民发明的一种传统智力玩具，其历史可以追溯到公元前一世纪。

明、清两代这一在民间广受喜爱的游戏逐渐流传至海外并有了一个新的名字“唐图”，至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.如图是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自阴影部分的概率为（）A ．516B ．1132C ．716D ．13325．在平面直角坐标系xOy 中，已知抛物线C 的顶点在坐标原点，焦点在x 轴上，若曲线C 经过点()1,4P ，则其焦点到准线的距离为（）A ．18B ．14C ．4D ．86．设0.43a =，π12b ⎫⎛= ⎪⎝⎭，log c =，则（） A ．a b c >>B ．c b a >>C ．b a c >>D ．a c b >> 7．已知π1cos 45α⎫⎛+= ⎪⎝⎭，α是第一象限角，则cos2α的值为（）A ．2325B ．2325-C ．25D ．25- 8．已知()1,2a =-，(),3b λ=满足()2b a a -⊥，则a b ⋅的值是（） A ．152- B ．52C ．6D ．2- 9．函数()sin 22x x x f x -=+（ππx -≤≤）的图象可能为（） A ． B ．C ．D ．10．在平面直角坐标系xOy xOy 中，圆C 的方程为2240x y x +-=，若直线21y x =+上存在一点P ，使过点P 所作的圆的两条切线相互垂直，则点P 的横坐标为（）A ．5±B ．3±C ．5±D ．3± 11．函数()sin g x x ω=（0ω>）的图象向左平移π5ω个单位长度得到函数()f x ，()f x 在[]0,2π上有且只有5个零点，则ω的取值范围是（）A ．812,55⎫⎛ ⎪⎝⎭B ．812,55⎫⎡⎪⎢⎣⎭C ．1229,510⎫⎛ ⎪⎝⎭D ．1229,510⎫⎡⎪⎢⎣⎭ 12．已知定义在π0,2⎫⎛⎪⎝⎭上的函数()f x ，()f x '是()f x 的导函数，且恒有()()cos sin 0xf x xf x '+>成立，则（）①ππ43f ⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭；②ππ36f ⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭；③ππ63f ⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭π64π⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭. A ．①③④ B ．①②③ C ．②③④ D ．①②④二、填空题：本题共4小题，每小题5分，共20分．13．已知双曲线2214x y m-=的焦点在直线330x y --=上，则实数m 的值为__________． 14．已知实数x ，y 满足50,220,0,x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩则目标函数2z x y =+的最大值为__________．15．在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知2b c -=，1cos 4A =-，ABC S =△则ABC △周长的值为__________．16．某市民广场有一批球形路障球（如图1所示）。

2021年广西高考文科数学真题及参考答案

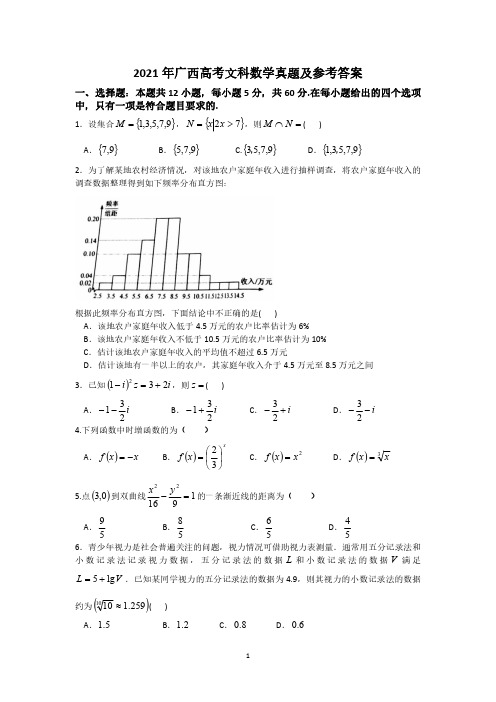
2021年广西高考文科数学真题及参考答案一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合{}9,7,5,3,1=M ，{}72>=x x N ，则=⋂N M ()A ．{}9,7B ．{}9,7,5 C.{}9,7,53，D ．{}9,7,53,1，2．为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是()A ．该地农户家庭年收入低于4.5万元的农户比率估计为6%B ．该地农户家庭年收入不低于10.5万元的农户比率估计为10%C ．估计该地农户家庭年收入的平均值不超过6.5万元D ．估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间3．己知()i z i 2312+=-，则=z ()A ．i 231--B ．i 231+-C ．i +-23D ．i --234.下列函数中时增函数的为（）A ．()xx f -=B ．()xx f ⎪⎭⎫⎝⎛=32C ．()2xx f =D ．()3xx f =5.点()0,3到双曲线191622=-y x 的一条渐近线的距离为（）A ．59B ．58C ．56D ．546．青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录法的数据V 满足V L lg 5+=．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为()259.11010≈()A ．5.1B ．2.1C ．8.0D ．6.07.在一个正方体中，过顶点A 的三条棱的中点分别为G F E ,,．该正方体截去三棱锥EFG A -后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是()A ．B ．C ．D ．8.在ABC ∆中，已知︒=120B ，19=AC ，2=AB ，则=BC （）A ．1B ．2C ．5D ．39.记n S 为等比数列{}n a 的前n 项和，若42=S ，64=S ，则=6S （）A ．7B ．8C ．9D ．1010.将3个1和2个0随机排成一行，则2个0不相邻的概率为（）A ．3.0B ．5.0C ．6.0D ．8.011.若⎪⎭⎫ ⎝⎛∈20πα，，αααsin 2cos 2tan -=，则=αtan ()A ．1515B ．55C ．35D ．31512.设()x f 是定义域为R 的奇函数，且()()x f x f -=+1.若3131=⎪⎭⎫ ⎝⎛-f ，则=⎪⎭⎫⎝⎛35f （）A ．35-B ．31-C ．31D ．35二、填空题：本题共4小题，每小题5分，共20分。

2021版《大高考》高考数学(文)一轮总复习高考AB卷：第8章立体几何初步第五节

1.(2021·大纲全国，11)已知正四棱柱ABCDA 1B 1C 1D 1中，AA 1＝2AB ，则CD 与平面BDC 1所成角的正弦值等于( ) A.23 B.33 C.23D.13解析如图，设AA 1＝2AB ＝2，AC 交BD 于点O ，连接OC 1，过C 作CH ⊥OC 1于点H ，连接DH .∵BD ⊥AC ，BD ⊥AA 1，∴BD ⊥平面ACC 1A 1.∴CH ⊂平面ACC 1A 1，∴CH ⊥BD .∴CH ⊥平面C 1BD .∴∠CDH 为CD 与平面BDC 1所成的角. OC 1＝CC 21＋OC 2＝4＋⎝ ⎛⎭⎪⎫222＝32. 由等面积法得OC 1·CH ＝OC ·CC 1， ∴32·CH ＝22×2.CH ＝23. ∴sin ∠CDH ＝CH CD ＝231＝23.故选A. 答案 A2.(2022·新课标全国Ⅰ，18)如图，已知正三棱锥P ABC 的侧面是直角三角形，P A ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连接PE 并延长交AB 于点G . (1)证明：G 是AB 的中点；(2)作出点E 在平面P AC 内的正投影F (说明作法及理由)，并求四周体PDEF 的体积.(1)证明由于P 在平面ABC 内的正投影为D ，所以AB ⊥PD .由于D 在平面P AB 内的正投影为E ，所以AB ⊥DE . 所以AB ⊥平面PED ，故AB ⊥PG .又由已知可得，P A ＝PB ，从而G 是AB 的中点.(2)解在平面P AB 内，过点E 作PB 的平行线交P A 于点F ，F 即为E 在平面P AC 内的正投影.理由如下：由已知可得PB ⊥P A ，PB ⊥PC ，又EF ∥PB ，所以EF ⊥P A ，EF ⊥PC ，因此EF ⊥平面P AC ，即点F 为E 在平面P AC 内的正投影.连接CG ，由于P 在平面ABC 内的正投影为D ，所以D 是正三角形ABC 的中心.由(1)知，G 是AB 的中点，所以D 在CG 上，故CD ＝23CG .由题设可得PC ⊥平面P AB ，DE ⊥平面P AB ，所以DE ∥PC ，因此PE ＝23PG ，DE ＝13PC .由已知，正三棱锥的侧面是直角三角形且P A ＝6，可得DE ＝2，PE ＝2 2. 在等腰直角三角形EFP 中，可得EF ＝PF ＝2. 所以四周体PDEF 的体积V ＝13×12×2×2×2＝43.3.(2022·新课标全国Ⅱ，19)如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H ，将△DEF 沿EF 折到△D ′EF 的位置. (1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积.(1)证明由已知得AC ⊥BD ，AD ＝CD ，又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF ，由此得EF ⊥HD ，折后EF 与HD 保持垂直关系，即EF ⊥HD ′，所以AC ⊥HD ′.(2)解由EF ∥AC 得OH DO ＝AE AD ＝14.由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4，所以OH ＝1，D ′H ＝DH ＝3，于是OD ′2＋OH 2＝(22)2＋12＝9＝D ′H 2，故OD ′⊥OH .由(1)知AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ，所以AC ⊥平面DHD ′，于是AC ⊥OD ′，又由OD ′⊥OH ，AC ∩OH ＝O ，所以OD ′⊥平面ABC .又由EF AC ＝DH DO 得EF ＝92.五边形ABCFE 的面积S ＝12×6×8－12×92×3＝694.所以五棱锥D ′ABCFE 的体积V ＝13×694×22＝2322.4.(2021·新课标全国Ⅰ，18)如图，四边形ABCD 为菱形，G 是AC 与BD的交点，BE ⊥平面ABCD . (1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC ，三棱锥EACD 的体积为63，求该三棱锥的侧面积. 解 (1)由于四边形ABCD 为菱形，所以AC ⊥BD .由于BE ⊥平面ABCD ，所以AC ⊥BE .故AC ⊥平面BED .又AC ⊂平面AEC ，所以平面AEC ⊥平面BED .(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得 AG ＝GC ＝32x ，GB ＝GD ＝x2.由于AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x .由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x .由已知得，三棱锥EACD 的体积V EACD ＝13×12AC ·GD ·BE ＝624x 3＝63.故x ＝2. 从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为 5.故三棱锥EACD 的侧面积为3＋2 5.5.(2022·新课标全国Ⅰ，19)如图，三棱柱ABCA 1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C . (1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABCA 1B 1C 1的高.(1)证明连接BC 1，则O 为B 1C 与B C 1的交点.由于侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1.又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ，又由于BC 1∩AO ＝O ，所以B 1C ⊥平面ABO . 由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)解作OD ⊥BC ，垂足为D ，连接AD .作OH ⊥AD ，垂足为H .由于BC ⊥AO ，BC ⊥OD ，AO ∩OD ＝O ，故BC ⊥平面AOD ，所以OH ⊥BC .又OH ⊥AD ，所以OH ⊥平面ABC .由于∠CBB 1＝60°，所以△CBB 1为等边三角形，又BC ＝1，可得OD ＝34.由于AC ⊥AB 1，所以OA ＝12B 1C ＝12. 由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114.又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217.故三棱柱ABCA 1B 1C 1的高为217.1.(2022·浙江，6)设m ，n 是两条不同的直线，α，β是两个不同的平面( ) A.若m ⊥n ，n ∥α，则m ⊥α B.若m ∥β，β⊥α，则m ⊥α C.若m ⊥β，n ⊥β，n ⊥α，则m ⊥α D.若m ⊥n ，n ⊥β，β⊥α，则m ⊥α解析选项A 、B 、D 中m 均可能与平面α平行、垂直、斜交或平面α内，故选C. 答案 C2.(2021·浙江，4)设m ，n 是两条不同的直线，α，β是两个不同的平面( ) A.若m ∥α，n ∥α，则m ∥n B.若m ∥α，m ∥β，则α∥βC.若m∥n，m⊥α，则n⊥αD.若m∥α，α⊥β，则m⊥β解析A选项中直线m，m可能平行，也可能相交或异面，直线m，n的关系是任意的；B选项中，α与β也可能相交，此时直线m平行于α，β的交线；D选项中，m也可能平行于β.故选C.答案 C3.(2022·北京，18)如图，在四棱锥P ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面P AC；(2)求证：平面P AB⊥平面P AC；(3)设点E为AB的中点，在棱PB上是否存在点F，使得P A∥平面CEF？说明理由.(1)证明∵PC⊥平面ABCD，DC⊂平面ABCD，∴PC⊥DC.又AC⊥DC，PC∩AC＝C，PC⊂平面P AC，AC⊂平面P AC，∴CD⊥平面P AC. (2)证明∵AB∥CD，CD⊥平面P AC，∴AB⊥平面P AC，AB⊂平面P AB，∴平面P AB⊥平面P AC.(3)解棱PB上存在点F，使得P A∥平面CEF.证明如下：取PB的中点F，连接EF，CE，CF，又由于E为AB的中点，∴EF为△P AB的中位线，∴EF∥P A.又P A⊄平面CEF，EF⊂平面CEF，∴P A∥平面CEF.4.(2022·浙江，18)如图，在三棱台ABCDEF中，平面BCFE⊥平面ABC，∠ACB＝90°，BE＝EF＝FC＝1，BC＝2，AC＝3.(1)求证：BF⊥平面ACFD；(2)求直线BD与平面ACFD所成角的余弦值.(1)证明延长AD，BE，CF相交于一点K，如图所示，由于平面BCFE⊥平面ABC，且AC⊥BC，所以AC⊥平面BCK，因此BF⊥AC.又由于EF∥BC，BE＝EF＝FC＝1，BC＝2，所以△BCK为等边三角形，且F为CK的中点，则BF⊥CK.所以BF⊥平面ACFD.(2)解由于BF⊥平面ACK，所以∠BDF是直线BD与平面ACFD所成的角.在Rt△BFD中，BF＝3，DF＝32，得cos ∠BDF＝217.所以，直线BD与平面ACFD所成角的余弦值为217.5.(2022·四川，17)如图，在四棱锥P ABCD中，P A⊥CD，AD∥BC，∠ADC＝∠P AB＝90°，BC＝CD＝12AD.(1)在平面P AD内找一点M，使得直线CM∥平面P AB，并说明理由.(2)证明：平面P AB⊥平面PBD.(1)解取棱AD的中点M(M∈平面P AD)，点M即为所求的一个点，理由如下：由于AD∥BC，BC＝12AD.所以BC∥AM，且BC＝AM.所以四边形AMCB是平行四边形，从而CM∥AB.又AB⊂平面P AB.CM⊄平面P AB.所以CM∥平面P AB.(说明：取棱PD的中点N，则所找的点可以是直线MN上任意一点)(2)证明由已知，P A⊥AB，P A⊥CD.由于AD∥BC，BC＝12AD，所以直线AB与CD相交，所以P A⊥平面ABCD.从而P A⊥BD.由于AD∥BC，BC＝12AD，所以BC∥MD，且BC＝MD.所以四边形BCDM是平行四边形，所以BM＝CD＝12AD，所以BD⊥AB.又AB∩AP＝A，所以BD⊥平面P AB.又BD⊂平面PBD，所以平面P AB⊥平面PBD.6.(2021·安徽，19)如图，三棱锥P-ABC中，P A⊥平面ABC，P A＝1，AB＝1，AC＝2，∠BAC＝60°.(1)求三棱锥P-ABC的体积；(2)证明：在线段PC上存在点M，使得AC⊥BM，并求PMMC的值.(1)解由题设AB＝1，AC＝2，∠BAC＝60°，可得S△ABC ＝12·AB·AC·sin 60°＝32.由P A⊥平面ABC，可知P A是三棱锥P-ABC的高，又P A＝1.所以三棱锥P-ABC的体积V＝13·S△ABC·P A＝36.(2)证明在平面ABC内，过点B作BN⊥AC，垂足为N，在平面P AC内，过点N作MN∥P A 交PC于点M，连接BM.由P A⊥平面ABC知P A⊥AC，所以MN⊥AC.由于BN∩MN＝N，故AC⊥平面MBN，又BM⊂平面MBN，所以AC⊥BM.在Rt△BAN中，AN＝AB·cos∠BAC＝12，从而NC＝AC－AN＝32，由MN∥P A，得PMMC＝ANNC＝13.7.(2021·湖北，20)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四周体称之为鳖臑.在如图所示的阳马P ABCD中，侧棱PD⊥底面ABCD，且PD＝CD，点E 是PC的中点，连接DE、BD、BE.(1)证明：DE⊥平面PBC.试推断四周体EBCD是否为鳖臑.若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由；(2)记阳马P ABCD的体积为V1，四周体EBCD的体积为V2，求V1V2的值.解(1)由于PD⊥底面ABCD，所以PD⊥BC，由底面ABCD为长方形，有BC⊥CD，而PD∩CD＝D，所以BC⊥平面PCD.而DE⊂平面PCD，所以BC⊥DE.又由于PD＝CD，点E是PC的中点，所以DE⊥PC.而PC∩BC＝C，所以DE⊥平面PBC.由BC⊥平面PCD，DE⊥平面PBC，可知四周体EBCD的四个面都是直角三角形，即四周体EBCD是一个鳖臑，其四个面的直角分别是∠BCD，∠BCE，∠DEC，∠DEB. (2)由已知，PD是阳马P ABCD的高，所以V1＝13S ABCD·PD＝13BC·CD·PD；由(1)知，DE是鳖臑DBCE的高，BC⊥CE，所以V2＝13S△BCE·DE＝16BC·CE·DE.在Rt△PDC中，由于PD＝CD，点E是PC的中点，所以DE＝CE＝22CD，于是V1V2＝13BC·CD·PD16BC·CE·DE＝2CD·PDCE·DE＝4.8.(2021·浙江，18)如图，在三棱柱ABCA1B1C1中，∠BAC＝90°，AB＝AC＝2，A1A＝4，A1在底面ABC的射影为BC的中点，D为B1C1的中点.(1)证明：A1D⊥平面A1BC；(2)求直线A1B和平面BB1C1C所成的角的正弦值.(1)证明设E为BC的中点，由题意得A1E⊥平面ABC，所以A1E⊥AE，由于AB＝AC，所以AE⊥BC.故AE⊥平面A1BC.由D，E分别为B1C1，BC的中点，得DE∥B1B且DE＝B1B，从而DE∥A1A且DE＝A1A，所以AA1DE为平行四边形.于是A1D∥AE.又由于AE⊥平面A1BC，所以A1D⊥平面A1BC.(2)解作A1F⊥DE，垂足为F，连接BF.由于A1E⊥平面ABC，所以BC⊥A1E.由于BC⊥AE，所以BC⊥平面AA1DE.所以BC⊥A1F，A1F⊥平面BB1C1C.所以∠A1BF为直线A1B和平面BB1C1C所成的角.由AB＝AC＝2，∠CAB＝90°，得EA＝EB＝ 2.由A1E⊥平面ABC，得A1A＝A1B＝4，A1E ＝14.由DE＝BB1＝4.DA1＝EA＝2，∠DA1E＝90°，得A1F＝7 2.所以sin ∠A1BF＝7 8.。

2021届广西玉林市、贵港市高中毕业班质量检测数学(文)试卷

2021年广西玉林市、贵港市高中毕业班质量检测数学（文）试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合2{|230}A x Z x x =∈--≤，{0,1}B =，则A C B =（） A ．{3,2,1}---B ．{1,2,3}-C ．{1,0,1,2,3}-D ．{0,1}2．若34z i =+，则zz（）A ．1B ．1-C ．3455i + D ．3455-i3．已知点2)A ，(03)B ，，(01)C ，，则BAC ∠=（） A ．30 B ．45︒ C ．60︒ D ．120︒4．随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，下图是某城市1月至8月的空气质量检测情况，图中一、二、三、四级是空气质量等级，一级空气质量最好，一级和二级都是质量合格天气，下面叙述不正确的是（）A ．1月至8月空气合格天数超过20天的月份有5个B ．第二季度与第一季度相比，空气达标天数的比重下降了C ．8月是空气质量最好的一个月D ．6月份的空气质量最差.5．有两张卡片，一张的正反面分别画着老鼠和小鸡，另一张的正反面分别画着老鹰和蛇，现在有个小孩随机地将两张卡片排在一起放在桌面上，不考虑顺序，则向上的图案是老鹰和小鸡的概率是（） A ．12B ．13C ．14D ．166．若cos 3sin 0θθ-=，则tan()4πθ-=（）A ．12-B ．2-C ．12D ．27．已知21log 34a =，12b =，51log 32c =，则（） A ．c a b <<B ．a b c <<C ．b c a <<D ．b a c <<8．执行如图所示的程序框图，如果输入的32n =，那么输出的M =（）A ．66B ．65C ．64D ．639．在ABC △中，tan 2C =，BC 边上的高为AD ，D 为垂足，且2BD DC =，则cos A =（）A ．310B．10CD10．小明在解决三视图还原问题时，错把图一的三视图看成图二的三视图.假设图一所对应几何体中最大面的面积为1S ，图二所对应几何体中最大面的面积为2S ，三视图中所有三角形均为全等的等腰三角形，则12S S =（）A ．1BCD11．网络用语“车珠子”，通常是指将一块原料木头通过加工打磨，变成球状珠子的过程，某同学有一圆锥状的木块，想把它“车成珠子”，经测量，该圆锥状木块的底面直径为12cm ，体积为396cm π，假设条件理想，他能成功，则该珠子的体积最大值是（）. A ．336cm πB ．312cm πC ．39cm πD ．372cm π12．已知O 为坐标原点，1F ，2F 分别是双曲线C ：22221x y a b-=的左右焦点，A 为C 的左顶点，P 为C 上一点，且1PF x ⊥轴.过点A 的直线l 与线段1PF 交于点M ，与y 轴交于点E ，若直线2F M 与y 轴交点为N ，2OE ON =，则C 的离心率为（） A ．13B ．2C ．23D ．34二、填空题13．若实数x ，y 满足条件10201x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩，则2log (2)x y +的最大值为__________．14．将函数()sin 22f x x x =+的图象向左平移ϕ（0ϕ>）个单位后看，所得到的图象关于y 轴对称，则ϕ的最小值为__________．15．已知椭圆：22182x y +=与抛物线22y px =（0p >）交于A 、B 两点，||2AB =，则p =__________．16．如图所示，()y f x =是可导函数，直线l ：3y kx =+是曲线()y f x =在1x =处的切线，若()()h x xf x =，则()h x 在1x =处的切线方程为：__________．三、解答题17．已知数列{}n a 中，11a =，()*1N 3nn n a a n a +=∈+．（1）证明数列112n a ⎧⎫+⎨⎬⎩⎭为等比数列，并求{}n a 的通项公式；（2）数列{}n b 满足()312nn n n nb a =-⋅⋅，数列{}n b 的前n 项和为n T ，求证4n T <． 18．2015男篮亚锦赛决赛阶段，中国男篮以9连胜的不败战绩赢得28届亚锦赛冠军，同时拿到亚洲唯一1张直通里约奥运会的入场券．赛后，中国男篮主力易建联荣膺本届亚锦赛MVP （最有价值球员），下表是易建联在这9场比赛中投篮的统计数据．注：（1）表中/a b 表示出手b 次命中a 次；（2）%TS （真实得分率）是衡量球员进攻的效率，其计算公式为： %2(TS =⨯全场得分投篮出手次数+0.44罚球出手次数)（1）从上述9场比赛中随机选择一场，求易建联在该场比赛中%TS 超过50%的概率；（2）我们把比分分差不超过15分的比赛称为“胶着比赛”.为了考察易建联在“胶着比赛”中的发挥情况，从“胶着比赛”中随机选择两场，求易建联在这两场比赛中%TS 至少有一场超过60%的概率；（3）用x 来表示易建联某场的得分，用y来表示中国队该场的总分，画出散点图如图所示，请根据散点图判断y 与x 之间是否具有线性相关关系？结合实际简单说明理由．19．如图，在四棱锥P ABCD -中，底面ABCD 是棱形，60DAB ∠=︒，PD ⊥平面ABCD ，1PD AD ==，点E 、F 分别为AB 和PC 中点，连接EF ，BF .（1）求证：直线EF 平面PAD ；（2）求三棱锥F PBE -的体积.20．已知抛物线E ：24y x =的焦点为F ，圆C ：222240x y ax a +-+-=.直线l 与抛物线E 交于点A 、B 两点，与圆C 切于点P .（1）当切点P 的坐标为4855，⎛⎫⎪⎝⎭时，求直线l 及圆C 的方程；（2）当2a =时，证明：||||||FA FB AB +-是定值，并求出该定值. 21．已知关于x 函数2()ln g x a x x=-（a R ∈），2()()f x x g x = （1）当2a =-时，求函数()g x 的单调区间；（2）若()f x 在区间1e e ⎛⎫ ⎪⎝⎭，内有且只有一个极值点，试求a 的取值范围； 22．已知平面直角坐标系xOy ，以O 为极点，x 轴的非负半轴为极轴建立极坐标系，P 点的极坐标为34，π⎛⎫⎪⎝⎭，曲线C 的极坐标方程为2cos 4πρθ⎛⎫=-⎪⎝⎭（θ为参数）. （1）写出点P 的直角坐标及曲线C 的直角坐标方程；（2）若Q 为曲线C 上的动点，求PQ 的中点M 到直线l ：2cos 4sin ρθρθ+=的距离的最小值.23．选修4-5：不等式选讲已知()|2||1|2|2|f x x x x =-++++. （1）求证：()5f x ≥；（2）若对任意实数x ，229152()1f x a a <<++都成立，求实数a 的取值范围.参考答案1．B 【解析】由题可知{}1,0,1,2,3A =-，则{}1,2,3AB =-．故本题选B ．2．D 【解析】由题3-4i 3-4i 34==-i |3+4i|555z z =．故本题答案选D ． 3．C 【解析】由题知()()3,1,3,1AB AC =-=--，则((()111cos 222AB AC BAC AB AC⨯+⨯-⋅∠===⨯，则3BAC π∠=．故本题答案选C ．点睛:本题主要考查向量的线性运算与坐标运算.向量的坐标运算主要是利用向量加,减,数乘运算的法则来进行求解的,若已知有向线段两端点的坐标,则应先求向量的坐标,向量的坐标运算,使得向量的线性运算都可用坐标来进行,实现了向量运算的完全代数化,将数与形紧密结合起来,就可以使很多几何问题的解答转化为我们熟悉的数量运算. 4．D 【解析】由图表可知5月空气质量合格天气只有13天，5月份的空气质量最差．故本题答案选D ． 5．C 【解析】将两张卡片排在一起，向上的一面组成的图案共4种，分别为：（老鼠，老鹰），（老鼠，蛇），（小鸡，老鹰），（小鸡，蛇），所以由古典概型概率公式可得组成的图案是老鹰和小鸡的概率14P =．选C ．点睛：古典概型计算的步骤：①判断试验是否是等可能的；②求出试验的基本事件有多少个；③事件A 是什么，它包含的基本事件有多少个；④根据古典概型概率公式求解．其中对是否为古典概型的判断是解题的关键，判断的关键是事件的发生是否具有的等可能性，事件是否有有限个． 6．A 【解析】由题知1tan 3θ=，则πtan 11tan 41tan 2θθθ-⎛⎫-==- ⎪+⎝⎭．故本题答案选A ． 7．A 【解析】由题可221log log 2a b =<==，又1lg34lg 2a ==511lg3log 322lg5c a ===<=，则c a b <<．故本题答案选A ．8．D 【解析】由程序框图可知1,0,32,1;2,16,3;4,8,347;8,4,7815;i M s M i s M i s M i s M ==========+====+=16,2,151631;32,1,313263i s M i s M ===+====+=．故本题答案选D ．点睛:本题主要考查程序框图中的循环结构.循环结构中都有一个累计变量和计数变量,累计变量用于输出结果,计算变量用于记录循环次数,累计变量用于输出结果,计数变量和累计变量一般是同步执行的,累加一次计数一次,哪一步终止循环或不能准确地识别表示累计的变量,都会出现错误.计算程序框图的有关的问题要注意判断框中的条件,同时要注意循环结构中的处理框的位置的先后顺序,顺序不一样,输出的结果一般不会相同. 9．B 【解析】由题可设CD a =,那么2BD a =,又tanC 2=,可得2AD a =.由勾股定理AC =;AB ==则3BC BD CD a =+=.由余弦定理可知222cos 2AB AC BC A AB AC +-==⋅.故本题答案选B . 10．D还原三视图,如图中几何体，可令三视图中等腰直角三角形的腰长为a .则图一对应的几何体中面积最大的面是直角边长为a 的直角三角形，其面积为22a ．图二对应的几何体2,.故本题答案选D . 11．A 【解析】由题可令圆锥的高为x 厘米,可得21π696π3x ⋅⋅=,则8x =,由底面直径为12,得母线长为10,可设轴截面的内切球半径为r ,由()1112810101222r ⨯⨯=⨯++,可得3r =.那么珠子的体积最大值为34π336π3⋅= 3cm .故本题答案选A .点睛：解决球与其他几何体的切，接的问题，关键在于选准最佳角度作出截面(要使这个截面尽可能多地包含球，几何体的各种元素以及体现这些元素之间的关系)，达到空间问题平面化的止的．球与旋转体的组合通常作它们的轴截面解题，球与多面体的组合通常过多面体的一条侧棱和球心，或”切点”，”接点”作出截面图，把空间问题化归为平面问题． 12．B 【解析】由1PF x ⊥轴可令(),M c t -,得()(),0,,0A a B a -.则AE tk a c=-,可得AE 的方程为()t y x a a c =+-,令0x =,知0,ta E a c ⎛⎫ ⎪-⎝⎭,又0,2t N ⎛⎫⎪⎝⎭且2OE ON =,可得22ta t a c =-,所以2c a =,即2ce a==.故本题答案选B . 13．2做出如图所示可行域,令2Z x y =+,结合图形可知经过1,10x x y =-+=的交点()1,2A 时Z 有最大值4,此时()2log 2z x y =+的最大值为2log 42=.故本题应填2.点睛:本题为线性规划问题.掌握常见的几种目标函数的最值的求法:①()0z ax by b =+≠利用截距的几何意义;②()0ay bz ac cx d+=≠+利用斜率的几何意义;③()()22z x a y b =-+-利用距离的几何意义.往往是根据题中给出的不等式,求出(),x y 的可行域,利用(),x y 的条件约束,做出图形.数形结合求得目标函数的最值. 14．12π【解析】由题可知π22223y sin x x sinx ==+（）,向左平移后可得解析式π2223y sin x ϕ=++（）,图像关于y 轴对称,函数为偶函数,也就是232212k k k Z ππππϕπϕ+=+=+∈，，．则ϕ最小值为12π.故本题应填12π.点睛:本题主要考查三角函数的图像性质.对于()sin y A x ωϕ=+和()cos y A x ωϕ=+的最小正周期为2T πω=.若()sin y A x ωϕ=+为偶函数,则当0x =时函数取得最值,若()sin y A x ωϕ=+为奇函数,则当0x =时,0f x .若要求()f x 的对称轴,只要令()2x k k Z πωϕπ+=+∈,求x .若要求()f x 的对称中心的横坐标,只要令()x k k Z ωϕπ+=∈即可.15．14【解析】由题可令()(),0,0A x y x y >>,又2AB =,可知1y =,代入椭圆方程可得2x =,再将()2,1A 代入抛物线方程可求得14p =.故本题应填14.16．1y x =+ 【解析】由直线3y kx =+是曲线y f x =（）在1x =处的切线，由图可得12（，）为切点，故()()'1132f k f k ==+=，，解得1k ，=-故'1112f f ==（）﹣，（），由h x xf x =（）（）可得''h x f x xf x =+（）（）（），'11'11112h f f h f =+===（）（）（），（）（），则h x （）在1x =处的切线方程为21y x -=-，即为10x y -+=．故本题应填10x y -+=．点睛：曲线()y f x =在点()00,P x y 处的切线是指以点P 为切点的切线，若存在，只有一条，其方程为()()000'y y f x x x -=-；而曲线()y f x =过点P 的切线，其切点不一定是P ，且切线也不一定只有一条，此时无论点是否在曲线()y f x =上，一般解法是先设切点为()()11,Q x f x ，切线方程为()()()112'y f x f x x x -=-，再把点P 坐标代入切线方程解得1x ，最后把解得的1x 代入切线方程，化简即可求得所求的切线方程．17．（1）证明见解析；231n n a =-；（2）1242n n n T -+=- 【分析】（1）先证明数列112n a ⎧⎫+⎨⎬⎩⎭是以3为公比，以111322a +=为首项的等比数列，从而111333222n n n a -+=⨯=，由此能求出{}n a 的通项公式；（2）由（1）推导出12n n nb -=，从而()0122111111123122222n n n T n n --=⨯+⨯+⨯+⋯+-⨯+⨯，利用错位相减法求和，利用放缩法证明4n T <．【详解】()1由nn 1n a a a 3+=+，*n N ∈，得n n 1n na 3131a a a ++==+， n 1n 11113a 2a 2+⎛⎫∴+=+ ⎪⎝⎭， ∴数列n 11a 2⎧⎫+⎨⎬⎩⎭是以3为公比，以1113a 22+=为首项的等比数列，从而nn 1n 11333a 222-+=⨯=， n n2.31a ∴=- ()2数列{}n b 满足()nn n n nb 31a 2=-⋅⋅， n n 1nb 2-∴=， ()n 012n 2n 111111T 123n 1n 22222--=⨯+⨯+⨯+⋯+-⨯+⨯，()n 12n 1n T 111112n 1n 22222-=⨯+⨯+⋯+-⨯+⨯，两式相减得：n 012n 1n n T 11111n 2n 22222222-+=+++⋯+-⨯=-， n n 1n 2T 4.2-+∴=-n 1n 202-+>，*n N ∀∈，n T 4.∴< 【点睛】本题主要考查等比数列的定义、通项公式与求和公式，以及错位相减法的应用，是中档题．一般地，如果数列{}n a 是等差数列，{}n b 是等比数列，求数列{}n n a b 的前n 项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列{}n b 的公比，然后作差求解, 在写出“n S ”与“n qS ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式.18．（1）8()9P A =;（2）13()18P B =;（3）不具有线性相关关系.【解析】试题分析:(1)由已知,结合古典概型计算公式可得:易建联在该场比赛中%TS 超过50%的概率;(2)由已知,结合古典概型计算公式可得: 易建联在该场比赛中%TS 超过60%的概率;(3)根据散点图,并不是分布在某一条直线的周围,可得结论.试题解析:（1）设易建联在比赛中%TS 超过50%为事件A ，则共有8场比赛中%TS 超过50%，故()89P A =，（2）设“易建联在这两场比赛中%TS 至少有一场超过60%”为事件B ，则从上述9场比赛中随机选择两场共有2936C =个基本事件，而从中任意选择两场中，两场%TS 都不超过60%的有2510C =个基本事件，那么两场至少有一场超过60%的基本事件为()3610-个基本事件．()3610133618P B -∴==．（3）不具有线性相关关系．因为散点图并不是分布在某一条直线的周围．篮球是集体运动，个人无法完全主宰一场比赛．19．（1）见解析（2【解析】试题分析:（1）取PD 中点M ，连接FM AM ，，由三角形中位线定理可得FM DC ，结合已知可得MF AE MFAE =，，则四边形AEFM 为平行四边形，则EF AM ，再由线面平行的判定可得直线EF PAD 平面；（2）连接DE ，解三角形可得DE AB ⊥，再由PD ABCD ⊥平面，得PD AB ⊥，得到AB PDE ⊥平面，有平面PDE PAB ⊥平面，过D 作DH PE H 于⊥，可得DH PAB ⊥平面，求解直角三角形得到DH ．则C 到平面PAB 的距离可求，进一步得F 到平面PAB 的距离，代入棱锥体积公式可得三棱锥F PBE ﹣的体积．试题解析:（1）证明：作//FM CD 交PD 于M ，连接AM .∵点F 为PC 中点，∴12FM CD =. ∵点E 为AB 的中点，∴12AE AB FM ==.又//AE FM ，∴四边形AEFM 为平行四边形，∴//EF AM ， ∴直线//EF 平面PAD .（2）已知60DAB ∠=︒，12AE =，1AD =，由余弦定理，得：DE AB ⊥，又//AB DC 则DE DC ⊥设F 到面BEC 的距离为h ，∵点F 为PC 的中点，∴12h PD =，从而有F PBE P BEF V V --== P BEC F BEC V V ---= ()1•3BEC S PD h ∆-= 11·32BEC S PD ∆1111•••3222=点睛:本题主要考查,线面间垂直的性质与判定,三棱锥的体积,空间想象能力,推理论证能力.在计算柱,锥,台的体积关键是根据条件找出相应的底面积和高.如果给出的几何体不规则 ,需要利用求体积的一些特殊方法:分割法,补体法,转化法等,它们是解决一些不规则几何体体积计算常用的方法,选择,填空题中使用居多,要熟练掌握.本题使用转化法,将底和高进行转化.20．（1）圆C ：224960525x y x ++-=，直线l ：1520440x y +-=（或31145y x =-+）；或圆C ：2240x y x +-=，直线l ：3440x y -+=（或314y x =+）.（2）定值为2. 【解析】试题分析:（1）将P 代入圆方程，即可求得a 的值，根据圆的方程求得圆心，再根据直线的斜率公式求得CP 的斜率k ，则直线l 的方程斜率为1k-，利用直线的点斜式方程，即可求得l 的方程；（2）将当l 垂直与x 轴时，求得A 和B 点坐标，利用两点之间的斜率公式，即可求得FA FB AB +﹣的值；当l 不垂直于x 轴时，由直线l 与圆C 相切，求得244kb b +=，将直线l 代入抛物线方程．利用韦达定理及弦长公式求得||AB ，利用抛物线的定义，12FA FB x x p +=++，即可求得FA FB AB +-是定值．试题解析:（1）把点P 代入圆C 的方程可得：2224842?40555a a ⎛⎫⎛⎫+-+-= ⎪ ⎪⎝⎭⎝⎭25a ⇒=-或2a =. （i ）当25a =-时，圆22416:055C x y x ++-=.∴圆心2,05C ⎛⎫- ⎪⎝⎭，804524355CP k -==--， ∴34l k =-，∴l 的方程为：834545y x ⎛⎫-=-- ⎪⎝⎭，化简得：1520440x y +-=.（ii ）当2a =时，圆22:40C x y x +-=，∴圆心()2,0C ，80454325CPk -==--， ∴34l k =，∴l 的方程为：834545y x ⎛⎫-=- ⎪⎝⎭，化简得：3440x y -+=.综上所述，圆22416:055C x y x ++-=，直线:1520440l x y +-=（或31145y x =-+）；或圆22:40C x y x +-=，直线:3440l x y -+=（或314y x =+）.（2）2a =时，由（1）知，圆22:40C x y x +-=. （i ）当l 垂直于x 轴时，:4l x =，()4,4A ，()4,4B -，∴5FA FB ==，8AB =.∴2FA FB AB +-=. （ii ）当直线l 不垂直于x 轴时，设直线():0l y kx b k =+≠. ∵直线l 与圆C2244kb b =⇒+=,∴0b ≠,1kb <.联立直线l 与抛物线C ，得24{y xy kx b=⇒=+ ()222240k x kb x b +-+=. ∴()222244kb k b ∆=--= ()216161644kb kb kb b-+=-++ 240b=>.又∵12224kb x x k -+=-，2122b x x k=，∴AB ======242kb k -=. 由抛物线的性质可知，12FA FB x x p +=++ 122x x =++， ∴2242kb AF BF k -+=-+，∴2FA FB AB +-=. 综上所述，FA FB AB +-是定值，且该定值为2.21．（1）()g x 在(01)，上单调递减，在(1)+∞，单调递增.（2）2a e =-或23a e> 【解析】试题分析:（1）先求出所给函数的导数，利用导数与函数单调性间的关系,解关于导函数的不等式，求出函数的单调区间即可；（2）根据零点存在定理得到1'?'e 0ef f （）（）＜，⋅解出a 的范围即可．试题解析:（1）当2a =-时，()22ln g x x x =+，()222222'(0)x g x x x x x -=-+=>. 当()0,1x ∈时，()'0g x <，此时函数()g x 单调递减；当()1,x ∈+∞时，()'0g x >，此时函数()g x 单调递增.所以函数()g x 在()0,1上单调递减，在()1,+∞单调递增.（2）()()222ln f x x g x x ax x ==-，其定义域为()0,+∞.()()'22ln f x a x x =-+.若0a =，则()'20f x =≠，不存在极值点，所以，0a ≠. 令()()()'22ln h x f x a x x x ==-+，()()'32ln h x a x =-+.当1,x e e ⎛⎫∈ ⎪⎝⎭时，32ln 0x +>.∴()'0h x >恒成立或者()'0h x <恒成立.∴()'f x 在1,e e ⎛⎫ ⎪⎝⎭是单调函数.∵()f x 在区间1,e e ⎛⎫ ⎪⎝⎭内有且只有一个极值点，∴()'f x 在1,e e ⎛⎫ ⎪⎝⎭有唯一解.由零点存在定理，得：()1''0f f e e ⎛⎫<⇒ ⎪⎝⎭ ()12230a ea e ⎛⎫+-< ⎪⎝⎭ 2a e ⇒<-或23a e>. 综上所述：2a e <-或23a e>.22．（1）点P ⎝⎭；22122x y ⎛⎫⎛⎫-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭（2 【解析】试题分析:(1)由P 的极坐标为3,4π⎛⎫⎪⎝⎭,利用cos {sin x y ρθρθ==可得P 点的直角坐标,曲线C 的参数方程展开可得:()22cos sin 2ρρθρθ=⨯+,利用cos {sin x y ρθρθ==以及222x y ρ=+可得出直角坐标方程;(2)直线l 的直角坐标方程为24x y +=设cos ,sin 22Q θθ⎛⎫++ ⎪ ⎪⎝⎭,则cos sin 22M θθ⎫⎪⎭,利用点到直线的距离公式与三角函数的单调性值域即可得出.试题解析:（1）点P 的直角坐标为,22⎛⎫⎪ ⎪⎝⎭；由2cos 4πρθ⎛⎫=-⎪⎝⎭得2cos sin ρθθ=①将222x y ρ=+，cos x ρθ=，sin y ρθ=代入①，可得曲线C的直角坐标方程为22122x y ⎛⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭．（2）直线:l2cos 4sin ρθρθ+=240x y +-=，设点Q的直角坐标为cos sin θθ⎫⎪⎪⎝⎭，则cos sin 22M θθ⎫⎪⎭，那么M 到直线l 的距离：d ===d ∴≥=（当且仅当()sin 1θϕ+=-时取等号），所以M 到直线:2cos 4sin l ρθρθ+=． 23．（1）见解析（2）a ≠【解析】试题分析:(1)通过零点分段讨论x 的范围,得到关于()f x 的分段函数,画出折线段的图象,从而求出()f x 的最小值;(2)根据基本不等式的性质求出a 的范围.试题解析:（1）()43,25,21{27,1243,2x x x f x x x x x --≤--<≤-=+-<≤+>，∴()f x 的最小值为5，∴()5f x ≥．（2）由（1）知：()152f x -的最大值等于5. ∵()2222991111a a a a +=++-++ 15≥=，“=”成立()22911a a ⇔+=+，即a =∴当a =2291a a ++取得最小值5.当a ≠时，22951a a +>+，又∵对任意实数x ，()152f x -< 2291a a ++都成立，∴a ≠.∴a 的取值范围为a ≠。

广西南宁二中2021届高三上学期10月考试数学文试卷Word版

南宁二中2021-2021学年第一学期10月份考试试卷高三文科数学〔考试时间：120分钟，总分值150分〕第I 卷〔选择题，共60分)一、单项选择题〔每题只有一个符合选项要求，每题5分，共60分)1．集合{}|02A x x =<<，{}2|340B x x x =+->，那么()B C A R 等于〔〕 A ．{}|01x x <≤B ．{}|12x x ≤<C ．{}|02x x <<D ．{}|12x x -≤<2．i 是虚数单位，x ∈R ，复数()()2z x i i =++为纯虚数，那么2x i -的模等于〔〕 A ．1BC．23．等比数列{}n a 各项为正数，354,,a a a -成等差数列，n S 为{}n a 的前n 项和，那么42S S =〔〕A ．2B ．78C ．98D ．544．a 、b 为不重合的直线，α为平面，以下命题：〔1〕假设a ∥b ，a ∥α，那么b ∥α；〔2〕假设a ∥α，b ⊂α，那么a ∥b ；〔3〕假设a ⊥b ，b ∥α，那么a ⊥α；〔4〕假设a ⊥α，b ⊥a ，那么b ∥α，其中正确的有个〔〕A ．0B ．1C ．2D ．35．0<α<2π<β<π，又sin α＝35，cos(α＋β)＝－45，那么sin β＝( )．A．0B．0或2425C．2425D．0或－24256．甲、乙两班在我校举行的“勿忘国耻，振兴中华⊂合唱比赛中，7位评委的评分情况如茎叶图所示，其中甲班成绩的中位数是81，乙班成绩的平均数是86，假设正实数a、b满足：a，G，b成等差数列且x，G，y成等比数列，那么14a b+的最小值为〔〕A．49B．2C．8D．947．,E F分别是长方体1111ABCD A B C D-的棱11,AB A B的中点，假设12AB AD AA===，那么四面体1C DEF-的外接球的外表积为( )A．π13B．16πC．18πD．20π8．函数2()cos2cos1f x x x x=++，那么〔〕A．()f x的最小正周期为π，最大值为3B．()f x的最小正周期为π，最大值为4C．()f x的最小正周期为2π，最大值为3D．()f x的最小正周期为2π，最大值为49．P是抛物线2:2(0)C y px p=>上的一点，F是抛物线C的焦点，O为坐标原点，假设||2PF=，3PFOπ∠=，那么抛物线C的方程为〔〕A．26y x=B．22y x=C．2y x=D．24y x=10．ABC中，a=，3Aπ=，b c+=，那么ABC的面积为〔〕A．58B11．过椭圆()2222:10x y C a b a b+=>>的左焦点F 的直线过C 的上端点B ，且与椭圆相交于点A ，假设3BF FA =，那么C 的离心率为〔〕A ．13B ．3C ．2D 12．定义在R 上的偶函数()f x 在[0,)+∞上单调递减，假设对[]1,3x ∈有不等式(ln 1)(ln 1)2(1)f ax x f ax x f -+++--≥恒成立，那么实数a 的取值范围为〔〕 A ．(2,)e B ．1[,)e +∞C ．1,e e ⎡⎤⎢⎥⎣⎦D ．12ln 3,3e +⎡⎤⎢⎥⎣⎦第II 卷〔非选择题，共90分)二、填空题〔每题5分，共20分)13．向量()12，=→a ，()3,4b =，(),2c k =，假设()3a b c -//，那么实数k =_________14．一个四棱锥的三视图如以下图所示，那么该几何体的体积＝．15．1sin 62πθ⎛⎫-= ⎪⎝⎭，且0,2πθ⎛⎫∈ ⎪⎝⎭，那么cos 3πθ⎛⎫-= ⎪⎝⎭_________. 16．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，假设cos 1cos2cos 1cos2b C C c B B +=+，C 是锐角，且a =1cos 3A =，那么ABC 的面积为______．三、解答题〔本大题共6小题，共70分，解容许写出必要的解答过程)〔一〕必考题：共60分17．〔12分〕等差数列{}n a 公差不为零，且满足：12a =，1a ，2a ，5a 成等比数列. 〔1〕求数列{}n a 的通项公式；〔2〕设3n n n b a =，求数列{}n b 的前n 项和.18．〔12分〕某学校为培养学生的兴趣爱好，提高学生的综合素养，在高一年级开设各种形式的校本课程供学生选择(如书法讲座、诗歌鉴赏、奥赛讲座等)．现统计了某班50名学生一周用在兴趣爱好方面的学习时间(单位：h)的数据，按照[0，2)，[2，4)，[4，6)，[6，8)，[8，10]分成五组，得到了如下的频率分布直方图．(1)⊂⊂⊂⊂⊂⊂⊂⊂⊂m⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂(2)⊂[4⊂6)⊂[6⊂8)⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂⊂6⊂⊂⊂⊂⊂6⊂⊂⊂⊂2⊂⊂⊂⊂⊂1⊂⊂[6⊂8)⊂⊂⊂⊂⊂⊂19．〔12分〕在三棱柱111ABC A B C -中，2,120AC BC ACB ==∠=︒，D 为11A B 的中点.〔1〕证明：1//A C 平面1BC D ；〔2〕假设11A A A C =，点1A 在平面ABC 的射影在AC 上，且侧面11A ABB 的面积为D BC A 11-的体积.20．〔12分〕椭圆E ：22221(0)x y a b a b +=>>的左，右焦点分别为1F ，2F ，离心率为2，且122F F =.〔1〕求椭圆E 的方程；〔2〕设椭圆的下顶点为B ，过右焦点2F 作与直线2BF 关于x 轴对称的直线l ，且直线l 与椭圆分别交于点M ，N ，O 为坐标原点，求OMN ∆的面积.21．〔12分〕函数3211()(1)132f x ax a x x =-+++〔1a ≥〕. 〔I 〕假设3a =，求曲线()y f x =在点(1,(1))f 处的切线方程；〔II 〕假设()f x 在R 上无极值点，求a 的值；〔III 〕当(0,2)x ∈时，讨论函数()f x 的零点个数，并说明理由.〔二〕选考题：共10分，请考生在22，23题中任选一题作答。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

绝密★启用前
2013年普通高等学校招生全国统一考试
数学（文科）
一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）设集合{}{}1,2,3,4,5,1,2,u U A A ===集合则
（A ）{}1,2 （B ）{}3,4,5 （C ）{}1,2,3,4,5 （D ）∅
（2）已知a 是第二象限角，5sin ,cos 13
a a ==则（A ）1213- （B ）513
- （C ）513 （D ）1213 （3）已知向量()()()()1,1,2,2,,=m n m n m n λλλ=+=++⊥-若则
（A ）4- （B ）3- （C ）-2 （D ）-1
（4）不等式222x -<的解集是
（A ）()-1,1 （B ）()-2,2 （C ）()
()-1,00,1 （D ）()()-2,00,2
（5）()862x x +的展开式中的系数是（A ）28 （B ）56 （C ）112 （D ）224
（6）函数()()()-121log 10=f x x f x x ⎛⎫=+
> ⎪⎝⎭的反函数（A ）()1021x x >- （B ）()1021
x x ≠- （C ）()21x x R -∈ （D ）()210x x -> （7）已知数列{}n a 满足{}12430,,103
n n n a a a a ++==-则的前项和等于（A ）()-10-61-3 （B ）()-1011-39
（C ）()-1031-3 （D ）()-1031+3
（8）已知()()1221
,0,1,0,F F C F x -是椭圆的两个焦点过且垂直于轴的直线交于 A B 、两点，且3AB =，则C 的方程为（A ）2212x y += （B ）22132x y += （C ）22143x y += （D ）22
154
x y += （9）若函数()()sin 0=y x ωϕωω=+>的部分图像如图，则
（A ）5 （B ）4 （C ）3 （D ）2
（10）已知曲线()42
1-128=y x ax a a =+++在点，处切线的斜率为，（A ）9 （B ）6 （C ）-9 （D ）-6
（11）已知正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中，则与平面所成角的正弦值等于
（A ）23 （B ）33 （C ）23 （D ）13
（12）已知抛物线()2:82,2,C C y x M k C =-与点过的焦点，且斜率为的直线与交于
,0,A B MA MB k ==两点,若则
（A ）12
（B ）22 （C ）2 （D ）2 二、填空题：本大题共4小题，每小题5分.
（13）设()[)()21,3=f x x f x ∈是以为周期的函数，且当时， .
（14）从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有种.（用数字作答）
（15）若x y 、满足约束条件0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩
则z x y =-+的最小值为 .
（16）已知圆O 和圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，
3602
OK O K =，且圆与圆所在的平面所成角为，则球O 的表面积等于 . 三、解答题：解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分10分）
等差数列{}n a 中，71994,2,a a a ==
（I ）求{}n a 的通项公式；
（II ）设{}1,.n n n n
b b n S na =求数列的前项和
18．（本小题满分12分）
设()(),,,,,.ABC A B C a b c a b c a b c ac ∆++-+=的内角的对边分别为
（I ）求;B
（II ）若
31sin sin , C.4A C -=求
19．（本小题满分12分）
如图，四棱锥902,P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中，，与都是边长为2的等边三角形.
（I ）证明：;PB CD ⊥
（II ）求点.A PCD 到平面的距离
20．（本小题满分12分）
甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比
赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为1,2
各局比赛的结果都相互独立，第1局甲当裁判.
（I ）求第4局甲当裁判的概率；
（II ）求前4局中乙恰好当1次裁判概率.
21．（本小题满分12分）
已知函数()32=33 1.f x x ax x +++
（I ）
求()f ;a x =的单调性；
（II ）若[)()2,0,.x f x a ∈+∞≥时，求的取值范围
22．（本小题满分12分）已知双曲线()22
1222:10,0x y C a b F F a b
-=>>的左、右焦点分别为，，离心率为3，
直线2y C =与
（I ）求,;a b ；
（II ）2F l C A B 设过的直线与的左、右两支分别相交于、两点，且 11,AF BF -证明：22.AF AB BF 、、成等比数列。