2-5指数与指数函数
指数与指数函数知识点

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载指数与指数函数知识点地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容指数函数(一)整数指数幂1.整数指数幂概念:2.整数指数幂的运算性质:(1)(2)(3)其中,.3.的次方根的概念一般地,如果一个数的次方等于,那么这个数叫做的次方根,即:若,则叫做的次方根,例如:27的3次方根,的3次方根,32的5次方根,的5次方根.说明:①若是奇数,则的次方根记作;若则,若则;②若是偶数,且则的正的次方根记作,的负的次方根,记作:;(例如:8的平方根 16的4次方根)③若是偶数,且则没意义,即负数没有偶次方根;④ ∴;⑤式子叫根式,叫根指数,叫被开方数。
∴..4.的次方根的性质一般地,若是奇数,则;若是偶数,则.(二)分数指数幂1.分数指数幂:即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式;如果幂的运算性质(2)对分数指数幂也适用,例如:若,则,,∴ .即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。
规定:(1)正数的正分数指数幂的意义是;(2)正数的负分数指数幂的意义是.2.分数指数幂的运算性质:整数指数幂的运算性质对于分数指数幂也同样适用即说明:(1)有理数指数幂的运算性质对无理数指数幂同样适用;(2)0的正分数指数幂等于0,0的负分数指数幂没意义。
二、指数函数1.指数函数定义:一般地,函数(且)叫做指数函数,其中是自变量,函数定义域是.2.指数函数在底数及这两种情况下的图象和性质:1.1 实数指数幂及其运算(一)(一)选择题1.下列正确的是( )A.a0=1 B. C.10-1=0.1 D.2.的值为( )A.±2B.2 C.-2 D.43.的值为( )A.B.C.D.4.化简的结果是( )A.a B.C.a2 D.a35.把下列根式化成分数指数幂的形式(其中a,b>0)(1)______;(2)=______;6.______.7.化简______.8.=______(三)解答题9.计算10.计算1.2 实数指数幂及其运算(二)(一)选择题(每道题的四个选择答案中有且只有一个答案是正确的) 1.下列说法正确的是(n∈N*)( )A.正数的n次方根是正数B.负数的n次方根是负数C.0的n次方根是0 D.是无理数2.函数的定义域为( )A.R B.[0,+∞)C.(0,+∞)D.(-∞,1] 3.可以简化为( )A.B.C.D.4.化简的结果是( )A.B.x2 C.x3 D.x4(二)填空题5.________,________________________.6.________.7.计算________.8.若a+a-1=3,则a2+a-2=______.10.若求的值.1.3 指数函数(一)(一)选择题(每道题的四个选择答案中有且只有一个答案是正确的)1.一种细胞在分裂时由一个分裂成两个,两个分裂成四个,四个分裂成八个……每天分裂一次.现在将一个该细胞放入一个容器,发现经过10天就可充满整个容器,则当细胞分裂到充满容器一半时需要的天数是( ) A.5 B.9 C.6 D.82.下列函数中为指数函数的是( )A.y=2·3x B.y=-3x C.y=3-x D.y=1x3.若0.2m=3,则( )A.m>0 B.m<0 C.m=0 D.以上答案都不对4.函数f(x)=ax+1(其中a>0且a≠1)的图象一定经过点( )A.(0,1) B.(0,2) C.(0,3) D.(1,3)(二)填空题5.若函数f(x)是指数函数且f(3)=8,则f(x)=______.6.函数的定义域为______,值域为______.7.函数y=2x-1的图象一定不经过第______象限;若函数的图象不经过第一象限,则实数b的取值范围是______.8.若2m>4,则m的取值范围是______;若(0.1)t>1,则t的取值范围是______.9.指数函数y=(a2-1)x在R上是减函数,则实数a的取值范围是______.(三)解答题10.根据函数f(x)=2x的图象,画出下列函数的草图.(1)y=-2x (2)y=-2x+1 (3)y=2|x|11.求函数的定义域和值域.12.已知a>0且a≠1,函数f1(x)=,f2(x)=,若f1(x)<f2(x),求x 的取值范围.1.4 指数函数(二)(一)选择题(每道题的四个选择答案中有且只有一个答案是正确的)1.若,则x的取值范围是( )A.(-∞,-3] B.(-∞,-3) C.[-3,+∞)D.R2.已知三个数M=0.32-0.32,P=0.32-3.2,Q=3.2-0.32,则它们的大小顺序是( )A.M<P<Q B.Q<M<P C.P<Q<M D.P<M<Q3.如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与0和1的大小关系是( )A.0<a<b<1<c<d B.0<b<a<1<d<cC.1<a<b<c<d D.0<a<b<1<d<c4.函数y=2x-2-x( )A.在R上减函数B.在R上是增函数C.在(-∞,0)上是减函数,在(0,+∞)上是增函数D.无法判断其单调性(二)填空题5.函数y=3x+1-2的图象是由函数y=3x的图象沿x轴向______平移______个单位,再沿y轴向______平移______个单位得到的.6.函数f(x)=3x+5的值域是______.7.函数y=ax-1+1(其中a>0且a≠1)的图象必经过点______.8.若指数函数y=ax在区间[0,1]上的最大值和最小值的差为,则底数a =______.9.函数g(x)=x2-x的单调增区间是______,函数y=的单调增区间是______.(三)解答题10.函数f(x)是R上的奇函数,且当x≥0时,f(x)=2x-1,求x<0时函数的解析式.11.若关于x的方程|2x-1|=a有两个解,借助图象求a的取值范围.12.已知函数f(x)=22x-2x+1-3,其中x∈[0,1],求f(x)的值域.您好,欢迎您阅读我的文章,本WORD文档可编辑修改,也可以直接打印。
2.5 指数与指数函数
2
2
2
∴a>-3.又 a<0,∴-3<a<0.
)a-7<1,
当 a≥0 时,不等式 f(a)<1 可化为 a<1.
∴0≤a<1,
综上,a 的取值范围为(-3,1).
命题点 2 与指数函数有关的复合函数的单调性
典例 (1)已知函数 f(x)= 2|2x-m| (m 为常数),若 f(x)在区间[2,+∞)上单调递增,则 m 的取值
( )1
画指数函数 y=ax(a>0,且 a≠1)的图象,应抓住三个关键点:(1,a),(0,1), -1, . a
2.指数函数的图象与底数大小的比较
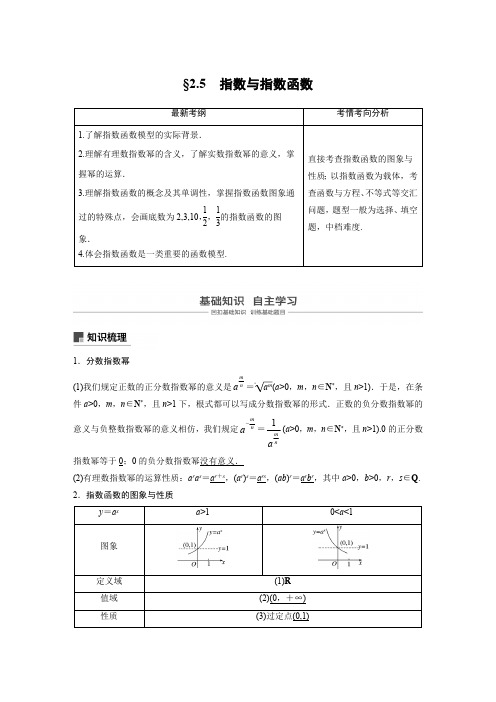
如图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx 的图象,底数 a,b,c,d 与 1 之间的 大小关系为 c>d>1>a>b>0.由此我们可得到以下规律:在第一象限内,指数函数 y=ax(a>0,a≠1) 的图象越高,底数越大. 3.指数函数 y=ax(a>0,a≠1)的图象和性质跟 a 的取值有关,要特别注意应分 a>1 与 0<a <1 来研究.
值等问题时,都要借助“同增异减”这一性质分析判断.
跟踪训练 (1)已知函数 f(x)=Error!的值域是[-8,1],则实数 a 的取值范围是
A.(-∞,-3]
B.[-3,0)
C.[-3,-1]
D.{-3}
答案 B
解析 当 0≤x≤4 时,f(x)∈[-8,1],
[ ( ) ) 1
当 a≤x<0 时,f(x)∈ - 2
(3)函数 f(x)=4x-2x+1 的单调增区间是________. 答案 [0,+∞) 解析 设 t=2x(t>0),则 y=t2-2t 的单调增区间为[1,+∞),令 2x≥1,得 x≥0,又 y=2x 在
高中数学-2.5 指数与指数函数

2.化简 2 3 × 1.5 × A.2 6 B.3 6
3
6
12的结果是( C.6
) D.12
关闭
2 3×
1 3
3
1.5 ×
6
12=2×3 ×
1 2
1 1 3 3 ×(3×4)6 =2×32 2
1
×3 ×2 ×3 ×
关闭
1 3
-
1 3
1 6
2 =6.故选 C.
C
解析
答案
第二章 1 2 3 4 5
2.5
指数与指数函数
知识梳理 双击自测 双击自测 核心考点 学科素养
考纲要求
-8-
3.已知函数f(x)=ax(a>0,且a≠1)的图像经过点(3,π),则函数f(x)的解 析式为( )
A.f(x)=π
x
B.f(x)= D.f(x)=
������ C.f(x)=π3
1 ������ π ������ 1 3 π
2.5
指数与指数函数
第二章
2.5
指数与指数函数
知识梳理 双击自测 核心考点 学科素养
考纲要求 考纲要求
-2-
考纲要求:1.了解指数函数模型的实际背景. 2.理解有理指数幂的 含义,了解实数指数幂的意义,掌握幂的运算. 3.理解指数函数的 概念及其单调性,掌握指数函数的图像通过的特殊点,会画底数为 1 1 2,3,10, , 的指数. 4.体会指数函数是一类重要的函数模型.
关闭
由f(x)=ax-b的图像可以看出,函数f(x)=ax-b在定义域上单调递减,所以0<a<1. 函数f(x)=ax-b的图像是在f(x)=ax的图像的基础上向左平移得到的,所以b<0.
指数函数公式运算法则

指数函数公式运算法则指数函数是一种常见的数学函数,其公式形式为f(x) = a^x,其中a为底数,x为指数。
指数函数在数学中有着广泛的应用,因此掌握指数函数的运算法则对于解决实际问题具有重要意义。
本文将介绍指数函数的运算法则,包括指数函数的加减乘除、指数函数的幂函数、指数函数的对数函数等内容。
一、指数函数的加减乘除1. 指数函数的加法当两个指数函数相加时,如果它们的底数相同,则可以将它们的指数相加,即a^x + a^y = a^(x+y)。
例如,2^3 + 2^4 =2^(3+4) = 2^7。
2. 指数函数的减法同样地,当两个指数函数相减时,如果它们的底数相同,则可以将它们的指数相减,即a^x - a^y = a^(x-y)。
例如,3^5 - 3^3 = 3^(5-3) = 3^2。
3. 指数函数的乘法当两个指数函数相乘时,如果它们的底数相同,则可以将它们的指数相加,即(a^x) * (a^y) = a^(x+y)。
例如,2^3 * 2^4 =2^(3+4) = 2^7。
4. 指数函数的除法当两个指数函数相除时,如果它们的底数相同,则可以将它们的指数相减,即(a^x) / (a^y) = a^(x-y)。
例如,3^5 / 3^3 =3^(5-3) = 3^2。
二、指数函数的幂函数指数函数的幂函数是指数函数的一种特殊形式,其公式为f(x) = (a^x)^n,其中a为底数,x为指数,n为幂次。
当计算指数函数的幂函数时,可以将指数函数的指数与幂次相乘,即(a^x)^n =a^(x*n)。
例如,(2^3)^2 = 2^(3*2) = 2^6。
三、指数函数的对数函数指数函数的对数函数是指数函数的逆运算,其公式为y =log_a(x),其中a为底数,x为指数,y为对数。
对数函数的作用是求解指数函数的指数,即log_a(x) = y 等价于 a^y = x。
例如,log_2(8) = 3 等价于 2^3 = 8。
指数与指数函数知识点

指数与指数函数知识点一、指数运算的基本性质1.任何数的0次方等于12.非零数的负指数等于该数的倒数。
3.相同底数的指数之间的乘方运算,底数保持不变,指数相加。
4.相同指数的指数之间的乘方运算,指数保持不变,底数相乘。
二、指数运算的规律1.法则1:a的m次方乘以a的n次方,等于a的m加n次方。
2.法则2:a的m次方除以a的n次方,等于a的m减n次方。
3.法则3:(a的m次方)的n次方,等于a的m乘n次方。
4.法则4:a的m次方的p次方,等于a的m乘p次方。
5.法则5:零的任何正次方都是0,零的0次方没有意义,规定为1三、指数函数的定义与性质指数函数的定义为:y=a^x,其中a>0且a≠1,a为底数,x为指数。
指数函数可以看作是以底数为底,自变量为指数的函数。
指数函数的性质如下:1.底数a大于1时,指数函数是递增的,即自变量x的增大,函数值y也增大。
2.底数a介于0和1之间时,指数函数是递减的,即自变量x的增大,函数值y也减小。
3.指数函数的图象都经过点(0,1),即当x=0时,y=14.指数函数的图象在直线x=0和y=0上均没有交点。
5.指数函数的图象没有水平渐近线,但有一条过点(0,0)的铅直渐近线。
指数函数常见的应用有:1.在金融领域中,指数函数可以用来描述货币的增长规律,例如复利计算。
2.在自然科学领域中,指数函数可以用来描述人口增长、病原体传播等现象。
3.在电路中,指数函数可以用来描述电容、电感等元件的充放电过程。
4.在计算机领域中,指数函数可以用来描述算法的时间复杂度、空间复杂度等特性。
总结:。
2-6第六节 指数与指数函数(2015年高考总复习)

解析
由 y=(a2-1)x 在(-∞,+∞)上为减函数,得 0<a2-
1<1,∴1<a2<2,即 1<a< 2或- 2<a<-1.
答案 (- 2,-1)∪(1, 2)
考源教学资源网
第20页
返回导航
第二章
第六节
高考总复习模块新课标
新课标A版数学
5. 若函数 f(x)=ax-1(a>0, 且 a≠1)的定义域和值域都是[0,2], 则实数 a=________.
在 y 轴右侧,图象从上到下相应的底数由大变小; 在 y 轴左侧,图象从下到上相应的底数由大变小; 既无论在 y 轴的左侧还是右侧,底数按逆时针方向变大.
考源教学资源网
第14页
返回导航
第二章
第六节
高考总复习模块新课标
新课标A版数学
基 础 自 评 1.下列等式能够成立的是( )
考源教学资源网
第35页
返回导航
第二章
第六节
高考总复习模块新课标
新课标A版数学
变式思考 2 ( )
(1)函数 y=ax-a(a>0,且 a≠1)的图象可能是
(2)k 为何值时,方程|3x-1|=k 无解?有一解?有两解?
考源教学资源网
新课标A版数学
题型二 【例 2】
指数函数图象的应用
已知 f(x)=|2x-1|,
(1)求 f(x)的单调区间; (2)比较 f(x+1)与 f(x)的大小. 【思维启迪】 (1)作出 f(x)的图象,数形结合求解.
(2)在同一坐标系中分别作出 f(x)、f(x+1)的图象,数形结合求 解.
考源教学资源网
4 3 1 B. 2, , , 3 10 5 1 3 4 D. , , , 2 5 10 3
2.5指数与指数函数

返回目录
退出
返回目录
退出
一、指数式与根式的计算
【例 1 】计算下列各式的值. (1) (2)
27 -3 8
2 1 2
+(0.002) -10( 5-2)-1+( 2 − 3)0; 3-1)0- 9-4 5;
-
1 -( 5+2
3
(3)
1 1(a>0,b>0). 1 1 4 (������ 4������ 2) ������ 3������3
请做演练巩固提升 4
返回目录
退出
二、指数函数的图象与性质的应用
【例 2 -1 】在同一坐标系中,函数 y=2 与 y= ( A ). A.关于 y 轴对称 B.关于 x 轴对称 C.关于原点对称 D.关于直线 y=x 对称
1 x 2
x
1 ������ 2
的图象之间的关系是
解析:∵ y=
=2-x,
∴ 它与函数 y=2x 的图象关于 y 轴对称.
返回目录 退出
3 .与指数函数有关的复合函数的单调性的求解步骤: (1)求复合函数的定义域; (2)弄清函数是由哪些基本函数复合而成的; (3)分层逐一求解函数的单调性; (4)求出复合函数的单调区间(注意 “同增异减 ”). 4 .函数 y=a f(x )的值域的求解,先确定 f(x)的值域 ,再根据指数函数的单调 性确定 y=a f(x )的值域.
返回目录
退出
而 y=
1 g (x ) 3
在 R 上单调递减.
所以 f(x)在(-∞,-2)上单调递减,在(-2,+∞)上单调递增, 即函数 f(x)的递增区间是(-2,+∞),递减区间是(-∞,-2).
浙江高考数学函数2.5指数与指数函数课件

C
解析
-18答案
考点一
考点二
考点三
指数函数的图象及其应用(考点难度★) 【例2】 (1)定义运算a*b= ������,������ ≤ ������, 则函数f(x)=1*2x的图象是 ������,������ > ������, ( )
关闭
因为当 x≤0 时,2x≤1; 当 x>0 时,2x>1. 2������ , ������ ≤ 0, x 则 f (x)=1*2 = 故选 A. 1, ������ > 0, A
解析
关闭
答案
-12知识梳理 双击自测
5.当a>0,且a≠1时,函数f(x)=ax-2-3的图象必经过定点
.
关闭
令x-2=0得x=2,此时,f(2)=-2. 因此,函数f(x)的图象必经过定点(2,-2). (2,-2)
解析
关闭
答案
-13知识梳理 双击自测
自测点评 1.根式的化简运算中要注意以下两个公式的区别:
( a) =a(n>1,n∈N ),
n
������
* ������
������������
=
������,������为奇数, |������|,������为偶数.
2.指数幂的运算中应注意:(1)运算的先后顺序;(2)化负数指数幂 为正数指数幂;(3)化根式为分数指数幂;(4)化小数为分数. 3.指数函数的单调性是由底数a的大小决定的,因此,应用单调性 解题时,应对底数a分为a>1和0<a<1两种情况进行讨论.
-16-
考点一
考点二
考点三
5 对点训练(1)化简: a2· ������3 ÷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则 2a+2c<2,且 2a+2c>1。故选 D。
答案 D
考点三 指数函数的性质及应用 微点小专题
微考向 1:比较大小
【例 3】 (1)(2019·全国Ⅰ卷)已知 a=log20.2,b=20.2,c=0.20.3,则
() A.a<b<c
B.a<c<b
C.c<a<b
D.b<c<a
解析 因为 a=log20.2<0,b=20.2>1,c=0.20.3∈(0,1), 所以 a<c<b。故选 B。 答案 B
y=|3x-1|与直线 y=m 有两个公共点,则实 数 m 的取值范围是(0,1)。答案 (0,1)
【互动探究】 (1)若本例(2)条件变为:方程 3|x|-1=m 有两个不同实根, 则实数 m 的取值范围是________。
解析 作出函数 y=3|x|-1 与 y=m 的图象如图所示,由图象知当 m>0 时,直线 y=3|x|-1 与直线 y=m 有两个交点,故实数 m 的取值范围是(0, +∞)。
解析
令
t=|2x-m|,则
t=|2x-m|在区间
m,+∞ 2
上单调递增,在区
间
-∞,m 2
上单调递减。而
y=2t
为
R
上的增函数,
所以要使函数 f(x)=2|2x-m|在[2,+∞)上单调递增,则有m≤2,即 m≤4, 2
所以 m 的取值范围是(-∞,4]。 答案 (-∞,4]
(2)函数 f(x)=12-x2+2x+1 的单调递减区间为________。
解析 令 g(x)=ax2+2x+3,由于 f(x)的值域是0,91,所以 g(x)的值域
a>0, 是[2,+∞)。因此有124aa-4=2, 解得 a=1,这时 g(x)=x2+2x+3,f(x)
=13x2+2x+3。由于 g(x)的单调递减区间是(-∞,-1],所以 f(x)的单调 递增区间是(-∞,-1]。
练习已知 f(x)=|2x-1|,当 a<b<c 时,有 f(a)>fc>f(b),则必有( )
A.a<0,b<0,c<0
B.a<0,b>0,c>0
C.2-a<2c
D.1<2a+2c<2
解析 作出函数 f(x)=|2x-1|的图象如图所示,因为 a<b<c,且有
f(a)>f(c)>f(b),所以必有 a<0,0<c<1,且|2a-1|>|2c-1|,所以 1-2a>2c-1,
1,1],所以 t∈ a,1a ,又函数 y=(t+1)2-2 在 a,1a 上单调递增,
则
ymax=
1+1 a
2-2=14,解得
a=13
(负值舍去)。综上,a=3 或 a=13。
答案 3 或1 3
【题组对点练】
1.(微考向 1)已知 a=0.50.8,b=0.80.5,c=0.80.8,则( )
1.判断下列说法是否正确(打“√”或“×”)。
n (1)
an与(n
a)n
都等于
a(n∈N*)。(×
)
(2)2a·2b=2ab。(× )
(3)函数 y=3·2x 与 y=2x+1 都不是指数函数。(√ )
(4)若 am<an(a>0,且 a≠1),则 m<n。(× )
2.化简4 16x8y4(x<0,y<0)得( )
5.若函数 f(x)=ax 在[-1,1]上的最大值为 2,则 a=________。
解析 若 a>1,则 f(x)max=f(1)=a=2; 若 0<a<1, 则 f(x)max=f(-1)=a-1=2,得 答案 π+8
答案 -12
指数幂运算的一般原则 1.指数幂的运算首先将根式、分数指数幂统一为分数指数幂,以便 利用法则计算。 2.先乘除后加减,负指数幂化成正指数幂的倒数。 3.底数是负数,先确定符号;底数是小数,先化成分数;底数是带 分数的,先化成假分数。 4.运算结果不能同时含有根号和分数指数,也不能既有分母又含有 负指数。
A.c<b<a
B.c<a<b
C.a<b<c
D.a<c<b
解析 因为函数 y=0.8x 在(-∞,+∞)上为减函数,所以 0.80.5>0.80.8, 即 b>c。因为函数 y=x0.8 在(0,+∞)上为增函数,所以 0.50.8<0.80.8,即 a<c, 所以 a<c<b。故选 D。
答案 D
2.(微考向 2)若函数 f(x)=13ax2+2x+3 的值域是0,91,则 f(x)的单调 递增区间是________。
解析 设 u=-x2+2x+1,因为 y=12u 在 R 上为减函数,所以函数 f(x) =12-x2+2x+1 的单调递减区间即为函数 u=-x2+2x+1 的单调递增区 间。又 u=-x2+2x+1 的单调递增区间为(-∞,1],所以函数 f(x)的单调 递减区间为(-∞,1]。
答案 (-∞,1]
6=ab, 24=b·a3,
结合 a>0,
且
a≠1,解得
a=2, b=3,
11 所以 f(x)=3·2x。要使 2 x+ 3 x≥m 在区间(-∞,1]
11 上恒成立,只需保证函数 y= 2 x+ 3 x 在区间(-∞,1]上的最小值不小于
11 m 即可。因为函数 y= 2 x+ 3 x 在区间(-∞,1]上为减函数,所以当 x=1
解析 令 ax=t,则 y=a2x+2ax-1=t2+2t-1=(t+1)2-2。当 a>1 时,
因为 x∈[-1,1],所以 t∈ 1a,a ,又函数 y=(t+1)2-2 在 1a,a 上单调递增,
所以 ymax=(a+1)2-2=14,解得 a=3(负值舍去)。当 0<a<1 时,因为 x∈[-
解 (1)由 f(x)=32⇒2x-21x=32⇒2·(2x)2-3·2x-2=0⇒ (2x-2)(2·2x+1)=0。 因为 2x>0,所以 2x=2,所以 x=1。
5.(配合例 5 使用)已知定义在 R 上的函数 f(x)=2x-21x。 (1)若 f(x)=3,求 x 的值;
2 (2)若 2tf(2t)+mf(t)≥0 对任意 t∈[1,2]恒成立,求实数 m 的取值范围。
11
时,y=
2
x+
3
x
有最小值5。所以只需 6
m≤5即可。所以 6
m
的最大值为5。 6
4.(加强练)当 x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0 恒成立,则
实数 m 的取值范围是( )
A.(-2,1)
B.(-4,3)
C.(-3,4)
D.(-1,2)
解析 原不等式变形为 m2-m<12x,又 y=12x 在(-∞,-1]上是减函
A.2x2y
B.2xy
C.4x2y
D.-2x2y
答案 D
4.函数 y=ax-1a(a>0,且 a≠1)的图象可能是(
)
A
B
C
D
解析 当 a>1 时,y=ax-1a为增函数,且在 y 轴上的截距为 0<1-1a<1,
此时四个选项均不对;当 0<a<1 时,函数 y=ax-1a是减函数,且其图象可
视为是由函数 y=ax 的图象向下平移1a1a>1个单位长度得到的。故选 D。 答案 D
②(ar)s= ars (a>0,r,s∈Q)。
③(ab)r= arbr (a>0,b>0,r∈Q)。
3.指数函数的图象与性质
1.指数函数图象的画法
画指数函数 y=ax(a>0,且 a≠1)的图象,应抓住三个关键点:(1,a),(0,1),
-1,1 a
。
2.指数函数的图象与底数大小的比较 如图是指数函数①y=ax,②y=bx,③y=cx,
第五节 指数与指数函数
1.根式 (1)根式的概念
(2)两个重要公式
a ②(n a)n= (注意 a 必须使n a有意义)。
2.有理数的指数幂 (1)幂的有关概念
③0 的正分数指数幂等于 0 ,0 的负分数指数幂 无意义 无意义 。
,0 的零次幂
(2)有理数指数幂的运算性质
①aras= ar+s (a>0,r,s∈Q)。
答案 B
比较指数式的大小的方法 1.能化成同底数的先化成同底数幂,再利用单调性比较大小。 2.不能化成同底数的,一般引入“ 1” “ 0” 等中间量比较大小。
微考向 2:复合型函数的单调性 【例 4】 (1)已知函数 f(x)=2|2x-m|(m 为常数),若 f(x)在区间[2,+∞) 上是增函数,则 m 的取值范围是________。
求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、 值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调 区间、最值等问题时,都要借助“同增异减”这一性质分析判断。
微考向 3:最值问题 【例 5】 如果函数 y=a2x+2ax-1(a>0,且 a≠1)在区间[-1,1]上的最 大值是 14,则 a 的值为________。
答案 D
(2)若曲线 y=|3x-1|与直线 y=m 有两个不同交点,则实数 m 的取值范 围是________。
解析 曲线 y=|3x-1|的图象是由函数 y=3x 的图象向下平移一个单位长度后,再把位于 x 轴 下方的图象沿 x 轴翻折到 x 轴上方得到的,而直 线 y=m 的图象是平行于 x 轴的一条直线,它的 图象如图所示,由图象可得,如果曲线
