指数与指数函数专题训练卷(含解析)

合集下载

指数函数的图象和性质专题训练卷(含答案详解)

2.1.2指数函数的图象和性质1．下列函数是指数函数的是( )．A ．y ＝x 5B ．y ＝4x 3C ．43x y ⎛⎫= ⎪⎝⎭D ．y ＝13x ⎛⎫- ⎪⎝⎭＋2 2．函数f (x )＝132a ⎛⎫- ⎪⎝⎭·a x 是指数函数，则12f ⎛⎫ ⎪⎝⎭的值为( )．A ．2B ．－2C ．-D ．3．函数||12x y -⎛⎫= ⎪⎝⎭的图象是( )．4．函数f (x )＝a x (a ＞0且a ≠1)对于任意的实数x ，y 都有( )．A ．f (xy )＝f (x )f (y )B ．f (xy )＝f (x )＋f (y )C ．f (x ＋y )＝f (x )f (y )D ．f (x ＋y )＝f (x )＋f (y )5．已知f (x )＝a －x (a ＞0且a ≠1)，且f (－2)＞f (－3)，则a 的取值范围是( )．A ．a ＞0B ． a ＞1C ．a ＜1D ．0＜a ＜16．函数y ( )．A ．[0，＋∞)B ．[0,4]C ．[0,4)D ．(0,4)7．若f (x )是指数函数，且f (2)－f (1)＝6，则f (x )＝__________.8．已知(a 2＋2a ＋5)3x ＞(a 2＋2a ＋5)1－x ，则x 的取值范围是__________．9．函数y =的定义域是__________．10．函数y ＝a x (a ＞0且a ≠1)在区间[1,2]上的最大值比最小值大2a ，求a 的值．参考答案1. 答案： C2. 答案：D解析：∵函数f (x )是指数函数， ∴12a －3＝1，a ＝8.∴f (x )＝8x ，12182f ⎛⎫== ⎪⎝⎭3. 答案：B4. 答案：C解析：f (x ＋y )＝a x ＋y ＝a x ·a y ＝f (x )·f (y )，故选C ．5. 答案：D 解析：由于f (x )＝a －x ＝1xa ⎛⎫ ⎪⎝⎭，而f (－2)＞f (－3)，说明f (x )是递增函数，从而11a >，0＜a ＜1，故选D ．6. 答案：C解析：∵4x ＞0，∴16－4x ＜16.∴函数y =[0,4)．7. 答案：3x解析：设f (x )＝a x (a ＞0且a ≠1)，则a 2－a ＝6，解得a ＝3，即f (x )＝3x .8. 答案：14⎛⎫+∞ ⎪⎝⎭，解析：对于任意实数a ，a 2＋2a ＋5＝(a ＋1)2＋4≥4＞1，故y ＝(a 2＋2a ＋5)x 是递增函数，因此有3x ＞1－x ，即14x >. 9. 答案：(－∞，0] 解析：由21402x -⎛⎫-≥ ⎪⎝⎭，得22－x ≥22，∴2－x ≥2，x ≤0.10. 解：当a ＞1时，y ＝a x 在[1,2]上是递增函数，∴y max ＝f (2)＝a 2，y min ＝f (1)＝a .∴f (2)－f (1)＝2a ，即a 2－a ＝2a .∴32a =. 当0＜a ＜1时， y ＝a x 在[1,2]上是递减函数， ∴y max ＝f (1)，y min ＝f (2)，即f (1)－f (2)＝2a ，即a －a 2＝2a . ∴12a =. 综上所述，12a =或32a =.。

(完整版)指数和指数函数练习题及答案

指数和指数函数一、选择题1．（36a 9）4（63a 9）4等于（）（C）a 4（A）a 16（B）a b 8（D）a -b 22.若a>1,b<0,且a +a =22,则a -a 的值等于（）-b b （A）6（B）±2（C）-2（D）22x 3．函数f（x）=(a -1)在R 上是减函数，则a 的取值范围是（）（A）a >1（B）a <2（C）a<2（D）1<a <4.下列函数式中，满足f(x+1)=(A)21f(x)的是( )211x -x(x+1) (B)x+ (C)2(D)224x 25.下列f(x)=(1+a )⋅a -x 是（）（A）奇函数（B）偶函数（C）非奇非偶函数（D）既奇且偶函数1a 1b116．已知a>b,ab ≠0下列不等式（1）a >b ,(2)2>2,(3)<,(4)a 3>b 3,(5)()<()33a b22a b 11中恒成立的有（）（A）1个（B）2个（C）3个（D）4个2x -17．函数y=x 是（）2+1（A）奇函数（B）偶函数（C）既奇又偶函数（D）非奇非偶函数8．函数y=1的值域是（）x 2-1（A）（-∞,1）（B）（-∞,0）⋃（0，+∞）（C）（-1，+∞）（D）（-∞，-1）⋃（0，+∞）+9．下列函数中，值域为R 的是（）（A）y=512-x（B）y=(1x 11-xx)（C）y=()-1（D）y=1-223e x -e -x10.函数y=的反函数是（）2（A）奇函数且在R 上是减函数（B）偶函数且在R 上是减函数++（C）奇函数且在R 上是增函数（D）偶函数且在R 上是增函数11．下列关系中正确的是（）++111111（A）（）3<（）3<（）3（B）（）3<（）3<（）3252225111111（C）（）3<（）3<（）3（D）（）3<（）3<（）352252221222122112212．若函数y=3+2的反函数的图像经过P 点，则P 点坐标是（）（A）（2，5）（B）（1，3）（C）（5，2）（D）（3，1）x -113．函数f(x)=3+5,则f (x)的定义域是（）（A）（０，＋∞）（B）（５，＋∞）（C）（６，＋∞）（D）（－∞，＋∞）x 14.若方程a -x-a=0有两个根，则a 的取值范围是（）（A）（1，+∞）（B）（0，1）（C）（0，+∞）（D）φ15．已知函数f(x)=a +k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数f(x)的表达式是（）x x x x (A)f(x)=2+5 (B)f(x)=5+3 (C)f(x)=3+4 (D)f(x)=4+316.已知三个实数a,b=a ,c=a a x x-1a a ,其中0.9<a<1,则这三个数之间的大小关系是（）（A）a<c<b （B）a<b<c （C）b<a<c （D）c<a<bx 17．已知0<a<1,b<-1,则函数y=a +b 的图像必定不经过（）(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限二、填空题1．若a <ax 322,则a 的取值范围是。

2020-2021学年数学第一册专题强化训练3指数运算与指数函数含解析

2020-2021学年新教材北师大版数学必修第一册专题强化训练3指数运算与指数函数含解析专题强化训练（三)指数运算与指数函数(建议用时:40分钟)一、选择题1．若a〈错误!，则化简错误!的结果是（）A．错误!B．－错误!C．错误!D．－错误!C［∵a〈错误!，∴2a－1<0，于是，原式＝错误!＝错误!。

］2．若函数f(x)＝错误!·a x是指数函数,则f错误!的值为（) A．2B．－2 C．－2错误!D．2错误!D[∵函数f(x)是指数函数，∴错误!a－3＝1，∴a＝8.∴f（x）＝8x，f错误!＝8错误!＝错误!＝2错误!.]3．函数y＝a x＋1（a＞0且a≠1)的图象必经过点(）A．（0，1) B．（1,0）C．(2，1) D．（0,2）D[因为a0＝1,所以,当x＝0时，y＝1＋1＝2。

]4．已知函数f（x）＝3x－错误!错误!，则f（x)（）A．是奇函数，且在R上是增函数B．是偶函数，且在R上是增函数C．是奇函数,且在R上是减函数D ．是偶函数，且在R 上是减函数A [∵函数f (x ）的定义域为R ,f （－x )＝3－x －错误!错误!＝错误!错误!－3x ＝－f (x ），∴函数f （x )是奇函数．∵函数y ＝错误!错误!在R 上是减函数，∴函数y ＝－错误!错误!在R 上是增函数．又∵y ＝3x 在R 上是增函数，∴函数f (x ）＝3x －错误!错误!在R 上是增函数．故选A 。

]5．函数f （x )＝(错误!)错误!的单调递减区间为( )A ．（－∞，＋∞)B ．［－3,3]C ．（－∞，3］D ．［3，＋∞)D ［令u ＝x 2－6x ＋5＝错误!错误!－4，则u 的单调递增区间为错误!，又y ＝错误!错误!是减函数，所以函数f （x ）＝（错误!）错误!的单调递减区间为［3，＋∞）]二、填空题6．方程3x －1＝19的解为________．－1 ［∵3x －1＝错误!＝3－2,∴x －1＝－2，∴x ＝－1.］7．我国的人口约13亿，如果今后能将人口数年平均增长率控制在1%，那么经过x 年后我国人口数为y 亿，则y 与x 的关系式为_____________．y ＝13×（1＋1%）x ，x ∈N * ［经过1年后人口数为13×(1＋1％)＝13（1＋1%）；经过2年后人口数为13×（1＋1%)2;…经过x年后人口数为13×（1＋1%）x。

4.1指数与指数函数-同步练习(含解析)高中数学人教B版(2019)必修第二册

4.1 指数与指数函数同步练习学校:___________姓名：___________班级：___________考号：___________一、单选题1．设0a >且1a ≠，若函数()()43x x xf x a =-是R 上的奇函数，则=a （）．A B C D 2．已知1122,0,()22,0x x x x m n x f x x -+-⎧⋅+⋅≥=⎨-<⎩是定义在R 上的偶函数，则m n -=（）A ．－4B ．0C ．2D ．43．若函数()f x 对任意1x ，2R x ∈都满足()()()12123f x x f x f x +=，则()f x 可以是（）A ．()23f x x=B ．()13x f x +=C ．()129x f x -=D ．()33f x x=4．已知函数()()e 11x x f x x +=-，则()f x 的部分图象大致为（）A ．B ．C ．D ．5．已知函数()y f x =的部分图象如图所示，则()f x 的解析式可能为（）．A ．()e 1e 1x xf x +=-B ．()e 1e 1x xf x -=+C ．()f x =D ．()f x =6．已知()f x 是定义域为R 的奇函数，满足(1)2f =，且对任意120x x ≤<，都有()()12121f x f x x x ->--，则不等式()2142x x f <--的解集为（）A ．(,0)-∞B ．(0,)+∞C ．(,1)-∞D ．(0,1)7．若函数()2442()x x f x x a -=-的图象关于点()1,0对称，则=a （）A ．0B ．1-C ．1D ．28．已知a 、b ∈R ，a b >，则下列不等式中不一定成立的是（）A ．22a b +>+B ．22a b>C ．22a b >D ．1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭二、多选题9．已知225552log (1)log (1)log ,log (1)log (1)log x x x y y y +=-++=-+，则（）A ．7x y +>B ．7x y +<C ．25x y<D ．25x y>10．对于实数,,a b c ，下列命题中正确的是（）A ．若0a b >>，则22ac bc >B ．若0a >，则12a a+≥C ．若a bc c>，则a b >D ．若a b >，1c >，则a bc c >11．已知函数()22x x f x -=-，若1120,0x x x <+>，则（）A ．()()0f x f x -->₁₂B ．()()0f x f x --<₁₂C ．()()0f x f x +>₁₂D ．()()0f x f x +<₁₂12．如图，已知直线l ：y x =与曲线C ：1e xy ⎛⎫= ⎪⎝⎭，设1P 为曲线C 上横坐标为1的点，过1P 作x 轴的平行线交直线l 于2Q ，过2Q 作x 轴的垂线交曲线C 于2P ；再过2P 作x 轴的平行线交直线l 于3Q ，过3Q 作x 轴的垂线交曲线C 于3P ……，设点123,,,,,n P P P P ⋅⋅⋅⋅⋅⋅的纵坐标分别为123,,,,,n a a a a ⋅⋅⋅⋅⋅⋅，则下列说法正确的是（）A ．11ea =B ．1ena n a -+=C ．20232024a a >D ．11n n n na a a a -+->-三、填空题13．已知函数()33x x f x -=+，若()()21f a f a =-，则=a．14．若实数a ，b 满足20a b -≥，则124ab+的最小值为 .15．已知()2xf x x =+，则不等式()233f x -<的解集为.16．设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数.例如：[]2.12=，[]3.14-=-.已知函数123()12x x f x ++=+，则()1f ⎡⎤-=⎣⎦，函数[]()y f x =的值域为.四、解答题17．设R a ∈，函数2()21x x af x +=-.(1)求a 的值，使得()y f x =为奇函数；(2)若(2)f a =，求满足()f x a >的实数x 的取值范围.18．已知函数()f x 是定义在R 上的奇函数，且当0x <时，()426(0)x xf x m m --=-+⋅+<.(1)求函数()f x 的解析式；(2)若[)1,x ∃∈+∞，使得()0f x <成立，求实数m 的取值范围.19．已知函数()423x xg x m =-⋅-(1)若函数()g x 在区间[]0,1上的最小值为1-，求实数m 的值；(2)若函数()f x 在其定义域内存在实数x 满足()()f x f x -=-，则称函数()f x 为“局部奇函数”，若函数()g x 是定义在R 上的“局部奇函数”，求实数m 的取值范围．20．已知函数()2m f x x x=-，且()742f =-.(1)求m 的值；(2)判断()f x 在()0,∞+上的单调性，并用定义证明.(3)求不等式()()2243x xf f +>+的解集.21．对于函数()f x ，若在定义域内存在实数x ，满足()()f x f x -=-，则称()f x 为“Ω函数”．(1)已知函数3(2)x f x =-，试判断()f x 是否为“Ω函数”，并说明理由；(2)若()423x x f x m =-⋅-为定义域在R 上的“Ω函数”，求实数m 的取值范围．参考答案：1．D【分析】根据(1)(1)f f -=-求出a ，然后代入验证即可.【详解】由于函数()()43x x xf x a =-是R 上的奇函数，故(1)(1)f f -=-，则112a a -=-，即2112a =．因为0a >，所以a =当a =()()43xx x f x =-，则()()()()4343xxx x x xf x f x ---+-=--+()(()(34434343431xx x xxx x x x xx x x x ⎡⎤⎢⎥--⎢⎥-=+⎣⋅-⎦=⋅(222434343304342233xx xx x x x x x x x x x x x x x x x -+-⎡⎤⎛⎫--⎢⎥==⋅-⋅-⋅= ⎪⎢⎥⎝⎭⋅⎣⎦⋅符合函数()f x 是R 上的奇函数故选：D ．2．A【分析】利用偶函数和0处函数值列方程求解即可.【详解】因为()f x 是定义在R 上的偶函数，所以(1)(1)f f =-，即232nm +=-，又1010(0)220f +-=-=，所以(0)0f m n =+=，联立2320n m m n ⎧+=-⎪⎨⎪+=⎩，解得2m =-，2n =，经检验，2m =-，2n =满足要求，故4m n -=-.故选：A.3．C【分析】根据已知条件，结合选项中的函数解析式，令121x x ==，可排除A 、B 、D 三个选项，利用指数运算判断C 对于任何1x ，2R x ∈都满足()()()12123f x x f x f x +=.【详解】A ：若()23f x x =，则将121x x ==分别代入()12f x x +，()()123f x f x 中，得()223212f =⨯=，()()31233327f f =⨯⨯=，1227≠，故A 不符合题意；B ：若()13x f x +=，则将121x x ==分别代入()12f x x +，()()123f x f x 中，得()212327f +==，()()22311333243f f =⨯⨯=，27243≠，故B 不符合题意；C ：若()129x f x -=，则()1212129x x f x x +-+=()()12111222129993x x f x f x --=⨯⨯=，故C 符合题意；D ：若()33f x x =，则将121x x ==分别代入()12f x x +，()()123f x f x 中，得()323224f =⨯=，()()31133327f f =⨯⨯=，2427≠，故D 不符合题意．故选：C ．4．C【分析】根据(0)1f =-与()0(1)f x x >>，结合排除法即可求解.【详解】由题意知，函数()f x 的定义域为{}1x x ≠，由(0)1f =-，排除选项A 、D ；当1x >时，e 0,10,10x x x >+>->，所以()0f x >，故排除选项B.故选：C 5．D【分析】根据()00f =排除A ，根据定义域排除B ，根据奇偶性排除C ，进而可得答案.【详解】对于A ， ()e 1e 1x xf x +=-在0x =处无意义，故A 错误；对于B ：()e 1e 1x x f x -=+的定义域为R ，故B 错误；对于C ：()f x =的定义域为{}|1x x ≠±，且()()2f x f x -==，则()f x 为偶函数，故C 错误；对于D ，()f x =满足图中要求，故D 正确.故选：D.6．C【分析】首先由()()12121f x f x x x ->--得出1122()()f x x f x x +<+，设()()g x f x x =+，得出()g x 在[0,)+∞上单调递增，根据()g x 的奇偶性得出()g x 为R 上的增函数，由不等式()2142x x f <--得)()21(1x g g -<，求解即可．【详解】由对任意120x x ≤<，都有()()12121f x f x x x ->--，可得1122()()f x x f x x +<+，令()()g x f x x =+，则函数()()g x f x x =+在[0,)+∞上单调递增，又x ∈R ，()()g x g x -=-，所以()g x 为R 上的奇函数，所以()g x 在R 上是增函数．不等式()2142x x f <--，且(1)2f =，得3()(2121(1)1)x x f f <=-++-，所以)()21(1x g g -<，所以211x -<，即1x <，故选：C ．7．C【分析】特殊值法：由图象关于点()1,0对称可得()()02f f =-代入计算求解，然后检验即可.【详解】解：()f x 的图象关于点()1,0对称，()()020f f ∴+=，即2231204(2)a a -+=-，解得()2441,2(1)x x a f x x -=∴=-，经检验知()f x 的图象关于点()1,0对称，故选：C.8．C【分析】根据不等式的性质即可求解ABC ，根据指数函数的单调性即可求解D.【详解】对于A ，由于a b >，所以22a b +>+，A 正确，对于B ，由a b >，则22a b >，故B 正确，对于C ，1,3a b ==-，满足a b >，但22a b <，故C 不一定成立，对于D ，由于12x y ⎛⎫= ⎪⎝⎭为单调递减函数，所以a b >，则1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，D 正确，故选：C 9．BC【分析】本题通过设元，将对数转化为指数，进而化成同底的对数，然后又将对数相等转化为指数相等，再利用指数函数的单调性，得到方程有两个相等的根，再根据零点存在定理，得出方程根的取值范围，进而得到,x y 的取值范围【详解】由已知，得1,1x y >>．令5log m x =，则5m x =，所以()()22log 51log 51m mm +=-+，所以()2log 51m+=()()222log 51log 2log 512m m m m ⎡⎤-+=-⎣⎦，所以51102m m m +=-．等式两边同时除以10m ，得21015m m m ---+=-，即251010m m m ---++-=．同理，令2log n y =，有25n n --++1010n --=．所以,m n 是方程251010x x x ---++-=的两个根．设()25101x x xf x ---=++-，则易知()f x 在区间(),-∞+∞上单调递减，所以m n =．又因为()()020,10.20f f =>=-<，所以(),0,1m n ∈．故52log log x y =，且15,12x y <<<<，所以7x y +<．又11122555155222m m m n n x y ---⨯⎛⎫===< ⎪⨯⎝⎭，所以25x y <．故选：BC ．【点睛】关键点点睛：本题考查了指数与对数的运算、函数的单调性，考查了转化与化归的思想，其关键在于指数与对数的相互转化，先将对数转化为指数，再换成同底对数，又利用对数相等转化为指数相等，从而可以利用指数函数的单调性求根，进而得到范围.10．BD【分析】根据不等式的性质即可求解AC ，根据基本不等式即可判断B ，由指数函数的单调性即可求解D.【详解】对于A 选项，若0a b >>，当0c =时，22ac bc =，故A 错误；对于B 选项，由0a >，利用基本不等式可得12a a+≥，当且仅当1a =等号成立，故B 正确；对于C 选项，若0a bc c c><,，则a b <，故C 错误；对于D 选项，因为a b >，1c >，由指数函数的单调性可知a b c c >，故D 正确；故选：BD 11．AC【分析】根据奇偶函数的定义和函数的单调性可知()f x 是奇函数且为增函数，结合()()1212,x x f x f x >->-即可判断选项.【详解】因为()()22x xf x f x --=-=-且定义域为R ，所以()f x 是奇函数.因为函数2x y =和2x y -=-都是增函数，所以()f x 是增函数.因为1120,0x x x <+>，所以()()1212,x x f x f x >->-，即()()120f x f x -->.故A 正确，B 错误；因为()()22f x f x =--，所以()()120f x f x +>，故C 正确，D 错误.故选：AC 12．ABD【分析】如图，将11P x =代入1()ex y =可得11e a =，即可判断A ；由1,nn nnP Q P Q y y x x +==推导可得11()en n a a +=，即可判断B ；由选项B 的分析，结合图形可得221n n a a ->、11n n n na a a a -+->-即可判断CD.【详解】如图，A ：11P x =，点1P 在函数1(ex y =图象上，所以11e P y =，即11e a =，故A 正确；B ：又21Q P y y =，所以21eQ y =，因为点2Q 在直线y x =上，所以21eQ x =，而22P Q x x =，所以21e P x =，又点2P 在函数1()ex y =图象上，所以21e 1()e P y =，即121()e a a =；所以321e 1()e Q P y y ==，得331e 1()e Q Q x y ==，所以331e 1()e P Q x x ==，得1e31()e 1()eP y =，即231(e a a =，以此类推，341(e aa =，，11(en n a a +=，故B 正确；C ：由选项B 的分析知，11()en n aa +=，且2143,a a a a >>，以此类推，，221n n a a ->，所以20242023a a >，故C 错误；D ：由图可知，2132431n n a a a a a a a a -->->->>- ，所以11n n n n a a a a -+->-，故D 正确.故选：ABD 13．1-或13【分析】由奇偶性定义可判断()f x 是偶函数，且结合()f x 在[)0,∞+上单调递增，即可求解.【详解】由题可知x ∈R ，()()33x x f x f x --=+=，所以()f x 是偶函数．由于函数y =[)0,∞+上单调递增，而0,=31x x t >> 且=3x t 单调递增，1y t t =+在[)1,t ∈+∞上单调递增，故33x x y -=+在[)0,∞+上单调递增，进而可得()f x 在[)0,∞+上单调递增，又()()21f a f a =-，所以21a a =-或21a a =-，解得13a =或1-．故答案为：1-或1314．2【分析】由已知20a >，104b>，20a b -≥，然后利用基本不等式求解即可.【详解】因为20a >，104b>，20a b -≥，所以21122242a a b b +=+≥=≥=，当且仅当2122ab =，即0a b ==时等号成立，所以124ab+的最小值为2.故答案为：2.15．(1,2)【分析】利用函数的单调性脱去法则，再解不等式即得.【详解】函数2,x y y x ==都是R 上的增函数，则函数()2x f x x =+是R 上的增函数，不等式()()23323(1)231f x f x f x -⇔-⇔-<，则1231x -<-<，解得12x <<，所以不等式()233f x -<的解集为(1,2).故答案为：(1,2)16． 1 {}0,1,2【分析】利用分离参数法可得115()1212x f x +⎛⎫=+ ⎪+⎝⎭，根据题意直接代入求解即可得()1f ⎡⎤-⎣⎦；根据指数函数性质可得()f x 的值域，进而可得[]()y f x =的值域.【详解】因为112315()112212x x x f x +++⎛⎫==+ ⎪++⎝⎭，所以()7114f ⎡⎤⎡⎤-==⎣⎦⎢⎥⎣⎦；又因为120x +>，则1121x ++>，可得110112x +<<+，所以()1,32f x ⎛⎫∈ ⎪⎝⎭，若()1,12f x ⎛⎫∈ ⎪⎝⎭，()0f x ⎡⎤=⎣⎦；若()[)1,2f x ∈，()1f x ⎡⎤=⎣⎦；若()[)2,3f x ∈，()2f x ⎡⎤=⎣⎦；综上所述：函数[]()y f x =的值域为{}0,1,2.故答案为：1；{}0,1,2.17．(1)1a =(2)(0,2)【分析】（1）由奇函数的性质可得(1)(1)f f -=-，代入解方程即可得出答案；（2）由(2)f a =，可得2a =，则22221x x +>-，由指数函数的单调性解不等式即可得出答案.【详解】（1）由()f x 为奇函数，可知(1)(1)f f -=-，即(12)(2)a a -+=-+，解得1a =，当1a =时，212112(),()()212112x x xx x x f x f x f x --+++=-===----对一切非零实数x 恒成立，故1a =时，()y f x =为奇函数.（2）由(2)f a =，可得43a a +=，解得2a =，所以2224()201242121x x x x x f x a +->⇔>⇔<⇔<<--解得：02x <<，所以满足()f x a >的实数x 的取值范围是(0,2).18．(1)()426,00,0426,0x x x x m x f x x m x --⎧-⋅->⎪==⎨⎪-+⋅+<⎩(2)()1,0-【分析】（1）由函数()f x 是定义在R 上的奇函数，则()00f =，设0x >，则0x -<，代入当0x <时，()426(0)x x f x m m --=-+⋅+<，则得到()f x 的解析式；（2）用换元法将()426x x f x m =-⋅-化为()26,2g t t mt t =--≥，再由[)“1,x ∞∃∈+，使得()0f x <成立”转化为[)“2,t ∞∃∈+，使得()0g t <成立”，通过分离参数，得到6m t t >-，由函数6y t t =-的单调性，从而得到实数m 的取值范围.【详解】（1）设0x >，则0x -<，因为()f x 是奇函数，所以()()()426426x x x x f x f x m m =--=--+⋅+=-⋅-.因为函数()f x 是定义在R 上的奇函数，所以()00f =.综上，()426,00,0426,0x x x x m x f x x m x --⎧-⋅->⎪==⎨⎪-+⋅+<⎩.（2）当0x >时，()426x x f x m =-⋅-.设2x t =，易知当1x ≥时，22x t =≥，令()26,2g t t mt t =--≥.[)“1,x ∞∃∈+，使得()0f x <成立”即为[)“2,t ∞∃∈+，使得()0g t <成立”，所以[)2,t ∞∃∈+，使得6m t t >-，又6y t t =-在[)2,+∞上单调递增，故1m >-，所以实数m 的取值范围是()1,0-.19．(1)1m =-(2){|2}m m ≥-【分析】（1）令2x t =，将问题转化为二次函数在区间上的最值问题，讨论对称轴和区间的位置关系列方程求解；（2）问题即为x ∃∈R 满足423423x x x x m m ---⋅-=-+⋅+，令2x t =，将问题转化为函数值域问题，通过参变分离求函数值域即可.【详解】（1）令2x t =，由01x ≤≤可得，12t ≤≤，原函数可化为()23h t t mt =--，为开口向上，对称轴2m t =，当22m ≥，即4m ≥时，()h t 在[]1,2上单调递减，则2t =时，函数取得最小值121m -=-，即1(m =舍)，当12m ≤，即2m ≤时，()h t 在[]1,2上单调递增，则1t =时，函数取得最小值21m --=-，即1m =-，当122m <<，即24m <<时，()h t 在[]1,2上先减后增，则2m t =时，函数取得最小值2314m --=-，此时m 不存在，故1m =-；（2）由题意得，x ∃∈R 满足423423x x x x m m ---⋅-=-+⋅+，即()22446x x x x m --+=+-，令()20,x t ∞=∈+，则存在()0,t ∞∈+满足2221116()8m t t t t t t ⎛⎫+=+-=+- ⎪⎝⎭，令12p t t =+≥=，当且仅当1t =时等号成立，则[)2,p ∞∃∈+满足28mp p =-，即8m p p=-，因为函数8y p p=-在[)2,+∞上单调递增，当2p =时，min 2y =-，所以2m ≥-，故m 的范围为{|2}m m ≥-．20．(1)1m =(2)()f x 在()0,∞+上的单调递减，证明见解析(3)()()2,0log 3,-∞+∞ 【分析】（1）由()742f =-可求得m 的值；（2）任取()12,0,x x ∈+∞，且12x x <，然后计算变形()()12f x f x -，再判断符号，可得结论；（3）由()f x 的单调性，将问题转化为2243x x +<+，再令2(0)x t t =>，可得243t t <+，求出t 的范围，从而可求得x 的范围.【详解】（1）由()174422m f =-=-，得44m =，则1m =.（2）()f x 在()0,∞+上的单调递减．证明如下：任取()12,0,x x ∈+∞，且12x x <，则()()12121222f x f x x x x x -=--+()()2121122x x x x x x -=+-()211221x x x x ⎛⎫=-+ ⎪⎝⎭，∵()12,0,x x ∈+∞，且12x x <，211220,10x x x x ∴->+>，∴()()120f x f x ->，即()()12f x f x >，()f x \在()0,∞+上单调递减.（3）由（2）可得，()f x 在()0,∞+上单调递减，而220,430x x +>+>，则由()()2243x x f f +>+可得2243x x +<+，令2(0)x t t =>，可得243t t <+.解得：01t <<或3t >.所以0x <或2log 3x >.不等式的解集为()()2,0log 3,-∞+∞ 21．(1)3(2)x f x =-是“Ω函数”，理由见解析(2)[2,)-+∞【分析】（1）根据“Ω函数”的定义，对于函数3(2)x f x =-求解方程()()0f x f x +-=即得；（2）由()423x x f x m =-⋅-为定义域在R 上的“Ω函数”可得4234230x x x x m m ---⋅-+-⋅-=，利用22x x t -=+换元，将其化成280t mt --=在[2,)+∞上有解，利用参变分离法即可求得m 的取值范围.【详解】（1）当3(2)x f x =-时，()()0f x f x +-=，即2260x x -+-=，令20x t =>，则得2610t t -+=，解得30t =±>．从而2260x x -+-=有解，函数3(2)x f x =-是“Ω函数”．（2）()423x x f x m =-⋅-为定义域在R 上的“Ω函数”，由()()0f x f x +-=，可得4234230x x x x m m ---⋅-+-⋅-=，化简得()442260x x x x m --+-⋅+-=（*）．令22x x t -=+，又222-+≥=x x ，当且仅当22-=x x ，即0x =时取等号，所以2t ≥，又2442x x t -+=-，从而方程（*）可化为：280t mt --=在[2,)+∞上有解，即8m t t=-在[2,)+∞上有解，令8()g t t t=-，[)2,t ∈+∞，则()g t 为[2,)+∞上的增函数，所以()(2)2g t g ≥=-，从而2m ≥-，即[2,)m ∈-+∞.。

2023年新高考数学一轮复习3-5 指数与指数函数(真题测试)含详解

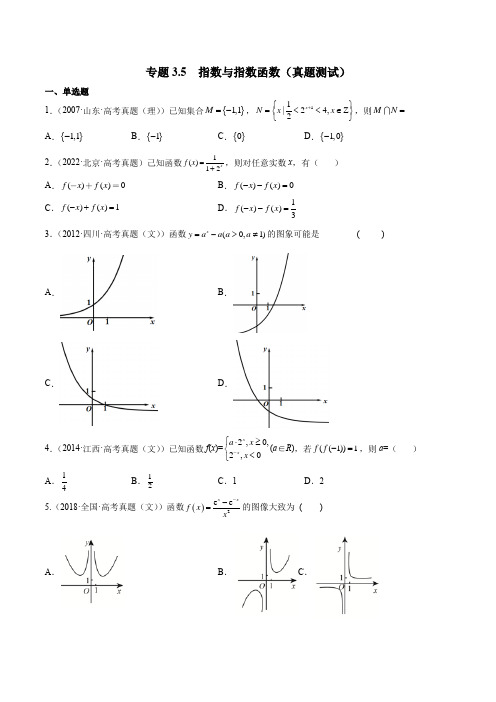
专题3.5 指数与指数函数（真题测试）一、单选题1．（2007·山东·高考真题（理））已知集合{}1,1M =-，11|24,Z 2x N x x +⎧⎫=<<∈⎨⎬⎩⎭，则MN =A ．{}1,1-B ．{}1-C ．{}0D ．{}1,0-2．（2022·北京·高考真题）己知函数1()12xf x =+，则对任意实数x ，有（） A ．()()0f x f x B ．()()0f x f x --= C ．()()1f x f x -+=D ．1()()3f x f x --=3．（2012·四川·高考真题（文））函数(0,1)x y a a a a =->≠的图象可能是 ( )A ．B ．C ．D ．4．（2014·江西·高考真题（文））已知函数f (x )=2,0,2,0x xa x x -⎧⋅≥⎨<⎩(a ∈R )，若((1))1f f -=，则a =（） A ．14B ．12C ．1D ．25.（2018·全国·高考真题（文））函数()2e e x xf x x --=的图像大致为 ( )A ．B ．C ．D ．6．（2013·全国·高考真题（文））若存在正数x 使2x （x -a ）＜1成立，则a 的取值范围是 A ．（-∞，+∞）B ．(-2, +∞)C ．(0, +∞)D ．（-1，+∞）7．（2015·山东·高考真题（文））设0.6 1.50.60.60.6 1.5a b c ===，，，则a b c ，，的大小关系是 A ．a b c ＜＜B ．a cb ＜＜ C ．b ac ＜＜D ．b c a ＜＜8．（2014·陕西·高考真题（文））下了函数中，满足“()()()f x y f x f y +=”的单调递增函数是A ．()3f x x =B ．()3xf x =C ．()23f x x = D ．()12xf x ⎛⎫= ⎪⎝⎭二、多选题9．（2021·江苏·南京市中华中学高三期中）已知a b >，0ab ≠，则（） A ．a b >B ．1133a b -->C ．33a b >D ．11a b< 10．（2022·全国·高三专题练习）已知函数()()()f x x a x b =--的图象如图所示，则()x g x a b =-的图象可能是（）A ．B ．C ．D ．11．（2022·山东潍坊·高三期末）已知函数x x x xe ef xe e，则下列结论中正确的是（）A ．()f x 的定义域为RB ．()f x 是奇函数C ．()f x 在定义域上是减函数D ．()f x 无最小值，无最大值12．（2022·全国·高三专题练习）已知函数2,0(),2,0x xa x f x a R a x -⎧-+<=∈⎨->⎩，下列结论正确的是（） A ．()f x 为奇函数B ．若()f x 在定义域上是增函数，则1a ≤C ．若()f x 的值域为R ，则1a <D ．当1a ≤时，若()(34)0f x f x ++>，则(1,0)(0,)x ∈-+∞ 三、填空题13．（2022·全国·高三专题练习）函数()f x =的定义域为______.14．（2012·山东·高考真题（文））若函数()(0,1)x f x a a a =>≠在［－1，2］上的最大值为4，最小值为m ，且函数()(14g x m =-[0,)+∞上是增函数，则a ＝______.15．（2015·山东·高考真题（理））已知函数()(0,1)x f x a b a a =+>≠ 的定义域和值域都是[]1,0- ，则a b +=_____________.16．（2022·浙江·乐清市知临中学模拟预测）设函数()2,111,12x a x f x x x --⎧≤⎪=⎨-+>⎪⎩，若()1f 是函数()f x 的最大值，则实数a 的取值范围为_______．四、解答题17．（2021·新疆·伊宁市第一中学高三期中（理））若(1)()42(1)2x a x f x a x x ⎧>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数，求实数a 的取值范围.18．（2021·福建龙岩·高三期中）已知()2221x m f x -=++是奇函数. (1)求m 的值；(2)求()f x 的值域.19．（2021·福建·永安市第三中学高中校高三期中）已知指数函数()(0xf x a a =>且1)a ≠的图象过点129⎛⎫ ⎪⎝⎭，．(1)求函数()xf x a =的解析式；(2)已知()()1f x f >，求x 的取值范围；20．（2021·安徽省六安中学高三阶段练习（文））已知函数()()33xf x k a b ⋅=++-(0a >，且1a ≠)是指数函数.(1)求k ，b 的值；(2)求解不等式()()2743f x f x ->-.21．（2021·重庆市涪陵高级中学校高三阶段练习）设()e e x x f x -=-()R x ∈．(1)判断并证明函数()y f x =的奇偶性；(2)解不等式()()22f x f x -≤．22．（2022·北京·高三专题练习）已知函数()33x xf x -=-．(1)利用函数单调性的定义证明()f x 是单调递增函数；(2)若对任意[]1,1x ∈-，()()24f x mf x ⎡⎤+≥-⎣⎦恒成立，求实数m 的取值范围．专题3.5 指数与指数函数（真题测试）一、单选题1．（2007·山东·高考真题（理））已知集合{}1,1M =-，11|24,Z 2x N x x +⎧⎫=<<∈⎨⎬⎩⎭，则MN =A ．{}1,1-B ．{}1-C ．{}0D ．{}1,0-【答案】B 【解析】【分析】利用指数函数的单调性化简集合N ，然后利用交集的定义运算即得. 【详解】函数2x y =是增函数，则不等式11242x +<<，即112222x -+<< ∴112,x -<+<即21x -<<，所以{}{}|21,Z 1,0N x x x =-<<∈=-，又{}1,1M =-， ∴{}1.M N ⋂=- 故选：B.2．（2022·北京·高考真题）己知函数1()12xf x =+，则对任意实数x ，有（） A ．()()0f x f x B ．()()0f x f x --= C ．()()1f x f x -+= D ．1()()3f x f x --=【答案】C 【解析】【分析】直接代入计算，注意通分不要计算错误．【详解】()()1121112121212x x x x xf x f x --+=+=+=++++，故A 错误，C 正确；()()11212121121212122121x x x x x x x xf x f x ----=-=-==-++++++，不是常数，故BD 错误；故选：C ．3．（2012·四川·高考真题（文））函数(0,1)x y a a a a =->≠的图象可能是 ( )A ． B ．C ．D ．【答案】C 【解析】【分析】对a 进行分类讨论，结合指数函数的单调性以及函数图像平移变换，即可得出答案. 【详解】①当1a >时，函数(0,1)x y a a a a =->≠可以看做函数x y a =的图象向下平移a 个单位，由于1a >，则A 错误；又1x =时，0y a a =-=，则函数(0,1)x y a a a a =->≠过点(1,0)，故B 错误；②当01a <<时，函数(0,1)x y a a a a =->≠可以看做函数x y a =的图象向下平移a 个单位，由于01a <<，则D 错误；又1x =时，0y a a =-=，则函数(0,1)x y a a a a =->≠过点(1,0)，故C 正确；故选：C4．（2014·江西·高考真题（文））已知函数f (x )=2,0,2,0x xa x x -⎧⋅≥⎨<⎩(a ∈R )，若((1))1f f -=，则a =（） A ．14B ．12C ．1D ．2【答案】A 【解析】【分析】先求出(1)f -的值，再求((1))f f -的值，然后列方程可求得答案【详解】解：由题意得(1)(1)22f ---==，所以2((1))(2)241f f f a a -==⋅==，解得a =14.故选：A5.（2018·全国·高考真题（文））函数()2e e x xf x x--=的图像大致为 ( ) A ． B ．C ．D ．【答案】B 【解析】【详解】分析：通过研究函数奇偶性以及单调性，确定函数图像.详解：20,()()()x xe e xf x f x f x x --≠-==-∴为奇函数，舍去A,1(1)0f e e -=->∴舍去D;243()()2(2)(2)()2,()0x x x x x xe e x e e x x e x ef x x f x x x ---+---++=='∴>'>，所以舍去C ；因此选B.点睛：有关函数图象识别问题的常见题型及解题思路（1）由函数的定义域，判断图象左右的位置，由函数的值域，判断图象的上下位置；②由函数的单调性，判断图象的变化趋势；③由函数的奇偶性，判断图象的对称性；④由函数的周期性，判断图象的循环往复．6．（2013·全国·高考真题（文））若存在正数x 使2x （x -a ）＜1成立，则a 的取值范围是 A ．（-∞，+∞） B ．(-2, +∞)C ．(0, +∞)D ．（-1，+∞）【答案】D 【解析】由题意知，存在正数x ，使12xa x >-，所以，而函数12xy x =-在(0,)+∞上是增函数，所以(0)1y y >=-，所以1a >-，故选D.7．（2015·山东·高考真题（文））设0.6 1.50.60.60.6 1.5a b c ===，，，则a b c ，，的大小关系是 A ．a b c ＜＜ B ． a c b ＜＜ C ．b a c ＜＜ D ．b c a ＜＜【答案】C 【解析】【详解】由0.6x y =在区间(0,)+∞是单调减函数可知， 1.50.600.60.61<<<，又0.61.51>，故选C . 8．（2014·陕西·高考真题（文））下了函数中，满足“()()()f x y f x f y +=”的单调递增函数是A ．()3f x x =B ．()3xf x =C ．()23f x x = D ．()12xf x ⎛⎫= ⎪⎝⎭【答案】B 【解析】【详解】试题分析：A 选项：由()()3f x y x y +=+，()()333()f x f y x y xy =⋅=，得()()()f x y f x f y +≠，所以A 错误；B 选项：由()3x y f x y ++=，()()333x y x y f x f y +=⋅=，得()()()f x y f x f y +=；又函数()3xf x =是定义在R 上增函数，所以B 正确；C 选项：由()()23f x y x y +=+，()()f x f y 2233x y =⋅23()xy =，得()()()f x y f x f y +≠，所以C 错误；D 选项：函数()12xf x ⎛⎫= ⎪⎝⎭是定义在R 上减函数，所以D 错误；故选B.二、多选题9．（2021·江苏·南京市中华中学高三期中）已知a b >，0ab ≠，则（） A ．a b >B ．1133a b -->C ．33a b >D ．11a b< 【答案】BC 【解析】对A ，D 可取反例；对B ，C 可利用函数的单调性判断；【详解】对A ，取1,2a b ==-，则||||a b >不成立，故A 错误；对B ，11a b a b >⇒->-，∴1133a b -->，故B 成立；对C ，33a b a b >⇒>，故C 成立；对D ，取1,1a b ==-，11a b<不成立；故选：BC10．（2022·全国·高三专题练习）已知函数()()()f x x a x b =--的图象如图所示，则()x g x a b =-的图象可能是（）A ．B ．C ．D ．【答案】AC 【解析】【分析】依题意可得a 、b 两个数一个大于1，一个大于0且小于1，再分类讨论，结合指数函数的性质判断即可；【详解】解：令()()()0f x x a x b =--=，解得1x a =、2x b =，根据二次函数图形可知，a 、b 两个数一个大于1，一个大于0且小于1，①当1a >，01b <<时，则()x g x a b =-在定义域上单调递增，且()001g a b b =-=-，即()001g <<，所以满足条件的函数图形为C ；②当1b >，01a <<时，则()x g x a b =-在定义域上单调递减，且()0010g a b b =-=-<，所以满足条件的函数图形为A ；故选：AC11．（2022·山东潍坊·高三期末）已知函数x x x xe ef x e e，则下列结论中正确的是（）A ．()f x 的定义域为RB ．()f x 是奇函数C ．()f x 在定义域上是减函数D ．()f x 无最小值，无最大值【答案】BD 【解析】【分析】求解0x x e e --≠，可判断A ；利用函数奇偶性的定义可判断B ；比较(1),(1)f f -可判断C ；分离常数得到2211x f x e ，分析单调性及函数值域可判断D【详解】选项A ，0x x e e --≠，解得0x ≠，故()f x 的定义域为{|0}x x ≠，选项A 错误；选项B ，函数定义域关于原点对称，且()()x x x x e ef x f x e e --+-==--，故()f x 是奇函数，选项B 正确；选项C ，()121212121110,(1)011e e e e e ef f e e e e e e ----++++-==<==>----，故(1)(1)f f -<，即()f x 在定义域上不是减函数，选项C 不正确；选项D ，()22212111x x x x x x x e e e f x e e e e --++===+---，令20x t e =>，211y t =+-，由于2x t e =在R 上单调递增，211y t =+-在(0,1),(1,)+∞分别单调递减，故函数()f x 在(,0),(0,)-∞+∞分别单调递减，且x →-∞时，()1f x →-，0x -→时，()f x →-∞，0x +→时，()f x →+∞，x →+∞时，()1f x →，故函数()f x 的值域为(,1)(1,-∞-⋃+∞），无最小值，无最大值，选项D 正确故选：BD12．（2022·全国·高三专题练习）已知函数2,0(),2,0x xa x f x a R a x -⎧-+<=∈⎨->⎩，下列结论正确的是（）A ．()f x 为奇函数B ．若()f x 在定义域上是增函数，则1a ≤C ．若()f x 的值域为R ，则1a <D ．当1a ≤时，若()(34)0f x f x ++>，则(1,0)(0,)x ∈-+∞ 【答案】ABD 【解析】【分析】分段函数奇偶性判断需要分段判断，分段函数的单调性需要列两段分别单调，衔接处单调即可. 【详解】当0x <时，0x ->，()2,()2(2)()x x x f x a f x a a f x ---=-+-=-=--+=-；当0x >时，0x -<，()2,()2()x x f x a f x a f x =--=-+=-．则函数()f x 为奇函数，故A 正确；若()f x 在定义域上是增函数，则0022a a --+≤-，即1a ≤，故B 正确；当0x <时，()2xf x a -=-+在区间(,0)-∞上单调递增，此时值域为(,1)a -∞-；当0x >时，()2x f x a =-在区间()0,∞+上单调递增，此时值域为(1,)a -+∞．要使得()f x 的值域为R ，则11a a ->-，即1a >，故C 错误；当1a ≤时，由于0022a a --+≤-，则函数()f x 在定义域上是增函数，由()(34)0f x f x ++>，得()(34)f x f x >--，则034034x x x x ≠⎧⎪--≠⎨⎪>--⎩解得(1,0)(0,)x ∈-+∞，故D 正确．故选：ABD. 三、填空题13．（2022·全国·高三专题练习）函数()f x =的定义域为______.【答案】[)()0,11,+∞【解析】【分析】结合分式型，二次根号型函数的定义即可求解. 【详解】由题知，021********x xx x x x x ⎧⎧≥-≥≥⎧⎪⎪⇒⇒⎨⎨⎨≠-≠-≠≠⎪⎪⎩⎩⎩且，所以()f x 的定义域为[)()0,11,+∞，故答案为：[)()0,11,+∞.14．（2012·山东·高考真题（文））若函数()(0,1)x f x a a a =>≠在［－1，2］上的最大值为4，最小值为m ，且函数()(14g x m =-[0,)+∞上是增函数，则a ＝______.【答案】14【解析】【详解】当1a >时，有214,a a m -==，此时12,2a m ==，此时()g x = 不合题意.若01a <<，则124,a a m -==，故11,416a m ==，检验知符合题意15．（2015·山东·高考真题（理））已知函数()(0,1)x f x a b a a =+>≠ 的定义域和值域都是[]1,0- ，则a b +=_____________. 【答案】32-【解析】【详解】若1a > ，则()f x 在[]1,0-上为增函数,所以11{10a b b -+=-+= ，此方程组无解；若01a << ，则()f x 在[]1,0-上为减函数,所以10{11a b b -+=+=- ，解得1{22a b ==- ，所以32a b +=-. 16．（2022·浙江·乐清市知临中学模拟预测）设函数()2,111,12x a x f x x x --⎧≤⎪=⎨-+>⎪⎩，若()1f 是函数()f x 的最大值，则实数a 的取值范围为_______．【答案】[1,2]【解析】【分析】由1x >，求得()f x 的范围，再求得||()2x a f x -=的单调性，讨论1a <，1a 时函数()f x 在1x 的最大值，即可得到所求范围．【详解】解：因为()2,111,12x a x f x x x --⎧≤⎪=⎨-+>⎪⎩，当1x >时()112f x x =-+函数单调递减且()12f x <，当1x ≤时()122x ax af x ---⎛⎫== ⎪⎝⎭，可得在x a >时函数单调递减，在x a <单调递增，若1a <，1x ，则()f x 在x a =处取得最大值，不符题意；若1a ，1x ，则()f x 在1x =处取得最大值，且11122a -⎛⎫≥⎪⎝⎭，解得12a ，综上可得a 的范围是[]1,2．故答案为：[]1,2 四、解答题17．（2021·新疆·伊宁市第一中学高三期中（理））若(1)()42(1)2x a x f x a x x ⎧>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数，求实数a 的取值范围. 【答案】[4,8). 【解析】【分析】根据分段函数的单调性的判定方法，列出不等式组，即可求解. 【详解】由题意，函数(1)()42(1)2xa x f x a x x ⎧>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数，则满足114024122a a a a⎧⎪>⎪⎪->⎨⎪⎪⎛⎫-⨯+≤ ⎪⎪⎝⎭⎩，解得48a ≤<，所以实数a 的取值范围[4,8).18．（2021·福建龙岩·高三期中）已知()2221x m f x -=++是奇函数. (1)求m 的值； (2)求()f x 的值域. 【答案】(1)-2 (2)11-（，）【解析】【分析】（1）因为()f x 为奇函数，且在0x =处有意义，所以()00f =，便可求出m 的值；（2）在（1）的前提下，对于复合函数分解成若干基本初等函数，然后逐个求其值域，从而求出()f x 的值域. (1)因为()f x 为奇函数，所以()00f =，即2022m +=，解得2m =-. 经检验：当2m =-时，()f x 为奇函数； (2)由（1）知()2121xf x -=-+，因为211x -+∈+∞（，），所以20221x -∈+（，），于是()11f x ∈-（，），因此()f x 的值域为11-（，）. 19．（2021·福建·永安市第三中学高中校高三期中）已知指数函数()(0xf x a a =>且1)a ≠的图象过点129⎛⎫ ⎪⎝⎭，．(1)求函数()xf x a =的解析式；(2)已知()()1f x f >，求x 的取值范围；【答案】(1)()13xf x ⎛⎫= ⎪⎝⎭(2)()1,1- 【解析】【分析】（1）将点129⎛⎫ ⎪⎝⎭，代入()(0xf x a a =>且1)a ≠，解之即可得出答案；（2）根据指数函数的单调性即可得出答案. (1)解：将点129⎛⎫ ⎪⎝⎭，代入()(0xf x a a =>且1)a ≠，得：219a =，解得13a =，所以()13xf x ⎛⎫= ⎪⎝⎭；(2)因为1013<<，所以函数()13xf x ⎛⎫= ⎪⎝⎭为减函数，由()()1f x f >，得1x <，解得11x -<<，所以()()1f x f >的解为()1,1-.20．（2021·安徽省六安中学高三阶段练习（文））已知函数()()33xf x k a b ⋅=++-(0a >，且1a ≠)是指数函数.(1)求k ，b 的值；(2)求解不等式()()2743f x f x ->-. 【答案】(1)2k =-，3b = (2)答案见解析【解析】【分析】（1）根据指数函数的定义列出方程，即可得解；（2）分1a >和01a <<两种情况讨论，结合指数函数的单调性即可得解. (1)解：因为()()33x f x k a b =++-(0a >，且1a ≠)是指数函数，所以31k +=，30b -=，所以2k =-，3b =； (2)解：由（1）得()xf x a =(0a >，且1a ≠)，①当1a >时，()xf x a =在R 上单调递增，则由()()2743f x f x ->-，可得2743x x ->-，解得2x <-；②当01a <<时，()xf x a =在R 上单调递减，则由()()2743f x f x ->-，可得2743x x -<-，解得2x >-，综上可知，当1a >时，原不等式的解集为(),2-∞-；当01a <<时，原不等式的解集为()2,-+∞.21．（2021·重庆市涪陵高级中学校高三阶段练习）设()e e x xf x -=-()R x ∈．(1)判断并证明函数()y f x =的奇偶性；(2)解不等式()()22f x f x -≤．【答案】(1)奇函数，证明见解析； (2)[]1,2- 【解析】【分析】（1）利用函数奇偶性的定义判断证明即可；（2）根据指数函数单调性以及函数单调性的性质判断()y f x =的单调性，再由单调性去掉f 转化为解一元二次不等式即可求解. (1)()e e x x f x -=-是R 上的奇函数，证明如下：()e e x x f x -=-的定义域为R 关于原点对称，()()()e e e e x x x x f x f x ---=-=--=-，所以()e e x xf x -=-是R 上的奇函数.(2)因为e x y =为R 上的增函数，1ee xxy -==为R 上的减函数，所以()e e x xf x -=-为R 上的增函数，若()()22f x f x -≤，则22x x -≤即220x x --≤，可得()()210x x -+≤，解得：12x -≤≤，所以不等式()()22f x f x -≤的解集为：[]1,2-.22．（2022·北京·高三专题练习）已知函数()33x xf x -=-．(1)利用函数单调性的定义证明()f x 是单调递增函数；(2)若对任意[]1,1x ∈-，()()24f x mf x ⎡⎤+≥-⎣⎦恒成立，求实数m 的取值范围．【答案】(1)证明见解析(2)[]4,4- 【解析】【分析】（1）利用单调性的定义，取值、作差、整理、定号、得结论，即可得证.（2）令33x x t -=-，根据x 的范围，可得t 的范围，原式等价为()2h t t mt =+，88,33t ⎡⎤∈-⎢⎥⎣⎦，只需()min 4h t ≥-即可，分别讨论823m -≤-、88323m -<-<和823m -≥三种情况，根据二次函数的性质，计算求值，分析即可得答案. (1)由已知可得()f x 的定义域为R ，任取12,x x ∈R ，且12x x <，则()()12f x f x -()()1122121121333331313x x x x x x x x x ---+⎛⎫=---=-+ ⎪⎝⎭，因为130x >，121103x x ++>，21130x x --<，所以()()120f x f x -<，即()()12f x f x <，所以()f x 在R 上是单调递增函数． (2)()()()()223333x x x xf x mf x m --⎡⎤+=-+-⎣⎦，令33x x t -=-，则当[]1,1x ∈-时，88,33t ⎡⎤∈-⎢⎥⎣⎦，所以()()22f x mf x t mt ⎡⎤+=+⎣⎦．令()2h t t mt =+，88,33t ⎡⎤∈-⎢⎥⎣⎦，则只需()min 4h t ≥-．当823m -≤-，即163m ≥时，()h t 在88,33⎡⎤-⎢⎥⎣⎦上单调递增，所以()min 86484393h t h m ⎛⎫=-=-≥- ⎪⎝⎭，解得256m ≤，与163m ≥矛盾，舍去；当88323m -<-<，即161633m -<<时，()h t 在8,32m ⎡⎤--⎢⎥⎣⎦上单调递减，在8,23m ⎡⎤-⎢⎥⎣⎦上单调递增，所以()2min424m m h t h ⎛⎫=-=-≥- ⎪⎝⎭，解得44m -≤≤；当823m -≥即163m ≤-时，()h t 在88,33⎡⎤-⎢⎥⎣⎦上单调递减，所以()min 86484393h t h m ⎛⎫==+≥- ⎪⎝⎭，解得256m ≥-，与163m ≤-矛盾，舍去．综上，实数m 的取值范围是[]4,4-．。

(完整版)指数和指数函数练习题及答案(可编辑修改word版)

2 62 指数和指数函数一、选择题 1．（3 6 a 9）4（ 6 3 a 9）4 等于（）（A ）a 16（B ）a 8（C ）a 4（D ）a 22. 若 a>1,b<0,且 a b+a -b=2,则 a b -a -b 的值等于（）（A ）（B ） ± 2（C ）-2（D ）23. 函数 f （x ）=(a 2-1)x在 R 上是减函数，则 a 的取值范围是（）（A ） a > 1 （B ） a < 2 （C ）a< （D ）1< a < 14. 下列函数式中，满足 f(x+1)= f(x)的是() 21 1 (A)(x+1)(B)x+(C)2x(D)2-x245.下列 f(x)=(1+a x )2⋅ a-x 是（）（A ）奇函数（B ）偶函数（C ）非奇非偶函数（D ）既奇且偶函数1 1 11 1 16．已知 a>b,ab ≠ 0 下列不等式（1）a 2>b 2,(2)2a>2b,(3) < ,(4)a 3 >b 3 ,(5)( )a <( )ba b 3 3中恒成立的有（）（A ）1 个（B ）2 个（C ）3 个（D ）4 个2 x - 17. 函数 y=是（）2 x+ 1 （A ）奇函数（B ）偶函数（C ）既奇又偶函数（D ）非奇非偶函数18. 函数 y=的值域是（）2 x- 1（A ）（- ∞,1）（B ）（- ∞, 0） ⋃ （0，+ ∞ ）（C ）（-1，+ ∞ ）（D ）（- ∞ ，-1） ⋃ （0，+ ∞ ）9. 下列函数中，值域为 R +的是（）1（A ）y=5 2-xe x - e - x1（B ）y=( )1-x（C ）y= 3（D ）y= 10. 函数 y= 的反函数是（）2（A ）奇函数且在 R +上是减函数（B ）偶函数且在 R +上是减函数（C ）奇函数且在 R +上是增函数（D ）偶函数且在 R +上是增函数11．下列关系中正确的是（）1 2 1 2 1 11 1 12 1 2（A ）（） 3 <（） 3 <（） 3（B ）（） 3 <（） 3 <（） 32 5 21 2 1 1 1 22 2 51 2 1 2 1 1（C ）（） 3 <（） 3 <（）3 （D ）（） 3 <（） 3 <（） 3 5 2 25 2 22 ( 1 ) x - 1 21 -2 xx 12. 若函数 y=3+2x-1的反函数的图像经过 P 点，则 P 点坐标是（）（A ）（2，5）（B ）（1，3）（C ）（5，2）（D ）（3，1）13. 函数 f(x)=3x +5,则 f -1(x)的定义域是（）（A ）（０，＋ ∞ ）（B ）（５，＋ ∞ ）（C ）（６，＋ ∞ ）（D ）（－ ∞ ，＋ ∞ ）14. 若方程 a x-x-a=0 有两个根，则 a 的取值范围是（）（A ）（1，+ ∞ ）（B ）（0，1）（C ）（0，+ ∞ ）（D ）15. 已知函数 f(x)=a x+k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数 f(x)的表达式是（）(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x+4(D)f(x)=4x+316. 已知三个实数 a,b=a a,c=a aa,其中 0.9<a<1,则这三个数之间的大小关系是（）（A ）a<c<b （B ）a<b<c （C ）b<a<c （D ）c<a<b17．已知 0<a<1,b<-1,则函数 y=a x+b 的图像必定不经过（） (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限二、填空题31.若 a2 <a 2 ,则 a 的取值范围是。

指数与指数函数练习题含答案

指数与指数函数练习题（1）1. 化简的结果是（）A.−2B.−2C.−2D.−22. 下列各函数中，值域为(0, +∞)的是（）A.y=2−x2 B.y=√1−2x C.y=x2+x+1 D.y=31x+13. 函数y=1sin x−x的一段大致图象是（）A. B.C. D.4. 函数f(x)=(12)x的值域是（）A.(0, +∞)B.(−∞, +∞)C.(0, 1)D.(1, +∞)5. 若函数f(x)＝a|2x−4|(a>0, a≠1)，满足f(1)=19，则f(x)的单调递减区间是（）A.(−∞, 2] B.[2, +∞) C.[−2, +∞) D.(−∞, −2]6. 如图是二次函数f(x)=x 2−bx +a 的部分图象，则函数g(x)=ln x +f′(x)的零点所在的区间是( )A.(14，12) B.(1, 2)C.(12，1)D.(2, 3)7. 奇函数f(x)在(−∞, 0)上单调递减，且f(2)=0，则不等式f(x)>0的解集是( ) A.(−∞, −2)∪(0, 2) B.(−∞, 0)∪(2, +∞) C.(−2, 0)∪(0, 2)D.(−2, 0)∪(2, +∞)8. 若2x ＝7，2y ＝6，则4x−y 等于（）A. B. C. D.9. 已知a >0，则2√a⋅√a 23=( )A.a 65B.a 56C.a −56D.a 5310. 下列运算结果中，一定正确的是（） A.a 3⋅a 4＝a 7 B.(−a 2)3＝a 6C.√a 88=aD.√(−π)55=−π11. 若函数(a >0，且a ≠1)是指数函数，则下列说法正确的是（）A.a ＝8B.f(0)＝−3C.D.a ＝4E.f(2)＝1612. 若a ＝log 20.5，b ＝20.5，c ＝0.52，则a ，b ，c 三个数的大小关系是（）A.a 0且a ≠1)的图象必经过点________；17. 已知函数f(x)=a⋅2x −12x +1的图象经过点(1,13)．（1）求a 的值；（2）求函数f(x)的定义域和值域．18. 求值：（1）；（2）已知2a ＝5b ＝m ，且，求实数m 的值．19. （1）计算：0.064−13−(−57)0+[(−2)3]−43+16−0.75； 19.（2）化简：•(a 23−1−12−12⋅b13√a⋅b 5620. 请根据给出的函数图象指出函数的极值点和最大（小）值点．21. 已知(a>0，且a≠1)．（1）讨论函数f(x)和g(x)的单调性．（2）如果f(x)<g(x)，那么x的取值范围是多少？22. 已知函数y＝a（）|x|+b的图象过原点，且无限接近直线y＝2但又不与该直线相交．（1）求该函数的解析式，并画出图象；（2）判断该函数的奇偶性和单调性．参考答案与试题解析指数与指数函数练习题（1）一、选择题（本题共计 9 小题，每题 5 分，共计45分） 1.【答案】 B【考点】有理数指数幂的运算性质及化简求值【解析】此题暂无解析【解答】此题暂无解答 2.【答案】 A【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】解：对于A ，y =2−x 2=(√22)x的值域为(0, +∞)；对于B ，因为1−2x ≥0，所以2x ≤1，x ≤0，y =√1−2x 的定义域是(−∞,0]，所以0<2x ≤1，所以0≤1−2x <1，所以y =√1−2x 的值域是[0,1)．对于C ，y =x 2+x +1=(x +12)2+34的值域是[34,+∞)；对于D ，因为1x+1∈(−∞,0)∪(0,+∞)，所以y =31x+1 的值域是(0,1)∪(1,+∞)．故选A ． 3.【答案】 A【考点】函数的图象与图象的变换【解析】根据函数的奇偶性和特殊值即可判断．【解答】f(−x)=−1sin x−x=−f(x)，∴y＝f(x)为奇函数，∴图象关于原点对称，∴当x＝π时，y=−1π<0，4.【答案】A【考点】指数函数的定义、解析式、定义域和值域【解析】根据指数函数的图象与性质，即可得出f(x)的值域是什么．【解答】解：∵函数f(x)=(12)x是指数函数，定义域是R，∴f(x)的值域是(0, +∞)．故选：A．5.【答案】B【考点】指数函数的单调性与特殊点【解析】由f(1)=19，解出a，求出g(x)＝|2x−4|的单调增区间，利用复合函数的单调性，求出f(x)的单调递减区间．【解答】由f(1)=19，得a2=19，于是a=13，因此f(x)＝(13)|2x−4|．因为g(x)＝|2x−4|在[2, +∞)上单调递增，所以f(x)的单调递减区间是[2, +∞)．故选：B．6.【答案】C【考点】二次函数的性质函数零点的判定定理【解析】由二次函数图象的对称轴确定b的范围，据g(x)的表达式计算g(12)和g(1)的值的符号，从而确定零点所在的区间．【解答】解：∵f(x)=x2−bx+a，结合函数的图象可知，二次函数的对称轴，12<x =b2<1 ∴ 10，∴ 函数g(x)=ln x +f′(x)的零点所在的区间是(12,1).故选C . 7.【答案】 A【考点】其他不等式的解法函数单调性的性质【解析】根据奇函数的性质求出f(−2)=0，由条件画出函数图象示意图，结合图象即可求出不等式的解集．【解答】解：∵ f(x)为奇函数，且f(2)=0，在(−∞, 0)是减函数， ∴ f(−2)=−f(2)=0，f(x)在(0, +∞)内是减函数， ∴ 在(−∞,0)上，f(x)>0的解为(−∞,2), 在(0,+∞)上，f(x)>0的解为(0,2).∴ 不等式f(x)>0的解集为(−∞, −2)∪(0, 2). 故选A ． 8. 【答案】 D【考点】有理数指数幂的运算性质及化简求值【解析】此题暂无解析【解答】此题暂无解答 9.【答案】 B【考点】有理数指数幂的运算性质及化简求值【解析】利用有理数指数幂的运算性质求解．【解答】2√a⋅√a23=a 2a 12⋅a 23=a 2a 76=a 56，二、多选题（本题共计 3 小题，每题 5 分，共计15分） 10.【答案】 A,D【考点】有理数指数幂的运算性质及化简求值【解析】根据有理数指数幂的运算法则计算．【解答】A 选项a 3⋅a 4＝a 3+4＝a 7，正确；B 选项(−a 2)3＝−a 6，错误；C 选项当a ≥0时，√a 88=a ，当a <0时，√a 88=−a ，错误； D 选项√(−π)55=−π，正确． 11.【答案】 A,C【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答 12.【答案】a ＝log 20.5＜0，b ＝20.5＞1，0＜c ＝0.52＜1，则a ＜c ＜b ，则选：C 【考点】指数函数的图象与性质【解析】根据对数函数以及指数函数的性质求出a ，b ，c 的大小即可．【解答】a ＝log 20.5<0，b ＝20.5>1，0<c ＝0.52<1，则a <c 0a −1≠1，解得a>1且a≠2；∴实数a的取值范围是(1, 2)∪(2, +∞)．故答案为：(1, 2)∪(2, +∞)．14.【答案】(0, 4)【考点】指数函数的单调性与特殊点【解析】此题暂无解析【解答】解：f(x)=a x+3的图象可以看作把f(x)=a x的图象向上平移3个单位而得到，且f(x)=a x一定过点(0, 1)，则f(x)=a x+3应过点(0, 4).故答案为：(0, 4).15.【答案】6,【考点】有理数指数幂的运算性质及化简求值【解析】此题暂无解析【解答】此题暂无解答16.【答案】(2, 0)【考点】指数函数的图象与性质【解析】结合指数函数过(0,1)点，结合题目条件，即可得出答案．【解答】令x−2=0，解得x=2当x=2时，y=−a2−2+1=0∴函数y=−a x−2+1(a>0且a≠1）图象过的定点为(2,0)答案：（20）四、解答题（本题共计 6 小题，每题 11 分，共计66分）17.【答案】【考点】函数的定义域及其求法函数的值域及其求法【解析】此题暂无解析【解答】此题暂无解答 18. 【答案】原式＝＝＝99；因为2a ＝5b ＝m ，所以a ＝log 2m ，b ＝log 5m ，所以，所以．【考点】有理数指数幂的运算性质及化简求值【解析】（1）直接利用有理数指数幂及根式的运算性质求解即可；（2）先利用指数式和对数式的互化，表示出a ，b 的值，然后利用对数的运算性质求解即可．【解答】原式＝＝＝99；因为2a ＝5b ＝m ，所以a ＝log 2m ，b ＝log 5m ，所以，所以．19. 【答案】原式＝0.4−1−1+2−4+2−3=52−1+116+18=2716．原式=a−13b 12⋅a −12⋅b 13a 16⋅b 56=a−13−12−16⋅b12+13−56=a −1=1a ．【考点】有理数指数幂的运算性质及化简求值【解析】（1）利用指数幂的运算性质即可得出．（2）利用指数幂的运算性质即可得出．【解答】原式＝0.4−1−1+2−4+2−3=52−1+116+18=2716．原式=a −13b 12⋅a −12⋅b 13a 16⋅b 56=a −13−12−16⋅b 12+13−56=a −1=1a ． 20.【答案】A ．函数的极大值点为x 2，极小值点为x 1，x 3，最大值点为a ，x 2，最小值点为x 3，B ．函数的极大值点为x 1，x 3极小值点为x 2，最大值点为x 1，最小值点为b ，C ．函数的极大值点为x 1，极小值点为x 2，最大值点为b ，最小值点为a【考点】函数的图象与图象的变换【解析】根据函数极值，最值与图象的关系进行判断即可．【解答】A ．函数的极大值点为x 2，极小值点为x 1，x 3，最大值点为a ，x 2，最小值点为x 3，B ．函数的极大值点为x 1，x 3极小值点为x 2，最大值点为x 1，最小值点为b ，C ．函数的极大值点为x 1，极小值点为x 2，最大值点为b ，最小值点为a 21.【答案】当0<a <1时，>1，则f(x)＝a x 在R 上单调递减，g(x)＝．当a >2时，0<，则f(x)＝a x 在R 上单调递增，g(x)＝．因为f(x)<g(x)，即a x <，即a x <a −x ，当0<a <7时，不等式即为x >−x ；当a >1时，不等式即为x <−x ，综上，当0<a <3时，+∞)，当a >1时，不等式的解集为(−∞．【考点】函数单调性的性质与判断利用导数研究函数的单调性【解析】此题暂无解析【解答】此题暂无解答22.【答案】根据题意，函数y＝a（）|x|+b的图象过原点，则有7＝a+b，则a＝−b，又由f(x)的图象无限接近直线y＝−2但又不与该直线相交，则b＝2，又由a+b＝6，则a＝−2，则f(x)＝−2×（）|x|+2，其图象如图：根据题意，f(x)＝−7×（）|x|+3，其定义域为R，有f(−x)＝−2×（）|x|+2＝f(x)，则f(x)是偶函数，又由f(x)＝，f(x)在(0, +∞)上为增函数，0)上为减函数．【考点】函数的图象与图象的变换函数奇偶性的性质与判断分段函数的应用【解析】此题暂无解析【解答】此题暂无解答。

指数函数试题及答案解析

指数函数试题及答案解析一、选择题1. 函数f(x)=2^{x}的值域是（）A. (0, +∞)B. (-∞, +∞)C. [0, +∞)D. [1, +∞)答案：A解析：指数函数f(x)=2^{x}，底数2大于1，因此函数是单调递增的，当x趋向负无穷时，函数值趋向0，但永远不会等于0，所以值域是(0, +∞)。

2. 函数y=a^{x}（a>0且a≠1）的图像恒过定点（）A. (0,1)B. (1,1)C. (0,0)D. (1,0)答案：B解析：指数函数y=a^{x}（a>0且a≠1）的图像恒过定点(1,1)，因为当x=1时，y=a^1=a，所以点(1,a)在图像上，而a>0且a≠1，所以a=1，因此定点为(1,1)。

3. 函数f(x)=a^{x}（a>0且a≠1）在区间（-∞，+∞）上是（）A. 增函数B. 减函数C. 先增后减D. 先减后增答案：A解析：指数函数f(x)=a^{x}（a>0且a≠1）在区间（-∞，+∞）上是增函数，因为底数a大于1，所以函数随着x的增加而增加。

二、填空题4. 函数f(x)=3^{x}的反函数是______。

答案：f^(-1)(x)=log3(x)解析：指数函数f(x)=3^{x}的反函数是f^(-1)(x)=log3(x)，因为3^{x}和log3(x)互为反函数。

5. 函数y=2^{x}的图象向左平移1个单位后，对应的函数解析式为______。

答案：y=2^{x+1}解析：函数y=2^{x}的图象向左平移1个单位，相当于将x替换为x+1，因此对应的函数解析式为y=2^{x+1}。

三、解答题6. 已知函数f(x)=2^{x}，求f(-1)的值。

答案：f(-1)=1/2解析：将x=-1代入函数f(x)=2^{x}中，得到f(-1)=2^{-1}=1/2。

7. 已知函数f(x)=a^{x}（a>0且a≠1），求证：当a>1时，f(x)是增函数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

指数与指数函数专题训练一、单选题1．（2020·嘉兴市第五高级中学高二期中）对任意的正实数a 及,m n Q ∈，下列运算正确的是（） A ．()nm m n a a += B ．()nnmm a a = C ．()nmm n a a -= D ．()nmmn a a =2．（2020·湖北省高三其他（文））已知()12|12|xxf x =+--，则()f x 的值域是（） A ．(],2-∞B ．(]0,2C ．(]03,D ．[]1,23．（2020·上海高一课时练习）若指数函数x y a =是减函数，则下列不等式中一定成立的是( )A ．1a >B ．0.2a <C ．(1)0a a -<D ．(1)0a a ->4．（2019·安徽省肥东县第二中学高一期中）已知在同一坐标系下，指数函数x y a =和x y b =的图象如图，则下列关系中正确的是（）A ．1a b <>D ．1b a >>5．（2019·宁夏回族自治区贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（） A ．（1，1）B ．（1，3）C ．（2，0）D ．（4，0）6．（2020·福建省高三其他（文））已知 1.22a =， 1.10.5b -=，0.44c =，则（） A ．c b a <-D ．1m ≤-9．（2020·湖北省高三其他（文））若0＜a ＜b ＜1，x ＝a b ，y ＝b a ，z ＝b b ，则x 、y 、z 的大小关系为（ A ．x ＜z ＜yB ．y ＜x ＜zC ．y ＜z ＜xD ．z ＜y ＜x10．（2019·安徽省肥东县第二中学高一期中）若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3二、多选题11．（2019·广东省佛山一中高一月考）下列运算结果中，一定正确的是（） A ．347a a a ⋅=B ．()326a a -=C ．88a a =D ．()55ππ-=-12．（2020·山东省高一期末）如图，某湖泊的蓝藻的面积y （单位：2m ）与时间t （单位：月）的关系满足ty a =，则下列说法正确的是（）A ．蓝藻面积每个月的增长率为100 %B ．蓝藻每个月增加的面积都相等C ．第6个月时，蓝藻面积就会超过260mD ．若蓝藻面积蔓延到2222,3,6m m m 所经过的时间分别是123, , t t t ，则一定有123t t t +=13．（2020·全国高一课时练习）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如：[ 3.5]4-=-，[2.1]2=.已知函数1()12=-+x xe f x e ，则关于函数()[()]g x f x =的叙述中正确的是（） A ．()g x 是偶函数B ．()f x 是奇函数C ．()f x 在R 上是增函数D ．()g x 的值域是{1,0,1}-E.()g x 的值域是{1,0}-14．（2020·湖南省宁乡一中高一开学考试）定义运算()()a ab a b b a b ⎧≥⎪⊕=⎨<⎪⎩，设函数()12xf x -=⊕，则下列命题正确的有（） A ．()f x 的值域为 [)1,+∞ B ．()f x 的值域为 (]0,1C ．不等式()()+12f x f x <成立的范围是(),0-∞D ．不等式()()+12f x f x <成立的范围是()0,+∞ 三、单空题15．（2020·上海高三专题练习）函数2233x y -=的单调递减区间是_________.16．（2020·上海高二课时练习）设21*718(,)n m m n N -+=∈，则21718n m ++=+_________. 17．（2020·上海高三专题练习）若曲线|y|＝2x ＋1与直线y ＝b 没有公共点，则b 的取值范围为________．四、双空题18．（2019·北京市第二十五中学高一期中）在①112-⎛⎫- ⎪⎝⎭、②122-、③1212-⎛⎫ ⎪⎝⎭④12-中，最大的数是________；最小的数值________（填序号）.19．（2020·上海高一课时练习）函数2x y =的图象与函数2x y -=的图象关于________对称，它们的交点坐标是_________.20．（2020·上海高一课时练习）已知函数22()2,[0,3]x xf x x -+=∈，则该函数的最大值为__________，最小值为_________.21．（2020·浙江省诸暨中学高二期中）设函数f （x ）2212x a x ax x ⎧+=⎨+≤⎩，＞，，若a ＝1，则f （f （2））＝_____；若f （x ）的值域为R ，则实数a 的取值范围是_____．五、解答题22．（2018·江苏省启东中学高一开学考试）若11a a --=，求下列各式的值:（1）22a a -+；（2）33a a --；（3）1a a -+；（4）3a - 23．（2020·上海高一课时练习）已知函数()2()2x xa f x a a a -=--（其中0a >且1a ≠）在R 上是增函数，求实数a 的取值范围.24．（2020·上海高三专题练习）已知[]3,2x ∈-，求11()142x x f x =-+的最小值与最大值． 25．（2019·黑龙江省大庆四中高一月考（文））已知函数2()(0,1,0)x f x a a a x -=>≠≥且的图像经过点(3,0.5)，（1）求a 值；（2）求函数2()(0)x f x ax -=≥的值域；26．（2019·攀枝花市第十五中学校高一月考）设函数()(0,1)x x f x a a a a -=->≠.（1）若11221()32f a a -=+=，求22a a -+的值.（2）若3(1)2f =，求函数()f x 的解析式；（3）在（2）的条件下，设22()2()xx g x aa mf x -=+-，()g x 在[1,)+∞上的最小值为1-，求m .27．（2020·山东省莱州一中高二月考）如图所示的函数()F x 的图象，由指数函数()xf x a =与幂函数()b g x x =“拼接”而成．（1）求()F x 的解析式；（2）比较b a 与a b 的大小；（3）已知(4)(32)bb m m --+<-，求m 的取值范围．二、单选题1．（2020·嘉兴市第五高级中学高二期中）对任意的正实数a 及,m n Q ∈，下列运算正确的是（） A ．()nm m n a a += B ．()nnmm a a = C ．()nmm n a a -= D ．()nmmn a a =【答案】D 【解析】根据指数的运算性质()nm mn a a =排除ABC.故选:D2．（2020·湖北省高三其他（文））已知()12|12|xxf x =+--，则()f x 的值域是（）A ．(],2-∞B ．(]0,2C ．(]03,D ．[]1,2【答案】B 【解析】当120x -≥，即0x ≤时，()()112122xxx f x +=+--=，则()02f x <≤，当120x -<，即0x >时，()()12122xxf x =++-=，∴()f x 的值域是(]0,2，故选：B ．3．（2020·上海高一课时练习）若指数函数x y a =是减函数，则下列不等式中一定成立的是( )A ．1a >B ．0.2a <C ．(1)0a a -<D ．(1)0a a ->【答案】C 【解析】由于指数函数xy a =是减函数，所以01a <<，所以10a -<，()10a a -<，所以ABD 选项错误，C 选项正确. 故选：C4．（2019·安徽省肥东县第二中学高一期中）已知在同一坐标系下，指数函数x y a =和x y b =的图象如图，则下列关系中正确的是（）A ．1a b <>D ．1b a >>【答案】C 【解析】很显然a ，b 均大于1；x y a =与1x =的交点在x y b =与1x =的交点上方，故b a <，综上所述:1a b >>. 故选:C.5．（2019·宁夏回族自治区贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（） A ．（1，1） B ．（1，3） C ．（2，0） D ．（4，0）【答案】B 【解析】由x ﹣1=0，解得x=1，此时y=1+2=3，即函数的图象过定点（1，3），故选B6．（2020·福建省高三其他（文））已知 1.22a =， 1.10.5b -=，0.44c =，则（） A ．c b a << B ．b a c << C ．b c a << D ．a b c <<【答案】A【解析】1.1 1.1 1.110.5()22b --===，0.420.40.84(2)2c ===.因为2xy =在R 上为增函数，所以0.8 1.1 1.2222<<. 即c b a <<. 故选：A7．（2020·萍乡市上栗中学高三二模（文））已知01a b <<<，则下列结论正确的是（） A ．a b b b ，故排除C ；a a b a >，故排除D ；由幂函数的性质得：b b a b <. 故选：B.8．（2020·上海高一课时练习）若函数2xy m =+的图像不经过第二象限，则m 的取值范围是( )A ．m 1≥B ．1m <C ．1m >-D ．1m ≤-【答案】D 【解析】指数函数2x y =过点0,1,则函数2xy m =+过点()0,1m +,若图像不经过第二象限,则10m +≤, 即1m ≤-, 故选：D9．（2020·湖北省高三其他（文））若0＜a ＜b ＜1，x ＝a b ，y ＝b a ，z ＝b b ，则x 、y 、z 的大小关系为（ A ．x ＜z ＜y B ．y ＜x ＜z C ．y ＜z ＜x D ．z ＜y ＜x【答案】A 【解析】因为01a b <<<，故()xf x b =单调递减；故a b y b z b =>=，幂函数()bg x x =单调递增；故b b x a z b =<=，则x 、y 、z 的大小关系为：x z y <<；故选：A10．（2019·安徽省肥东县第二中学高一期中）若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3【答案】B 【解析】函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增， ()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ．二、多选题11．（2019·广东省佛山一中高一月考）下列运算结果中，一定正确的是（） A ．347a a a ⋅= B ．()326a a -=Ca =Dπ=-【答案】AD 【解析】34347a a a a +==，故A 正确；当1a =时，显然不成立，故B 不正确；88a a =，故C 不正确；()55ππ-=-，D 正确，故选AD.12．（2020·山东省高一期末）如图，某湖泊的蓝藻的面积y （单位：2m ）与时间t （单位：月）的关系满足ty a =，则下列说法正确的是（）A ．蓝藻面积每个月的增长率为100 %B ．蓝藻每个月增加的面积都相等C ．第6个月时，蓝藻面积就会超过260mD ．若蓝藻面积蔓延到2222,3,6m m m 所经过的时间分别是123, , t t t ，则一定有123t t t += 【答案】ACD 【解析】由图可知，函数ty a =图象经过()1,2，即12a =，则2a =，∴2ty =；∴1222t t t +-=不是常数，则蓝藻每个月的面积是上个月的2倍，则每个月的增长率为100 %，A 对、B 错；当6t =时，626460y ==>，C 对；若蓝藻面积蔓延到2222,3,6m m m 所经过的时间分别是123, , t t t ，则122t =，22 3 t =，326t =，则122223t t ⋅=⨯，即1226t t +=，则123t t t +=，D 对；故选：ACD ．13．（2020·全国高一课时练习）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如：[ 3.5]4-=-，[2.1]2=.已知函数1()12=-+x xe f x e ，则关于函数()[()]g x f x =的叙述中正确的是（） A ．()g x 是偶函数 B ．()f x 是奇函数C ．()f x 在R 上是增函数D ．()g x 的值域是{1,0,1}-E.()g x 的值域是{1,0}- 【答案】BCE 【解析】根据题意知，e 111()1e 221ex x xf x =-=-++. ∵e1(1)[(1)]01e 2g f ⎡⎤==-=⎢⎥+⎣⎦， 11(1)[(1)]112g f e ⎡⎤-=-=-=-⎢⎥+⎣⎦，(1)(1),(1)(1)g g g g ∴≠-≠--，∴函数()g x 既不是奇函数也不是偶函数，A 错误；e 111()()1e 21e 2x x xf x f x ---=-=-=-++， ∴()f x 是奇函数，B 正确；由复合函数的单调性知11()21x f x e =-+在R 上是增函数，C 正确； e 0x>，1e 1x ∴+>，1101,10,11x xe e<<-<-<++ 11()22f x ∴-<<，()[()]{1,0}g x f x ∴==-，D 错误，E 正确.故选:BCE .14．（2020·湖南省宁乡一中高一开学考试）定义运算()()a ab a b b a b ⎧≥⎪⊕=⎨<⎪⎩，设函数()12xf x -=⊕，则下列命题正确的有（） A ．()f x 的值域为 [)1,+∞ B ．()f x 的值域为 (]0,1C ．不等式()()+12f x f x <成立的范围是(),0-∞D ．不等式()()+12f x f x <成立的范围是()0,+∞ 【答案】AC 【解析】由函数()12xf x -=⊕，有1(12)()2(12)x xxf x ---⎧≥=⎨<⎩, 即2(0)()1(0)xx f x x -⎧<=⎨≥⎩，作出函数()f x 的图像如下，根据函数图像有()f x 的值域为[1,)+∞，若不等式()()+12f x f x <成立，由函数图像有当210x x <+≤即1x ≤-时成立，当2010x x <⎧⎨+>⎩即10x -<<时也成立.所以不等式()()+12f x f x <成立时，0x <. 故选：AC. 三、单空题15．（2020·上海高三专题练习）函数2233x y -=的单调递减区间是_________. 【答案】()0,∞+ 【解析】令223u x =-，则3u y =，u 在(),0x ∈-∞上递增，在()0,x ∈+∞上递减，而3uy =是增函数，∴原函数的递减区间为()0,∞+，故答案为()0,∞+.【方法点睛】判断复合函数单调性要注意把握两点：一是要同时考虑两个函数的的定义域；二是同时考虑两个函数的单调性，正确理解“同增异减”的含义（增增→ 增，减减→ 增，增减→ 减，减增→ 减）.16．（2020·上海高二课时练习）设21*718(,)n m m n N -+=∈，则21718n m ++=+_________. 【答案】21487n -⨯ 【解析】21*718(,)n m m n N -+=∈，21781n m -∴=- 21212217747=79n n n +--⨯=⨯，217149811=49(88)4n m m +∴+=⨯-+⨯- =8+48848=8+48(81)m m m m ⨯-⨯- 21=8+487n m -⨯故答案为：21487n -⨯17．（2020·上海高三专题练习）若曲线|y|＝2x ＋1与直线y ＝b 没有公共点，则b 的取值范围为________．【答案】[－1,1] 【解析】画出曲线|y|＝2x ＋1与直线y ＝b 的图象如图所示由图象可得|y|＝2x ＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1，1]．四、双空题18．（2019·北京市第二十五中学高一期中）在①112-⎛⎫- ⎪⎝⎭、②122-、③1212-⎛⎫ ⎪⎝⎭④12-中，最大的数是________；最小的数值________（填序号）.【答案】③. ①. 【解析】①1122-⎛⎫-=- ⎪⎝⎭；②122222-==；③11221222-⎛⎫== ⎪⎝⎭；④1122-=. 所以最大的是③，最小的是①. 故答案为：(1). ③. (2). ①.19．（2020·上海高一课时练习）函数2x y =的图象与函数2xy -=的图象关于________对称，它们的交点坐标是_________.【答案】y 轴 ()0,1 【解析】函数2x y =的图象与函数2xy -=的图象如下：由指数函数的性质可知，函数2xy =的图象与函数2xy -=的图象关于y 轴对称，它们的交点坐标是()0,1.故答案为：y 轴；()0,1.20．（2020·上海高一课时练习）已知函数22()2,[0,3]x xf x x -+=∈，则该函数的最大值为__________，最小值为_________. 【答案】2 18【解析】函数()()22211g x x x x =-+=--+在[0,1)上单调递增，在(1,3]上单调递减，且()()0=033g g =-，，()11g =()[3,1]g x ∴∈-，函数2xy =单调递增，()1228g x ∴≤≤，即函数()f x 的最大值为2，最小值为18. 故答案为：2；1821．（2020·浙江省诸暨中学高二期中）设函数f （x ）2212x a x ax x ⎧+=⎨+≤⎩，＞，，若a ＝1，则f （f （2））＝_____；若f （x ）的值域为R ，则实数a 的取值范围是_____．【答案】9 [3，+∞）【解析】若a ＝1，则f (f (2))＝f (3）＝23+1＝9，当x ＞2时，f （x ）＝2x +a ＞4+a ，当x ≤2时，由函数的值域为R 可知，a ＞0，此时f (x )≤2a +1，结合分段函数的性质可知，2a +1≥a +4即a ≥3．故答案为：9；[3，+∞）．五、解答题22．（2018·江苏省启东中学高一开学考试）若11a a --=，求下列各式的值: （1）22a a -+；（2）33a a --；（3）1a a -+；（4）3a -【答案】（1）3（2）4（3）4【解析】（1）11a a --=，1222()21a a a a --∴-=+-=， 223a a -∴+=．（2）33122()(1)1(31)4a a a a a a ----=-++=⨯+=．（3）1222()2325a a a a --+=++=+=，1a a -∴+=（4）33122()(1)(32)a a a a a a ---+=++-=-=即33a a -+=2）得：334a a --=，3a -∴=23．（2020·上海高一课时练习）已知函数()2()2x xa f x a a a -=--（其中0a >且1a ≠）在R 上是增函数，求实数a 的取值范围.【答案】(0,1))⋃+∞ 【解析】函数()2()2x x af x a a a -=--（其中0a >且1a ≠）在R 上是增函数，当1a >时，x y a =和xy a -=-单调递增，故只需满足202a a >-，故a > 当01a <<时，x y a =和xy a -=-单调递减，故只需满足202a a <-，故01a <<；综上所述：(0,1)(2,)a ∈+∞.24．（2020·上海高三专题练习）已知[]3,2x ∈-，求11()142x xf x =-+的最小值与最大值．【答案】最小值34；最大值57 【解析】()221113142122124224x x x x x x x f x -----⎛⎫=-+=-+=-+=-+ ⎪⎝⎭,∵[]3,2x ∈-, ∴1284x -≤≤. 则当122x-=,即1x =时,()f x 有最小值34；当28x -=,即3x =-时，()f x 有最大值 25．（2019·黑龙江省大庆四中高一月考（文））已知函数2()(0,1,0)x f x a a a x -=>≠≥且的图像经过点(3,0.5)，（1）求a 值；（2）求函数2()(0)x f x a x -=≥的值域；【答案】（1）12a =（2）0,4]（【解析】（1）函数()2x f x a-=的图像经过点()3,0.5320.5a -∴=12a ∴=（2）由（1）可知()()2102x f x x -⎛⎫=≥ ⎪⎝⎭1012<< ()f x ∴在[0,+∞）上单调递减，则()f x 在0x =时有最大值 ()()21042maxf x f f -⎛⎫∴=== ⎪⎝⎭又()0f x >∴函数()f x 的值域为0,4]（26．（2019·攀枝花市第十五中学校高一月考）设函数()(0,1)x x f x a a a a -=->≠.（1）若11221()32f a a -=+=，求22a a -+的值.（2）若3(1)2f =，求函数()f x 的解析式；（3）在（2）的条件下，设22()2()x xg x a a mf x -=+-，()g x 在[1,)+∞上的最小值为1-，求m .【答案】（1）7；（2）2；（3【解析】（1）由题意知11223a a -+=，可得112122()29a a a a --+=++=，可得17a a -+=，又由1222(249a a a a--+=++=），可得2247a a -+=.（2）由函数()xxf x a a-=-，且3(1)2f =，可得132a a -=，整理得22320a a --=，解得2a =或12a =-（舍去），所以函数()f x 的解析式为()22x xf x -=-.（3）由（2）知()22x xf x -=-，可得()2222()2()22222xx x x x x g x aa mf x m ---=+-=+--()()2222222x x x x m --=---+，令()22x x t f x -==-，可得222()22()2h t t mt t m m =-+=-+-，又由函数()22x xf x -=-为增函数，因为1x ≥，所以3(1)2t f ≥=，当32m ≥，当t m =时，2min ()21h t m =-=-，即3m =±，解得3m =，当32m <，当32t =时，min 17()314h t m =-=-，解得7342m =>，舍去. 综上可知3m =.27．（2020·山东省莱州一中高二月考）如图所示的函数()F x 的图象，由指数函数()x f x a =与幂函数()b g x x =“拼接”而成．（1）求()F x 的解析式；（2）比较b a 与a b 的大小；（3）已知(4)(32)bb m m --+<-，求m 的取值范围．【答案】（1）x 1211,164()1,4x F x x x ⎧⎛⎫≤⎪ ⎪⎪⎝⎭=⎨⎪>⎪⎩；（2）b a a b <；（3）12(,)33-.【解析】（1）将11,42⎛⎫ ⎪⎝⎭分别代入()xf x a =，()bg x x =，求得11612a b ⎧=⎪⎪⎨⎪=⎪⎩，所以x 1211,164()1,4x F x x x ⎧⎛⎫≤⎪ ⎪⎪⎝⎭=⎨⎪>⎪⎩；（2）因为3211()22<，所以1116321611()()22⎡⎤<⎢⎥⎣⎦，即b a a b <；（3）由题意1122(4)(32)m m --+<-，根据定义域和单调性，有40,{320,432,m m m m +>->+>-解得1332m -<<. 试题解析：（1）由题意得14b 12,1142a ⎧=⎪⎪⎨⎪=⎪⎩解得1,16{1,2a b ==∴x 1211,164()1,4x F x x x ⎧⎛⎫≤⎪ ⎪⎪⎝⎭=⎨⎪>⎪⎩（2）因为3211()22<，所以1116321611()()22⎡⎤<⎢⎥⎣⎦，即b a a b <．（3）由题意1122(4)(32)m m --+<-，所以40,{320,432,m m m m +>->+>-解得1332m -<<，所以m 的取值范围是12(,)33-．。