3-5稳定性分析
5-5稳定裕度和稳定性能分析

-1
0
1
临界稳定
相角裕度的含义:保持系统稳定的前提下,开环 频率特性允许增加的滞后相角。 幅值裕度的含义:保持系统稳定的前提下,开环 频率特性的幅值允许增加到的倍数。
j 1/h j
-1
ωx
b a
ω =∞
0
γ <0
1
ωc
-1 b 0 a
ωx
ω =∞
1
γ >0
ωc
1/h
ω =0
ω =0
γ >0 稳定系统 h > 1 ω < ω x c
转折频率:0.5 斜率: -40
-20 -40
L(ω)曲线 曲线
L(ω)
[-20] 40db [-40] 20db 0db 0.1 -20db --40db 0.5 1 2
40 (0.5s + 1) G ( s ) H (s ) = 1 s ( 2s + 1)( s + 1) 30
[-20] 10
20
25
30
K=6
Nyquist Diagram 0.5 0 -0.5 Imaginary Axis -1 -1.5 -2 -2.5 -3 -3 0 Amplitude 1.5 2 Step Response
1
0.5
-2
-1
0 Real Axis
1
2
3
0
5
10
15
20
25
30
35
Time (sec)
已知单位反馈系统开环传函如下,绘制闭 环系统的频率特性图:
11.7 G ( s) = s (1 + 0.05s )(1 + 0.1s )
第5章李雅普诺夫稳定性分析

第5章 李雅普诺夫稳定性分析
第五章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性 5.2 李雅普诺夫第一法(间接法) 5.3 李雅普诺夫第二法(直接法) 5.4 线性定常系统的李雅普诺夫稳定性分析
4
第5章 李雅普诺夫稳定性分析
5.1 李雅普诺夫意义下的稳定性
1.自治系统
没有外输入作用时的系统称为自治系统,可 用如下系统状态方程来描述:
如果时变函数V(x,t)有一个正定函数作为下限, 也就是说,存在一个正定函数W(x) ,使得
V ( x ,t) W ( x), V (0,t) 0, t t0
则称时变函数V(x,t)在域S(域S包含状态空间的 原点)内是正定的。
24
第5章 李雅普诺夫稳定性分析
3. 负定函数:如果-V(x)是正定函数,则标量函数 V(x)为负定函数。
则称平衡状态xe在李雅普诺夫意义下是稳定的。
在上述稳定的定义中,实数δ通常与ε和初始时
刻t0都有关,如果δ只依赖于ε ,而和t0的选取无关,
则称平衡状态是一致稳定的。
9
第5章 李雅普诺夫稳定性分析
5. 渐近稳定性
若系统的平衡状态xe不仅具有李雅普诺夫意 义下的稳定性,且有
lim
t
||
x(t;
x0 ,
(s)
则 m(s) 为矩阵A的最小多项式。
注:换言之,矩阵A的最小多项式就是(sI-A)-1
中所有元素的最小公分母。
17
第5章 李雅普诺夫稳定性分析
例5-1(补充):判断下述线性定常系统的稳定性
0 0 0
x 0 0
0
x
0 0 1
解:1)系统矩阵A为奇异矩阵,故系统存在无穷
隧道稳定性分析与设计方法讲座之三:隧道设计理念与方法

隧道稳定性分析与设计方法讲座之三: 隧道设计理念与方法
T u n n e l D e s i g nI d e aa n dT u n n e l D e s i g nMe t h o d
Z H E N GY i n g r e n ,A B I E r d i ,X I A N GY u z h o u
( D e p a r t m e n t o f C i v i l E n g i n e e r i n g ,L o g i s t i c a l E n g i n e e r i n gU n i v e r s i t y ,C h o n g q i n g4 0 0 0 4 1 ,C h i n a ) A b s t r a c t :T h ep a p e r r e v i e w s t h r e e t u n n e l d e s i g nm e t h o d s u s e da t p r e s e n t a n dp u t s f o r w a r dt h e s t r a t u m s t r u c t u r e m e t h o d b a s e do nn u m e r i c a l l i m i t a n a l y s i s .T h em e t h o dc a nw o r ko u t t h e s a f e t y f a c t o r o f s u r r o u n d i n g r o c kn e e d e di nt h e d e s i g n , s o t h e c u r r e n t s u b j e c t i v e p r o b l e m s c a nb e s o l v e d . T h e p a p e r s t u d i e s t h e s e p a r a t r i x b e t w e e ns h a l l o wt u n n e l s a n dd e e pt u n n e l s a n da l s o e v a l u a t e s t h e a d v a n t a g e s a n dd i s a d v a n t a g e s o f t h e t w o d i v i d i n g s t a n d a r d s .F i v e b a s i c i d e a s o f t u n n e l d e s i g n a n dc a l c u l a t i o na r ed i s c u s s e di nt h ep a p e r :1 )T h et u n n e l d e s i g nm u s t s a t i s f yt h es a f e t yr e q u i r e m e n t s d u r i n go p e r a t i o n a n dc o n s t r u c t i o na n dt h es a f e t yf a c t o r o f s u r r o u n d i n gr o c ka f t e r p r i m a r ys u p p o r t m u s t e n s u r et h ec o n s t r u c t i o ns a f e t y ;2 ) T h ed e s i g na n dc a l c u l a t i o nm o d e l s h o u l da d a p t t od i f f e r e n t g e o l o g i c a l c o n d i t i o n s ,d i f f e r e n t s u r r o u n d i n gr o c kp r e s s u r e c h a r a c t e r i s t i c s a n dd i f f e r e n t p r a c t i c a l m e c h a n i c a l s t a t e o f t h e t u n n e l ; 3 )T h e d e s i g na n dc a l c u l a t i o no f t u n n e l m u s t b e i n a c c o r d a n c ew i t ht h em o d e r np r e s s u r et h e o r yo f s u r r o u n d i n gr o c ka n ds u p p o r t i n gp r i n c i p l ea n dm u s t m a k ef u l l u s eo f t h e s e l f s u p p o r t c a p a b i l i t yo f s u r r o u n d i n gr o c k ;4 )T h et u n n e l s t r u c t u r em o d e l s h o u l da l s oa d a p t t ot h ep r a c t i c a l m e c h a n i c s t a t ea n dt h en e wi d e at h a t t h ep r i m a r ys u p p o r t i st h er e i n f o r c e m e n t m a t e r i a l o f s u r r o u n d i n gr o c ka n dt h a t c a l c u l a t i o n s h o u l db e m a d e a c c o r d i n g t o t h e p l a s t i c t h e o r y s h o u l db e e s t a b l i s h e d ; 5 )R e a s o n a b l e c a l c u l a t i o nm e t h o da n dc a l c u l a t i o n p a r a m e t e r s s h o u l db eu s e dt oe n s u r es c i e n t i f i ct u n n e l d e s i g na n dc a l c u l a t i o n .F i n a l l y ,t a k i n g a s u b w a y s t a t i o na s a ne x ,t h ep a p e r i n t r o d u c e s t h ed e s i g nm e t h o do f t u n n e l s i nG r a d eI I ,G r a d eI I I a n dG r a d eVs u r r o u n d i n gr o c k . a m p l e K e yw o r d s :s t a b i l i t ya n a l y s i s ;a n a l y t i cc r i t e r i ao f t h es t a b i l i t yo f s u r r o u n d i n gr o c k ;F E Ms t r e n g t hr e d u c t i o nm e t h o d ; s a f e t yf a c t o r o f s h e a r ;f a i l u r es u r f a c e ;s o i l t u n n e l ;r o c kt u n n e l
精品文档-自动控制原理及其应用(第二版)温希东-第3章

能够用一阶微分方程描述的系统称为一阶系统,它的典型 形式是一阶惯性环节,即
(3-9)
第3章 时 域 分 析 法
20
1. 一阶系统的单位阶跃响应 当r(t)=1(t)时,有
第3章 时 域 分 析 法
对上式进行拉氏反变换,得
根据式(3-10),可得出表 3-1 所列数据。
21 (3-10)
第3章 时 域 分 析 法
第3章 时 域 分 析 法
63
图 3-14 二阶系统单位阶跃响应包络线
第3章 时 域 分 析 法
第3章 时 域 分 析 法
57
2) 求峰值时间tp 由峰值时间tp的定义知,tp为c(t)响应超过其终值到达第 一个峰值所需的时间。
由式(3-14)和式(3-19)得
(3-21)
第3章 时 域 分 析 法
58
根据数学求极值概念,令
即
第3章 时 域 分 析 法
59
因为
所以
由此可得, ωdtp=π, 则 (3-22)
28
3.3 二阶系统的动态响应
用二阶微分方程描述的系统称为二阶系统。从物理上讲, 二阶系统总包含两个储能元件,能量在两个元件之间交换,从 而引起系统具有往复的振荡趋势。当阻尼不够充分大时,系统 呈现出振荡的特性,这样的二阶系统也称为二阶振荡环节。
第3章 时 域 分 析 法
29
二阶系统的典型传递函数为
当r(t)=1(t)时,有
则
第3章 时 域 分 析 法
44
对上式进行拉氏反变换,可得
(3-17)
其响应曲线如图 3-10所示,系统为无阻尼等幅振荡。该种情况 实际系统不能用。
第3章 时 域 分 析 法
45
第5章现代控制理论之系统运动的稳定性分析

由稳定性定义知,球域S(δ) 限制着初始状态x0的取值,球域
S(ε)规定了系统自由运动响应 xt xt; x0的, t0边 界。
简单地说:1.如果 x t; x0, t0 有界,则称 xe 稳定;
2.如果 x t; x0, t0 不仅有界,而且当t→∞时收敛于原点,则
5.1.1 平衡状态
李雅普诺夫关于稳定性的研究均针对平衡状态而言。
1. 平衡状态的定义
设系统状态方程为: x f x,t , x Rn
若对所有t ,状态 x 满足 x 0 ,则称该状态x为平衡状
态,记为xe。故有下式成立:f xe ,t 0
由平衡状态在状态空间中所确定的点,称为平衡点。
2.平衡状态的求法
由定义,平衡状态将包含在 f x,t 这样0 一个代数方程组
中。
对于线性定常系统 x A,x其平衡状态为 xe 应满足代数
方程 。Ax 0
只有坐标原点处是线性系统的平衡状态点。
对于非线性系统,方程 方程而定。
如:
x1 x2
x1 x1
x2
x
3 2
f x的,t 解 可0 能有多个,视系统
稳定性是系统的重要特性,是系统正常工作的必要条件。
稳定性是指系统在平衡状态下受到扰动后,系统自由运动 的性质。因此,系统的稳定性是相对于系统的平衡状态而 言的。它描述初始条件下系统方程是否具有收敛性,而不 考虑输入作用。
1. 线性系统的稳定性只取决于系统的结构和参数,与系统 初始条件及外作用无关; 2. 非线性系统的稳定性既取决于系统的结构和参数,也与 系统初始条件及外作用有关;
当稳定性与 t0 的选择无关时,称一致全局渐近稳定。
6SIGMA专业术语

6SIGMA专业术语6SIGMA专业术语DMAIC定义、测量、分析、改进、管理CTQ质量特性值FMEA故障模式及影响分析QFD质量功能展开PTS : Project Tracking System课题跟踪系统DPU单位产品缺陷数;DPO每个机会的缺陷数;DPMO为DPO乘以1000000。
VOC顾客的要求 (voice of the customer)Project课题Process过程;Procedures程序Sample样本QCD质量、成本、交货期USL规格上限;LSL规格下限;Target公差中心COPQ劣质成本б标准差(Standard Deviation,σ) : 表示数据(质量特性值)离公差中心值远近的分散程度的统计参数α犯第一种错误的概率;β犯第二种错误的概率R&R重复性和再现性Cp短期过程能力指数,以 Process Capability Index表示过程能力指数.(Cp=T/6σ,T为技术规范的公差幅度);Cpk长期过程能力指数,平均值与目标值不同时(产品质量分布的均值与公差中心不重合时)的过程能力指数。
PPM : 以Parts per Million在百万个中表示不合格品数的单位.Output输出;INPUT输入Process Mapping流程图T公差幅度,公差范围,顾客要求的规格范围3P : Product, Process, People产品,过程,人Master Blackbelt黑带主管;Blackbelt黑带;Greenbelt绿带 Champion冠军Brainstorming头脑风暴法RTY(Rolled Throughput Yield) : 流通合格率(过程从头到尾各工序合格率的连乘积。
量测系统分析作业程序精品资料网()专业提供企管培训资料1.目的:为了解量测系统是否能满足制程使用需求,确定新购及可能有缺陷或经维护后校验合格的量具设备在重新使用时是否亦能提供客观正确的分析评价,以评估量测设备的适用性,确保产品品质。
第五节-壳体的稳定性分析
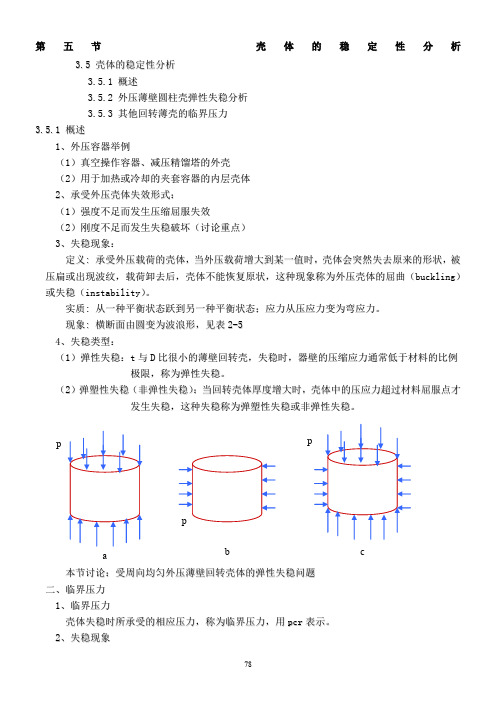
第五节 壳体的稳定性分析3.5 壳体的稳定性分析3.5.1 概述3.5.2 外压薄壁圆柱壳弹性失稳分析3.5.3 其他回转薄壳的临界压力3.5.1 概述1、外压容器举例(1)真空操作容器、减压精馏塔的外壳(2)用于加热或冷却的夹套容器的内层壳体2、承受外压壳体失效形式:(1)强度不足而发生压缩屈服失效(2)刚度不足而发生失稳破坏(讨论重点)3、失稳现象:定义: 承受外压载荷的壳体,当外压载荷增大到某一值时,壳体会突然失去原来的形状,被压扁或出现波纹,载荷卸去后,壳体不能恢复原状,这种现象称为外压壳体的屈曲(b u c k l i n g )或失稳(i n s t a b i l i t y )。
实质: 从一种平衡状态跃到另一种平衡状态;应力从压应力变为弯应力。
现象: 横断面由圆变为波浪形,见表2-54、失稳类型:(1)弹性失稳:t 与D 比很小的薄壁回转壳,失稳时,器壁的压缩应力通常低于材料的比例极限,称为弹性失稳。
(2)弹塑性失稳(非弹性失稳):当回转壳体厚度增大时,壳体中的压应力超过材料屈服点才发生失稳,这种失稳称为弹塑性失稳或非弹性失稳。
本节讨论:受周向均匀外压薄壁回转壳体的弹性失稳问题 二、临界压力1、临界压力壳体失稳时所承受的相应压力,称为临界压力,用p c r 表示。
2、失稳现象pab c外载荷达到某一临界值,发生径向挠曲,并迅速增加,沿周向出现压扁或波纹。
见表2-53、影响p c r 的因素:对于给定外直径D o 和厚度,t p c r 与圆柱壳端部约束之间距离和圆柱壳上两个刚性元件之间距离L 有关;p c r 随着壳体材料的弹性模量E 、泊松比μ的增大而增加;非弹性失稳的p c r 还与材料的屈服点有关。
注意: 外压容器失稳的根本原因是由于壳体刚度不足,并不是由于壳体存在椭圆度或材料不均匀所致。
即椭圆度和材料不均匀对失稳的性质无影响,只影响使p c r ↓。
3.5.2 外压薄壁圆柱壳弹性失稳分析目的:求cr p 、cr σ、cr L理论: 理想圆柱壳小挠度理论假设:①圆柱壳厚度t 与半径D 相比是小量,位移w 与厚度t 相比是小量(t D ↓↓,w t↓↓) ②失稳时圆柱壳体的应力仍处于弹性范围。
数据结构——排序——8种常用排序算法稳定性分析

数据结构——排序——8种常⽤排序算法稳定性分析⾸先,排序算法的稳定性⼤家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
在简单形式化⼀下,如果Ai = Aj, Ai原来在位置前,排序后Ai还是要在Aj位置前。
其次,说⼀下稳定性的好处。
排序算法如果是稳定的,那么从⼀个键上排序,然后再从另⼀个键上排序,第⼀个键排序的结果可以为第⼆个键排序所⽤。
基数排序就是这样,先按低位排序,逐次按⾼位排序,低位相同的元素其顺序再⾼位也相同时是不会改变的。
另外,如果排序算法稳定,对基于⽐较的排序算法⽽⾔,元素交换的次数可能会少⼀些(个⼈感觉,没有证实)。
回到主题,现在分析⼀下常见的排序算法的稳定性,每个都给出简单的理由。
(1)冒泡排序冒泡排序就是把⼩的元素往前调或者把⼤的元素往后调。
⽐较是相邻的两个元素⽐较,交换也发⽣在这两个元素之间。
所以,如果两个元素相等,我想你是不会再⽆聊地把他们俩交换⼀下的;如果两个相等的元素没有相邻,那么即使通过前⾯的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是⼀种稳定排序算法。
(2)选择排序选择排序是给每个位置选择当前元素最⼩的,⽐如给第⼀个位置选择最⼩的,在剩余元素⾥⾯给第⼆个元素选择第⼆⼩的,依次类推,直到第n-1个元素,第n个元素不⽤选择了,因为只剩下它⼀个最⼤的元素了。
那么,在⼀趟选择,如果当前元素⽐⼀个元素⼩,⽽该⼩的元素⼜出现在⼀个和当前元素相等的元素后⾯,那么交换后稳定性就被破坏了。
⽐较拗⼝,举个例⼦,序列5 8 5 2 9,我们知道第⼀遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是⼀个稳定的排序算法。
(3)插⼊排序插⼊排序是在⼀个已经有序的⼩序列的基础上,⼀次插⼊⼀个元素。
当然,刚开始这个有序的⼩序列只有1个元素,就是第⼀个元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、稳定的基本概念 如果一个稳定的系统在外作用的影响下, 如果一个稳定的系统在外作用的影响下,离开了初始的稳 定状态,但是当外作用消失后, 定状态,但是当外作用消失后,系统经过足够长的时间它还能 回复到原来的稳定状态, 回复到原来的稳定状态,则称这样的系统为稳定的系统 。否则 为不稳定的系统。 为不稳定的系统。 或定义为:设初始条件为零时, 或定义为:设初始条件为零时,输入为一个理想的单位脉 冲函数 δ (t),即R(S)=1。当作用时间 时,δ (t) =0,这相当 ) 。当作用时间t>0时 , 给系统一个扰动。 给系统一个扰动。如果系统的输出脉冲响应
17:53
S平面
不 稳 Re 定 区
5
注意:稳定性是线性定常系统的一个属性, 注意:稳定性是线性定常系统的一个属性,只与系统本身的结构 参数有关,表现在传递函数中就只与特征根有关, 参数有关,表现在传递函数中就只与特征根有关,即只与极点有 与零点无关,也与输入输出信号无关; 关,与零点无关,也与输入输出信号无关; 对于一阶系统,s + a0 对于一阶系统a , 1 系统是稳定的。 系统是稳定的。
17:53 11
[例1]:特征方程为: s3 + a2s2 + a1s + a0 = 0 ,试判断稳定性。 例 :特征方程为: 试判断稳定性。 a3 [解]:劳斯阵为: 3 解 :劳斯阵为: s
a3 a1 a0 0 0
s2 a2 s1 s0 a
a2a1 − a3a0 a2
0
稳定的充要条件为: 稳定的充要条件为:
c13 c23 c33 c43 L c15 c25 c35 c45 L M M M M M
sn−3 c14 c24 c34 c44 L s M s0
n−4
a1 c34 = − c13
c1,n+1 c2,n+1 c3,n+1 c4,n+1L
以下各行各列的元素值可依上几式的规律依次算得.
17:53
10
sn
c(t) = ∑ci e
i=1 k pit
+ ∑e j ( Aj cosω j t + Bj sin ω j t)
j =1
r
σt
(t ≥ 0)
上式中第一项是指数函数,根为 pi ;第二项是指数函数与正弦 上式中第一项是指数函数, 函数的乘积, 要想系统稳定, 函数的乘积,根的实部为 σ j 。 要想系统稳定,两个指数函数 p 必须是衰减的,也就是说, 必须是负数。因此有, 必须是衰减的,也就是说, i 和 σ j 必须是负数。因此有, 线性 系统稳定的充要条件是: 系统稳定的充要条件是:闭环系统特征方程的所有根均具有负 实部;或者说,闭环传递函数的极点均分布在复平面的左半部。 实部;或者说,闭环传递函数的极点均分布在复平面的左半部。 为什么? 为什么?
17:53 4
如果特征方程中有一对共轭虚根, 如果特征方程中有一对共轭虚根,它的对应 于等幅的周期振荡,称为临界平衡状态( 于等幅的周期振荡,称为临界平衡状态(或临界 稳定状态)。 稳定状态)。 从控制工程的角度认为临界稳定状态属于不 从控制工程的角度认为临界稳定状态属于不 稳定。 稳定。
Im
稳 临 定 界 区 稳 定
n−4
面两行构成劳思行列表的 表头, 表头 表中其它各行各列 的元素值按如下公式计算: 的元素值按如下公式计算
a0 a1 a1 a0
a2 a3 a4 a1 a1a2 − a0a3 = a1
c15 c25 c35 c45 L c13 = − M M M M M
c1,n+1 c2,n+1 c3,n+1 c4,n+1Lc = − a1 a5 = a1a4 − a0a5 23
17:53 3
如果特征方程中有一个正实根, 如果特征方程中有一个正实根,它所对应 的指数项将随时间单调增长; 的指数项将随时间单调增长; • 如果特征方程中有一对实部为正的共轭 复根,它的对应项是发散的周期振荡。 复根,它的对应项是发散的周期振荡。 • 上述两种情况下系统是不稳定的。 上述两种情况下系统是不稳定的。 • 如果特征方程中有一个零根(1/s项), 如果特征方程中有一个零根(1/s项),拉 氏反变换对应于一个常系数项, 氏反变换对应于一个常系数项,系统可在 任何状态下平衡,称为随遇平衡状态( 任何状态下平衡,称为随遇平衡状态(如 系统本来是稳定的再加入这个根则还是稳 本来不稳定则还是不稳定); 定,本来不稳定则还是不稳定); •
17:53 6
2 − a1 ± a1 − 4a2a0 对于二阶系统, 对于二阶系统, 2s2 + a1s + a0 = 0, s1,2 = a 2a2
三、 劳斯稳定性判据 设线性系统的特征方程为
D(s) = a0s + a1s
n
n− 1
+L+ an−1s + an = 0
式中 a0 > 0 , 构造如下劳斯行列表 构造如下劳斯行列表:
a0 都大于零, = 0, s = − 只要 a0 ,a1都大于零, , a1
都大于零,系统才稳定。(负实根或实部为负) 。(负实根或实部为负 只有 a0 , a1, a2 都大于零,系统才稳定。(负实根或实部为负) 对于三阶或以上系统,求根是很烦琐的。 对于三阶或以上系统,求根是很烦琐的。于是就有了以下 描述的代数稳定性判据。 描述的代数稳定性判据。
17:53
13
例3: 设系统的特征方程 D(s) = s5 + 2s4 + s3 + 3s2 + 4s + 5 = 0 为 用劳思稳定判据判别系统是否稳定? 用劳思稳定判据判别系统是否稳定
s5 解: s4 s3 s2 s1 s0 1 2 1 3 4 5
− 0.5 9 16/ 9 5
1.5 5
因为第一列有-0.5, 且正﹑负号 且正﹑ 因为第一列有 改变两次, 所以系统不稳定, 改变两次 所以系统不稳定 且有两个根在s的右半平面上 的右半平面上. 且有两个根在 的右半平面上
用劳思稳定判据判别系统是否稳定? 用劳思稳定判据判别系统是否稳定
解:
s3 1 100 s2 4 500 s1 − 25 0 s0 500 0
因为第一列有-25, 且正﹑负号改变 且正﹑ 因为第一列有 两次, 所以系统不稳定, 两次 所以系统不稳定 且有两个 根在s的右半平面上 的右半平面上. 根在 的右半平面上 也是因为系数的乘积差4*100<1*500 也是因为系数的乘积差
17:53
14
四.劳斯判据的特殊情况 劳斯判据的特殊情况 1)劳思表某行第一个列项为零,其余均不为零。 )劳思表某行第一个列项为零,其余均不为零。
[处理办法一 :用很小的正数 ε 代替零的那一项,然后据此计算出劳 处理办法一]: 代替零的那一项, 处理办法一 斯阵列中的其他项。 斯阵列中的其他项。 设系统特征方程为s 例3 设系统特征方程为 4+2s3+s2+2s+2=0 ;试用劳斯稳定判据判 断系统的稳定性。 断系统的稳定性。 解:列出劳斯表 s4 s3 s2 s1 s0 1 2 取代0) 取代 ε(取代 2-4/ε ε 2 1 2 2 2 0
a0 a6 a7 a1 a1a6 − a0a7 = L , a1 c14 = − a1 a1 a3 c13 a1 c13 c23 c13a3 − a1c23 = c13
9
c33 = −
17:53
s s s
n n−1 n−2
a0 a1
a2 a3
a4 a5
a6 a7
L L
c24 = − a1 c13 a5 c33 c13 a7 c43 c13 = c13a7 − a1c43 L , c13 = c13a5 − a1c33 c13
a0
a2 a3 c24 c25 M
a4 a5 c33 c34 c35 M
a6 a7
L L
sn−1 a 1 sn−3 c 14 sn−4 c 15 M s0 M
sn−2 c c23 13
c43 L c44 L c45 L M M
c ,n+1 c2,n+1 c3,n+1 c4,n+1L 1
则线性系统稳定的充要条件是 劳斯表中第一列各值均大于零. 劳斯表中第一列各值均大于零 如劳斯表第一列中出现小 于零的数值, 系统就不稳定, 且第一列各数值符号的改变次数, 于零的数值 系统就不稳定 且第一列各数值符号的改变次数 就是系统特征方程的正实部根的数目, 就是系统特征方程的正实部根的数目 即系统在极点平面的右 半平面上的极点个数. 半平面上的极点个数
limc(t) = 0
t→ ∞
即输出增量收敛于原平衡工作点,则系统是稳定的。 即输出增量收敛于原平衡工作点,则系统是稳定的。
17:53 1
二 稳定的必要条件 闭环系统的传递函数为: 闭环系统的传递函数为:
C(s) bmsm + bm−1sm−1 +L+ b1s + b0 B(s) Φ(s) = = = n n−1 R(s) ans + an−1s +L+ a1s + a0 D(s)
[
][
]
2
17:53
r αjs + βj B(s) B(s) k ci =∑ +∑ C(s) = R(s) = D(s) D(s) i=1 s − pi j=1[s − (σ j + jωj )][s − (σ j − jωj )]
对上式进行拉氏反变换,得到理想脉冲函数作用下的输出: 对上式进行拉氏反变换,得到理想脉冲函数作用下的输出:
可见第一列元素的符号改变两次,故系统是不稳定的且在 右半平 可见第一列元素的符号改变两次,故系统是不稳定的且在S右半平 面上有两个极点。 面上有两个极点。
