二年级奥数:有趣的图形计数
二年级奥数.计数.有趣的图形计数

把一些正方体堆在一起你会数吗?无论是平面图形还是几何图形,在数复杂图形的个数时,只要我们认真仔细观察图形特点,有次序地去数,不遗漏不重复,就能数得又对又快。
今天这节课我们也去闯一闯几何王国,让我们用我们的智慧去挑战这些图形吧!立体图形包括正方体、长方体等,如果把许多的正方体堆成不同的图形你会数吗?如果把一个 大的长方体切成许多的小正方体你又会数吗?【例1】 下面的图形有多少个?你会数吗?( )条线段 ( )个长方形( )个正方形 ()个三角形 ( )个圆【例2】 数一数,图 1和图 2中各有多少黑方块和白方块?【例3】 迪斯尼乐园里米老鼠又住上了新房子,下图是他新房子的侧面墙,你能根据这个侧面图算算砌 好图1图2例题精讲知识框架有趣的图形计数 巧求周长【例4】你喜欢下跳棋吗?你知道跳棋盘有多少个孔吗?仔细数一数。
【例5】数一数,下面的方块各有多少?【例6】下面的图形中一共有几个小方块?【例7】下面这堆木方块共有多少块?(中间打阴影部分从上到下是空心)【例9】下面是用小正方体堆成的图形,现在把这个图形的表面涂上黄色,想一想有多少个小正方形没有被涂色【例10】有一天大头儿子做手工,把一个正方体木块表面涂上绿色,然后再把它切成8个小正方体,想一想每个小正方体有几个面没有颜色?课堂检测【随练1】下面两个图形能拼成一个长方体吗?【随练2】 下图是一个正方体木块,在它的表面涂上蓝色,然后沿正方体上面直线垂直切开。
切成了( )个三棱柱。
每个三棱柱没有涂颜色的面共有( )个,这些三棱柱一共有( )个面没有被涂色。
【随练3】 一个大正方体的表面上都涂上绿色,然后切成27个小立方体(切线如图中虚线所示)。
在这些切成的小立方体中,问:(1)1面涂成绿色的有( )个。
(2)2面涂成绿色的有( )个。
(3)3面涂成绿色的有( )个。
(4)1个面也没有被涂成绿色的有( )个【作业1】 数一数.【作业2】 如图所示砖墙是由正六边形的特型砖砌成,问需要几块正六边形的砖才能把它补好?( )个正方形( )个三角形()个三角形家庭作业【作业3】下面是用方块砌成的台阶,一共用了多少方块?【作业4】下面的图形被云彩遮住了,你能数出有多少个方块吗?(中间阴影部分是空心的)【作业5】这堆木方块共有多少块?(中间打阴影部分是空心)【作业6】如图所示为一堆砖.中央最高一摞是10块,它的左右两边各是9块,再往两边是8块、7块、6块、5块、4块、3块、2块、1块.问:这堆砖共有多少块?【作业7】下图中每个图形各由几个小正方体拼成,至少再增加几个小正方体就可以把这个图形拼成一个长方体?。
小蜗班二年级趣味图形奥数题
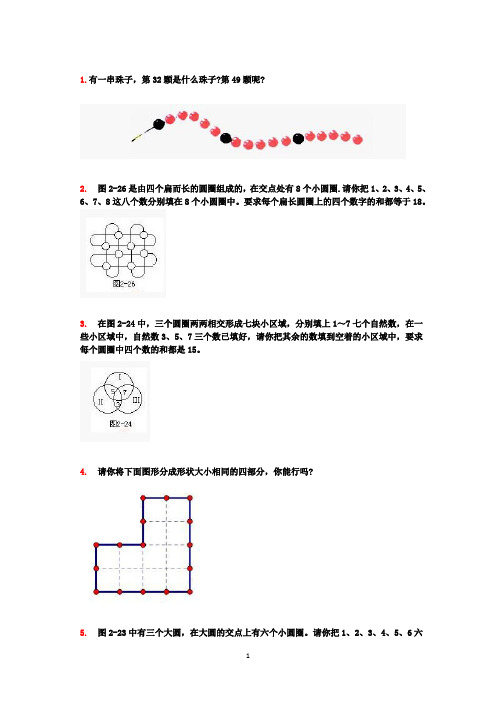
1.有一串珠子,第32颗是什么珠子?第49颗呢?2.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
3.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
4.请你将下面图形分成形状大小相同的四部分,你能行吗?5.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
6.请你将下面的图形拼成一个大长方形的宣传板,上面从左到右写着"快乐学习"几个字。
请你在大长方形图中将这几个字表示出来。
7.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
8.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?9.你能将下面的图形分成形状大小相同的四部分吗?其中AB=AD=EF=BC,DE=FC10.请看下图,共有多少个正方形?11.如图有5个点,在两个点之间可以画出一条线段,画出的图形中一共可以得到( )条线段.12.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?13.将14个大小一样的小正方体摆成下面的图形,然后将表面涂成红色再分开,有( )个小正方形的面没有被涂色。
14.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
15.有十一根火柴棍,摆成如图所示的算式。
这个算式显然是不对的,你能只移动其中一根,使等式成立吗?16.请把下图中长方形分成形状相同、大小相等的两块,然后再拼成一个正方形.17.在图中,一共有_____个四边形,_______条线段18.在空格中填入合适的数19.找出下面图形变化的规律,并在横线上画出第四幅图。
奥数2年级图形计数

图形计数:计算某一图形的个数。
要求: 1、计数时不重复,即不能 把同一图
形计数两次。 2、不遗漏。 3、要按一定的顺序或按一某一个标
准统一分类去计算,即有规律地 计数。
图形计数方法: 1、线段端点法 2、基本图形数量法 3、分式法 4、分类法
典型例题 例1:下图中有多少条线段?
AB C
D
练习: 下图中有多少条线段?
练习: 下图中有多少条线段?
……
A C1 C2
C20 B
典型例题 例2:下图中有多少个三角形?
练习 下图中有多少个三角形?
典型例题 例3:下图中有多少个三角形?
A
D NM
BF E
CHale Waihona Puke 练习 下图中有多少个三角形?
典型例题 例4:下图中有多少个长方形?
练习 下图中有多少个长方形?
典型例题 例4:下图中有多少个正方形?
练习 下图中有多少个正方形?
从武汉到上海的客船,中途要停靠5 站,航运公司要为这艘客船准备多 少种不同的船票价?
有10个小朋友,每个小朋友都要和 其他小朋友拍手,这些小朋友一共 要拍多少次手?
二年级上册奥数:《画图凑数法》

二年级上册奥数:《画图凑数法》笫十五讲画图凑数袪例1 一只鸡有一个头2只脚,一只兔有一个头4只脚.如果一个笼子里关着的鸡和兔共有10个头和26只脚,你知道笼子里有几只鸡、有几只兔吗?例2 —辆自行车有2个轮子.一辆三轮车有3个轮子.车棚里放着自行车和三轮车共10辆,数数车轮共有26个.问自行车几辆,三轮车几辆?例3 —只妁贱&条腿,一只蜘殊8条腿.现有姑蛾和螂鎌共1Q只,共有68条腿.问轴姗几只,蜘蛛几只?例4笼中有兔又有鸡,数数腿36,数数脑袋11,问几只兔子几只鸡?例5今有五分的和一角的两种汽车票,共10张,总钱数是七角五分.问每种各几张?答案笫十五讲画图凑数法例1 一只鸡有一个头2只脚,一只兔有一个头q只脚.如果一个笼子里关着的鸡和兔共有io个头和26只脚,你知道笼子里有几只鸡、有几只兔吗?解:这是古代的民间趣题,叫"鸡兔同笼”问题.见图15-1 (1)、C2)、〔3)•①先画10个头’因15-1( 1 )②每个头下画上两条腿;圈 15T(2)数一数,共有20条腿,比题中给岀的腿数少26-20二6条腿.③给一些鸡添上两条腿,叫它变成兔.边添腿边数,凑够26条腿.每把一只鸡添上两条腿,它就变成了兔,显然添6条腿就变岀来3只兔.这祥就得岀答案,笼中有3只兔和7只鸡.例2 —辆自行车有2个轮子,一辆三轮车有3个轮子.车棚里放着自行车和三轮车共10辆,数数车轮共有26个.问自行车几辆,三轮车几辆?解:发挥熄像力和创造力,你可以画一个简图代表车身,见图15-2 ⑴、⑵、⑶■①先画10个车身;LLLLLLLLLLU 15-2( 1 )②在每个车身下配上两个轮子,它就成了自行车,LLLLLLLLLLE] 15-2( 2)③数一数共20个车轮,比题中给岀的轮子数少26-20=6个轮子,在自行车下面添轮子,每添一个轮子,这个自行车就成了三轮车.边添边凑数,凑岀2&个轮子岀来.乙厶 4 厶---------- 6辆三轮车--------- ° ——辆自行车——/H15-2 ( 3 )最后数一数,共有6辆三轮车,4辆目行车.注意,用这种画图凑数法解 题,很直观,也比较快,为了使解题速度更快,可以把三个歩骤合起来,就能 得岀答案.例3 —只岫岫6条腿,一只蜘蛛8条腿.现有岫轴和蜘蛛共10只,共有68条 腿•问嗽轴几只,蜘蛛几只?解:此题要想个更简单的亦法,见图15-3 C1)、(2).① 先画10个头,在每个头下写上数字“ 6",代表6只腿,--即先假设10 只都是««,则如:② 数一数,算一算,6X10=60,即共有60条腿,比题中给岀的腿数少昭- 60二8条腿.所以就要在下面再添腿,每在一个头下添2条腿〔写个“ 2”),它 就变成了一只蜘塢 共添上8条腿,就使总腿数凑够倔条腿了.^)15-3 ( 2 ) 职后数1数,共勺4只螂蛛,6只WW-解这道题时,我们用数字代表腿数,使我们省去了画"腿"的麻烦.其 实,也可以完全省去画图,我们只要把解题想法和算式摘出来就行了!第一步,先把10只全部看成是轴蝸,那么一共就有=6X10=60 条腿.第二步,算一算少了多少条腿?少了 &8-&0二8条腿.666666666 6^)15-3 ( 1 )66666666 62 2 2 、-- &只轴抽 ------- '第三步,把一个蚁赋给它添上2条腿,使它变成了聊蛛,可以变成几只蜘蛛呢?8-2=4只(蜘蛛),笫四步,再算出轴岫的只数出来:10-4=6;只(iftH).这样一来,我们就不必借助于画圈的直观形象,也可以解这类题目了.如杲能这样,我们的思维能力就又提高一步了!特别重要的是,我们这样就可以不用“凑数”的尝试方法了.例4笼中有兔又有鸡,数数腿36,数数脑袋11,问几只兔子几只鸡?解;方法1;先用画图凑数法解,见图15-4 C1)、(2)、(3)・①先画11个头’②再在头下填腿:③数一数,共有2XII二22条腿.还少36-22二14条腿,每添2条腿,就使一只鸡变成兔・数一数,共变出了7只兔;14-2=7.最后数一数,笼中共有7只兔,4只鸡.方法2:①把11只全部看成鸡,共有2XII二22条腿.②比题中给岀的腿数少了36-22二14条腿.③给一只鸡添2条腿使它变成一只兔,共变成;14^2=7只(兔)・④再算岀鸡数为:11-7二4只(鸡).例5今有五分的和一角的两神汽车票,井10张,总钱数是七角五分•问每种各几张?解:方法1:分歩列式法:若10张全是5分的,栈数应为:5X10二50分,即5角.比题中给的钱数少:75-50=25分.每给一张5分车票加5分,它就变成了1张[角车票了,共变出:25 *5二5张(1角车票)5分车票有10-5二5张(5分车票).方袪2:用画图凑数法.见图15-5 (1)、(2)■①先都画成5分的:國國國國函函國國國國图15-5 ( 1 )②算-算共5X10二50分(即5角).比题中给的钱数少花分-50二25分.③给有些5分车票加钱,使它变成1角的,凑出总钱数与题目相符合.⑤⑤⑤⑤图⑤国⑤⑤⑤+ 5 +5 +5 +5 +5图15-5( 2)最后数一数,可知1角的车票5张,5分的车票5张.习题十五1. 笼中有兔又有鸡,数数腿三十整,数数脑袋一十一,几只兔子几只鸡?2. 今有雉兔同笼,上有三十五头,下有九十四足问雉兔各几何?(这是一道古代趣题.雉,即野鸡,"各几何”是各多少的意思.) 3. 有一首中国民谣:“一队猎手一队狗,二臥排着一起走,数头一共三百 六,数腿一共八百九多少猎手多少狗? ”4. 扌巴99粒棋子放在两种型号的17个盒子里,每个大盒子里放12粒,每个小 盒子里放5粒,恰好放完•问大、小盒子各多少个。
二年级奥数之巧数图形

猜一猜下图每个图中一共有多少个小方块?看不见的小方块有几个?
请问这首诗中,去掉标点后,这首诗一共有几个字?
鹅、鹅、鹅,
曲项向天歌,
白毛浮绿水,
红掌拨清波。
【拓展】★★★
数数看,下边这张床是由多少个小正方体组成的?
下面的图形是用火柴棒摆成的,你知道用了多少根火柴棒吗?
【例5】★★★★
⑴三角形数:
第8个三角形数是多少?小小飞天王,吐丝织罗网,摆开八卦阵,蚊蝇美美尝。
这是( )。
①蜘蛛网中心有一个点。
织到第一层一共有( )个
点。
织到第二层一共有( )个点……
现在这个蜘蛛网上共有多少个点?
现在这个蜘蛛网上一共有多少个点?
②如果蜘蛛网织到第八层,一共有多少个点?
小朋友们都玩过跳棋吧!你知道跳子棋盘上有多少个圆洞吗?数一数。
一、平面图形
、平面图形(不规则)
方法:分类数。
二年级奥数数学巧数图形课件

例题五(★ ★ ★ ★ )
(2)正方形
第7个正方形数是 多少?
在正方形数中, 第1个是1×1=1 第3个是3×3=9 以此类推
例题五(★ ★ ★ ★ )
小小飞天王,吐丝织罗网,摆开八卦阵,蚊蝇美美尝。这是( ) ①蜘蛛网中心有一个点。织到第一 层一共有(17)个点。织到第二层一共有() 个点……现在这个蜘蛛网上一共有多少个点?
拓展(★ ★ ★ )
下面的图形是用火柴棒摆成的,你知道用了多少根火柴棒吗?
方法二: 方层数 第一层:3根 第二层:6根 第三层:9根 第四层:12根
一共有:3+6+9+12=30(根)
例题五(★ ★ ★ ★ ) ⑴三角形数:
第8个三角形数是 多少?
第8个三角形数是: 1+2+3+4+5+6+7+8=36
例题【四】(★ ★ ★ ★)
像下图这样摆出一个长方形,一共用了多少根小棒?摆出一个正方形 , 一共用了多少根小棒?
方法二 3×8+1=25(根)
例题【四】(★ ★ ★ ★)
像下图这样摆出一个长方形,一共用了多少根小棒?摆出一个正方形 , 一共用了多少根小棒?
(2)方法一 横着:3×4=12(根) 一共:12+12=24(根)
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
春季 第二讲有趣的图形计数
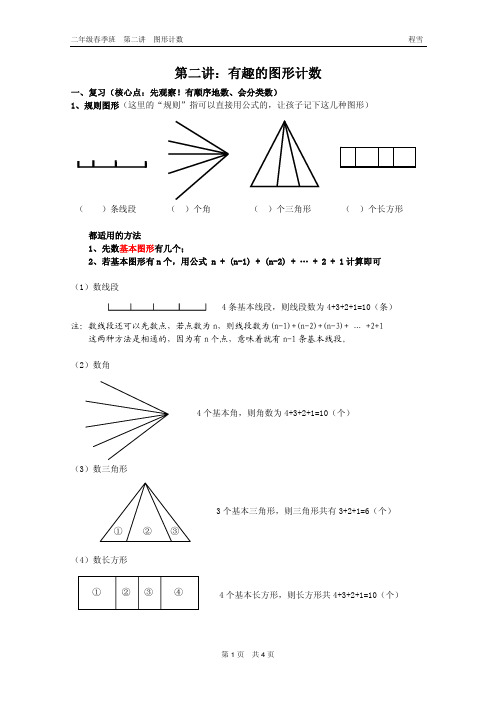
四、染色问题 简单情况仍然使用观察法。 复杂一些的可使用分类法,思路如下: 1、没被染色的面即为粘在一起的面,粘一处少两个面(两个方块各少一面)。 2、粘的情况分两类:横着粘的和竖着粘的
“横着”粘的(粘的面是水平的),这个数量就是上层粘下层的数量,所以就看看除了最 下面一层,上面有多少个方块,就粘了多少处;“竖着”粘的,这个数量是同一层中相互挨着 的方块所粘的数量,就把各层的平面图画出来,找公共边就可以了,比如说一层有四个方块, 拼成了一个“田”字,那就画出这个平面图(即一个田字格),一共四条公共边,则本层竖着 就粘了四处。
(1)数线段
4 条基本线段,则线段数为 4+3+2+1=10(条) 注:数线段还可以先数点,若点数为 n,则线段数为(n-1)+(n-2)+(n-3)+ … +2+1
这两种方法是相通的,因为有 n 个点,意味着就有 n-1 条基本线段。
(2)数角
4 个基本角,则角数为 4+3+2+1=10(个)
(3)数三角形
8×4=32(块) 思路二:补 先把空心补上,则成了一个长方体
9×4-4=32(块)
2、补方块 简单的可使用观察法,复杂一些的应先计算完整的正方体需要多少方块,再减去已有的就是 需要添加的了。 正方体求方块数:边长×边长×边长
提高例 4 尖子例 3(图略 讲解第 3 小题) 先找最长的边是 4,得知最后拼成的正方体边长是 4 总方块数:4×4×4=64(块) 已 有:19 块 缺 少:64-19=25(块)
复习 :分层数(从上往下,一层一层数,最后再求和) 每层的数量 = 这层你能看见的 + 上层数量。 关键:“你能看见的”指从上往下能看见的,即能看见“顶”的。
二年级奥数:《飞速图形计数》
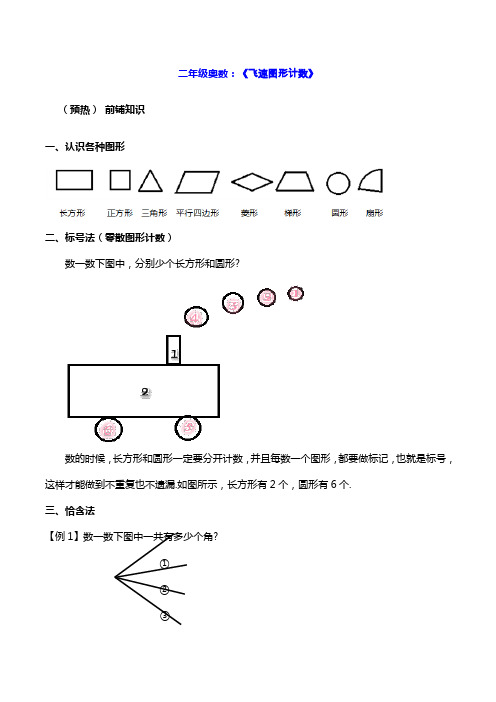
二年级奥数:《飞速图形计数》(预热)前铺知识一、认识各种图形二、标号法(零散图形计数)数一数下图中,分别少个长方形和圆形?数的时候,长方形和圆形一定要分开计数,并且每数一个图形,都要做标记,也就是标号,这样才能做到不重复也不遗漏.如图所示,长方形有2个,圆形有6个.三、恰含法【例1】数一数下图中一共有多少个角?①②③恰含1个角的:①、②、③,共3个;恰含2个角的:①+②、②+③,共2个;恰含3个角的:①+②+③,共1个.一共:3+2+1=6(个)答:一共有6个角.【例2】数一数下图有多少个长方形?①⑤②③④恰含1个长方形的:①、②、③、④、⑤,共5个;恰含2个长方形的:①+②、②+③、③+④、④+⑤,共4个;恰含3个长方形的:②+③+④,共1个.一共:5+4+1=10(个)答:一共有10个长方形.四、其他分类方法1、按大小分类有4个小正方形,3个大正方形.2、按位置分类中间有2个圆,周围有3个圆.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《飞速图形计数》知识点精讲【知识点总结】复习1、枚举法(标号法)2、恰含法(通用)新知识一、简单规整图形(肩并肩、手拉手排成一排)开火车大法总数=火车头(基本图形数)依次加到1二、多层规整图形分层数(相合不能忘)三、不规整图形分类法:①分部分②分大小(恰含法)③分方向注:常见的【简单规整图形】(特别:数正方形不能用开火车大法)线段角【例1】数一数下面一共有多少条线段?①②③④方法1:恰含1条:4条恰含2条:①②、②③、③④3条恰含3条:①②③、②③④2条恰含4条:①②③④1条总数:4+3+2+1=10(条)方法2:基本线段有4条,所以从4开始依次加到14+3+2+1=10(条)答:一共有10条线段.【例2】数一数图中有多少个三角形?每层个数:4+3+2+1=10(个)层数:3层总数:10×3=30(个)答:一共有30个三角形.【例3】数一数右侧图形中一共有多少个三角形?左边:3+2+1=6(个)右边:3+2+1=6(个)合起来:3个总数:6+6+3=15(个)答:一共有15个三角形.【例4】数一数右侧图形中一共有多少个三角形?恰含1个:①、②、③、④、⑤、⑥6个Array恰含2个:①②、③④、⑤⑥3个恰含3个:①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②6个恰含6个:①②③④⑤⑥1个6+3+6+1=16(个)答:一共有16个三角形.【例5】数一数下面图形中一共有多少个正方形?方法:先按照正的和斜的这两个不同方向,把图形拆分出来.正的:按大小分类数,斜的:一个田字格,有5个正方形最小:4个中等大小:5个最大:1个共4+5+1=10(个)总数:10+5=15(个)答:一共有15个正方形.【学习建议】本讲讲的是数图形的方法,根据不同类型的图形有不同的巧妙方法,同学们要仔细辨认图形的种类,像是简单规整图形和多层规整图形都是有巧妙方法的;如果是不规则图形,那么一定要注意分类,分类的依据是什么,数的时候思路要清楚,这样才不会数错.《飞速图形计数》补充题1.数一数下面两幅图中分别有多少条线段?2. 在一条直线上有10个端点,那么在这条直线上可以数出多少条线段?3. 下图中有多少个三角形?4、数一数,下面有多少个长方形?5、数一数图中有多少个正方形?6、数一数下面一共有几个正方形.7、数一数,下图中包含有苹果的三角形有几个?8、数一数下图中一共有多少个平行四边形?答案解析1、(1)5+4+3+2+1=15(条)答:这幅图中有15条线段.(2)(3+2+1)+(2+1)=9(条)答:这幅图中有9条线段.2、基本线段数:10-1=9(条)总线段数:9+8+7+6+5+4+3+2+1=45(条)答:这条直线上有45条线段.3、每层个数:5+4+3+2+1=15(个)层数:3层总数:15×3=45(个)答:图中共有45个三角形.4、长边线段数:3+2+1=6(条)宽边线段数:4+3+2+1=10(条)长方形总个数:10×6=60(个)答:图中共有60个长方形.5、恰含1个:5×3=15(个)恰含4个:8个恰含9个:3个正方形总个数:15+8+3=26(个)答:图中共有26个正方形.6、按照正的和斜的两个方向,先把原图形拆分成如下两个图形.恰含1个:4×4=16(个)一个田字格有5个正方形恰含4个:3×3=9(个)恰含9个:2×2=4(个)恰含16个:1×1=1(个)共:16+9+4+1=30(个)所以一共有:30+5=35(个)正方形答:一共有35个长方形.7、按照三角形从小到大的顺序,且时刻注意题目要求,要包含苹果.恰含1个:2个恰含4个:6个恰含9个:5个恰含16个:3个最大的:1个共:2+6+5+3+1=17(个)答:含有苹果的三角形一共有17个.8、是简单规整图形,肩并肩、手拉手,可以用开火车大法.6+5+4+3+2+1=21(个)答:一共有21个平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二年级奥数:有趣的图形计数知识点总结
一、平面图形计数
1.规则图形——跑火车
基本图形数依次加到1
2.不规则图形——
分层数
分类(大小分类,方向分类)
3.方法:观察规律,变加为乘
二、立体图形计数——分层数
每层个数=上层个数+本层露出头顶的个数
二、染色问题
1重合2不染
知识点精讲
一、平面图形
1、规则图形
公式法(跑火车)(适用于数线段、数角、数三角形等)
例数线段
分析:有3条基本线段(火车头是3),所以一共有3+2+1=6(条)线段例数角
分析:有3个基本角,共有3+2+1=6(个)角
例数三角形
分析:有4个基本三角形,共有4+3+2+1=10(个)三角形
(2)不规则图形
①分层数
例数多层长方形(分层数)
分析:每层有3+2+1=6(个),有3层,所以共有6╳3=18(个)
也可以,长边上线段总数3+2+1=6(个)
宽边上线段总数2+1=3(个)
总共有:3×6=18(个)
例图中有多少个三角形?
解析:观察本图不是规则图形,不能直接用公式.但可以将它分成2层(中间横线以上是一层,去掉横线是一层),且每层都是一个规则的数三角的图形.每层个数:3+2+1=6(个)层数:2层总个数6×2=12(个)
②分类数:大小、方向
例数三角形
方法:标号法(适用于任何基本的平面图形,建议重点掌握)
分析:用标号法如图
小三角形有6个,
两个小三角形拼成的有(2,3)(4,5)(6,1)3个
三个小三角形拼成的有(1,2,3)(2,3,4)(3,4,5)(4,5,6)(5,6,1)(6,1,2)6个六小三角形拼成的有1个
共6+3+6+1=16(个)
二、其它平面图形计数
1、数棋盘:细观察,找规律,变加为乘
2、数方块: 补、拆
三、立体图形计数
1、数立方体
推荐方法:从上往下一层一层的数
每层个数=上层个数+本层露出头顶的个数
例数一数下图有多少块立方体?
分析:如图,从上往下,一层一层的数
即1+3+6+10=20(块)
2、补成大正方体/长方体
推荐方法:要补的块数=总数-现有的块数
例至少添加多少个小正方体可以组成一个较大的正方体?
分析:先观察发现这幅图有4层,那么要想拼出一个大正方体,那么每层应该有4行4列,所以拼成的大正方体至少得4╳4╳4=64块,现在有3+4+5+7=19块,所以至少得补64-19=45块
3、染色问题
简单情况可使用观察法
没被染色的面即为粘在一起的面(重合面),粘一处少两个面,(两个方块各少一个面)例下面是用小正方体堆成的图形,现在把这个图形的表面涂上红色,数一数有多少个小正方形没有被涂色?
分析:“横着”粘的:第一层+第二层的块数1+2=3处。
