初等几何研究试题答案(6)
初等几何研究试题答案(李长明版)

初等几何研究试题答案(I)、线段与角的相等1. O O、O Q相交于A B, O O的弦BC交O Q于E, O 02的弦BD交O0于F,求证:(1)若2 DBA2 CBA贝卩若DF二CE则 / DBA M CBA.证明:⑴连接AC AE AF、AD在O 0 中,由/ CBA W DBA得AC=AF在O O 中,由/ CBA W DBA得AE=AD由A C、B、E四点共圆得/仁/2由A D B、E四点共圆得/ 3二/4所以△ ACE^A AFD••• DF=CE(2) 由(1)得/ 仁/ 2, / 3=2 4v DF=CE• △ACE^A AFD••• AD=AE在O Q 中,由AD=AE^得/ DBA M CBA2. 在厶ABC中,AC=BC,Z ACB=90,D是AC上的一点,AE丄BD的延长线于E,又AE=1BD,2求证:BD平分/ ABC.证明:延长AE,BC交于点F7 AED "BCA =90 ADE "BDC•CBD =/CAF又7 ACF BCA = 90 AC 二BC•ACF 三BCD . AF = BD1 1又、:AE BD . AE AF2 2又ABEE _ BE■ BE平分ABF即BD平分.ABC3. 已知在凸五边形ABCDE中, / BAE=3 ,BC=CD=DE M/ BCD玄CDE=180-求证:/ BAC 2 CAD h DAE.证明:过点B 作BDL BC,交圆周于点D,连结CD ©D•••/ DBC=90, • CD 是直径,则/CAD=90证明:连接BD,得△ CBD 是等腰三角形且底角是/ CDB=[18(0-(180o — 2 - )] -2=.:丄 BDE=(180° — 2G )-O (=180O — 3«••• A B 、D E 共圆同理A C D E 共圆• h BAC h CAD h DAE4. 设H 为锐角△ ABC 的垂心,若AH 等于外接圆的半径由题,可得AH L BC, BH丄AC••• BD// AH, AD// BH二四边形ADBH是□••• AH=BD又;AH等于外接圆的半径(R)• BD=R M CD=2R•••在Rt △ BCD中,CD=2BD即/ BCD=30• / BDC=60又;/ BAC K BDC BAC M BDC=605. 在厶ABC中, / C=90,BE是/B的平分线,CD是斜边上的高,过BE CD之交点0且平行于AB的直线分别交AC BC于F、G,求证AF=CE.证明:如图;/ 1 = 2 3, / 仁/2. 2二/ 3, • GB = GO,;2 5=2 4=2 6, • CO =CE,;FG// AB,「. AF/CF二B$CG二G0CG,又;△ FCO^COG/. CO7CF=G/CG=A/CF,• CO=AF;CO=CE,\ AF=CE.6. 在厶ABC中,先作角A B的平分线,再从点C作上二角的平分线值平行线,并连结它们的交点 D E,若DE// BA,求证:△ ABC等腰.证:如图所示设AG ED的交点为Fv AD是/ A的平分线•••/仁/2T DE// AB 仁/ 3v CE// AD :丄 3二/ 5, / 4二/ 2•/仁/2二/3=Z 4=2 5则厶FAD ffi^ FCE是等腰三角形•A F=DF,EF=CF•A C=DE同理可证BC=DE•A C=BC• △ ABC是等腰三角形7. 三条中线把△ ABC分成6个三角形,若这六个三角形的内切圆中有4个相等.求证:△ ABC是正三角形.AB D C证明:•/△ AOF △ AOE △ COD △ COE △ BOF △ BOD面积都相等--S A OFE=S A OEC即: 11111 1BF X 叶一FOX 叶BO X r= CEX 叶一OE< 叶一OC X r 2 2 2 2 2 21 12 (BF+FO+BO X r= - (CE+OE+OC X r••• BF+FO+BO二CCE+OE+OC••• CE+OE+OC-OG-OI二CE+OE+OC-OL-OJ• 2DH+2BH=2FK+2CK• 2BF=2CE又F、E分别为AB AC之中点••• AB=AC同理:AB=BC故厶ABC是正三角形.8. 平行四边形被对角线分成四个三角形中,若有三个的内切圆相等证明:该四边形为菱形.C证明:又•••△ AOBA BOC、△ CODA DOA四个三角形的面积相等1 1OD DC OC r OB BC OC r2 2CD OC OD 二BC OB OCOD OC DC - OE - OG = OB OC BC - Ol - OG二2DF +2CF =2BH +2CH二2DC =2BC=DC =BC•四边形为菱形9. 凸四边形被对角线分成4个三角形,皆有相等的内切圆,求证:该四边形是菱形证明:连结O i 、O 2,分别作O i 、O 2到AC 的垂线,垂足分别为P 、M•••在厶ABC 中 ,BO 是。
初等几何研究答案

《初等几何研究》作业一、填空题1、对直线a 上任意两点A 、B ,把B 以及a 上与B 在A 同侧的点的集合称作 射线(或半直线),; ,并记作 AB 。
2、在绝对几何中,外角定理的内容是: 三角形的外角大于任一不相邻的内角 。
3、第四组公理由 两 条公理组成,它们的名称分别是 度量公理(或阿基米德公理)和康托儿公理 。
4、欧氏平行公理是:对任意直线a 及其外一点A ,在a 和A 决定的平面上,至多有一条过A 与a 不相交的直线 。
5、罗氏几何公理系统与欧氏几何公理系统的共同之处是 前4组公理(或绝对几何) ,不同之处是 平行公理 。
6、几何证明的基本方法,从推理形式上分为 演绎 法与归纳法;从思维方向上分为 综合 法与分析法;从命题结构上分为 直接 证法与间接证法,其中间接证法包括 反证 法与 同一 法。
7、过反演中心的圆,其反演图形是 不过 (过或不过)反演中心的 直线 。
8、锐角三角形的所有内接三角形中,周长最短的是 垂足三角形。
9、锡瓦定理:设⊿ABC 的三边(所在直线)BC 、CA 、AB 上分别有点X 、Y 、Z ,则AX 、BY 、CZ 三线共点(包括平行)的充要条件是1=⋅⋅ZBAZYA CY XC BX 。
10、解作图问题的常用方法有: 交轨法 、三角奠基法、 代数法 、 变换法 等。
11、数学公理系统的三个基本问题是 相容性、 独立性和 完备 性.33.①答案不惟一.34.①(0,+∞),②,(0,π/2),③连续,④单调递减. 35.①平移,②旋转,③轴对称.36. ①1=⋅⋅ZB AZYA CY XC BX (或-1)37.①写出已知与求作,②分析,③作法,④证明,⑤讨论.12、对于共面的直线a和a外两点A、B,若a与(AB)相交,则称A、B在a的异侧,否则称A、B在a的同侧.13、命题:“过直线外一点,至少有一条直线与已知直线共面但不相交”是外角定理的推论.14、证明直线和圆的连续性时,主要依据了戴德金分割原理.15、罗氏平行公理是:对任意直线a及其外一点A,在a和A决定的平面上,至多有一条过A与a不相交的直线.,16、在罗氏几何中,共面的两条直线有3种关系,它们分别是平行,相交,分散.17、几何证明的通用方法一般有化归法、类比法、构造法、数形结合法、变换法、模型法等.18、等边三角形外接圆周上任一点到三顶点的连线段中,最长线段与另两条线段之和具有相等的关系.19、尺规可作图的充要条件是所求的量可用已知量的有理式或只含平方根的无理式表出.20.由公理可以证明,线段的合同关系具有反身性、对称性、传递性和可加性.21.如果线段与角对应,那么线段的中点与角的角平分线对应.22.命题:“线段小于任意一条连接其两个端点的折线”是外角定理的推论.23.绝对几何包括有四组公理,它们分别是结合公理、顺序公理、合同公理、连续公理. 24.写出一条与欧氏平行公理等价的命题:.25.在罗氏几何中,两条直线为分散线的充要条件是.26、.常用的几何变换有合同变换、相似变换、射影变换、反演变换等27.托勒密定理:四边形ABCD是圆内接四边形,则1=⋅⋅ZBAZYACYXCBX(或-1).28.请写出两条作图公法:过两点可作一条直线(或其部分)。
初等几何研究复习题

习题1.设梯形两底之和等于一腰,则此腰两邻角的平分线必通过另一腰的中点。
已知:如图,梯形ABCD 中,AD ∥BC,AB=AD+BC,E 是DC 中点求证:∠DAB 与∠ABC 的平分线必经过E 点。
证明(同一法):设∠DAB 与∠ABC 的角平分线交于E ′点,只需证E ′点与E 点重合。
∵AD ∥BC∴∠DAB+∠ABC=180° ∵∠1=∠2, ∠3=∠4, ∴∠2+∠3=90° ∴∠A E ′B=90°作Rt △ABE ′的斜边AB 上的中线 FE ′,则 FE ′=21AB=AF=BF∴∠2=∠A E ′F, ∠3=∠B E ′F ∴∠1=∠2=∠A E ′F , ∴E ′F ∥AD ∥BC连结EF,则EF 为梯形 ABCD 的中位线, E F ∥AD ∥BC ∴E ′F 与EF 共线∵FE ′=21AB=21(AD+BC), FE =21(AD+BC)∴E ′F = E F∴E ′与E 重合,证毕.习题2.A 是等腰三角形ABC 的顶点,将其腰AB 延长至D ,使BD=AB 。
知CD=10厘米,求AB 边上中线的长。
解:过B 作BF ∥AC 交CD 于F , 则BF 是△DAC 的中位线。
∴BF 21AC∴∠FBC=∠ACB又∠ACB=∠ABC ,AB=AC ∴∠FBC=∠ABC ,BF=21AB=BE21∴△EBC ≌△FBC (SAS ) ∴CE=CF=21CD=21×10=5cm即△ABC 中边上的中线CE 的长为5厘米。
习题3.证明:等腰三角形底边延长线上任一点到两腰距离之差为常量。
已知:如图,等腰三角形ABC 中,AB=AC 。
D 为BC 延长线上一点,过D 作DE ⊥ AB 于E ,作DF ⊥ AC 延长线于F 。
求证:DE -DF 为常量。
证明:作△ABC 的边AB 上的高CH ,再作CG ⊥DE 于G ,则四边形CHEG 为矩形。
初等几何研究综合测试题(十六)

《初等几何研究》综合测试题(十六)适用专业:数学教育专业 考试时间:120分钟一、选择题(本题共8小题,每小题3分,共24分)1.已知ABCD 为平行四边形,下列判断正确的是__________。
A.若∠A=90°,则ABCD 为正方形;B.若AB=BC ,则ABCD 为菱形;C.对角线互相平分垂直;D.以上都不对。
2. 下列判断正确的是_________。
A.任意两个等腰三角形都相似;B.任意两个直角三角形都相似; C .有一个角相等且有两边对应成比例的两个三角形都相似; D.任意两个等腰直角三角形都相似。
3.如图,Rt AB C 中,CD 是斜边AB 上的高,DE ⊥AC 于E,AC:CB=4:5,则AE:EC 等于_______。
A.4:5;C.16:25;D.以上都不对。
4.等腰三角形一腰上的高与底边所成的角等于__________。
A.顶角的一半;B.底角的一半; C.90°减去顶角的一半;D. 90°减去底角的一半。
5.如图,圆锥的底面半径OA=3cm ,高SO=4cm ,则它的侧面积 为__________2cm .A.12π;B.15π;C.16π;D.20π.6. 6.下列命题中能用来判断一条线段是半径的命题是__________。
A.过圆心且垂直于切线的直线必经过切点;B.过切点且垂直于切线的直线必经过圆心;C.圆的切线垂直于过切点的半径;D.过半径的外端且垂直于这条半径的直线是圆的切线。
7.下列图形中,不一定为轴对称图形的是_________。
A.直角;B.线段;C.直角三角形;D.等腰直角三角形。
8.如图,有A 、B 、C 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在_________。
A.在AC 、BC 两边高线的交点处; B.在AC 、BC 两边中线的交点处;C.在AC 、BC 两边垂直平分线的交点处;D.在∠A 、∠B 两内角平分线的交点处。
初等几何研究试题答案(6)李长明版
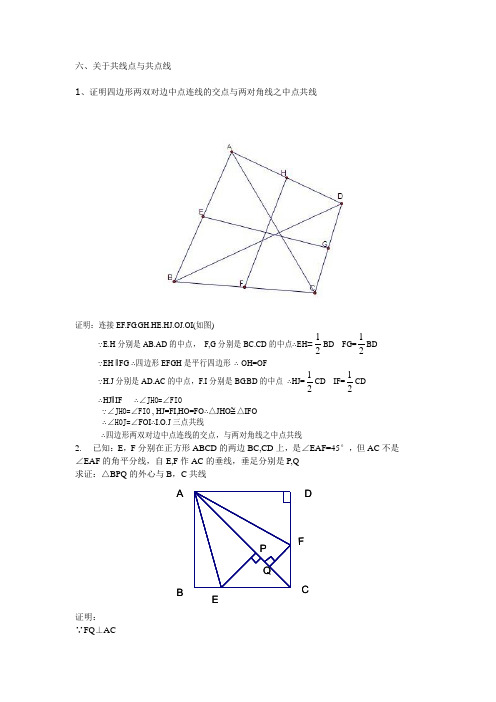
六、关于共线点与共点线1、证明四边形两双对边中点连线的交点与两对角线之中点共线证明:连接EF.FG.GH.HE.HJ.OJ.OI(如图)∵E.H 分别是AB.AD 的中点, F,G 分别是BC.CD 的中点∴EH =12BD FG=12BD ∵EH ∥FG ∴四边形EFGH 是平行四边形 ∴ OH=OF∵H.J 分别是AD.AC 的中点,F.I 分别是BG.BD 的中点 ∴HJ=12CD IF=12CD ∴HJ ∥IF ∴∠JHO=∠FIO∵∠JHO=∠FIO , HJ=FI,HO=FO ∴△JHO ≅△IFO ∴∠HOJ=∠FOI ∴I.O.J 三点共线∴四边形两双对边中点连线的交点,与两对角线之中点共线2. 已知:E ,F 分别在正方形ABCD 的两边BC,CD 上,是∠EAF=45°,但AC 不是∠EAF 的角平分线,自E,F 作AC 的垂线,垂足分别是P,Q 求证:△BPQ 的外心与B ,C 共线A DCFBEP Q证明: ∵FQ ⊥AC∴∠ABE=∠AQF 又∵∠EAF=45° ∴∠BAE=∠QAF ∴△ABE ∽△AQF 可得AQ AB AFAE同理可得,△AEP ∽△AFD 即AD AP=AFAE∴AQ AB =ABAP利用切割线定理之逆定理,因△BPQ 的外心在BC 上,等价于AB,APQ 是切,割线 ∴△BPQ 的外心在BC 上3.在Rt △AB 为斜边,CH 为斜边上 的高,以AC 为半径作☉A ,过B 作☉A 的任一割线交☉A 于D 、E ,交CH 于F(D 在B 、F 之间),又作∠ABG=∠ABD ,G 在☉A 上,G 与D 在AB 异侧。
求证:(1)A 、H 、D 共圆。
(2)E 、H 、G 共线。
(3)FD 、FE 、BD 、BE 四线段成比例证明:如图所示:连结AE 、AD(1)∵BC 2=BH ·BA(摄影定理) BC 2=BD ·BE(割线定理) ∴BD ·BE=BH ·BA∴A 、H 、D 、E 四点共圆 (2)∵∠ABD=∠ABG∴∠GBH=∠DBH(对称性) 又∵A 、H 、D 、E 四点共圆∴∠FEA=∠DHB(对角等于内对角) ∠AHE=∠EDA (同弧所对的角) 又∵AE=AD ∴∠AEF=∠ADF∴∠AEF=∠DHB=∠GHB=∠ADE=∠AHE ∴∠GHB=∠AHE (对顶角) ∴E 、H 、G 三点共线 (3)∵∠ABD=∠ABG∴由对称知:HB 平分∠DHG(∠GHB=∠DHB) 又∵ CH 垂直AB E 、H 、G 三点共线 ∴HC 平分∠DHE∴HC 、HB 是∠DHE 的内外角平分线 ∴FE DF =HE HD =BEBD4.设P是正方形ABCD内的一点,使PA:PB:PC=1:2:3,将BP 绕B 点朝着BC 旋转90BP 至Q.求证:A 、P 、 Q 共线.证明:连接 CQ ,∵PA:PB:PC= 1:2:3设AP=1 则 BP=2 CP=3 ∵BP 绕B 点朝着BC 旋转90° ∴∠PBQ=90°BP=BQ=2 ①∠BPQ=∠BQP=45°∴PQ =√BP 2+BQ 2=2√2 又∵四边形ABCD 是正方形 ∴AB=BC ②∴∠ABC=∠PBQ= 90°即∠ABP+∠PBC=∠CBQ +∠PBC=90°∴∠ABP=∠CBQ ③∴△ABP≌△CBQ(由①②③可得到)∴PA=QC=1又∵PQ2+QC2=(2√2)2+12=32=PC2∴∠PQC=90°,∠BQC=∠PQC+∠BQP=90+45°=135°又∵∠APB=180°-45°=135°∴∠BQC=∠APB=135°即A、P、Q共线(∠APB、∠BQP是邻补角)5. 在∆ABC中,D,E,F分别在AB.BC.CA上,使得DE=BE,EF=CE.求证:∆ADF的外心O 在∠DEF的角平分线上。
初等几何研究试卷5

第 1 页 (共 2 页)5一、填空题(本大题共 9题,每空 2 分,共 20分)1、当欲证某图形具有某种性质而又不易直接证明时,可以先作出具有所示性质的图形,然后证明所作的图形跟所给的图形就是同一个,这种证法叫做 ;2、在ABC ∆中,,BE AC CF AB ⊥⊥,若AB AC >,则BE 与CF 的大小关系是 ;3、已知ABC ∆的三边分别为5cm,8cm,11cm ,则ABC ∆的面积S= ;4、从圆O 外一点P 引这个圆的两条切线,其夹角为60º,如果PO=6,那么圆的半径等于 ;5、圆内接四边形ABCD 中,已知AB=6cm,BC=CD=4cm,AD=8cm ,则对角线AC ·BD= ;6、在一些作图题中,解题的关键在于一些线段的算出,这种利用代数解作图题的方法称为 ;7、设点C 在线段AB 上且满足关系式2AC AB CB =⋅,则点C 称为线段AB 的 ; 8、设一线段在互垂三平面上的射影为123,,r r r ,则此线段的长为 ; 9、到两定点A 、B 的距离的平方差为定值k 的点的轨迹是垂直于AB 的一条直线,称为 ,点A 到垂足H 的距离AH= . 二、计算题(本大题共 2 题,第1小题8 分,第2小题10分,共 18 分) 1、在ABC ∆中,AD 是BC 边上的中线,E 是AD 的中点,连接BE 与AC交于点P,求:BE EP 的值。
2、已知Rt ABC ∆所在平面外一点P 到直顶角C 的距离为24,到两直角边的距离为求PC 与平面ABC 所成的角。
三、证明题(本大题共 4 题,每小题10 分,共40 分)1、 圆的两弦AB 与CD 相交于一点E ,由E 引AD 的平行线与直线BC 交于F ,过F 作圆的切线FG ,G 为切点,证明EF=FG.2、设梯形ABCD 的两底之和AD+BC=CD ,求证D ∠与C ∠的平分线交于AB 的中点处。
CE第 2 页 (共 2 页)3、AD 、BE 、CF 是ABC ∆的高线,从垂足D 引DM BE ⊥于M ,引DN CF ⊥于N ,求证MNFE4、证明三角形的中线小于夹此中线两边的半和,而大于这半和与第三边一半的差。
初等几何研究

1.(证明线段相等)例1:在ABC ∆的两边AB 、AC 上向外做正方形ABEF 和ACGH ,则BC 边上的高线AD 平分FH 。
证明:过点F 作PQ FQ ⊥,过点H 作DP HP ⊥在ΔADB 和ΔFQA 中⎪⎩⎪⎨⎧=∠=∠=∠=∠AB AF DBA QAF ADB FQA90AD FQ ΔADB ΔFQA =⇒≅∴在中ΔCAD 和ΔAFP⎪⎩⎪⎨⎧=∠=∠=∠=∠AC AH DAC PHA 90CDA APHAD PH ΔCAD ΔAHP =⇒≅∴HP FQ =∴在中和HPM FQM ∆∆⎪⎩⎪⎨⎧=∠=∠∠=∠HP FQ HMP FMQ PHM QFM ΔH P M ΔF Q M ≅∴ HM FM =∴即M 为FH 的中点。
2:C 是弦AB 的中点,通过C 引弦PQ ,并在此弦两端作圆的切线PX 和QY 。
它们交直线AB 于X 、Y 。
证PX=QY 、AX=BY 。
3:AB 是圆的直径,从圆上一点C 作AB CD ⊥于D 。
且在A 、C 两点的切线相交于E ,证明:BE 平分CD 。
证明:过点B 作AB BF ⊥交EC 于FEA//CD//BF ∴ECDM AE DM AB BD EF CF EF BF EC CM ===== DM CM =∴即BE 平分CD 。
4:设AD 、BE 、CF 是ABC ∆的高线,则DEF ∆称为ABC ∆垂足三角形。
证明这些高线平分垂足三角形的内角或外角。
证明: FCDM 共圆FDM FCM ∠=∠∴DBEM 共圆EDM EBM ∠=∠∴90BAC EBM BAC FCM =∠+∠=∠+∠EBM FCM ∠=∠∴EDM FDM ∠=∠∴即AD 平分FDE ∠同理可得BF 平分DFE ∠,CE 平分FED ∠即这三条高线平分DEF ∆的内角或外角。
5:二圆外切于P ,一圆在其上一点C 的切线交另一圆于A 、B 。
求证:PC 是APB ∠的外角平分线。
6:等边三角形外接圆周上任意一点到顶点连线中最长的等于其余两线之和。
初等几何研究试题

初等几何研究试题一、选择题 (5分⨯4=20分)1. 如图,CD EF AB ||||,已知20=AB ,,80=CD 100=BC 那么,EF 的值是____. A. 10, B.12, C.16, D.20第1题图 第2题图 2. 如图,在ABC ∆中,P 是AC 上的点,取BP 的中点Q ,连结CQ 并延长与AB 交于D ,则ABP S ∆与ACD S ∆的关系是_____.A. ABP ACD S S ∆∆<B. ABP ACD S S ∆∆=C. ABP ACD S S ∆∆>D. 不能确定.3. 如图,在ABC ∆中,BE 、CF 分别是AC 、AB 边上的高,o A 45=∠,那么,FBCE AEF S S :=______.A 1:1B 2:1C 3:1D 4:1第3题图 第4题图4. 如图,ABCD 是面积为1的正方形,PCB ∆是正三角形,PBD ∆的面积为_____.A.213- B. 8132- C. 43D. 413-二、填空题 (5分⨯4=20分)1.如图,已知正方形ABCD 的边长为1,E 为AD 的中点,P 为CE 的中点,F 为BP 的中点,则BFD S =_____.第1题图 第2题图 2.如图,AB 是圆O 直径,4=AB ,弦3=BC ,ABC ∠的平分线交半圆于D ,BC AD ,的延长线交于E ,DCE ABCD S S :=______.3.已知圆O 是ABC ∆的外接圆,半径为r ,CO BO AO ,,分别交对边于F E D ,,, 则:CF BE AD 111++=______.(用r 表示)4.ABC ∆的三条高分别为c b a h h h ,,,又ABC ∆内任一点P 到三边距离分别为c b a p p p ,,,则=++c c b b a a h p h p h p ______.三、证明题(12分⨯5=60分)1. 在ABC ∆中,过点A 作直线BC l ||,B ∠的平分线交AC 于D ,交直线l 于E ,C ∠的平分线交AB 于F ,交直线l 于G ,且FG DE =,求证: ABC ∆是等腰三角形.2.M是以AB为直径的上不同于BA、的任一点,C是直径AB上的定点,过M作CM 垂直的直线交过处BD、,求证:A、的切线于E(1)ED,成等比数列;BM,EC(2)BEAD⋅是定值.3.三条中线把ABC∆分成6个三角形,若这6个三角开的内切圆中有4个相等,求ABC∆是正三角形.4.从等腰ABC ∆的底边AC 上的中点M 作BC 边的垂线MH ,点P 为线段MH 的中点,求证:BP AH ⊥.5.已知: ABC ∆内接于圆O ,N M L ,,分别是弧AB CA BC ,,的中点,连结LM NM ,分别交BC AB ,于E D ,;I 是ABC ∆的内心,求证: (1)BC DE ||;(2)IE DI DE +=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S
B' C' A' Q R A C P
B
证明:如图 在△SBC 和截线 PC'B'中根据梅氏定理可得:
BP CC ' SB ' . . 1 PC C ' S B ' B
①
在△SCA 与截线 QA'C'中根据梅氏定理可得:
CQ AA ' SC ' . . 1 QA A ' S C ' C
∴O 在∠DEF 的角平分线上。
6.在△ABC 中,∠A、∠B 的平分线分别交于对边于 D、E,∠C 的 外角平分线交于对边延长线于 F,求证:D、E、F 共线。
证: ∵AD 平分∠A ∴BD/DC=AB/AC ∵BE 平分∠B ∴CE/EA=BC/BA ∵CF 平分∠C 的外角 ∴AF/BF=CA/CB …③ …② …①
E、H、G 三点共线
4.
设
P
是 正 方 形
ABCD
内 的 一 点 , 使
PA:PB:PC=1:2:3,将 BP 绕 B 点朝着 BC 旋转 90
BP 至 Q. 求证:A、P、 Q 共线.
证明:连接 CQ,∵PA:PB:PC= 1:2:3 设 AP=1 则 BP=2 CP=3 ∵BP 绕 B 点朝着 BC 旋转 90° ∴∠PBQ=90°BP=BQ=2 ① ° ∠BPQ=∠BQP=45 2 2 ∴PQ=√BP +BQ =2√2 又∵四边形 ABCD 是正方形 ∴AB=BC ② ∴∠ABC=∠PBQ= 90°即∠ABP+∠PBC= ∠CBQ +∠PBC=90° ∴∠ABP=∠CBQ ③ ∴△ABP≌△CBQ(由①②③可得到) ∴PA=QC=1
2. 已知:E,F 分别在正方形 ABCD 的两边 BC,CD 上,是∠EAF=45°,但 AC 不是 ∠EAF 的角平分线,自 E,F 作 AC 的垂线,垂足分别是 P,Q 求证:△BPQ 的外心与 B,C 共线
证明: ∵FQ⊥AC ∴∠ABE=∠AQF 又∵∠EAF=45° ∴∠BAE=∠QAF ∴△ABE∽△AQF 可得
10. 有两个正方形 ABCD 与 AB1C1D1,B 与 B1 不重合。求证:直线 BB1、CC1 和 DD1 共点。
B
2
1· · 1' B1 3
A
D1 3' 2' C C1 D P
证明: 设 BB1、CC1 交于 P,在连结 AC、AC1,则有 2 2 ' A、B、C、P共圆
2 2 ' 1 1' ∆ABB'∞∆ACC' 3 3'
2
2
2
2
2
2
°
在∠DEF 的角平分线上。
1
2
证明:∵∠ DEF=180O- ∠ 1- ∠ 2=180O-(180O-2 ∠ B)- ∠ 1=180O-(180O-2 ∠ B)-(180O-2 ∠ C)=2(∠B+∠C)-180O=180O-2∠A 又∵∠DOF=2∠A ∴D.E.F.O 四点共圆 ∵O 是外心 ∴FO=DO ∴∠FEO=∠DEO
由①②③可得:BD/DC*CE/EA*AF/BF=-1 根据梅涅劳斯定理得:D、E、F 共线
7,若三角形的三边两两不等。求证:三外角平分线与对边的交点共线。
D
E
A
C
F
B
证明:如图所示: D 为∠C 外角平分线与 AB 延长线的交点,E 为∠B 外角平分线与 AC 延长线的交点,F 为∠A 外角平分线与 BC 延长线的交点。 ∵ BE 为∠B 外角平分线,CD 为∠C 外角平分线,AF 为∠A 外角平分线 ∴有
②
在△SAB 与截线 RA'B'中根据梅氏定理可得:
AR BB ' SA ' . . 1 RB B ' S S ' A
将上式①②③相乘可得:
③
BP CQ AR . . 1 PC QA RB
根据梅氏定理可得 P、Q、R 三点共线。
9. □EFGH 的顶点在□ABCD 各边,求证:对角线 AC,BD,EG, FH 共点
AB AE AQ AF AE AF
同理可得,△AEP∽△AFD 即
AP = AD
∴
AB AP = AQ AB
利用切割线定理之逆定理,因△BPQ 的外心在 BC 上,等价于 AB,APQ 是切,割线 ∴△BPQ 的外心在 BC 上
3.在 Rt △AB 为斜边,CH 为斜边上 的高,以 AC 为半径作 ☉ A,过 B 作☉A 的任一割线交☉A 于 D、E,交 CH 于 F(D 在 B、F 之间),又作∠ ABG=∠ABD,G 在☉A 上,G 与 D 在 AB 异侧。
再由四边形垂直又有 LAB*+lCD*=lBC*+lAB* (2) (1)*-(2)再除以 2,得 lAB•lCD=lBC•lAB (3) (1) (3)两式表明:lAB lCD lBC lDA 都是 X*+px+q=0 的一对根,故只有如下两种情况 LAB=lBC, lCD=lAB 或 lAB=lAD,lCD=lBC 前者表明 BD 为对称轴,如右图所示,后者断定 AC 是对称轴 ,由此得证 证(2)∵∠1=∠2=∠3=∠4 QS 过点 E 同理:PR 也过点 E 13. △ABC 的内切圆⊙I 分别切三边 BC,CA 和 AB 于 A1,B1 和 C1,线段 AI,BI,和 CI 分别 与⊙I 交于 A2,B2,C2. 求证:直线 A1A2,B1B2,C1C2 共点。 A
∵H.J 分别是AD.AC 的中点,F.I 分别是BG.BD 的中点 ∴HJ=
1 1 CD IF= CD 2 2
∴HJ∥IF
∴∠JHO=∠FIO
∵∠JHO=∠FIO , HJ=FI,HO=FO∴△JHO≅△IFO
∴∠HOJ=∠FOI∴I.O.J 三点共线
∴四边形两双对边中点连线的交点,与两对角线之中点共线
A、B'、C'、P 共圆
又 A、B、C、P
P 是两正方形外接圆的交点 P 在 DD'上 直线 BB1、CC1 和 DD1 共点。
11. I 为△ABC 的内心,X、Y 分别为内切圆与 AB、BC 的切
点,D、E 分别为 BC、CA 的中点. 求证:AI、XY 与 ED 共点.
A
X I P B D Y C
求证: (1)A、H、D 共圆。 (2)E、H、G 共线。 (3)FD、FE、BD、BE 四线段成比例
证明:如图所示:连结 AE、AD (1)∵BC =BH·BA(摄影定理) BC =BD·BE(割线定理) ∴BD·BE=BH·BA ∴A、H、D、E 四点共圆 (2)∵∠ABD=∠ABG ∴∠GBH=∠DBH(对称性) 又∵A、H、D、E 四点共圆 ∴∠FEA=∠DHB(对角等于内对角) ∠AHE=∠EDA(同弧所对的角) 又∵AE=AD ∴∠AEF=∠ADF
初等几何研究试题(6)
六、关于共线点与共点线 1、证明四边形两双对边中点连线的交点与两对角线之中点共线
证明:连接EF.FG.GH.HE.HJ.OJ.OI(如图) ∵E.H 分别是AB.AD 的中点, F,G 分别是BC.CD 的中点∴EH=
1 1 BD FG= BD 2 2
∵EH ∥FG ∴四边形EFGH 是平行四边形 ∴ OH=OF
12. 四边形 ABCD 外切于圆 O,AC⊥BD 并交于 E,P、Q、R、S 顺次为边 AB、BC、CD、 DA 上的切点,连结 PR、QS, 求证: (1)四边形 ABCD 以其一条对角线为对称轴 (2)PR 与 QS 都过 E. A
P E
S
B 2 Q
1 4 3
D O R
C 证明: 设 lAB、 lBC、 lCD 、lDA 分别表示四边形 ABCD 各边之长,则由四边形 ABCD 外切于圆。可知 lAB+ LCD= lBC+ lAB (1)
AX s a
同理
BX s b
a BD BY DY s b DY 2
DY s b a 2
DE AB,BX BY DP DY s b a 2
又
PE DE DP c (s b a ) b AE 2 2 2 AE 再由 DE AB 即知 AP 平分
H
2 2
∴∠AEF=∠DHB=∠GHB=∠ADE=∠AHE ∴∠GHB=∠AHE(对顶角) ∴E、H、G 三点共线 (3)∵∠ABD=∠ABG ∴由对称知:HB 平分∠DHG(∠GHB=∠DHB) 又∵ CH 垂直 AB ∴HC 平分∠DHE ∴HC、HB 是∠DHE 的内外角平分线 ∴
DF HD BD = = FE HE BE
又∵PQ +QC =(2√2) +1 =3 =PC ∴∠PQC=90°, ° ∠BQC=∠PQC+∠BQP=90+45 =135° 又∵∠APB=180°-45 =135° ∴∠BQC=∠APB=135° 即 A、P、Q 共线(∠APB、∠BQP 是邻补 角)
5. 在∆ABC 中,D,E,F 分别在 AB.BC.CA 上,使得 DE=BE,EF=CE. 求证:∆ADF 的外心 O
A2 C1 B1
I
B2 B A1 C
证明:连接 A1,B1 和 C1 ∵圆 I 内切于△ABC, ∴AI,BI,CI 分别平分∠A,∠B,∠C, 即 AI,BI,CI 分别平分弧 B1C1,C1A1,B1A1 ∴A1A2,B1B2,C1C2 是△A1B1C1 的内角平分线 ∴A1A2,B1B2,C1C2 共点。
A
E
D
接 BE,DG 在□ABCD 中,∠B=∠D,AD∥BC ∴∠BGE=∠DEG 在□EFGH 中,EH=FG, EH∥FG, ∴∠FGE=∠HEG ∴∠FGB=∠HED ∴△FBG≌△HDE ∴BG=DE ∴四边形 BGDE 为平行四边形,BD,EG 为对角线 同理四边形 AFCH 为平行四边形,AC,FH 为其对角线 ∴AC,BD,EG, FH 共点
