机械优化设计实例教学文稿
机械优化设计案例
机械优化设计案例：某生产线自动送料机构的改进
在制造领域，生产线上的自动送料机构是确保生产流程顺畅、高效的关键环节。
然而，传统的自动送料机构往往存在效率低下、易损坏、维护成本高等问题。
为了解决这些问题，我们采用了机械优化设计的方法，对某生产线上的自动送料机构进行了改进。
该自动送料机构的主要任务是将原材料从存储区输送到生产线，并确保每次输送的数量准确。
但是，在长时间使用后，传统的送料机构常常出现卡顿、输送不准确等问题。
经过分析，我们发现这些问题主要是由于机构中的某些部件设计不合理，导致机械效率降低。
为了解决这些问题，我们采用了以下优化策略：
结构优化：利用拓扑优化技术，对送料机构的主体结构进行了重新设计，使其在满足强度和刚度的同时，减轻了重量，从而减少了动力消耗。
传动系统优化：采用了新型的齿轮和链条传动系统，减少了传动过程中的摩擦和能量损失，提高了传动效率。
控制系统优化：引入了PLC和传感器技术，实现了对送料过程的精确控制，确保了每次输送的数量准确。
维护性优化：设计了易于拆卸和维护的结构，减少了维护时间和成本。
经过上述优化后，新的自动送料机构的性能得到了显著提升。
与传统的送料机构相比，新的机构在输送速度、准确性、使用寿命和维护成本等方面都有了显著的优势。
经过实际生产验证，新的自动送料机构不仅提高了生产效率，还降低了生产成本，为企业带来了显著的经济效益。
机械优化设计第二版教学设计
机械优化设计第二版教学设计一、引言机械优化设计是机械工程专业课中非常重要的一门课程，可以帮助学生掌握优化设计的方法和技能，提高机械产品的效率、稳定性和可靠性等指标。
本文档旨在介绍机械优化设计第二版的教学设计，内容包括教学目标、教学方式、教学内容和评估方式等。
二、教学目标机械优化设计第二版的教学目标如下：1.了解优化设计的基本概念和理论；2.掌握优化设计的方法和技能，能够应用优化设计的方法解决实际问题；3.了解优化设计在机械产品设计中的应用，提高机械产品的效率、稳定性和可靠性等指标；4.培养学生的创新意识和实际动手能力。
三、教学方式机械优化设计第二版的教学方式采用“理论教学+实验教学”的模式，其中理论教学包括课堂讲授和案例分析，实验教学包括个人实验和小组实验。
1.理论教学理论教学部分将采用面授、讨论等方式，主要内容包括优化设计的基本概念、优化设计的方法和技术、优化设计的应用等。
在授课的过程中，将结合一些典型案例进行分析，以帮助学生更好地理解和掌握优化设计的方法和技能。
2.实验教学实验教学部分将采用个人实验和小组实验相结合的方式，主要内容包括优化设计的基础实验和综合实验。
个人实验主要是为了让学生掌握优化设计的基本操作和方法，小组实验则是为了让学生通过团队协作解决实际问题的能力。
四、教学内容机械优化设计第二版的教学内容主要包括以下方面：1.优化设计的基本概念和理论•优化设计的基本概念和发展历程；•优化设计的基本原理和方法；•优化设计的优化目标和指标；•优化设计的问题模型及其解法。
2.优化设计的方法和技能•描述优化设计的流程；•采用单目标、多目标等优化方法进行机械优化设计；•不同算法的优缺点、适用范围及其应用案例；•通过计算机仿真进行机械优化设计。
3.优化设计在机械产品设计中的应用•解析、设计机械产品时所需要考虑的问题；•使用优化设计方法提高机械产品的效率、稳定性和可靠性等指标；•采用优化设计方法解决机械产品设计中的实际问题。
机械优化设计教案第二篇
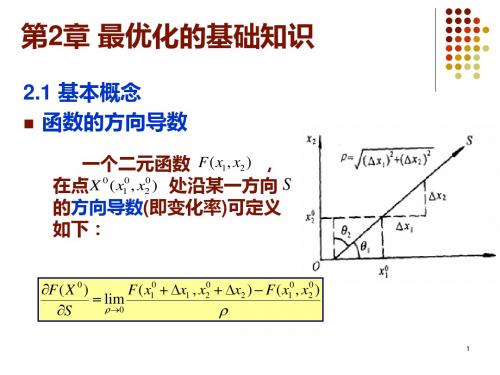
2 例2 1 ：求二元函数 F(X) πx1 x2 / 4 在X 0 [1,1]T 点
1 / 4 1 / 3 沿S1 和S 2 的方向导数。 2 / 4 2 / 6
6
分析:
F ( X ) T F ( X ) S F ( X ) S cos( F ( X ), S ) S 函数F(X)沿S方向的方向导数等于向量▽ F(X)在S方 向上的投影。 当cos（ ▽ F(X) ， S ）＝1时，即S 与 ▽ F(X)方向相 同时，向量▽ F(X) 在 S 方向上的投影最大，其值为 F ( X )
函数F(X)在点X处的梯度▽F(X), 可记作grad F(X)
F ( X ) F ( X ) x1 F ( X ) x2
T
方向S的单位向量
S cos1 cos2
S 1
5
n元函数 F ( x1 , x2 ,, xn ) 的梯度:
F ( X ) F ( X ) F ( X ) F ( X ) , , , x2 xn x1
极小值点●1 a b
X
16
无约束优化问题的极值
对 于n元 函 数 F ( X ) F ( x1 , x2 , , xn )的 无 约 束 极 值 问 题 min F ( X ), X R n 点X *为 一 个 局 部 极 值 点 的 分 充必 要 条 件 是 ：
不等式约束条件下的优化解 不等式约束条件下，可行区域是满足不等式约束的 区域，此区域内有无穷多个解，且必有一个最优解。
14
2.3 极值原理
高等数学中的极值原理实际上是一种无约束优化方法。 由于它是最基本或最简单且广泛应用于工程实际，这里 简单介绍一元函数的极值原理。 设一元函数y=f(x)的定义域为a≤x≤b。在开区间 a<x<b上y=f(x)的极值点X*求法如下：
机械优化设计经典实例演示文稿
第28页，共53页。
1.3.3 数组运算
3). 数组点乘 两数组的对应元素相乘a.*b 结果： [a1＊b1 a2＊b2…an＊bn]
（a与b的维数必须相同）
第29页，共53页。
1.3.3 数组运算
4). 数组点正除（右除） 使两数组的对应元素正除 a./b 结果为:
第43页，共53页。
2.2 无约束非线性优化函数
[结果] x=
1.0e-008 * -0.7512 0.2479
fval =
1.3818e-016
第44页，共53页。
2.3 约束优化函数
[函数] fmincon
[格式]
x= fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x= fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon, options)
[x,fval] = fmincon(…)
第45页，共53页。
2.3 约束优化函数—盖板优化实例：
第46页，共53页。
目标函数：
f(x ) 2 6t 0 2 0 .5 h 1x 2 1 x 0 2
6.1(2 x12x22)x31 0 6
第10页，共53页。
设计实例1:
g 1 ( X ) d 4 D 4 1 . 2 D 1 7 5 x 2 0 4 x 1 4 1 . 2 1 5 7 0 0 g 2 ( ) 1 D 4 . 3 5 d D 44 4 D D d 3 /2 1 x 1 4. 3 5 x 2 x 4 1 4 4 x 1 x 1 x 2 3 /2 0
1.4.3 M-文件的操作
机械优化设计课程设计
目录摘要 (3)关键词 (3)一、概述 (3)二、优化方法介绍 (3)（一）、一维搜索方法 (3)（二）无约束优化方法 (5)1）共轭方向的生成 (6)2）基本算法 (6)3)改进算法的基本步骤如下 (7)三、优化设计实例 (10)1）模型 (10)2）变量 (10)3）优化设计源程序 (10)4）分析结果 (20)四、课程总结 (20)《机械优化设计》课程设计论文摘要：随着社会经济的迅速发展，机械优化设计作为一门为工程设计提供手段的学科，在这样的时代背景下应运而生。
针对具体的课题，通过一些设计变量而建立起目标函数的过程，称为数学建模；应用优化方法为工程设计寻找出最优解是现代优化设计所研究的主要课题与方向。
关键词：机械优化设计；设计变量；目标函数；数学模型；优化方法一、概述优化设计是20世纪60年代初发展起来的一门新学科，它是将最优化原理与计算技术应用于设计领域，为工程设计提供一种重要的科学设计方法的手段。
利用这种新的设计方法，人们就可以从众多的设计方案中寻找出最佳设计方案，从而大大提高设计效率和设计质量。
因此优化设计是现代设计理论和方法的一个重要领域，它已广泛应用于各个工业部门，成为现代工程设计的一个重要手段！二、优化方法介绍（一）、一维搜索方法一维搜索方法可分为两类，一类称为试探法，这类方法是按某种给定的规律来确定区间内插入点的位置，此点位置的确定仅仅按照区间缩短如何加快，而不顾及函数值的分布关系，例如黄金分割法，裴波那契法等。
另一类一维搜索法称作插值法或函数逼近法。
这类方法是根据某些点处的某些信息，如函数值，一阶导数，二阶导数等，构造一个插值函数来逼近原来的函数，用插值函数的极小点作为区间的插入点，这类方法主要有二次插值法，三次插值法等。
在此重点讨论黄金分割法。
黄金分割法适用于[a, b]区间上的任何单谷函数求极小值问题，对函数除要求“单谷”外不作其他要求，甚至可以不连续。
因此，这种方法的适应面相当广。
机械优化设计实例
机械优化设计实例公司生产的机械设备是用来处理废气的，该设备由风机和过滤系统组成。
一些客户反映在高温环境下，设备的性能下降严重，需要频繁维护和更换零部件。
为了解决这个问题，公司决定进行机械优化设计，提高设备在高温环境下的性能和可靠性。
首先，公司通过实地调研和用户反馈，发现高温环境下设备性能下降的主要原因是风机的叶轮脆性破坏和过滤系统的滤芯耐高温能力差。
因此，公司决定对风机和过滤系统进行优化设计。
风机优化设计的一项重要措施是改变叶轮材料。
公司与材料科学研究院合作，选用一种可耐高温的新型材料。
这种新材料具有良好的耐腐蚀性和高强度，能够在高温环境下保持稳定的性能。
通过对风机进行新材料叶轮的更换，可以大大提高设备在高温环境下的可靠性和寿命。
过滤系统的优化设计主要包括滤芯材料的改进和结构的优化。
公司与滤芯制造商进行合作，针对高温环境下滤芯易损的情况，选用了一种能够耐受高温的特殊材料制作滤芯。
该材料具有优异的耐热性和抗腐蚀性，能够有效过滤废气中的有害物质。
此外，公司还对滤芯的结构进行优化设计，增加了滤芯的表面积，提高了吸附效率和容尘量。
除了对零部件的优化设计，公司还对设备的工艺流程进行了改进。
在原有的设备上增加了高温预热和冷却系统，可以避免温度的突变对设备的影响，提高了设备的稳定性和寿命。
经过优化设计，该公司的机械设备在高温环境下的性能得到了显著提高。
经实际运行验证，设备在高温环境下能够稳定工作，无需频繁维护和更换零部件，极大地减少了停机时间和维修成本。
同时，设备的可靠性和寿命也得到了显著提升，增强了客户的信任和满意度。
这个实例充分展示了机械优化设计的重要性和成功应用。
通过对机械结构、工艺流程和材料的优化，可以提高机械产品的性能、效率和可靠性，满足客户的需求，提升企业的竞争力。
机械优化设计第五版教学设计 (2)
机械优化设计第五版教学设计一、教学目标1.掌握机械优化设计的基本概念和设计方法。
2.能够理解和应用CAD/CAM软件进行机械优化设计。
3.能够自主设计和制作简单的机械产品，达到工业实际应用水平。
二、教学内容1. 机械优化设计基础1.1 机械优化设计的基本概念与原理 1.2 机械优化设计的设计流程与主要方法2. CAD/CAM软件的使用2.1 CAD软件基础 2.2 CAM软件基础 2.3 CAD/CAM协同设计3. 机械设计实例分析3.1 零件分析与选材 3.2 设计思路和方案比较 3.3 机械设计的优化和改进三、教学方法教学方法以讲授、实践操作、案例分析结合为主，注重学生的互动和个性化教学。
讲授环节：由教师进行机械优化设计基础理论的讲解和CAD/CAM软件的使用方法演示。
实践操作环节：学生在教师的指导下，使用CAD/CAM软件进行操作实践，从而能够熟练地掌握机械优化设计和软件使用。
案例分析环节：通过对实际机械产品的设计案例进行分析，学生能够理解机械设计的思路和方法，同时能够学到好的设计习惯和经验。
四、考核方式1.平时成绩占总成绩的30%，其中包括实验成绩和平时作业等。
2.期末考试占总成绩的70%，主要考核学生对机械优化设计理论的掌握程度和软件的操作能力。
五、参考教材1.《机械优化设计基础》2.《CAD/CAM设计与应用》3.《机械设计手册》六、教学进度安排教学单元授课时间实践时间第一单元：机械优化设计2周1周第二单元：CAD/CAM软件2周1周第三单元：案例分析与实践2周1周七、教学总结本课程的主要目的是使学生能够较深入地理解机械优化设计的基本概念和设计方法，并能够熟练使用CAD/CAM软件进行机械产品的设计。
教师在授课中应重视案例分析，在帮助学生熟练掌握机械优化设计基础和软件操作方面，还要注意培养学生的动手能力和团队协作能力。
学生也应在实践操作中不断探索和创新，不断完善自己的设计思维和实践能力，达到真正意义上的工程应用水平。
机械优化设计范例
1 / 8例题：用一批长度为4ｍ的圆钢,下长度为698ｍｍ的零件4000个和长度为518ｍｍ的零件3600个。
如何下料才能使消耗的圆钢数量最少?解：（一） 建立机械优化设计数学模型（设计变量、目标函数、约束条件）设698ｍｍ的零件记为①,518ｍｍ的零件记为②。
对本例题,若只用4ｍ长的圆钢,则总共有6种下料方案:下5个零件①,0个零件②,利用率87% （%87%10040005698=⨯⨯） 方案一 下0个零件①,7个零件②,利用率91% （%91%10040007518=⨯⨯） 方案二下4个零件①,2个零件②,利用率96% （%96%100400025184698=⨯⨯+⨯） 方案三下3个零件①,3个零件②,利用率91% （ %91%100400035183698=⨯⨯+⨯） 方案四 (1)下2个零件①,5个零件②,利用率99% （%99%100400055182698=⨯⨯+⨯） 方案五下1个零件①,6个零件②,利用率95% （%95%100400065181698=⨯⨯+⨯） 方案六从式(1)可知,用4ｍ长的圆钢总共有6种下料方法。
现用1X 、2X 、3X 、4X 、5X 、6X 分别表示按这种方式下料所需的圆钢数量,则下料方案可用表1表示。
2 / 8表1 下料方案Tab.1 Cutting material plan 原钢种类（m ）数量零件① 零件② 方 案 4 1X5 0 方案一 4 2X0 7 方案二 4 3X 4 2 方案三 4 4X 3 3 方案四 4 5X 2 5 方案五 46X16方案六表示为数学模型就是Min 654321654321),,,,,(X X X X X X X X X X X X f +++++= (2)51X +43X +34X +25X +6X ≥4000 (3) 72X +23X +43X +55X +66X ≥3600 (4) Ｘ1≥0,Ｘ2≥0,Ｘ3≥0,Ｘ4≥0,Ｘ5≥0,Ｘ6≥0 (5)3 / 8式(2)称为目标函数，式(3)、式(4)和式(5)都称为约束条件。
机械优化设计说课稿
《优化设计的数学模型》说课稿张华我说课的题目是：《优化设计的数学模型》。
本章是中国石化出版社第一版《现代设计方法》第二章第二节的内容。
我主要从教材分析，教法设计，学法指导，教学设计四个方面进行阐述。
一、教材分析：从以下三方面加以分析。
1、地位作用：本节主要讲授建立优化设计数学模型的三要素：即目标函数、设计变量和约束条件，建立优化设计问题的数学模型，是进行实际问题优化设计首要环节，它为后续进行优化设计算法和编程，以及得出准确的优化结果奠定良好的基础。
本小节是第二章的教学重点章节。
2、教学目标：根据大纲要求，结合学生特点，我将教学目标定为知识目标，能力目标，情感目标三个方面。
知识目标： 1）理解优化设计问题数学模型的组成。
2）掌握优化设计问题数学模型的建立方法。
能力目标： 1）培养学生从实际问题进行抽象、概括、归纳优化设计数学模型的能力。
2）培养学生主动探究、协作学习的能力。
情感目标：培养学生迎难而上克服困难的精神和正确认识事物本质的方法论。
3、学情分析本门课的授课对象是普通本科机械电子工程专业大三学生，他们前续已经学习了《高等数学》、《机械设计》、《机械原理》、《现代工程图学》、《三维软件基础》等课程，具有产品设计研发的基本思路和方法，但工程实践经验不足，概括和抽象能力有待提升。
4、重点与难点由于工程优化问题的复杂难易程度有差异，所以其数学模型的建立也有难易，而建立其优化设计的数学模型是开展后续优化环节的首要步骤，数学模型建立是否准确，直接决定了后续优化结果的可靠性，所以它是本章的重点。
而要使学生掌握优化设计数学模型的建立方法，需要学生有数学建模的基本理论，有工程问题抽象思维的能力，而这对于机电专业普通本科生而言是有一定的难度的，所以把它定为教学难点。
二、教法设计：主要采用演示法、启发诱导法和研讨法的教学方法，通过“动画演示、创设问题情境提出问题、探究验证回答问题、发现一般规律、共同讨论得出结论”等环节，体现“教为主导，学为主体”的教学原则。
第八章机械优化设计实例
机械与材料学院
×
2、目标函数： 、目标函数：
考虑主轴最轻， 考虑主轴最轻，所以机床主轴优化设计的 目标函数为
材料的密度
机械与材料学院
×
3、约束条件： 、约束条件：
1）刚度约束条件：由于主轴刚度是一个重要 ）刚度约束条件： 的性能指标，其外伸端的挠度y不得超过规定值 不得超过规定值y 的性能指标，其外伸端的挠度 不得超过规定值 0 所以可依此建立性能约束： 所以可依此建立性能约束：
例子
机械与材料学院
×
尺度变换前的等值线图
尺度变换后的等值线图
机械与材料学院
×
2、设计变量的尺度变换 、 ——对设计变量进行重新标度，使它们称 对设计变量进行重新标度， 对设计变量进行重新标度 为无量纲和规格化的设计变量。 为无量纲和规格化的设计变量。 方法： 方法：
原 设 计 变 量 新 设 计 变 量
机械与材料学院
×
2、目标函数的确定 、
目标函数——一项设计所追求的指标的数学反映 一项设计所追求的指标的数学反映 目标函数 要求： 要求： 能够用来评价设计的优劣 必须是设计变量的可计算函数
机械与材料学院
×
1）、优化目标的选择： ）、优化目标的选择： ）、优化目标的选择
应当对所追求的各项指标进行细致分析， 应当对所追求的各项指标进行细致分析，从 中选择最重要、 中选择最重要、最具代表性的指标作为优化 目标
机械与材料学院
×
•在性能约束中，又有复杂和简单之分 在性能约束中， 在性能约束中 约束函数有的很简单，可以表示成显式形式， 约束函数有的很简单，可以表示成显式形式， 即反映设计变量之间明显的函数关系，这类约束叫 即反映设计变量之间明显的函数关系， 显式约束。 做显式约束。例如设计曲柄连杆机构时的曲柄存在 约束条件 有的只能表示成隐式形式，例如复杂结构的性 有的只能表示成隐式形式， 能约束函数（变形、应力、频率等） 能约束函数（变形、应力、频率等），需要通过有 限元或动力学计算求得，机构的运动误差要用数值 限元或动力学计算求得， 积分来计算，这类约束叫做隐式约束 隐式约束。 积分来计算，这类约束叫做隐式约束。
第八章机械优化设计实例
第八章机械优化设计实例机械优化设计是指通过优化设计方法和技术，提高机械产品的性能、降低成本和改善产品的可靠性和可维修性。
在本章中，我们将介绍两个机械优化设计实例，分别是汽车发动机和风力发电机的优化设计。
汽车发动机的优化设计是目前汽车行业的热点问题。
传统的汽车发动机具有功率输出低、能效低和排放高等问题。
为解决这些问题，可以通过优化设计改善发动机的气缸设计、燃烧室设计和可变气门技术等。
例如，通过增加气缸数和减小气缸直径来提高发动机的功率输出和燃烧效率；通过优化燃烧室形状和喷射系统来提高燃烧效率和降低排放；通过采用可变气门技术来提高发动机的响应速度和燃烧效率。
风力发电机的优化设计是提高风力发电机转化效率的重要途径。
传统的风力发电机的转化效率较低，主要是由于叶片的设计不合理和气动噪声等。
为此，可以通过优化叶片的形态和材料，改善气动性能和降低噪声水平。
例如，通过增加叶片的长度和调整叶片的弯曲角度来提高叶片的气动效率；通过选择具有良好耐候性和强度的材料来延长叶片的使用寿命。
此外，还可以通过改进整个风力发电机的结构和控制系统，提高发电机的运行稳定性和可靠性。
以上两个实例都是典型的机械优化设计案例，通过采用优化设计方法和技术，可以显著提高机械产品的性能和质量，降低生产成本和维护成本，同时还可以减少对环境的影响，提高产品的竞争力和市场占有率。
机械优化设计的核心是在设计阶段充分考虑产品的性能、成本和可靠性等因素，通过系统性的优化设计方法和工具，找出最佳设计方案。
优化设计的过程包括问题定义、设计参数选择、设计方案生成和评估等。
其中，设计参数的选择是非常重要的，设计参数的合理选择可以显著影响产品性能和成本。
在实际的优化设计中，可以使用模拟软件和实验方法进行参数优化和设计方案评估。
在机械优化设计实例中，我们提到了汽车发动机和风力发电机的优化设计。
这两个实例都是当今社会中具有重要意义的机械产品，它们的性能和质量对整个行业的发展和进步起着重要的推动作用。
机械优化设计
机械优化设计课题货箱优化设计姓名：xxxx学号：xxxxxx班级：xxxxxx目录一、问题描述 (3)二、问题分析 (3)三、建立数学模型 (3)四、优化方法的选择 (4)五、设定初始点 (5)六、利用matlab进行数学运算分析 (6)七、结果分析 (7)八、Matlab 程序源代码 (7)总结 (11)一、问题描述现用薄板制造一个货箱，是一个长度不小于5m的无上盖的立方体货箱，高度不小于2m，宽度不小于1m，要求该货箱的钢板耗费量最少，试确定货箱的长、宽、高尺寸。
二、问题分析（1）目标：用料最少，即货箱的表面积最小。
（2）设计参数确定：长x1 、宽x2 、高x3；（3）设计约束条件：（a）长度要求（b）宽度要求（c）高度要求三、建立数学模型(1 )参数及条件分析；设计参数：x1, x2 ,x3设计目标; f(x)min=x1x2+2x2x3+2x1x3约束条件; g1=x1>=5g2=x2>=1g3=x3>=2其数学模型为；Minf(x)=f(x1,x2,x3)s.t. x1>=5x2>=1x3>=2四、优化方法的选择本设计是含有不等式约束的优化问题，是在三个不等式约束条件所确定的可行域内，寻求最优解。
可以将这个约束优化问题中的约束函数进行特殊的加权处理，和目标函数结合起来，构成一个新的目标函数，即将约束优化问题转化为一个无约束优化问题。
然后对新的目标函数进行无约束优化计算。
因而根据此思路可以通过构造惩罚函数把约束优化问题转化为一些列无约束优化问题，进而用无约束最优化方法求解，本题采用外点法进行优化。
利用外点法将不等式和等式约束函数经过加权转化后，和原目标函数结合成新的目标函数即惩罚函数如下；F(x)min=x1x2+2x2x3+2x1x3+r(x1-5)^2+r(x2-1)^2+r(x3-2)^2对于这个无约束优化问题，首先求其海赛（Hessian ）矩阵如下 r r r222221212由于惩罚因子r>0，所以各阶顺序主子式都大于零，海赛矩阵在可行域内是正定的，满足凸性条件，因此可以判断这个函数是凸函数，属于凸规划。
机械优化设计课程教学设计
《机械优化设计》课程教学设计（一）基本描述课程编号：S4080270课程名称：机械优化设计课程英文名称：OPTIMAL DESIGN OF MACHINE总学时：30 讲课学时：30 习题课学时：0 实验学时：0 上机学时：0 学分：2开课单位：机电工程学院机械制造及其自动化系授课对象：机电工程学院机械设计制造及其自动化专业，其它相关专业。
先修课程：高等数学理论力学材料力学机械原理机械设计机械制造装备设计高级语言程序设计。
开课时间：第七学期教材与主要参考书：孙靖民．《机械优化设计》机械工业出版社2003年6月孙全颖．《机械优化设计》哈尔滨工业大学出版社2005年（二）课程性质、研究对象及任务机械优化设计是机械类专业的专业选修课，其目的是使学生树立优化设计的思想，掌握优化设计的基本概念和基本方法，获得解决机械优化设计的初步能力，进一步提高学生的分析问题和解决问题的水平。
通过本课程的学习，培养学生具备以下几个方面的能力。
1、树立优化设计的思想，理论联系实际，具有创新设计的能力。
2、掌握机械优化设计的思想、方法和规律。
在学习优化设计基本理论的基础上，应具备数学模型的建立、优化方法的选择、软件使用、优化结果分析等方面的能力。
3、正确的运用已经学过的机械优化设计基础理论和基础知识，能够初步解决其它领域的最优化问题。
4、正确掌握本领域出现的新技术、新原理和新方法，初步具备进行机械结构优化与综合研究的能力。
机械优化设计是高等工科院校中机械设计制造及其自动化专业现代设计方法模块的一门主干课，它能够综合的运用先修课程所学到的知识与技能，在进一步加强数学基础理论知识培养的同时，重点训练学生运用数学方法解决机械设计问题的能力，为学生今后从事机械优化设计及其它相关工作打下一定的基础。
（三）教材选择分析目前全国已经编写出版的机械优化设计的教材比较多，合起来不少于十几本。
但是，综合起来讲，还是由机械工业出版社出版，由哈尔滨工业大学孙靖民教授主编的机械优化设计教材比较合适。
机械优化设计方法讲课文档
,
,...
x1
x2
xn
沿d方向的方向向量
cos 1
d
c
o
s
2
...
c
o
s
n
即
f d x0
f x0 T d
fx0T cosf,d
第四十二页，共202页。
图2-5 梯度方向与等值面的关系
第四十三页，共202页。
第二节 多元函数的泰勒展开 若目标函数f(x)处处存在一阶导数，则极值点 的必要条件一阶偏导数等于零，即
xx1 x2 ... xnT
第十八页，共202页。
图2-4 设计空间
第十九页，共202页。
二、约束条件
一个可行设计必须满足某些设计限制条件，这 些限制条件称作约束条件，简称约束。
性能约束 约束 （按性质分） 侧面约束
按数学表达形式分 ：
针对性能要求
只对设计变量的取值范 围限制（又称边界约束）
第二十页，共202页。
f x 1 (0 ) x 1 ,x 2 0 x 2f x 1 0 ,x 2 0 x 2 x 1
x 1
f
x10,x20 x2 f
x10,x20
x2
x2
f x0
f x0
x1
cos1 x2
cos2
第三十九页，共202页。
二、二元函数的梯度
对于二维函数 f x1, x2 在 x 0 点处的梯度
T=0.25cm,
105
1钢0 3管k g材m料3 的弹性模量E=2.y 1 × Mpa，材料密度ρ=7.8 ×
/ ，许用压应 力y = 420MPa。 求e 在钢管压应力
不超过许用压应力 和失稳临界应力 的条件下，人字
机械优化设计实例
机械优化设计实例以机械设备的流体传动系统为例，该系统由电机、泵、阀门等构成，用于传动液体介质。
现有系统存在的问题是效率低、能耗高以及噪音大等。
为了改善这些问题，进行了机械优化设计。
首先，针对效率低和能耗高这两个问题，通过增大泵的转速和修改泵的设计参数来提高泵的效率。
同时，通过更换高效的电机，以减小能耗。
此外，对于传动介质进行优化选择，使用黏度小的液体介质，进一步提高系统的效率。
其次，针对噪音大的问题，从系统的结构和材料方面考虑进行优化。
通过增加隔音隔震材料，减少噪音的传递和扩散。
在设计阀门和管道连接处增加密封材料，减少泄漏和冲击声发生。
另外，通过优化系统的结构，减少振动和共振现象，降低噪音产生。
此外，还可以通过加入传感器和自动控制系统来实现对流体传动系统的自动监控和控制，进一步提高系统的效率和稳定性。
通过传感器检测系统的工作状态和参数，通过控制系统对电机、泵和阀门等进行自动调整和优化控制，实现系统的自动化运行。
最后，对整个流体传动系统进行整体优化设计。
通过数值模拟和实验验证，调整和改进系统的设计参数。
通过减少系统的阻力和压降，提高系统的流动性能。
同时，优化系统的结构布局，减少空间占用和安装方便。
通过以上的优化措施，改进了机械设备的流体传动系统的性能。
系统的效率得到提高，能耗减少，同时噪音也得到了降低。
同时，通过自动控制系统的应用，实现了对系统的自动监控和优化，提高了整个系统的可靠性和稳定性。
这也是一个典型的机械优化设计实例。
总结起来，机械优化设计可以通过对机械结构、零部件、工艺等方面进行修改和改进，提高机械性能、降低成本和提高效率。
在实际应用中，需要根据具体问题进行针对性的优化设计，并进行数值模拟和实验验证，以达到最佳的优化效果。
机械优化设计实例
机械优化设计作业一、优化设计问题的提出预制一无盖水槽，现有一块长为4m，宽为3m的长方形铁板作为原材料，想在这块铁板的四个角处剪去相等的正方形以制成无盖水槽，问如何剪法使水槽的底面积最大？二、建立问题的数学模型为了建成此无盖水槽，可设在这块铁板的四个角处剪去相等的正方形的边长为X,所建造水槽的底面积为S，分析问题有次问题变成在约束条件：X≥04-2X≥03-2X≥0限制下,求目标函数：S（X）=（4-2X）(3-2X)=4-14X+12的最大值。
由此可得此问题的数学模型为：Min S（X）=4约束条件：（ =-X ≤0 （ = -（4-2X ）≤0（ =-（3-2X ）≤0 算法为黄金分割法。
四、外推法确定最优解的搜索区间用外推法确定函数S （X ）=4 索区间。
设初始点 ， =S( )=12; = +h=0+1=1， =S( )=2;比较 和 ，因为 < h=2h=2x1=2， = +h=1+2=3, 比较 和 ，因为 > ,面，故搜索区间可定为[a,b]=[1，3]。
五、算法框图六、算法程序#include <math.h>#include <stdio.h>double obfunc(double x){double ff;ff=4*X*X-14*X+12;return(ff);}void jts(double x0,double h0,double s[],int n,double a[],double b[]) {int i;double x[3],h,f1,f2,f3;h=h0;for(i=0;i<n;i++)x[0]=x0;f1=obfunc(x[0]);for(i=0;i<n;i++) x[1]=x[0]+h*s[i];f2=obfunc(x[1]);if(f2>=f1){h=-h0;for(i=0;i<n;i++)x[2]=x[0];f3=f1;for(i=0;i<n;i++){x[0]=x[1];x[1]=x[2];}f1=f2;f2=f3;}for(;;){h=2.0*h;for(i=0;i<n;i++)x[2]=x[1]+h*s[i];f3=obfunc(x[2]);if(f2<f3)break;else{for(i=0;i<n;i++){x[0]=x[1];x[1]=x[2];}f1=f2;f2=f3;}}if(h<0)for(i=0;i<n;i++){a[i]=x[2];b[i]=x[0];}elsefor(i=0;i<n;i++){a[i]=x[0];b[i]=x[2];}printf("%4d",n);}double gold(double a[],double b[],double eps,int n,double xx) double f1,f2,ff,q,w;double x[3];for(i=0;i<n;i++){x[0]=a[i]+0.618*(b[i]-a[i]);x[1]=a[i]+0.382*(b[i]-a[i]);}f1=obfunc(x[0]); f2=obfunc(x[1]);do{if(f1>f2){for(i=0;i<n;i++){b[i]=x[0];x[0]=x[1];}f1=f2;for(i=0;i<n;i++)x[1]=a[i]+0.382*(b[i]-a[i]);f2=obfunc(x[1]);}else{for(i=0;i<n;i++){a[i]=x[1];x[1]=x[0];}f2=f1;for(i=0;i<n;i++)x[0]=a[i]+0.618*(b[i]-a[i]);f1=obfunc(x[0]);}q=0;for(i=0;i<n;i++)q=q+(b[i]-a[i])*(b[i]-a[i]);w=sqrt(q);}while(w>eps);for(i=0;i<n;i++)xx=0.5*(a[i]+b[i]);ff=obfunc(xx);printf("xx=ff=%5.2f,,,,%5.2f",xx,ff);return(ff);}void main(){int n=1;double a[1],b[1],xx;double s[]={1},x0=0;double eps1=0.001,h0=0.1;jts(x0,h0,s,n,a,b);gold(a,b,eps1,n,xx);七、程序运行结果与分析（1）程序运行结果（截屏）（2）结果分析、对与函数S（X）=（4-2X）(3-2X)=4-14X+12，令(X)=8X-14=0可解的X=1.75，说明程序运行结果正确。
第8章_机械优化设计实例
第8章_机械优化设计实例1.引言机械优化设计是用于提高机械系统性能的重要方法之一、本章将介绍两个机械优化设计实例，分别是电动车的电动机设计和汽车发动机排气系统设计。
通过对这两个实例的分析和优化，可以了解到机械优化设计的基本原理和方法。
2.电动车的电动机设计电动车的电动机是其动力系统的核心部件，其设计和性能直接影响到电动车的续航里程、加速性能和整车效率等。
在进行电动机设计时，需要考虑功率、转速范围、效率等因素。
在优化设计电动机时，首先需要确定其电机类型，常见的有直流电机（DC motor）、异步电机（Asynchronous motor）和同步电机（Synchronous motor）等。
根据电动车的使用条件和要求，选择合适的电机类型。
其次，需要确定电动机的参数，如磁极数、线圈匝数、齿槽数等。
通过改变这些参数，可以改变电动机的转速范围和功率输出等性能。
同时，还需要优化电动机的效率，提高其能量利用率。
最后，还需要对电动机进行热设计，确保其工作时不会过热。
通过合理的散热设计和冷却系统，可以有效降低电动机的温度，提高其稳定性和寿命。
3.汽车发动机排气系统设计汽车发动机排气系统是排放控制和动力性能的重要组成部分，其设计直接影响到发动机的功率输出和排放性能。
在进行排气系统设计时，需要考虑排气阻力和噪声等因素。
优化排气系统设计的方法之一是通过改变排气管的形状和长度来降低排气阻力。
通过数值模拟和实验测试，可以确定最佳的排气管尺寸和形状，以提高发动机的功率输出和燃烧效率。
另一方面，还可以通过改变排气系统的消声器和消音器等部件来降低排气噪声。
通过优化消声器的结构和材料，可以有效降低排气系统的噪声水平，提高车辆的驾驶舒适度。
此外，还需要考虑排气系统对发动机的冷却效果。
通过合理设计排气系统的散热器和风道等部件，可以提高发动机的冷却效果，降低发动机的温度，提高整车的性能和可靠性。
4.结论机械优化设计是提高机械系统性能的重要手段之一、通过上述两个机械优化设计实例的分析，可以看出在机械优化设计中需要考虑多个方面的因素，如功率、效率、排气阻力、噪声等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机械优化设计实例压杆是一根足够细长的直杆，以学号为p值，自定义有设计变量的尺寸限制值，求在p 一定时d i、d2和丨分别取何值时管状压杆的体积或重量最小？（内外直径分别为d i、d2）两端承向轴向压力，并会因轴向压力达到临界值时而突然弯曲，失去稳定性，所以，设计时，应使压应力不超过材料的弹性极限，还必须使轴向压力小于压杆的临界载荷。
解：根据欧拉压杆公式，两端铰支的压杆，其临界载荷为:I ――材料的惯性矩，EI为抗弯刚度1、设计变量现以管状压杆的内径d i、外径d2和长度l作为设计变量2、目标函数以其体积或重量作为目标函数3、约束条件以压杆不产生屈服和不破坏轴向稳定性，以及尺寸限制为约束条件，在外力为p的情况下建立优化模型：min F〔孟）=oiia 右詡异）=—一和）J2） '压杆的最优化设计也㈤皿也2亟刍-皿。
4勿（忙）=韵佃1 dJ = P -卩匕型—瘩辽（茁—町）I2~M?嵐二（工）==止皿_£］玉o血（兀）=呂.SJ =右 ~ ^lmax —°3) .3 ■■' -J」j -工—二.g$ (光)~ & (£) —^2 2JHK—"」^W = ^W = U-/^ogO劭刘罚函数:反耐皿上严）二7寓-町）f +円｛［诡［o,［cr］-+ mm[ Q@『+nun[鸥『+min[ 0,?]3 + ■■■)传递扭矩的等截面轴的优化设计2、目标函数JT 讪(為4-d「)―^—胡解：1、设计变量:冈区I3、约束条件:式中：――轴所传递的最大扭矩勿（匿）二內⑴二兰拿-罔空J7EZ2）要求扭转变形小于许用变形。
即:式中：G――材料的剪切弹性模数32M T13）结构尺寸要求的约束条件:若轴中间还要承受一个集中载荷，则约束条件中要考虑：根据弯矩联合作用得出的强度与扭转约束条件、弯曲刚度的约束条件、对于较重要的和转速较高可能引起疲劳损坏的轴，疲劳强度校核的安全系数法，增加一项疲劳强度不低于许用值的约束条件。
Jp ――极惯性矩，对实心轴:以轴的重量最轻作为目标函数:a = = --- Ip41）要求扭矩应力小于许用扭转应力，即:抗扭截面系数。
对实心轴16应采用二级齿轮减速器的传动比分配二级齿轮减速器，总传动比i=4，求在中心距A最小下如何分配传动比？设齿轮分度圆直径依次为d i、d2、d3、d4。
第级减速比分别为i 1、i 2。
假设d i=d3,则:1 1 4 1 4」飞3化)+囲+血)］飞如+ 訂二护［卄廿2］七辊矫直实验罚函数法是一种对实际计算和理论研究都非常有价值的优化方法，广泛用来求解约束问题。
其原理是将优化问题中的不等式约束和等式约束加权转换后，和原目标函数结合成新的目标函数，求解该新目标函数的无约束极小值，以期得到原问题的约束最优解。
考虑到本优化程序要处理的是一个兼而有之的问题，故采用混合罚函数法。
-)、优化过程(1)、设计变量以试件通过各矫直辊时所受到的弯矩为设计变量:X -M3- [x1工4 x5]r(2)、目标函数住用在轿直辗上的压力以矫直机的驱动功率为目标函数式中：——矫直速度，mm/s匸一一矫直辊直径，mm耳一一传动效率亠」二一一作用在辊子上的总传动力矩叽=M t+皿+心: --- 轧件弯曲变形所需的转动力矩，N.mmM t=十十亞占+ M补丄一4%M" ' ――克服轧件与辊子间滚动摩擦所需的转动力矩，N.mm山――克服辊子轴承的摩擦及支承辊与工作辊间的滚动摩擦所需力矩，.mm上式表明，编制程序时也可以把目标函数简化为求弯矩和的最小值。
简化问题，可以将程序中的目标函数改为工X =兀+兀$十工4 +屯+兀&（3）、不等式约束首先，试件应满足咬入条件，即式中：丁二一一一、二辊之间的相对压下量口一一试件与矫直辊之间的滑动摩擦系数其次，要保证试件每经过一个矫直单元，实现一次反向弯曲，且弯矩值在极限范围内，即式中：门』一一使试件产生反向弯曲的最小弯矩值，N.mm为了使试件变形充分、均匀，在经过第一、第二个矫直单元时反弯曲率值与原始曲率值应尽量接近。
也就是说，前几个矫直单元采用大变形矫直方案。
试件从最后一个矫直辊中出来后, 要满足质量要求，符合国家有关标准，即有C式中：L门——有关标准规定的残余曲率值，对于本试件[cj= Z.OxlO'5mm~x(4)、等式约束式中：*--、•-＞、・’匸、•’工——分别为相邻两辊之间的相对压下量二)、优化数据以原始曲率半径为2000mm的08F双层焊管为例，得到优化矫直力矩为X 二｛百花花石x.y =(21274.6 22321 9 22045.Z 21983.2 21874.7)7优化矫直力为P={P l马E 耳耳死耳f 二{274.4 820.8 1088.6 1079.5 1062.8 783.4 分别对原始双层曲率半径为1500mm 2500mm和3000mmB勺断面系数相同的5级齿轮传动的传动比分配在指挥仪及精密仪器中，常用如图所示的多级减速器。
为了提高运动精度，不仅要求减重，还要求转动惯量小。
已知总减速比为i,假定各级小齿轮参数相同，各级减速比分别为,且有一：。
下面推导转动惯量和中心距的表达式。
解：i.总转动惯量’」式中一1为小齿轮转动惯量，■- ■-。
若令"-等于下式右端括号内各项，即当1 一定时，对'1求极小，则必为极小，「称传动的转动惯量系数。
2•中心距-进行矫直力矩优化，得到的优化值与原始曲率半径为2000mm的值相差不大。
£二㊁哄力十弓+%+九+258.2)r08F 双层卷焊管式中T为小齿轮分度圆直径。
令-7等于下式右端括号内各项，则T一定下，对-八求极小，必使二亦极小，这意味着重量亦小。
-称中心距系数，即二」-本问题要求减速器重量和转动惯量小，这是双目标优化问题，设计变量为•- ■- ■-，可用线形加权法构造双目标转化为单目标无约束优化问题，即匚:」-式中的=1、笑=1 为权因子，表明设计者对禺（标志转动惯量）和疋2 （标志重量）的重要程度而选定的系数，一般有空一-，例如选二」-，二」- 等。
选取不同□一 - 、二」- 求解，可了解它们对传动比分配的影响，从中选设计者认为满意的解。
曲柄摇杆机构运动规律的最优化设计（复合形法）并且其传动角「（机构的连杆I•与摇杆之间的夹角）的最大值及最小值应分别不大于、不小于其许用值，即『叱站；込］=4罗。
Illi柄掘朴机构简图当曲柄人由其初始位置册转到% 2列规律运动：时，要求摇杆由其极限角” 1开始按下曲柄揺杆机构简图1. 确定设计变量考虑到机构杆长按比例变化时不会改变其运动规律，因此在计算时常取曲柄为单位长度， 即打一 1,而其他杆长则按比例取为 U 的倍数；机架长 二常由结构布置事先给定，分析上图得关 系式：陆]-arccos[啊-arccos[因此，仅为独立变量，是二维最优化设计问题,可根据期望与偏差为最小的要求，来建立目标函数:弘口二旳-瓯尸i-0式中*——期望输岀角1'――实际输出角他 H [ V! i :岬’t h 工网:勺H■禹）盘€俐< 2^由右图求得摇杆匚与BD连线夹角3 . 2 _ 2CL= arccosf—--- --- )S心机架7与BD连线夹角2 ； _ 1 2毘=心七产BD连线长度诩曲将杆『杓EL什楚押聞・h U15A■:J炯空口沁'沆;式中I'' '■ I （单位长度）、二为已定常量。
3.给定约束条件曲柄与机架处于共线位置时:+叮我鮎2=留=arccos[ ]>[r^] = 45°込煜之［8£怙］及^ ' 得约束条件:Si（蜀二一彳-琉-忑心心+&+几r < o自（K）= £ +请-忑心心-（存一许卩< 04.设计变量的可行域曲柄存在的条件:十厶A 斗+/丄 厶+4-4冋右+他一切幼殆©0 = I —丐 <0 刘3)=1-尢沙0务(X)= 71 +.) ■耳■屯兰°S6(^) = 7i -几)+可-码盖o 场 UD - (fl -ZJ- +A 3 <0取单位长度即'1 '■ ^'，只有二、'二:和-J-':为起作用约束，它们是两个椭圆方程。
min f(X) = min £ 仏-陽J_ 2-0 .s,i.g L (X) = _兀：一就- Ji 兀*] +36 <0 乞(刃=兀十理-72%^2-16 £0这是一个带有不等式约束具有两个设计变量的小型最优化设计问题，可采用直接法来求解曲柄摇杆机构如图所示，当曲柄 AB 整周转动时，连杆 BC 上一点M 实现给定轨迹，轨迹坐标方程为可=0.4 + an{ 2jr[(nr - ^I2ir- 0 16]}=■ 2 + 0 5sin(疋-肋要求确定各构件的长度，使点 M 的实际轨迹与给定轨迹间的偏差最小。
2. 建立目标函数:取各构件的杆长1 :为设计变量，即解：1.确定设计变量：T" = *1丿2丿*4人山『得约束条件:最后的数学模型为按连杆上点M实际实现的轨迹与要求实现的轨迹的均方偏差最小的原则建立目标函数，其函数形式可表达为，'"'(町一心尸+ 3-丿』一式中，(s表示将曲柄转角■分成s等份)；一'丁，，山为连杆上点M第j个位置所要求实现的坐标值；*： ^为点M实际实现的坐标值与I；可按下列公式计算得到：卞：=CGS密』+ '二g ¥$一%sin 丫$yj= z L sin 巒+■?」tin y,4-^cosy = +^3 cos^r - s L cossin y = (z l sin 爭一巧sin 叭"】-丘±(肝-4加严CQSkT = --------------2Z4 = 2?+以B=2KLy C^K^-M2K工2^ -23J j - 22-154 COS (pL = 2広样斗一2S］巧cos tp其中第三式中的根号前的正负号应参照运动连续性来选取。
3.确定约束条件：首先要保证曲柄AB能作整周回转。
若结构上要求'' ，则可取下列约束条件(曲柄存在条件)：gj® 二 6 一勾一屯+^4< 0也(刃=习+石一习-2A<0其次考虑机构具有较好的传力性能，按最小传动角大于」：“写成的约束条件为gj(Z)二习'+空：—(习一习尸—Ng屯cos45° < 0g^(Z) =-z23- r53+ (z4+ Z-!)3- 2z a z3co.'45° 兰Q综上所述，这一优化设计问题的数学模型可表示为求设计变量 - 一-一一亠一一一_，使min y（z）- £〔勺・兀» +Cx广打）满足于约束条件■- -4.计算结果:以u - -为例，计算结果为:简化的机床主轴当跨距1,夕卜伸端a求轴的内、外径d、D取何值的时候，主轴重量最轻?解：1、确定设计变量由于材料一定时，主轴内孔只与机床型号有关，所以设计变量为:x = [ x i X2 X3]T =[l D a]T 2、目标函数：考虑主轴最轻，所以min二—（D 2 一沪）（f 十盘）’p -（xf —d ‘）（厲十与）44式中：p ——材料密度3、约束条件：由于主轴刚度是一个重要的性能指标，其外伸端的挠度y 不得超过规定值 y 。