人教版八年级数学上册全等三角形课时练及答案

合集下载

(完整)人教版八年级数学上全等三角形课时练习及答案.docx

E
D
B
AFC
6．如图，△ABC中，∠C=90°，AD是△ABC的角平分线，（1）求证：AC =BE；（2）求∠B的度数。
A
DE⊥AB于E，AD=BD．
C
D
EB
（第6题）
8
第页
第9课时
角平分线的性质
（2）
一、选择题
1．三角形中到三边距离相等的点是（
）
A．三条边的垂直平分线的交点
B．三条高的交点
C．三条中线的交点
A
E
F
B
D
C
（第5题）
6．如图，AD为△ABC的高，E为AC上一点，BE交AD于点F，且有BF=AC，FD=CD．
求证：BE⊥AC．
A
E
F
BDC
（第6题）
6
第页
第7课时
三角形全等的条件（
6）
一、选择题
1．下列条件中，不一定能使两个三角形全等的是
（
）
A．三边对应相等
B．两角和其中一角的对边对应相等
C．两边和其中一边的对角对应相等
E
A
C
D
E
O
C
B
ADF
B
（第3题）
（第2
题）
三、解答题
4．已知：如图，AC=DF，BF=CE，AB⊥BF，DE⊥BE，
垂足分别为B，E．
A
D
5
第页
BFCE
求证：AB=DE
（第4题）
5．如图，△ABC中，D是BC边的中点, AD平分∠BAC，DE⊥AB于E，DF⊥AC于F.
求证：（1）DE= DF；（2）∠B =∠C．
）
A．2对
B．3对

八年级上册数学人教版课时练《12.1 全等三角形》01(含答案解析)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！《12.1全等三角形》课时练考点1全等图形的认识1．下列说法中，正确的有（）①正方形都是全等形；②等边三角形都是全等形；③形状相同的图形是全等形；④大小相同的图形是全等形；⑤能够完全重合的图形是全等形．A．1个B．2个C．3个D．4个2．如图所示的图形是全等图形的是()A．B．C．D．3．下列四个图形中，全等的图形是（）A．①和②B．①和③C．②和③D．③和④4．下列说法不正确的是（）A．如果两个图形全等，那么它们的形状和大小一定相同；B．面积相等的两个图形是全等图形；C．图形全等，只与形状、大小有关，而与它们的位置无关；D．全等三角形的对应边相等，对应角相等；5．如图，将一张长方形纸片ABCD沿对角线AC折叠后，点D落在点E处，与BC交与点F，图中共有全等三角形（）A．2对B．3对C．4对D．5对考点2全等三角形的概念6．下列说法正确的是（）A．直角三角形是轴对称图形B．两个等边三角形一定全等C．面积相等的两个三角形一定全等D．轴对称图形的对称轴是任何一对对应点连线段的中垂线7．下列说法正确的是（）A．形状相同的两个三角形全等B．面积相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等腰三角形都全等8．下列说法:①全等三角形的形状相同、大小相等②全等三角形的面积相等③周长相等的两个三角形全等④全等三角形的对应边相等、对应角相等其中正确的说法为（）A．②③④B．①②③C．①②④D．①②③④9．下列四个命题中真命题的是（）①有一个角相等的两个等腰三角形全等②有一个钝角相等且有一条边相等的两个等腰三角形全等③有两边相等的两个等腰直角三角形全等④一个三角形的底和腰与另一个三角形的底和腰对应相等的两个等腰三角形全等A．①②B．②③C．②④D．③④考点3全等三角形的性质10．如图所示，若△ABE≌△ACF，且AB=5，AE=2，则EC的长为（）A．2B．3C．5D．2.5Ð等于()11．已知图中的两个三角形全等，则1A ．70°B ．50°C ．60°D ．120°12．如图，△ABC ≌△DEF ，下列结论不正确的是()A ．AB=DEB ．BE=CFC ．BC=EFD ．AC=DE13．三个全等三角形按如图的形式摆放，则1 23Ð+Ð+Ð的度数是（）A ．120°B ．135°C ．150°D ．180°14．若△ABC ≌△DEF ，AB ＝2，AC ＝4，且△DEF 的周长为奇数，则EF 的值为（）A ．3B ．4C ．1或3D ．3或515．对于两个全等的三角形，下列结论正确的有（）①两个三角形的周长相等；②两个三角形的面积相等；③两个三角形对应角的平分线相等；④两个三角形对应边上的中线相等A ．1个B ．2个C ．3个D ．4个16．如图所示中的44´的正方形网格中，1234567Ð+Ð+Ð+Ð+Ð+Ð+Ð=（）A．330 B．315 C．300o D．24517．如图，已知△AOC≌△BOD，∠A＝30°，∠C＝20°，则∠COD＝()A．50°B．80°C．100°D．130°18．下列说法中，正确的是（）A．全等三角形的角平分线相等B．全等三角形的中线相等C．全等三角形的高相等D．全等三角形的周长相等参考答案1．A2．B3．D4．B5．C6．D7．C8．C9．D 10．B11．C12．D13．D14．D15．D16．B17．B18．D。

2020年人教版八年级数学上册课时作业全等三角形判定一(SSS)(含答案)

2020年人教版八年级数学上册课时作业全等三角形判定一(SSS)一、选择题1.如图所示，如果AB=A′B′，BC=B′C′，AC=A′C′，那么下列结论正确的是()A.△ABC≌△A′B′C′B.△ABC≌△C′A′B′C.△ABC≌△B′C′A′D.这两个三角形不全等2.如图，AB=A 1B 1，BC=B 1C 1，AC=A 1C 1，且∠A=110°，∠B=40°，则∠C 1=()A.110°B.40°C.30°D.20°3.如图所示，在△ABC 和△DBC 中，已知AB=DB，AC=DC，则下列结论中错误的是()A.△ABC≌△DBCB.∠A=∠DC.BC 是∠ACD 的平分线D.∠A=∠BCD4.已知△ABC 的三边长分别为3，5，7，△DEF 的三边长分别为3，3x－2，2x－1，若这两个三角形全等，则x 等于()A.73 B.4 C.3 D.不能确定5.如图，AB=AC，AD=AE，BE=CD，∠2=110°，∠BAE=60°，下列结论错误的是()A.△ABE≌△ACDB.△ABD≌△ACEC.∠ACE=30°D.∠1=70°二、填空题6.如图所示，AD=BC，AC=BD，用三角形全等的判定“SSS”可证明△ADC≌或△ABD≌.7.如图，下列三角形中，与△ABC全等的是.8.如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连接AD，CD.若∠B=65°，则∠ADC的大小为.三、解答题9.如图，OA=OB，AC=BC.求证：△AOC≌△BOC.10.已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，求证：△ABD≌△ACD.11.如图，AB=AC，AD=AE，CD=BE.求证：∠DAB=∠EAC.12.如图，AB=AC，DB=DC，EB=EC.(1)图中有几对全等三角形？请一一写出来；(2)选择(1)中的一对全等三角形加以证明.13.如图，点B，F，C，E在直线l上(F，C之间不能直接测量)，点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.(1)求证：△ABC≌△DEF；(2)指出图中所有平行的线段，并说明理由.14.如图，已知AB=AC，AD=AE，BD=CE，求证：∠3=∠1＋∠2.15.如图，已知AB=DC，DB=AC.求证：∠B=∠C；参考答案1.答案为：A；2.答案为：C；3.答案为：D；4.答案为：C；5.答案为：C；6.答案为：△BCD，△BAC；7.答案为：③；8.答案为：65°；9.证明：在△AOC和△BOC中，∴△AOC≌△BOC(SSS).10.证明：∵AD是BC边上的中线，∴BD=CD.在△ABD和△ACD中，∴△ABD≌△ACD(SSS).11.证明：在△ADC和△AEB中，∴△ADC≌△AEB.∴∠DAC=∠EAB.∴∠DAC－∠BAC=∠EAB－∠BAC.∴∠DAB=∠EAC.12.解：(1)有3对全等三角形：△ABD≌△ACD，△ABE≌△ACE，△DBE≌△DCE.(2)以△ABD≌△ACD为例.证明：在△ABD和△ACD中，∴△ABD≌△ACD(SSS).13.解：(1)证明：∵BF=EC，∴BF＋FC=EC＋CF，即BC=EF.又∵AB=DE，AC=DF，∴△ABC≌△DEF.(2)AB∥DE，AC∥DF.理由：∵△ABC≌△DEF，∴∠ABC=∠DEF，∠ACB=∠DFE.∴AB∥DE，AC∥DF.14.证明：在△ABD和△ACE中，∴△ABD≌△ACE(SSS).∴∠BAD=∠1，∠ABD=∠2.∵∠3=∠BAD＋∠ABD，∴∠3=∠1＋∠2.15.解：证明：连接AD，在△BAD和△CDA中，，，，∴△BAD≌△CDA(SSS).∴∠B=∠C(全等三角形的对应角相等).。

2021年人教版数学八年级上册12.1《全等三角形》课时练习(含答案)

人教版数学八年级上册12.1《全等三角形》课时练习一、选择题1.下列说法不正确的是（）A.如果两个图形全等，那么它们的形状和大小一定相同。

B.图形全等，只与形状、大小有关，而与它们的位置无关。

C.全等图形的面积相等，面积相等的两个图形是全等形。

D.全等三角形的对应边相等，对应角相等。

2.如图，若△ABC≌△DEF，则∠E等于（）A.30°B. 50°C.60°D.100°3.边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为（）A.3B.4C.5D.3或4或54.如图所示，在△ABC中，D、E分别是边AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为（）A.15°B.20°C.25°D.30°5.如下图，△ABC≌△ADE,∠B=70°，∠C=26°，∠DAC=20°，则∠EAC=( )A.20°B.64°C.30°D.65°6.已知△ABC≌△DEF，BC=EF=6cm，△ABC的面积为18 cm2，则EF边上的高的长是( ).A.3cmB.4cmC.5cmD.6cm7.如图已知△ABE≌△ACD, AB=AC, BE=CD，∠B=40°,∠AEC=120°则∠DAC的度数为（）A.80°B.70°C.60°D.50°8.已知图中的两个三角形全等，则∠1等于（）A.50°B.58°C.60°D.72°9.如图（1），已知两个全等三角形的直角顶点及一条直角边重合．将△ACB绕点C按顺时针方向旋转到△A′CB′的位置，其中A′C交直线AD于点E，A′B′分别交直线AD、AC于点F、G，则在图（2）中，全等三角形共有（）A．5对 B．4对 C．3对 D．2对10.如图，△ABE、△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3=7：2：1，则∠α的度数为( )A.90°B.108°C.110°D.126°二、填空题11.如图所示，△AOB≌△COD，∠AOB=∠COD，∠A=∠C，则∠D的对应角是__________，图中相等的线段有__________.12.如图，△ABC≌△DEF，请根据图中提供的信息，写出x=________13.如图所示，已知△ABC≌△DEF，AB=4cm，BC=6cm，AC=5cm，CF=2cm，∠A=70°，∠B=65°，则∠D=__________，∠F=__________，DE=__________，BE=__________.14.如图，△ABC中，点A的坐标为（0，1），点C的坐标为（4，3），如果要使△ABD与△ABC 全等，那么点D的坐标是．三、作图题15.如图，把大小为4×4的正方形方格图形分别分割成两个全等图形，例如图①，请在下图中，沿着虚线画出四种不同的分法，把4×4的正方形分割成两个全等图形．四、解答题16.如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边，∠A=∠C=35°，∠CDE=100°，∠DEB=10°，求∠AEC的度数.17.△ACF≌△DBE，∠E=∠F，若AD=11，BC=7，求线段AB的长.18.如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数.参考答案1.C2.D3.B4.D5.B6.D7.A8.B9.B10.B11.答案为：∠OBA，OA=OC、OB=OD、AB=CD12.答案为：2013.答案为：70° 45° 4cm 2cm14.答案为：（4，﹣1）或（﹣1，3）或（﹣1，﹣1）15.解：如图所示：16.解:因为AB、EC是对应边，所以∠AEB=∠CDE=100°，又因为∠C=35°，所以∠CED=180°-35°-100°=45°，又因为∠DEB=10°，所以∠BEC=45°-10°=35°，所以∠AEC=∠AEB-∠BEC=100°-35°=65°.17.解：∵△ACF≌△DBE，∴AC=BD，∴AC－BC=BO－BC，即AB=CD，∴2AB＋BC=AO，∴2AB＋7=11，∴AB=218.解：∵△ABC≌△ADE，∴∠DAE=∠BAC=（∠EAB﹣∠CAD）=. ∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°∠DGB=∠DFB﹣∠D=90°﹣25°=65°.综上所述：∠DFB=90°，∠DGB=65°.。

人教版八年级数学上册《三角形全等的判定》课堂同步练习题含答案(6课时)

∠AOB 是一个任意角，在边 OA，OB 上分别取 OM=ON，移动角尺，使角尺两边相同的刻度分别与 M，N 重合，过角尺顶点 C 作射线 OC。由做法得 △MOC≌△NOC 的依据是____ __ __.
11 题图
10．如图，已知 AC = FE ，BC = DE ，点 A、D、
B、F 在一条直线上，要使△ ABC ≌△ FDE ，还需添加一．个．条件，这个条件
7
12.2 三角形全等的判定
一、选择题
第 1 课时边边边（SSS）
1. B 2. A 3.C 4.C 5.C 6.B 7.D 8.B
二、填空题
9. sss
10. AB = FD （答案不惟一，也可以是 AD = FB ）
11. 76
12. sss 13 .20 14. AB=AC
16. ②①③ 17. EC, △ABF≌△DCE
[来源:Z+xx+]
21．（2010 浙江金华）如图，在△ABC 中，D 是 BC 边上的点（不与 B，C 重合），
F，E 分别是 AD 及其延长线上的点，CF∥BE. 请你添加一个条件，使△BDE
≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．
（1）你添加的条件是：（2）证明：
∴∠A＝∠C（全等三角形的对应角相等）
21. 解：（1）
(或点 D 是线段 BC 的中点)， FD = ED， CF = BE 中
任选一个即可﹒
（2）以 BD = DC 为例进行证明：
∵CF∥BE，
[来源:]
∴∠FCD﹦∠EBD．
又∵ BD = DC ，∠ FDC﹦∠EDB， ∴△BDE≌△CDF．
A．BC=EC，∠B=∠E

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析一、选择题（每小题3分，共30分） 1.下列说法正确的是（）A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等 2. 如图所示，a,b,c 分别表示△ABC 的三边长，则下面与△ABC 一定全等的三角形是（）3.如图所示，已知△ABE ≌△ACD ，∠1=∠2，∠B=∠C ，下列不正确的等式是（） B.∠BAE=∠CADA.AB=AC C.BE=DC D.AD=DE 4. 在△ABC 和△A /B /C /中,AB=A /B /,∠B=∠B /,补充条件后仍不一定能保证△ABC ≌△A /B /C /,则补充的这个条件是( )A ．BC=B /C / B ．∠A=∠A / C ．AC=A /C /D ．∠C=∠C / 5.如图所示，点B 、C 、E 在同一条直线上，△ABC 与△CDE都是等边三角形，则下列结论不一定成立的是（）A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA6. 要测量河两岸相对的两点A,B 的距离，先在AB 的垂线BF 上取两点C,D ，使CD=BC ，再作出BF 的垂线DE ，使A,C,E 在一条直线上（如图所示），可以说明△EDC ≌△ABC ，得ED=AB ，因此测得ED 的长就是AB 的长，判定△EDC ≌△ABC 最恰当的理由是（）第3题图第5题图第2题图第6题图AB C DA.边角边B.角边角C.边边边D.边边角7.已知：如图所示，AC=CD ，∠B=∠E=90°，AC ⊥CD ，则不正确的结论是（）A ．∠A 与∠D 互为余角B ．∠A=∠2C ．△ABC ≌△CED D ．∠1=∠28. 在△ABC 和△FED 中，已知∠C=∠D ，∠B=∠E ，要判定这两个三角形全等，还需要条件（） A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F 9.如图所示，在△ABC 中，AB=AC ，∠ABC 、∠ACB 的平分线BD ，CE 相交于O 点，且BD 交AC 于点D ，CE 交AB 于点E ．某同学分析图形后得出以下结论：①△BCD ≌△CBE ； ②△BAD ≌△BCD ；③△BDA ≌△CEA ；④△BOE ≌△COD ；⑤△ACE ≌△BCE ，上述结论一定正确的是（） A.①②③ B.②③④ C.①③⑤ D.①③④10、下列命题中：⑴形状相同的两个三角形是全等形；⑵在两个三角形中，相等的角是对应角，相等的边是对应边；⑶全等三角形对应边上的高、中线及对应角平分线分别相等，其中真命题的个数有( ) A 、3个 B 、2个 C 、1个 D 、0个二、填空题（每题3分，共21分）11．如图６，ＡＣ＝ＡＤ，ＢＣ＝ＢＤ，则△ＡＢＣ≌ ；应用的判定方法是．12．如图７，△ＡＢＤ≌△ＢＡＣ，若ＡＤ＝ＢＣ，则∠ＢＡＤ的对应角为．13．已知ＡＤ是△ＡＢＣ的角平分线，ＤＥ⊥ＡＢ于Ｅ，且ＤＥ＝３cm ，则点Ｄ到ＡＣ的距离为．ＢＣＤＡ图6 D O CBA 图8 A D CB图7 第9题图第7题图14．如图８，ＡＢ与ＣＤ交于点Ｏ，ＯＡ＝ＯＣ，ＯＤ＝ＯＢ，∠ＡＯＤ＝，根据可得△ＡＯＤ≌△ＣＯＢ，从而可以得到ＡＤ＝．15．如图９，∠Ａ＝∠Ｄ＝９０°，ＡＣ＝ＤＢ，欲使ＯＢ＝ＯＣ，可以先利用“ＨＬ”说明 ≌ 得到ＡＢ＝ＤＣ，再利用“ ”证明△ＡＯＢ≌ 得到ＯＢ＝ＯＣ． 16．如果两个三角形的两条边和其中一边上的高分别对应相等，那么这两个三角形的第三边所对的角的关系是．17．如图10，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带________去配，这样做的数学依据是是．三、解答题（共29分）18. （6分）如右图，已知△ABC 中，AB ＝AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由．解： ∵AD 平分∠BAC∴∠________＝∠_________（角平分线的定义）在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∴△ABD ≌△ACD （） 19．（8分）如图，已知△≌△是对应角．（1）写出相等的线段与相等的角；（2）若EF=2.1 cm ，FH=1.1 cm ，HM=3.3 cm ，求MN和HG 的长度.第19题图图10 DCBA20．（7分）如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC＝CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理．21．（8分）已知AB∥DE，BC∥EF，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．四、解答题（共20分）22．（10分）已知：BE⊥CD，BE＝DE，BC＝DA，求证：①△BEC≌△DAE；②DF⊥BC．B C EF A23．（10分）如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．12章·全等三角形（详细答案）一、选择题 CBDCD BDCDC二、填空题 11、△ABD SSS 12、∠ABC 13、3cm 14、∠COB SAS CB 15、△ABC △DCB AAS △DOC 16、相等 17、○3 两角和它们的夹边分别相等的两个三角形全等三、解答题18、AD CAD AB=AC ∠BAD=∠CAD AD=AD SAS19、B 解：(1)EF=MN EG=HN FG=MH ∠F=∠M ∠E=∠N ∠EGF=∠MHN (2)∵△EFG ≌△NMH ∴MN=EF=2.1cm∴GF=HM=3.3cm ∵FH=1.1cm ∴HG=GF －FH=3.3－1.1=2.2cm 20、解：∵DE ∥AB ∴∠A=∠E在△ABC 与△CDE 中∠A=∠E BC=CD∠ACB=∠ECD∴△ABC ≌△CDE(ASA)∴AB=DE21、证明：∵AB ∥DE∴∠A=∠EDF∵BC ∥EFCA∴∠ACB=∠F∵AD=CF∴AC=DF在△ABC与△DEF中∠A=∠EDFAC=DF∠ACB=∠F△ABC≌△DEF(ASA)四、解答题22、证明：①∵ＢＥ⊥ＣＤ∴∠ＢＥＣ＝∠ＤＥＡ＝９０°在Ｒｔ△ＢＥＣ与Ｒｔ△ＤＥＡ中ＢＣ＝ＤＡＢＥ＝ＤＥ∴Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ（ＨＬ）②∵Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ∴∠Ｃ＝∠ＤＡＥ∵∠ＤＥＡ＝９０°∴∠Ｄ＋∠ＤＡＥ＝９０°∴∠Ｄ＋∠Ｃ＝９０°∴∠ＤＦＣ＝９０°∴ＤＦ⊥ＢC23、证明：在△ABC与△ADC中1=∠2AC=AC3=∠4∴△ABC≌△ADC(ASA)∴CB=CD在△ECD与△ECB中CB=CD∠3=∠4CE=CE∴△ECD≌△ECB(SAS)∴∠5=∠6第十二章全等三角形一、填空题（每小题4分,共32分）.1．已知：///ABC A B C ∆∆≌，/A A ∠=∠，/B B ∠=∠，70C ∠=︒，15AB cm =，则/C ∠=_________，//A B =__________．2．如图1，在ABC ∆中，AB=AC ，AD ⊥BC 于D 点，E 、F 分别为DB 、DC 的中点，则图中共有全等三角形_______对．图1 图2 图33．已知△ABC ≌△A ′B ′C ′，若△ABC 的面积为10 cm 2，则△A ′B ′C ′的面积为______ cm 2，若△A ′B ′C ′的周长为16 cm ，则△ABC 的周长为________c m ． 4．如图2所示，∠1=∠2，要使△ABD ≌△ACD ，需添加的一个条件是________________(只添一个条件即可)．5．如图3所示，点F 、C 在线段BE 上，且∠1=∠2，BC =EF ，若要使△ABC ≌△DEF ，则还需补充一个条件________，依据是________________．6．三角形两外角平分线和第三个角的内角平分线_____一点，且该点在三角形______部． 7．如图4，两平面镜α、β的夹角 θ，入射光线AO 平行于β，入射到α上，经两次反射后的出射光线CB 平行于α，则角θ等于________．8．如图5，直线AE ∥BD ，点C 在BD 上，若AE ＝4，BD ＝8，△ABD 的面积为16，则ACE △ 的面积为______．二、选择题（每小题4分,共24分） 9．如图6，AE ＝AF ，AB ＝AC ，E C 与B F 交于点O ，∠A ＝600，∠B ＝250，则∠E OB 的度数为（）A 、600B 、700C 、750D 、85010．△ABC ≌△DEF ，且△ABC 的周长为100 cm ，A 、B 分别与D 、E 对应，且AB ＝35 cm ，DF =30 cm ，则EF 的长为( ) A ．35 cm B ．30 cm C ．45 cm D ．55 cm11．图7是一个由四根木条钉成的框架，拉动其中两根木条后，它的形状将会改变，若固定其形状，下列有四种加固木条的方法，不能固定形状的是钉在________两点上的木条．( )A ．A 、FB ．C 、E C ．C 、AD ．E 、F12．要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD= BC ，再定出BF 的垂线DE ，使A 、C 、E 在一条直线上，可以证明△EDC ≌△ABC ，得到ED=AB ，因此测得ED 的长就是AB 的长（如图8），判定△EDC ≌△ABC 的理由是（）NAMC B图7 图8 图9 图10A．边角边公理 B．角边角公理； C．边边边公理 D．斜边直角边公理13．如图9，在△ABC中，∠A:∠B:∠C=3:5:10，又△MNC≌△ABC，则∠BCM：∠BCN等于（）A．1:2 B．1:3C．2:3 D．1:414．如图10，P是∠AOB平分线上一点，CD⊥OP于F，并分别交OA、OB于CD，则CD_____P点到∠AOB两边距离之和．( )A．小于B．大于C．等于D．不能确定三、解答题（共46分）中，∠ACB=90°，延长BC至B'，使15．已知如图11，ABCC B'=BC，连结A B'．求证：△AB B'是等腰三角形．图11第十二章全等三角形。

人教版八年级数学上册 12.2 全等三角形的判定课时训练(含答案)

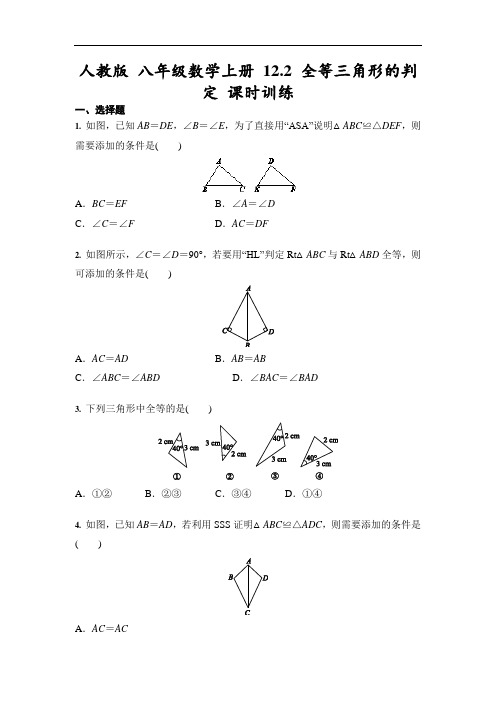
人教版八年级数学上册12.2 全等三角形的判定课时训练一、选择题1. 如图，已知AB＝DE，∠B＝∠E，为了直接用“ASA”说明△ABC≌△DEF，则需要添加的条件是()A．BC＝EF B．∠A＝∠DC．∠C＝∠F D．AC＝DF2. 如图所示，∠C＝∠D＝90°，若要用“HL”判定Rt△ABC与Rt△ABD全等，则可添加的条件是()A．AC＝AD B．AB＝ABC．∠ABC＝∠ABD D．∠BAC＝∠BAD3. 下列三角形中全等的是()A．①②B．②③C．③④D．①④4. 如图，已知AB＝AD，若利用SSS证明△ABC≌△ADC，则需要添加的条件是()A．AC＝ACB．∠B＝∠DC．BC＝DCD．AB＝CD5. 如图，要用“SAS”证明△ABC≌△ADE，若已知AB＝AD，AC＝AE，则还需添加条件()A．∠B＝∠D B．∠C＝∠EC．∠1＝∠2 D．∠3＝∠46. 如图，点B，E，C，F在同一直线上，AB∥DE，∠A＝∠D，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是()A．BE＝CF B．∠ACB＝∠FC．AC＝DF D．AB＝DE7. 如图，BE⊥AC，CF⊥AB，垂足分别是E，F.若BE＝CF，则图中全等三角形有()A．1对B．2对C．3对D．4对8. 如图所示，P是∠BAC内一点，且点P到AB，AC的距离PE，PF相等，则△PEA≌△PF A的依据是()A．HL B．ASA C．SSS D．SAS9. 已知△ABC的六个元素，下列甲、乙、丙三个三角形中标出了某些元素，则与△ABC全等的三角形是()A．只有乙B．只有丙C．甲和乙D．乙和丙10. 如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A.BC=FD，AC=EDB.∠A=∠DEF，AC=EDC.AC=ED，AB=EFD.∠A=∠DEF，BC=FD二、填空题11. 如图，AB＝DE，∠1＝∠2，添加一个适当的条件，使△ABC≌△DEC，则需添加的条件是__________(不添加任何辅助线，填一个即可)．12. 如图，在△ABC中，AD⊥BC于点D，要使△ABD≌△ACD，若根据“HL”判定，还需要添加条件：____________．13. 如图，在Rt△ABC中，∠C=90°，∠B=20°，以点A为圆心，小于AC的长为半径画弧与AB，AC分别交于点M，N，再分别以点M，N为圆心，大于MN 的长为半径画弧，两弧相交于点P，连接AP并延长交BC于点D，则∠ADB=°.14. 如图所示，AE=AD，∠B=∠C，BE=4，AD=5，则AC=.15. 如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是.三、解答题16. 如图是一个平分角的仪器，其中AB＝AD，BC＝DC，将点A放在角的顶点，AB和AD沿着角的两边放正，沿AC画一条射线AE，则AE就是角平分线，请你说明其中的道理．17. 如图，BM平分∠ABC，D是BM上一点，过点D作DE⊥AB于点E，DF⊥BC 于点F，P是BM上的另一点，连接PE，PF.(1)若∠EDF＝124°，求∠ABC的度数；(2)求证：PE＝PF.18. 如图所示，在一条笔直的海岸线上有A，B两个观测点，点B在点A的正东方，海岛C在观测点A的正北方，海岛D在观测点B的正北方，从观测点A看海岛C，D的视角∠CAD与从观测点B看海岛C，D的视角∠CBD相等，那么海岛C，D到观测点A，B所在海岸线的距离相等吗?为什么?19. 如图，AD∥BC，AB⊥BC于点B，连接AC，过点D作DE⊥AC于点E，过点B作BF⊥AC于点F.(1)若∠ABF＝63°，求∠ADE的度数；DE＝BF＋EF.20. 杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语．其具体信息汇集如下．如图，AB∥OH∥CD，相邻两平行线间的距离相等．AC、BD相交于O，OD⊥CD，垂足为D.已知AB＝20米，请根据上述信息求标语CD的长度．人教版八年级数学上册 12.2 全等三角形的判定课时训练-答案一、选择题 1. 【答案】B2. 【答案】A3. 【答案】A[解析] ①②符合证明三角形全等的判定方法“SAS”．③④中相等的角所对的边不相等，所以不可能全等．故选A.4. 【答案】C5. 【答案】C[解析] 还需添加条件∠1＝∠2.理由：∵∠1＝∠2，∴∠1＋∠EAC ＝∠2＋∠EAC ，即∠BAC ＝∠DAE. 在△ABC 和△ADE 中，⎩⎨⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE(SAS)．6. 【答案】B7. 【答案】C[解析] ①∵BE ⊥AC ，CF ⊥AB ，∴∠CFB ＝∠BEC ＝90°.在Rt △BCF 和Rt △CBE 中，⎩⎨⎧CF ＝BE ，BC ＝CB ，∴Rt △BCF ≌Rt △CBE(HL)．②∵BE ⊥AC ，CF ⊥AB ，∴∠AFC ＝∠AEB ＝90°.在△ABE 和△ACF 中，⎩⎨⎧∠AEB ＝∠AFC ，∠A ＝∠A ，BE ＝CF ，∴△ABE ≌△ACF(AAS)． ③设BE 与CF 相交于点O. ∵BE ⊥AC ，CF ⊥AB ， ∴∠OFB ＝∠OEC ＝90°.∵△ABE ≌△ACF ，∴AB ＝AC ，AE ＝AF. ∴BF ＝CE.在△BOF 和△COE 中，⎩⎨⎧∠OFB ＝∠OEC ，∠BOF ＝∠COE ，BF ＝CE ，∴△BOF ≌△COE(AAS)．8. 【答案】A9. 【答案】D10. 【答案】C[解析] A .添加BC=FD ，AC=ED ，可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ，AC=ED ，可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ，AB=EF ，不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ，BC=FD ，可利用“AAS”判定△ABC ≌△EFD.二、填空题11. 【答案】答案不唯一，如∠B ＝∠E12. 【答案】AB ＝AC13. 【答案】125[解析] 由题意可得AD 平分∠CAB.∵∠C=90°，∠B=20°，∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°. 14. 【答案】915. 【答案】①②③[解析] 由△ABO ≌△ADO ，得AB=AD ，∠AOB=∠AOD=90°，∠BAC=∠DAC.又因为AC=AC ，所以△ABC ≌△ADC ，则CB=CD.所以①②③正确.三、解答题16. 【答案】解：在△ABC 与△ADC 中，⎩⎨⎧AB ＝AD ，BC ＝DC ，AC ＝AC ，∴△ABC ≌△ADC(SSS)．∴∠BAC ＝∠DAC ，即AE 平分∠BAD.17. 【答案】解：(1)∵DE ⊥AB ，DF ⊥BC ， ∴∠DEB ＝∠DFB ＝90°. ∵∠EDF ＝124°，∴∠ABC ＝360°－90°－90°－124°＝56°.(2)证明：∵BM 平分∠ABC ，DE ⊥AB ，DF ⊥BC ， ∴∠ABM ＝∠CBM ，DE ＝DF.∵∠BDE ＝90°－∠ABM ，∠BDF ＝90°－∠CBM ， ∴∠BDE ＝∠BDF. ∴∠EDP ＝∠FDP.在△EDP 和△FDP 中，⎩⎨⎧DE ＝DF ，∠EDP ＝∠FDP ，DP ＝DP ，∴△EDP ≌△FDP(SAS)．∴PE ＝PF.18. 【答案】解:相等.理由:设AD ，BC 相交于点O.∵∠CAD=∠CBD ，∠COA=∠DOB ， ∴由三角形内角和定理，得∠C=∠D. 由已知得∠CAB=∠DBA=90°. 在△CAB 和△DBA 中，∴△CAB ≌△DBA. ∴CA=DB.∴海岛C ，D 到观测点A ，B 所在海岸线的距离相等.19. 【答案】解：(1)∵AD ∥BC ，AB ⊥BC ， ∴∠ABC ＝∠BAD ＝90°. ∵DE ⊥AC ，BF ⊥AC ， ∴∠BFA ＝∠AED ＝90°.∴∠ABF ＋∠BAF ＝∠BAF ＋∠DAE ＝90°. ∴∠DAE ＝∠ABF ＝63°.∴∠ADE ＝27°.(2)证明：由(1)得∠DAE ＝∠ABF ，∠AED ＝∠BFA ＝90°.在△DAE 和△ABF 中，⎩⎨⎧∠DAE ＝∠ABF ，∠AED ＝∠BFA ，AD ＝BA ，∴△DAE ≌△ABF(AAS)． ∴AE ＝BF ，DE ＝AF.∴DE ＝AF ＝AE ＋EF ＝BF ＋EF.20. 【答案】解：∵AB ∥CD ，OD ⊥CD ， ∴OB ⊥AB ，∵相邻两平行线间的距离相等， ∴OB ＝OD.(3分)在△ABO 与△CDO 中，⎩⎨⎧∠ABO ＝∠CDOOB ＝OD∠AOB ＝∠COD， ∴△ABO ≌△CDO(ASA )，(6分) ∴CD ＝AB ＝20(米)．(7分)。

12.1 全等三角形初中数学人教版八年级上册课时习题(含答案)

12.1全等三角形一、选择题（本大题共8小题，在每小题列出的选项中，选出符合题目的一项）1.下列图形中，是全等图形的是( )A. 形状相同的两个五角星B. 腰长相等的两个等腰三角形C. 周长相等的两个长方形D. 面积相等的两个正方形2.下列说法正确的是( )A. 两个面积相等的图形一定是全等图形B. 两个全等图形形状一定相同C. 两个周长相等的图形一定是全等图形D. 两个正三角形一定是全等图形3.如图所示的各组图形中，不是全等形的是( )A. B.C. D.4.下列各组图形中，属于全等图形的是( )A.B.C.D.5.如图所示，在△ABC中，D，E分别是边AC，BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为( )A. 15°B. 20°C. 25°D. 30°6.若△ABC≌△DEF，则根据图中提供的信息，可得出x的值为( )A. 30B. 27C. 35D. 407.如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是( )A. 15°B. 20°C. 25°D. 30°8.如图，△ABC≌△ADE，∠B=25°，∠E=105°，∠EAB=10°，则∠BAD为( )A. 50°B. 60°C. 80°D. 120°二、填空题（本大题共4小题）9.如图，在由6个相同的小正方形拼成的网格中，∠2―∠1=______°.10.________的两个图形叫做全等形．11.如图，△ABC≌△EDC，∠C=90°，点D在线段AC上，点E在线段CB延长线上，则∠1+∠E=°.12.已知△ABC≌△DEF，△DEF的周长为32cm，DE=9cm，EF=12cm，则AC=______．三、解答题（本大题共6小题，解答应写出文字说明，证明过程或演算步骤）13.说出图(2)、图(3)中两个全等三角形的对应边、对应角．14.如图，△ABC≌△CDA，AB和CD，BC和DA是对应边．写出其他对应边及对应角．15.沿着图中的虚线，用四种不同的方法将下面的图形分成两个全等的图形．16.如图，△OCA≌△OBD，点C和点B，点A和点D是对应顶点．说出这两个三角形中相等的边和角．17.如图，△ABC≌△DEC，CA和CD，CB和CE是对应边．∠ACD和∠BCE相等吗？为什么？18.如图，△ACF≌△DBE，其中点A、B、C、D在一条直线上．(1)若BE⊥AD，∠F=62°，求∠A的大小；(2)若AD=9cm，BC=5cm，求AB的长．参考答案1.【答案】D2.【答案】B3.【答案】B4.【答案】C5.【答案】D6.【答案】A7.【答案】D8.【答案】B9.【答案】9010.【答案】能够完全重合11.【答案】9012.【答案】11cm13.【答案】解：在图(2)中，AB和DB，AC和DC，BC和BC是对应边；∠A和∠D，∠ABC和∠DBC，∠ACB和∠DCB是对应角．在图(3)中，AB和AD，AC和AE，BC和DE是对应边；∠B和∠D，∠C和∠E，∠BAC和∠DAE是对应角．14.【答案】解：其他对应边是AC和CA；对应角是∠B和∠D，∠ACB和∠CAD，∠CAB和∠ACD．15.【答案】解：如图所示：．16.【答案】解：相等的边有AC=DB，OC=OB，OA=OD；相等的角有∠A=∠D，∠C=∠B，∠AOC=∠DOB．17.【答案】解：相等．理由：∵△ABC≌△DEC，∴∠ACB=∠DCE(全等三角形的对应角相等)．∴∠ACB―∠ACE=∠DCE―∠ACE(等式的基本性质)，即∠BCE=∠ACD．18.【答案】解：(1)∵BE⊥AD，∴∠EBD=90°，∵△ACF≌△DBE，∴∠FCA=∠EBD=90°，∵∠F=62°，∴∠A=90°―∠F=28°；(2)∵△ACF≌△DBE，∴CA=BD，∴CA―CB=BD―BC，即AB=CD，∵AD=9cm，BC=5cm，∴AB+CD=9―5=4(cm)，∴AB=2cm．。

人教版八年级数学上册课时练：第十二章《全等三角形》 (培优篇)解析版

课时练：第十二章《全等三角形》（培优篇）一．选择题1．已知△ACB≌△A'CB'，∠CBA＝30°，则∠CB'A'的度数为（）A．20°B．30°C．35°D．40°2．在下列条件中，能判断两个直角三角形全等的是（）A．一个锐角对应相等B．两锐角对应相等C．一条边对应相等D．一条斜边和另外一条直角边对应相等3．如图，点B、F、C、E在同一直线上，BF＝CE，AB∥DE，添加下列条件，其中不能判定△ABC≌△DEF的是（）A．∠A＝∠D B．AC＝DF C．AB＝DE D．∠ACB＝∠DFE 4．如图，在△ABC中，∠ABC＝45°，AC＝9cm，F是高AD和BE的交点，则BF的长是（）A．4cm B．6cm C．8cm D．9cm5．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC＝32，DE＝4，AB ＝6，则AC的长是（）A．8 B．9 C．10 D．116．如图，已知△ABC≌△DEF，CD平分∠BCA，若∠A＝28°，∠CGF＝85°，则∠E的度数是（）A．38°B．36°C．34°D．32°7．如图，方格纸中△DEF的三个顶点分别在小正方形的顶点上，像这样的三个顶点都在格点上的三角形叫格点三角形，则图中与△DEF全等的格点三角形有（）个．A．9 B．10 C．11 D．128．如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO．下列结论错误的是（）A．CB＝CD B．DA＝DC C．AB＝AD D．△ABC≌△ADC 9．如图，在△ABC中，∠B＝90°，点O是∠CAB、∠ACB平分线的交点，且BC＝4cm，AC＝5cm，则点O到边AB的距离为（）A．1cm B．2cm C．3cm D．4cm10．如图，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD 延长线上的点，∠EAF＝∠BAD，若DF＝1，BE＝5，则线段EF的长为（）A．3 B．4 C．5 D．6二．填空题11．如图，已知点A，D，C，F在同一条直线上，AB＝DE，且∠B＝∠E．则添加条件，可得△ABC≌△DEF．12．如图，四边形ABCD中，AC＝BC＝BD，且AC⊥BD，若AB＝a，则△ABD的面积为．（用含a的式子表示）13．如图，在四边形ABCD中，AC是四边形的对角线，∠CAD＝30°，过点C作CE⊥AB 于点E，∠B＝2∠BAC，∠ADC﹣∠BAC＝90°，若AB＝20，CD＝16，则BE的长为．14．如图，在△ABC中，CD是它的角平分线，DE⊥AC于点E．若BC＝8cm，DE＝3cm，则△BCD的面积为cm2．15．如图，△ABC中，∠C＝60°，取BC上一点D，连接AD，使AD＝BD，延长CA至E，连接ED，且∠DAE＝2∠AED，若BC＝4AE，AC＝3，则BC的长度为．三．解答题16．已知，如图，A、D、C、B在同一条直线上AD＝BC，AE＝BF，CE＝DF，求证：（1）DF∥CE；（2）DE＝CF．17．如图，已知△ABC中，AB＝AC＝10cm，BC＝8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由点B向C点运动，同时，点Q在线段CA上由点C向A点运动．（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由．（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？18．如图，已知∠ABC＝90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ，连接QE并延长交BP于点F．试说明：（1）△ABP≌△AEQ；（2）EF＝BF．19．在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C．且BD ＝CD，点E，F分别在边AM和AN上．（1）如图1，若∠BED＝∠CFD，请说明DE＝DF；（2）如图2，若∠BDC＝120°，∠EDF＝60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由．20．已知：直线m∥n，点A，B分别是直线m，n上任意两点，在直线n上取一点C，使BC＝AB，连接AC，在直线AC上任取一点E，作∠BEF＝∠ABC，EF交直线m于点F．（1）如图1，若点E是线段AC上任意一点，EF交AB于H，求证：EF＝BE；（2）如图2，点E在线段AC的延长线上时，∠ABE与∠AFE互为补角，若∠ABC＝90°，请判断线段EF与BE的数量关系，并说明理由．参考答案一．选择题1．解：∵△ACB≌△A'CB'，∠CBA＝30°，∴∠CB'A'＝∠CBA＝30°．故选：B．2．解：A、一个锐角对应相等，不能判定两直角三角形全等，故此选项不符合题意；B、两锐角对应相等，不能判定两直角三角形全等，故此选项不符合题意；C、一条边对应相等，不能判定两直角三角形全等，故此选项不符合题意；D、一条斜边和另外一条直角边对应相等能判定两直角三角形全等，故此选项符合题意；故选：D．3．解：∵BF＝CE，∴BC＝EF，∵AB∥DE∴∠B＝∠E，当∠A＝∠D时，且BC＝EF，∠B＝∠E，由“AAS”可证△ABC≌△DEF，当AC＝DF时，不能判定△ABC≌△DEF，当AB＝DE时，且BC＝EF，∠B＝∠E，由“SAS”可证△ABC≌△DEF，当∠ACB＝∠DFE时，且BC＝EF，∠B＝∠E，由“ASA”可证△ABC≌△DEF，故选：B．4．解：如图所示：∵AD⊥BC，BE⊥AC，∴∠ADC＝∠ADB＝90°，∠BEA＝90°，又∵∠FBD+∠BDF+∠BFD＝180°，∠FAE+∠FEA+∠AFE＝180°，∠BFD＝∠AFE，∴∠FBD＝∠FAE，又∵∠ABC＝45°，∠ABD+∠BAD＝90°，∴∠BAD＝45°，∴BD＝AD，在△FBD和△CAD中，，∴△FBD≌△CAD（AAS），∴BF＝AC，又∵AC＝9cm，∴BF＝9cm．故选：D．5．解：作DF⊥AC于F，如图，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DF⊥AC，∴DE＝DF＝4，∵S△ADB+S△ADC＝S△ABC，∴×6×4+×AC×4＝32，∴AC＝10．故选：C．6．解：∵CD平分∠BCA，∴∠ACD＝∠BCD＝∠BCA，∵△ABC≌△DEF，∴∠D＝∠A＝28°，∵∠CGF＝∠D+∠BCD，∴∠BCD＝∠CGF﹣∠D＝57°，∴∠BCA＝114°，∴∠B＝180°﹣28°﹣114°＝38°，∵△ABC≌△DEF，∴∠E＝∠B＝38°，故选：A．7．解：如图示2×3排列的每6个小正方形上都可找出4个全等的三角形，所以共有12个全等三角形，除去△DEF外有11个与△DEF全等的三角形：△DAF，△BGQ，△CGQ，△NFH，△AFH，△WBI，△QBI，△CKR，△KRW，△CGR，△KIW．故选：C．8．解：∵△ABO≌△ADO．∴AB＝AD，选项C正确，∠BAC＝∠DAC，在△ABC与△ADC中，∴△ABC≌△ADC（SAS），选项D正确∴CB＝CD，选项A正确；故选：B．9．解：∵点O为∠CAB与∠ACB的平分线的交点，∴点O在∠ACB的角平分线上，∴点O为△ABC的内心，过O作OP⊥AB，连接OB，S＝＝OP•（AB+BC+AC），△ABC又∵AC＝5，BC＝4，△ABC为直角三角形，∠B＝90°∴AB＝3，∴×3×4＝•OP（3+4+5），解得：OP＝1．故选：A．10．解：在BE上截取BG＝DF，∵∠B+∠ADC＝180°，∠ADC+∠ADF＝180°，∴∠B＝∠ADF，在△ADF与△ABG中，∴△ADF≌△ABG（SAS），∴AG＝AF，∠FAD＝∠GAB，∵∠EAF＝∠BAD，∴∠FAE＝∠GAE，在△AEG与△AEF中，∴△AEG≌△AEF（SAS）∴EF＝EG＝BE﹣BG＝BE﹣DF＝4．故选：B．二．填空题（共5小题）11．解：添加条件：BC＝EF；理由如下：在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）；故答案为：BC＝EF（答案不唯一）12．解：过D作DE⊥AB交BA的延长线于E，过C作CF⊥AB交AB于F，∵AC⊥BD，CF⊥AB，∴∠ACF+∠FAC＝90°，∠ABD+∠BAC＝90°，∴∠ACF＝∠ABD∵AC＝BC，CF⊥AB，∴AF＝BF＝，∠ACF＝∠BCF∴∠ABD＝∠BCF，∵∠DEB＝∠AFC＝90°，∠ABD＝∠BCF，BC＝BD∴△BDE≌△CBF（AAS）∴BF＝ED＝，∴△ABD的面积＝×AB×DE＝a2，故答案为a2．13．解：在EA上截取EF＝EB，连接CF，作FM⊥AC于M，作CN⊥AD于N，如图所示：∵CE⊥AB，∴CB＝CF，∴∠CFB＝∠B＝2∠BAC，∵∠CFB＝∠FCA+∠BAC，∴∠FCA＝∠BAC，∴AF＝CF，∵FM⊥AC，∴CM＝AM＝AC，∵CN⊥AD，∠CAD＝30°，∴CN＝AC，∴AM＝CN，∵∠ADC﹣∠BAC＝90°，∴∠ADC＝90°+∠BAC，∵∠ADC＝∠N+∠DCN＝90°+∠DCN，∴∠BAC＝∠DCN，在△AFM和△CDN中，，∴△AFM≌△CDN（ASA），∴AF＝CD＝16，∴BF＝AB﹣AF＝20﹣16＝4，∴BE＝BF＝2；故答案为：2．14．解：作DF⊥BC于F，∵CD是它的角平分线，DE⊥AC，DF⊥BC，∴DF＝DE＝3，∴△BCD的面积＝×BC×DF＝12（cm2），故答案为：12．15．解：延长CE至H，使CH＝CB，连接BH，作DG∥CH交BH于G，延长AC至F，使AF＝AD，连接DF、EG，如图所示：则∠ADF＝∠AFD，∠EDG＝∠AED，∠DGB＝∠H，设∠AED＝x，∵∠DAE＝2∠AED＝2x，∴∠ADF＝∠AFD＝∠DAE＝x＝∠AED＝∠DEG，∴DE＝DF，∵∠ACB＝60°，AH＝CB，∴△BCH是等边三角形，∴CB＝BH，∠CBH＝∠H＝60°，∴∠DGB＝∠CBH＝60°，∴△BDG是等边三角形，∴BD＝GD＝BG＝AD＝AF，∴GH＝BG＝，在△ADF和△GED中，，∴△ADF≌△GED（SAS），∴AF＝AD＝GE＝DG，∠ADF＝∠GED＝x，∴∠AEG＝2x＝∠EAD，∴∠GEH＝∠DAC，在△HEG和△CAD中，，∴△HEG≌△CAD（AAS），∴EH＝AC＝3，∵BC＝CH＝3+AE+3，BC＝4AE，∴6+AE＝4AE，解得：AE＝2，∴BC＝8；故答案为：8．三．解答题（共5小题）16．证明：（1）∵AD＝BC，∴AC＝BD，又AE＝BF，CE＝DF，∴△ACE≌△BDF（SSS）∴∠FDC＝∠ECD，∴DF∥CE；（2）由（1）可得∠A＝∠B，AD＝BC，AE＝BF，∴△ADE≌△BCF（SAS），∴DE＝CF17．解：（1）经过1秒后，PB＝3cm，PC＝5cm，CQ＝3cm，∵△ABC中，AB＝AC，∴在△BPD和△CQP中，，∴△BPD≌△CQP（SAS）．（2）设点Q的运动速度为x（x≠3）cm/s，经过ts△BPD与△CQP全等；则可知PB＝3tcm，PC＝8﹣3tcm，CQ＝xtcm，∵AB＝AC，∴∠B＝∠C，根据全等三角形的判定定理SAS可知，有两种情况：①当BD＝PC，BP＝CQ时，②当BD＝CQ，BP＝PC时，两三角形全等；①当BD＝PC且BP＝CQ时，8﹣3t＝5且3t＝xt，解得x＝3，∵x≠3，∴舍去此情况；②BD＝CQ，BP＝PC时，5＝xt且3t＝8﹣3t，解得：x＝；故若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为cm/s时，能够使△BPD与△CQP全等．18．解：（1）∵△ABE和△APQ是等边三角形，∴AB＝AE，AP＝AQ，∠BAE＝∠PAQ＝∠ABE＝∠AEB＝60°，∴∠BAE﹣∠PAE＝∠PAQ﹣∠PAE，∴∠BAP＝∠EAQ．在△ABP和△AEQ中，，∴△QAE≌△PAB（SAS）；（2）∵△QAE≌△PAB∴∠ABP＝∠AEQ＝90°．∴∠AEF＝90°，∴∠ABP＝∠AEF∴∠ABP﹣∠AEB＝∠AEF﹣∠ABE，∴∠BEF＝∠EBF，∴BF＝EF．19．解：（1）∵DB⊥AM，DC⊥AN，∴∠DBE＝∠DCF＝90°，在△BDE和△CDF中，∵∴△BDE≌△CDF（AAS）．∴DE＝DF；（2）EF＝FC+BE，理由：过点D作∠CDG＝∠BDE，交AN于点G，在△BDE和△CDG中，，∴△BDE≌△CDG（ASA），∴DE＝DG，BE＝CG．∵∠BDC＝120°，∠EDF＝60°，∴∠BDE+∠CDF＝60°．∴∠FDG＝∠CDG+∠CDF＝60°，∴∠EDF＝∠GDF．在△EDF和△GDF中，，∴△EDF≌△GDF（SAS）．∴EF＝GF，∴EF＝FC+CG＝FC+BE．20．（1）证明：如图1，在直线m上，取点M，使ME＝EA，∴∠EMA＝∠EAM，∵BC＝AB，∴∠CAB＝∠ACB，∵m∥n，∴∠MAC＝∠ACB，∠FAB＝∠ABC，∴∠MAC＝∠CAB，∴∠CAB＝∠EMA，∵∠BEF＝∠ABC，∴∠FAB＝∠BEF，∵∠AHF＝∠EHB∴∠AFE＝∠EBA，∴△AEB≌△MEF（AAS），∴EF＝EB；（2）解：EF＝BE．理由如下：如图2，在直线m上截取AN＝AB，连接NE，∵∠ABC＝90°，∴∠CAB＝∠ACB＝45°，∵m∥n，∴∠NAE＝∠ACB＝∠CAB＝45°，∠FAB＝90°，∵AE＝AE∴△NAE≌△ABE（SAS），∴EN＝EB，∠ANE＝∠ABE，∵∠ABE+∠EFA＝180°，∠ANE+∠ENF＝180°∴∠ENF＝∠EFA，∴EN＝EF，∴EF＝BE．。

八年级初二上册数学人教版课时练《三角形全等的判定》01(含答案)

二、填空题
1．如图，AB=DC，AD=BC，E、F是DB上两点且BE=DF，若∠AEB=100°，∠ADB= ，=AC，BE、CF是中线，则由可得。
4．如图AB=CD，AD=BC，O为BD中点过O点作直线与DA、BC延长线交于E、F，若，EO=10，则∠DBC=，FO=。
∴∠1=∠2、∠3=∠4（全等三角形对应角相等）
∴∠EFB=∠BCE又∵AB=ED∴AC=FD
在△FDB与△ACE中 ∴ （SAS）
∴ （全等三角形对应角相等）
2．
证明：在与中， ∴ （SAS）
∴ 、（全等三角形对应角相等）∴AC=DB
在与中 ∴ （AAS）
∴AE=EB在与中，
∴ （SSS）∴ ∴OE平分∠AOB
4．已知∠1=∠2，∠3=∠4，∠B=∠D，AF=CE，求证：AB=ED。
参考答案
一、选择题
1．B 2．B 3．D 4．A 5．C 6．C 7．D 8．B 9．D 10．D
二、填空题
1．70°2．27°3．SAS 4．60°；10 5．28°
三、解答题
1．
证明：连结FC，在与中， ∴ （SSS）
A．AD=BE B．AD=2BE C．AD=3BE D．以上都不对
9．如图AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则（）
A．∠1=∠EFD B．BE=EC C．BF=DF=CD D．FD∥BC
10．如图△ABC中，AD⊥BC，D为BC中点，则以下结论不正确的是（）
A． B．
C．AD是 A的平分线D．∠ABC是等边三角形
5．如图，AB=AC，BD=DC，若，则。
三、解答题
1．如图已知BF=CE，BC=EF，AB=DE，求证：∠A=∠D。

第12章《全等三角形》人教版八年级数学上册课时练能力篇(含答案)

课时练：第十二章《全等三角形》（能力篇）一．选择题1．下列说法正确的是（）A．形状相同的两个三角形全等B．能完全重合的两个三角形全等C．两个等腰直角三角形全等D．面积相等的两个三角形全等2．如图所示，OA＝OB，OC＝OD，∠O＝50°，∠D＝35°，则∠OBC的度数是（）A．130°B．85°C．105°D．95°3．如图，∠ADC＝∠AEB＝90°，补充下列一个条件，仍无法判定△ABE≌△ACD的是（）A．AD＝AE B．∠B＝∠C C．BE＝CD D．AB＝AC4．如图，△ABC≌A′CB′，若∠BCB′＝40°，AC⊥A′B′，则∠A′的度数是（）A．50°B．60°C．70°D．80°5．用尺规作图，不能唯一确定一个直角三角形的是（）A．已知两直角边B．已知一个直角边和斜边C．已知两个锐角D．已知一斜边和一锐角6．如图，AB，BC，AC表示的是三条河流，现决定在这三条河流中间修建一个木材厂，使该厂到三条河流的距离相等，以便利用走水路向外运木柴，则这个木柴长应建在（）A．AC，BC两边高线的交点处B．AC，BC两边中线的交点处C．AC，BC两边垂直平分线的交点处D．∠A，∠B两角的平分线的交点处7．如图，在△ABC中，∠ACB＝90°，AE为∠BAC的平分线，DE⊥AB，AB＝7cm，AC＝3cm，则BD等于（）A．1cm B．2cm C．3cm D．4cm8．小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、4的四块），你认为将其中的哪一块带去玻璃店，就能配一块与原来一样大小的三角形玻璃．应该带（）A．第4块B．第3块C．第2块D．第1块9．如图所示，△ABC中，AB＝AC，BE＝CF，AD⊥BC，则图中共有全等三角形（）A．4对B．3对C．2对D．1对10．如图，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，将△ABC沿直线BC方向平移2.5个单位得到△DEF，AC与DE相交于G点，连接AD，AE，则下列结论：①△AGD≌△CGE；②△ADE为等腰三角形；③AC平分∠EAD；④四边形AEFD的面积为9．其中正确的个数是（）A．1个B．2个C．3个D．4个二．填空题11．如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需要加条件．12．在平面直角坐标系中，点A（2，0），B（0，4），作△BOC，使△BOC与△ABO全等，则点C坐标为．（点C不与点A重合）13．如图，BD是△ABC的角平分线，DE⊥AB，垂足为E，△ABC的面积为70，AB＝16，BC＝12，则DE的长为．14．如图，在△ABC中，∠C＝90°，DE⊥AB于D，BC＝BD，若AC＝4cm，则AE+DE＝．15．如图，△ABC≌△ADE，且∠EAB＝120°，∠B＝30°，∠CAD＝10°，∠CFD＝°．三．解答题16．已知如图，在△ABC中，BE、CF分别是AC、AB边上的高，在BE的延长线上截取BM ＝AC，在CF的延长线上截取CN＝AB，请说明：（1）AM＝AN．（2）AM⊥AN．17．如图，△ABC中，BD⊥AC于点D，CE⊥AB于点E，且BD、CE交于点F，点G是线段CD上一点，连接AF、GF，若AF＝GF，BD＝CD．（1）求∠CAF的度数；（2）判断线段FG与BC的位置关系，并说明理由．18．（1）如图①，在Rt△ABC中，∠C＝90°，∠B＝45°，AD平分∠BAC，交BC于点D．如果作辅助线DE⊥AB于点E，则可以得到AC、CD、AB三条线段之间的数量关系为；（2）如图，△ABC中，∠C＝2∠B，AD平分∠BAC，交BC于点D．（1）中的结论是否仍然成立？若不成立，试说明理由；若成立，请证明．19．如图，在△ABC中，D是BC的中点，过点D的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF，交AB于点E，连接EG，EF．（1）求证：EG＝EF．（2）请你判断BE+CF与EF的大小关系，并说明理由．20．已知，点D是△ABC内一点，满足AD＝AC（1）已知∠CAD＝2∠BAD，∠ABD＝30°，如图1，若∠BAC＝60°，∠ACB＝80°，请判断BD和CD的数量关系（直接写出答案）（2）如图2，若∠ACB＝2∠ABC，BD＝CD，试证明∠CAD＝2∠BAD．参考答案一．选择题1．解：A、如教师用的三角板和学生用的三角板形状相同，但不全等，故本选项错误；B、能够完全重合的两个三角形全等，故本选项正确；C、如图：图中的两个等腰直角三角形不全等，故本选项错误；D、当一个三角形的底是2，对应的高是1，而另一个三角形的底是1，对应的高是2，两三角形的面积相等，但是两三角形不全等，故本选项错误；故选：B．2．解：∵在△OAD和△OBC中，，∴△OAD≌△OBC，（SAS）∴∠OBC＝∠OAD＝180°﹣∠O﹣∠D＝95°，故选：D．3．解：A、在△ABE和△ACD中，，∴△ABE≌△ACD（ASA），故本选项错误；B、根据∠A＝∠A，∠AEB＝∠ADC，∠B＝∠C不能推出△ABE≌△ACD（ASA），故本选项正确；C、在△ABE和△ACD中，，∴△ABE≌△ACD（AAS），故本选项错误；D、在△ABE和△ACD中，，∴△ABE≌△ACD（AAS），故本选项错误；故选：B．4．解：∵△ABC≌A′CB′，∴∠ACB＝∠B′CA′，∴∠BCB′＝∠ACA′＝40°，∵AC⊥A′B′，∴∠A′＝90°﹣∠ACA′＝50°，故选：A．5．解：A、符合全等三角形的判定定理SAS，所以能作出唯直角一三角形．故本选项不符合题意；B、符合全等三角形的判定定理HL，所以能作出唯一直角三角形．故本选项不符合题意；C、因为已知两个锐角，而边长不确定，故这样的三角形可作很多，而不是唯一的．故本选项符合题意；D、故选符合全等三角形的判定定理AAS，所以能作出唯直角一三角形．故本选项不符合题意；故选：C．6．解：根据角平分线的性质，木材厂应建在∠A、∠B两内角平分线的交点处．故选：D．7．解：∵AC⊥BC，AE为∠BAC的平分线，DE⊥AB，∴CE＝DE，在Rt△ACE和Rt△ADE中，，∴Rt△ACE≌Rt△ADE（HL），∴AC＝AD，∵AB＝7cm，AC＝3cm，∴BD＝AB﹣AD＝AB﹣AC＝7﹣3＝4cm．故选：D．8．解：1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，只有第2块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．故选：C．9．解：∵AD⊥BC，AB＝AC，∴∠ADB＝∠ADC＝90°，BD＝DC，∵BE＝CF，∴DE＝DF，∵AD⊥BC，∴AE＝AF，在△ADB和△ADC中，，∴△ADB≌△ADC（SAS），同理△ADF≌△ADE，在△AEB和△AFC中，，∴△AEB≌△AFC（SSS），∵BE＝CF，∴BE+EF＝CF+EF，∴BF＝CE，在△AEC和△AFB中，，∴△AEC≌△AFB（SSS），即共4对全等三角形．故选：A．10．解：由平移的性质得：AD∥BE，AD＝BE＝2.5，∵∠BAC＝90°，AB＝3，AC＝4，∴BC＝＝＝5，∴CE＝2.5，∴AD＝CE，∵AD∥BE，∴∠DAG＝∠ECG，在△AGD和△CGE中，，∴△AGD≌△CGE（AAS），∴①正确；∵∠BAC＝90°，BE＝CE，∴AE＝BC＝CE＝2.5，∴AE＝AD，∴△ADE为等腰三角形，∴②正确；∵AE＝CE，∴∠EAC＝∠ECG，∵∠DAG＝∠ECG，∴∠EAC＝∠DAG，∴AC平分∠EAD，∴③正确；作AH⊥BC于H，如图所示：∵△ABC的面积＝BC•AH＝AB•AC，∴AH＝＝，∴四边形AEFD的面积＝（AD+EF）×AH＝（2.5+5）×＝9，∴④正确；正确的个数有4个，故选：D．二．填空题（共5小题）11．解：还需添加条件AB＝AC，∵AD⊥BC于D，∴∠ADB＝∠ADC＝90°，在Rt△ABD和Rt△ACD中，，∴Rt△ABD≌Rt△ACD（HL），故答案为：AB＝AC．12．解：如图所示：有三个点符合，∵点A（2，0），B（0，4），∴OB＝4，OA＝2，∵△BOC与△AOB全等，∴OB＝OB＝4，OA＝OC＝2，∴C1（﹣2，0），C2（﹣2，4），C3（2，4）．故答案为：（2，4）或（﹣2，0）或（﹣2，4）．13．解：作DF⊥BC于F，∵BD是△ABC的角平分线，DE⊥AB，DF⊥BC，∴DF＝DE，∴×AB×DE+×BC×DF＝70，∴DF＝DE＝5．故答案为：5．14．解：∵DE⊥AB，∴∠C＝∠BDE，在Rt△CBE和Rt△DBE中∴Rt△CBE≌Rt△DBE（HL），∴CE＝DE，∴AE+DE＝AE+CE＝AC＝4cm，故答案为：4cm．15．解：∵△ABC≌△ADE，∴∠EAD＝∠CAB，∵∠EAB＝120°，∠CAD＝10°，∴∠EAD＝∠CAB＝55°，∴∠CFD＝∠FAB+∠B＝10°+55°+30°＝95°，故答案为：95．三．解答题（共5小题）16．证明：（1）∵CF⊥AB，BE⊥AC，∴∠AEB＝∠AFC＝90°，∴∠ABE＝∠ACF＝90°﹣∠BAC，在△AMB和△ANC中，，∴△AMB≌△NAC（SAS），∴AM＝AN；（2）∵△AMB≌△NAC，∴∠BAM＝∠N，∵∠N+∠NAF＝90°，∴∠BAM+∠NAF＝90°，∴∠MAN＝90°，∴AM⊥AN．17．解：（1）∵BD⊥AC，CE⊥AB，∴∠BEF＝∠CDF＝90°，∵∠EFB＝∠DFC，∴∠EBF＝∠FCD，∵BD＝CD，∠ADB＝∠CDF，∴△ABD≌△FCD，∴AD＝DF，∴△ADF是等腰直角三角形，∴∠CAF＝45°；（2）FG∥BC，理由是：∵AF＝FG，∴∠FGA＝∠CAF＝45°，∵BD⊥AC，BD＝CD，∴△BDC是等腰直角三角形，∴∠DCB＝45°，∴∠FGA＝∠DCB，∴FG∥BC．18．解：（1）如图1，∵AD平分∠BAC，∴∠CAD＝∠EAD，在△CAD和△EAD中，∴△CAD≌△EAD（AAS），∴CD＝DE，AC＝AE，∵∠B＝45°，∠DEB＝90°，∴DE＝EB，∴DC＝BE，∴AE+BE＝AC+DC＝AB；故答案为：AB＝AC+CD．（2）成立．证明：如图2，在AB上截取AE＝AC，连接DE．∵在△ACD和△AED中，∴△ACD≌△AED（SAS），∴CD＝ED，∠C＝∠AED，又∵∠C＝2∠B，∴∠AED＝2∠B，又∵∠AED＝∠B+∠EDB，∴2∠B＝∠B+∠EDB，∴∠B＝∠EDB，∴ED＝EB∵AB＝AE+EB，ED＝EB＝CD，AE＝AC，∴AB＝AC+CD．19．解：（1）∵BG∥AC，∴∠DBG＝∠C，在△DBG和△DCF中，，∴△DBG≌△DCF，∴DG＝DF，∵DE⊥GF，∴EG＝EF．（2）结论：BE+CF＞EF．理由：∵△DBG≌△DCF，∴CF＝BG，在△EBG中，∵BE+BG＞EG，∵BG＝CF，EG＝EF，∴BE+CF＞EF．20．解：（1）BD和CD的数量关系是BD＝CD；理由：∵在△ABC中，∠BAC＝60°，∠ACB＝80°，∴∠ABC＝40°，∵∠CAD＝2∠BAD，∴∠CAD＝40°，∠BAD＝20°，又∵AD＝AC，∴∠ADC＝∠ACD＝70°，∴∠DBC＝∠ABC﹣∠ABD＝40°﹣30°＝10°，∠DCB＝∠ACB﹣∠ACD＝80°﹣70°＝10°，∴∠DBC＝∠DCB，∴DB＝DC；（2）作∠EBC＝∠ACB，使EB＝AC，连接ED、EA，则四边形AEBC是等腰梯形，∴AE∥BC，∴∠EAB＝∠ABC，∵BD＝CD，∴∠DBC＝∠DCB，∴∠EBD＝∠ACD，在△EBD和△ACD中∴△EBD≌△ACD（SAS），∴ED＝AD，∵∠ACB＝2∠ABC，∠EBC＝∠ACB，∴∠EBC＝2∠ABC，∴∠ABE＝∠ABC，∴∠EAB＝∠ABE，∴BE＝AE，∵AD＝AC＝EB，∴EA＝ED＝AD，∴△AED是等边三角形，∴∠EAD＝60°，∴∠BAD＝60°﹣∠EAB＝60°﹣∠ABC，∴2∠BAD＝120°﹣2∠ABC＝120°﹣∠ACB，∵AE∥BC，∴∠ACB+∠EAC＝180°，∴∠ACB＝180°﹣∠EAC，∵∠EAC＝60°+∠DAC，∴2∠BAD＝120°﹣（180°﹣60°﹣∠DAC）＝∠DAC，∴∠DAC＝2∠BAD．。

全等三角形-人教版数学八年级上第十二章12.1第一课时练习和答案

第十二章全等三角形12.1 全等三角形测试题知识点：全等形的概念1.如图11.1-4，5个全等的正六边形A、B、C、D、E，请仔细观察A、B、C、D四个图案，其中与E图案完全相同的是（）2.下列说法中正确的有（1）用一张底片冲洗出来的10张一寸相片是全等形（2）我国国旗上的4颗小五角星是全等形（3）所有的正方形是全等形（4）全等形的面积一定相等A. 1个B. 2个C. 3个D. 4个知识点：全等三角形的概念和表示法3.如图所示，图中两个三角形能完全重合，下列写法正确的是（）A．△ABE≌△AFB B．△ABE≌△ABFC．△ABE≌△FBA D．△ABE≌△FAB4.如果△ABC和△DEF全等，△DEF和△GHI全等，则△ABC和△GHI______全等，如果△ABC和△DEF不全等，△DEF和△GHI全等，则△ABC和△GHI______全等。

（填“一定”或“不一定”或“一定不”）5.直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是（）A．形状相同B．周长相等C．面积相等D．全等知识点：全等三角形的对应元素6.如图，△AOC≌△BOD，则对应角是______________，对应边是________________。

7.如图，把△ABC绕A点旋转一定角度，得到△ADE，则对应角是________________，对应边是______________________。

8.如图，沿着直线AC对折，△ABC和△ADC重合，则△CAB≌，AB的对应边是，∠BCA的对应角是。

知识点：全等三角形的性质9.若△ABC和△DEF全等，点A和点E、点B和点D分别是对应点，则下列结论是错误的是（）。

A．BC=EFB．∠B=∠DC．∠C=∠F D．AC=EF10.如图，△ABD≌△ACE，点B和点C是对应顶点，AB=8，AD=6，BD=7，则BE的长是（）。

A．1 B．2 C．4 D．611.如图，△ABC≌△ADE，∠B＝100°，∠BAC＝30°，那么∠AED＝______。

2020八年级数学上册第12章全等三角形 12.1 全等三角形课时练 (新版)新人教版

第十二章 12.1 全等三角形学校：姓名：班考号：①只有两个三角形才能完全重合;②如果两个图形是全等形,那么它们的形状和大小一定都相同;③两个正方形一定是全等形;④边数相同的图形一定能互相重合.A. ①③④B. ①②③C. ①③D. ①④2. 如图所示,已知△ABC ≌△AEF ,AB=BC ,∠B=∠E ,则下列结论中正确的个数为( )①AC=AF ; ②∠FAB=∠EAB ;③AE=EF ; ④∠EAB=∠FAC.A. 1B. 2C.3 D. 43. 已知△ABC ≌△A'B'C',等腰三角形ABC 的周长为18 cm,BC=8 cm,那么△A'B'C'中底边的长等于( )A. 5 cmB. 2 cm 或5 cmC. 8 cmD. 2 cm 或8 cm4. 如图所示,△ABC ≌△DEF ,BE=4,AE=1,则DE 的长是( )A. 5B. 4C.3 D. 25. 如图,△ACB ≌△A 1CB 1,∠BCB 1=30°,则∠ACA 1的度数为( )A. 20°B. 30°C.35° D. 40°20206. 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A 和点B是对应点,下列结论中,错误的是()A. AF∥BEB. CF∥DEC.AB=CD D. ∠ACF=∠EBD7. 如图,已知△ABC中,△ACD≌△BFD,F是高AD和BE的交点,CD=4,则线段DF的长度为()A. 2B. 4C.6 D. 38. 如图所示,△PAC≌△PBD,∠A=45°,∠BPD=20°,则∠PCD的度数为()A. 25°B. 45°C.65° D. 115°9. 如图所示,将△ABC沿BC翻折,使点A落在点D处,则△ABC≌△DBC,其中∠ABC的对应角为()A. ∠ACBB. ∠BCDC.∠BDC D. ∠DBC二、填空题,B,E,C,F在同一条直线上.如果AB=8 cm,BE=4 cm,DH=3 cm,则图中阴影部分的面积为cm2.11. 已知△ABC≌△DEF,AB=6 cm,△ABC的面积为24 cm2,则DE边上的高为.12. 已知△ABC≌△DEF,且△DEF的周长是13,若AB=4,BC=6,则DF的长是.13. 如图所示,若把△ABC绕点A旋转一定的角度就得到△ADE,那么________≌________;对应边AB=________,AC=________,BC=________;对应角∠CAB=________,∠B=________,∠C=________.14. 将长方形ABCD的一角沿AE折叠,使点D落在点D'处,得到如图所示的图形,若∠CED'=56°,则∠D'AB= 度.三、解答题ACD,∠AEB与∠ADC是对应角,根据这两个全等三角形,写出对应边和其他的对应角.16. 如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,BC的延长线分别交AD,ED于点F,G,求∠EGF的度数.17. 如图,已知CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=30°,AB=8,AD=4,G为AB延长线上一点,求∠EBG的度数和CE的长.18. 如图所示,A,D,E三点在同一条直线上,且△BAD≌△ACE,试说明:(1)BD=DE+CE;2020 (2)当△ABD满足什么条件时,BD∥CE?参考答案1. 【答案】A【解析】形状、大小相同的图形放在一起能够完全重合,这两个图形叫做全等形.由此定义可知, ①③④错误.2. 【答案】C【解析】由全等三角形的性质及∠FAB为∠EAF与∠CAB的公共角,可知①③④正确,由已知条件无法判定②是否正确,故选C.3. 【答案】D【解析】因为等腰三角形ABC的周长为18 cm,所以当BC=8 cm为腰时,△ABC 的底边为2 cm;当BC=8 cm为底边时, △ABC的腰长为5 cm,符合题意.又△ABC≌△A'B'C',综上,故△A'B'C'中底边的长等于2 cm或8 cm.4. 【答案】A【解析】易知AB= BE + AE =5,又因为△ABC≌△DEF,所以DE=AB=5,故选A.5. 【答案】B【解析】因为△ACB≌△A1CB1,所以∠ACB=∠A1CB1,又因为∠ACB=∠ACA1+A1CB,∠A1CB1=∠A1CB+∠BCB1,∠BCB1=30°,即∠ACA1+A1CB=∠A1CB+30°,所以∠ACA1=30°,故选B.6. 【答案】D【解析】由△ACF≌△BDE,点F和点E是对应点,点A和点B是对应点,可得点C 和点D是对应点.所以①∠A=∠EBD,∴AF∥BE；②∠D=∠FCA，∴CF∥DE;③AC=BD,AC-BC=BD-BC, ∴AB=CD；所以A，B，C均正确;④∠ACF=∠BDE,而题中未给出三角形两边相等的条件，故D不正确.7. 【答案】B【解析】∵△ACD≌△BFD,∴对应边DF=DC=4.故选B.8. 【答案】C【解析】因为△PAC≌△PBD,对应角相等得∠APC=∠BPD=20°,所以∠PCD=∠A+∠APC=45°+20°=65°.9. 【答案】D【解析】由三角形翻折得到的△ABC≌△DBC可知,点A和点D,点B和点B,点C 和点C分别是对应点,所以∠ABC和∠DBC是对应角.10. 【答案】2611. 【答案】8 cm12. 【答案】313. 【答案】△ABC △ADE AD AE DE ∠EAD ∠D ∠E14. 【答案】3418.(1) 【答案】∵△BAD≌△ACE,∴BD=AE,AD=CE.∵AE=AD+DE,∴AE= DE + CE,∴BD= DE + CE.(2) 【答案】当△ABD中∠ADB=90°时,BD∥CE.理由:若BD∥CE，则∠EDB=∠CED.又∵△BAD≌△ACE, ∴∠ADB=∠CED.∴∠ADB=∠DEB.又∵∠ADB+∠BDE=180°,∴∠ADB=90°.。

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析

第12章《全等三角形》人教版八年级数学上册课时练能力篇(含答案)

课时练：第12章《全等三角形》（能力篇）一．选择题1．下列结论正确的是（）A．形状相同的两个图形是全等图形B．全等图形的面积相等C．对应角相等的两个三角形全等D．两个等边三角形全等2．到三角形三边距离相等的点是（）A．三角形的两条平分线的交点B．三角形的两条高的交点C．三角形的三条中线的交点D．三角形的三条边的垂直平分线的交点3．如图，已知△ABC≌△DEF，点B与点E是对应点，点A与点D是对应点，下列说法不一定成立的是（）A．AB＝DE B．AC＝DF C．BE＝EC D．BE＝CF4．如图，点E在线段AB上，若AC＝AD，CE＝DE，则图中的全等三角形共有（）A．1对B．2对C．3对D．4对5．如图，△ABC中，∠B＝∠C＝∠EDF＝α，BD＝CF，BE＝CD，则下列结论正确的是（）A．2α+∠A＝180°B．α+∠A＝90°C．2α+∠A＝90°D．α+∠A＝180°6．如图，AC是△ABC和△ADC的公共边，下列条件中不能判定△ABC≌△ADC的是（）A．∠2＝∠1，∠B＝∠D B．AB＝AD，∠3＝∠4C．∠2＝∠1，∠3＝∠4 D．AB＝AD，∠2＝∠17．如图，已知EA⊥AB，BC∥EA，EA＝AB＝2BC，D为AB的中点，则下面式子中不能成立的是（）A．∠1+∠3＝90°B．DE⊥AC且DE＝ACC．∠3＝60°D．∠2＝∠38．如图，在△ABC中，点D在边BC上，若∠BAD＝∠CAD，AB＝6，AC＝3，S＝3，△ABD ＝（）则S△ACDA．3 B．6 C．D．9．如图，在Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，则下列结论中正确的是（）A．BD+ED＝AC B．BD+ED＝AD C．DE平分∠ADB D．ED+AC＞AD 10．△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：①∠DAE＝∠F；②∠AGH＝∠BAE+∠ACB；③S△AEB ：S△AEC＝AB：CA；④∠ABC+∠ACB＝2∠AHG，其中正确的结论有（）个．A．1 B．2 C．3 D．4二．填空题11．工人师傅常用角尺平分一个任意角．作法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C作射线OC．由作法得△MOC≌△NOC的依据是．12．如图，已知∠AOB＝30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC＝4，则PD等于．13．一个三角形的三边为2、7、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y＝．14．如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需要加条件．15．如图，已知点P到AE、AD、BC的距离相等，下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P在∠BAC、∠CBE、∠BCD的平分线的交点上，其中正确的是．（填序号）16．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．17．在△ABC中，已知∠A＝60°，∠ABC的平分线BD与∠ACB的平分线CE相交于点O，∠BOC的平分线交BC于F，则下列说法中正确的是．①∠BOE＝60°，②∠ABD＝∠ACE，③OE＝OD④BC＝BE+CD三．解答题18．在△ABC中，AB＝AC，∠BAC＝60°，点E为直线AC上一点，D为直线BC上的一点，且DA＝DE．当点D在线段BC上时，如图①，易证：BD+AB＝AE；当点D在线段CB的延长线上时，如图②、图③，猜想线段BD，AB和AE之间又有怎样的数量关系？写出你的猜想，并选择一种情况给予证明．19．如图，AD＝CB，E、F是AC上两动点，且有DE＝BF．（1）若点E、F运动至如图（1）所示的位置，且有AF＝CE，求证：△ADE≌△CBF；（2）若点E、F运动至如图（2）所示的位置，仍有AF＝CE，则△ADE≌△CBF还成立吗？为什么？（3）若点E、F不重合，则AD和CB平行吗？请说明理由．20．如图1，在平面直角坐标系xOy中，点A在y轴上，点B是第一象限的点，且AB⊥y 轴，且AB＝OA，点C是线段OA上任意一点，连接BC，作BD⊥BC，交x轴于点D．（1）依题意补全图1；（2）用等式表示线段OA，AC与OD之间的数量关系，并证明；②连接CD，作∠CBD的平分线，交CD边于点H，连接AH，求∠BAH的度数．21．如图1，图2，在△ABC中，∠ACB＝90°，AC＝BC，AB＝8，点D时AB边长的中点，点E时AB边上一动点（点E不与点A、B重合），连接CE，过点B作BF⊥CE于F，交射线CD于点G．（1）当点E在点D的左侧运动时，（图1），求证：△ACE≌△CBG；（2）当点E在点D的右侧运动时（图2），（1）中的结论是否成立？请说明理由；（3）当点E运动到何处时，BG＝5，试求出此时AE的长．22．如图1，有两个全等的直角三角形△ABC和△EDF，∠ACB＝∠F＝90°，∠A＝∠E＝30°，点D在边AB上，且AD＝BD＝CD．△EDF绕着点D旋转，边DE，DF分别交边AC于点M，K．（1）如图2、图3，当∠CDF＝0°或60°时，AM+CK MK（填“＞”，“＜”或“＝”），你的依据是；（2）如图4，当∠CDF＝30°时，AM+CK MK（填“＞”或“＜”）；（3）猜想：如图1，当0°＜∠CDF＜60°时，AM+CK MK，试证明你的猜想．参考答案一．选择1．解：A．形状相同的两个图形不一定是全等图形，是相似形，故A错误；B．根据全等图形的性质，可得全等图形的面积相等，故B正确；C．对应角相等且对应边相等的两个三角形全等，故C错误；D．两个边长相等的等边三角形全等，故D错误，故选：B．2．解：∵点到两边距离相等，∴这个点在两边夹角的平分线上，同理可知，这个点在任意两边夹角的平分线上，∴这个点是三角形的两条平分线的交点，故选：A．3．解：∵△ABC≌△DEF，∴AB＝DE，AC＝DF，BC＝EF，∴BE＝CF，故选：C．4．解：图中的全等三角形共有3对．∵AC＝AD，CE＝DE，AE公共，∴△ACE≌△ADE．（SSS）进而得出△CEB≌△DEB，△ABC≌△ABD；故选：C．5．解：A、正确．∵∠A+∠B+∠C＝180°，∠B＝∠C＝α，∴2α+∠A＝180°．B、错误．不妨设，α+∠A＝90°，∵2α+∠A＝180°，∴α＝90°，这个显然与已知矛盾，故结论不成立．C、错误．∵2α+∠A＝180°，∴2α+∠A＝90°不成立．D、错误．∵2α+∠A＝180°，∴α+∠A＝180°不成立．故选：A．6．解：A、在△ABC和△ADC中，，∴△ABC≌△ADC（AAS）；B、在△ABC和△ADC中，，∴△ABC≌△ADC（SAS）；C、在△ABC和△ADC中，，∴△ABC≌△ADC（ASA）；D、在△ABC和△ADC中，AB＝AD，AC＝AC，∠2＝∠1，∴无法证出△ABC≌△ADC．故选：D．7．解：∵EA⊥AB，∴∠EAD＝90°，∵EA∥BC，∴∠CBA+∠EAD＝180°，∴∠B＝∠EAD＝90°，∵AB＝2BC，D为AB的中点，∴AD＝BC，在△EAD和△ABC中，，∴△EAD≌△ABC（SAS），∴DE＝AC，∠C＝∠3，∠E＝∠1，∵∠E+∠2＝90°，∴∠1+∠3＝90°，故A正确．∴∠AFD＝90°，AF⊥DE，故B正确，∵∠1+∠2＝90°，∠1+∠3＝90°，∴∠2＝∠3，故D正确，故选：C．8．解：过D作DP⊥AC交AC的延长线于P，DQ⊥AB于Q，∵∠BAD＝∠CAD，∴DP＝DQ，＝AB•DQ＝•DQ＝3，∵S△ABD∴DQ＝1，∴DP＝1，∴S＝•AC•DP＝，△ACD故选：C．9．解：∵AD平分∠CAB，DE⊥AB于E，DC⊥AC，∴DE＝DC，∴在△ADC中，有AC+CD＞AD，即DE+AC＞AD，故选：D．10．解：如图，①∵AD⊥BC，FG⊥AE，∴∠ADE＝∠AMF＝90°，∵∠AED＝∠MEF，∴∠DAE＝∠F；故①正确；②∵∠DAE＝∠F，∠FDG＝∠FME＝90°，∴∠AGH＝∠MEF，∵AE平分∠BAC交BC于E，∴∠BAE＝∠CAE，∵∠MEF＝∠CAE+∠ACB，∴∠AGH＝∠CAE+∠ACB，∴∠AGH＝∠BAE+∠ACB；故②正确；③∵AE平分∠BAC交BC于E，∴，∵S△AEB ：S△AEC＝＝，∴S△AEB ：S△AEC＝AB：CA；故③正确；④∵∠AMH＝90°，∴∠AHG＝90°﹣∠CAE＝90°﹣∠BAC，∵∠BAC＝180°﹣∠ABC﹣∠ACB，∴∠AHG＝90°﹣（180°﹣∠ABC﹣∠ACB）＝（∠ABC+∠ACB），即∠ABC+∠ACB＝2∠AHG；故④正确．故选：D．二．填空题（共7小题）11．解：∵OM＝ON，CM＝CN，OC为公共边，∴△MOC≌△NOC（SSS）．故答案为SSS．12．解：作PE⊥OA于E，∵CP∥OB，∴∠OPC＝∠POD，∵P是∠AOB平分线上一点，∴∠POA＝∠POD＝15°，∴∠ACP＝∠OPC+∠POA＝30°，∴PE＝PC＝2，∵P是∠AOB平分线上一点，PD⊥OB，PE⊥OA，∴PD＝PE＝2，故答案为：2．13．解：∵两个三角形全等，∴x＝6，y＝7，∴x+y＝7+6＝13．故答案为：1314．解：还需添加条件AB＝AC，∵AD⊥BC于D，∴∠ADB＝∠ADC＝90°，在Rt△ABD和Rt△ACD中，，∴Rt△ABD≌Rt△ACD（HL），故答案为：AB＝AC．15．解：∵点P到AE、AD的距离相等，∴点P在∠BAC的平分线上，①正确；∵点P到AE、BC的距离相等，∴点P在∠CBE的平分线上，②正确；∵点P到AD、BC的距离相等，∴点P在∠BCD的平分线上，③正确；∴点P在∠BAC、∠CBE、∠BCD的平分线的交点上，④正确，故答案为：①②③④．16．解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△BAD和△CAE中，∴△BAD≌△CAE（SAS），∴∠2＝∠ABD＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°，故答案为：55°．17．解：①如图，∵∠A＝60°，∴∠ABC+∠ACB＝180°﹣60°＝120°，∵BD、CE分别是∠ABC和∠BCA的平分线，∴∠OBC+∠OCB＝×120°＝60°，∴∠BOE＝∠OBC+∠OCB＝60°故①正确；②∵BD、CE分别是∠ABC和∠BCA的平分线，∴∠ABD＝∠ABC，∠ACE＝∠ACB，当AB＝AC时，∠ABC＝∠ACB，而已知AB和AC没有相等关系，故②不正确；③∵∠OBC+∠OCB＝60°，∴∠BOC＝120°，∵OF平分∠BOC，∴∠BOF＝∠COF＝60°，∴∠BOE＝60°，在△BOE和△BOF中，∵，∴△BOE≌△BOF（ASA），∴OE＝OF，同理得：△CDO≌△CFO，∴OD＝OF，∴OD＝OE，故③正确；④∵△BOE≌△BOF，△CDO≌△CFO，∴BF＝BE，CF＝CD，∴BC＝CF+BF＝BE+CD，故④正确；则下列说法中正确的是：①③④故答案为①③④．三．解答题（共5小题）18．解；如图②中，结论：BD+AE＝AB．理由：作EM∥AB交BC于M，∵△ABC是等边三角形，∴∠ABC＝∠C＝∠BAC＝60°，AB＝BC＝AC，∴∠CEM＝∠CAB＝60°，∠CME＝∠CBA＝60°，∴△CME是等边三角形，∴CE＝CM＝EM，∠EMC＝60°，∴AE＝BM，∵DA＝DE，∴∠DAE＝∠DEA，∴∠BAC+∠DAB＝∠C+∠EDM，∴∠DAB＝∠EDM，∵∠ABD＝180°﹣∠ABC＝120°，∠EMD＝180°﹣∠EMC＝120°，在△ABD和△DEM中，，∴△ABD≌△DEM，∴DB＝EM＝CM，∴DB+AE＝CM+BM＝BC＝AB．如图③中，结论：BD﹣AE＝AB．理由：作EM∥AB交BC于M，∵△ABC是等边三角形，∴∠ABC＝∠C＝∠BAC＝60°，AB＝BC＝AC，∴∠CEM＝∠CAB＝60°，∠CME＝∠CBA＝60°，∴△CME是等边三角形，∴CE＝CM＝EM，∠EMC＝∠MEC＝60°，∴AE＝BM，∵DA＝DE，∴∠DAE＝∠DEA，∴∠C+∠ADC＝∠MEC+∠DEM，∴∠ADB＝∠DEM，∵∠ABD＝180°﹣∠ABC＝120°，∠EMD＝180°﹣∠EMC＝120°，∴∠ABD＝∠DME，在△ABD和△DEM中，，∴△ABD≌△DME，∴DB＝EM＝CM，∴DB﹣AE＝CM﹣BM＝BC＝AB．19．解：（1）证明：∵AF＝CE，∴AF+EF＝CE+EF，即AE＝CF，在△ADE和△CBF中，∵，∴△ADE≌△CBF（SSS）；（2）△ADE≌△CBF成立，∵AF＝CE，∴AF﹣EF＝CE﹣EF，即AE＝CF，在△ADE和△CBF中，∵，∴△ADE≌△CBF（SSS）；（3）AD与CB不一定平行，在△ADE和△CBF中，仅有AD＝CB、DE＝BF不能判定它们全等，即不能得出∠A＝∠C，故AD与CB不一定平行．20．解：（1）如图1所示，（2）①OA+AC＝OD，过B作BE⊥x轴于E，则四边形AOEB是矩形，∴BE＝AO，∠ABE＝90°，∵AB＝AO，∴AB＝BE，∵BD⊥BC，∴∠CBD＝90°，∴∠ABC＝∠DBE，在△ABC与△BDE中，，∴△ABC≌△BDE，∴AC＝DE，∵OE＝AB＝OA，∴AO+AC＝OD；②如图2由（1）知：△ABC≌△BDE，∴BC＝BD，∵BD⊥BC，∴△BCD是等腰直角三角形，∴∠BCD＝45°，∵BH平分∠CBD，∴∠BHC＝90°，∵∠BAO＝90°，过H作HN⊥OA，HM⊥AB，∴四边形ANMH是矩形，∴∠NHM＝90°，∴∠NHC＝∠MHB，∴△CNH≌△BHM，∴HN＝HM，∴AH平分∠CAB，∴∠BAH＝45°．21．解：（1）在Rt△ABC中，∵AC＝BC，∴∠A＝∠ABC＝45°．∵点D是AB的中点，∴∠BCG＝∠ACB＝45°，∴∠A＝∠BCG．∵BF⊥CE，∴∠CBG+∠BCF＝90°．∵∠ACE+∠BCF＝90°，∴∠CBG＝∠ACE，在△ACE和△CBG中，，∴△ACE≌△CBG；（2）结论仍然成立，即△ACE≌△CBG．理由如下：在Rt△ABC中，∵AC＝BC，∴∠A＝∠ABC＝45°．∵点D是AB的中点，∴∠BCG＝∠ACB＝45°，∴∠A＝∠BCG．∵BF⊥CE，∴∠CBG+∠BCF＝90°．∵∠ACE+∠BCF＝90°，∴∠CBG＝∠ACE，∴△ACE≌△CBG；（3）在Rt△ABC中，∵AC＝BC，点D是AB的中点，∴CD⊥AB，CD＝AD＝BD＝AB＝4，在Rt△BDG中，DG＝＝3．点E在运动的过程中，分两种情况讨论：①当点E在点D的左侧运动时，CG＝CD﹣DG＝1，∵△ACE≌△CBG，∴AE＝CG＝1；②当点E在点D的右侧运动时，CG＝CD+DG＝7，∵△ACE≌△CBG，∴AE＝CG＝7．22．解：（1）在Rt△ABC中，D是AB的中点，∴AD＝BD＝CD＝AB，∠B＝∠BDC＝60°又∵∠A＝30°，∴∠ACD＝60°﹣30°＝30°，又∵∠CDE＝60°，或∠CDF＝60°时，∴∠CKD＝90°，∴在△CDA中，AM（K）＝CM（K），即AM（K）＝KM（C）（等腰三角形底边上的垂线与中线重合），∵CK＝0，或AM＝0，∴AM+CK＝MK；（2）由（1），得∠ACD＝30°，∠CDB＝60°，又∵∠A＝30°，∠CDF＝30°，∠EDF＝60°，∴∠ADM＝30°，∴AM＝MD，CK＝KD，∴AM+CK＝MD+KD，∴在△MKD中，AM+CK＞MK，（3）AM+CK＞MK，证明：作点A关于ED的对称点G，连接GK，GM，GD．∵点G是点A关于直线DE的对称点∴AD＝GD，GM＝AM，∠GDM＝∠ADM，∵Rt△ABC中，D是AB的中点，∴AD＝CD＝GD．∵∠A＝∠E＝30°，∴∠CDA＝120°，∠EDF＝60°，∴∠GDM+∠GDK＝60°，∠ADM+∠CDK＝60°，∴∠GDK＝∠CDK，在△GDK和△CDK中，∵，∴△GDK≌△CDK（SAS），∴GK＝CK，∵GM+GK＞MK，∴AM+CK＞MK．。

人教版八年级数学上册课时练：第12章《全等三角形》 (培优篇)

课时练：第12章《全等三角形》（培优篇）一．选择题1．如果两个三角形全等，那么下列结论不正确的是（）A．这两个三角形的对应边相等B．这两个三角形都是锐角三角形C．这两个三角形的面积相等D．这两个三角形的周长相等2．如图，已知△ABE≌△ACD，∠1＝∠2，∠B＝∠C，不正确的等式是（）A．AB＝AC B．∠BAE＝∠CAD C．BE＝DC D．AD＝DE3．一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．你认为下列四个答案中考虑最全面的是（）A．带其中的任意两块去都可以B．带1、2或2、3去就可以了C．带1、4或3、4去就可以了D．带1、4或2、4或3、4去均可4．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE、下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（）A．1个B．2个C．3个D．4个5．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A．线段CD的中点B．OA与OB的中垂线的交点C．OA与CD的中垂线的交点D．CD与∠AOB的平分线的交点6．已知△ABC≌△DEF，∠A＝80°，∠E＝50°，则∠F的度数为（）A．30°B．50°C．80°D．100°7．如图，已知AB＝CD，∠1＝∠2，AO＝3，则AC＝（）A．3 B．6 C．9 D．128．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，BC 恰好平分∠ABF，下列结论错误的是（）A．DE＝DF B．AC＝3BF C．BD＝DC D．AD⊥BC9．如图，∠A＝∠EGF，点F为BE、CG的中点，DB＝4，DE＝7，则EG长为（）A．1.5 B．2 C．3 D．5.510．如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）A．m+n＞b+c B．m+n＜b+c C．m+n＝b+c D．无法确定二．填空题11．如图，B、C、E共线，AB⊥BE，DE⊥BE，AC⊥DC，AC＝DC，又AB＝2cm，DE＝1cm，则BE＝．12．如图，若△ABC≌△ADE，且∠B＝60°，∠C＝30°，则∠DAE＝．13．如图，AC＝AD，∠1＝∠2，只添加一个条件使△ABC≌△AED，你添加的条件是．14．如图，△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm．点P从A点出发沿A→C→B路径向终点运动，终点为B点；点Q从B点出发沿B→C→A路径向终点运动，终点为A点．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．设运动时间为t秒，则当t＝秒时，△PEC与△QFC全等．15．如图，△ABC的周长是12，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，则△ABC的面积是．＝36cm2，AB＝18cm，BC＝12cm，则DE 16．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝cm．17．如图所示的方格中，∠1+∠2+∠3＝度．三．解答题18．如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1＝48°，求∠BDE的度数．19．如图，在等腰三角形△ABC中，AC＝BC，D、E分别为AB、BC上一点，∠CDE＝∠A．（1）如图①，若BC＝BD，求证：CD＝DE；（2）如图②，过点C作CH⊥DE，垂足为H，若CD＝BD，EH＝，直接写出CE﹣BE的值为．20．（1）已知△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC＝∠DCE，若∠A等于60°（如图①）．求证：EB＝AD；（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变（如图②），（1）的结论是否成立，并说明理由．21．如图、在△ABC中，∠ABC＝60°，AC＝2AB，AD平分∠BAC交BC于点D，延长DB点F，使BF＝BD，连接AF．（1）求证：AF＝CD；（2）若CE平分∠ACB交AB于点E，试猜想AC、AF、AE三条线段之间的数量关系，并证明你猜想的结论．22．如图1，在△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE 的延长线于F，且AF＝BD，连接BF．（1）求证：点D是线段BC的中点；（2）如图2，若AB＝AC＝13，AF＝BD＝5，求四边形AFBD的面积．23．已知∠MAN＝120°，AC平分∠MAN．（1）在图1中，若∠ABC＝∠ADC＝90°，求证：AB+AD＝AC；（2）在图2中，若∠ABC+∠ADC＝180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．参考答案一．选择题1．解：因为能够完全重合的两个三角形是全等三角形，所以：A、这两个三角形的对应边相等，正确；B、直角三角形，钝角三角形也能全等，所以全等三角形可以是锐角三角形、直角三角形或钝角三角形，故本选项错误；C、能够完全重合，所以这两个三角形的面积相等，正确；D、能够完全重合，所以这两个三角形的周长相等，正确．故选：B．2．解：∵△ABE≌△ACD，∠1＝∠2，∠B＝∠C，∴AB＝AC，∠BAE＝∠CAD，BE＝DC，AD＝AE，故A、B、C正确；AD的对应边是AE而非DE，所以D错误．故选：D．3．解：带③、④可以用“角边角”确定三角形，带①、④可以用“角边角”确定三角形，带②④可以延长还原出原三角形，故选：D．4．解：∵AD是△ABC的中线，∴BD＝CD，又∠CDE＝∠BDF，DE＝DF，∴△BDF≌△CDE，故④正确；由△BDF≌△CDE，可知CE＝BF，故①正确；∵AD是△ABC的中线，∴△ABD和△ACD等底等高，∴△ABD和△ACD面积相等，故②正确；由△BDF≌△CDE，可知∠FBD＝∠ECD∴BF∥CE，故③正确．故选：D．5．解：利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P．故选：D．6．解：∵△ABC≌△DEF，∴∠D＝∠A＝80°∴∠F＝180﹣∠D﹣∠E＝50°故选：B．7．解：∵AB＝CD，∠1＝∠2，∠AOB＝∠COD，∴△AOB≌△COD（AAS）∴AO＝CO＝3，∴AC＝6故选：B．8．解：∵BF∥AC，∴∠C＝∠CBF，∵BC平分∠ABF，∴∠ABC＝∠CBF，∴∠C＝∠ABC，∴AB＝AC，∵AD是△ABC的角平分线，∴BD＝CD，AD⊥BC，故CD正确，在△CDE与△DBF中，，∴△CDE≌△DBF，∴DE＝DF，CE＝BF，故A正确；∵没有指明AE＝2BF，∴不能得出AC＝3BF，故B错误．故选：B．9．解：∵∠A＝∠EGF，∠AGD＝∠EGF，∴∠A＝∠AGD，∴AD＝DG，设AD＝x，则DG＝x，在△EGF和△BCF中，∵，∴△EGF≌△BCF（SAS），∴BC＝EG，∠E＝∠EBC，∴EG∥BC，∴∠AGD＝∠C＝∠A，∴BC＝AB＝x+4＝EG，∵DE＝7，∴x+x+4＝7，x＝，∴EG＝x+4＝＝5.5．故选：D．10．解：在BA的延长线上取点E，使AE＝AC，连接EP，∵AD是∠A的外角平分线，∴∠CAD＝∠EAD，在△ACP和△AEP中，，∴△ACP≌△AEP（SAS），∴PE＝PC，在△PBE中，PB+PE＞AB+AE，∵PB＝m，PC＝n，AB＝c，AC＝b，∴m+n＞b+c．故选：A．二．填空题（共7小题）11．解：∵AC⊥DC，∴∠ACB+∠ECD＝90°∵AB⊥BE，∴∠ACB+∠A＝90°，∴∠A＝∠ECD，在△ABC和△CED中，，∴△ABC≌△CED（AAS），∴AB＝CE＝2cm，BC＝DE＝1cm，∴BE＝BC+CE＝3cm．故答案为3cm．12．解：∵在△ABC中，∠B＝60°，∠C＝30°，∴∠BAC＝180°﹣∠B﹣∠C＝90°，∵△ABC≌△ADE，∴∠DAE＝∠BAC＝90°，故答案为：90°．13．解：添加∠C＝∠D或∠B＝∠E或AB＝AE．（1）添加∠C＝∠D．∵∠1＝∠2，∴∠1+∠BAD＝∠2+∠BAD，∴∠CAB＝∠DAE，在△ABC与△AED中，，∴△ABC≌△AED（ASA）；（2）添加∠B＝∠E．∵∠1＝∠2，∴∠1+∠BAD＝∠2+∠BAD，∴∠CAB＝∠DAE，在△ABC与△AED中，，∴△ABC≌△AED（AAS）；（3）添加AB＝AE∵∠1＝∠2∴∠1+∠BAD＝∠2+∠BAD∴∠CAB＝∠DAE在△ABC与△AED中，，∴△ABC≌△AED（SAS）故填：∠C＝∠D或∠B＝∠E或AB＝AE．14．解：分为三种情况：①如图1，P在AC上，Q在BC上，∵PE⊥l，QF⊥l，∴∠PEC＝∠QFC＝90°，∵∠ACB＝90°，∴∠EPC+∠PCE＝90°，∠PCE+∠QCF＝90°，∴∠EPC＝∠QCF，则△PCE≌△CQF，∴PC＝CQ，即6﹣t＝8﹣3t，t＝1；②如图2，P在BC上，Q在AC上，∵由①知：PC＝CQ，∴t﹣6＝3t﹣8，t＝1；t﹣6＜0，即此种情况不符合题意；③当P、Q都在AC上时，如图3，CP＝6﹣t＝3t﹣8，t＝；④当Q到A点停止，P在BC上时，AC＝PC，t﹣6＝6时，解得t＝12．P和Q都在BC上的情况不存在，∵P的速度是每秒1cm，Q的速度是每秒3cm；故答案为：1或或12．15．解：如图，过点O作OE⊥AB于E，作OF⊥AC于F，∵OB、OC分别平分∠ABC和∠ACB，OD⊥BC，∴OE＝OD＝OF＝3，∴△ABC的面积＝×12×3＝18．故答案为：18．16．解：过点D作DF⊥BC于点F，∵BD是∠ABC的平分线，DE⊥AB，∴DE＝DF，∵AB＝18cm，BC＝12cm，∴S△ABC ＝S△ABD+S△BCD＝AB•DE+BC•DF＝DE•（AB+BC）＝36cm2，∴DE＝2.4（cm）．故答案为：2.4．17．解：如图，根据网格结构可知，在△ABC与△ADE中，，∴△ABC≌△ADE（SSS），∴∠1＝∠DAE，∴∠1+∠3＝∠DAE+∠3＝90°，又∵AD＝DF，AD⊥DF，∴△ADF是等腰直角三角形，∴∠2＝45°，∴∠1+∠2+∠3＝90°+45°＝135°．故答案为：135．三．解答题（共6小题）18．证明：（1）∵∠ADE＝∠1+∠C ∴∠2+∠BDE＝∠1+∠C，且∠1＝∠2，∴∠C＝∠BDE，且AE＝BE，∠A＝∠B，∴△AEC≌△BED（AAS）；（2）∵△AEC≌△BED，∴ED＝EC，∠BDE＝∠C，∴∠EDC＝∠C＝＝66°．19．（1）证明：∵AC＝BC，∠CDE＝∠A，∴∠A＝∠B＝∠CDE，∵∠CDB＝∠A+∠ACD＝∠CDE+∠BDE∴∠ACD＝∠BDE，又∵BC＝BD，∴BD＝AC，在△ADC和△BED中，，∴△ADC≌△BED（ASA），∴CD＝DE；（2）解：∵CD＝BD，∴∠B＝∠DCB，由（1）知：∠CDE＝∠B，∴∠DCB＝∠CDE，∴CE＝DE，如图②，在DE上取点F，使得FD＝BE，在△CDF和△DBE中，，∴△CDF≌△DBE（SAS），∴CF＝DE＝CE，又∵CH⊥EF，∴FH＝HE，∴CE﹣BE＝DE﹣DF＝EF＝2HE＝2×＝．20．证明：（1）作DF∥BC交AC于F，如图①所示：则∠ADF＝∠ABC，∠AFD＝∠ACB，∠FDC＝∠DCE，∵△ABC是等腰三角形，∠A＝60°，∴△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∴∠DBE＝120°，∠ADF＝∠AFD＝60°＝∠A，∴△ADF是等边三角形，∠DFC＝120°，∴AD＝DF，∵∠DEC＝∠DCE，∴∠FDC＝∠DEC，ED＝CD，在△DBE和△CFD中，，∴△DBE≌△CFD（AAS），∴EB＝DF，∴EB＝AD；（2）解：EB＝AD成立；理由如下：作DF∥BC交AC的延长线于F，如图②所示：同（1）得：AD＝DF，∠FDC＝∠ECD，∠FDC＝∠DEC，ED＝CD，又∵∠DBE＝∠DFC＝60°，∴在△DBE和△CFD中，，∴△DBE≌△CFD（AAS），∴EB＝DF，∴EB＝AD．21．（1）证明：如图1，取AC的中点G，连接DG，∴AC＝2AG＝2CG，∵AC＝2AB，∴AG＝AB＝CG，∵AD平分∠BAG，∴∠BAD＝∠GAD，在△ADB和△ADG中，∵，∴△ADB≌△ADG（SAS），∴BD＝DG，∠ABD＝∠AGD，∴∠DGC＝∠ABF，∵BD＝BF，∴BF＝DG，在△ABF和△CGD中，∵，∴△ABF≌△CGD（SAS），∴AF＝CD；（2）解：AC＝AE+AF，理由是：如图2，在AC上取一点H，使AH＝AE，连接OH，同理得△AOE≌△AOH（SAS），∴∠AOE＝∠AOH，∵∠ABO＝60°，∴∠BAC+∠ACB＝120°，∵AD平分∠BAC，CE平分∠ACB，∴∠BAO＝∠OAC，∠ACE＝∠BCE，∴∠OAC+∠ACO＝∠AOE＝60°，∴∠AOH＝60°，∴∠COH＝∠COD＝60°，∵∠HCO＝∠DCO，OC＝OC，∴△HCO≌△DCO（ASA），∴CD＝CH，∴AC＝AH+CH＝AE+CD＝AE+AF．22．（1）证明：如图1，∵点E是AD的中点，∴AE＝DE，∵AF∥BC，∴∠AFE＝∠DCE，∠FAE＝∠CDE．在△EAF和△EDC，∴△EAF≌△EDC，∴AF＝DC，∵AF＝BD，∴BD＝DC，即D是BC的中点；（2）解：如图2，∵AF∥BD，AF＝BD，∴四边形AFBD是平行四边形，∵AB＝AC，又由（1）可知D是BC的中点，∴AD⊥BC，在Rt△ABD中，AD＝＝12，∴矩形AFBD的面积＝BD•AD＝60．23．解：（1）在Rt△ACD中，∠DCA＝30°，Rt△ACB中，∠BCA＝30°∴AC＝2AD，AC＝2AB，∴2AD＝2AB∴AD＝AB∴AD+AB＝AC．（2）（1）中的结论AD+AB＝AC成立，理由如下：如图2，在AN上截取AE＝AC，连接CE，∵∠CAE＝60°，∴△ACE是等边三角形，∴∠DAC＝∠CEB＝60°，∵∠ADC+∠ABC＝180°，∠ABC+∠EBC＝180°，∴∠ADC＝∠EBC，∵在△ADC和△EBC中，，∴△ADC≌△EBC∴DA＝BE∵△CAE为等边三角形，∴AC＝AE，∴AD+AB＝AB+BE＝AE＝AC，∴AD+AB＝AC．。

人教版八年级数学上册全等三角形课时练及答案之欧阳美创编

ABE CD（第5题）ABCD E（第4题）A ODBC（第1题）第十三章全等三角形第1课时全等三角形一、选择题1．如图，已知△ABC≌△DCB ，且AB=DC ，则∠DBC 等于（）A ．∠A B．∠DCB C．∠ABC D．∠ACB 2．已知△ABC≌△DEF，AB=2，AC=4，△DEF 的周长为偶数，则EF 的长为（）A ．3B ．4 C ． 5D ．6二、填空题3．已知△ABC≌△DEF，∠A=50°，∠B=65°，DE=18㎝，则∠F=___°，AB=____㎝．4．如图，△ABC 绕点A 旋转180°得到△AED，则DE 与BC 的位置关系是___________，数量关系是___________．三、解答题5．把△ABC 绕点A 逆时针旋转，边AB 旋转到AD ，得到△ADE，用符号“≌”表示图中与△ABC 全等的三角形，并写出它们的对应边和对应A CF E DABFEDC （第6题）（第7题）角．6．如图，把△ABC 沿BC 方向平移，得到△DEF ．求证：AC ∥DF 。

7．如图，△ACF ≌△ADE ，AD =9，AE =4，求DF的长．ADBC（第2题）A F E CDB （第3题）AB C （第4题）一、选择题1．如果△ABC 的三边长分别为3，5，7，△DEF 的三边长分别为3，3x －2，2x －1，若这两个三角形全等，则x 等于（）A ．B ．3C ．4D ．5 二、填空题2．如图，已知AC=DB ，要使△ABC≌△DCB ，还需知道的一个条件是________．3．已知AC=FD ，BC=ED ，点B ，D ，C ，E 在一条直线上，要利用“SSS”，还需添加条件___________，得△ACB≌△_______．4．如图△ABC 中，AB=AC ，现想利用证三角形全等证明∠B=∠C，若证三角形全等所用的公理是SSS 公理，则图中所添加的辅助线应是_____________________．二、解答题5．如图，A ，E ，C ，F 在同一条直线上，AB=FD ，BC =DE ，AE=FC ．求证：△ABC ≌△FDE ．6．如图，AB=AC ，BD=CD ，那么∠B 与∠C 是否相等？为什么？ 7．如图，AB=AC ，AD = AE ，CD=BE ．求证：∠DAB=∠EAC ．D C EFB A（第5题） A B C D DEAACDBE F（第2题）A BEDC（第1题）ABCED一、填空题 1．如图，AB ＝AC ，如果根据“SAS”使△ABE≌△ACD，那么需添加条件________________．2．如图，AB ∥CD ，BC ∥AD ，AB=CD ，BE=DF ，图中全等三角形有_____________对．3．下列命题：①腰和顶角对应相等的两个等腰三角形全等；②两条直角边对应相等的两个直角三角形全等；③有两边和一角对应相等的两个三角形全等；④等腰三角形顶角平分线把这个等腰三角形分成两个全等的三角形．其中正确的命题有_____________．二、解答题4．已知：如图，C 是AB 的中点，AD ∥CE ，AD=CE ．求证：△ADC ≌△CEB ．5．如图， A ，C ，D ，B 在同一条直线上，AE=BF ，AD=BC ，AE∥BF .求证：FD ∥EC ．6．已知：如图，AC⊥BD，BC=CE ，AC=DC ．求证：∠B+∠D=90°；第4课时三角形全等的条件（3）（第4AB CDEDCF BAE（第5ABC DOAECBDABFE DC（第4题）1．下列说法正确的是（）A ．有三个角对应相等的两个三角形全等B ．有一个角和两条边对应相等的两个三角形全等C ．有两个角和它们夹边对应相等的两个三角形全等D ．面积相等的两个三角形全等二、填空题2．如图，∠B＝∠DEF，BC ＝EF, 要证△ABC≌△DEF，（1）若以“SAS”为依据，还缺条件；（2）若以“ASA”为依据，还缺条件．3．如图，在△ABC 中，BD ＝EC ，∠ADB＝∠AEC， ∠B＝∠C ，则∠CAE＝．三、解答题4．已知：如图，AB∥CD ，OA=OC ．求证：OB=OD5．已知：如图，AC⊥CE ，AC=CE ，∠ABC=∠CDE=90°，求证：BD=AB+ED6．已知：如图，AB=AD ，BO=DO ，求证：AE=AC第5课时三角形全等的条件（4）EAC（第3题）（第5题）（第2题）ADBCoABEDCF（第3题）（第5题）（第6题）（第4题）1．已知△ABC 的六个元素，则下面甲、乙、丙三个三角形中和△ABC 全等的图形是（）A ．甲和乙B ．乙和丙C ．只有乙D ．只有丙二、填空题2．如图，已知∠A=∠D ，∠A BC =∠DCB ，AB=6,则DC=．3．如图，已知∠A=∠C ，BE∥DF ，若要用“AAS ”证△ABE≌△CDF ，则还需添加的一个条件是．（只要填一个即可）三、解答题4．已知：如图，AB=CD ，AC=BD ，写出图中所有全等三角形，并注明理由．5．如图，如果AC ＝EF ，那么根据所给的数据信息，图中的两个三角形全等吗？请说明理由．6．如图，已知∠1＝∠2，∠3＝∠4，EC ＝AD ，求证：AB ＝BE第6课时三角形全等的条件（5） DCB A（第2ABDFCE（第3题）（第4题）1．使两个直角三角形全等的条件是（）A ．一个锐角对应相等B ．两个锐角对应相等C ．一条边对应相等D 。

最新人教版八年级数学上册课时同步练：全等三角形的判定(含答案)

课时同步练：全等三角形的判定基础题训练（一）：限时35分钟1．如图，在△ABC和△DBE中，点D在边AC上，BC与DE交于点P，AB＝DB，∠A＝∠BDE，∠ABD＝∠CBE．（1）求证：BC＝BE；（2）若AD＝DC＝2.5，BC＝4，求△CDP与△BEP的周长之和．2．如图，AB∥CD，∠B＝∠D，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）试判断AD与BE有怎样的位置关系，并说明理由；（2）试说明△AOD≌△EOC．3．如图，已知AD＝AE，BD和CE相交于点O，BD＝CE，∠B＝∠C．求证：AB＝AC．小明同学的证明过程如下框．小明同学的证法是否正确？若正确，请在方框内打“√”；若错误，请写出你的证明过程．4．已知两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD 是一个筝形，其中AD＝CD，AB＝CB，小明在探究筝形的性质时，得到如下结论：①BD平分∠ADC；②AO＝CO＝AC；③AC⊥BD；④S四边形ABCD＝AC•BD．（1）在以上结论中，正确的有（只填序号）；（2）请选择一个你认为正确的结论进行证明．5．如图，△ACD中，∠ACD＝60°，以AC为边作等腰三角形ABC，AB＝AC，E、F分别为边CD、BC上的点，连结AE、AF、EF，∠BAC＝∠EAF＝60°（1）求证：△ABF≌△ACE；（2）若∠AED＝70°，求∠EFC的度数；（3）请直接指出：当F点在BC何处时，AC⊥EF？6．填空：把下面的推理过程补充完整，并在括号内注明理由，如图，已知△ABC中，E、F分别是AB、AC上的两点，且EF∥BC，D为EF上一点，且BD＝CD，ED＝FD，请说明BE＝CF．解：∵BD＝CD（已知）∴∠DBC＝∠DCB（）∵EF∥BC（已知）∴∠EDB＝∠DBC∠FDC＝（）∴∠EDB＝∠FDC（等量代换）在△EBD和△FCD中，∴△EBD≌△FCD（）∴BE＝CF（）7．如图，点P是△ABC内一点，E、F分别是边AC、BC上的两点，连接PE、PF，且PE＝PF，点D为AC延长线上一点，连接PD，且DE＝BF，∠AEP+∠BFP＝180°．（1）求证：△DEP≌△BFP；（2）已知AB＝AE+BF，若∠ACB＝80°，求∠APB的度数．基础题训练（二）：限时35分钟8．如图，在∠ABC＝90°，∠DBE＝90°，BA＝BC，BD＝BE，连接AE、CD，AE所在直线交CD于点F，连接BF．（1）连接AD，EC，求证：AD＝EC；（2）若BF⊥AF，求证：点F为CD的中点．9．在△ABC和△ADE中，点E在BC边上，∠EAC＝∠DAB，∠B＝∠D，AB＝AD．（1）求证：△ABC≌△ADE；（2）如果∠AEC＝70°，求∠BAD的度数．10．（1）如图1，已知，AB∥CD，AD∥BC．求证：△ABC≌△CDA；（2）如图2，已知AB＝DC，AE＝DF，BF＝CE．求证：AF＝DE．11．如图，边长为a的正方形ABCD被两条与正方形的边平行的线段EF，GH分割成四个小矩形，EF与GH交于点P，连接AF，AH．（1）若BF＝DH，求证：AF＝AH．（2）连接FH，若∠FAH＝45°，求△FCH的周长（用含a的代数式表示）．12．如图，在△ABC中，AB＝AC，DE是过点A的直线，BD⊥DE 于点D，CE⊥DE于点E，AD＝CE．（1）若BC在DE的同侧（如图①）．求证：AB⊥AC．（2）若BC在DE的两侧（如图②），其他条件不变，（1）中的结论还成立吗？（不需证明）13．如图，已知BC是△ABD的角平分线，BC＝DC，∠A＝∠E＝30°，∠D＝50°．（1）写出AB＝DE的理由；（2）求∠BCE的度数．14．如图，点M是线段AB中点，AD、BC交于点N，连接AC、BD、MC、MD，∠1＝∠2，∠3＝∠4．（1）求证：△AMD≌△BMC；（2）图中在不添加新的字母的情况下，请写出除了“△AMD≌△BMC”以外的所有全等三角形，并选出其中一对进行证明．15．已知，如图，△ABC中，AB＝AC，∠ABC＝30°，过点B作BD ⊥AB交CA延长线于点D，过点C作CE⊥AC交BA延长线于点E，点F为AE中点，连接CF．（1）求证：AD＝BF；（2）请直接写出长度等于CF的线段（线段CF本身除外）．参考答案1．（1）证明：∵∠ABD＝∠CBE，∴∠ABC＝∠DBE，∵∠A＝∠BDE，AB＝BD，∴△ABC≌△DBE（SAS），∴BC＝BE；（2）∵△ABC≌△DBE，∴DE＝AC＝AD+DC＝2.5+2.5＝5，BE＝BC＝4，∴△CDP和△BEP的周长和＝DC+DP+CP+BP+PE+BE＝DC+DE+BC+BE＝15.5．2．解：（1）AD∥BE，理由：∵AB∥CD，∴∠B＝∠DCE，∵∠B＝∠D，∴∠DCE＝∠D，∴AD∥BE；（2）∵O是CD的中点，∴DO＝CO，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D＝∠OCE，在△ADO和△ECO中，∴△AOD≌△EOC（ASA）．3．解：小明同学的证法不正确．证明：∵∠B＝∠C，∠BOE＝∠COE，∴∠BDC＝∠BEC，∴∠ADB＝∠AEC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AB＝AC．4．解：在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），∴∠BDA＝∠BDC，故①正确，∵DA＝DC，∴DO⊥AC，∴∠AOD＝∠COD＝90°，AO＝OC，∴AC⊥DB，故②③正确；四边形ABCD的面积＝S△ADB+S△BCD＝DB×OA+DB×OC＝AC•BD，故④正确；故答案为①②③④5．（1）证明：∵∠BAC＝∠EAF＝60°，∴∠BAC﹣∠CAF＝∠EAF﹣∠CAF，∴∠EAC＝∠BAF，∵AB＝AC，∴∠B＝∠ACB＝（180°﹣6°）÷2＝60°，∵∠ACD＝60°，∴∠ACD＝∠D，在△CAE和△BAF中，，∴△CAE≌△BAF．（2）解：∵△CAE≌△BAF，∴AE＝AF，∠AEC＝∠AFB，∴∠AEF＝∠AFE＝（180°﹣60°）÷2＝60°，∵∠AEC+∠AED＝∠AFC+∠AFB＝180°，∴∠AED＝∠AFC＝70°，∴∠EFC＝∠AFC﹣∠AFE＝70°﹣60°＝10°．（3）解：当F点是BC的中点时，AC⊥EF．理由：∵△CAE≌△BAF．∴AE＝AF，CE＝BF，∵BF＝CF，∴CE＝CF，∴AC⊥EF．6．解：∵BD＝CD（已知）∴∠DBC＝∠DCB（等边对等角）∵EF∥BC（已知）∴∠EDB＝∠DBC∠FDC＝∠DCB（两直线平行，内错角相等）∴∠EDB＝∠FDC（等量代换）在△EBD和△FCD中，，∴△EBD≌△FCD（SAS）∴BE＝CF（全等三角形的对应边相等），故答案为：等边对等角；∠DCB；两直线平行，内错角相等；SAS；全等三角形的对应边相等．7．（1）证明：∵∠AEP+∠BFP＝180°，∠AEP+∠DEP＝180°，∴∠DEP＝∠BFP，∴DE＝BF，PE＝FP，∴△DEP≌△BFP．（2）解：∵△DEP≌△BFP，∴BF＝DE，PB＝PD，∠D＝∠FBP，∵AB＝AE+BF＝AE+DE＝AD，AP＝AP，∴△APD≌△APB，∴∠D＝∠ABP＝∠FBP，∠PAD＝∠PAB，∵∠ACB＝80°，∴∠CAB+∠CBA＝100°，∴∠PAB+∠PBA＝50°，∴∠APB＝130°．8．证明：（1）∵∠ABC＝90°，∠DBE＝90°，∴∠ABD＝∠EBC，又∵AB＝BC，BD＝BE，∴△ABD≌△BEC，∴AD＝EC．（2）如图2中：作CP⊥BF交BF的延长线于P，作DN⊥BF于N．∵∠ABC＝90°，BF⊥AE∴∠ABF+∠A＝90°，∠ABF+∠PBC＝90°∴∠A＝∠PBC，且AB＝BC，∠P＝∠AFB＝90°∴△ABF≌△BPC∴BF＝CP∵∠DBN+∠EBF＝90°，∠DBN+∠BDN＝90°，∴∠BDN＝∠EBF，∵∠DNB＝∠BFE＝90°，BD＝BE，∴△DNB≌△BFE，∴DN＝BF＝CP，∵∠DNF＝∠FPC，∠DEN＝∠PFC，∴△PFC≌△NFD，∴DF＝FC即点F是CD中点．9．证明：（1）∵∠EAC＝∠DAB，∴∠BAC＝∠DAE，在△ABC和△ADE中∵，∴△ABC≌△ADE；（2）∵△ABC≌△ADE，∴AC＝AE，∴∠C＝∠AEC＝70°，∴∠CAE＝180°﹣∠C﹣∠AEC＝40°，∴∠BAD＝40°．10．（1）证明：∵AB∥CD，∴∠BAC＝∠DCA，∵AD∥BC∴∠BCA＝∠DAC，在△ABC和△CDA中∴△ABC≌△CDA（ASA）（2）∵BF＝CE，∴BF+EF＝CE+EF．∴BE＝CF．在△ABE和△DCF中∴△ABE≌△DCF（SSS）．∴∠B＝∠C，在△ABF和△DCE中∴△ABF≌△DCE（SAS）∴AF＝DE．11．证明：（1）∵四边形ABCD是正方形，∴AD＝AB，∠D＝∠B＝90°，在△ABF和△ADH中，，∴△ABF≌△ADH（SAS），∴AF＝AH；（2）将△ADH绕点A顺时针旋转90°到△ABM的位置，如图所示，则AM＝AH，∠DAH＝∠BAM，∵∠FAH＝45°，∠DAB＝90°，∴∠DAH+∠BAF＝45°，∴∠BAM+∠BAF＝45°，即∠FAM＝45°，∴∠FAM＝∠FAH，在△FAM和△FAH中，，∴△FAM≌△FAH（SAS），∴MF＝HF，∵MF＝BF+BM＝BF+DH，∴△FCH的周长为：CF+CH+FH＝CF+CH+BF+DH＝BC+CD＝2a，即△FCH的周长为2a．12．（1）证明：∵BD⊥DE于点D，CE⊥DE于点E，∴△ABD和△CAE均为直角三角形．在Rt△ABD和Rt△CAE中，，∴Rt△ABD≌Rt△CAE（HL），∴∠ABD＝∠CAE．又∵∠ABD+∠BAD＝90°，∴∠CAE+∠BAD＝90°，∴∠BAC＝180°﹣（∠CAE+∠BAD）＝90°，∴AB⊥AC．（2）解：AB⊥AC，理由如下：同（1）可证出：Rt△ABD≌Rt△CAE（HL），∴∠ABD＝∠CAE．又∵∠ABD+∠BAD＝90°，∴∠BAC＝∠CAE+∠BAD＝90°，∴AB⊥AC．13．解：（1）∵BC是△ABD的角平分线，∴∠CBD＝∠CBA，∵BC＝DC，∴∠CBD＝∠D＝50°，∴∠CBD＝∠CBA，在△CDE和△CBA中，，∴△CDE≌△CBA，∴DE＝AB；（2）由（1）知，∠CBD＝∠D＝50°，∴∠BCD＝80°，∴∠ACB＝100°由（1）知，△CDE≌△CBA，∴∠DCE＝∠BCA，∴∠BCD＝∠ACE＝80°，∴∠BCE＝∠ACB﹣∠ACE＝20°．14．（1）解：∵点M是AB中点，∴AM＝BM，∵∠1＝∠2，∴∠AMD＝∠BMC，在△AMD和△BMC中，，∴△AMD≌△MBC（ASA）；（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．理由：∵△AMD≌△MBC，∴AD＝BC，∵∠3＝∠4，AB＝BA，∴△BAD≌△ABC（SAS），∴AC＝BD，∠BDN＝∠ACN，∵∠ANC＝∠BND，∴△ANC≌△BND（AAS），∵AC＝BD，∠CAM＝∠DBM，AM＝BM，∴△AMC≌△BMD（SAS）．15．（1）证明：∵BD⊥AB，EC⊥CA，∴∠DBA＝∠ECA＝90°，在△DBA和△ECA中，，∴△DBA≌△ECA（ASA），∴AD＝AE，∵AB＝AC，∴∠ABC＝∠ACB＝30°，∴∠FAC＝∠ABC+∠ACB＝60°，∵AF＝FE，∠ACE＝90°，∴CF＝AF＝EF，∴△AFC是等边三角形，∴AF＝AC＝FC＝AB＝EF，∴BF＝AE，∴BF＝AE，∴AD＝BF．（2）∵AF＝FE，∠ECA＝90°，∴CF＝AF＝EF，∵AB＝AC，∴∠ABC＝∠ACB＝30°，∴∠FAC＝∠ABC+∠ACB＝60°，∴△CAF是等边三角形，∴AC＝CF，∴与CF相等的线段有AB，AC，AF，EF．。

人教版八年级数学上册全等三角形课时练及答案

(完整)人教版八年级数学上全等三角形课时练习及答案.docx

八年级上册数学人教版课时练《12.1 全等三角形》01(含答案解析)

2020年人教版八年级数学上册 课时作业 全等三角形判定一(SSS)(含答案)

2021年人教版数学八年级上册12.1《全等三角形》课时练习(含答案)

人教版八年级数学上册《三角形全等的判定》课堂同步练习题含答案(6课时)

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析

人教版八年级数学上册 12.2 全等三角形的判定 课时训练(含答案)

12.1 全等三角形 初中数学人教版八年级上册课时习题(含答案)

人教版八年级数学上册课时练：第十二章 《全等三角形》 (培优篇)解析版

八年级初二上册数学人教版课时练《 三角形全等的判定》01(含答案)

第12章《全等三角形》人教版八年级数学上册课时练能力篇(含答案)

全等三角形-人教版数学八年级上第十二章12.1第一课时练习和答案

2020八年级数学上册 第12章 全等三角形 12.1 全等三角形课时练 (新版)新人教版

人教版八年级数学上册《第十二章全等三角形》课后练习及答案解析

第12章《全等三角形》人教版八年级数学上册课时练能力篇(含答案)

人教版八年级数学上册课时练：第12章 《全等三角形》 (培优篇)

人教版八年级数学上册全等三角形课时练及答案之欧阳美创编

最新人教版八年级数学上册课时同步练：全等三角形的判定(含答案)

2020年人教版八年级数学上册课时作业全等三角形判定一(SSS)(含答案)

人教版八年级数学上册 12.2 全等三角形的判定课时训练(含答案)

12.1 全等三角形初中数学人教版八年级上册课时习题(含答案)

人教版八年级数学上册课时练：第十二章《全等三角形》 (培优篇)解析版

八年级初二上册数学人教版课时练《三角形全等的判定》01(含答案)

2020八年级数学上册第12章全等三角形 12.1 全等三角形课时练 (新版)新人教版

人教版八年级数学上册课时练：第12章《全等三角形》 (培优篇)