高中三视图练习含答案56340
三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一,它能够以三个不同的视角展示一个物体的外观和内部结构,帮助人们更好地理解和分析物体的形状和构造。
为了提高对三视图的理解和应用能力,下面将给出一些三视图练习题及答案,希望对读者有所帮助。
1. 请根据给出的三视图,画出物体的立体图。
答案:根据三视图,我们可以确定物体的形状和尺寸,然后利用透视法将其转化为立体图。
在绘制过程中,需要注意比例和透视关系,以保证立体图的准确性。
2. 给出一个物体的立体图,请根据立体图绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察立体图中的各个面,然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意比例和尺寸的准确性,以确保三视图能够准确地表达立体图的形状和结构。
3. 请根据给出的三视图,判断物体的形状是什么?答案:通过观察三视图中的线条和面,我们可以判断物体的形状。
例如,如果正视图中的线条是直的,侧视图中的线条是弯曲的,那么物体可能是一个圆柱体。
通过观察三视图中的特征,我们可以逐步推断出物体的形状。
4. 给出一个物体的形状,请根据形状绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察物体的形状和结构,然后根据其特征来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意线条的粗细和长度,以确保三视图能够准确地表达物体的形状和结构。
通过以上的练习题和答案,我们可以提高对三视图的理解和应用能力。
练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构,还可以提高我们的制图能力和空间想象力。
在实际工程设计和制图中,三视图是非常重要的表达方式,掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。
总之,通过不断地练习和应用,我们可以提高对三视图的掌握程度,为工程设计和制图提供更准确、更有效的表达方式。
希望以上的练习题和答案能够对读者有所帮助,进一步提高对三视图的理解和应用能力。
三视图习题50道含答案

三视图习题50道(含答案)三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是( )(A )2 (B )1 (C )23 (D )132、一个几何体的三视图如图,该几何体的表面积是 ( ) (A )372 (B )360 (C )292 (D )2803、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 (A )3523cm 3(B )3203cm3(C )2243cm 3(D )1603cm 34、一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为:( )第1第2第35、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面..积.等于 ( )A.3 B.2 C.23 D.66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm7、一个几何体的三视图如图所示,则这个几何体的体积为。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.第69、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图)是( )10、一空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B.423π+ C. 2323π+ D. 2343π+22侧22 2 正俯第俯视图 正(主)视图 侧(左)视图 2 3 22 第1111、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.9πB.10πC.11πD.12π12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m)为()(B)48+24(C)36+12(A)48+1213、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是3cm.14、设某几何体的三视图如上图所示。
(完整版)高中数学3三视图课后习题(带答案)

(完整版)高中数学3三视图课后习题(带答案)332 正视图侧视图俯视图图1 三视图课后习题1.(陕西理5)某几何体的三视图如图所示,则它的体积是A .283π-B .83π-C .82π-D .23π2.(全国新课标理6)。
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为3.(湖南理3)设图1是某几何体的三视图,则该几何体的体积为A .9122π+B .9182π+C .942π+D .3618π+4.(广东理7)如图1-3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为A .63 B .93C .123D .1835.(北京理7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A .8B .62C .10D .826.(安徽理6)一个空间几何体的三视图如图所示,则该几何体的表面积为(A )48 (B )32+817 (C )48+817 (D )807.(辽宁理15)一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是.8.(天津理10)一个几何体的三视图如右图所示(单位:m ),则该几何体的体积为__________3m9.(2010湖南文数)13.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h= cm10.(2010浙江理数)(12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是___________3cm .11.(2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为 .12.(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.13.(2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为。
高中数学1.2.1空间几何体的三视图练习新人教版A版必修2【含答案】
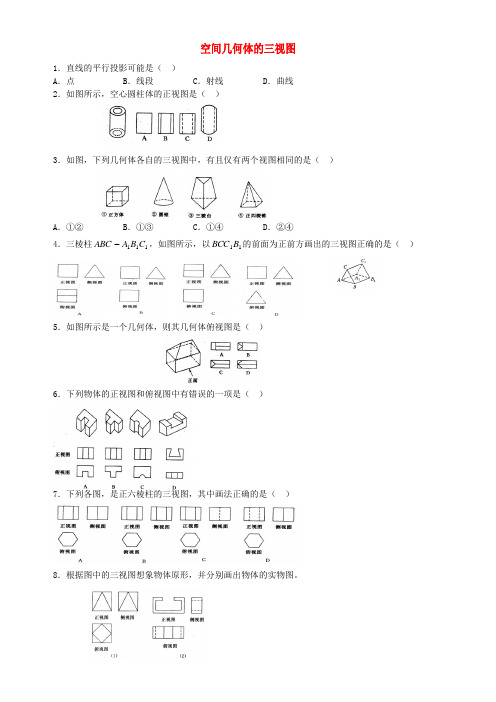
空间几何体的三视图1.直线的平行投影可能是( )A .点B .线段C .射线D .曲线2.如图所示,空心圆柱体的正视图是( )3.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④4.三棱柱111C B A ABC ,如图所示,以11B BCC 的前面为正前方画出的三视图正确的是()5.如图所示是一个几何体,则其几何体俯视图是( )6.下列物体的正视图和俯视图中有错误的一项是( )7.下列各图,是正六棱柱的三视图,其中画法正确的是( )8.根据图中的三视图想象物体原形,并分别画出物体的实物图。
10.如图,E 、F 分别是正方体1AC 的面11A ADD 和面11B BCC 的中心,则四边形E BFD 1在该正方体的面上的正投影(投射线垂直于投影面的投影)可能是图中 (把所有可能图形的序号都填上)。
空间几何体的直观图1.利用斜二测画法叙述正确的是( )A .正三角形的直观图是正三角形B .平行四边形的直观图是平行四边形C .矩形的直观图是矩形D .圆的直观图一定是圆2.下列结论正确的是( )A .相等的线段在直观图中仍然相等B .若两条线段平行,则在直观图中对应的两条线段仍然平行C .两个全等三角形的直观图一定也全等D .两个图形的直观图是全等的三角形,则这两个图形是全等三角形3.直角坐标系中一个平面图形上的一条线段AB 的实际长度为4cm ,若AB//x 轴,则画出直观图后对应的线段=''B A ,若y AB //轴,则画出直观图后对应的线段B A ''= 。
4.水平放置的ABC ∆的斜二测直观图如图所示,已知2,3=''=''C B C A ,则AB 边上的中线的实际长度为 。
四、典例剖析1.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积是( )A .16B .64C .16或64D .都不对分析:根据直观图的画法,平行于x 轴的线段长度不变,平行于y 轴的线段变为原来的一半,于是长为4的边如果平行于x 轴,则正方形边长为4,面积为16,边长为4的边如果平行于y 轴,则正方形边长为8,面积是64。
(2021年整理)高中数学必修二之三视图练习题

(完整)高中数学必修二之三视图练习题(完整)高中数学必修二之三视图练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)高中数学必修二之三视图练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)高中数学必修二之三视图练习题的全部内容。
1三视图练习题一、选择题1.对几何体的三视图,下列说法正确的是( ) A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽2.一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其圆心,那么这个几何体为( )A.棱锥B.棱柱C.圆锥D.圆柱3.(2011-2012·安徽淮南高三模拟)下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①②B.①③C.①④D.②④4。
一个几何体的三视图如图,则组成该几何体的简单几何体为()A.圆柱和圆锥B.正方体和圆锥C.四棱柱和圆锥D.正方体和球5.一个几何体的三视图如图,则组成该组合体的简单几何体为()A.圆柱与圆台B.四棱柱与四棱台C.圆柱与四棱台D.四棱柱与圆台6.(2010·北京理,3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为( )27.如图所示几何体的正视图和侧视图都正确的是( )9.如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是BB1、BC的中点,则图中阴影部分在平面ADD1A1上的正投影是()8.(2011·新课标全国高考)在一个几何体的三视图中,主视图和俯视图如下图所示,则相应的侧视图可以为( )10.某几何体的三视图如图所示,那么这个几何体是()3A.三棱锥 B.四棱锥C.四棱台 D.三棱台二、填空题11.下列图形:①三角形;②直线;③平行四边形;④四面体;⑤球.其中投影不可能是线段的是________.12.(2011·烟台高一检测)已知某一几何体的正视图与侧视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有________.13.(2011-2012·湖南高三“十二校联考")一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为4的正方体.三、解答题14.如图所示是一个四棱柱铁块,画出它的三视图.15.依所给实物图的形状,画出所给组合体的三视图.4516.说出下列三视图表示的几何体:17.根据下列图中所给出的一个物体的三视图,试画出它的形状.67详解答案1[答案] C 2[答案] C 3[答案] D[解析] 视图和侧视图相同;③三棱台,三视图各不相同台,正视图和侧视图相同.[点评] 熟悉常见几何体的三视图特征,对于画几何体的直观图是基本的要求.下图是最基本的常见几何体的三视图.几何体 直观图形 正视图 侧视图 俯视图正方体长方体圆柱圆锥圆台 [解析] 由正视图和侧视图可知,该几何体的上部可能为棱锥或圆锥,下部可能为棱柱和圆柱,结合俯视图为圆和圆心及正方形知,上部是圆锥,下部是四棱柱.5[答案] B[解析] 该几何体形状如图.上部是一个四棱柱,下部是一个四棱台.6[答案]C[解析]由正视图和侧视图知,该长方体上面去掉的小长方体,从正前方看在观察者左侧,从左向右看时在观察者右侧,故俯视图为C.7[答案] B8[答案] D[解析] 此几何体为一个半圆锥和一个半三棱锥的组合体,只有D项符合题意.9[答案]A[解析]N点投影为AD中点,M点投影为AA1中点,故选A.10[答案]B[解析]由正视图与侧视图知,该几何体为棱锥,由俯视图知,该几何体是四棱锥.11[答案]②④⑤[解析] 三角形的投影是线段成三角形;直线的投影是点或直线;平行四边形的投影是线段或平行四边形;四面体的投影是三角形或四边形;球的投影是圆.12[答案]①②③④13[答案]3[解析] 该几何体是四棱锥,其底面是边长为4的正方形,高等于4,如图(1)所示的四棱锥A-A1B1C1D1,如图(2)所示,三个相同的四棱锥A-A1B1C1D1,A -BB1C1C,A-DD1C1C可以拼成一个棱长为4的正方体.14[答案]正视图、俯视图、侧视图分别如图所示.8915[解析] 图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:16[解析]17[答案] 所对应的空间几何体的图形为:。
三视图习题50道(含答案)

word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题(单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2(主)视图与侧(左)视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示,则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图,该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示,则其侧.面积等于(A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h=7、 一个几何体的三视图如图所示 ,则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图(也称主视图)是()8、如图,网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形,)S 2a.俯视图正(主)视图侧(左)视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示,则该几何体的体积为().A.2 2.3B. 4 2 . 3侧(左)视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c m2)为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。
三视图练习题(含答案)
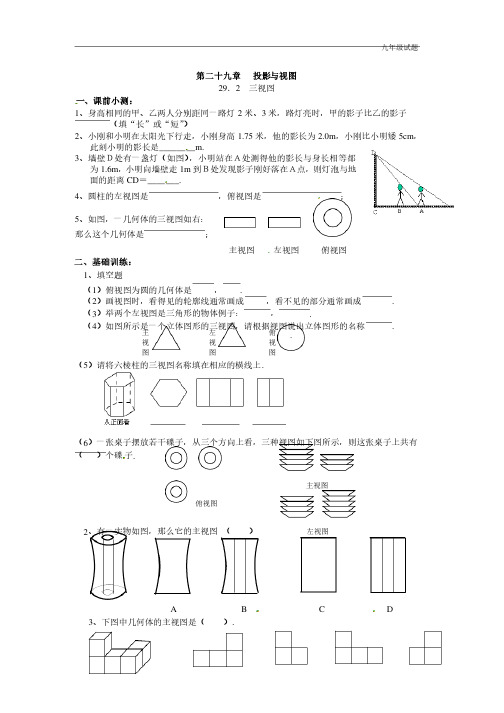
第二十九章投影与视图29.2 三视图一、课前小测:1、身高相同的甲、乙两人分别距同一路灯2米、3米,路灯亮时,甲的影子比乙的影子(填“长”或“短”)2、小刚和小明在太阳光下行走,小刚身高1.75米,他的影长为2.0m ,小刚比小明矮5cm ,此刻小明的影长是________m.3、墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m ,小明向墙壁走1m 到B处发现影子刚好落在A点,到B处发现影子刚好落在A点,则灯泡与地则灯泡与地面的距离CD =_______.4、圆柱的左视图是,俯视图是;5、如图,一几何体的三视图如右:那么这个几何体是;主视图左视图俯视图二、基础训练:1、填空题(1)俯视图为圆的几何体是,.(2)画视图时,看得见的轮廓线通常画成,看不见的部分通常画成. (3)举两个左视图是三角形的物体例子:,.(4)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称.(5)请将六棱柱的三视图名称填在相应的横线上.(6)一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有()个碟子.2、有一实物如图,那么它的主视图()AB C D 3、下图中几何体的主视图是(). 俯视图主视图左视图主视图左视图俯视图俯视图主(正)视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有(有( ) (A )5桶 (B ) 6桶(C )9桶 (D )12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是方体的前面,则这个正方体的后面是 ( ) ( )A .OB O B.. 6C 6 C.快.快.快D D D.乐.乐.乐三、综合训练:1.小明从正面观察下图所示的两个物体,看到的是(.小明从正面观察下图所示的两个物体,看到的是( )2、右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是(的小立方块的个数是( )A 5个B 6个C 7个D 8个3、如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )4、下面是空心圆柱在指定方向上的视图,正确的是…(、下面是空心圆柱在指定方向上的视图,正确的是…( )B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图:实物的三视图:第二十九章 投影与视图29.2 三视图三视图 参考答案:考答案: 课前小测:课前小测:1、短、短2、35723、15644、矩形,圆、矩形,圆5、空心圆柱、空心圆柱 二、基础训练:二、基础训练:1、(1)球,圆柱体;(2)实线,虚线;(3)圆锥,正四棱锥,倒放的正三棱柱等;(4)圆锥;(5)俯视图,正视图,左视图;(6)12.2、A ;3、C4、B5、B三、综合训练:三、综合训练:1、C2、D3、B ;4、A ;5、题图:图:主视图左视图俯视图。
高中三视图练习(含答案56340

专题练习:1. 一个几何体的三视图如图所示,其中 俯视图为正三角形,则该几何体的表面积为2. 一个几何体的三视图如下图所示,则该几何体的表面积为 __________ .三视图第3题图3.如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为(A . 3B. 2C.3D.424.右图是一个几何体的三视图,则该几何体侧(左)视3侧视图卜仁-2正视图剧f 左[徵图的体积为 ( )4A . 6B . 8C . 16D. 245. 一空间几何体的三视图如图所示,则该几何体的体积为6. 一个棱锥的三视图如图,则该棱锥的全面积(单位:c m 2 )为正(主)视图 侧(左)视图 C.2.3 3(B ) 48+24.2(C ) 36+12 2(D ) 36+24 2(A ) 48+12 27.若某几何体的三视图则此几何体的体积是( ).(单位:cm )如图所示, 3cm .的体积为 ( )48.设某几何体的三视图如下(尺寸的长度单位为 m>9.如图是一个几何体的三视图,若它的体积是3丽,则a体的俯视图可以是10.如右图,某几何体的正视图与侧视图都是边长为i 的正方形,且体积为 1。
则该集合2则该几何体的体积为3'211.右图是一个几何体的三视图,根据图中数据, 可得该几何体的表面积是答案:1. 24 .3 2. 24 12注意第6题二项分布与超几何分布辨析山东韩文文二项分布与超几何分布是两个非常重要的、应用广泛的概率模型,实际中的许多问 题都可以利用这两个概率模型来解决•在实际应用中,理解并区分两个概率模型是至关 重要的•下面举例进行对比辨析.例 袋中有8个白球、2个黑球,从中随机地连续抽取 3次,每次取1个球.求: (1)有放回抽样时,取到黑球的个数X 的分布列;(2)不放回抽样时,取到黑球的个数Y 的分布列.(A)9 n (B ) 10n(C)11 n(D)12n.3常険田 IE解:(1)有放回抽样时,取到的黑球数X 可能的取值为0, 1 到黑球的概率均为,3次取球可以看成 3次独立重复试验,则 X ~ B 35P(X 1)C3 11 2448 . ;551252 1亠2 14 12P(X 2) C 3 ——.551253—3 1 4 1P(X 3) C3 —— 125 .55因此,X的分布列为2.不放回抽样时,取到的黑球数Y 可能的取值为0, 1, 2,且有:因此,Y 的分布列为辨析:通过此例可以看出:有放回抽样时,每次抽取时的总体没有改变,因而每次 抽到某物的概率都是相同的,可以看成是独立重复试验,此种抽样是二项分布模型•而 不放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种1, 2,3.又由于每次取1••• P (X 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
俯视
侧(左)视
2
4
主(正)视图
三视图
专题练习:
1.一个几何体的三视图如图所示,其中
俯视图为正三角形,则该几何体的表面积为___________.
2.一个几何体的三视图如下图所示, 则该几何体的表面积为______.
3.如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为( ) A . π3 B . π2 C . π2
3 D . π4
4.右图是一个几何体的三视图,则该几何体 的体积为 ( ) A .6 B .8 C .16D .24
正视图侧视图俯视图
1223112231第3题图
主视图俯视图
左视图
5.一空间几何体的三视图如图所示,则该几何体的体积为( ).
A.223
π+ B. 423
π+ C. 23
2
3
π+ D.
23
4
3
π+
6.一个棱锥的三视图如图,则该棱锥的全面积(单位:c2
m)为
(A)2(B)2(C)2(D)2
7.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是3
cm.
2
2
2
正(主)视图
2
2
侧(左)视图
俯视图
8.设某几何体的三视图如下(尺寸的长度单位为m)。
则该几何体的体积为3
m 9.如图是一个几何体的三视图,若它的体积是33,则
a_______
10.如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为1
2。
则该集合
体的俯视图可以是
11.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是
(A)9π (B )10π (C)11π (D)12π
答案:1. 24+ 2. 2412π+ . . . . . 9.
注意第6题二项分布与超几何分布辨析
山东 韩文文
二项分布与超几何分布是两个非常重要的、应用广泛的概率模型,实际中的许多问题都可以利用这两个概率模型来解决.在实际应用中,理解并区分两个概率模型是至关重要的.下面举例进行对比辨析.
例 袋中有8个白球、2个黑球,从中随机地连续抽取3次,每次取1个球.求: (1)有放回抽样时,取到黑球的个数X的分布列; (2)不放回抽样时,取到黑球的个数Y的分布列. 解:(1)有放回抽样时,取到的黑球数X可能的取值为0,1,2,3.又由于每次取
到黑球的概率均为,3次取球可以看成3次独立重复试验,则1~35X B ⎛⎫
⎪⎝⎭,.
3
03
1464(0)55125
P X C ⎛⎫⎛⎫
==⨯= ⎪ ⎪⎝⎭⎝⎭∴;
12
13
1448(1)55125P X C ⎛⎫⎛⎫
==⨯= ⎪ ⎪⎝⎭⎝⎭
;
21
23
1412(2)55125
P X C ⎛⎫⎛⎫
==⨯= ⎪ ⎪⎝⎭⎝⎭;
30
33
141(3)55125
P X C ⎛⎫⎛⎫
==⨯= ⎪ ⎪⎝⎭⎝⎭.
因此,X 的分布列为
2.不放回抽样时,取到的黑球数Y可能的取值为0,1,2,且有:
03283107(0)15C C P Y C ===;12283107(1)15
C C P Y C ===;21
283101
(2)15C C
P Y C ===.
因此,Y 的分布列为
辨析:通过此例可以看出:有放回抽样时,每次抽取时的总体没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复试验,此种抽样是二项分布模型.而不放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模型.因此,二项分布模型和超几何分布模型最主要的区别在于是有放回抽样还是不放回抽样.所以,在解有关二项分布和超几何分布问题时,仔细阅读、辨析题目条件是非常重要的.
超几何分布和二项分布都是离散型分布 超几何分布和二项分布的区别:
超几何分布需要知道总体的容量,而二项分布不需要; 超几何分布是不放回抽取,而二项分布是放回抽取(独立重复)
当总体的容量非常大时,超几何分布近似于二项分布.........。
