上海师范大学高数试题 (10)
上海市上海师范大学附中2025届数学高三第一学期期末复习检测试题含解析

上海市上海师范大学附中2025届数学高三第一学期期末复习检测试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量a 与向量()4,6m =平行,()5,1b =-,且14a b ⋅=,则a =( )A .()4,6B .()4,6--C .1313⎛⎫ ⎪ ⎪⎝⎭D .1313⎛-- ⎝⎭2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB = A .{}3 B .{}5C .{}3,5D .{}1,2,3,4,5,73.已知函数2()sincos 444f x x x x πππ=,则(1)(2)...(2020)f f f +++的值等于( ) A .2018B .1009C .1010D .2020 4.关于函数22tan ()cos 21tan x f x x x=++,下列说法正确的是( ) A .函数()f x 的定义域为RB .函数()f x 一个递增区间为3,88ππ⎡⎤-⎢⎥⎣⎦C .函数()f x 的图像关于直线8x π=对称D .将函数2y x =图像向左平移8π个单位可得函数()y f x =的图像 5.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的x 的值为1,输出的x 的值为( )A .6481B .3227 C .89 D .16276.已知α是第二象限的角,3tan()4πα+=-,则sin 2α=( )A .1225B .1225- C .2425 D .2425-7.已知a ,b 是两条不同的直线,α,β是两个不同的平面,且a β⊂,b αβ=,则“//a α”是“//a b ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.在ABC ∆中,“tan tan 1B C >”是“ABC ∆为钝角三角形”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不充分也不必要条件9.若函数12log,01,()(1)(3),1,x x f x x x x x <⎧⎪=⎨⎪--->⎩函数()()g x f x kx =+只有1个零点,则k 的取值范围是( )A .(1,0)-B .(,0)(1,)-∞⋃+∞C .(,1)(0,)-∞-+∞D .(0,1)10. “1cos 22α=-”是“3k παπ=+,k Z ∈”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件11.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( )A .36 cm 3B .48 cm 3C .60 cm 3D .72 cm 312.复数12z i =+,若复数12,z z 在复平面内对应的点关于虚轴对称,则12z z 等于( ) A .345i +- B .345i + C .34i -+ D .345i -+ 二、填空题:本题共4小题,每小题5分,共20分。
上海师范学校2020年高三数学文下学期期末试卷含解析

上海师范学校2020年高三数学文下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设,则“”是“”的()A.充分不必要条件B.必要不充分条件 C.充分必要条件D.既不充分也不必要条件参考答案:A2. 双曲线中,F2为其右焦点,A1为其左顶点,点B(0,b)在以A1F2为直径的圆上,则此双曲线的离心率为( )A. B. C. D.参考答案:D3. 已知分别是定义在上的偶函数和奇函数,且,则 ( )A.-3 B.-1 C. 1 D.3参考答案:C略4. 设动点在直线上,为坐标原点,以为直角边,为直角顶点作等腰,则动点的轨迹是()A.圆 B.两条平行直线 C.抛物线 D.双曲线参考答案:B略5. 设M(,)为抛物线C:上一点,F为抛物线C的焦点,以F为圆心、为半径的圆和抛物线C的准线相交,则的取值范围是 ( )A.(0,2) B.[0,2] C.(2,+∞) D.[2,+∞)参考答案:C由题意只要即可,而所以,简单考查抛物线的方程、直线与圆的位置关系、抛物线的定义及几何性质,是简单题。
6. 若偶函数在上是增函数,则下列关系式中成立的是高考资源A. B.C. D.参考答案:D7. 已知函数f(x)=4x3﹣ax+1存在n(n∈N)个零点对应的实数a构成的集合记为A(n),则()A.A(0)=(﹣∞,3] B.A(1)={2} C.A(2)=(3,+∞)D.A(3)=(3,+∞)参考答案:D【考点】函数零点的判定定理.【分析】令f(x)=0得出a=4x2+,令h(x)=4x2+,判断h(x)的单调性,作出h(x)的函数图象,利用函数图象判断方程h(x)=a的解的个数,从而得出A(n).【解答】解:令f(x)=0得a=4x2+,∴当f(x)有n个零点时,方程a=4x2+有n个不同的解.设h(x)=4x2+,则h′(x)=8x﹣=,∴当x>时,h′(x)>0,当x<0或0时,h′(x)<0.作出h(x)=4x2+的大致函数图象如下:由图象可知当a<3时,h(x)=a只有一解,当a=3时,h(x)=a有两解,当a>3时,h(x)=a有三解.∴A(0)=?,A(1)=(﹣∞,3),A(2)={3},A(3)=(3,+∞).故选D.8. 一个几何体的三视图如图所示,则该几何体的表面积为()A. 3πB. 4πC. 2π+4D.3π+4参考答案:D该几何体为半圆柱,底面为半径为1的半圆,高为2,因此表面积为,选D.9. 对于函数,若存在常数,使得取定义域内的每一个值,都有,则称为准偶函数,下列函数中是准偶函数的是 ( )A.B. C. D.参考答案:【知识点】抽象函数及其应用.A 解:对于函数,若存在常数,使得取定义域内的每一个值,都有,则称为准偶函数,∴函数的对称轴是x=a,a≠0,选项B、C、D函数没有对称轴;函数f(x)=cos(x+1),有对称轴,且x=0不是对称轴,选项A正确.故选:A.【思路点拨】由题意判断f(x)为准偶函数的对称轴,然后依次判断选项即可.10. 若.则()A. B. C. D.参考答案:A【分析】利用诱导公式及同角三角函数的商数关系可得,再利用诱导公式及同角三角函数的平方关系化简,求值即可。
2019-2020学年上海师范学校高三数学理期末试题含解析

2019-2020学年上海师范学校高三数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 当时,复数(为虚数单位)子复平面内对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限参考答案:2.已知函数,(C为复数),则等于A、B、 C、D、参考答案:答案:C解析:∵∴故选C3. 设是虚数单位,若复数为纯虚数,则实数的值为....参考答案:依题意.由复数为纯虚数可知,且,求得.故选.【解题探究】本题主要考查复数的基本概念与复数的运算.解题的关键是利用复数运算法则进行复数的乘法、除法运算,求解时还需要注意理解纯虚数的概念.4. 已知函数f t(x)=﹣(x﹣t)2+t(t∈R),设a>b,f(x)=,若函数y=f(x)﹣x+a﹣b有四个零点,则b﹣a的取值范围是( )A.(﹣∞,﹣2﹣)B.(﹣∞,2﹣) C.(﹣2﹣,0)D.(2﹣.0)参考答案:A【考点】根的存在性及根的个数判断;函数的零点与方程根的关系.【专题】函数的性质及应用.【分析】解方程f a(x)=f b(x)得交点坐标,函数f(x)的图象与直线l:y=x+b﹣a有四个不同的交点,由图象知,点P在l下方,由此解得b﹣a的取值范围.【解答】解:作函数f(x)的图象,且解方程f a(x)=f b(x)得,﹣(x﹣a)2+a=﹣(x﹣b)2+b,解得x=,此时y=﹣(﹣b)2+b=﹣()2+b,即交点坐标为(,﹣()2+b),若y=f(x)﹣x+a﹣b有四个零点,即f(x)﹣x+a﹣b=0有四个根,即f(x)=x+b﹣a,分别作出f(x)与y=x+b﹣a的图象如图:要使函数y=f(x)﹣x+a﹣b有四个零点,即函数f(x)的图象与直线l:y=x+b﹣a有四个不同的交点.由图象知,点P在下方,所以﹣()2+b<+b﹣a,即()2>,设t=a﹣b,则t>0,则方程等价为>,即t2﹣4t﹣1>0,即t<2,或t>2+,∵t>0,∴t>2+,故b﹣a=﹣t<﹣2﹣,即b﹣a的取值范围是(﹣∞,﹣2﹣),故选:A【点评】本题主要考查根的存在性以及根的个数判断,函数的零点与方程的根的关系,体现了转化的数学思想,利用数形结合是解决本题的关键.5. 下面关于复数的四个结论,正确的是①②③④A.①② B.②③ C.②④D.③④参考答案:C6. 已知是虚数单位,则=A. B. C. D.参考答案:A略7. 若k∈R,则“k>3”是“方程﹣=1表示双曲线”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件参考答案:A考点:双曲线的标准方程.专题:压轴题.分析:根据双曲线定义可知,要使方程表示双曲线k﹣3和k+3同号,进而求得k的范围即可判断是什么条件.解答:解:依题意:“方程﹣=1表示双曲线”可知(k﹣3)(k+3)>0,求得k>3或k<﹣3,则“k>3”是“方程﹣=1表示双曲线”的充分不必要条件.故选A.点评:本题主要考查了双曲线的标准方程.解题时要注意讨论焦点在x轴和y轴两种情况.8. 在△ABC中,已知,,则的值为()A.B.C.D.参考答案:【知识点】平面向量数量积的运算.F3【答案解析】D 解析:∵=,∴sinA=;∴cosA=±∴==4×1×(±)=±2,故选:D.【思路点拨】先根据三角形的面积公式可求得A的正弦值,从而可求得余弦值,根据向量的数量积运算可得到的值.9. 若二次函数y=ax2(a>0)的图象与不等式组表示的平面区域无公共点,则实数a的取值范围为()A.(,2)B.(,)C.(0,)∪(,+∞)D.(0,)∪(2,+∞)参考答案:D【考点】简单线性规划.【专题】函数思想;数形结合法;不等式.【分析】先画出满足条件的平面区域,求出临界点的坐标,从而求出a的范围即可.【解答】解:画出满足条件的平面区域,如图示:,将A(1,2)代入y=ax2,解得:a=2,将B(3,2)代入y=ax2,解得:a=,若二次函数y=ax2(a>0)的图象与不等式组表示的平面区域无公共点,则a∈(0,)∪(2,+∞),故选:D.【点评】本题考查了二次函数的性质,考查简单的线性规划问题,考查数形结合思想,是一道基础题.10. 已知集合,,则()A. B.{ } C.{ } D.{}参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 已知某几何体的三视图如右图所示,则该几何体的外接球体积为___________.参考答案:【知识点】由三视图求面积、体积G2由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,其四个顶点是以俯视图为底面,以2为高的三棱柱的四个顶点,故其外接球,即为以俯视图为底面,以2为高的三棱柱的外接球,由底面两直角边长分别为,,故相当于棱长分别为,,2的长方体的外接球,故满足,所以,几何体的外接球的体积为,故答案为:.【思路点拨】由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,求出其外接球的半径,代入体积公式,可得答案.12. 设函数的最大值为M,最小值为m,则M+m=____________.参考答案:2略13. 记为不超过实数的最大整数,例如,,,.设为正整数,数列满足,,现有下列命题:①当时,数列的前3项依次为5,3,2;②对数列都存在正整数,当时总有;③当时,;④对某个正整数,若,则.其中的真命题有_________.(写出所有真命题的编号)参考答案:①③④略14. 已知、是方程的两根,且、,则;参考答案:答案:15. 某同学为了研究函数的性质,构造了如图所示的两个边长为的正方形和,点是边上的一个动点,设,则.那么,可推知方程解的个数是_________个参考答案:216. 设奇函数的定义域为R,且周期为5,若,则实数a 的取值范围是参考答案:17. 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知,,则b+c的最大值为.参考答案:6在中,∵,∴整理可得:,∴,∴,∴,∴,可得:,∴由余弦定理可得:,∴解得:,∴,当且仅当时,.故答案为:.三、解答题:本大题共5小题,共72分。
(NEW)上海师范大学数理学院861高等代数历年考研真题汇编(含部分答案)

2003年上海师范大学444高等代数考研真题(含答 案)
2002年上海师范大学438高等代数考研真题(含答 案)
2001年上海师范大学432高等代数考研真题
第2部分 其他院校高等代数最新真题
2016年华南理工大学864高等代数考研真题
2016年湘潭大学832高等代数考研真题
2016年中山大学868高等代数考研真题
第2部分 其他院校高等代数最新真题 2016年华南理工大学864高等代数考研真题 2016年湘潭大学832高等代数考研真题 2016年中山大学868高等代数考研真题
第1部分 上海师范大学高等代数考研真题
2007年上海师范大学高等代数考研真题
2005年上海师范大学461高等代数考研真题(含答 案)
目 录
第1部分 上海师范大学高等代数考研真题 2007年上海师范大学高等代数考研真题 2005年上海师范大学461高等代数考研真题(含答案) 2004年上海师范大学448高等代数考研真题(含答案) 2003年上海师范大学444高等代数考研真题(含答案) 2002年上海师范大学438高等代数考研真题(含答案) 2001年上海师范大学432高等代数考研真题
2020年上海师范学校高一数学理上学期期末试卷含解析

2020年上海师范学校高一数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 对数式中,实数的取值范围是()A. B. C. D.参考答案:C2. 直线当变动时,所有直线都通过定点()A.(0,0)B.(0,1)C.(3,1)D.(2,1)参考答案:C3. 设函数,则下列说法中正确的是()A.在区间内均有零点.B.在区间内均无零点.C.在区间内有零点,在内无零点.D.在区间内无零点,在内有零点.参考答案:D略4. 设等差数列{a n}满足,,S n是数列{a n}的前n项和,则使得{S n}取得最大值的自然数n是()A.4 B. 5 C.6 D.7参考答案:B5. 要使与轴的两个交点分别位于原点的两侧,则有()A. B. C. D.参考答案:D6. 已知,,则的值为().A. B. C. D.参考答案:A【分析】根据角的范围可知,;利用同角三角函数的平方关系和商数关系构造方程可求得结果.【详解】由可知:,由得:本题正确选项:A7. 已知函数f(x)的定义域为(0,1),则函数f(2x+1)的定义域为( )A.(﹣1,1)B.C.(﹣1,0)D.参考答案:B考点:函数的定义域及其求法.专题:函数的性质及应用.分析:直接由2x+1在函数f(x)的定义域内求解x的取值集合得答案.解答:解:∵函数f(x)的定义域为(0,1),由0<2x+1<1,得.∴函数f(2x+1)的定义域为.故选:B.点评:本题考查了函数的定义域及其求法,考查了复合函数的定义域,是高考常见题型,属基础题,也是易错题8. 半径为的球内接一个正方体,则该正方体的体积是().[来源:学&科&网]A. B. C. D.参考答案:C略9. 已知x∈[-π,π],则“x∈”是“sin(sin x)<cos(cos x)成立”的()A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件参考答案:C试题分析:当x∈时,sinx+cosx≤所以0≤sinx<-cosx≤于是sin(sinx)<sin(-cosx)=cos(cosx),充分性成立.取x=-,有sin(sinx)=sin(-)=-sin<0cos(cosx)=cos(-)=cos>0所以sin(sinx)<<cos(cosx)也成立,必要性不成立故选C考点:三角函数的性质,充要条件10. 函数的部分图象如图所示,则函数表达式为()A. B.C. D.参考答案:D由图象可以看出,,则,将点代入中,得,,又函数表达式,故选D.二、填空题:本大题共7小题,每小题4分,共28分11. 函数的最小值为.参考答案:12. 函数的定义域是.参考答案:令且,得,解得,故填.13. 等差数列{a n}的首项a1=1,且a2是a1和a6的等比中项,那么公差d= _________ .参考答案:0或314. 给出下列命题:①是幂函数;②函数在上有3个零点;③的解集为;④当时,幂函数的图象与两坐标轴不相交;其中真命题的序号是(写出所有正确命题的编号).参考答案:②④15. 关于x的方程= p x有4个不同的实数根,则p的取值范围是。
【全国百强校】上海市上海师范大学...

【全国百强校】上海市上海师范大学...一、填空题(本大题共有14题,每题4分,满分56分.)1.集合{}*|03,A x x x N =≤<∈的真子集的个数是 .【答案】3【解析】试题分析:{}*|03,={1,2}A x x x N =≤<∈,真子集个数22-1=3,所以答案应填:3.考点:集合的子集概念.2.命题“如果,a b 都是奇数,那么a b +是偶数”的逆否命题是 .【答案】如果a b +不是偶数,那么,a b 不都是奇数【解析】试题分析:命题的条件和结论否定后交换,所以答案应填:如果a b +不是偶数,那么,a b 不都是奇数.考点:逆否命题. 3.已知函数()922-=x x x f ,()3-=x x g ,()33+=x x x h ,则()()()=+x h x g x f .【答案】(3)x x ≠±考点:函数的定义域.4.已知集合{223}A y y x x ==--,集合{}2213B y y x x ==-++,则AB = .【答案】[4,14]-【解析】试题分析:由2223=1)44y x x x =----≥-(,22213(1)1414y x x x =-++=--+≤,知 A B =[4,14]-,所以答案应填:[4,14]-.考点:1、集合;2、二次函数值域.5.函数2()|1|||f x x x a =-+-(常数a R ∈),若(2)1f =,则(1)f = .【答案】3【解析】试题分析:(2)1f =得:4a =,故(1)3f =,所以答案应填:3.考点:函数概念.6.已知全集{}0,1,2,3,4,5U =,且{}1,2U BC A =,{}5U A C B =,{}0,4U U C A C B =,则集合A = .【答案】{3,5}考点:1、集合的交集2、集合的补集.7.已知集合{|A a =关于x 的方程211x a x +=-有唯一实数解,}a R ∈,用列举法表示集合 A = .【答案】51,1,4??--【解析】试题分析:由211(1)(1)x a x a x x x ++==--+,当1x a x +=-或1x a x +=+时,方程有一解,当21x a x +=-有一解时,0?=,54a =-,所以答案应填:51,1,4??--.考点:含参分式方程.8. 对于集合,A B ,定义运算:{}A B x x A x B -=∈?且,()()A B AB B A ?=--.若{}1,2A =, {}2,B x x x Z =<∈,则A B ?= .【答案】{}1,0,2-【解析】试题分析:{}1,2A =,{}2,{1,01}B x x x Z =<∈=-,,()(){2}{1,0}{1,0,2}A B B A --=-=-,所以答案应填:{}1,0,2-.考点:集合的运算.9. 已知全集U R =,实数,a b 满足0a b >>,集合{|},{|}2a b M x b x N x x a +=<<=<<,则U M C N = .【答案】(b考点:集合的交集、补集.10.已知关于x 的不等式022>++c x ax 的解集为)21,31(-,其中,a c R ∈,则关于x 的不等式 022>-+-a x cx 的解集是 .【答案】)3,2(-【解析】试题分析:由不等式022>++c x ax 的解集为)21,31(-知211321 6a c a-=-+=-??,解得122a c =-??=?,所以022>-+-a x cx 即为260x x -++>,解得23x -<<,所以答案应填:)3,2(-.考点:1、一元二次不等式;2、一元二次方程.【思路点晴】本题主要考查的是含参一元二次不等式的解法,属于中档题.解题时一定注意不等式的解集端点与相应方程的关系,即端点是方程的根,再根据根与系数关系得出a ,c ,从而解出022>-+-a x cx 的解集.11.对于实数x ,若1,n x n ≤<+规定[]x n =()n Z ∈,则不等式[][]2420210x x -+<的解集是.【答案】【解析】。
上海市上海师范大学附属中学2024-2025学年高三上学期10月月考数学试卷

上海市上海师范大学附属中学2024-2025学年高三上学期10月月考数学试卷一、填空题1.函数()f x =2.已知0a >. 3.已知幂函数()f x 的图象经过点13,9⎛⎫⎪⎝⎭,求(3)f -=.4.若1sin 3α=,则cos(2)πα-=.5.已知集合{|3sin ,}M y y x x =∈=R ,{|||}N x x a =<,若M N ⊆,则实数a 的取值范围是. 6.设a ,b ∈R .已知关于x 的不等式250ax x b -+>的解集为21,34⎛⎫- ⎪⎝⎭,则不等式250ax x b ++<的解集为.7.已知锐角α的顶点为原点,始边为x 轴的正半轴,将α的终边绕原点逆时针旋转π6后交单位圆于点1,3P y ⎛⎫- ⎪⎝⎭,则sin α的值为.8.已知()()()()1f x x x a x b =+++.若()y f x =为奇函数,则()0f '=.9.如图,某同学为测量鹳雀楼的高度MN ,在鹳雀楼的正东方向找到一座建筑物AB ,高约为37m ,在地面上点C 处(,,B C N 三点共线)测得建筑物顶部A ,鹳雀楼顶部M 的仰角分别为30o 和45o ,在A 处测得楼顶部M 的仰角为15o ,则鹳雀楼的高度约为m .10.对于函数()f x 和()g x ,设(){}|0x f x α∈=,(){}|0x g x β∈=,若存在α,β,使得1αβ-<,则称()f x 与()g x 互为“零点相邻函数”.若函数()1e 2x f x x -=+-与()21g x x ax =-+互为“零点相邻函数”,则实数a 的取值范围是.11.若函数()y f x =的图像上存在不同的两点M x 1,y 1 和N x 2,y 2 ,满足1212x x y y +≥()y f x =具有性质P ,给出下列函数: ①()sin f x x =;②()x f x e =;③1(),(0,)f x x x x=+∈+∞;④()||1f x x =+.其中其有性质p 的函数为(填上所有正确序号).12.已知函数()ln 1f x b x =--,若关于x 的方程()0f x =在2e,e ⎡⎤⎣⎦上有解,则22a b +的最小值为.二、单选题13.已知a b ∈R ,且0ab ≠,则“22a b >”是“11a b<”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件14.设函数()sin f x x =,若对于任意5π2π,63α⎡⎤∈--⎢⎥⎣⎦,在区间[0,]m 上总存在唯一确定的β,使得()()0f f αβ+=,则m 的值可能是( )A .π6B .π3C .2π3 D .5π6 15.已知在ABC V 中,0P 是边AB 上一定点,满足023P B AB =u u u r u u u r,且对于边AB 上任意一点P ,都有00PB PC P B P C ⋅≥⋅u u u r u u u r u u u r u u u r,则ABC V 是( )A .钝角三角形B .直角三角形C .锐角三角形D .无法确定16.设函数,()2,2x x P f x x x M x∈⎧⎪=⎨+∈⎪⎩其中,P M 是实数集R 的两个非空子集,又规定(){(),},(){(),}A P y y f x x P A M y y f x x M ==∈==∈∣∣,有下列命题:①对任意满足P M ⋃=R 的集合P 和M ,都有()()A P A M ⋃=R ; ②对任意满足P M ⋃≠R 的集合P 和M ,都有()()A P A M ⋃≠R , 则对于两个命题真假判断正确的是( )A .①和②都是真命题B .①和②都是假命题C .①是真命题,②是假命题D .①是假命题,②是真命题三、解答题17.已知向量3sin ,,(cos ,1)4a x b x ⎛⎫==- ⎪⎝⎭r r .(1)当a b r r∥时,求tan 2x 的值;(2)设函数()2()f x a b b =+⋅r rr ,且π0,2x ⎛⎫∈ ⎪⎝⎭,求()f x 的值域.18.已知函数()22x x af x =+其中a 为实常数.(1)若()07f =,解关于x 的方程()5f x =; (2)判断函数()f x 的奇偶性,并说明理由.19.某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y (万元)随投资收益x (万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.(1)若建立函数()f x 模型制定奖励方案,试用数学语言表述公司对奖励函数()f x 模型的基本要求;(2)现有两个奖励函数模型:①()2150xf x =+;②()ln 2f x x =-;问这两个函数模型是否符合公司要求,并说明理由?20.已知函数()y f x =的定义域为区间D ,若对于给定的非零实数m ,存在0x ,使得()()00f f x x m =+,则称函数()y f x =在区间D 上具有性质()P m .(1)判断函数()2f x x =在区间[]1,1-上是否具有性质12P ⎛⎫ ⎪⎝⎭,并说明理由;(2)若函数()sin f x x =在区间()()0,0>n n 上具有性质4P π⎛⎫⎪⎝⎭,求n 的取值范围;(3)已知函数()y f x =的图像是连续不断的曲线,且()()02f f =,求证:函数()y f x =在区间[]0,2上具有性质13P ⎛⎫⎪⎝⎭.21.已知函数()e (,1),()(,)k x f x x k k g x cx m c m =∈≥=+∈N R ,其中e 是自然对数的底数.(1)当1k =时,若曲线()y f x =在1x =处的切线恰好是直线()y g x =,求c 和m 的值; (2)当1k =,e m =-时,关于x 的方程()()f x g x =有正实数根,求c 的取值范围:(3)当2,1k m ==-时,关于x 的不等式2()e ()f x ax bx g x -≥+≥对于任意[1,)x ∈+∞恒成立(其中,a b ∈R ),当c 取得最大值时,求a 的最小值.。
(完整)上海师范大学高数试题(10)
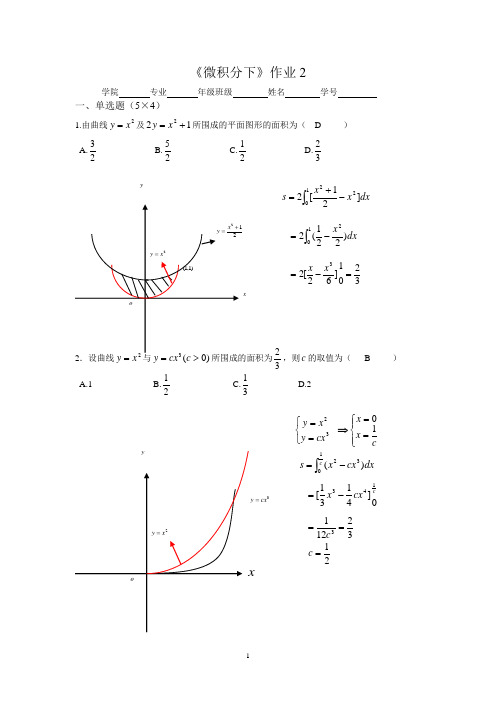
《微积分下》作业2学院 专业 年级班级 姓名 学号一、单选题(5×4)1.由曲线2x y =及122+=x y 所围成的平面图形的面积为( D ) A.23 B.25 C.21 D.32dx x x s ]21[22102-+=⎰dx x )221(2210-=⎰ 3201]62[23=-=x x32,则c 的取值为( B ) A.1 B.21 C.31D.2⎩⎨⎧==32cx y x y ⇒⎪⎩⎪⎨⎧==c x x 10 dx cx x s c )(132⎰-=0]4131[143c cx x -=321213==c 21=cy3cx y =3. 由曲线)0(sin 23π≤≤=x x y 与x 轴围成的图形绕x 轴旋转所成旋转体的体积为( C ) A.34 B.32 C.π34 D.π32 4.抛物线x y 22=与直线4-=x y 所围成的图形的面积为( A )A.18B.58 C.518D.8 5.曲线x y ln =与x 轴及直线e x ex ==,1所围成的图形的面积是( B )A.e e 1-B.e 22-C.e e 2-D.ee 1+二﹑综合题(2×10)1.求心形线)0)(cos 1(>+=a a ϕρ与圆a =ρ所围各部分的面积。
解:(1)圆内,心形线内部分1A221212()22A d a πππρϕϕ=+⎰=22222)cos 1(a d a πϕϕππ++⎰=ϕϕϕπππd aa ]22cos 1cos 21[2222⎰++++ =ππϕϕϕπ222]2sin 41sin 223[2+++a a =)245(]243[2222-=-+πππa a a (2)圆内,心形线外部分2A)42(2122ππ-=-=a A a A(3) 圆外,心形线内部分3Aϕϕπd a a A ])cos 1([212222203-+=⎰=ϕϕϕπd a ]1cos cos 21[2022-++⎰=ϕϕϕπd a]cos cos 2[2022⎰+=)42(2π+a2.设1D 是由抛物线22x y =和直线a x =,2=x ,及0=y 所围成的平面区域,2D 是由抛物线22x y =和直线0=y ,a x =所围成的平面区域,其中20<<a .(1)试求1D 绕x 轴旋转而成的旋转体体积1V ,2D 绕y 轴旋转而成的旋转体体积2V ; (2)问当a 为何值时,21V V +取得最大值?试求此最大值.解:(1))32(54)2(52221a dx x V a-==⎰ππ420222222a dy y a a V a πππ=-⋅=⎰(2)4521)32(54a a V V V ππ+-=+=)1(43a a V -='π令0='V 1=⇒a10<<a 0>'V 1>A 0<'V 1=∴a 是极大值点即最大值点且最大值为π5129。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《微积分下》作业2
学院 专业 年级班级 姓名 学号
一、单选题(5×4)
1.由曲线2x y =及122+=x y 所围成的平面图形的面积为( D ) A.23 B.25 C.21 D.3
2
dx x x s ]2
1
[221
02-+=⎰
dx x )2
21(22
1
0-
=⎰ 3
201]62[23=-=x x
3
2
,则c 的取值为( B ) A.1 B.21 C.3
1
D.2
⎩⎨⎧==32cx y x y ⇒⎪⎩
⎪⎨⎧==c x x 1
0 dx cx x s c )(1
32⎰
-=
0]4
131[143c cx x -=
32
1213
==
c 21=c
y
3
cx y =
3. 由曲线)0(sin 2
3π≤≤=x x y 与x 轴围成的图形绕x 轴旋转所成旋转体的体积为
( C ) A.
34 B.32 C.π34 D.π3
2 4.抛物线x y 22=与直线4-=x y 所围成的图形的面积为( A )
A.18
B.
58 C.5
18
D.8 5.曲线x y ln =与x 轴及直线e x e
x ==,1
所围成的图形的面积是( B )
A.e e 1-
B.e 22-
C.e e 2-
D.e
e 1+
二﹑综合题(2×10)
1.求心形线)0)(cos 1(>+=a a ϕρ与圆a =ρ所围各部分的面积。
解:(1)圆内,心形线内部分1A
221
212()22A d a πππρϕϕ=+⎰=22
222)cos 1(a d a πϕϕππ++⎰
=
ϕϕ
ϕπ
π
π
d a
a ]2
2cos 1cos 21[2
2
2
2⎰
++
++ =ππϕϕϕπ
2
22]2sin 41
sin 223[2+++a a =
)24
5(]243[
2
222-=-+π
ππ
a a a (2)圆内,心形线外部分2A
)4
2(2122
π
π-
=-=a A a A
(3) 圆外,心形线内部分3A
ϕϕπ
d a a A ])cos 1([2
1222220
3
-+=⎰
=ϕϕϕπ
d a ]1cos cos 21[2
022-++⎰
=ϕϕϕπd a
]cos cos 2[2
22
⎰
+=)4
2(2π
+
a
2.设1D 是由抛物线2
2x y =和直线a x =,2=x ,及0=y 所围成的平面区域,2D 是由抛物线
22x y =和直线0=y ,a x =所围成的平面区域,其中20<<a .
(1)试求1D 绕x 轴旋转而成的旋转体体积1V ,2D 绕y 轴旋转而成的旋转体体积2V ; (2)问当a 为何值时,21V V +取得最大值?试求此最大值.
解:(1))32(54)2(5
22
21a dx x V a
-=
=⎰ππ
4202
2222
2a dy y a a V a πππ=-⋅=⎰ (2)4521)32(5
4a a V V V ππ
+-=+= )1(43a a V -='π令0='V 1=⇒a
10<<a 0>'V 1>A 0<'V 1=∴a 是极大值点即最大值点
且最大值为π5
129。
