锐角三角函数(一)
§1.1 锐角三角函数(1)

§1.1 锐角三角函数(1)【教学目标】1.探索直角三角形中锐角三角函数值与三边之间的关系。
2.掌握三角函数定义式:sinA=斜边的对边A ∠, cosA=斜边的邻边A ∠,【重点难点】重点:三角函数定义的理解。
难点:直角三角形中锐角三角函数值与三边之间的关系及求三角函数值。
【教学过程】 一、情境导入1、∠A=30°,则ABBC= ,这个比值和B 点的位置有关系吗?2、在∠A 的一边上任取两点B 与B 1,分别作BC ⊥AC 于点C ,B 1C 1⊥AC 1于点C 1.比值AB BC 与1111B A C B 有什么关系?3、比较1和2中的两个比值是否相等?如果∠A =50°时,这个比值和40°时有变化吗? 二、新课教学 1、结论:当锐角α确定时,比值AB BC 是一个唯一确定的值;当锐角α变化时,比值ABBC也随之变化.简单地说:角度不变,比值不变,角度改变,比值改变边与2、2、三角函数的定义在Rt △ABC 中,如果锐角A 确定,那么∠A 的对斜边的比、邻边与斜边的比也随之确定.∠A 的对边与邻边的比叫做∠A 的正弦(sine),记作sinA ,即sinA=ABBC =斜边的对边A ∠∠A 的邻边与斜边的比叫做∠A 的余弦(cosine),记作cosA ,即cosA=ABAC =斜边的邻边A ∠∠A 的对边与∠A 的邻边的比叫做∠A 的正切(tang e nt ),记作tan A , 即的斜边的对边A tan ∠∠==A AC BC A 锐角A 的正弦、余弦和正切统称∠A 的三角函数. 三、课堂练习: 1. 根据图形填空:sin A = ; cos A = ; tan A =tanA=∠A的对边∠A的邻边 A 30° BCAB 1 BC CC 140°AαBCC4532. 如图,在Rt △ABC 中,∠C = Rt ∠ ,AC =2, AB=13 . 求 : (1) sin A 、 cos A 、tan A 的值 (2) sin B 、 cos B 、tan B 的值;3、在Rt △ABC 中, ∠C =Rt ∠,AC ︰BC =1︰2. 求tan B 、sin B 、 cos B 的值.4、在Rt △ABC 中, ∠C =Rt ∠,sin A = ,则sin B 的值为( )(A) (B) (C) (D)5、 在Rt ⊿ABC 中,∠C=Rt ∠, CD ⊥AB ,求锐角∠DCB 的余弦四、回顾总结:1. 一个概念:锐角三角函数2. 一个关系:直角三角形中边角关系3、对任意锐角 ,下列结论成立吗?请说明理由. ① 0<sin <1, ② 0<cos <1, ③sin +cos >1 , ④tan >0感谢您的阅读,祝您生活愉快。
锐角三角函数(1)

锐角三角函数一:【知识梳理】1.直角三角形的边角关系(如图)(1)边的关系(勾股定理):AC 2+BC 2=AB 2;(2)角的关系:∠A+∠B=∠C=900; (3)边角关系:①:00901230C BC AB A ⎫∠=⎪⇒=⎬∠=⎪⎭②:锐角三角函数:∠A 的正弦=A a sin A=c∠的对边,即斜边;∠A 的余弦=A b cos A=c∠的邻边,即斜边,∠A 的正切=A a tan=A b∠的对边,即∠的邻边注:三角函数值是一个比值.2.特殊角的三角函数值.3.三角函数的关系(1) 互为余角的三角函数关系.sin (90○-A )=cosA , cos (90○-A )=sin Atan (90○-A )= cotA cot (90○-A )=tanA (2) 同角的三角函数关系.①平方关系:sin 2 A+cos 2A=l ②倒数关系:tanA ·cotA=1③商数关系:sin cos tan ,cot cos sin A AA A A A==4.三角函数的大小比较(1) 同名三角函数的大小比较①正弦、正切是增函数.三角函数值随角的增大而增大,随角的减小而减小. ②余弦、余切是减函数.三角函数值随角的增大而减小,随角的减小而增大。
(2) 异名三角函数的大小比较①tanA >SinA ,由定义,知tanA=a b ,sinA=a c ;因为b <c ,所以tanA >sinA②cotA >cosA .由定义,知cosA=b c,cotA=b a;因为 a <c ,所以cotA >cosA .③若0○<A <45○,则cosA >sinA ,cotA >tanA ;若45○<A <90○,则cosA <sinA ,cotA <tanA5.解直角三角形分类:(1)已知斜边和一个锐角解直角三角形;(2)已知一条直角边和一个锐角解直角三角形;(3)已知两边解直角三角形. 6.在实际问题中常用的几种角 ①俯角和仰角在测量时,视线与水平线所成的角中,视线在水平线上方的角叫做仰角;视线在水平线下方的角叫做俯角.②坡度与坡角hα通常坡面的竖直高度h 和水平宽度l 的比叫做坡度,用字母i 表示,即lhi ==αtan ,其中α是坡面与水平面的夹角即坡角。
锐角三角函数(1)

第1课时 锐角三角函数(1)
课 前 小 测 课 堂 精 讲
课 后 作 业
Page 1
课 前 小 测
关键视点 1.如图,在 中,如果锐角A确定,那么 的对边与邻边的 比 便随之确定,这个比叫做 的 正切 ,记作 即
2.坡面的 铅直高度 与 水平宽度 的比称为坡度 (或坡比).常用来描述山的坡度.
Page 6
课 堂 精 讲
考点2 坡度 【例2】(2016闵行区一模)已知一条斜坡, 向上前进5米,水平高度升高了4米,那么坡比 为 1:0.75 .
【分析】先求出水平方向上前进的距离,然后 根据坡比=竖直方向上升的距离:水平方向前 进的距离,即可解题. 【解答】解:如图所示: AC=5米,BC=4米, 则AB= =3米, 则坡比= = =1:0.75.
Page 4
课 堂 精 讲
解:(1)tan∠BOA= = = ;
(2)点C的坐标是(﹣2,4)
类 比 精 练
1.如图,△ABC的三个顶点 都在正方形网格的格点上, 则tan∠A的值为( B )
A.
B.
C.
D.
Page 5
课 堂 精 讲
【分析】在正方形网格中构造一个∠A为锐角的 直角三角形,然后利用正切的定义求解. 【解答】解:如图, 在Rt△ADB中, tan A= 故选B. = .
Page 3
课 堂 精 讲
考点1 正切 【例1】如图,在平面直角坐标系中,已知点 B(4,2),BA⊥x轴于A. (1)求tan∠BOA的值; (2)将点B绕原点逆时针方向旋转90°后记作点 C,求点C的坐标. 【分析】(1)根据正切的定义 ,对边与相邻的斜边的比,即 可求解; (2)根据图形,确定旋转以后 的位置,可以直接写出坐标.
1.1锐角三角函数(第1课时)课件

比值大的梯子陡.
图③
图④
知识点 1 正切的定义
B
B B2 B1
A
C2 C1 C
C
如图,B1,B2是梯子AB上的点,B1C1⊥AC,垂足为点C1,
B2C2⊥AC,垂足为点C2.小明想通过测量B1C1及AC1,算出它们
的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2
及AC2,算出它们的比,也能说明梯子的倾斜程度.
应用新知,典例剖析
例1.下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较
陡?
A
E
4m 甲
┐ 8m α
C 甲梯
B
13 m 乙
F
β
乙梯
5m
┌
D
解:甲梯中 tan 4 1 .
82
乙梯中 tan 5 5 .
132 52 12
∵ tanα> tanβ ∴甲梯更陡
知识点 3 坡度和坡角
如图,正切也经常用来描述山坡的坡度.例如, 有一山坡在水平方向上每前进100m就升高60m,那 么山坡的坡度i(即tanα)就是:
(3).如图 (2) tan A BC ( AB
(4).如图 (2) tan B 10 ( 7
). A
).
7┍m
C A 10m C
(1)
(2)
). (6).如图 (2)
). tan A 0.7,
( ).
(5).如图 (2) tanA = 0.7 ( ). tan A 0.7或 tan A 0.7
生活中的梯子
梯子是我们日常生活中常见的物体.
情境导入
你会比较两个梯子哪个更陡吗?你有哪些办法?
知识讲授
锐角三角函数(第一课时)课件ppt

对边与斜边的比 BC ,你能得出什
么结论?
AB
C
B
在Rt△ABC中,∠C=90°,由于∠A=45°,所以Rt△ABC是
等腰直角三角形,由勾股定理得
AB2 AC2 BC2 2BC2
AB 2BC
因此 BC BC 1 2
AB 2BC 2 2
即在直角三角形中,当一个锐角等于45°时,不管这 个直角三角形的大小如何,这个角的对边与斜边的比都 等于 2
(2)直角三角形中一个锐角的度数越大,它的 对边与斜边的比值越大
结论
如图,Rt△ABC中,直角边AC、BC小于斜边AB,
B
sin A BC AB
<1
sin B AC <1 AB
A
C
所以0<sinA <1, 0<sinB <1,
如果∠A < ∠B,则BC<AC ,
那么0< sinA <sinB <1
C
AB
在Rt△BCD中, sin B CD BC
A
D
B
因为∠B=∠ACD,所以
sin B sin ACD AD AC
请分别计算60度的锐角对边与斜边的比值 你能发现什么规律吗?
sin 45 2 2
sin 45 2 2
sin30 1
2
(1)直角三角形中,锐角大小确定后,这个角的 对边与斜边的比值随之确定;
意大利的伟大科学家C 伽俐 .略,曾在斜塔的顶
层做过自由落体运动的实 验.
B
“斜而未倒” AB=54.5m BC=5.2m
α
A
情
问题 为了绿化荒山,某地打算从位于山脚下的机井 房沿着山坡铺设水管,在山坡上修建一座扬水站,
锐角三角函数练习题及答案
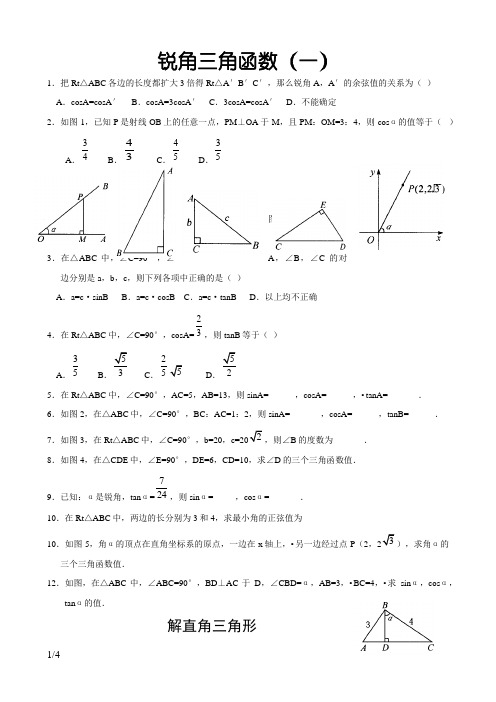
锐角三角函数(一)1.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A,A′的余弦值的关系为()A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定2.如图1,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值等于()A.34 B.43 C.45 D .35图 1 图 2 图3 图4图53.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确4.在Rt△ABC中,∠C=90°,cosA=23,则tanB等于()A.35 B.53 C.255 D.525.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,•tanA=_______.6.如图2,在△ABC中,∠C=90°,BC:AC=1:2,则sinA=_______,cosA=______,tanB=______.7.如图3,在Rt△ABC中,∠C=90°,b=20,c=202,则∠B的度数为_______.8.如图4,在△CDE中,∠E=90°,DE=6,CD=10,求∠D的三个三角函数值.9.已知:α是锐角,tanα=724,则sinα=_____,cosα=_______.10.在Rt△ABC中,两边的长分别为3和4,求最小角的正弦值为10.如图5,角α的顶点在直角坐标系的原点,一边在x轴上,•另一边经过点P(2,23),求角α的三个三角函数值.12.如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3,•BC=4,•求sinα,cosα,tanα的值.解直角三角形一、填空题1. 已知cosA=23,且∠B=900-∠A ,则sinB=__________.2. 在Rt △ABC 中,∠C 为直角,cot(900-A)=1.524,则tan(900-B)=_________.3. ∠A 为锐角,已知sinA=135,那么cos (900-A)=___________.4. 已知sinA=21(∠A 为锐角),则∠A=_________,cosA_______,tanA=__________.5. 用不等号连结右面的式子:cos400_______cos200,sin370_______sin420.6. 若cot α=0.3027,cot β=0.3206,则锐角α、β的大小关系是______________. 7. 计算: 2sin450-3tan600=____________. 8. 计算: (sin300+tan450)·cos600=______________.9. 计算: tan450·sin450-4sin300·cos450+6cot600=__________.10. 计算: tan 2300+2sin600-tan450·sin900-tan600+cos 2300=____________. 二、选择题:1. 在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=( )A . 43;B . 34;C .53;D . 54.2. 在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21;B .23;C .1;D .223. 在Rt △ABC 中,∠C 为直角,∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+;D .414. 当锐角A>450时,sinA 的值( )A .小于22; B .大于22; C .小于23; D .大于235. 若∠A 是锐角,且sinA=43,则( )A .00<∠A<300; B .300<∠A<450;C .450<∠A<600;D . 600<∠A<9006. 当∠A 为锐角,且tanA 的值大于33时, ∠A( )A .小于300; B .大于300; C .小于600; D .大于6007. 如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43;B .34;C .53;D .548. Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135; B .cosA=1312; C . tanA=1213;D . cotA=1259. 已知α为锐角,且21<cos α<22,则α的取值范围是( )A .00<α<300;B .600<α<900;C .450<α<600;D .300<α<450.三、解答题1、 在△ABC 中,∠C 为直角,已知AB=23,BC=3,求∠B 和AC .2、在△ABC 中,∠C 为直角,直角边a=3cm ,b=4cm ,求sinA+sinB+sinC 的值.3、在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知b=3, c=14. 求∠A 的四个三角函数.4、在△ABC 中,∠C 为直角,不查表解下列问题: (1)已知a=5,∠B=600.求b ; (2)已知a=52,b=56,求∠A .5、在△ABC 中,∠C 为直角, ∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知a=25,b=215,求c 、∠A 、∠B .6、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1) 已知a =156, b =56,求c; (2) 已知a =20, c =220,求∠B ; (3) 已知c =30, ∠A =60°,求a ;(4) 已知b =15, ∠A =30°,求a .7、已知:如图,在ΔABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠B =30°,CD =6,求AB 的长.8、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡度为︒30︒=∠30DCB ,400=CD 米),测得A 的仰角为︒60,求山的高度DCAB9、会堂里竖直挂一条幅AB,如图5,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
初三 锐角三角函数(一)

A C锐角三角函数(一)知识要点1.锐角三角函数的定义在Rt △ABC 中,∠C=90°。
∠A 的正弦:sin aA c=(对边比斜边) ∠A 的余弦: cosA=bc (邻边比斜边) ∠A 的正切: tanA=a b(对边比邻边) cotA=a b(邻边比对边)2.特殊角度的三角函数值113.三角函数的范围:0<sinA <1,0<cosA <1。
引入操场里有一个旗杆,老师让小明去测量旗杆高度。
小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。
你想知道小明怎样算出的吗?典型例题例1.(1)在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.(2)在Rt △ABC 中,∠B =90°,若a =16,c =30,则b =______, sin A =______,cos A =______,tan A =______, sin C =______,cos C =______,tan C =______.(3)在Rt △ABC 中,∠C =90°,若∠A =30°,则∠B =______, sin A =______,cos A =______,tan A =______,︒341米10米?(1)3A(2)sin B =______,cos B =______,tan B =______.例2:在Rt △ABC 中, ∠C =90°,BC=6, 53sin =A ,求cos A 和tanB 的值.例3:(1)如图(1), 在Rt △ABC 中,∠C =90°,6=AB ,3=BC ,求A ∠的度数.(2)用一片半径为2,面积为π2的扇形纸片围成如图(2)的圆锥,求圆锥的高OA 及α.例4.计算下列式子的值(1)cos45°+3tan30°+cos30°+2sin60°-2tan45°(2)︒+︒+︒+︒-︒45sin 30cos 30tan 130sin 145cos 222例5.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,⋅=31sin A (1)求AB 边上的高CD ;(2)求△ABC 的面积S ; (3)求tan B .例6.(四川自贡,第10题4分)如图,在半径为1的⊙O 中,∠AOB=45°,则sinC 的值为( )A.22B.222-C. 222+ D.42经典练习1.在Rt △ABC 中,∠C =90°,若a =1,b =3,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.2.因为对于锐角α 的每一个确定的值,sin α 、cos α 、tan α 分别都有____________与它______,所以sin α 、cos α 、tan α 都是____________.又称为α 的____________. 3(滨州,第11题3分)在Rt △ACB 中,∠C =90°,AB =10,sinA =53,cosA =54,tanA =43,则BC 的长为( )4.(江苏宿迁)如图,△ABC 的顶点都是正方形网格中的格点,则sin ∠ABC 等于( )ABCD A. 5 B.552 C. 55 D.325.﹙黑龙江﹚ 在△ABC 中,∠C=90°,BC=2,sinA=23,则边AC 的长是( )A .13B .3C .43D . 56.﹙成都﹚如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D.已知AC=5,BC=2,那么sin ∠ACD =( )A .35B .32 C .552 D .257.在△ABC 中,∠C =90°,a ,b ,c 分别是∠A 、∠B 、∠C 的对边,则有( ) A.B. C . D .8.如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,且AB =5,BC =3. 则sin ∠BAC= ;sin ∠ADC= .9.(广西贺州,第18题3分)网格中的每个小正方形的边长都是1,△ABC 每个顶点都在网格的交点处,则sinA = .10.(广西玉林市、防城港市,第16题3分)如图,直线MN 与⊙O 相切于点M ,ME =EF 且EF ∥MN ,则cos ∠E = .11.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB和cos B .AB12.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.13.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.巩固练习1.如图,在直角△ABC 中,∠C =90o,若AB =5,AC =4,则sinA =( ) A .35 B .45 C .34 D .43 2.求下列各式的值:(1)︒︒+︒+︒45sin 30sin 245cos 60cos 22CB A(2)︒+︒︒-︒+︒-︒︒+︒45cos 30sin 45cos 60cos 45sin 60cos 45sin 60cos3.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2. 求:sin B 、cos B 、tan B .4.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC .。
锐角三角函数1

教师备课稿学科_ 数学__ _九_年级第_下册教师朱晶_课题1.1锐角三角函数(1)第课时教学目标1.经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念.2.掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数.3.掌握在直角三角形中,锐角三角函数与边之比的关系.4.了解锐角的三角函数值都是正实数,会根据锐角三角函数的定义求锐角三角函数值.重难点教学重点:锐角的正弦、余弦、正切和锐角三角函数的概念. 教学难点:锐角三角函数的概念.教具、学具准备ppt课件学教安排教法及学法指导、反思课前准备一、创设情境,引入新课小红在上山过程中,下列哪些量是变量,哪些量是常量(坡角,上升高度,所走路程)?她在斜坡上任意位置时,上升的高度和所走路程的比值变化吗?小强呢?(通过学生自主探索,教师引导,从而发现小红在上山过程中,坡角是常量,上升高度和所走路程是变量.她在斜坡上任意位置时,上升的高度和所走路程的比值不会变化.)定义:一般地,对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,则比值BCAB,ACAB,BCAC都是一个确定的值,与点B在角的边上的位置无关,因此,比值BCAB,ACAB,BCAC都是锐角α的三角函数.比值BCAB叫做∠α的正弦(sine),记做sinα.比值ACAB叫做∠α的余弦(cosine) ,记做cosα.30°B45°西东比值BCAC叫做∠α的正切(tangent) ,记做tanα.注意:1、在三角函数的表示中,用希腊字母或单独一个大写英文字母表示的角前面的“∠”一般省略不写.2、sinα、cosα、tanα是一个完整的符号,单独的“sin”没有意义.如果∠A是Rt△ABC的一个锐角(如图),则有sin cos tanAAAAAAA∠=∠=∠=∠的对边斜边的邻边斜边的对边的邻边那么B∠呢?追问:你能求出sinA 与cosA的取值范围吗?.三、新知运用用一用1.如图△ABC中,∠C=90°,BC=5,AC=12.判断:(1)sinA=513(√)(2)tanB=512(×)2.如图,在Rt△ABC中,∠C=90°.⑴若BC=8,AB=17,求sinA, cosA,tanA的值;⑵若BC︰AB=1︰2 ,求sinA, cosA,tanA的值;⑶若sinA=513, 求sinB的值.解后语:已知直角三角形中的两边或两边之比,就能求出锐角三角函数值.例1.如图:在Rt△ABC中,∠B=90ο,AC=200, sinA=0.6.求BC的长.解后反思:本题属于简单题,属于知识的简单运用.练一练:1.在Rt△ABC中,∠C为Rt∠,AC:BC=1:2,求sinA+cosA的值.四、课堂小结1.正弦,余弦和正切的概念;2.三角函数的概念;3.如果∠A是直角三角形的一个锐角,那么它的三角函数与边的关系.4.锐角三角函数的值都是哪一类数,正弦和余弦有什么范围限制?课后反思感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 3 2
B. 1 C. 5 D. 2
2
5
2
9
课堂导学
知识点2:由正弦值求三角形的边长
【例2】在△ABC中,∠C=90°,BC=6,
sinA=23,则AB边的长是____9______.
【解析】根据正弦的定义来解决,由
sinA=2 ,则AB=2 BC=9.
3
3
10
课堂导学
【点拔】运用正弦值求线段时,要根据 正弦的概念找准相应的边,要注意,正 弦值只是一个比值,不能直接当作边长 用.
BC=5,则sinA的值为( D )
5 A. 12
B.
12 5
C. 12 13
D. 5 13
7
课堂导学
2.如右下图,P(4,3)是∠α的边OA上一
点,则sinα 等于( C )
A.
3 4
B.
4 3
C. 3
D. 4
5
5
8
课堂导学
3.如下图,△ABC的顶点都在方格纸的
格点上,则sinA的值是( C )
第11题
17
课后巩固
12.如下图,在菱形ABCD中,DE⊥AB
于E,BE=16cm,sinA =1123 ,求此菱形的周长. 由sinA=DADE =1123 ,设DE=12x,AD= 13x,则AE=5x,所以5x+16=13x,
得x=2,∴AD=26,周长为104.
18
课后巩固
13.在直角三角形ABC中,已知∠C= 90°,AB=15,AC=9,求sinA. 解:∵∠C=90°,AB=15,AC=9, ∴BC= 152-92=12, ∴sinA=BACB =1125 =45,
︵︵ ∠OAC,∴ DC =BC ,∴DC=BC.
23
能力培优
(2)求CE的长; (2)由△ABC∽△ACE,∴ AB =BC 得
AC CE CE=152 . (3)求sin∠DCE的值.
(3)又DC=BC=3,∴DE= CD2-CE2 =
9 5
,∴sin∠DCE=
3 5
.
24
感谢聆听
25
再用正弦的定义求
sinA和sinB的值.
5
课堂导学
【答案】解:在Rt△ABC中,∵∠C=90°,
AC=
AB2-BC2
=12.∴sinA=BACB=
5 13
,
sinB=AC =12 . AB 13
【点拔】求一个角的正弦,只需要求
出这个角所在直角三角形的对边与斜
边的比值. 6
对点训练一
课堂导学
1.在Rt△ABC中,∠C=90°,AC=12,
28.1 锐角三角函数(一)
1
核心目标 ……………..…
2 …课…前…预…习…..… 3 …课…堂…导…学…..… 4 …课…后…巩…固…..…
5 …能…力…培…优…..… 1
核心目标
理解正弦的概念,能根据正弦概念正 确进行计算.
2
课前预习
1.如下图,在Rt△ABC中,∠C=90°,我 们把锐角A的____对______边与____斜______边 的比叫做∠A的正弦,记作____s_in__A___,
a 即sinA=___c___.
第1题图3
课前预习
2.如上图,在Rt△ABC中,∠C=90°, 3
AB=5,BC=3,则sinA的值是__5___.
第2题图
4
课堂导学
知识点1:求锐角的正弦值 【例1】 如右图,在Rt△ABC中,∠C=
90°,求sinA和sinB的值.
【解析】利用勾股
定理求出AC的长,
19
课后巩固
14. 如下图所示在直角三角形ABC中,
∠ACB=90°,CD⊥AB于D,已知AC= 5 ,
AB=3,求sin∠ACD的值. 解:∵直角三角形ABC
中,∠ACB=90°,
CD⊥AB,∴∠ACD+∠BCD=90°,∠BCD
+∠B=90°,∴∠ACD=∠B,则sin∠ACD
=sinB=AACB
11
对点训练二
课堂导学
4.已知,在Rt△ABC中,∠C=90°, AB=5,sinA=2 ,那么BC=___2___.
5
5.已知,在Rt△ABC中,∠C=90°, sinA=3 ,且AB=10,则AC=__8__.
5
12
课堂导学
6.如右图,菱形ABCD的边长为12cm, DE⊥AB,sinA=2 ,则这个菱形的面积
ห้องสมุดไป่ตู้
=
5 3
,故答案为:
5 3
20
课后巩固
15.如下图,点A(t,4)在第一象限,OA 与 解x:轴过所A夹作的AB锐⊥角x为轴α于,B.sin∴αs=in23α,=求AOt的BA,值. ∵sinα=23,∴ AOBA=23, ∵A(t,4),∴AB=4,
∴OA=6,
∴t= 62-42=2 5.
21
能力培优
3 为____9__6____cm2.
13
课后巩固
7.△ABC中,AB=AC=5,BC=8,那
么sinB=( C )
A.
5 8
B. 45
C.
3 5
D.
3 4
8.在Rt△ABC中,sinA=13(5),则
sinB=( A )
A. 12 13
B. 135
C. 5 12
D. 5 8
14
课后巩固
9.如右图,在Rt△ABC中,∠C=90°, AB=26cm,sinA= 5,则AC边的长
13 度为___2__4_____.
15
课后巩固
10.如下图,已知AB是⊙O的直径,点 C、D在⊙O上,AB=5,BC=3,则
3 sin∠BAC=____5______,sin∠ADC=
4 ___5_______.
第10题16
课后巩固
11.如上图所示,在矩形ABCD中, DE⊥AC于点2E0,已知sin∠CDE=45 ,AB= 4,则AC=__3_____.
17.△ABC内接于⊙O,AB是⊙O的直径, 点D在⊙O 上,过点C的切线交AD的延 长线于点E,且 AE⊥CE,连接 CD,已知AB=5, AC=4.
22
能力培优
(1)求证:DC=BC; (1)连接OC,则OC⊥CE,又AE⊥CE, ∴OC∥AE,∴∠OCA=∠CAD,∵OC= OA,∴∠OCA=∠OAC,∴∠CAD=
