锐角三角函数_第一课时-课件
合集下载
《锐角三角函数》PPT教学课件(第1课时)
BC AC
= 12 =
AC
34，所以AC=9.故填9.
随堂训练
AB 6.如图，在Rt△ABC中，∠C＝90°，BC
17 15
,则tan
15 A＝_8__．
由正切定义可知tan A＝BACC , 因为 AB 17 , 可设BC＝15a，AB＝17a，从而可
BC 15
用勾股定理表示出第三边AC＝8a，再用正切的定义求解得 tan A＝ BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义： 如图，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻
边的比便随之确定，这个比叫做 ∠A的正切，记作tan A， 即tan A＝ A的对边
A的邻边
2.tanA的值越大，梯子（坡）越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它 的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮 船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫
23.1锐角的三角函数第一课时+课件+2024—2025学年沪科版数学九年级上册
平长度三者中的任何一个，可以判断
坡面的倾斜程度吗?
比较坡面的长度、铅直高度、水平长度三者中的任何一个都不
能判断哪个坡面更陡.
新课探究
既然只用一边不行，如何改进呢?我们尝试综合考虑两条边.
如图，坡面的长度、铅直高度、水平长度
构成了一个直角三角形。两个锐角一样大的
直角三角形对应的坡面的倾斜程度是一样的，
改变。∠A的对边与∠A的邻边的比(即 )随∠A的变化而变化，并且对于
∠A的每一个值，都有唯一确定的值与之对应。你认为与∠A这两个变量之
间是一种什么关系? (函数关系)
新课探究
如图，在Rt△ABC中，我们把锐角A的对边与邻边的比叫做
∠A的正切(tangent)，记作tan A，即
tan A
∴ = 2 + 2 = 36 + 4 = 2 10 米 .
D.6米
课堂练习
3. 如图所示，A，B，C三点在正方形网格线的交点处，
网格中，小正方形的边长均为1，若将△ACB绕着点A
1
逆时针旋转得到△AC'B'，则tan B'的值为_______.
3
B′
C′
A
C
B
锐角的正切问题，必须放在直角三角形中．
正切：
课堂小结
在Rt△ABC中，我们把锐角A的对边与邻边的比叫做
∠A的正切(tangent)，记作tan A，即
正
切
tan A
∠A的对边 BC a
.
∠A的邻边 AC b
坡度：
坡面的铅直高度h和水平长度l的比叫做坡面的坡度
h
i
(坡度通常写成h∶l的形式) ．
坡面的倾斜程度吗?
比较坡面的长度、铅直高度、水平长度三者中的任何一个都不
能判断哪个坡面更陡.
新课探究
既然只用一边不行，如何改进呢?我们尝试综合考虑两条边.
如图，坡面的长度、铅直高度、水平长度
构成了一个直角三角形。两个锐角一样大的
直角三角形对应的坡面的倾斜程度是一样的，
改变。∠A的对边与∠A的邻边的比(即 )随∠A的变化而变化，并且对于
∠A的每一个值，都有唯一确定的值与之对应。你认为与∠A这两个变量之
间是一种什么关系? (函数关系)
新课探究
如图，在Rt△ABC中，我们把锐角A的对边与邻边的比叫做
∠A的正切(tangent)，记作tan A，即
tan A
∴ = 2 + 2 = 36 + 4 = 2 10 米 .
D.6米
课堂练习
3. 如图所示，A，B，C三点在正方形网格线的交点处，
网格中，小正方形的边长均为1，若将△ACB绕着点A
1
逆时针旋转得到△AC'B'，则tan B'的值为_______.
3
B′
C′
A
C
B
锐角的正切问题，必须放在直角三角形中．
正切：
课堂小结
在Rt△ABC中，我们把锐角A的对边与邻边的比叫做
∠A的正切(tangent)，记作tan A，即
正
切
tan A
∠A的对边 BC a
.
∠A的邻边 AC b
坡度：
坡面的铅直高度h和水平长度l的比叫做坡面的坡度
h
i
(坡度通常写成h∶l的形式) ．
锐角三角函数(1) 课件
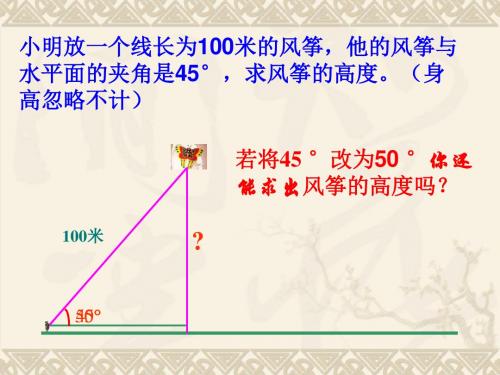
图 19.3.2
AB1
可见，在Rt△ABC中，对于锐角A的每一个 确定的值，其对边与斜边的比值是唯一确定 的.
想一想
图 19.3.2
对于锐角A的每一个确定的值，其邻 边与斜边、对边与邻边的比值也是唯 一确定的 吗？
在Rt△ABC中，对于锐角A的每一个 确定的值，其对边与斜边、邻边与斜 边、邻边与对边的比值也是唯一确定 的.
温馨提示： sin50 °≈0.来自7当堂测评 ：1．在Rt△ABC中，∠C=90°，a=1，c=4， 则sinA的值是（ ）． 15 1 1 15 B. C. D. A． 15 4 3 4 2．在△ABC中，AC=3，BC=4，AB=5， 则tanB的值是（ ） 4 4 C． 3 D． 3 B． A． 5 5 4 3 3．在△ABC中，∠C=90°，BC=2， cos A=0.5 ，则边AC的长是（ ）
B•
50
A C （1）、计算 的值（结果保留2个有效数字）， 并将所得的结果与你同伴所得的结果进行比较。 （2）、将你所取的AB的值和你的同伴比较。
观察图19.3.2中的Rt△AB1C1、
Rt△AB2C2和Rt△AB3C3， 它们之间有什么关系？
Rt△AB1C1 ∽ Rt△AB2C2 ∽ Rt△AB3C3 B3C3 B2C2 B1C1 AB3 ＝__________=__________. AB2 所以 ：
例1：求出图19.3.3所示的Rt△ABC中∠A的
三个三角函数值.
8 15
图 19.3.1
现在同学们能否求 出小明风筝的高度
解：设风筝的高度为x 米，由题意得
在直角三角形中
X sin50 °= 100
∴ x=100× sin50 ° ≈ 100 ×0.77 =77(米） 答:风筝的高度是77米
锐角三角函数(第一课时)课件ppt
对边与斜边的比 BC ，你能得出什
么结论？
AB
C
B
在Rt△ABC中，∠C＝90°，由于∠A＝45°，所以Rt△ABC是
等腰直角三角形，由勾股定理得
AB2 AC2 BC2 2BC2
AB 2BC
因此 BC BC 1 2
AB 2BC 2 2
即在直角三角形中，当一个锐角等于45°时，不管这 个直角三角形的大小如何，这个角的对边与斜边的比都 等于 2
（2）直角三角形中一个锐角的度数越大，它的 对边与斜边的比值越大
结论
如图，Rt△ABC中，直角边AC、BC小于斜边AB，
B
sin A BC AB
＜1
sin B AC ＜1 AB
A
C
所以0＜sinA ＜1, 0＜sinB ＜1,
如果∠A ＜ ∠B,则BC＜AC ,
那么0＜ sinA ＜sinB ＜1
C
AB
在Rt△BCD中， sin B CD BC
A
D
B
因为∠B=∠ACD，所以
sin B sin ACD AD AC
请分别计算60度的锐角对边与斜边的比值 你能发现什么规律吗？
sin 45 2 2
sin 45 2 2
sin30 1
2
(1)直角三角形中，锐角大小确定后，这个角的 对边与斜边的比值随之确定；
意大利的伟大科学家C 伽俐 ．略，曾在斜塔的顶
层做过自由落体运动的实 验.
B
“斜而未倒” AB=54.5m BC=5.2m
α
A
情
问题 为了绿化荒山，某地打算从位于山脚下的机井 房沿着山坡铺设水管，在山坡上修建一座扬水站，
(课件1)25.2锐角三角函数
股定理求出，试一试吧，用心做一做，我相信， 你 一 定 能 又 准 又 快 的 做 好 的 ---
特殊角的三角函数值
sin 30 , sin 45 , sin 60 的 函 数 值 分 别 是 多 少 啊 ？ 有哪些规律啊？（可以从它们的分子分母上去观察） cos 30 , cos 45 , cos 60 呢 ？ 与 正 弦 有 什 么 联 系 呢 ？ tan 30 , tan 45 , tan 60 的 大 小 规 律 是 什 么 啊 ？ cot 30 , cot 45 , cot 60 的 大 小 规 律 与 锐 角 的 正 弦 类 似 ， 还是与余弦类似啊？
定义的应用(一）
取值范围：
AC AB
在以后的计算过程中， 如果出现了一个锐角 的正弦值或是余弦值 大于1—你啊，快点 回头检查，一定在哪 一步出现了错误！
sin B
中 , A C 为 直 角 边 ， AB为 斜 边 ， AC AB
sin B 1
想 一 想 ： 为 什 么 “ sin B 0” 呢 ？ 你 能 不 能 根 据 以 上 推 理 ， 得 出 “ 0 sinB 1 这个结论吗？
, 斜 边 A B是 直 角 边 AC的
答案（1-----3题）
1 . 1 .原 式 3 3 3 3
2 .原 式
3 2 2
1
2。 答 ： 这 个 三 角 形 是 钝 角 三 角 形 。 原 因 ： A=45 , B 30
C 180 45 30 105 90
解直角三角形 -锐角三角函数
• 华东师大版第25章第二节 • 九年级上册
锐角三角函数的内容
北师大版数学九年级下册1.1锐角三角函数第1课时课件
＋4＝0的两个正整数根之一，且另两边长为BC＝4，AB＝6，求
tan A.
合作探究
解:设方程x2＋mx＋4＝0的两根分别为x1，x2，
根据根与系数的关系可知x1·x2＝4，
∵x1、x2为正整数解，∴x1、x2可为1、4或2、2.
又∵BC＝4，AB＝6，∴2＜AC＜10，∴AC＝4，∴AC＝BC
＝4，∴△ABC为等腰三角形.
过点C作CD⊥AB(如图)，∴AD＝3，∴CD＝ ，tan A＝
＝ .
合作探究
方法归纳交流 求解图形中有关角的正切值，在直角三角
形中可直接运用正切的定义求值，无直角三角形的要作辅助线
构造直角三角形求值.
合作探究
1.如图，在Rt△ABC中，∠C＝90°，CD是斜边AB上的高，
如果CD＝3，BD＝2.求tan A的值.
◎重点:正切、倾斜程度、坡度的数学意义.
预习导学
激趣导入
如图，这是上海东方明珠塔的图片，它于1994年10月1日建
成.在各国广播电视塔的排名榜中，当时其高度列亚洲第一、世
界第三，与外滩的“万国建筑博览群”隔江相望.在塔顶俯瞰上
海风景，美不胜收.你能测出东方明珠塔的高度吗？那么就开始
本章的学习之旅吧！
A.
B.
C.
D.
合作探究
在Rt△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、
∠C的对边，若b＝2a，则tan A＝
.
直角三角形两边的比为3∶4，则最小角的正切为
或
.
若某人沿坡度i＝3∶4的斜坡前进10米，则他所在的位
置比本来的位置升高了 6 米.
tan A.
合作探究
解:设方程x2＋mx＋4＝0的两根分别为x1，x2，
根据根与系数的关系可知x1·x2＝4，
∵x1、x2为正整数解，∴x1、x2可为1、4或2、2.
又∵BC＝4，AB＝6，∴2＜AC＜10，∴AC＝4，∴AC＝BC
＝4，∴△ABC为等腰三角形.
过点C作CD⊥AB(如图)，∴AD＝3，∴CD＝ ，tan A＝
＝ .
合作探究
方法归纳交流 求解图形中有关角的正切值，在直角三角
形中可直接运用正切的定义求值，无直角三角形的要作辅助线
构造直角三角形求值.
合作探究
1.如图，在Rt△ABC中，∠C＝90°，CD是斜边AB上的高，
如果CD＝3，BD＝2.求tan A的值.
◎重点:正切、倾斜程度、坡度的数学意义.
预习导学
激趣导入
如图，这是上海东方明珠塔的图片，它于1994年10月1日建
成.在各国广播电视塔的排名榜中，当时其高度列亚洲第一、世
界第三，与外滩的“万国建筑博览群”隔江相望.在塔顶俯瞰上
海风景，美不胜收.你能测出东方明珠塔的高度吗？那么就开始
本章的学习之旅吧！
A.
B.
C.
D.
合作探究
在Rt△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、
∠C的对边，若b＝2a，则tan A＝
.
直角三角形两边的比为3∶4，则最小角的正切为
或
.
若某人沿坡度i＝3∶4的斜坡前进10米，则他所在的位
置比本来的位置升高了 6 米.
《锐角三角函数》课件
锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
第1课时 锐角三角函数 公开课获奖课件
根据“在直角三角形中，30°角所对的直角边等于斜边的一半”，即 ∠A斜的边对边＝ABCB＝21， 可得 AB＝2BC＝70 m，即需要准备 70 m 长的水管． 思考 1：在上面的问题中，如果使出水口的高度为 50 m，那么需要准备 多长的水管？ 学生按与上面相似的过程，自主解决． 结论：在一个直角三角形中，如果一个锐角等于 30°，那么不管三角形
sinB＝∠B斜的边对边＝bc.
思考 3：一般地，当∠A 取一定度数的锐角时，它的邻边与斜边的比是否 也是一个固定值？
探究：如图，在 Rt△ABC 与 Rt△A′B′C′中，∠C＝∠C′＝90°，∠ A＝∠A′＝α，那么AACB与AA′′CB′′有什么关系？
教师用类比的方法引导学生思考、讨论． 结论：在直角三角形中，当锐角 A 的度数一定时，不管三角形的大小如 何改变，∠A 的邻边与斜边的比是一个固定值． 余弦的概念： 在 Rt△ABC 中，∠C＝90°，把锐角 A 的邻边与斜边的比叫做∠A 的余 弦，记作 cosA，即 cosA＝∠A斜的边邻边＝bc.
•
蔡琰（作者有待考证）的《胡笳十八拍》
郭璞的《游仙诗》
鲍照的《拟行路难》
庾信的《拟咏怀》
都特别喜欢。不过都是组诗，太长了，就不贴了orz。
最后还想推一下萧绎的《幽逼诗》四首：
【南史曰：元帝避建邺则都江陵，外迫强敌，内失人和。魏师至，方征兵四方，未至而城见克。在幽逼求酒，饮之，制诗四绝。后为梁王詧所害。】 南风且绝唱，西陵最可悲。今日还蒿里，终非封禅时。 人世逢百六，天道异贞恒。何言异蝼蚁，一旦损鲲鹏。 松风侵晓哀，霜雰当夜来。寂寥千载后，谁畏轩辕台。 夜长无岁月，安知秋与春。原陵五树杏，空得动耕人。
的大小如何，这个角的对边与斜边的比值都等于12.
1.1锐角的三角函数第1课时正切与坡度课件(共33张PPT)北师大版九年级数学下册
在图中，梯子的倾斜程度与 tanA 有关系吗？
梯子的倾斜程度与tanA有关系吗？
tanA的值越大， 梯子越陡.
A
B1 B2
C2
C1
归纳总结
在 Rt△ABC 中，如果锐角 A 确定，那么 ∠A
的对边与邻边的比便随之确定，这个比叫做 ∠A
的正切，记作 tanA，即 tanA =
∠A的对边 ∠A的邻边
1.5
D
C
4
2. 如图，某人从山脚下的点A走了200m后到达山顶的点B. 已知点B到山脚的垂直距离为55m，求山坡的坡度. (结果精确到0.001m)
B
A
C
解 tan A BC = 55 ≈0.286. AC 2002 552
1. 在 Rt△ABC中，∠C= 90°，AC=5，AB= 13，求tan A 和tan B.
(2)
B1C1 AC1
和
B2C2 AC2
有什么关系？B1C1 B2C2
AC1 AC2
B3
B2
B1
(3) 如果改变 B2 在梯子上的位置. A C3 C2 C1
(如 B3C3 )呢？Rt△AB1C1∽Rt△AB2C2∽ Rt△AB3C3
议一议
B1C1 B2C2 B3C3 AC1 AC2 AC3
相似三角形的 对应边成比例
E
A 6m
4m
2m
B
CF 3m D
问题2 ：在下图中，梯子 AB 和 EF 哪个更陡？ 你是怎样判断的？
当铅直高度与水平宽度的比越大，梯子越陡.
倾斜角越大，梯子越陡.
A
E
总结：铅直高度与水平宽度
的比和倾斜角的大小都可用
4m
3.5 m
人教版九年级下册数学教学课件锐角三角函数第一课时
人教版·九年级下册
导入新课
意大利比萨斜塔1350年落成时就已倾斜，其塔顶 中心点偏离垂直中心点2.1 m．1972年比萨地区发生 地震，这座高54.5 m的斜塔在大幅度摇摆后仍魏然屹 立，但塔顶中心点偏离垂直中心线5.2 m，而且还在 继续倾斜，有倒塌的危险．当地从1990年对斜塔进行 维修纠偏，2001年竣工，此时塔顶中心点偏离垂直中 心的距离减少了43.8 cm．
28.1 锐角三角函数（1） ∠A的正弦、余弦、正切都是∠A的锐角三角函数（trigonometric function of acute angle）．
答：我们前面研究了直角三角形中角与角之间的关系（两锐角互余）、三边之间的关系（勾股定理），还可以研究边与角之间的关系 ． 2．锐角三角函数的定义 2．在Rt△ABC中，∠C=90°，a=3，c=5，求sin A和tan A的值． 1 锐角三角函数（1）
13
巩固练习
2．在Rt△ABC中，∠C=90°，a=3，c=5，求sin A和
tan A的值．
解：在Rt△ABC中，∵a=3，c=5，
∴ b c2 a2 52 32 4 ．
∴sin A= a 3 ，tan A= a 3 ．
c5
b4
课堂小结
1．正弦、余弦、正切的定义
如图，在Rt△ABC中，∠C=90°，∠A，∠B，∠C 当∠A=45°时，∠A的对边与斜边的比都等于 ，它也是一个固定值．由此你能猜想出什么一般的结论呢？
1．在△ABC中，若三边BC、CA、AB满足BC︰CA︰AB=5︰12︰13，则cos B=（ ）．
解：在理Rt△）ABC，中，∵还a=3，可c=5以， 研究边与角之间的关系．
导入新课
从实际需要看，要描述比萨斜塔的倾斜程度，我 们需要研究直角三角形中边与角之间的关系：从数学 内部看，我们已经研究了直角三角形的边与边的关 系、角与角的关系，边与角之间有什么关系呢？本节 课我们一起来学习“锐角三角函数”——锐角的正弦、 余弦、正切．
导入新课
意大利比萨斜塔1350年落成时就已倾斜，其塔顶 中心点偏离垂直中心点2.1 m．1972年比萨地区发生 地震，这座高54.5 m的斜塔在大幅度摇摆后仍魏然屹 立，但塔顶中心点偏离垂直中心线5.2 m，而且还在 继续倾斜，有倒塌的危险．当地从1990年对斜塔进行 维修纠偏，2001年竣工，此时塔顶中心点偏离垂直中 心的距离减少了43.8 cm．
28.1 锐角三角函数（1） ∠A的正弦、余弦、正切都是∠A的锐角三角函数（trigonometric function of acute angle）．
答：我们前面研究了直角三角形中角与角之间的关系（两锐角互余）、三边之间的关系（勾股定理），还可以研究边与角之间的关系 ． 2．锐角三角函数的定义 2．在Rt△ABC中，∠C=90°，a=3，c=5，求sin A和tan A的值． 1 锐角三角函数（1）
13
巩固练习
2．在Rt△ABC中，∠C=90°，a=3，c=5，求sin A和
tan A的值．
解：在Rt△ABC中，∵a=3，c=5，
∴ b c2 a2 52 32 4 ．
∴sin A= a 3 ，tan A= a 3 ．
c5
b4
课堂小结
1．正弦、余弦、正切的定义
如图，在Rt△ABC中，∠C=90°，∠A，∠B，∠C 当∠A=45°时，∠A的对边与斜边的比都等于 ，它也是一个固定值．由此你能猜想出什么一般的结论呢？
1．在△ABC中，若三边BC、CA、AB满足BC︰CA︰AB=5︰12︰13，则cos B=（ ）．
解：在理Rt△）ABC，中，∵还a=3，可c=5以， 研究边与角之间的关系．
导入新课
从实际需要看，要描述比萨斜塔的倾斜程度，我 们需要研究直角三角形中边与角之间的关系：从数学 内部看，我们已经研究了直角三角形的边与边的关 系、角与角的关系，边与角之间有什么关系呢？本节 课我们一起来学习“锐角三角函数”——锐角的正弦、 余弦、正切．
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)
观察以上计算结果,你发现了什么?
sinA=cosB ，cosA=sinB (∠A+∠B=90）
tanA·tanB=1
(∠A+∠B=90）
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图，在△ABC中，若AB=5，BC=3，则下列结论正确
锐角A，A′的余弦值的关系为（ ） A
A．cosA=cosA′ B．cosA=3cosA′ C．3cosA=cosA′ D．不能确定 2．如图，已知P是射线OB上的任意一点，PM⊥OA于M，
且PM：OM=3：4，则cosα的值等于（ C）
3 A．4
4 B．3
C．4 5
3
D．
5
3．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦，余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine)，记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ，记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ，记做tanα.
b，c，则下列各项中正确的是（ ） B
A．a=c·sinB B．a=c·cosB C．a=c·tanB D．以上均不正确
4．在Rt△ABC中，∠C=90°，cosA= 2 ，则tanB等于（ ）
C
26.1 锐角三角函数 - 第1课时课件(共19张PPT)
提示:过点A作AD垂直于BC于点D.求锐角三角函数时,勾股定理的运用是很重要的.
3.如图,正方形ABCD的边长为4,点M在BC上,M,N两点关于对角线AC对称, 若DM=1，求tan∠ADN的值.
解：由正方形的性质可知，∠ADN=∠DNC，BC=DC=4，∵ M、N两点关于对角线AC对称, ∴ DM=1BN=DM=1.tan∠AND=tan∠DNC= .
知识点 正切的概念
新知探究
思考
在两个直角三角形中，当一对锐角相等时，这两个直角三角形相似，从而两条对应直角边的比相等，即当∠A（小于90°）确定时，以∠A为锐角的Rt△ABC的两条直角边的比 是确定的.
发现
正切
如图，在Rt△ABC中，∠C＝90°，∠A的对边与邻边的比叫做∠A的正切，记作：tanA ，即
在Rt△ABC中，∠C＝90°.（1）如图（1），∠A=30°，求tanA，tanB的值．（2）如图（2），∠A=45°，求tanA的值．
例1
例题示范
随堂演练
1.在△ABC中，已知AC=5，BC=4，AB=3.那么下列各式正确的是（ ）A.tanA= B.tanA=CtanC= DtanC=
课堂小结
正切
定义
对边与邻边的比
表示方法
有关计算
与锐角的大小有关，与三角形边的长短无关
同学们再见！
授课老师：
时间：2024年9月15日
A
2.在Rt△ABC中，锐角A的对边和邻边同时扩大100倍，tanA的值（ ） A.扩大100倍 B.缩小 C.不变 D.不能确定
C
3. 如图， P是平面直角坐标系上的一点，且点P的坐标为（3，4），则tan α = .
第 二十六章 解直角三角形
3.如图,正方形ABCD的边长为4,点M在BC上,M,N两点关于对角线AC对称, 若DM=1，求tan∠ADN的值.
解：由正方形的性质可知，∠ADN=∠DNC，BC=DC=4，∵ M、N两点关于对角线AC对称, ∴ DM=1BN=DM=1.tan∠AND=tan∠DNC= .
知识点 正切的概念
新知探究
思考
在两个直角三角形中，当一对锐角相等时，这两个直角三角形相似，从而两条对应直角边的比相等，即当∠A（小于90°）确定时，以∠A为锐角的Rt△ABC的两条直角边的比 是确定的.
发现
正切
如图，在Rt△ABC中，∠C＝90°，∠A的对边与邻边的比叫做∠A的正切，记作：tanA ，即
在Rt△ABC中，∠C＝90°.（1）如图（1），∠A=30°，求tanA，tanB的值．（2）如图（2），∠A=45°，求tanA的值．
例1
例题示范
随堂演练
1.在△ABC中，已知AC=5，BC=4，AB=3.那么下列各式正确的是（ ）A.tanA= B.tanA=CtanC= DtanC=
课堂小结
正切
定义
对边与邻边的比
表示方法
有关计算
与锐角的大小有关，与三角形边的长短无关
同学们再见！
授课老师：
时间：2024年9月15日
A
2.在Rt△ABC中，锐角A的对边和邻边同时扩大100倍，tanA的值（ ） A.扩大100倍 B.缩小 C.不变 D.不能确定
C
3. 如图， P是平面直角坐标系上的一点，且点P的坐标为（3，4），则tan α = .
第 二十六章 解直角三角形
锐角三角函数--课件
D
A
F
E
C
B
哪个轨道更陡？
你是如何判断的？
问题1：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
问题2：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
E
(1)
B
(2)
4m
6m
A
2m C
D
3m
F
问题3：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
(1)
B
(2)
E
4m
A
3m C
3m
D
2m F
（2）若AC=9，AB=15，求
tanA和tanB
B
C
如图，某人从小山坡下的B点走了15米到达坡顶的A， 已知点A到坡脚的垂直距离为9m，求坡的坡度.
A
坡角
B
C
练 如图:求tanC=( C
(A) 1 (B) 5 (C) 4
6
3
B
) (D) 5
3
5
5
4
构造直角三角形
A 3 D6 3 C
在非直角三角形中求角的正切值，要作辅助 线构造直角三角形来解决问题.
小组活动3：
探索30°，45°，60 ° 角的正切值.
小组活动4：
如图，△ABC是等腰直角三角形，
∠C=90°. 若 AD是BC边上的角平
分线， 求∠BAD的正切值.
B
D
A
C
将本堂课记录的角度及 它的正切值填入表格
（按角的度数从小到大排列）
1、谈谈本节课的收获. 2、说说团队合作的感受.
作业布置：
邻边的比值改变吗？
B
B1
A
C1
A
F
E
C
B
哪个轨道更陡？
你是如何判断的？
问题1：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
问题2：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
E
(1)
B
(2)
4m
6m
A
2m C
D
3m
F
问题3：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
(1)
B
(2)
E
4m
A
3m C
3m
D
2m F
（2）若AC=9，AB=15，求
tanA和tanB
B
C
如图，某人从小山坡下的B点走了15米到达坡顶的A， 已知点A到坡脚的垂直距离为9m，求坡的坡度.
A
坡角
B
C
练 如图:求tanC=( C
(A) 1 (B) 5 (C) 4
6
3
B
) (D) 5
3
5
5
4
构造直角三角形
A 3 D6 3 C
在非直角三角形中求角的正切值，要作辅助 线构造直角三角形来解决问题.
小组活动3：
探索30°，45°，60 ° 角的正切值.
小组活动4：
如图，△ABC是等腰直角三角形，
∠C=90°. 若 AD是BC边上的角平
分线， 求∠BAD的正切值.
B
D
A
C
将本堂课记录的角度及 它的正切值填入表格
（按角的度数从小到大排列）
1、谈谈本节课的收获. 2、说说团队合作的感受.
作业布置：
邻边的比值改变吗？
B
B1
A
C1
1.1锐角三角函数(第一课时)课件(共17张PPT)浙教版数学九年级下册
cosA=
=
∠的邻边
温馨提醒：以正弦为例
sinA（省去角的符号），
30°的正弦表示为sin30°，比值 叫做∠A的正切值，记做tanA，即
斜边
∠BAC的正弦表示为sin∠BAC
，∠1的正弦表示为:sin∠1.
tanA=
∠的对边
∠的邻边
=
概念运用
①BC=8，AC=6
概念
cosA=
= ，
tanA=
4
3
sinA=
4
5
3
= ，
5
= .
解后反思：在直角三角
形中，已知什么条件可
以求三角函数值?
课堂练习
1.如图，在Rt△ABC中，∠ACB=90°，作CD⊥AB于
点D，若BC=5，BD=4，求sin∠A.
C
A
B
思路1：求AB的长
思路2：等角转化
△BCD∽△BAC
B"
P
C" Q
图（1）
图（2）
角为30°
’’ 1
""
=
= =
’’ 2
"
’’
3 "
=
=
=
’’
2
"
’’
3 ""
=
=
=
’’
3
"
请先按暂停键！
思考完成后
再按回播放键！
边的比值为定值
探索规律
当∠PAQ发生改变时，刚才所获得的发现是否还成立呢？
解:设AB=5k，AC=3k，
28章锐角三角函数全章ppt课件
问题（1）当梯子与地面所成的角a为75°时，梯子顶端与地面的 距离是使用这个梯子所能攀到的最大高度．
问题（1）可以归结为：在Rt △ABC中，已知∠A＝75°，斜
边AB＝6，求∠A的对边BC的长．
B
由 sin A BC 得 AB
BC AB sin A 6sin 75
由计算器求得 sin75°≈0.97
α
A
C
所以 BC≈6×0.97≈5.8
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
对于问题（2），当梯子底端距离墙面2.4m时，求梯子与地面所成的 角a的问题，可以归结为：在Rt△ABC中，已知AC＝2.4，斜边AB＝6， 求锐角a的度数
由于
B
cos a AC 2.4 0.4
AB 6
tan A BC 8k 8 AC 15k 15
例题示范
例3： 如图，在Rt△ABC中，∠C＝90° B
1.求证：sinA=cosB，sinB=cosA
2.求证：tan A sin A ;tan A 1
cos A
tan B
3.求证：sin2 A cos2 A 1
A
C
sin2 A sin A sin A
如图，Rt△ABC中，直角边AC、BC小于斜边AB，
sin A BC ＜1
AB
sin B AC AB
＜1
A
C
所以0＜sinA ＜1, 0＜sinB ＜1, 如果∠A ＜ ∠B,则BC＜AC , 那么0＜ sinA ＜sinB ＜1
探究
精讲
如图，在Rt△ABC中，∠C＝ 90°，当锐角A确定时，∠A 的对边与斜边的比就随之确 定，此时，其他边之间的比 是否也确定了呢？为什么？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c 斜边
a
对边
A
C
b
注意：1、sinA不是sin与A的乘积，而是一个整体；
思2考、：正∠弦B的的三正种弦表怎示么方表式示：？s要in求A、一s个in5锐6°角、的sin正∠弦D值EF，； 我们需要3、知si道nA直是角两三线角段形之中比的，哪故些si边nA？是一个数，没有单位。
知ቤተ መጻሕፍቲ ባይዱ回顾 问题探究 课堂小结 探究三：什么是正弦？
活动1 理论提升，认识正弦
如图，在Rt△ABC中，∠A、∠B、∠C所对的边分别记
为a、b、c，在Rt△ABC中，∠C=90°，我们把锐角A的对边
与斜边的比叫做∠A的正弦，记作sinA.则sin30°= 1 ，sin45°=
sinA＝ AA的 的对 斜边 边
a c
2
B
1
2 2
（举例说明：若a=1，c=3，则sinA=3）
知识梳理
知识回顾 问题探究 课堂小结
（1）在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边 的比叫做∠A的正弦，记作sinA= a
c
（2）sin30°=
1 ，sin45°= 2
2 2
重难点突破
知识回顾 问题探究 课堂小结
（1）运用正弦计算时，关键是找准角的对边与斜边。
（2）如果一个锐角没有在直角三角形中，要构造直角三角形求解。
有什么关系？
分析：由于∠C=∠C´=90°，
∠A=∠A´=α，所以
Rt△ABC∽Rt△A´B´C´，BB'CC' AA'BB，'
即
BC B'C'
结AB论：A'B在' 直角三角形中，当锐角A的度数一定时，不管三
角形的大小如何，∠A的对边与斜边的比也是一个固定值。
知识回顾 问题探究 课堂小结 探究三：什么是正弦？
2
知识回顾 问题探究 课堂小结 探究二：在直角三角形中，任意锐角的对边比斜边是固定值吗？
活动1 大胆猜想，归纳推理
一般地，当∠A取其他一定度数的锐角时，它的对边与斜边
的比是否也是一个固定值？
如图：Rt△ABC与Rt△A´B´C´，∠C=∠C´=90°，∠A=∠A´=α，
那么
BC AB
与
B'C' A' B'
知识回顾 问题探究 课堂小结
求sinA就是要确定∠A的对边与斜边 的比，求sinB就是要确定∠B的对边与斜 边的比。
谢谢
活动2 初步运用，简单求值
例1：在Rt△ABC中，∠C=90°，求sinA和sinB的值。
B
B
13
3
5
A
4
C
（1）
C
（2）
A
解：（1）在Rt△ABC中，AB= AC2 BC2 = 42 32 =5 因此，sinA= BC = 3，sinB= AC = 4
三（角2）形点在中拨R，：t△只正AAB要弦BC已是中知直5，任角sin意三A=两角BACBA条形B=边中153的锐5，条角AC件的=下对A，边B2 都与 B可斜C2根边=据之13勾比2 股，52定在=理直12求角 出因第此三，边sin，B=进AAC而B =求1123出正弦值。在解题中，准确画出图形并找出所 求锐角是关键。
∠A=30°，BC=35m，求AB的长。
根据“在直角三角形中，30°角所对的直角
结边论等：于在斜一边个的直一角半三”角，形即中，如果一个锐角等于30°，那么不管
三角形的可大得小A如B何=2，B这C=个70角m的，对即边需与要斜准边备的70比m长值都等于 的水管。同理，若BC=50m，则易求得
1 2
。
知识回顾 问题探究 课堂小结
（4）相似三角形性质：相似三角形对应角相等、对应边成 比例；相似三角形对应线段（中线、高、角平分线）之比等 于相似比；相似三角形的周长之比等于相似比、面积之比等 于相似比的平方。
知识回顾 问题探究 课堂小结 探究一：在直角三角形中，30°、45°角的对边比斜边是固定值吗？
活动1 创设情境，引出问题
为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水 管，在山坡上修建一座扬水站，对坡面的绿地进行灌溉。现测得斜坡
与水平面所成角的度数是30°，为使出水口的高度为35m，那么需要准 备多长的水管？如果使出水口的高度为50m，那么需要准备多长的水管？
分析：
问题转化为：在Rt△ABC中，∠C=90°，
锐角三角函数
第一课时
知识回顾 问题探究 课堂小结
（1）在直角三角形中，30°角所对的直角边等于斜边的一半。
（2）勾股定理：在直角三角形中，两直角边的平方和等于斜边 的平方。
（3）相似三角形的判定：三边对应成比例的两三角形相似；两 边对应成比例且夹角相等的两三角形相似；两角对应相等的两 三角形相似；斜边和一条直角边成比例的两个直角三角形相似。
AB=100m
知识回顾 问题探究 课堂小结 探究一：在直角三角形中，30°、45°角的对边比斜边是固定值吗？
活动2 类比思考，举一反三
如图，任意画一个Rt△ABC，使∠C=90°，∠A=45°，计算∠A的 对边与斜边的比 BC ，能得到什么结论？
AB
结论：在一个直角三角形中，如果一个锐角等于45°， 那么不管三角形的大小如何，这个角的对边与斜边的比值 都等于 2 。