数学列方程解应用题的常用公式
完整版)初一数学列方程解应用题归类含答案

完整版)初一数学列方程解应用题归类含答案一、等积变形问题常见几何图形的面积、体积、周长计算公式,依据形状变化,但体积不变。
①圆柱体的体积公式为V=底面积×高=S·h=πrh②长方体的体积为V=长×宽×高=abc1.一段铁丝围成长方形,发现长比宽多2cm;围成正方形时,边长刚好为4cm。
求所围成的长方形的长和宽各是多少?解:设长方形的长为x,宽为x-2,则有x+x-2+4=4x,解得x=6,所以长方形的长为6cm,宽为4cm。
2.用一个底面半径为40mm,高为120mm的圆柱形玻璃杯向一个底面半径为100mm的大圆柱形玻璃杯中倒水,倒了满满10杯水后,大玻璃杯的液面离杯口还有10mm,大玻璃杯的高度是多少?解:由于10杯水的体积为10×40×40×π×120=π mm³,而大玻璃杯的底面积为100×100×π=π mm²,所以大玻璃杯的高度为π/π-10=22mm。
3.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成。
现有长为35米的竹篱笆,小王打算用它围成一个鸡场,其中长比宽多5米;小赵也打算用它围成一个鸡场,其中长比宽多2米。
你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?解:设鸡场的长为x,宽为y,则有x+y=35,x-14=y+5或x-14=y+2,解得x=24,y=11或x=21,y=14.所以小王的设计符合实际,鸡场的面积为24×11=264平方米。
4.将一个装满水的内部长、宽、高分别为300毫米,300毫米和80毫米的长方体铁盒中的水,倒入一个内径为200毫米的圆柱形水桶中,正好倒满,求圆柱形水桶的高(精确到0.1毫米,π≈3.14)。
解:长方体铁盒中的水的体积为300×300×80=xxxxxxxmm³,而圆柱形水桶的体积为π×100×100×h=πh,所以h=xxxxxxx/(π)=229.18mm。
求应用二元一次方程组-增收节支导学案

求应用二元一次方程组——增收节支【学习过程】模块一 预习反馈学习准备1.列二元一次方程组解应用题的关键是:2.列二元一次方程组解应用题的步骤是:3.常用公式:(1)增长(亏损)率问题:原量(1+增长率)=新量;原量(1—亏损率)=新量;%100-100%⨯=⨯=原来的量原来的量现在的量原来的量增长的量增长率 (2)银行利率问题: 利息=本金×利率×期数,本息和=本金+利息(3)行程问题:路程=速度×时间(4)百分率问题:%100⨯=原量增(减)量百分率 (5)利润(率)问题:利润=售价-进价(成本价)=进价(成本价)×利润率;%100⨯=商品及进价商品利润商品利润率; %100-⨯=总产值总支出总产值产品利润率 教材精读例1 某工厂去年的利润(总产值—总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元,去年的总产值、总支出各是多少万元?设去年的总产值为x 万元,总支出为y 万元,则有根据题意得: ⎩⎨⎧.______________________,__________ 解得⎩⎨⎧==.______,y x 答:去年的总产值为2000万元,总支出1800万元,归结:将实际问题转化成二元一次方程组的数学模型;会用图表分析数量关系。
实践练习:一、二班共有100名学生,他们的体育达标率(达到标准的百分率)为81%,如果一班的学生的体育达标率为87%,二班的达标率为75%,那么一、二班的学生数各是多少?教材拓展例2 甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2时,那么他们在乙出发2.5时后相遇;如果乙比甲先走2时,那么他们在甲出发3时后相遇,甲、乙两人每时各走多少千米?模块二 合作探究例3 祥福中学去年有学生1500名,今年比去年减少12%,其中寄宿学生增加了12.5%,走读学生减少了40%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x 名,走读学生y 名,则可列出方程组为 。
初数学列方程解应用题精选

初数学列方程解应用题精选班级_________姓名__________一、和、差、倍、分问题:这类问题的基本相等关系式是:各分量之和等于总量.1.丢番图的墓志铭:“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一.又过十二分之一,两颊长胡,再过七分之一,点燃结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”你知道丢番图去世时的年龄吗?请你列出方程解答.2.一批商界人士在露天茶座聚会,他们先是两人一桌,服务员给每桌送上1瓶果汁.后来他们又改为三人一桌,服务员给每桌送上1瓶葡萄酒.不久他们改坐成四人一桌,服务员给每桌送上1瓶啤酒.此外他们每人都要了一瓶可口可乐.聚会结束时服务员收拾到了100个空瓶.如果没有人带走瓶子,那么聚会有多少人参加?二、盈余与不足问题:这类问题的基本相等关系式是:不同分法所得的总量相等.3.某中学有住校生若干人,若每间宿舍住8人,则有5人无处住;若每间宿舍增加1人,则还空35张床位,问有宿舍多少间?住校生多少人?4.用一队卡车运一批货物,若每辆装7吨,尚余10吨货物装不完;若每辆装8吨,则最后一辆只装3吨就装完了货物.问这批货物共几吨?5.用绳子量井深,把绳子三折来量,井外余绳4尺;把绳四折来量,井外余绳1尺.求井深和绳长各是多少?三、配套问题此类问题的基本相等关系式是:每一套中所涉及物体之间的倍数关系.6.用白铁皮做罐头盒,每张铁皮可制盒身16个或制盒底48个,一个盒身与两个盒底配成一套.现有100张白铁皮,应怎样分配制盒身与盒底才能配套?7.某车间每天能生产甲种零件120个,或者乙种零件100个.甲、乙两种零件分别取3个、2个才能配套.要在36天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数?8. 服装厂要生产一批某种型号的服装,已知每3米的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的布料生产这种服装,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?四、劳力调配问题此类问题的基本相等关系式是:各部分分量之和等于总量.9. 若在甲处工作的有31人,在乙处工作的有20人,现调来18人分别派往甲、乙两处,使在甲处工作的人数是在乙处工作的人数的2倍,则应往甲、乙两处各派多少人?10. 青海省玉树县发生地震后,甲、乙两工程队奔赴灾区支援建设工作,其中甲工程队人数是乙工程队人数的2倍.因工作需要,从甲工程队抽调16人支援乙工程队,使得甲工程队人数比乙工程队人数的一半少3人,试求甲、乙两工程队原来各有多少人?五、年龄问题解决有关年龄问题时,抓年龄差...这个不变量建立方程.11.父亲今年38岁,女儿今年14岁,则哪一年时,父亲的年龄是女儿年龄的7倍?12.学生问数学老师:“你今年多少岁”?老师说:“当你是我现在的年龄时,我35岁;当我是你现在的年龄时,你2岁.”问老师今年多少岁?学生今年多少岁?六、数字、日历问题13.一个两位数,个位上的数字是十位上的数字的2倍,如果把十位与个位上的数字对调,那么所得的两位数比原来两位数大36,求原来的两位数.14.初一(2)班的数学课代表苗苗问数学老师家的电话号码是多少?老师说:“我家的电话号码是八位数,这个数的前四位数字相同,后面四位数字是连续的自然数、全部数字之和恰好等于号码的最后两位数,巧的是,这个号码的后五位数也是连续的自然数.”请你把老师家的电话号码求出来.(提示:求整体,设部分)15.有四个数,其中每三个数之和分别为22,20,17,25,求此四个数.(提示:求部分,设整体)16.把99拆成四个数之和,使得第一个数加上2,第二个数减去2,第三个数乘2,第四个数除以2,所得的结果都相等,求所拆成的四个数.(提示:设特征量)17.小华在日历上任意找出一个数,发现它连同上、下、左、右的共5个数的和为85,请求出小华找的数是当月的几号?七、工程问题工程问题中的基本关系式:工作总量=工作效率×工作时间;各部分工作量之和=工作总量18.一件工作,甲独做需20小时,乙独做需12小时. (1)如果把总工作量看做“1”,甲的工效是____,乙的工效是____,甲、乙合作1小时的工作量是_______.(2)若先由甲独做4小时,剩下由甲、乙合作,还需多少小时完成?(3)若先由甲独做4小时,剩下由甲、乙合作,共需多少小时完成?19.食堂存煤若干吨,原来每天烧煤4吨,用去15吨后,改进设备,耗煤量改为原来的一半,结果多烧了10天,求原存煤量.20.整理一批图书,如果由一个人单独做要花60小时.现先由一部分人用一小时整理,随后增加15人和他们一起又做了两小时,恰好完成整理工作.假设每个人的工作效率相同,那么先安排整理的人员有多少人?21.两支等长粗细不同的蜡烛,细蜡烛4小时燃完,粗蜡烛5小时燃完.某时,天突然起雾,同时点燃这两支蜡烛,雾散去时,一支剩下的长度是另一支的两倍.问点燃多少时间?22.一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完.现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?八、行程问题1.基本公式:路程=速度×时间2.基本类型:相遇问题、追及问题、环形跑道问题、航行问题(飞行)问题.3.航行问题的数量关系:(1)顺水航行的路程=逆水航行的路程;(2)顺水速度=静水速度+水速;逆水速度=静水速度-水速飞行问题基本等量关系:顺风速度=无风速度+风速;逆风速度=无风速度-风速23.A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发.(1)若两车相向而行,请问B车行了多长时间后与A车相遇?(2)若两车同向而行(B车在A车前面),请问B车行了多长时间后被A车追上?(3)若两车相向而行,请问B车行了多长时间后两车相距20千米?24.甲、乙两人在400米长的环形跑道上练习跑步,甲每秒跑5米,乙每秒跑3米. (1)若两人同时同地同向出发,多长时间两人首次相遇?(2)若两人同时同地反向出发,多长时间两人首次相遇?25.一小船由A港口顺流航行到B港口需行驶6小时,由B港口到A港口需行驶8小时,一天,小船由A港口出发顺流到达B港口时发现一救生圈中途落水,立即返回,1小时后找到救生圈,若水流速度是2千米/时.(1)小船在静水中的速度是多少?(2)救生圈是何时掉入水中的?26.一架飞机飞行两城之间,顺风时需要5小时30分钟,逆风时需要6小时,已知风速为每小时24公里,求两城之间的距离?27.一铁路桥长1200米,现在有一列火车从桥上匀速通过,测得火车从上桥到完全过桥共用时50秒,整列火车完全在桥上的时间是30秒,求火车的长度和速度.28.一列客车和一列货车在平行的轨道上同向匀速行驶,客车在货车的后方,客车的长是200米,货车的长是280米,客车的速度与货车的速度比是5 :3,客车赶上货车的交叉时间是1分钟,求各车的速度;若两车相向行驶,它们的交叉时间是多少分钟?九、销售利润问题基本关系式:商品利润= 商品售价—商品进价 %100⨯=进价利润利润率 10打折数标价商品售价⨯= 利润率)(商品进价商品售价+⨯=1 29. 小华的妈妈为爸爸买了一件衣服和一条裤子,共用了306元.其中衣服按标价打七折,裤子按标价打八折,衣服的标价为300元,则裤子的标价为 元.30.某商品的标价是3000元,进价是2000元,需打_____折才能使利润率为5%.31.某商品因换季准备打折出售,如果按定价的七五折出售将赔25元;而按定价的九折出售将赚20元,求这种商品的定价是多少?32.某商店在某一时间以每件60元的价格卖出A 、B 两类衣服,其中A 类一件盈利25%,B 类一件亏损25%.(1)A 、B 两类衣服每一件的成本价分别是多少元?(2)A 、B 各卖一件总收入是盈利还是亏损?或是不盈不亏?(3)若A 类衣服每件的标价是66元,商场要打折促销,并要获得10﹪的利润,请计算一下应打几折?(4)现商店准备A 类衣服每件卖60元,B 类每件卖120元.有两种出售方式:方式一,全部9折优惠;方式二,每买4件B 类衣服赠送一件A 类衣服.我校初一22班准备买班服,其中A 类需要15件,B 类需要40件.问怎样购买花钱最少?十、方案设计33. 某县要印制高中招生的录取通知书,有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折优惠收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元价格不变,而制版费900元则六折优惠.回答下列问题:①印刷多少份时,两厂所需费用相等;②如何根据印刷的数量选择比较合算的印刷厂,举例说明;③如果要印刷3000份录取通知书,那么应当选择哪个厂?需要多少费用?34. 某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元;制成酸奶销售,每吨可获利润1200元;制成奶片销售,每吨可获利润2000元,该厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片每天加工1吨,受人员限制,两种加工方式不可同时进行;受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂设计了两种可行方案,方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.你认为选择哪种方案获利较多?为什么?十一、其他问题35. 如右图,宽为50cm的长方形图案由10个大小相同的小长方形拼成.其中一个小长方形的面积为 cm2.36. 某学生在署假期间观察了x天的天气情况,其结果是:①共有7天上午是晴天;②共有5个下午是晴天;③共下了8次雨,在上午或下午;④上午下雨的那天,下午是晴天.则x等于()A.8B.9C.10D.1137.参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1000元.那么此人住院的医疗费是()38. 旅游车上乘坐着日本、美国、法国三个国家的游客,现知道日本游客有18人,法国游客有9人;成年男游客中,美国5人,法国3人;成年女游客中,法国3人,日本5人;男孩子中,日本3人,美国2人,法国2人;女孩子中,美国2人,法国1人.还知道成年女游客比成年男游客少2人,而男孩和女孩一样多,则美国游客有人.39. 张老师在出版社出版了一本书,并从出版社一次性取得稿酬收入若干元,按个人所得税法的规定,稿酬扣除800元后的余额,按照14%的比例征收个人所得税,张老师应缴个人所得税210元,则张老师领取税后稿酬元.40.全国足球联赛赛完8轮,胜一场得3分,平一场得1分,负一场得0分.到目前为止,上海国际队踢平的场数是所负场数的2倍,共得17分,则该队胜了________场.41.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:档次每户每月用电数(度)执行电价(元/度)第一档小于等于200 0.55第二档大于200小于400 0.6第三档大于等于400 0.85例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?42.某校初2021届1到4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:班级1班2班3班4班实际购数量(本)3321实际购数量与计划购数量的差值(本)+12﹣8﹣9(1)完成表格;(2)根据记录的数据可知4个班实际一共购书_________本?(3)书店给出两种优惠方案,方案甲:一次购买不少于15本,其中2本书免费;乙方案:如果一次性购书不少于20本,总价9折优惠,假设每本书售价为30元,请你计算初2021届1班实际购书最少花费多少元?43.【新知理解】如图①,点C在线段AB上,图中的三条线段AB、AC和BC.若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.(1)填空:线段的中点这条线段的巧点;(填“是”或“不是”或“不确定是”)【问题解决】(2)如图②,点A和B在数轴上表示的数分别是﹣20和40,点C是线段AB的巧点,求点C在数轴上表示的数.【应用拓展】(3)在(2)的条件下,动点P从点A发,以每秒2个单位长度的速度沿AB向点B匀速运动;动点Q从点B出发,以每秒4个单位长度的速度沿BA向点A匀速运动.点P、Q同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为t秒,当t为何值时,A、P、Q三点中,其中一点恰好是另外两点为端点的线段的巧点?并求出此时巧点在数轴上表示的数.(直接写出答案).。
一元一次方程公式大全

一元一次方程公式大全一元一次方程是初中数学学习中的重要内容,也是数学建模和解决实际问题的基础。
在学习一元一次方程时,我们需要熟练掌握一元一次方程的基本概念、解法和应用。
本文将为大家详细介绍一元一次方程的相关知识,包括一元一次方程的定义、一元一次方程的解法、一元一次方程的应用以及一元一次方程的实例分析,希望能够帮助大家更好地理解和掌握这一部分内容。
一、一元一次方程的定义。
一元一次方程是指未知数只有一个,且未知数的最高次数为一的方程。
一元一次方程的一般形式为ax+b=0,其中a和b是已知数,a≠0,x是未知数。
在解一元一次方程时,我们的目标是找到未知数x的值,使得方程成立。
二、一元一次方程的解法。
解一元一次方程的常用方法有,等式性质法、加减消去法、乘除消去法、代入法等。
下面我们分别来介绍这些解法的具体步骤。
1. 等式性质法,根据等式两边相等的性质,可以对方程进行等式性质变形,最终得到方程的解。
2. 加减消去法,通过加减消去,将方程中的一些项相互抵消,从而简化方程,最终求得方程的解。
3. 乘除消去法,通过乘除消去,可以将方程中的一些项进行消去,从而简化方程,最终求得方程的解。
4. 代入法,将已知的数代入方程中,求解未知数的值,从而得到方程的解。
三、一元一次方程的应用。
一元一次方程在日常生活中有着广泛的应用,例如,小明买了若干本书,每本书的价格是10元,他一共花了60元,那么小明买了几本书?这个问题可以用一元一次方程来表示和解决。
又如,某商品原价100元,现在打8折出售,打折后的价格是多少?这个问题也可以用一元一次方程来表示和解决。
四、一元一次方程的实例分析。
现在我们通过几个实例来分析一元一次方程的具体应用。
例1,某数的3倍加上5等于20,求这个数。
解,设这个数为x,根据题意可以列出方程3x+5=20,然后通过等式性质变形,得到3x=15,最终求得x=5。
所以这个数是5。
例2,某数的一半加上3等于7,求这个数。
第15课时列方程(组)解应用题

2、反之,若为两次降低,则
平均降低率公式为 a(1-x)2=b
练习:
1、某种药品,原来每盒售价96元,由于两 次降价,现在每盒售价54元,平均每次降 价百分之几?
2、某人想把10000元钱存入银行,存两 年。一年期定期年利率6%,两年期定期 年利率为6.2%.哪一种存款更划算? 注:一年期存两年与两年期存款的本息和 的计算公式是不一样的。前者是m(1+a1)2, 后者是m(1+2a2).请同学们注意!
解得, x1=0.2 x2=-2.2 (不合题意), 答:平均每个月增长的百分率是20%.
例1.某钢铁厂去年1月某种钢的产量为5000 吨,3月上升到7200吨,这两个月平均每个月 增长的百分率是多少?
分析:则2月份比一月份增产__5_0_0_0_x__ 吨. 2月份的产量是 ____5_0_0_0_(1_+__x_) ___吨 3月份比2月份增产__5_0_0_0_(_1_+_x_)_x_ 吨 3月份的产量是 ___5_0_00_(_1_+_x_)2__ 吨
a(1x)2 b
数字类型应用题
例1、两个连续奇数的积是323,求这两个数。
解:设较小的一个奇数为x,则另一个为
x+2, 根据题意得:x(x+2)=323
整理后得:x2+2x-323=0
解这个方程得:x1=17 x2=-19 由x1=17 得:x+2=19 由 x2=-19 得:x+2=-17 答:这两个数奇数是17,19,或者-19,-17
40cm
25cm
图1
图2
想 如图1有一张长40cm,宽25cm的长方 形硬纸片,裁去角上四个小正方形之后,
五年级上册(秋季班)-14列方程解决问题-教师版-徐汇

列方程解决问题【教学目标】1.能根据题意正确寻找等量关系;2.能用方程解答简单的实际问题。
【教学重点】1.正确寻找题中的等量关系;2.列方程解应用题的步骤。
【教学难点】寻找题中的等量关系列出方程。
【知识点精讲】知识点1:正确寻找题中的等量关系(1)列方程解应用题的关键是寻找到题目中数量之间的相等关系,根据等量关系列出方程求出解。
一般情况下,题目中会有一句话反映出数量之间的相等关系,只要找到这句话,也就找到了等量关系。
(2)常用的等量关系:①行程问题公式: 路程=速度×时间; 路程÷时间=速度; 路程÷速度=时间相遇问题: 速度和×相遇时间=相遇路程追及问题: 速度差×追及时间=追及路程流水问题: 顺水速度=船速+水速逆水速度=船速-水速顺水行程=(船速+水速)×顺水时间逆水行程=(船速-水速)×逆水时间②平均数问题公式:总数量÷总份数=平均数工程问题公式:工效×工时=工作总量工作总量÷工作时间=工效效率工作总量÷工作效率=工作时间④面积问题公式:长方形面积=长×宽正方形面积=边长×边长知识点2:列方程解应用题的步骤:(1)找出一个合适的未知数,用字母表示。
(2)找出应用题中的等量关系。
(3)根据等量关系列出方程。
(4)解方程并检验、验算,写出答案。
例1、说出下列各题中的等量关系。
(1)篮球和足球共40只。
篮球只数+足球只数=40(2)红花的朵数是黄花的4倍。
红花朵数=黄花朵数×4(3)每只足球的价格比每根跳绳的价格的4倍还多5元。
每只足球的价格=每根跳绳的价格×4+5例2、看图列方程。
(1)x人唱歌50人跳舞150人唱歌跳舞方程是: x+50=150801本故事书借走了18本还剩下x本方程是: 18+x=801(3)方程是: 4x=128(4)方程是: x-10=30例3、列方程解决问题(1) 停车场停放着290辆公共汽车,开出一部分后,还剩下143辆,开出了几辆公共汽车?解:设开出了x 辆公共汽车。
七上数学列方程解应用题公式

七上数学列方程解应用题公式
七年级上册数学列方程解应用题公式主要包括以下几种:
1. 追及问题:甲、乙两物体在同一直线上运动,如果甲、乙做匀速直线运动,那么追及问题的等量关系为:甲的路程+乙的路程=甲与乙的初始距离。
2. 相遇问题:甲、乙两物体在某地相向而行,经过一段时间它们相遇了。
相遇问题的等量关系是:甲的路程+乙的路程=两地的距离。
3. 航行问题:航行问题可以分为顺水航行和逆水航行两种情况。
在顺水航行中,船的速度等于船在静水中的速度加上水流的速度;在逆水航行中,船的速度等于船在静水中的速度减去水流的速度。
4. 劳力调配问题:这类问题一般涉及三个等量关系,设工作总量为“1”,
若完成某项工作的人数增加,则工作时间减少;若完成某项工作的人数减少,则工作时间增加。
5. 比例问题:若甲、乙两数的比是 k,那么我们可以得到以下等量关系:甲/乙=k,或者甲=k×乙。
6. 工程问题:在工程问题中,工作量、工作时间和工作效率之间的关系非常重要。
一般来说,工作量=工作时间×工作效率。
这些是七年级上册数学列方程解应用题的主要公式和等量关系。
需要注意的是,这些公式和等量关系都是根据实际问题的情况而定的,具体问题需要具体分析。
在解题过程中,还需要注意单位的统一和换算。
八年级(下)数学 同步讲义 列方程解应用题(解析版)
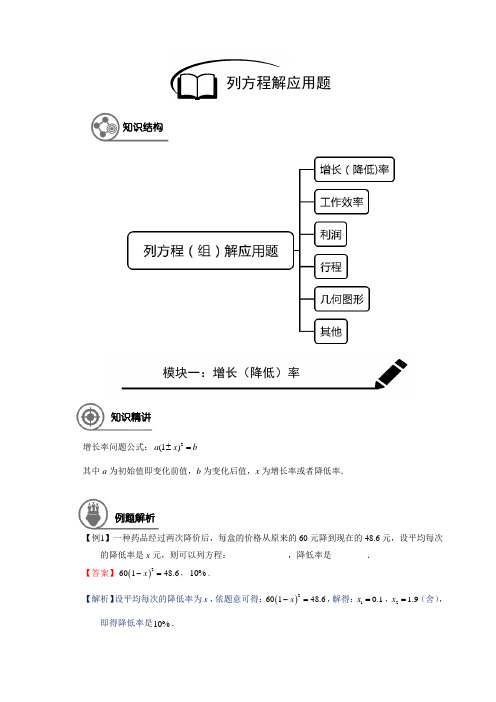
增长率问题公式:2(1)a x b ±=其中a 为初始值即变化前值,b 为变化后值,x 为增长率或者降低率.【例1】一种药品经过两次降价后,每盒的价格从原来的60元降到现在的48.6元,设平均每次的降低率是x 元,则可以列方程:_____________,降低率是________. 【答案】()260148.6x -=,10%.【解析】设平均每次的降低率为x ,依题意可得:()260148.6x -=,解得:10.1x =,2 1.9x =(舍),即得降低率是10%.列方程解应用题知识结构例题解析知识精讲模块一:增长(降低)率【总结】考查降低(增长)率问题的应用.【例2】某公司2014年各项经营收入中,经营电脑配件收入为500万元,占全部经营总收入的13,该公司预计2016年经营总收入达到2160万元,求从2014年到2016年每年经营总收入的平均年增长率.【答案】()2150012160x +=,20%.【解析】设从2014年到2016年每年经营总收入的平均年增长率为x ,依题意可得: ()2150012160x +=,解得:10.2x =,2 2.2x =-(舍),即得平均增长率是20%. 【总结】考查降低(增长)率问题的应用.【例3】一辆汽车,新车的购买价是20万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二、三年的年折旧率相同.已知在第三年年末,这辆车折旧后的价值是 11.56万元,求这辆车第二、三年的折旧率. 【答案】15%.【解析】设这辆车第二、三年的折旧率为x ,依题意可得:()()220120%111.56x --=, 解得:10.15x =,2 1.85x =(舍),即得这辆车第二、三年的折旧率是15%. 【总结】考查降低(增长)率问题的应用.【例4】某工厂甲、乙两个车间在6月份共生产231台仪器,每个车间都比上月增产,且增产的百分率相同,已知甲车间上个月月产量不少于100台,6月份比上个月增产5台,乙车间上月生产120台.问:甲车间上月生产多少台?6月份每个车间增产的百分率是多少? 【答案】甲车间上月生产100台,增产百分率是5% 【解析】设甲车间上月生产x 台,则6月份生产()5x +台,依题意可得:551201231x x ⎛⎫+++= ⎪⎝⎭,整理得21066000x x -+=,解得:1100x =,26x =(舍),即得甲车间上月生产100台,每个车间增产百分率为5100%5%100⨯=. 【总结】考查降低(增长)率问题的应用.【例5】某农户种植花生,原来种植的亩产量为200千克,出油率为50%,现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量增长率的12,求新产品花生亩产量的增长率? 【答案】20%.【解析】设新产品花生亩产量的增长率x ,则出油率增长率为12x ,依题意可得:()1200150%11322x x ⎛⎫+⨯+= ⎪⎝⎭,整理得22575160x x +-=,解得:10.2x =,2 3.2x =-(舍),即得新产品花生亩产量增长率是20%. 【总结】考查降低(增长)率问题的应用.【例6】某工厂今年头三个月生产甲、乙两种产品,已知甲种产品1月份生产16件,以后每月比上月增长相同的百分率;乙种产品每月比上月增产10件.又知2月份的甲、乙两种产品的产量之比为2:3,且3月份的两种产品的产量之和为65件,求甲种产品每月的增长率和乙种产品1月份的产量.【答案】甲产品每月产量增长率是25%,乙产品1月份的产量为20件.【解析】设甲种产品每月的增长率为x ,则甲2月份的产量为()161x +,3月份的产量为()2161x +,则乙3月份产量为()265161x -+,2月份的产量为()26516110x -+-,依题意可得:()()2161:65161102:3x x ⎡⎤+-+-=⎣⎦,整理得21656150x x +-=,解得:10.25x =,2 3.75x =-(舍),即得甲产品每月产量增长率是25%, 乙产品1月份的产量为()26516125%101020-⨯+--=件. 【总结】考查降低(增长)率问题的应用,注意各个月份产量的表示.工作效率问题:工作总量=工作效率⨯工作时间; 假设工作总量是1,则工作效率是1工作时间.【例7】(1)一项工程甲单独做需要a 天完成,乙单独做需要b 天完成,则甲乙合作需要_____天完成;(2)甲、乙两个工程队合作修筑一条通道,已知甲工程队比乙工程队每天多修5米,甲工程队修筑80米所用的时间与乙工程队修筑70米所用的时间相同,那么甲工程队每天修________米,如果设甲工程队每天修x 米,则可列出方程__________.【答案】(1)ab a b +;(2)40,80705x x =-.【解析】(1)设工程量为1,则甲的工作效率为1a ,乙的工作效率为1b, 合作完成需要的天数为111aba ba b=++; (2)依题意可得80705x x =-,解得:40x =,经检验40x =是原方程的解,且符合题意, 故甲工程队每天修40米.【总结】考查工程问题和相应工作效率的表示,注意分式方程解完要检验.例题解析知识精讲模块二:工作效率【例8】某服装厂准备加工300套演出服,在加工了60套后,采用了新技术,使每天的工作效率是原来的2倍,结果共用了9天完成任务,求该厂原来每天加工多少套演出服. 【答案】20【解析】设该厂原来每天加工x 套演出服,依题意可得:603006092x x-+=, 解得:20x =,经检验20x =是原方程的解,且符合题意, 即该厂原来每天加工20套演出服.【总结】考查工程问题一个量作设一个量列式,注意分式方程要检验.【例9】汛期到来之前,某施工队承接了一段长300米的河提加固任务,加固80米后,接到防汛指挥部的指示,要求加快施工速度,为此施工队在保证质量的前提下,每天多加工15米,这样一共用了6天完成了任务,问接到指示后,施工队每天加固河堤多少米. 【答案】55.【解析】设指示后施工队每天加固河堤x 米,则指示前每天加工()15x -米,依题意可得:8030080615x x-+=-,解得:55x =, 经检验55x =是原方程的解,且符合题意,故接到指示后施工队每天加固河堤55米. 【总结】考查工程问题一个量作设一个量列式,注意分式方程要检验.【例10】有一项工程,甲单独做比甲、乙合作的天数多5天,如果甲、乙先合作4天,再由乙单独做3天,才能完成全部工作的一半,问甲、乙单独完成此项工程各需要多少天. 【答案】甲单独完成需要15天,乙单独完成需要30天.【解析】设甲单独完成需要x 天,则甲乙合作完成需要()5x -天,乙单独完成需要2151155x x x x -=--天,依题意可得215143552x x x ⋅+⋅=--,整理得213300x x -+=,解得:115x =,22x =-(舍),经检验均是原方程的解,但22x =-不符合题意,舍去,即甲单独完成需要15天,乙单独完成需要215515305-⨯=天. 【总结】考查工程问题一个量作设一个量列式,注意分式方程要检验.【例11】某工厂甲、乙两个车间各生产300个零件,按原来的工效,乙车间需要比甲车间多用一天的时间完成,现在甲、乙两车间都提高了工效,其中甲车间工效提高了20%,而乙车间提高了一倍,结果生产同样的300个零件,乙车间比甲车间少用了2天就可完成,问甲、乙两车间原来生产300个零件各需要多少天?【答案】甲车间原来生产300个零件需要7.5天,乙车间需要8.5天. 【解析】设甲原来需要x 天,则乙原来需要()1x +天,依题意可得:12120%2x x +-=+,解得:7.5x =,即甲车间原来生产300个零件需要7.5天,乙车间需要8.5天. 【总结】考查工程问题一个量作设一个量列式.【例12】已知甲、乙、丙三人做某项工作,甲独做所需要的时间是乙、丙两人合做这件工作的a 倍,乙独做需要的时间是甲、丙两人合做这件工作的b 倍,求丙独做所用的时间是甲、乙两人合做此工作的几倍.【答案】21a b ab ++-.【解析】设甲、乙、丙需要的工作时间分别为x ,y ,z ,依题意可得111x a y z=⋅+,111y b x z=⋅+,分别整理可得()111a x ab z +=-,()111b y ab z+=-, 相加得()1121a b x y ab z+++=-,由此得2111a b z ab x y ⎛⎫++=+ ⎪-⎝⎭.【总结】考查工程问题的应用,注意找准字母之间的关系.【例13】一个水池有甲、乙两个进水管,单独开放甲管注满水池比单独开放乙管少用10小时,如果单独开放甲管10个小时后,加入乙管,需要6个小时把水池注满,那么单独开放一个水管,需要多少小时才可以把水池注满?【答案】单独开放甲注水管需要20小时注满水池,单独开放乙注水管需要30小时注满水池.【解析】设甲需要xh ,则乙需要()10x h +,依题意可得10116110x x x ⎛⎫++= ⎪+⎝⎭,整理得2121600x x --=,解得:120x =,28x =-, 经检验均是原方程的解,但28x =-不符合题意,舍去,故单独开放甲注水管需要20小时注满水池,单独开放乙注水管需要30小时注满水池. 【总结】考查工程问题的应用,合作加独做合为单位“1”,注意分式方程要检验..单件利润=售价-成本; 总利润=单件利润⨯销售件数.【例14】某各个体户以2元/kg 的价格购进一种食品,以3元/kg 的价格出售,每天可售出200kg ,为促销,该个体户决定降价销售,经调查,这种食品每降价0.1元/kg ,每天可多售出40kg ,另外每天房租等固定成本24元,此人想每天盈利200元,应将售价降低为多少元/kg ? 【答案】应将售价降低为2.7元/千克.【解析】设应将售价降低为x 元/kg ,依题意可得:()3220040242000.1x x -⎛⎫-+⋅-= ⎪⎝⎭, 整理得2502753780x x -+=,即()()51410270x x --=,解得:1 2.7x =,2 2.8x =, 因为是促销,即应将售价每千克应降低为2.7元. 【总结】考查利润问题的应用,总利润=单个利润×总销量.例题解析知识精讲模块三:利润【例15】甲、乙两家便利店到批发站采购一批饮料,共25箱,由于两店所处的地理位置不同,因此甲店的销售价格比乙店的销售价格每箱多10元.当两店将所进的饮料全部售完后,甲店的营业额为1000元,比乙店少350元,求甲乙两店各进货多少箱饮料? 【答案】甲店进货10箱饮料,乙店进货15箱饮料. 【解析】设甲店进货x 箱饮料,则乙店进货()25x -箱饮料,依题意可得100010003501025x x+-=-,整理得226025000x x -+=, 解得:110x =,2250x =,经检验均是原方程的解,但2250x =不符合题意,舍去, 故甲店进货10箱饮料,乙店进货15箱饮料. 【总结】考查销售问题,注意对题意的准确理解.【例16】某水果店在水果批发市场用100元购进一批甲种水果,再用100元购进一批乙种水果,已知购进的乙种水果比甲种水果多10千克,乙种水果的批发价比甲种水果的批发价低 0.5元/千克.(1) 求甲乙两种水果各购进了多少千克?(2) 购进水货当天,甲乙两种水果都按照2.8元/千克出售,乙种水果很快售完,而甲种水果先售出35,剩余的按售价打5折出售,这一天的水果买卖是否赚钱?如果赚钱了,赚多少?如果不赚钱,那么赔了多少?【答案】(1)甲种水果购进40千克,乙种水果购进50千克;(2)赚了29.6元【解析】(1)设购进甲种水果x 千克,乙种水果x +10千克,由题意得1001000.510x x -=+,解得:x =40,经检验x =40是原方程的解,且符合题意,故购进甲种水果是40千克,乙种水果是40+10=50千克;(2)利润为:3250(2.82)40(2.8 2.5)40(1.4 2.5)29.6055⨯-+⨯-+⨯-=>,故赚了29.6元.【总结】本题主要考察了利润问题,找出题目中的等量关系再列方程.【例17】某中学库存960套旧课桌椅,准备修理后捐助给贫困山区学校,现在有甲乙两个木工小组都希望承揽这项业务,经协商研究得知:甲小组单独修理这批桌椅比乙小组单独修理要多用20天;乙小组每天比甲小组多修理8套;学校每天需要付甲乙小组修理费分别是80元和120元;(1) 求甲乙两个小组每天各修理课桌椅多少套?(2) 在修理桌椅的过程中,学校委派一名维修工进行质量监控,由学校每天发出10元钱作为生活补贴;现在有三种修理方案:方案一由甲单独修理;方案二由乙单独修理;方案三由甲乙共同修理;选择哪种方案,更省钱?【答案】(1)甲小组每天修理16套旧桌椅,则乙小组每天修理24套旧桌椅;(2)方案三. 【解析】(1)设甲小组每天修理x 套旧桌椅,则乙小组每天修理()8x +套旧桌椅,依题意可得960960208x x -=+,整理得283840x x +-=,解得:116x =,224x =-, 经检验均是原方程的解,但224x =-不符合题意,舍去,即得甲小组每天修理16套旧桌椅,则乙小组每天修理24套旧桌椅; (2)方案一需要的费用为(8010)960165400+⨯÷=元; 方案二需要的费用为(12010)960245200+⨯÷=元;方案三需要的费用为(8012010)960(1624)5040++⨯÷+=元,可知方案三更省钱. 【总结】考查工程问题的应用,注意分式方程要检验.行程问题中三个变量:路程、速度和时间,关系如下: 路程=速度⨯时间可以通过等式的相关计算推导出速度、和时间的相关计算公式.知识精讲模块四:行程【例18】小王从甲地到乙地需要m 分钟,若小李同时从乙地到甲地,则两人经过n 分钟相遇,则小李从乙地到甲地需要_________分钟(用含m 、n 的代数式表示).【答案】mnm n -.【解析】小李需要的分钟数为111mnm nn m=--. 【总结】考查行程问题的应用,注意平均速度的求解.【例19】甲、乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时,二人每小时各走多少米?【答案】甲每小时走6千米,乙每小时走5千米.【解析】设甲每小时走x 千米,则乙每小时走()1x -千米,依题意可得:1515112x x -=-, 整理得2300x x --=,解得:16x =,25x =-(舍), 经检验均是原方程的解,但25x =-不符合题意,故舍去, 所以甲每小时走6千米,乙每小时走5千米. 【总结】考查行程问题的应用,注意分式方程要检验..【例20】已知A 、B 两地相距125km ,甲乙两人同时A 、B 两地出发,相向而行,每走10km 甲比乙快36分钟,经5小时两人相遇,求甲乙两人的速度.【答案】甲的速度为50/3km h ,乙的速度为25/3km h .【解析】设甲的速度为/xkm h ,依题意可得1051251035x x +=+(),整理得232512500x x +-=, 解得:1503x =,225x =-,经检验均是原方程的解,但225x =-不符合题意,故舍去, 所以甲的速度为50/3km h ,乙的速度为1255025/533km h -=. 【总结】考查行程问题的应用,注意分式方程要检验.【例21】甲、乙两人分别从相距27千米的A 、B 两地同时出发,相向而行,3小时相遇,随后两人按照原来的速度继续前进,甲到达B 地比乙到达A 地少用1小时21分钟,求两人的速度.例题解析【答案】甲的速度为5/km h ,乙的速度为4/km h . 【解析】设甲的速度为/xkm h ,乙的速度为/ykm h .依题意可得()32727272720x y y x ⎧+=⎪⎨-=⎪⎩,解得:54x y =⎧⎨=⎩,经检验54x y =⎧⎨=⎩是原方程组的解,且符合题意,故甲的速度为5/km h ,乙的速度为4/km h .【总结】考查行程问题的应用,,注意分式方程组要检验..(1) 关于线段长度类问题,主要列无理方程求解; (2) 与面积相关的问题; (3) 图形中的动点问题.【例22】函数y =2x 图像上一点P 到点A (5,0)的距离是5,求点P 的坐标.【答案】()124P ,,()200P ,. 【解析】设()2P x x ,,依题意可得()()22525x x -+=,解得:12x =,20x =,经检验12x =,20x =均是原方程的解,故得()124P ,或()200P ,. 【总结】考查点坐标的求取,根据点所在的直线设点坐标,注意无理方程要验根.【例23】已知直角三角形的两条直角边的差是2cm ,它的面积是12cm 2,求这两条直角边的长. 【答案】两直角边长分别为6cm 和4cm 、【解析】设较长一边为xcm ,则另一直角边为()2x cm -,依题意可得()12122x x -=,整理得22240x x --=,解得:16x =,24x =-(舍),例题解析知识精讲模块五:几何图形即得一边长为6cm ,另一边长为624cm -=. 【总结】考查根据面积的相应表示进行列方程求解.【例24】将一条长为20cm 的铁丝剪成两段,并以每一段铁丝的长度围成一个正方形,两个正方形的面积之和可能等于12cm 2吗?若能,求出两段铁丝的长度,若不能,请说明理由. 【答案】不能.【解析】设一个正方形边长为xcm ,则另一个边长为()5x cm -,依题意可得()512x x -=, 方程无解,即不可能.【总结】考查面积问题的应用,一边作设,一边相应表示出来列方程求解即可.【例25】如图,笔直公路上A 、B 两点相距10千米,C 、D 为两居民区,DA ⊥AB 于A ,CB ⊥AB 于B ,已知DA =6千米,CB =8千米,现要在公路AB 段上建一超市E ,使C 、D 两居民区到E 的距离相等,则超市E 应建在离A 处多远处. 【答案】离A 处处【解析】设AE xkm =,则10BE x =-,6.4x =, 经检验 6.4x =是原方程的解, 故超市应建在离A 处6.4km 处.【总结】考查根据勾股定理确定相应长度表示进行求解.ABCDE【例26】有一块长x 米,宽120米(x >120)的长方形,投资方计划将它分成甲乙丙三部分,其中甲和乙为正方形,甲为住宅区,乙为商场,丙为公司,若已知丙地的面积为3200米,求x 的值. 【答案】160或200.【解析】依题意可得()()1201201203200x x ---=⎡⎤⎣⎦,整理得2360320000x x -+=,解得:1160x =,2200x =,即x 的值为160或200. 【总结】考查根据面积的相应表示进行列方程求解.【例27】有一块长为80米,宽为50米的长方形绿地,其中有三条直路(图中的阴影部分,道路的一边AD 与长方形绿地的一边平行,且道路的出入口AB 、CD 、EF 、KI 、GH 、IJ 的长度都相等,其余部分种植绿化).已知道路的面积为352平方米,求道路出入口的边的长度【答案】2m【解析】设边的长度为xm ,依题意可得2802502352x x x +⋅-=,整理得2901760x x -+=,解得:12x =,288x =(舍), 即得路宽为2m .【总结】考查根据面积的相应表示进行列方程求解.【例28】等腰Rt △ABC 中,8 cm AB BC ==,动点P 从点A 出发,沿AB 向点B 移动.通过点P引平行于BC 、AC 的直线与AC 、BC 分别交于点R 、Q ,问:AP 等于多少厘米时,平行四边形PQCR 的面积等于16cm 2. 【答案】4cm【解析】设AP xcm =,则8BP x =-,由题意可知APR ∆和PBQ ∆ 均为等腰直角三角形,依题意可得()816x x -=, 解得:124x x ==,即AP 长为4cm . 【总结】考查动点问题的应用求解.【例29】m 、n 为两条互相垂直的笔直公路,工厂A 在公路n 上,距公路m 为1千米,B 与工厂A 在公路m 的同侧,且距公路m 为2千米,距公路n 为3千米.现要在公路m 上建造一个ABC PQRA B甲乙丙n m车站P ,使它与A 、B 的距离之和为P 的位置.【答案】点P 在两道路交点上下方2km 或211km 处.【解析】以公路n 、m 分别为x 、y 轴建立平面直角坐标系,依题意得()10A ,,()123B ,或()23B -,,设()0P y ,,=, 整理得2112440y y -+=或2112440y y ++=, 解得:12y =,2211y =,32y =-,4211y =-,经检验均是原方程的解,但32y =-,4211y =-不符合题意,故舍去, 所以点P 在两道路交点上下方2km 或211km 处. 【总结】考查根据题目条件建立平面直角坐标系进行点坐标的确定进而确定相应位置.【例30】已知A (0,-1),B (0,4),点P 在坐标轴上,且P A +PB =P 的坐标.【答案】()120P ,,()220P -,,30P ⎛ ⎝⎭,40P ⎛ ⎝⎭.【解析】当P 在x 轴上时,设()0P x ,= 解得:12x =,22x =-,即得()120P ,,()220P -,;当P 在y 轴上时,设()0P x ,,依题意可得41x x -++=解得:1x 2x =30P ⎛ ⎝⎭,40P ⎛ ⎝⎭. 【总结】考查根据题目条件进行相应作设求解,注意分类讨论.【例31】有一个非零数,它与4的和的正平方根再加上2后恰好等于它本身,求这个数. 【答案】5【解析】设这个数为x ,依题意可得42x x ++=,解得:15x =,20x =(舍),即这个数是5. 【总结】考查数位问题根据题目条件作设求解.【例32】有一个两位数,如果个位上的数与十位上的数的和是5,并且个位上的数的平方比十位上的数大1,求这个两位数. 【答案】32.【解析】设十位数为x ,则个位数为5x -,依题意可得()251x x --=,整理得211240x x -+=,解得:13x =,28x =(舍), 则这个数个位上是2,这个数是32. 【总结】考查数位问题根据题目条件作设求解.【例33】某剧场有座位800个,每排的座位数一样多,在每排增加5个座位,并增加2排后就有座位1020个,问原来座位多少排?原每排多少个座位.【答案】这个剧院有10排,每排有80个座位;或这个剧院有32排,每排有25个座位.【解析】设原来有x 排,则每排有800x 个座位,依题意可得()800251020x x ⎛⎫++=⎪⎝⎭, 整理得2423200x x -+=,解得:110x =,232x =,经检验均是方程的解且符合题意. 即这个剧院有10排,每排有8008010=个座位; 或这个剧院有32排,每排有8002532=个座位. 【总结】考查根据题目条件进行相应方程求解列式的应用,注意两种解都成立,另分式方程解完别忘记检验.【例34】植树节前,园林局把植数1600棵的任务交给了一个小队,小队被分成若干个组,计划每个组植树的棵树相同,但后来又4个组另有任务不能参加,所以其他组就要比原计划多例题解析模块六:其他植树20棵,每个小分队共分成了多少个组. 【答案】20【解析】设共分成了x 个小组,依题意可得16001600204x x-=-, 整理得243200x x --=,解得:120x =,216x =-(舍),即共分成了20个小组. 【总结】考查工程问题的应用,解完别忘记检验.【例35】学校甲、乙、丙三个摄影兴趣小组进行了一次摄影作品交流活动,活动时,每位同学向不同组的每个组员送一张摄影作品,这样互相交流的摄影作品共310张,已知甲组人数是丙组人数的2倍,乙组比甲组少3人,这三个摄影小组各有多少人? 【答案】甲组有10人,乙组有7人,丙组有5人.【解析】设丙组有x 人,则甲组有2x 人,乙组有()23x -人,依题意可得()()()()223232232310x x x x x x x x x +-+-++-+=,整理得2891550x x --=,即()()58310x x -+=,解得:15x =,2318x =-(舍), 即丙组有5人,甲组有10人,乙组有7人. 【总结】考查握手问题的应用.【例36】小强放学回家后,向爸爸、妈妈询问火箭队与雄鹿队的当天的篮球比赛的结果,妈妈说:“本场比赛火箭队的姚明比雄鹿的易建联多得了12分”.爸爸说:“如果把姚明的分数乘以易建联的得分再加上36分,恰好等于他们两人的得分之和的15倍,并且,如果姚明的得分不超过30分,则雄鹿队胜,否则,火箭队胜”,请你帮小强算一下,这场比赛,究竟是哪个队胜了?姚明和易建联各得了多少分?【答案】姚明得分为36分,易建联得分为24分,火箭队获胜. 【解析】设姚明得分为x 分,则易建联得分为()12x -分,依题意可得()()12361512x x x x -+=+-,整理得242+2160x x -=, 解得:136x =,26x =(舍),即姚明得分为36分,则易建联得分为24分,可知火箭队获胜.【总结】考查根据题意列方程进行方程的求解.【习题1】某公司1996年出口创收135万元,1997年、1998年每年都比上一年增加a%,那么1998年这个公司出口创收_________元.【答案】()21351%a+.【解析】考查增长率问题的应用.【习题2】甲、乙两个工程队合修一条路要6天完成,如果各队单独修路,则甲队比乙队少用5天,设甲、乙两队单独修路所需天数分别为x天和y天,则可列方程组为()A.65x yx y+=⎧⎨=-⎩B.65x yx y+=⎧⎨=+⎩C.11165x yx y⎧+=⎪⎨⎪=-⎩D.11165x yx y⎧+=⎪⎨⎪=+⎩【答案】C【解析】考查工程问题的应用.随堂检测【习题3】 已知点A (12,2),B (3,-1),在x 轴上找一点P ,使P A =2PB .【答案】()160P ,,()260P -,【解析】设()0P x ,=,整理得236x =,解得:16x =,26x =-,即得()160P ,或()260P -,. 【总结】考查满足一定条件的点坐标求取的应用.【习题4】 甲、乙两组工人合做某项工作,10天以后,因甲组另有任务,乙组再单独做2天才完成,如果单独完成这项工作,甲组比乙组可以快4天,求各组单独完成这项工作所需要的天数.【答案】甲单独做需要20天,则乙单独做需要24天. 【解析】设甲单独做需要x 天,则乙单独做需要()4x +天,依题意可得111102144x x x ⎛⎫++⋅= ⎪++⎝⎭,整理得218400x x --=, 解得:120x =,22x =-,经检验均是原方程的解,但22x =-不符合题意,故舍去. 即甲单独做需要20天,则乙单独做需要20424+=天. 【总结】考查工程问题的应用,注意分式方程解完要检验.【习题5】 有一面积为150平方米的长方形饲养场,饲养场一边靠墙(墙长18米),另三边用竹篱笆围成,如果竹篱笆的长为35米,求饲养场的长和宽. 【答案】饲养场长为15m ,宽为10m .【解析】设饲养场长为xm ,依题意可得351502xx -⋅=,整理得2353000x x -+=,解得:115x =,220x =(舍), 即饲养场长为15m ,宽为10m . 【总结】考查面积问题的应用.【习题6】 修建360米长的一段高速公路,甲工程队单独修建比乙工程队多用10天,甲工程队每天比乙工程队少修建6米.甲工程队每天修建的费用为2万元,乙工程队每天修建的费用为3.2万元.(1)求甲、乙两个工程队每天各修建多少米;(2)为在35天内完成修建任务应请哪个工程队修建这段高速公路才能在按时完成任务的前提下所花费用较少?并说明理由【答案】(1)甲每天修12m ,则乙每天修18m ;(2)甲. 【解析】(1)设甲每天修xm ,则乙每天修()6x m +,依题意可得360360106x x -=+,整理得262160x x +-=, 解得:112x =,218x =-(舍), 即甲每天修12m ,则乙每天修18m ;(2)甲需要30天,乙需要20天,所以在35天内都可以完成.甲所需的费用为30260⨯=万元,乙所需的费用为20 3.264⨯=万元,6064<,所以选择甲. 【总结】考查工程问题的应用.【习题7】 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛. 【答案】8【解析】设应邀请需要x 个队参赛, 依题意可得()1472x x -=⨯,整理得2560x x --=,解得:18x =,27x =-(舍), 即应邀请6个队参赛.【总结】考查比赛问题,注意赛制是单循环还是双循环.【习题8】 初二(1)班班委会主动为班级上一位生病住院的同学筹集部分医药费,计划筹集600元,由全体班委同学分担,后来又6位同学知道消息后也自愿参加了捐助和班委同学一起分担,因此每个班委的同学比原来少分担了50元,问:该班委有几个人?按照原计划每个班委平均分摊多少元.【答案】班委有6个人,原计划每个班委分摊100元【解析】设班委有x 个人, 依题意可得600600506x x -=+,整理得26720x x +-=,解得:16x =,212x =-, 经检验均是原方程的解,但212x =-不符合题意,故舍去.即班委有6个人,原计划每个班委分摊6001006=元. 【总结】考查列方程解应用题的应用,注意分式方程解完要检验.【习题9】 制造一种产品,原来每件的成本是500元,销售价是625元,经市场预测,该产品销售价第一个月将降低20%,第二个月将比第一个月提高6%,为了使两个月后的原销售利润不变,该产品的成本价平均每月应降低多少?【答案】10%【解析】设成本价平均每月降低x ,依题意可得:()()()2625120%16%5001625500x -+--=-,解得:10.1x =,2 1.9x =(舍),即成本价平均每月降低10%.【总结】考查利润问题的应用,根据题目条件找到等量关系.【习题10】 一汽艇用一定速度驶完一段路程,若汽艇每小时少走8千米,则走完全程要多用4小时,若汽艇每小时多走8千米,则走完全程可少用2小时,试求这段路的长度以及汽艇原来的速度.【答案】这段路长192km ,汽艇原来速度为24/km h .【解析】设这段路长为xkm ,汽艇原来的速度为/ykm h ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列方程解应用题的常用公式:(1)行程问题:距离=速度·时间时间距离速度= 速度距离时间=;(2)工程问题:工作量=工效·工时工时工作量工效= 工效工作量工时=;(3)比率问题:部分=全体·比率全体部分比率= 比率部分全体=;(4)顺逆流问题:顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;(5)商品价格问题:售价=定价·折·101 ,利润=售价-成本,%100×−=成本成本售价利润率;(6)周长、面积、体积问题:C圆=2πR,S圆=πR2,C长方形=2(a+b),S长方形=ab,C正方形=4a,S正方形=a2,S环形=π(R2-r2),V长方体=abc ,V正方体=a3,V圆柱=πR2h ,V圆锥=31πR2h方程和方程组(一)基本概念方程:含有未知数的等式. 方程的解:使方程左右两边相等的未知数的值. 根据方程的解的定义,要判断一个数是不是方程的解,可将这个数分别代入方程左右两边进行计算,如果左右两边相等,那么这个数就是方程的解.(如果要求把检验的过程写出来,同学们应注意格式)解方程:求方程的解的过程. 一元一次方程:含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1的方程. 二元一次方程:含有两个未知数,并且未知项的次数都是1的整式方程. 二元一次方程组:两个二元一次方程合在一起构成的方程组. 二元一次方程组的解:使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值. (二)基本方法方程的两种基本变形:⑴方程两边都加上或减去同一个数或同一个整式,方程的解不变. ⑵方程两边都乘以或都除以同一个不为零的数,方程的解不变. 解一元一次方程的一般步骤和方法及注意事项:变形名称具体做法注意事项去分母在方程两边都乘以各分母的最小公倍数 1.不要漏乘2.分子不是一个整体,去分母后应加上括号去括号先去小括号,再去中括号,最后去大括号不要漏乘括号里的项不要弄错符号移项把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(记住移项要变号)移项要变号不要丢项合并同类项把方程化成ax=b(a≠0)形式字母及字母的指数不变系数化成1 在方程两边都除以未知数的系数a,得到方程的解不要把分子、分母搞颠到解二元一次方程组:⑴解二元一次方程组的基本思想是:消元⑵解二元一次方程组消元时,常用的两种方法是:代入消元法和加减消元法. 即:二元一次方程组一元一次方程代入消元法的思路是:选择一个系数简单的方程变形,用一个未知数的代数式表示另一个未知数,然后代入另一个方程通过消去一个未知数,从而进行求解. 加减消元法的思路是:使两个方程中对应的同类项系数变成相等或(互为相反数),然后把两个方程相减或(相加),通过消去一个未知数,从而进行求解. (三)方程和方程组的应用 1.方程和方程组的应用主要体现在两个方面:⑴解决一些纯数学的简单问题. ⑵解决实际问题(即列方程或方程组解应用题).其一般步骤主要是:⑴理解题意(审题)⑵把问题转化为方程或方程组(即建立方程或方程组的数学模型)⑶解方程或方程组⑷检验并作答即:问题方程(组)解答 2.解决实际问题的分析和抽象通常包括:⑴设元(用字母表示适当的未知数)⑵找出问题所给出的数量的相等关系⑶分析题意中的数量关系,列出相等关系需要的代数式. 上述过程,应当注意的是:设元有直接设元和简接设元,恰当的设元,会给建立方程(组)带来方便。
分析相等关系以及数量关系时,可借助一些方法比如“列表法”、“图示法”等帮助分析。
另外在实际解决问题时,上面三项的顺序也并非固定的。
3.解实际问题的常见题型及数量关系:⑴行程问题:路程=速度×时间⑵工程问题:工作总量=工作效率×工作时间⑶浓度问题:溶质=溶液×浓度⑷利率问题:本息和=本金+利息,利息=本金×利率×期数⑸利润问题:利润=成本×利润率,利润=售价-成本⑹价格问题:总价=单价×数量⑺水流问题:顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度此外还有:等积变形问题、数字问题、比例问题、调配问题、与几何图形相关的问题、…等。
应当注意的是:我们列出这些类型,并非让同学们按类型去解应用题,努力地去掌握分析问题的本领,才是学好的关健。
二、多边形(一)最简单的多边形-三角形 1.三角形及有关概念三角形:由三条不在同一条直线上的线段首尾顺次连结组成的平面图形. 三角形的外角:三角形一边的延长线与三角形的另一边组成的角. 如图1,∠ACD是△ABC的一个外角. 三角形的中线:连结三角形的一个顶点和它对边中点的线段. 如图2,AD是△ABC的中线,则BD=CD=BC 三角形的角平分线:三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段. 如图2,AE是△ABC的角平分线,则∠BAE=∠CAE=∠BAC 三角形的高:从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段. 如图2,AF是△ABC的高,则∠AFB =∠AFC=90°或AF⊥BC. 请你分别在一个三角形中,画它的三条中线、三条角平分线、三条高,想一想,你能发现结论? 2.三角形的分类⑴按角分类: (2)按边分类:三角形的按角分类很重要,在解决一些有关三角形的问题时,我们常将三角形按角分类,进行讨论. 3.三角形的一般性质⑴三角形的三边关系:三角形任意两边的和大于第三边三角形任意两边的差小于第三边⑵三角形角之间的关系:三角形内角的关系:三角形内角的和等于180°三角形外角与内角间的关系:相等关系:三角形的一个外角等于和它不相邻的两个内角的和不等关系:三角形的一个外角大于任何一个和它不相邻的内角⑶三角形的边与角间的关系:在三角形中相等的边所对的角也相等(即:等边对等角)在三角形中相等的角所对的边也相等(即:等角对等边)此外,三角形还具有稳定性.即:如果一个三角形的三边确定,则这个三角形的形状和大小就完全确定了. (二)多边形 1.研究多边形的有关问题常将多边形转化为三角形的问题,常用的一种方法是,从多边形的一个顶点出发作多边形的对角线,如图3所示,那么⑴从n边形的一个顶点出发可作条对角线. ⑵从n边形的一个顶点出发的对角线把n边形分成个三角形此外,还可以怎样把多边形分割为三角形,请想一想? 2.多边形的内角和与外角和⑴n 边形的内角和为:(n-2)—180°⑵n边形的外角和为:360°注意:多边形的外角和是指:在多边形的每一个顶点处取一个外角相加,得到的和. 3.正多边形的有关计算正n边形的内角:方法一(n-2)—180°/n ,方法二180°-360°/n. 正n边形的外角:360°/n.. (三)多边形知识的一个应用:用正多边形铺地板 1.用多边形围绕一点拼成一个不留空隙又不重叠的平面图形的关键是:几个多边形的内角相加为360°. 2.用一种正多边形能铺满地面的是:正三角形、正方形、正六边形. 3.用两种正多边形能铺满地面的常见组合是:⑴正三角形与正方形⑵正三角形与正六边形⑶正八边形与正方形⑷正三角形与正十二边形三、轴对称(一)轴对称 1.轴对称图形与轴对称的概念⑴定义轴对称图形:一个图形沿某条直线对折,对折的两部分能够完全重合,那么这个图形就叫做轴对称图形. 轴对称:把一个图形沿某条直线对折,如果它能够与另一个图形重合,就说这两个图形成轴对称. ⑵区别和联系区别:⑴轴对称是对两个图形说的,轴对称图形是对一个图形说的. ⑵轴对称表示两个图形之间的对称关系,轴对称图形表示某个图形特性. 联系:⑴定义中都有一条直线,都要沿这条直线折叠后重合. ⑵可互相转化. 把轴对称图形的两部分看成两个图形,就是轴对称;把轴对称的两个图形看成一个图形,就是轴对称图形. 2.性质⑴轴对称图形的对应线段相等,对应角相等. ⑵轴对称图形的对称点的连线的垂直平分线,就是该图形的对称轴.⑶轴对称图形的对应线段或延长线相交,其交点一定在对称轴上.(此条供了解) 3.画法如果图形是直线、线段、或射线组成时,那么在画它关于某条直线的对称图形时,只要画出图形中的特殊点的对称点,然后连结对称点,就可以画出关于这条直线的对称图形. 画一个点的对称点分三步:作垂直---------顺延长--------取相等(二)简单的轴对称图形 1.线段垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫做中垂线⑴线段是轴对称图形,对称轴是它本身所在的直线和它的垂直平分线. 如图4所示. ⑵线段的垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等. 如图5,直线CD垂直平分AB,P是CD上任意一点,则PA=PB 做一做:任意画一个三角形,分别画出它三边的垂直平分线,根据线段的垂直平分线的性质,你能得到什么结论?. 2.角⑴角是轴对称图形,对称轴是它的角平分线所在的直线. 如图 6 所示⑵角的平分线的性质:角平分线上的点到角两边的距离相等. 如图7,OC平分∠AOB,点P是OC上任意一点,PD⊥OA,PE⊥OB,则PD=PE 做一做:任意画一个三角形,分别画出它的三条角平分线,根据角的平分线的性质,你能得到什么结论?. 3.等腰三角形⑴定义:有两条边相等的三角形叫做等腰三角形. ⑵性质:等腰三角形是特殊的三角形,一般三角形具有的性质它都具有,另外它还具有:①等腰三角形是轴对称图形,对称轴是底边的垂直平分线,如图8. ②等腰三角形两底角相等.(简称为:等边对等角)③等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(简称为:等腰三角形“三线合一”的性质)怎样运用等腰三角形“三线合一”的性质呢?在等腰三角形中,只要已知一条线段是等腰三角形顶角的平分线、底边上的中线、底边上的高这三条线段中的其中一种线段,就可以得出这条线段也是另外两种线段. 如图9,在△ABC中,下面的空格你能填出来吗?(括号里填根据)Ⅰ.∵AB=AC,AD⊥BC ()∴∠=∠,=;()Ⅱ.∵AB=AC,AD是中线()∴⊥,∠=∠;()Ⅲ.∵AB=AC,AD是角平分线()∴⊥,=. ()⑶识别:①方法一:根据定义,看一个三角形是否有两条边相等. ②方法二:如果一个三角形有两个角相等,那么这两个角所对的边也相等. (简称为:等角对等边) 4.等边三角形⑴定义:三条边都相等的三角形叫做等边三角形. ⑵性质:等边三角形是特殊的等腰三角形,因此它具有一般三角形,等腰三角形所具有的所有性质,另外它还有:①是轴对称图形,如图10所示. ②等边三角形的各个内角都相等,并且每一个内角都等于60°. ⑶识别:①方法一:根据定义,看一个三角形是否三边都相等. ②方法二:三个角都相等的三角形是等边三角形.③方法三:有一个角是60°的等腰三角形是等边三角形.。
