南京市2011-2012学年度第一学期高二期末调研文科数学
2012年高二文科期末考试数学试卷

2011年高二年级期末数学试卷★祝考试顺利★考试时间:120分钟,试卷满分:150分一.选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题中正确的是…………………………………………………………( ) (A )若b a >,则22bc ac >(B )若22bc ac >,则b a > (C )若b a >||,则ba 1||1<(D )若c b a >>,则))((2c b b a a --> 2、已知点M (a ,b )(ab ≠0)是图222r y x =+内一点,直线g 是以M 为中点的弦所在直线,直线l 的方程为02=++r by ax ,则( ) A .g l //,且与圆相离 B .g l ⊥,且与圆相切 C .g l //,且与圆相交 D .g l ⊥,且与圆相离3、某社区有400个家庭,其中高等收入家庭120户,中等收入家庭180户,低收入家庭100户.为了调查社会购买力的某项指标,要从中抽取一个容量为100的样本,记作①;某校高一年级有13名排球运动员,要从中选出3人调查学习负担情况,记作②.那么,完成上述2项调查宜采用的抽样方法是( B )A .①用简单随机抽样,②用系统抽样B .①用分层抽样,②用简单随机抽样C .①用系统抽样,②用分层抽样D .①用分层抽样,②用系统抽样4、如果实数y x ,满足等式22(2)3x y -+=,那么yx的最大值是 ( ) A 、12B 、33C 、32D 、35、在大小相同的5个球中,有3个是红球,2个是白球,若从中任取2个球,则所取的2个球中至少有一个白球的概率是A.710B.310C.25D.356、在两个变量y 与x 的回归模型中,分别选择了四个不同的模型,它们的相关指数2R 如下,其中拟合效果最好的为A.模型①的相关指数为0.351B.模型②的相关指数为 0.766C.模型③的相关指数为0.076D.模型④的相关指数为0.9067、圆(x-3)2+(y+4)2=2关于直线x+y=0的对称圆的标准方程是( )A.(x+3)2+(y-4)2=2B.(x-4)2+(y+3)2=2C.(x+4)2+(y-3)=2D.(x-3)2+(y-4)2=28、当2x =时,下面的程序段结果是 ( ) 1i = 0s =WHILE 4i <= *1s s x =+ 1i i =+ WENDPRINT s ENDA. 3B. 7C. 15D. 179、投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A ,B 中至少有一件发生的概率是( ) A 、512 B 、 12 C 、 712 D 、 3410.若圆错误!未找到引用源。
南京市2010-2011学年第一学期高二数学期末试卷

2010~2011学年度第一学期期末学情调研高二数学说明:本试卷共160分,考试时间120分钟.请在答卷纸上作答.一、填空题:本大题共14小题,每小题5分,共70分1.已知复数11z i =-,21z i =+,那么21z z = ▲ . 2.函数2()f x x =在区间[]1,4上的平均变化率为 ▲ .3.已知函数()cos f x x =,则/()4f π= ▲ . 4.命题:p 20x x -<;命题:q 22x -<<,则p 是q 的 ▲ 条件.5.复数12z =-+,则z = ▲ . 6.函数()x f x e ex =-的单调减区间为 ▲ .7.已知函数1()2x f x x -=+,[]0,2x ∈,则函数()f x 的最小值为 ▲ . 8.若椭圆1422=+y m x 的离心率为21,则m 的值为 ▲ . 9.曲线2ln y x x =-在点(1,2)处的切线方程是 ▲ .10.(文)已知抛物线顶点在坐标原点,焦点在x 轴上,抛物线上一点M (4,b )到焦点的距离等于5,则抛物线的方程为 ▲ .(理)已知向量a =(1, -1,0)和b =(1,0, -1)是平面α内的两个向量,则平面α的一个法向量为 ▲ .(写出一个就行)11.若方程22131x y t t +=-- 所表示的曲线为C ,给出下列四个命题: ①若C 为椭圆,则13t <<; ②若C 为双曲线,则3t >或1t <;③曲线C 不可能是圆; ④若C 表示椭圆,且长轴在x 轴上,则12t <<. 其中真命题的序号为 ▲ (把所有正确命题的序号都填在横线上).12.函数32()31f x ax x x =+-+在区间(,)-∞+∞上是减函数,则a 的取值范围是 ▲ .13.已知⊙A :221x y +=,⊙B: 22(3)(4)16x y ++-=,P 是平面内一动点,过P 作⊙A 、⊙B 的切线,切点分别为D 、E ,若PE PD =,则P 到坐标原点距离的最小值为 ▲ . 14.我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k ,那么甲的面积是乙的面积的k 倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是22221(0)x y a b a b+=>>与222x y a +=,运用上面的原理,可求得图③中椭圆的面积为 ▲.二、解答题:本大题有6大题,满分90分.解答应写出文字说明,证明过程或演算步骤15.(本题满分14分)已知复数()22(4)32z m m m i =-+-+,求分别满足下列条件的实数m 的值或范围:(1)z 为纯虚数;(2)z 在复平面上对应的点在第三象限.16.(本题满分14分)已知m ∈R ,设命题p :[]21,2,0x x m ∀∈-≥;命题q :2,220x R x mx m ∃∈++-<.求使“p 且q ”为真命题的m 的取值范围.17.(本题满分15分)如图,用长为36m 的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1.(1)设长方体的宽为x ,试把体积表示成x 的函数,并求其定义域;(2)问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?l① ② ③(将l 向右平移) x。
江苏省南京市数学高二上学期文数期末考试试卷

江苏省南京市数学高二上学期文数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2017高二下·洛阳期末) 命题“若a>b,则ac>bc”的逆否命题是()A . 若a>b,则ac≤bcB . 若ac≤bc,则a≤bC . 若ac>bc,则a>bD . 若a≤b,则ac≤bc2. (2分)已知函数的图象与直线交于点P,若图象在点P处的切线与x轴交点的横坐标为,则++…+的值为()A . -1B . 1-log20132012C . -log20132012D . 13. (2分) (2015高二下·上饶期中) 如图,椭圆的中心在坐标原点,焦点在x轴上,A1 , A2 , B1 , B2为椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PB2为钝角,则该椭圆离心率的取值范围是()A . (,1)B . (0,)C . (0,)D . (,1)4. (2分) (2015高二下·克拉玛依期中) 命题:“∀x∈R,x2﹣x+2≥0”的否定是()A . ∃x∈R,x2﹣x+2≥0B . ∀x∈R,x2﹣x+2≥0C . ∃x∈R,x2﹣x+2<0D . ∀x∈R,x2﹣x+2<05. (2分)已知函数的图象上一点及邻近一点,则等于()A . 4B . 4+2 xC . 4+ xD .6. (2分)设抛物线,直线l过抛物线C的焦点F,且与C的对称轴垂直,l与C交于,两点, S为C的准线上一点,若的面积为8,则P=()A .B . 2C .D . 47. (2分)(2017·九江模拟) 设椭圆的左右交点分别为F1 , F2 ,点P在椭圆上,且满足• =9,则| |•| |的值为()A . 8B . 10C . 12D . 158. (2分)椭圆的离心率是,则双曲线的渐近线方程是()A .B .C .D .9. (2分)设,则对任意实数a,b,a+b≥0是f(a)+f(b)≥0的()A . 充分必要条件B . 充分而非必要条件C . 必要而非充分条件D . 既非充分也非必要条件10. (2分) (2018高二下·河南期中) 下列说法正确的是()A . 命题“若,则”的否命题是“若,则”B . 若,则“ ”是“ ”的必要不充分条件C . 函数的最小值为D . 命题“ ,”的否定是“ ,”11. (2分) (2016高二下·龙海期中) 函数f(x)=﹣(a<b<1),则()A . f(a)=f(b)B . f(a)<f(b)C . f(a)>f(b)D . f(a),f(b)大小关系不能确定12. (2分)若在上是减函数,则b的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高一上·舟山期末) 给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次为A,B,C,D;如果线段AB,BC,CD的长度按此顺序构成一个等差数列,则直线l的方程为________14. (1分)如果质点A按照规律s=5t2运动,则在t=3时的瞬时速度为________.15. (1分) (2018高三上·西宁月考) 已知函数 . 表示中的最小值,若函数恰有三个零点,则实数的取值范围是________.16. (1分)(2017·海淀模拟) 抛物线y2=8x的焦点到双曲线的渐近线的距离是________.三、解答题 (共6题;共30分)17. (5分)设函数,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊊P,则求实数a的取值范围.18. (5分)(2017·广西模拟) 赵州桥是当今世界上建造最早、保存最完整的我国古代单孔敞肩石拱桥(图一).若以赵州桥跨径AB所在直线为x轴,桥的拱高OP所在直线为y轴,建立平面直角坐标系(图二),有桥的圆拱APB所在的圆的方程为x2+(y+20.7)2=27.92 .求|OP|.19. (5分) (2016高二上·上杭期中) 已知p:﹣x2+2x﹣m<0对x∈R恒成立;q:x2+mx+1=0有两个正根.若p∧q为假命题,p∨q为真命题,求m的取值范围.20. (5分)已知函数f(x)=在x=e上取得极值,a,t∈R,且t>0.(Ⅰ)求a的值;(Ⅱ)求函数g(x)=(x﹣1)•f(x)在(0,t]上的最小值;(Ⅲ)证明:对任意的x1 ,x2∈(,+∞),且x1≠x2 ,都<t.21. (5分)(2017·黑龙江模拟) 椭圆C:过点P(,1)且离心率为,F为椭圆的右焦点,过F的直线交椭圆C于M,N两点,定点A(﹣4,0).(Ⅰ)求椭圆C的方程;(Ⅱ)若△AMN面积为3 ,求直线MN的方程.22. (5分) (2016高三上·山西期中) 已知函数f(x)=lnx,g(x)= ax2+bx,a≠0.(Ⅰ)若b=2,且h(x)=f(x)﹣g(x)存在单调递减区间,求a的取值范围;(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1 ,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共30分)17-1、18-1、19-1、20-1、21-1、。
南京市数学高二上学期文数期末考试试卷(I)卷
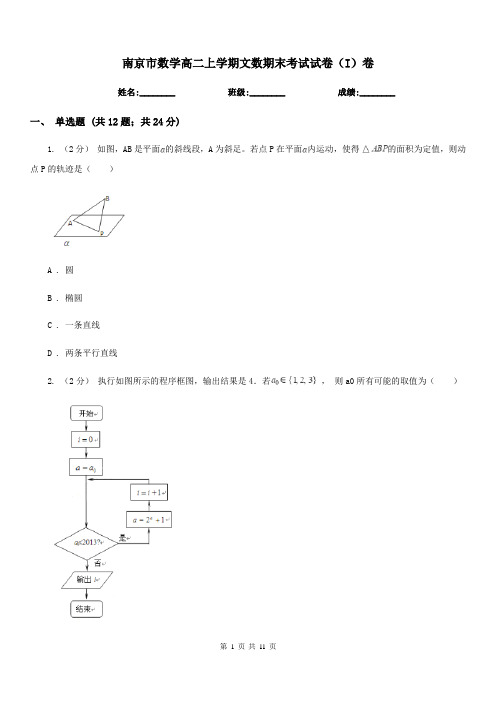
南京市数学高二上学期文数期末考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)如图,AB是平面的斜线段,A为斜足。
若点P在平面内运动,使得的面积为定值,则动点P的轨迹是()A . 圆B . 椭圆C . 一条直线D . 两条平行直线2. (2分)执行如图所示的程序框图,输出结果是4.若,则a0所有可能的取值为()A . 1,2,3B . 1C . 2D . 1,23. (2分)设命题p:函数f(x)=lg(ax2-x+ a)的定义域为R;命题q:不等式3x-9x<a对一切正实数均成立.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围().A . 0≤a<1B . 0≤aC . a≤1D . 0≤a≤14. (2分)椭圆的离心率为,右焦点为,方程的两个实根分别为和,则点()A . 必在圆内B . 必在圆上C . 必在圆外D . 以上三种情形都有可能5. (2分)(2018·郑州模拟) 执行如图所示的程序框图,若输出的结果是7,则判断框内的取值范围是()A .B .C .D .6. (2分) (2018高一上·徐州期中) 已知函数是定义在区间上的偶函数,当时,是减函数,如果不等式成立,则实数的取值范围是()A .B .C .D .7. (2分) (2018高二上·浙江月考) 设分别是双曲线的左、右焦点.若点在双曲线上,且,则()A .B .C .D .8. (2分) (2018高二上·南山月考) 1037和425的最大公约数是()A . 9B . 3C . 51D . 179. (2分)已知命题p:“∃x>0,sinx≥1”,则¬p为()A . ∀x>0,sinx≥1B . ∀x≤0,sinx<1C . ∀x>0,sinx<1D . ∀x≤0,sin≥110. (2分)用秦九韶算法计算当x=3时,多项式f(x)=3x9+3x6+5x4+x3+7x2+3x+1的值时,求得v5的值是()A . 84B . 252C . 761D . 228411. (2分)过双曲线的一个焦点作实轴的垂线,交双曲线于A,B两点,若线段AB的长度恰等于焦距,则双曲线的离心率为()A .B .C .D .12. (2分)如图,抛物线的焦点为,准线为,经过且斜率为的直线与抛物线在轴上方的部分相交于点,,垂足为,则的面积是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)下列关于算法的说法,正确的是________ .①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是明确的,不能有歧义或模糊;④算法执行后一定产生确定的结果.14. (1分) (2017高一上·葫芦岛期末) 已知圆C1:x2+y2﹣6x﹣7=0与圆C2:x2+y2﹣6y﹣27=0相交于A、B两点,则线段AB的中垂线方程为________.15. (1分)已知一个学生2016年的高考语文成绩为120分,数学成绩为135分,英语成绩为100分,理科综合成绩为249分,求他的总分与平均分的一个算法如下,请补充完整.第一步,取A=120,B=135,C=100,D=249.第二步, .第三步,________.第四步,输出计算结果.16. (1分) (2019高二上·集宁月考) 设F为抛物线的焦点,A、B、C为该抛物线上的三点,若,则 ________.三、解答题 (共6题;共55分)17. (5分)下面是一个问题的自然语言叙述的算法过程:第一步输入x;第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x﹣800);否则y=25+0.1(x﹣1300);第三步输出y;第四步结束.(1)请写出该算法的功能(用算式表示)(2)用基本算法语句写出相应的程序(注:不可用框图).18. (20分)在一次模拟打飞机的游戏中,小李接连射击了两次,设命题p1“第一次射击击中飞机”,命题p2“第二次射击击中飞机”,试用p1、p2及连接词“或”“且”“非”表示下列命题:(1)两次都击中飞机;(2)两次都没击中飞机;(3)恰有一次击中飞机;(4)至少有一次击中飞机.19. (5分) (2017高三上·涪城开学考) 已知p:|1﹣|≤2,q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的充分而不必要条件,求实数m的取值范围.20. (5分)(1)已知圆C经过O(0,0),Q(﹣2,2)两点,且被直线y=1截得的线段长为2.求圆C 的方程.(2)已知点P(1,1)和圆x2+y2﹣4y=0,过点P的动直线l与圆交于A,B两点,求线段AB的中点M的轨迹方程.21. (10分) (2017高二下·平顶山期末) 已知抛物线C:y2=2px(p>0)(1)若直线x﹣y﹣2=0过抛物线C的焦点,求抛物线C的方程,并求出准线方程;(2)设p=2,A,B是C上异于坐标原点O的两个动点,满足OA⊥OB,△ABO的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.22. (10分) (2016高二上·福田期中) 已知,椭圆C过点A ,两个焦点为(﹣1,0),(1,0).(1)求椭圆C的方程;(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分)17-1、18-1、18-2、18-3、18-4、19-1、20-1、答案:略21-1、答案:略21-2、答案:略22-1、22-2、第11 页共11 页。
江苏省南京市2013-2014学年度高二第一学期期末调研数学(理)试题(含答案)

南京市2013-2014学年度第一学期高二期末调研数学卷(理科) 2014.01注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡.一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答题卡相应位置.......上 1.命题“∀x ∈N ,x 2≠x ”的否定是 ▲ .2.在平面直角坐标系xOy 中,焦点为F (5,0)的抛物线的标准方程是 ▲ . 3.已知a ,b ∈R ,a +b i =(1+2i)(1-i) (i 为虚数单位),则a +b 的值为 ▲ . 4.记函数f (x )=x +1x的导函数为f '(x ),则 f '(1)的值为 ▲ .5.已知实数x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -4≤0,x -y ≥0,y ≥0,则z =x +2y 的最大值为 ▲ .6.记命题p 为“若α=β,则cos α=cos β”,则在命题p 及其逆命题、否命题、逆否命题中,真命题的个数是 ▲ .7.在平面直角坐标系xOy 中,已知焦点在x 轴上的双曲线的渐近线方程为x ±2y =0,则该双曲线的离心率为 ▲ .8.如图,已知四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是矩形,AB =4,AA 1=3, ∠BAA 1=60︒,E 为棱C 1D 1的中点,则→AB ⋅→AE = ▲ .9.已知函数f (x )=e x -ax 在区间(0,1)上有极值,则实数a 的取值范围是 ▲ .10.“a =1”是“函数f (x )=x +a cos x 在区间(0,π2)上为增函数”的 ▲ 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空). 11.已知圆柱的体积为16π cm 3,则当底面半径r = ▲ cm 时,圆柱的表面积最小.CDA 1B 1C 1D 1E(第8题图)12.在平面直角坐标系xOy 中,已知椭圆x 24+y 23=1的左焦点为F ,直线x -y -1=0,x -y +1=0与椭圆分别相交于点A ,B ,C ,D ,则AF +BF +CF +DF = ▲ . 13.定义在R 上的函数y =f (x )的图像经过坐标原点O ,且它的导函数y =f (x )的图像是如图所示的一条直线,则y =f (x )的图像一定不经过第 ▲ 象限. 14.已知A 是曲线C 1:y =ax -2(a >0)与曲线C 2:x 2+y 2=5的一个公共点.若C 1在A 处的切线与C 2在A 处的切线互相垂直,则实数a 的值是 ▲ .二、解答题:本大题共6小题,共计58分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分8分)已知m ∈R ,设p :复数z 1=(m -1)+(m +3)i (i 是虚数单位)在复平面内对应的点在第二象限,q :复数z 2=1+(m -2)i 的模不超过10.(1)当p 为真命题时,求m 的取值范围;(2)若命题“p 且q ”为假命题,“p 或q ”为真命题,求m 的取值范围.16.(本题满分10分)在平面直角坐标系xOy 中,曲线y =x 2-2x -3与坐标轴的交点都在圆C 上. (1)求圆C 的方程;(2)若直线x +y +a =0与圆C 交于A ,B 两点,且AB =2,求实数a 的值.17.(本题满分10分)在长方体ABCD -A 1B 1C 1D 1中,AB =AD =2,AA 1=a ,E ,F 分别为AD ,CD 的中点.(第13题图)(1)若AC 1⊥D 1F ,求a 的值;(2)若a =2,求二面角E -FD 1-D 的余弦值.18.(本题满分10分)已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x 元/件(1≤x ≤2),今年新增的年销量......(单位:万件)与(2-x )2成正比,比例系数为4. (1)写出今年商户甲的收益y (单位:万元)与今年的实际销售单价x 间的函数关系式;(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.19.(本题满分10分)已知函数f (x )=ax 2-(4a +2)x +4ln x ,其中a ≥0. (1)若a =0,求曲线y =f (x )在点(1,f (1))处的切线方程;A BCD C 1B 1A 1D 1EF(第17题图)(2)讨论函数f (x )的单调性.20.(本题满分10分)在平面直角坐标系xOy 中,△ABC 的顶点B 、C 的坐标为B (-2,0),C (2,0),直线AB ,AC 的斜率乘积为-14,设顶点A 的轨迹为曲线E .(1)求曲线E 的方程;(2)设曲线E 与y 轴负半轴的交点为D ,过点D 作两条互相垂直的直线l 1,l 2,这两条直线与曲线E的另一个交点分别为M ,N .设l 1的斜率为k (k ≠0),△DMN 的面积为S ,试求S∣k ∣的取值范围.南京市2013-2014学年度第一学期高二期末调研数学参考答案及评分标准(理科) 2014.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题3分,共42分)1.∃x ∈N ,x 2=x 2.y 2=20x 3.4 4.-1 5.6 6.2 7.528.14 9.(1,e) 10.充分不必要. 11.2 12.8 13.1 14.2二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤) 15.解(1)因为复数z 1=(m -1)+(m +3)i 在复平面内对应的点在第二象限,所以⎩⎨⎧m -1<0,m +3>0.解得-3<m <1,即m 的取值范围为(-3,1). ……………… 3分 (2)由q 为真命题,即复数z 2=1+(m -2)i 的模不超过10,所以12+(m -2)2≤10,解得-1≤m ≤5. ……………… 5分 由命题“p 且q ”为假命题,“p 或q ”为真命题得⎩⎨⎧p 为真命题,q 为假命题,或 ⎩⎨⎧p 为假命题,q 为真命题. 所以⎩⎨⎧-3<m <1,m <-1或m >5,或⎩⎨⎧m ≤-3或m ≥1,-1≤m ≤5,即-3<m <-1或1≤m ≤5.所以m 的取值范围为(-3,-1)∪[1,5]. ……………… 8分 16.解 (1)曲线与y 轴的交点是(0,-3).令y =0,得x 2-2x -3=0,解得x =-1或x =3.即曲线与x 轴的交点是(-1,0),(3,0). ……………… 2分设所求圆C 的方程是x 2+y 2+Dx +Ey +F =0,则⎩⎪⎨⎪⎧9-3E +F =0,1-D +F =0,9+3D +F =0,解得D =-2,E =2,F =-3.所以圆C 的方程是x 2+y 2-2x +2y -3=0. ……………… 5分(2)圆C 的方程可化为(x -1)2+(y +1)2=(5)2,所以圆心C (1,-1),半径r =5. ……………… 7分 圆心C 到直线x +y +a =0的距离d =|1+(-1)+a |2=|a |2. 由于d 2+(12AB )2=r 2,所以(|a |2)2+12=(5)2,解得a =±2 2 . ……………… 10分 17.解 如图,以D 为坐标原点,DA 所在直线为x 轴,DC 所在直线为y 轴,DD 1所在直线为z 轴,建立坐标系.(1)由题意得A (2,0,0),D 1(0,0,a ),C 1(0,2,a ),F (0,1,0).故→AC 1=(-2,2,a ),→D 1F =(0,1,-a ). …… 2分因为AC 1⊥D 1F ,所以→AC 1·→D 1F =0,即(-2,2,a )·(0,1,-a )=0.从而2-a 2=0,又a >0,故a =2. ……………… 5分 (2)平面FD 1D 的一个法向量为m =(1,0,0). 设平面EFD 1的一个法向量为n =(x ,y ,z ),因为E (1,0,0),a =2,故→EF =(-1,1,0),→D 1F =(0,1,-2). 由n ⊥→EF ,n ⊥→D 1F ,得-x +y =0且y -2z =0,解得x =y =2z .故平面EFD 1的一个法向量为n =(2,2,1). ……………… 8分因为cos<m ,n >=m ·n |m |·|n |=(1,0,0)·(2,2,1)1×3=23,且二面角E -FD 1-D 的大小为锐角,所以二面角E -FD 1-D 的余弦值为23. ……………… 10分18.解 (1)由题意知,今年的年销售量为1+4(x -2)2 (万件).因为每销售一件,商户甲可获利(x -1)元,所以今年商户甲的收益y =[1+4(x -2)2](x -1)=4x 3-20x 2+33x -17,(1≤x ≤2). ……………… 4分(2)由(1)知y =4x 3-20x 2+33x -17,1≤x ≤2, 从而y ′=12x 2-40x +33=(2x -3)(6x -11).令y ′=0,解得x =32,或x =116.列表如下:……………… 7分又f (32)=1,f (2)=1,所以f (x )在区间[1,2]上的最大值为1(万元).而往年的收益为(2-1)×1=1(万元),所以,商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.……………… 10分19.解(1)当a =0时,f (x )=-2x +4ln x ,从而f ′(x )=-2+4x ,其中x >0. ……………… 2分所以f ′(1)=2.又切点为(1,-2),所以所求切线方程为y +2=2(x -1),即2x -y -4=0. ……………… 4分(2)因为f (x )=ax 2-(4a +2)x +4ln x ,所以f ′(x )=2ax -(4a +2)+4x =2ax 2-(4a +2)x +4x =2(ax -1)(x -2)x ,其中x >0.①当a =0时,f ′(x )=-2(x -2)x,x >0.由f ′(x )>0得,0<x <2,所以函数f (x )的单调增区间是(0,2);单调减区间是(2,+∞);……………… 6分②当0<a <12时,因为1a >2,由f ′(x )>0,得x <2或x >1a.所以函数f (x )的单调增区间是(0,2)和(1a ,+∞);单调减区间为(2,1a);……………… 8分③当a =12时,f ′(x )=(x -2)2x ≥0,且仅在x =2时,f ′(x )=0,所以函数f (x )的单调增区间是(0,+∞);④当a >12时,因0<1a <2,由f ′(x )>0,得0<x <1a或x >2,所以函数f (x )的单调增区间是(0,1a )和(2,+∞);单调减区间为(1a ,2).综上,当a =0时,f (x )的单调增区间是(0,2),单调减区间是(2,+∞); 当0<a <12时,f (x )的单调增区间是(0,2)和(1a ,+∞),减区间为(2,1a );当a =12时,f (x )的单调增区间是(0,+∞);当a >12时,f (x )的单调增区间是(0,1a )和(2,+∞),减区间为(1a,2).……………… 10分20.解(1)设顶点A 的坐标为(x ,y ),则k AB =y x +2,k AC =yx -2, ………… 2分 因为k AB ⋅k AC =-14,所以y x +2⋅ y x -2=-14, 即x 24+y 2=1.(或x 2+4y 2=4).所以曲线E 的方程为 x 24+y 2=1(x ≠±2) . ……………… 4分(2)曲线E 与y 轴负半轴的交点为D (0,-1).因为l 1的斜率存在,所以设l 1的方程为y =kx -1, 代入x 24+y 2=1,得M (8k1+4k 2,4k 2-11+4k 2),从而DM =(8k 1+4k 2)2+(4k 2-11+4k 2+1)2=8∣k ∣1+k 21+4k 2. ……………… 6分 用-1k 代k 得DN =81+k 24+k 2.所以△DMN 的面积S =12⋅8∣k ∣1+k 21+4k 2⨯81+k 24+k 2=32(1+k 2)∣k ∣(1+4k 2)(4+k 2). ……………… 8分 则S∣k ∣= 32(1+k 2)(1+4k 2)(4+k 2), 因为k ≠0且k ≠±12,k ≠±2,令1+k 2=t ,则t >1,且t ≠54,t ≠5,从而S ∣k ∣=32t (4t -3)(t +3)=32t 4t 2+9t -9=329+4t -9t , 因为4t -9t >-5,,且4t -9t ≠-115,4t -9t ≠915.所以9+4t -9t >4且9+4t -9t ≠345,9+4t -9t ≠1365,从而 S ∣k ∣<8且S ∣k ∣≠8017,S ∣k ∣≠2017, 即 S ∣k ∣∈(0,2017)∪(2017,8017)∪(8017,8). ……………… 10分。
南京市2011-2012学年度第一学期高二期末调研文科

南京市2011-2012学年度第一学期高二期末调研文科数学卷 2012.01注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答卷纸的密封线内.试题的答案写在答卷纸...上对应题目的答案空格内.考试结束后,交回答卷纸.一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答.卷纸..相应位置....上 1.命题“ x ∈R ,x 2≥0”的否定是 ▲ .2.已知函数f (x )=x 2-x ,则f ′(x )= ▲ .3.已知复数z =2+i (i 为虚数单位),则_z 对应的点在第 ▲ 象限.4.双曲线x 25-y 24=1的焦点坐标是 ▲ . 5.设直线l 1:ax -2y +1=0,l 2:(a -1) x +3y =0,若l 1// l 2,则实数a 的值是 ▲ .6.顶点在原点,焦点在x 轴上的抛物线经过点(2,2),则此抛物线方程为 ▲ .7.已知双曲线x 2-y 2b 2=1(b >0)的一条渐近线的方程为y =2x ,则b 的值是 ▲ . 8.函数f (x )=12x -sin x 在区间[0,π]上的最小值是 ▲ . 9.设椭圆x 2a 2+y 2b 2=1(a >b >0)的右准线与x 轴的交点为M ,以椭圆的长轴为直径作圆O ,过点M 引圆O 的切线,切点为N ,若△OMN 为等腰直角三角形,则椭圆的离心率为 ▲ .10.如图,直线l 是曲线y =f (x )在x =4处的切线,则f ′(4)= ▲ .11.若圆x 2+y 2=r 2(r >0)与圆(x 的取值范围是 ▲ .12.给出下列命题①“a >b ”是“a 2>b 2”的充分不必要条件;②“lg a =lg b ”是“a =b ”的必要不充分条件;③若x , y ∈R ,则“|x |=|y |”是“x 2=y 2”的充要条件;④△ABC 中,“sin A >sin B ”是“A >B ”的充要条件.其中真命题是 ▲ .(写出所有真命题的序号)13.观察下列等式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…从中可归纳得出第n 个等式是 ▲ .14.设函数f (x )在其定义域D 上的导函数为f ′(x ).如果存在实数a 和函数h (x ),其中h (x )对任意的x ∈D 都有h (x )>0,使得f ′(x )=h (x )(x 2-ax +1),则称函数f (x )具有性质P (a ).给出下列四个函数:①f (x )=13x 3-x 2+x +1;②f (x )=ln x +4x +1;③f (x )=(x 2-4x +5)e x ;④f (x )=x 2+x 2x +1,其中具有性质P (2)的函数是 ▲ .(写出所有满足条件的函数的序号)二、解答题:本大题共6小题,共计58分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分8分)已知复数z1=m(m-1)+(m-1)i是纯虚数.(1)求实数m的值;(2)若(3+z1) z=4+2i,求复数z.16.(本题满分8分)已知命题p:函数y=log a x在(0,+∞)上是增函数;命题q:关于x的方程x2-2ax+4=0有实数根.若p ∧q为真,求实数a的取值范围.17.(本题满分10分)设直线l:4x+3y+a=0和圆C:x2+y2+2x-4y=0.(1)当直线l过圆C的圆心时,求实数a的值;(2)当a=3时,求直线l被圆C所截得的弦长.18.(本题满分10分)某公司需制作容积为216 ml的长方体形饮料盒,饮料盒底面的长是宽的2倍.当饮料盒底面的宽为多少时,才能使它的用料最省?19.(本题满分10分)已知椭圆C 的焦点为F 1(-5,0),F 2(5,0),焦点到短轴端点的距离为210.(1)求椭圆C 的标准方程;(2)设点P 是椭圆C 上的一点,且在第一象限.若△PF 1F 2为直角三角形,试判断直线PF 1与圆O :x 2+y 2=52的位置关系.20.(本题满分12分)已知函数f (x )=a ln x +12x 2+(a +1)x +1. (1)当a =-1时,求函数f (x )的单调增区间;(2)若函数f (x )在(0,+∞)上是增函数,求实数a 的取值范围;(3)若a >0,且对任意x 1,x 2∈(0,+∞),x 1≠x 2,都有| f (x 1)-f (x 2)|>2| x 1-x 2|,求实数a 的最小值.南京市2011-2012学年度第一学期高二期末调研答卷纸(文科数学)2012.01一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答.卷纸..相应位...置.上. 1. 2. 3.4. 5. 6.7. 8. 9.10. 11. 12.13. 14.二、解答题:本大题共6小题,共58分.请在答.卷纸..指定区域内.....作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分8分)16.(本小题满分8分)17.(本小题满分10分)18.(本小题满分10分)19.(本小题满分10分)20.(本小题满分12分)南京市2011-2012学年度第一学期高二期末调研文科数学参考答案及评分标准卷2012.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题3分,共42分)1.ヨx ∈R ,x 2<0 2.2x -1 3.四 4.(±3,0) 5.256.y 2=4x 7.2 8.π6-32 9.22 10.1211.(1,11) 12.③④ 13.n +(n +1)+(n +2)+…+[n +2(n -1)]=(2n -1)2(n ∈N*) 14.①②③二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤)15.(本题满分8分,第1小题4分,第2小题4分)解:(1)由题意得⎩⎨⎧m (m -1)=0, m -1≠0.………………………………………………………………2分 解得m =0. ………………………………………………………………………………4分(2)当m =0时,z 1=-i .由(3+z 1) z =4+2i ,即(3-i) z =4+2i ,得z =4+2i 3-i………………………………………………………………………………6分 =1+i . ………………………………………………………………………………8分16.(本题满分8分)解: 当p 为真命题时,a >1. ………………………………………………………………2分 当q 为真命题时,△=4a 2-16≥0.解得a ≤-2或a ≥2. ………………………………………………………………………4分 因为p ∧q 为真,所以p 和q 都是真命题.⎩⎨⎧a >1,a ≤-2或a ≥2.…………………………………………………………………6分 所以实数a 的取值范围是[2,+∞). ………………………………………………………8分17.(本题满分10分)解:(1)由x 2+y 2+2x -4y =0,得(x +1)2+(y -2)2=5.所以圆C 的圆心为(-1,2),半径为5. ……………………………………………………2分 因为直线l 过圆C 的圆心,所以-4+6+a =0.解得a =-2. …………………………………………………………………………4分(2)当a =3时,圆心(-1,2)到直线l :4x +3y +3=0的距离为d =|4×(-1)+3×2+3|42+32=1. ……………………………………………………………………7分 则2r 2-d 2=4.所以直线l 被圆C 所截得的弦长为4. ………………………………………………………10分18.(本题满分10分)解:设饮料盒底面的宽为x cm ,高为h cm ,则底面长为2x cm .根据V =x ·2x ·h ,可得h = 2162x 2.…………………………2分 所以,表面积S (x )=2(x ·2x +x ·h +2x ·h )=2(2x 2+3x ·2162x 2)=4(x 2+162x) (x >0) ……………………………………4分 由S '(x )=4(2x -162x2)=0, ………………………………………………………………………6分 得x =33. ……………………………………………………………………………………8分 当0<x <33时,S '(x )<0,函数S (x ) 在(0,33)是减函数;当x >33时,S '(x ) >0,函数S (x ) 在(33,+∞)是增函数.所以,当x =33时,S (x )取得极小值,且是最小值.答:当饮料盒底面的宽为3 3 cm 时,才能使它的用料最省.…………………………………10分19.(本题满分10分,第1小题4分,第2小题6分)解:(1)由题意可得a =210,c =5, …………………………………………………………2分 则b 2=15.所以椭圆C 的方程为x 240+y 215=1. …………………………………………………………………4分 (2)圆O :x 2+y 2=52的圆心为原点,半径r =102. ①当∠PF 2F 1为直角时,点P 的坐标为(5,3104). ……………………………………………5分 直线PF 1的方程为y =3410(x +5). 此时圆心到直线PF 1的距离为1513<102. 所以直线PF 1与圆O :x 2+y 2=52相交. …………………………………………………………7分 ②当∠F 1PF 2为直角时,设点P 的坐标为(x ,y ).解⎩⎨⎧x 240+y 215=1, x 2+y 2=52.得⎩⎨⎧x =4,y =3. 所以点P 的坐标为(4,3). …………………………………………………………………………9分 则点P 到椭圆右焦点(5,0)的距离为10.此时圆心O 到直线PF 1的距离为102. 所以直线PF 1与圆O :x 2+y 2=52相切. ……………………………………………………10分20.(本题满分12分)解:(1)当a =-1时,f (x )=-ln x +12x 2+1. 则f ′(x )=-1x+x . ………………………………………………………………………………2分 令f ′(x )>0,得x <0或x >1.所以函数函数f (x )的单调增区间为(1,+∞).………………………………………………4分(2)因为函数f (x )在(0,+∞)上是增函数,所以f ′(x )==x 2+(a +1) x +a x =(x +1)( x +a )x≥0对x ∈(0,+∞)恒成立. ………………6分 即x +a ≥0对x ∈(0,+∞)恒成立.所以a ≥0. ………………………………………………………………………………8分 即实数a 的取值范围是[0,+∞).(3)因为a >0,所以函数f (x )在(0,+∞)上是增函数.因为x 1,x 2∈(0,+∞),x 1≠x 2,不妨设x 1>x 2,所以f (x 1)>f (x 2).由| f (x 1)-f (x 2)| 2| x 1-x 2|恒成立,可得f (x 1)-f (x 2)>2(x 1-x 2),即f (x 1)-2x 1>f (x 2)-2x 2恒成立.令g (x )=f (x )-2x ,则在(0,+∞)上是增函数. …………………………………………10分所以g ′(x )=a x +x +(a +)-2=x 2+(a -1) x +a x≥0对x ∈(0,+∞)恒成立. 即x 2+(a -1) x +a ≥0对x ∈(0,+∞)恒成立.即a ≥-x 2-x x +1对x ∈(0,+∞)恒成立 因为-x 2-x x +1=-(x +1+2x +1-3)≤3-22(当且仅当x +1=2x +1即x =2-1时取等号), 所以a ≥3-22.所以实数a 的最小值为3-22. ……………………………………………………………12分。
2011-2012年市统考文科数学试题
2011—2012学年第二学期高二数学(文科)质量检测说明:满分150分,考试用时间120分钟一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}11A x x =-<<,{}02B x x =<<,则A B 等于( ) A {}12x x -<< B {}01x x << C {}10x x -<< D {}12x x << 2. 命题:“2,0x R x x ∃∈-≤”的否定是( )A “ 2,0x R x x ∀∈->”B “2,0x R x x ∃∈->” C “2,0x R x x ∀∈-≤” D “2,0x R x x ∃∉-≤”3. 设向量(1,2)a = ,(2,)b t =-,若//a b ,则t 等于( )A 1-B 1C 4D 4- 4. 已知1tan 2α=-,且(,)2παπ∈,则cos α等于( )AB C D 5. 设α、β是两个不同的平面,a 、b 是两条不同的直线,下列四个命题中,其中真命题的是( )A 若//a α, //b α,则//a bB 若 //a α,//b β,//a b ,则//αβC 若a α⊥,b β⊥,a b ⊥,则αβ⊥D 若a 、b 在平面α内的射影互相垂直,则a b ⊥6. 已知奇函数()f x 在R 上单调递减,且(1)(2)0f x f -+>,则x 的取值范围为( ) A (,1)-∞- B (1,)-+∞ C (,3)-∞ D (3,)+∞7. 在等差数列{}n a 中,410a =,616a =,则10a 等于( ) A 24 B 26 C 28 D 308. 已知椭圆22221x y a b+=的一个焦点与抛物线24y x =的焦点重合,且椭圆的离心率为2,则椭圆的方程为( ) A 2212x y += B 22132x y += C 22143x y += D 22154x y +=9. 在区间[]1,1-内随机取两个数a 、b ,则函数22()21f x x ax b =+-+有零点的概率为( ) A 18π-B 14π-C 12π-D 314π-10. 在R 上定义运算:(1)x y x y ⊗=-,若存在x R ∈,使得()()1x a x a -⊗+>成立,则实数a 的取值范围为( )A 13(,)(,)22-∞-+∞ B 13(,)22- C 31(,)22- D 31(,)(,)22-∞-+∞二、填空题:本大题共4小题,每小题5分,满分20分11. 若复数2(1)(1)z a a i =-++为纯虚数,则实数a 的值为_______________.12.若实数x 、y 满足约束条件01001x y x y x +≥⎧⎪-+≥⎨⎪≤≤⎩,则z x y =-的最大值为_________.13. 程序框图(即算法流程图)如图所示,其输出 结果是 。
20112012学年度上学期期末考试高二数学试卷
2011—2012学年度上学期期末考试高二数学试卷(文科)gkxx123@本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,注意事项: 1.第Ⅰ卷的答案填在答题卷方框里,第Ⅱ卷的答案或解答过程写在答题卷指定处,写在试题卷上的无效。
2.答题前,考生务必将自己的“姓名”、“班级”、和“考号”写在答题卷上。
3.考试结束,只交答题卷。
第Ⅰ卷(选择题共50分)一、选择题(每小题5分,共10个小题,本题满分50分) 1.如果命题“()p q ⌝或”为假命题,则( )A .p ,q 均为真命题B .p ,q 中至少有一个为真命题C .p ,q 均为假命题D .p ,q 中至多有一个为真命题 2.下列说法正确的是( )A .命题“若22am bm <”,则“a b <”的逆命题是真命题 B .命题“若2,0x R x x ∃∈->”,的否定是“2,0x R x x ∀∈-≤”C .命题“p 或q ”,则命题“p ”和命题“q ”均为真命题D .已知x R ∈,则“x>1”是“x>2”的充分不必要条件 3.根据右边程序判断输出结果为( )A .8B . 9C .10D .114.函数20()32,[5,5]f x x x x =-+∈-,任取0x 使0()0f x ≥的概率为( )A .110 B .15 C .910 D .455.下列命题中真命题的是( )A .在同一平面内,动点到两定点的距离之差(大于两定点间的距离)为常数的点的轨迹是双曲线B . 在平面内,F 1,F 2是定点,|F 1F 2|=6,动点M 满足|MF 1|+|MF 2|=6,则点M 的轨迹是椭圆C .“若-3<m<5则方程22153x y m m +=-+是椭圆” D .存在一个函数,它既是奇函数,又是偶函数 6.记定点M 10(3,)3与抛物线22y x =上的点P 之间的距离为d 1,P 到抛物线的准线l 距离为d 2,则当d 1+d 2取最小值时,P 点坐标为( )A .(0,0)B .C .(2,2)D .11(,)82-7.已知双曲线中心在原点,且一个焦点为F ,直线y=x-1与其相交于M 、N 两点,MN 中点的横坐标为23,则此双曲线方程为( )A .22134x y -= B .22143x y -= C .22152x y -= D .22125x y -= 8.若点00(,)x y 满足2004y x <,就叫点00(,)x y 在抛物线24y x =的内部。
江苏省南京市高二数学上学期期末调研试题 文 苏教版
南京市2013-2014学年度第一学期高二期末调研数学卷(文科)注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡. 一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答题卡相应位置.......上1.命题“∀x ∈N ,x 2≠x ”的否定是 ▲ .2.在平面直角坐标系xOy 中,焦点为F (5,0)的抛物线的标准方程是 ▲ .3.设复数z 满足z ·i =3+4i (i 是虚数单位),则复数z 的模为 ▲ .4.椭圆x 28+y 24=1的右准线方程是 ▲ . 5.记函数f (x )=x +1x的导函数为f '(x ),则 f '(1)的值为 ▲ . 6.已知实数x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -4≤0,x -y ≥0,y ≥0,则z =x +2y 的最大值为 ▲ . 7.记命题p 为“若α=β,则cos α=cos β”,则在命题p 及其逆命题、否命题、逆否命题中,真命题的个数是 ▲ .8.在平面直角坐标系xOy 中,已知焦点在x 轴上的双曲线的渐近线方程为x ±2y =0,则该双曲线的离心率为 ▲ .9.在平面直角坐标系xOy 中,抛物线y 2=4x 的焦点为F ,点P 在抛物线上,若PF =2,则点P 到抛物线顶点O 的距离是 ▲ .10.已知函数f (x )=e x -ax 在区间(0,1)上有极值,则实数a 的取值范围是 ▲ .11.“a =1”是“函数f (x )=x +a cos x 在区间(0,π2)上为增函数”的 ▲ 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).12.已知圆柱的体积为16π cm 3,则当底面半径r = ▲ cm 时,圆柱的表面积最小.13.在平面直角坐标系xOy 中,已知椭圆x 24+y 23=1的左焦点为F ,直线x -y -1=0,x -y +1=0与椭圆分别相交于点A ,B ,C ,D ,则AF +BF +CF +DF = ▲ . 14.定义在R 上的函数y =f (x )的图像经过坐标原点O ,且它的导函数y =f '(x ) 的图像是如图所示的一条直线,则y =f (x )的图像一定不经过第 ▲ 象限.二、解答题:本大题共6小题,共计58分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分8分)已知a 为实数,复数z 1=2-i ,z 2=a +i (i 为虚数单位).(1)若a =1,指出z 1+—z 2在复平面内对应的点所在的象限;(第14题图)(2)若z 1· z 2为纯虚数,求a 的值.16.(本题满分10分)已知a ∈R ,设p :函数f (x )=x 2+(a -1)x 是区间(1,+∞)上的增函数,q :方程x 2-ay 2=1表示双曲线.(1)若p 为真命题,求实数a 的取值范围;(2)若“p 且q ”为真命题,求实数a 的取值范围.17.(本题满分10分)在平面直角坐标系xOy 中,曲线y =x 2-2x -3与坐标轴的交点都在圆C 上.(1)求圆C 的方程;(2)若直线x +y +a =0与圆C 交于A ,B 两点,且AB =2,求实数a 的值.18.(本题满分10分)已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x ≤2),今年新增的年销量......(单位:万件)与(2-x )2成正比,比例系数为4. (1)写出今年商户甲的收益y (单位:万元)与今年的实际销售单价x 间的函数关系式;(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.19.(本题满分10分)已知函数f (x )=ax 2-(4a +2)x +4ln x ,其中a ≥0.(1)若a =0,求曲线y =f (x )在点(1,f (1))处的切线方程;(2)讨论函数f (x )的单调性.20.(本题满分10分)如图,在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,短轴长是2. (1)求a ,b 的值;(2)设椭圆C 的下顶点为D ,过点D 作两条互相垂直的直线l 1,l 2,这两条直线与椭圆C的另一个交点分别为M ,N .设l 1的斜率为k (k ≠0),△DMN 的面积为S ,当S ∣k ∣>169时,求k 的取值范围.南京市2013-2014学年度第一学期高二期末调研数学参考答案及评分标准(文科) 2014.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题3分,共42分)1. x ∈N ,x 2=x 2.y 2=20x 3.5 4.x =4 5.-16.6 7.2 8.52 9. 5. 10.(1,e) 11.充分不必要 12.2 13.8 14.1二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤)15.解 (1)因为a =1,所以z 1+—z 2=(2-i)+(1-i)=3-2i . ………………… 2分所以z 1+—z 2在复平面内对应的点为(3,-2),从而z 1+—z 2在复平面内对应的点在第四象限. ………………… 4分(2)z 1· z 2=(2-i) (a +i)=(2a +1)+(2-a ) i . ………………… 6分因为a ∈R ,z 1· z 2为纯虚数,所以2a +1=0,且2-a ≠0,解得a =-12. ………………… 8分 16.解 (1)因为p 为真命题,即函数f (x )=x 2+(a -1)x 是(1,+∞)上的增函数,(第20题图)所以-a -12≤1. ………………… 3分解得a ≥-1.即实数a 的取值范围是[-1,+∞). ………………… 5分(2)因为“p 且q ”为真命题,所以p 为真命题,且q 也为真命题. …………… 7分 由q 为真命题,得a >0.所以a ≥-1且a >0,即a >0.所以实数a 的取值范围是(0,+∞). ………………… 10分17.解 (1)曲线与y 轴的交点是(0,-3).令y =0,得x 2-2x -3=0,解得x =-1或x =3,即曲线与x 轴的交点是(-1,0),(3,0). ……………… 2分 设所求圆C 的方程是x 2+y 2+Dx +Ey +F =0,则⎩⎪⎨⎪⎧9-3E +F =0,1-D +F =0,9+3D +F =0,解得D =-2,E =2,F =-3. 所以圆C 的方程是x 2+y 2-2x +2y -3=0. ……………… 5分(2)圆C 的方程可化为(x -1)2+(y +1)2=(5)2,所以圆心C (1,-1),半径r =5. ……………… 7分 圆心C 到直线x +y +a =0的距离d =|1+(-1)+a | 2=|a | 2.由于d 2+(12AB )2=r 2,所以(|a | 2)2+12=(5)2,解得a =±2 2 . ……………… 10分18.解 (1)由题意知,今年的年销售量为1+4(x -2)2 (万件).因为每销售一件,商户甲可获利(x -1)元,所以今年商户甲的收益y =[1+4(x -2)2](x -1)=4x 3-20x 2+33x -17,(1≤x ≤2). ……………… 4分(2)由(1)知y =4x 3-20x 2+33x -17,1≤x ≤2,从而y ′=12x 2-40x +33=(2x -3)(6x -11).令y ′=0,解得x =32,或x =116.列表如下:……………… 7分又f (32)=1,f (2)=1,所以f (x )在区间[1,2]上的最大值为1(万元).而往年的收益为(2-1)×1=1(万元),所以,商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.……………… 10分19.解(1)当a =0时,f (x )=-2x +4ln x ,从而f ′(x )=-2+4x,其中x >0. ……………… 2分 所以f ′(1)=2.又切点为(1,-2),所以所求切线方程为y +2=2(x -1),即2x -y -4=0. ……………… 4分(2)因为f (x )=ax 2-(4a +2)x +4ln x ,所以f ′(x )=2ax -(4a +2)+4x =2ax 2-(4a +2)x +4x =2(ax -1)(x -2)x,其中x >0. ①当a =0时,f ′(x )=-2(x -2)x,x >0. 由f ′(x )>0得,0<x <2,所以函数f (x )的单调增区间是(0,2);单调减区间是(2,+∞);……………… 6分②当0<a <12时,因为1a >2,由f ′(x )>0,得x <2或x >1a. 所以函数f (x )的单调增区间是(0,2)和(1a ,+∞);单调减区间为(2,1a); ……………… 8分③当a =12时,f ′(x )=(x -2)2x≥0,且仅在x =2时,f ′(x )=0, 所以函数f (x )的单调增区间是(0,+∞);④当a >12时,因0<1a <2,由f ′(x )>0,得0<x <1a或x >2, 所以函数f (x )的单调增区间是(0,1a )和(2,+∞);单调减区间为(1a,2). 综上,当a =0时,f (x )的单调增区间是(0,2),单调减区间是(2,+∞);当0<a <12时,f (x )的单调增区间是(0,2)和(1a ,+∞),减区间为(2,1a); 当a =12时,f (x )的单调增区间是(0,+∞); 当a >12时,f (x )的单调增区间是(0,1a )和(2,+∞),减区间为(1a,2). ……………… 10分20.解(1)设椭圆C 的半焦距为c ,则由题意得⎩⎪⎨⎪⎧c a =32,b =1,又a 2=b 2+c 2, 解得a =2,b =1. ……………… 4分(2)由(1)知,椭圆C 的方程为x 24+y 2=1, 所以椭圆C 与y 轴负半轴交点为D (0,-1).因为l 1的斜率存在,所以设l 1的方程为y =kx -1.代入x 24+y 2=1,得M (8k 1+4k 2,4k 2-11+4k 2), 从而DM =(8k 1+4k 2)2+(4k 2-11+4k 2+1)2=8∣k ∣1+k21+4k 2. ……………… 6分用-1k 代k 得DN =81+k24+k 2. 所以△DMN 的面积S =12⋅8∣k ∣1+k 21+4k 2⨯81+k24+k 2=32(1+k 2)∣k ∣(1+4k 2)(4+k 2). ……………… 8分 则S ∣k ∣= 32(1+k 2)(1+4k 2)(4+k 2),因为S ∣k ∣>169,即32(1+k 2)(1+4k 2)(4+k 2)>169,整理得4k 4-k 2-14<0,解得-74<k 2<2所以0<k 2<2,即-2<k <0或0<k < 2 .从而k 的取值范围为(-2,0)∪(0,2).。
南京市2013-2014学年高二上学期期末(文)调研含答案
绝密★启用前2013-2014学年江苏省南京市高二上学期期末文科调研考试一、填空题1.命题“∀x ∈N ,x 2≠x ”的否定是 .【答案】∃x ∈N ,x 2=x 【解析】试题分析:根据全称命题“,x p ∀”的否定为“,x p ∃⌝”,得命题“∀x ∈N ,x 2≠x ”的否定“20,x x x ∃>=”,解决此类问题须注意条件x ∈N 不能变.考点:全称命题的否定2.在平面直角坐标系xOy 中,焦点为F(5,0)的抛物线的标准方程是 .【答案】y 2=20x 【解析】试题分析:焦点为F(5,0),所以抛物线开口向右,标准方程可设为22(0)y px p =>,又52p =所以10p =,抛物线的标准方程是y 2=20x 考点:抛物线的焦点坐标与方程关系3.设复数z 满足z ·i =3+4i (i 是虚数单位),则复数z 的模为 . 【答案】5 【解析】试题分析:本题有两种解法,一是解出3443iz i i+==-,再根据复数模的定义求出||5z ==,二是利用复数模的性质:1212||||||z z z z ⋅=⋅得到|||||||||34z i z i z i ⋅=⋅==+= 考点:复数模,复数运算4.椭圆22184x y +=的右准线方程是 . 【答案】x =4【解析】试题分析:本题知识点简单,就是利用椭圆22221(0)x y a b a b +=>>的准线方程为2a x c=,得到右准线方程为4x =考点:椭圆的准线方程 5.记函数1()x f x x+=的导函数为f '(x),则f '(1)的值为 . 【答案】-1 【解析】试题分析:根据商的导数运算法则得22(1)1()x x f x x x -+'==-,所以(1)1f '=-解此类问题要注意顺序,不能将题目做成求(1)f 的导数考点:商的导数运算法则试卷第2页,总9页6.已知实数x ,y 满足约束条件4000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩,则z =x +2y 的最大值为 .【答案】6 【解析】试题分析:解线性规划求最值问题,首先要正确作出可行域,本题可行域为一个三角形,(0,0),(2,2),(2,0)ABC A B C,然后研究目标函数,本题目标函数是一条斜率确定的直线,所以当它过点(2,2)B 时,取最大值6.考点:线性规划求最值7.记命题p 为“若α=β,则cos α=cos β”,则在命题p 及其逆命题、否命题、逆否命题中,真命题的个数是 . 【答案】2 【解析】试题分析:命题p 为“若α=β,则cos α=cos β”,显然为真命题,所以其逆否命题也为真命题;命题p 的逆命题为“若cos α=cos β,则α=β”为假命题,所以其逆否命题,即命题p的否命题也为假命题. 真命题个数是2. 考点:四种命题关系及真假判断8.在平面直角坐标系xOy 中,已知焦点在x 轴上的双曲线的渐近线方程为x ±2y =0,则该双曲线的离心率为 . 【解析】试题分析:因为焦点在x 轴上的双曲线22221(0,0)x y a b a b-=>>的渐近线方程为byx a =±,所以122b a b c e a =⇒=⇒=⇒=考点:双曲线渐近线方程9.在平面直角坐标系xOy 中,抛物线y 2=4x 的焦点为F ,点P 在抛物线上,若PF =2,则点P 到抛物线顶点O 的距离是 .【解析】试题分析:点P 到抛物线焦点距离等于点P 到抛物线准线距离,即22114P P P PF x x y ==+⇒=⇒=因此OP ==考点:抛物线定义10.已知函数f(x)=e x-ax 在区间(0,1)上有极值,则实数a 的取值范围是 . 【答案】(1,e) 【解析】试题分析:函数f(x)=e x-ax 在区间(0,1)上有极值,就是导函数()0x f x e a '=-=在区间(0,1)上有解,即(1,)x a e e =∈ 考点:函数极值11.“a =1”是“函数f(x)=x +acosx 在区间(0,)2π上为增函数”的 条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空). 【答案】充分不必要 【解析】试题分析:当a =1时,()cos f x x x =+,()1sin 0f x x '=-≥,函数()f x 在区间(0,2π上为增函数,所以充分性成立;反之,若函数()f x 在区间(0,)2π上为增函数,则()1sin 0f x a x '=-≥对(0,)2x π∈恒成立,min 1()sin a x ≤,而当(0,)2x π∈,11sin x>,所以1a ≤,因此必要性不成立.考点:利用导数求增减性,充要关系判定12.已知圆柱的体积为16πcm 3,则当底面半径r = cm 时,圆柱的表面积最小. 【答案】2 【解析】试题分析:圆柱的体积为221616V r h r h ππ==⇒=,圆柱的表面积22232162222()S rh r r r πππππ=+=+=+,由2162(2)0S r π'=-+=得2r =,当底面半径r =2时,圆柱的表面积最小.考点:利用导数求最值,13.在平面直角坐标系xOy 中,已知椭圆22143x y +=的左焦点为F ,直线x -y -1=0,x -y+1=0与椭圆分别相交于点A ,B ,C ,D ,则AF +BF +CF +DF = .【答案】8 【解析】试题分析:椭圆22143x y +=的左焦点为(1,0)F -,右焦点为(1,0)F ',所以直线x -y -1=0过右焦点,直线x -y +1=0过左焦点,由对称性得,DF AF CF BF ''==,因此48AF BF CF DF AF AF BF BF a ''+++=+++==考点:椭圆定义14.定义在R 上的函数y =f(x)的图像经过坐标原点O ,且它的导函数y =f '(x)的图像是如图所示的一条直线,则y =f(x)的图像一定不经过第 象限.【答案】一 【解析】试题分析:设导函数y =f '(x)的零点为00,(0)x x <,所以当0x x <时,()f x 单调增;当试卷第4页,总9页0x x >时,()f x 单调减,又(0)0f =,则由图像知()f x 一定不经过第一象限.考点:导函数与原函数的关系二、解答题15.已知a 为实数,复数z 1=2-i ,z 2=a +i(i 为虚数单位). (1)若a =1,指出12z z +在复平面内对应的点所在的象限; (2)若z 1·z 2为纯虚数,求a 的值. 【答案】(1)第四象限(2)12a =- 【解析】试题分析:(1)复数(,)z a bi a b R =+∈与复平面内点(,)a b 一一对应,要确定复数在复平面内对应的点所在的象限,关键在于正确求出复数.由于互为共轭的两个复数,实部相等,虚部相反,所以2z a i =-,因此z 1+2z =(2-i)+(1-i)=3-2i ,所以z 1+2z 在复平面内对应的点为(3,-2),在第四象限,(2)复数为纯虚数,有两个条件,一是实部为零,二是虚部不为零.由z 1·z 2=(2-i)(a +i)=(2a +1)+(2-a)i 得2a +1=0,且2-a ≠0,解得12a =- 试题解析:(1)因为a =1,所以z 1+2z =(2-i)+(1-i)=3-2i . 2分 所以z 1+2z 在复平面内对应的点为(3,-2),从而z 1+2z 在复平面内对应的点在第四象限. 4分 (2)z 1·z 2=(2-i)(a +i)=(2a +1)+(2-a) i . 6分 因为a ∈R ,z 1·z 2为纯虚数,所以2a +1=0,且2-a ≠0,解得12a =-. 8分 考点:复数与复平面内点的对应关系,纯虚数概念,共轭复数概念16.已知a ∈R ,设p :函数f(x)=x 2+(a -1)x 是区间(1,+∞)上的增函数,q :方程x 2-ay 2=1表示双曲线.(1)若p 为真命题,求实数a 的取值范围;(2)若“p 且q ”为真命题,求实数a 的取值范围. 【答案】(1)[-1,+∞)(2)(0,+∞) 【解析】试题分析:(1)因为p 为真命题,即函数f(x)=x 2+(a -1)x 是(1,+∞)上的增函数,由于二次函数单调性决定于对称轴与定义区间的相对位置关系,所以结合图像可得对称轴在区间(1,+∞)左侧时,函数单调增即:112a --≤,解得a ≥-1,(2)因为“p 且q ”为真命题,所以p 为真命题,且q 也为真命题.由(1)可得p 为真命题时有a ≥-1;由q 为真命题,即方程x 2-ay 2=1表示双曲线,因而有a >0;两者要同时成立,就是求其交集,为a >0. 试题解析:(1)因为p 为真命题,即函数f(x)=x 2+(a -1)x 是(1,+∞)上的增函数, 所以112a --≤. 3分 解得a ≥-1.即实数a 的取值范围是[-1,+∞). 5分(2)因为“p 且q ”为真命题,所以p 为真命题,且q 也为真命题. 7分 由q 为真命题,得a>0.所以a ≥-1且a >0,即a >0.所以实数a 的取值范围是(0,+∞). 10分 考点:复合命题的真假17.在平面直角坐标系xOy 中,曲线y =x 2-2x -3与坐标轴的交点都在圆C 上. (1)求圆C 的方程;(2)若直线x +y +a =0与圆C 交于A ,B 两点,且AB =2,求实数a 的值. 【答案】(1)x 2+y 2-2x +2y-3=0(2)a =±【解析】试题分析:(1)曲线y =x 2-2x -3与坐标轴的交点有三个交点,本题就是求过三个点的圆的方程,因此设圆方程的一般式x 2+y 2+Dx +Ey +F =0,若从图形看,则圆的方程又可设成x 2+y 2-2x +Ey-3=0,再利用过点(0,2)-求出2,E =(2)先将圆的一般式化为标准式:222(1)(1)x y -++=,明确圆心和半径,涉及圆的弦长问题,利用由半径、半弦长、圆心到弦所在直线距离构成的直角三角形,列等量关系:221a +=⇒=±试题解析:解 (1)曲线与y 轴的交点是(0,-3).令y =0,得x 2-2x -3=0,解得x =-1或x =3.即曲线与x 轴的交点是(-1,0),(3,0). 2分设所求圆C 的方程是x 2+y 2+Dx +Ey +F =0,则93010930E F D F D F -+=⎧⎪-+=⎨⎪++=⎩,解得D =-2,E =2,F =-3. 所以圆C 的方程是x 2+y 2-2x +2y-3=0. 5分 (2)圆C 的方程可化为222(1)(1)x y -++=,所以圆心C(1,-1),半径r =. 7分 圆心C 到直线x +y +a =0的距离d ==2221()2d AB r +=试卷第6页,总9页所以2221+=,解得a=± 10分考点:圆的一般式方程,圆的弦长18.已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件,今年拟下调销售单价以提高销量,增加收益.据测算,若今年的实际销售单价为x元/件(1≤x≤2),今年新增的年销量......(单位:万件)与(2-x)2成正比,比例系数为4.(1)写出今年商户甲的收益y(单位:万元)与今年的实际销售单价x间的函数关系式;(2)商户甲今年采取降低单价,提高销量的营销策略是否能获得比往年更大的收益(即比往年收益更多)?说明理由.【答案】(1)y=4x3-20x2+33x-17,(1≤x≤2)(2)不能【解析】试题分析:(1)根据收益等于单件利润与销售量的乘积,列等量关系.注意今年销售量等于原销售量与新增的年销量之和,另外还要注意交代函数定义域;y=[1+4(x-2)2](x-1)=4x3-20x2+33x-17,(1≤x≤2).(2)本题实际需求本年收益范围,即需求函数y=4x3-20x2+33x-17,1≤x≤2的值域,这可借助于导数研究.求导后可知函数图像先增后减再增,因此其最大值在极大值及2x=处取到,比较大小知f(x)在区间[1,2]上的最大值为f(2)=1,即为往年的收益,所以商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.试题解析:解(1)由题意知,今年的年销售量为1+4(x-2)2 (万件).因为每销售一件,商户甲可获利(x-1)元,所以今年商户甲的收益y=[1+4(x-2)2](x -1)=4x3-20x2+33x-17,(1≤x≤2). 4分(2)由(1)知y=4x3-20x2+33x-17,1≤x≤2,从而y′=12x2-40x+33=(2x -3)(6x-11).令y′=0,解得x=3,或x=11.列表如下:7分又f(32)=1,f(2)=1,所以f(x)在区间[1,2]上的最大值为1(万元).而往年的收益为(2-1)×1=1(万元),所以,商户甲采取降低单价,提高销量的营销策略不能获得比往年更大的收益.10分考点:函数解析式,利用导数求函数最值19.已知函数f(x)=ax2-(4a+2)x+4lnx,其中a≥0.(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性.【答案】(1)2x-y-4=0,(2)当a=0时,f(x)的单调增区间是(0,2),单调减区间是(2,+∞);当0<a <12时,f(x)的单调增区间是(0,2)和(1a ,+∞),减区间为(2,1a);当a =12时,f(x)的单调增区间是(0,+∞);当a >12时,f(x)的单调增区间是(0,1a)和(2,+∞),减区间为(1a,2)【解析】 试题分析:(1)利用导数集合意义,在1x =处导数值等于该点处切线的斜率,因为4()2f x x'=-+,所以 k =f ′(1)=2, 又切点为(1,-2),所以所求切线方程为y +2=2(x -1),(2)函数f(x)的单调性之所以要讨论,就是由于导函数为零时根的不确定性.因为2(1)(2)()ax x f x x--'=,所以当a =0时,方程()0f x '=在定义域内只有一根;当0a >时,需讨论两根1,2a 的大小,三种情况0<a <12,a =12,及a >12需一一讨论.解题过程中,最易忽视的是两根相等的情况;答题时最易出错的是将两个单调性相同的不连续区间用“并集”“或”合并写.试题解析:解(1)当a =0时,f(x)=-2x +4lnx ,从而4()2f x x'=-+,其中x >0. 2分 所以f ′(1)=2. 又切点为(1,-2),所以所求切线方程为y +2=2(x -1),即2x -y -4=0. 4分(2)因为f(x)=ax 2-(4a +2)x +4lnx ,所以242(42)42(1)(2)()2(42)ax a x ax x f x ax a x x x x-++--'=-++==,其中x >0.①当a =0时,2(2)()x f x x-'=-,x >0. 由f ′(x)>0得,0<x <2,所以函数f(x)的单调增区间是(0,2);单调减区间是(2,+∞); 6分②当0<a <12时,因为1a >2,由f ′(x)>0,得x <2或x >1a. 所以函数f(x)的单调增区间是(0,2)和(1a ,+∞);单调减区间为(2,1a); 8分③当a =12时,2(2)()0x f x x-'=≥,且仅在x =2时,f ′(x)=0, 所以函数f(x)的单调增区间是(0,+∞);④当a >12时,因0<1a <2,由f ′(x)>0,得0<x <1a或x >2, 所以函数f(x)的单调增区间是(0,1a )和(2,+∞);单调减区间为(1a,2).综上,当a =0时,f(x)的单调增区间是(0,2),单调减区间是(2,+∞); 当0<a <12时,f(x)的单调增区间是(0,2)和(1a ,+∞),减区间为(2,1a);试卷第8页,总9页当a =12时,f(x)的单调增区间是(0,+∞); 当a >12时,f(x)的单调增区间是(0,1a )和(2,+∞),减区间为(1a,2). 10分考点:利用导数求函数切线方程,利用导数求函数单调区间20.如图,在平面直角坐标系xOy中,椭圆C :22221(0)x y a b a b +=>>短轴长是2.(1)求a ,b 的值;(2)设椭圆C 的下顶点为D ,过点D 作两条互相垂直的直线l 1,l 2,这两条直线与椭圆C 的另一个交点分别为M ,N .设l 1的斜率为k(k ≠0),△DMN 的面积为S ,当16||9S k >时,求k 的取值范围.【答案】(1)a =2,b =1(2)(⋃. 【解析】试题分析:(1)两个未知数,两个独立条件.由21c a b ⎧=⎪⎨⎪=⎩a 2=b 2+c2,解得a =2,b =1.正确解答本题需注意短轴长为2,b 而不是,b (2)本题关键是用l 1的斜率为k 表示出△DMN 的面积,因为为直线l 1与椭圆C 的交点,所以由直线l 1方程与椭圆C 的方程联立方程组得M坐标为222841(,)1414k k k k -++,从而有28|14k DM k==+.由于N 与M 相似性,可用1k -代k 直接得24DN k=+,所以△DMN 的面积S =222132(1)||2(14)(4)k k DM DN k k +⋅=++,到此只需将S 代入16||9S k >,并化简可得k 的取值范围为(⋃. 试题解析:(1)设椭圆C 的半焦距为c ,则由题意得21c a b ⎧=⎪⎨⎪=⎩,又a 2=b2+c 2,解得a =2,b =1. 4分(2)由(1)知,椭圆C 的方程为2214x y += 所以椭圆C 与y 轴负半轴交点为D(0,-1).因为l 1的斜率存在,所以设l 1的方程为y =kx -1.代入2214x y +=,得222841(,1414k k M k k-++, 从而28||14k DMk==+. 6分 用1k -代k 得24DN k =+所以△DMN 的面积S =222132(1)||2(14)(4)k k DM DN k k +⋅=++ 8分则||S k = 22232(1)(14)(4)k k k +++因为16||9S k >,即22232(1)16(14)(4)9k k k +>++ 整理得4k 4-k 2-14<0,解得74-<k 2<2 所以0<k 2<2,即k <0或0<k 从而k 的取值范围为(⋃. 考点:椭圆中基本量,直线与椭圆交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市2011-2012学年度第一学期高二期末调研文科数学卷 2012.01注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为100分,考试时间为100分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答卷纸的密封线内.试题的答案写在答卷纸...上对应题目的答案空格内.考试结束后,交回答卷纸. 一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答.卷纸..相应位置....上1.命题“ x ∈R ,x 2≥0”的否定是 ▲ . 2.已知函数f (x )=x 2-x ,则f ′(x )= ▲ .3.已知复数z =2+i (i 为虚数单位),则_z 对应的点在第 ▲ 象限. 4.双曲线x 25-y 24=1的焦点坐标是 ▲ .5.设直线l 1:ax -2y +1=0,l 2:(a -1) x +3y =0,若l 1// l 2,则实数a 的值是 ▲ . 6.顶点在原点,焦点在x 轴上的抛物线经过点(2,2),则此抛物线方程为 ▲ . 7.已知双曲线x 2-y 2b2=1(b >0)的一条渐近线的方程为y =2x ,则b 的值是 ▲ .8.函数f (x )=12x -sin x 在区间[0,π]上的最小值是 ▲ .9.设椭圆x 2a 2+y 2b2=1(a >b >0)的右准线与x 轴的交点为M ,以椭圆的长轴为直径作圆O ,过点M 引圆O 的切线,切点为N ,若△OMN 为等腰直角三角形,则椭圆的离心率为 ▲ .10.如图,直线l 是曲线y =f (x )在x =4处的切线,则f ′(4)= ▲ .11.若圆x 2+y 2=r 2(r >0)与圆(x 的取值范围是▲ . 12.给出下列命题①“a >b ”是“a 2>b 2”的充分不必要条件; ②“lg a =lg b ”是“a =b ”的必要不充分条件;③若x , y ∈R ,则“|x |=|y |”是“x 2=y 2”的充要条件; ④△ABC 中,“sin A >sin B ”是“A >B ”的充要条件. 其中真命题是 ▲ .(写出所有真命题的序号)13.观察下列等式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…从中可归纳得出第n 个等式是 ▲ .14.设函数f (x )在其定义域D 上的导函数为f ′(x ).如果存在实数a 和函数h (x ),其中h (x )对任意的x ∈D 都有h (x )>0,使得f ′(x )=h (x )(x 2-ax +1),则称函数f (x )具有性质P (a ).给出下列四个函数:①f (x )=13x 3-x 2+x +1;②f (x )=ln x +4x +1;③f (x )=(x 2-4x +5)e x ;④f (x )=x 2+x2x +1,其中具有性质P (2)的函数是 ▲ .(写出所有满足条件的函数的序号)二、解答题:本大题共6小题,共计58分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分8分)已知复数z1=m(m-1)+(m-1)i是纯虚数.(1)求实数m的值;(2)若(3+z1) z=4+2i,求复数z.16.(本题满分8分)已知命题p:函数y=log a x在(0,+∞)上是增函数;命题q:关于x的方程x2-2ax+4=0有实数根.若p∧q为真,求实数a的取值范围.17.(本题满分10分)设直线l:4x+3y+a=0和圆C:x2+y2+2x-4y=0.(1)当直线l过圆C的圆心时,求实数a的值;(2)当a=3时,求直线l被圆C所截得的弦长.18.(本题满分10分)某公司需制作容积为216 ml 的长方体形饮料盒,饮料盒底面的长是宽的2倍.当饮料盒底面的宽为多少时,才能使它的用料最省?19.(本题满分10分)已知椭圆C 的焦点为F 1(-5,0),F 2(5,0),焦点到短轴端点的距离为210. (1)求椭圆C 的标准方程;(2)设点P 是椭圆C 上的一点,且在第一象限.若△PF 1F 2为直角三角形,试判断直线PF 1与圆O :x 2+y 2=52的位置关系.20.(本题满分12分)已知函数f (x )=a ln x +12x 2+(a +1)x +1.(1)当a =-1时,求函数f (x )的单调增区间;(2)若函数f (x )在(0,+∞)上是增函数,求实数a 的取值范围;(3)若a >0,且对任意x 1,x 2∈(0,+∞),x 1≠x 2,都有| f (x 1)-f (x 2)|>2| x 1-x 2|,求实数a的最小值.南京市2011-2012学年度第一学期高二期末调研答卷纸(文科数学)2012.01一、填空题:本大题共14小题,每小题3分,共42分.请把答案填写在答.卷纸..相应位置....上. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.二、解答题:本大题共6小题,共58分.请在答.卷纸..指定区域内.....作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分8分)16.(本小题满分8分)17.(本小题满分10分)18.(本小题满分10分)19.(本小题满分10分)20.(本小题满分12分)南京市2011-2012学年度第一学期高二期末调研文科数学参考答案及评分标准卷 2012.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题3分,共42分)1.ヨx ∈R ,x 2<0 2.2x -1 3.四 4.(±3,0) 5.25 6.y 2=4x 7.28.π6-32 9.22 10.1211.(1,11) 12.③④ 13.n +(n +1)+(n +2)+…+[n +2(n -1)]=(2n -1)2(n ∈N*) 14.①②③二、解答题(本大题共6小题,共58分.解答应写出文字说明、证明过程或演算步骤) 15.(本题满分8分,第1小题4分,第2小题4分)解:(1)由题意得⎩⎨⎧m (m -1)=0,m -1≠0. (2)分解得m =0. (4)分(2)当m =0时,z 1=-i .由(3+z 1) z =4+2i ,即(3-i) z =4+2i ,得z =4+2i 3-i ………………………………………………………………………………6分=1+i . (8)分 16.(本题满分8分)解: 当p 为真命题时,a >1. ………………………………………………………………2分当q 为真命题时,△=4a 2-16≥0.解得a ≤-2或a ≥2. ………………………………………………………………………4分因为p ∧q 为真,所以p 和q 都是真命题.⎩⎨⎧a >1,a ≤-2或a ≥2. …………………………………………………………………6分所以实数a 的取值范围是[2,+∞). ………………………………………………………8分 17.(本题满分10分) 解:(1)由x 2+y 2+2x -4y =0,得(x +1)2+(y -2)2=5. 所以圆C 的圆心为(-1,2),半径为5. (2)分因为直线l 过圆C 的圆心,所以-4+6+a =0.解得a =-2. (4)分(2)当a =3时,圆心(-1,2)到直线l :4x +3y +3=0的距离为 d =|4×(-1)+3×2+3|42+32=1. ……………………………………………………………………7分则2r 2-d 2=4.所以直线l 被圆C 所截得的弦长为4. (10)分 18.(本题满分10分)解:设饮料盒底面的宽为x cm ,高为h cm ,则底面长为2x cm . 根据V =x ·2x ·h ,可得h =2162x 2.…………………………2分 所以,表面积S (x )=2(x ·2x +x ·h +2x ·h )=2(2x 2+3x ·2162x 2)=4(x 2+162x ) (x >0) ……………………………………4分由S '(x )=4(2x -162x2)=0, (6)分得x =33. (8)分 当0<x <33时,S '(x )<0,函数S (x ) 在(0,33)是减函数; 当x >33时,S '(x ) >0,函数S (x ) 在(33,+∞)是增函数. 所以,当x =33时,S (x )取得极小值,且是最小值.答:当饮料盒底面的宽为3 3 cm 时,才能使它的用料最省.…………………………………10分 19.(本题满分10分,第1小题4分,第2小题6分) 解:(1)由题意可得a =210,c =5, …………………………………2分 则b 2=15.所以椭圆C 的方程为x 240+y 215=1. ……………………………………4分(2)圆O :x 2+y 2=52的圆心为原点,半径r =102.①当∠PF 2F 1为直角时,点P 的坐标为(5, 3104). ……………5分直线PF 1的方程为y =3410(x +5). 此时圆心到直线PF 1的距离为1513<102.所以直线PF 1与圆O :x 2+y 2=52相交. …………………………7分②当∠F 1PF 2为直角时,设点P 的坐标为(x ,y ).解⎩⎨⎧x 240+y 215=1,x 2+y 2=52.得⎩⎨⎧x =4,y =3.所以点P 的坐标为(4,3). …………………………………………9分则点P 到椭圆右焦点(5,0)的距离为10.此时圆心O 到直线PF 1的距离为102.所以直线PF 1与圆O :x 2+y 2=52相切. …………………………10分20.(本题满分12分)解:(1)当a =-1时,f (x )=-ln x +12x 2+1.则f ′(x )=-1x +x . ……………………………………2分令f ′(x )>0,得x <0或x >1.所以函数函数f (x )的单调增区间为(1,+∞).………………4分(2)因为函数f (x )在(0,+∞)上是增函数,所以f ′(x )==x 2+(a +1) x +a x =(x +1)( x +a )x ≥0对x ∈(0,+∞)恒成立.…6分 即x +a ≥0对x ∈(0,+∞)恒成立.所以a ≥0. ……………………………………8分即实数a 的取值范围是[0,+∞).(3)因为a >0,所以函数f (x )在(0,+∞)上是增函数.因为x 1,x 2∈(0,+∞),x 1≠x 2,不妨设x 1>x 2,所以f (x 1)>f (x 2).由| f (x 1)-f (x 2)| 2| x 1-x 2|恒成立,可得f (x 1)-f (x 2)>2(x 1-x 2),即f (x 1)-2x 1>f (x 2)-2x 2恒成立.令g (x )=f (x )-2x ,则在(0,+∞)上是增函数. ……………10分所以g ′(x )=a x +x +(a +)-2=x 2+(a -1) x +ax ≥0对x ∈(0,+∞)恒成立.即x 2+(a -1) x +a ≥0对x ∈(0,+∞)恒成立.即a ≥-x 2-xx +1对x ∈(0,+∞)恒成立因为-x 2-x x +1=-(x +1+2x +1-3)≤3-22(当且仅当x +1=2x +1即x =2-1时取等号),所以a ≥3-22.所以实数a 的最小值为3-22. …………………………12分。
