拱桥荷载受力计算
毕业设计(论文)_拱桥静载受力分析和模态分析计算
目录摘要第一章绪论.................................................1.1拱桥概述............................................拱桥的特点..............................................国内外发展状况 ........................................我国拱桥的发展方向及主要结构型式........................我国拱桥的施工方法......................................1.2论文简述............................................课题介绍 ...........................................建模依据 ...........................................第二章ANSYS软件介绍.....................................2.1 ANSYS 发展........................................2.2主要功能及特点......................................2.3典型的分析过程.....................................2.4负载定义及附表...................................... 第三章有限元分析 ........................................3.1模型参数............................................3.2建模过程............................................3.3加载及后处理........................................简述自重(deadweight) 作用在中跨处施加车辆荷载(load)第四章模型实验简介第五章数据分析比较4.1 .....................第六章结论...........展望 .............致谢 .............参考文献 .........拱桥静载受力分析和模态分析计算摘要：本文对跨度为3米，矢跨比为1/6的系杆拱桥在一定外力作用下的应力、应变、位移和拱桥模态利用an sys软件，进行了有限元建模和分析计算，得到了相应的计算结果，并与实验结果进行了比对，证明了建模是合理的，计算结果是可信的。
§9.3拱桥的计算
y1ds ∫s EI (9.21) ys = ds EI f (chξk − 1) (6) y1 = m −1
dx l1 = = dξ = l 1 + tg 2ϕ dξ ds cos ϕ cos ϕ 2
l = 1 + η 2 sh 2 kξ dξ 2
f ys = ⋅ m −1
∫0 (chkξ − 1)
2
−1
(
)
(7 )
（2）若已知m，则y1由（6）求得，换言之，当跨径和矢 高确定后， y1仅随m而变化，故有不同的m可得到不同的 拱轴线形状。其线形特征可用1/4点纵坐标的大小表示：
y1 =
4
f ⎛ k ⎞ ⎜ ch − 1⎟ m − 1⎝ 2 ⎠
k chk + 1 m +1 Q ch = = 2 2 2
y1 ∴
4
f
=
m +1 −1 1 2 = m −1 2(m + 1) + 2
(8)
可见，随m 增大，拱轴线抬高
（3）一般的拱桥中，
g j > gd
故 m>1(悬连线拱的拱轴系数，宜采用2.814~1.167， 随跨径的增大或矢跨比的减小而减小)； 当m=1时，表示恒载压力均布，压力线为二次抛物 线，
9.3 拱桥的计算
拱桥计算包括成桥状态受力分析和强度、刚度、稳定验 算以及必要的动力分析，施工阶段结构受力分析和验算。
9.3.1 悬链线拱的拱轴方程及几何性质
（一）实腹式悬链线拱 采用恒载压力线（不计弹性压缩）作为拱轴线
M d = 0 Qd = 0
Hg
1、悬链线拱轴方程
Mx 对任意截面取矩： y1 = Hg
' 22
拱桥计算书
设计计算书一、设计资料（一）设计标准设计荷载：汽车-20级，挂车-100，人群荷载3KN/m2 净跨径：L0=16m净矢高：f0=2.28m桥面净宽：净6.5+2*（0.25+1.5m人行道）(二)材料及其数据拱顶填土厚度h d=0.5m,γ3=22KN/m3拱腔填料单位重γ=20KN/m3腹孔结构材料单位重γ2=24KN/m3主拱圈用10号砂浆砌号60块石,γ1=24KN/m3,极限抗压强度R j a=9.0MP a,弹性模量E＝800R a j。
(三)计算依据1、交通部部标准《公路桥涵设计通用规范（JTJ021-89）》，人民交通出版社，1989年。
2、交通部部标准《公路砖石及混凝土桥涵设计规范（JTJ022-85）》，人民交通出版社，1985年。
3、《公路设计手册-拱桥》（上、下册），人民交通出版社，1994年。
4、《公路设计手册-基本资料》，人民交通出版社，1993年。
二、上部结构计算（一）主拱圈1、主拱圈采用矩形横截面，其宽度b0＝10.0m,主拱圈厚度d=mkl01/3=6*1.2*16001/3=84.2cm,取d=85cm。
假定m=1.988,相应的y1/4/f=0.225,查《拱桥》附表（Ⅲ）-20（9）得Ψj=33003′32″,sinΨj=0.54551, cosΨj=0.83811 2、主拱圈的计算跨径和矢高L=l0+dsinΨj=16+0.85*0.54551=16.4637mf=f0+d/2-dcosΨ/2=2.28+0.85/2-0.85*0.83811/2=2.3488j3、主拱圈截面坐标将拱中性轴沿跨径24等分，每等分长Δl=l/24=0.6860m,每等分点拱轴线的纵坐标y1=[《拱桥》（上册）表（Ⅲ）-1值]f,相应拱背曲面的坐标y′1=y1-y上/cosΨ,拱腹曲面相应点的坐标y″1=y1+y下/cosΨ,具体位置见图1-1，具体数值见表1-1。
主拱圈截面计算表表1-1(二)拱上结构1、主拱圈拱上每侧对称布置截面高度d′＝0.25m的石砌等截面圆弧线腹拱圈，其净跨径l′＝1.5m,净矢高f′＝0.3m,净矢跨比为1/5。
拱桥的计算例题
2008-4-6
桥梁工程
解：
y1/4
2008-4-6
桥梁工程
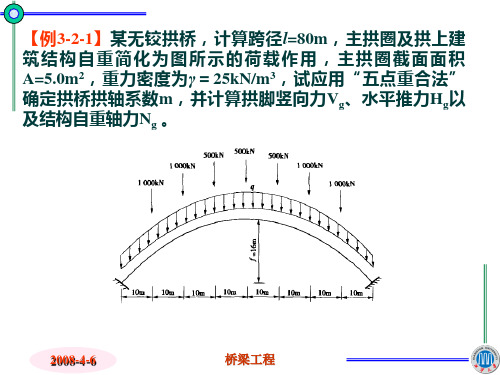
【例3-2-2】某无铰拱桥，计算跨径l=80m，主拱圈及拱上建 筑结构自重简化为图所示的荷载作用，主拱圈截面面积 A=5.0m2，重力密度为γ＝25kN/m3，由“五点重合法”确定 拱桥拱轴系数m=2.24，截面抗弯惯矩I=1.0m4，计算考虑弹性 压缩后，拱脚竖向力Vg、水平推力Hg以及结构自重轴力Ng， 以及弹性压缩引起的拱脚截面弯矩。
V KVV 216.8790.1662250 280.6kN N H1 cos j V sin j 819.2 0.7357 280.6 0.68284 790.1kN
2、拱脚最大负弯矩及相应轴力
1）根据
l 50m
拱脚最大负M及汽车-20查《基本资料》第79页的等代荷载：
KM 23.547kN / m, KH 10.932, KV 16.724kN / m
M1/4
1
f M j 2(m 1) 2
半拱悬臂集中力荷载作用时：
1)假定拱轴系数m=2.514, f/l=16/80 =1/5,查 表(III)-19得:
所有荷载: 所以
2008-4-6
桥梁工程
需重新计算
2)假定拱轴系数m=2.24
所有荷载:
所以 小于半级，因此取拱轴系数m=2.24
3)查表(III)-19得半拱悬臂自重对拱脚截面的竖向剪力为 半拱悬臂集中力对拱脚截面的竖向剪力为:
拱桥的计算
gd o
y1
第三章 拱桥的计算
3.1.2. 空腹式悬链线拱 五点重合法
三铰拱的情形
M A 0 H g
Mj f
M B 0 H g
Ml 4 yl 4
yl 4
Ml 4
f Mj
B
A l1=l/4
Δy l1=l/4
Hg y1/4
f
y1 4 f
1
2m 1 2
3.1.1. 实腹式悬链线拱 实腹式悬链线拱轴系数的确定
φj
φj
d
hj h d /cosφj
d /cosφj
r1 r2 r
hd
d
x=ξl1
f
φj
l1=l/2
第三章 拱桥的计算
3.1.1. 实腹式悬链线拱 拱轴系数与悬链线线 形的关系
m gj
gj
gd
y1 4 f
1
2m 1 2
x
yl 4
Ml 4
f Mj
2
m
1 2
f yl
4
2
1
第三章 拱桥的计算
3.1.2. 空腹式悬链线拱 五点重合法 三铰拱的实际压力线与按五点重合法 确定的悬链线的差异
Δy B
压力线与拱轴线偏离在拱中产生 附加内力
A l1=l/4
l1=l/4
A Mp=ΔyHg B
Hg y1/4
d 2M dx2
x
gd Hg
1 (m 1)
y1 f
x=ξl1 dx=l1dξl1
d 2 y1
d 2
l12 gd Hg
拱桥内力计算51
Hg
Mj f
半拱恒载对拱脚的弯矩
Vg P （半拱恒载重力）
N Hg
cos
三、拱桥内力计算
偏离的影响可按式计算出的 X1, X 2 然后根据静力平
衡条件计算任意截面的轴力N，弯矩M和剪力Q。
N X 2 cos M X1 X 2 ( y1 ys ) H g y Q X 2 sin
向缩短l（右图所示）。由于在实际
结构中，拱顶没有相对水平位移，其 变形受到约束，则在弹性中心处必有
一水平拉力Hg
三、拱桥内力计算
Hg的计算
由变形相容方程有：
其中：
H
g
' 22
l
0
H g
l '
22
l
l
0
dx
sds cos
s
Nds EA
cos
N Hg
N H1
c os
拱顶：数值很小，可不考虑
拱脚： Q H1 sin j V cos j 拱顶：数值较小，可不考虑
三、拱桥内力计算
由于活载弹性压缩产生的内力
活载弹性压缩与恒载弹性压缩计算相似，也在弹性中心产生赘余水平 力H，其大小为：
H
l '
22
Nds cos
s EA
' 22
取脱离体如下图，将各力投影到水平方向有：
N H1 Q sin H1 (1 Q sin )
cos
cos H1
Q sin 相对较小，可近似忽略，则有：
H1
N H1 cos
三、拱桥内力计算
拱桥结构计算书
B2= -12.15810
C2= -10.6084
D2= -3.7665
A2*B1-A1*B2= -32.3521
aEcI= 462424.49
根据《公路桥涵地基与基础设计规范》JTG D63-2007附录P第 P.0.4第三条规定 ：
−
h =αh
13.46 m＞2.5m时， kh=0
(1)当H0=1时
Pmix= 95.6214 kN
2）、桩基最大水平位移的验算
按《公路桥涵地基与基础设计规范》JTG D63-2007附录P表P.0.4中公式计算 x0
x0
=
δ H (0) 0 HH
+
M
0δ
(0) HM
=
0.0058 m
= 5.80 ＜6mm
φ0 值：
符合设计要求
φ0
=
−(H0δM(0H)
+
M0δ
(0) MM
所以，b1=
1.58 m
（2）、桩的变形系数
α = 5 mb1 式中EI=0.8EcI= 1099560 EI
KN/m2
承台底以下hm=2(d+1)= 4
m深度内深度内只有一层土 故m值直接查《公路桥涵地基
与基础设计规范》JTG D63-2007附录P表P.0.2-1取用，即m=
3000
则α =
0.34
根据《公路桥涵设计手册 墩台与基础》中得到：
ρ=
fcd fsd
.
Br − A(ηe0) C(ηe0) − Dgr
=
= 0.0111
1.113 %
Nu = Ar2 fcd +Cρr2 fsd = 1876.63 KN ＞ 1377.01 kN
拱桥计算理论
（4）建模时，根据联合作用的大小，选择主拱或拱圈和拱 上建筑的建模图式。
一、概 述 Introduction
1、联合作用：荷载作用下拱上建筑参与主拱圈共同受力；
（5）主拱圈不计联合作用的计算偏于安全，但拱上结构不 安全，不合理。
（6）梁板式拱上建筑不考虑联合作用，拱式拱上建筑考虑 联合作用。
（7）整体型上承式拱桥必须考虑联合作用。
一、概 述 Introduction
2、活载横向分布：活载作用不论是否在桥面中心， 使主拱截面应力不均匀的现象。
（1）活载横向分布与许多因素有关，主要与桥梁的横向 构造形式有直接关系。
（2）在板拱、箱拱情况下常常不计荷载横向分布，认为 主拱圈全宽均匀承担荷载。
（ Calculation of Arch Bridges ）
一、拱轴线的选择与确定 二、主拱圈结构恒载与使用荷载内力计算 三、主拱附加内力计算 四、主拱在横向水平力及偏心荷载下计算 五、拱上建筑计算 六、连拱作用计算简介 七、拱桥动力及抗震计算要点 八、主拱内力调整 九、考虑几何非线性发主拱内力计算简介 十、主拱圈结构验算
程。
经典线性理论基于三个基本假定，这些假定使得三组基本方程成为线
性。材料的应力、应变关系满足广义虎克定律；位移是微小的；约束 是理想约束。
只要研究对象不能满足线性问题基本假定中任何一个时，就转化为各
种非线性问题。
一、概 述 Introduction
3、非线性影响考虑
（1）什么是非线性？ Odin说过“ 我们生活在一个非线性世界里”。 线性理论在许多情况下并不适用，开始了对非线性力学问题的研究。 固体力学中有三组基本方程，即：本构方程、几何运动方程和平衡方
拱桥的计算
1 f m ( 2) 2 1 2 y1/ 4
2
悬链线
应当注意，用上述方法确定空腹 拱的拱轴线，仅与其三铰拱恒载 压力线保持五点重合，其它截面， 拱轴线与三铰拱恒载压力线都有 不同程度的偏离。对大跨度空腹 拱桥，这种偏离影响必须加以考 虑
(a)
悬链线 (b)
大量计算证明，从拱顶到1/4点， 一般压力线在拱轴线之上；而从 1/4点到拱脚，压力线则大多在拱 (c) 轴线之下。拱轴线与相应三铰拱恒 载压力线的偏离类似于一个正弦波。
（2）、布集度 gd
gd 1hd 2 d
拱脚恒载分布集度
gj
d g j 1hd 2 3h cos j
其中
1, 2 , 3
d
拱顶填料、拱圈及拱腹填料的容重
hd 拱顶填料厚度
拱圈厚度
j 拱脚处拱轴线的水平倾角 d d hf 2 2cos j
l x l1 2
ds
其中：
则：
这样：
ds
l 1 2 sh 2 k 2
ys
y1ds
s
ds
s
f 0 m 1
1
(chk 1) 1 2 sh 2 k d
1
0
1 2 sh 2 k d
（三）、恒载内力计算
(a)
悬链线 (b) 三铰拱恒载压力线 /4 /4
对称无铰拱若从拱顶切开取基本结构，多余力M（弯
矩），H （轴力）为对称，而V（剪力）是反对称的， 故知副系数
13 31 0 23 32 0
ys 引用弹性中心，设“ 刚臂 ”长为 y1ds s EI 可以证明当 ys ds 时，弹性中心处 12 21＝0 s EI
拱桥设计计算内容及方法
拱桥设计计算内容及方法
2.拱桥整体受力计算：拱桥是一个整体结构，因此需要进行整体的受
力计算。
这包括确定整个拱桥受力的大小、方向和分布情况，以及确定拱
桥的整体稳定性。
常用的方法包括静力学平衡方法、弹性力学方法和有限
元方法等。
3.拱桥的固有频率计算：拱桥是一个动力结构，其固有频率对于设计
的安全性是非常重要的。
因此，需要计算拱桥的固有频率，以评估其在自
然频率下的抗风、抗震等性能。
4.应力和变形计算：拱桥在使用过程中会受到荷载的作用，因此需要
计算拱桥在荷载作用下的应力和变形情况，以评估拱桥的安全性能。
常用
的方法包括弹性力学法、有限元法等。
5.断面设计：根据拱桥的受力情况，进行断面设计，包括确定构件的
尺寸和材料。
断面设计需要满足强度和刚度的要求，同时还要考虑构件的
自重和施工的可行性等因素。
6.水力条件计算：对于水上拱桥来说，还需要计算水流对拱桥的冲击
力和涌浪力等水力条件，以评估拱桥的稳定性和安全性。
在进行拱桥设计计算时，常用的工具和软件包括AutoCAD、ANSYS、STAAD.Pro等。
这些工具可以帮助工程师进行受力分析、应力计算和断面
设计等。
同时，还需要参考相关的设计规范和规范，如公路桥梁设计规范、钢结构设计规范等，以确保拱桥的设计计算符合规范和标准的要求。
总之，拱桥设计计算是一项复杂而关键的工作，需要对拱桥结构进行
全面的受力、应力和变形分析，并根据工程实际要求和设计规范进行设计。
只有进行合理的设计计算，才能保证拱桥的安全性和可靠性。
拱桥计算书
等截面悬链线圬工拱桥计算一． 设计资料（一） 设计标准1．设计荷载公路二级，人群荷载3kN/㎡。
2．跨径及桥宽净跨径l 0=40m ，净失高m f 8= ,净失跨比5100=l f 。
桥面净宽为净7+2×（0.25+0.75m 人行道），m B 9= 。
（二） 材料及其数据中国范文网【/】详细出处参考：/post/215.html 还有海量相关文章1.拱上建筑拱顶填料厚度，m h d 5.0=，包括桥面系的计算厚度为0.736m ，平均重力密度31/20m kN ＝γ。
拱上护拱为浆砌片石，重力密度32/23m kN =γ。
腹孔结构材料重力密度33/24m kN =γ。
主拱拱腔填料为砂、砾石夹石灰炉渣黄土，包括两侧侧墙的平均重力密度4γ=kN/3m 2.主拱圈M10砂浆砌MU40块石，重力密度33/24m kN =γ。
轴心抗压强度设计值cd f =2323/1012.42.1/1044.3m kN m kN ⨯=⨯⨯。
抗剪强度设计值MPa f vd 073.0=。
弹性模量MPa E m 073.0=。
拱圈设计温差为C 15± 3.桥墩地基土为中等密实的软石夹沙、碎石，其容许承载力[0σ]=500kN/㎡。
基础与地基间的滑动摩擦系数取5.0=μ。
(三)设计依据1.交通部部标准《公路桥涵设计通用规范》，（JTG D60-2004）2004年。
简称《桥规1》；2.交通部部标准《公路圬工桥涵设计规范》（JTG D61-2005）2005年，人民交通出版社，《简称桥规2》；3.交通部部标准《公路桥涵地基与基础设计规范》，人民交通出版社，简称《桥规3》；4.《公路设计手册-拱桥》上下册，人民交通出版社，1978。
简称《拱桥》。
二、主拱圈计算（一）确定拱轴系数拱轴系数m 值的确定，一般采用“五点重合法”，先假定一个m 值，定出拱轴线，拟定上部结构各种几何尺寸，计算出半拱恒载对拱桥截面形心的弯矩j M ∑和自拱顶至4l 跨的恒载对4l跨截面形心的弯矩4l M ∑。
拱桥计算
gx d 2 y1 1 d 2M 2 2 dx H g dx Hg
（3）
由上式可知，为了计算拱轴线（压力线）的一般方程，需首先知道恒载 的分布规律，对于实腹式拱，其任意截面的恒载可以用下式表示：
g x g d y1 gd
拱顶处恒载强度；
（4）
拱上材料的容重。
由上式，取y1=f，可得拱脚处恒载强度 g j 为：
反双曲余弦函数对数表示
（10）
当m=1时 gx=gj，可以证明，在均布荷载作用下的压力线为二次抛 物线，其方程变为：
y1 f 2
由悬链线方程可以看出，当拱的跨度和失高确定后，拱轴线各点的坐 标取 确于拱轴系数m。其线形特征可用l/4点纵坐标y1/4的大小表示： 当
1 2
时， y1 y1/ 4 ；代
拱轴线与压力线不相符
不考虑弹性压缩
弹性压缩
1、不考虑弹性压缩的恒载内力 1）实腹拱 实腹式悬链线的拱轴线与压力线重和，恒载作用拱的任意截面存 在轴力，而无弯矩，此时拱中轴力可按以下公式计算。 在进行悬链线方程推导时有：
l12 g d k (m 1) Hg f
2
（11）
恒载水平推力Hg ：利用上式有
y1
f (chk 1) m 1
（9）
上式为悬链线方程。
其中ch k为双曲余弦函数：
e k e k chk 2
对于拱脚截面有：=1，y1=f，代入式（9）可得：
chk m
通常m为已知，则可以用下式计算k值：
k ch1m ln(m m 2 1)
2、拱轴系数m值的确定 （1）实腹式拱m值的确定
m
gj gd
拱顶恒载分布集度 gd
稳定性验算拱桥
5
五、施工阶段的主拱计算 主拱的受力在不同的施工阶段是不同的，且与成桥后的主拱受力情况相 差较大，必须验算施工阶段主拱的强度和稳定性。
（一）缆索吊装施工阶段的主拱验算
1、拱肋（箱）脱模吊运过程中的验算 •将预制拱肋（箱）顶起脱离底板模板时，应进行脱模验算 可近似不考虑拱肋曲率，按直线梁计算，支点位置由千斤顶或吊 机的吊点确定
1、纵向稳定验算
•对砖、石及混凝土主拱圈
对于长细比不大，且f/l在0.3 以下的拱，其纵向稳定性验 算一般可以表达为强度校核 的形式，即将拱圈（肋）换 算为相当长度的压杆，按平 均轴向力计算，以强度效核 控制稳定，对砖、石及混凝 N 土主拱圈（拱肋），其验算 公式为：
f
N H cosm
Nj AaR j /m
EI b ) EI a
倍；
以上计算没有考虑拱轴在荷载作用下变形的影响
3
2、横向稳定性检算
宽跨度比小于1/20的拱桥、肋拱桥、特大跨拱桥以及无支架施工的 拱圈均存在横向稳定问体，设计时必须检算，检算公式如下：
K2
NL' Nj
4~5
式中：K2为纵向稳定安全系数：
N
' L
拱横向失稳时的平均临界轴力；
•对于板拱或采用单肋合龙时的拱肋，可以近似地用矩形等截面抛
梁设计规范的有关规定采用，主拱为偏心受压构件时，按下式计算
1
12[11.33(e0 )2]
rw
式中：为与砌体砂浆有关的系数，对于5号、2.5号、1号砂浆， 分
别采用0.002、0.0025、0.004；对混凝土通常采用0.002
l0 hw
l0 rw
对矩形截面 非矩形截面
拱桥计算书
推荐方案：钢混组合梁蝶形拱桥计算分析1 主桥结构概况主桥为双索面的下承式系杆拱桥，主桥跨径为156m；主拱肋为钢箱形拱结构，副拱肋、连杆和横联均为圆管结构，桥面系为钢混组合梁结构。
吊杆为平行钢丝吊索。
拱肋分为主拱和副拱，主拱外倾，副拱内倾。
两片副拱肋之间设置“一”字撑使其连成整体。
1.计算模型成桥状态模拟计算分析图式结构分析采用空间模型建立全桥计算图式，主梁、主拱、副拱、连杆、横撑、横梁等结构采用空间梁单元，吊杆采用空间桁架单元。
计算模型如图所示。
桥面系采用双梁计算模型，计算程序采用MIDAS CIVIL 2010软件。
2.计算荷载计算主要考虑荷载：桥梁结构自重，二期铺装和管线等附属设施，车辆荷载、人群荷载、温度荷载以及风荷载。
1）恒载2）温度荷载体系整体按升温+30°C，降温-30°C计。
桥面板局部升降温按《公路桥涵设计通用规范》（JTG D60-2004）梯度温度效应计算。
3）活载公路－Ⅰ级，根据桥宽，横向按双向四车道或六车道进行加载，横向偏载系数1.15。
3.施工过程模拟1）支架施工主梁、横梁和拱肋；2）安装吊杆，安装预制桥面板并现浇湿接缝，拆除支架，张拉第一轮拉力；3）上桥面铺装，张拉成桥吊杆力，调整系杆力；2 结构空间静力计算单位及符号说明：轴力单位为kN，以拉为正，以压为负；弯矩单位为kN*m，下缘受拉为正；位移单位mm；应力单位MPa，以受拉为正，受压为负。
1. 成桥阶段计算结果（1）成桥阶段主拱轴力图（2）成桥阶段主拱弯矩图（3）成桥阶段副拱轴力图（4）成桥阶段副拱弯矩图（5）成桥阶段主梁轴力图（6）成桥阶段主梁弯矩图（7）成桥阶段主拱应力图（8）成桥阶段副拱应力图（9）成桥阶段连杆应力图（10）成桥阶段钢梁上缘应力图（11）成桥阶段钢梁下缘应力图（12）成桥阶段主梁混凝土板上缘应力图（13）成桥阶段主梁混凝土桥面板下缘应力图2. 正常使用阶段计算结果经计算表明，本桥最不利荷载工况为恒载+车辆+人群+温度的组合。
拱桥内力计算
s EI
EI
l 2
0
1 2sh2k d l3
EI
式中： 1 , , 1
为系数，可查相应的表格得到；
2kf
l(m 1)
为了计算变位，在计算MP时，可利 用对称性，将单位荷载分解为正对
称和反对称两组荷载，并设荷载作
用在右半拱。
1P
M1M P ds s EI
2P
M
2 1
ds
l
s EI EI
l 0
12sh2k d l 1 EI 1
22
M
2 2
ds
s EI
l
EI
l 0
f m 1
(chk
1)
f m 1
chk
1 2sh2k d
lf 2
EI
33
M
2 3
ds
l3
l
l H g dx
0 EAcos
Hg
l dx
0 EAcos
' 22
M 22ds s EI
N
2 2
ds
s EA
y2ds s EA
cos2 ds
s EA
(1 ) y2ds
s s
（1－2－45）
在设计中小跨径的空腹式拱桥时可以偏于安全地不考虑偏离弯 矩的影响。大跨径空腹式拱桥的恒载压力线与拱轴线一般比中、 小跨径偏离大，一般要计入偏离的影响。
2、弹性压缩引起的内力
在恒载产生的轴向压力作用下，拱圈的弹性变 性表现为拱轴长度的缩短。首先将拱顶切开， 假设拱桥圈可以自由变形，并假设弹性压缩会
拱桥计算书
目录1.方案比选 (3)设计原则 (3)方案设计 (3)方案选择 (6)2.设计要求及基本数据 (7)设计要求和数据 (7)3.结构计算 (7)主拱圈截面要素及尺寸拟定 (7)拱轴系数的确定 (9)上部结构设计 (9)上部恒载计算 (11)内力计算 (15)主拱圈内力计算 (15)桥面系计算 (19)盖梁计算 (28)立柱计算 (37)各结构的配筋计算及应力验算 (39)空心板配筋计算及应力验算 (39)盖梁配筋计算及应力验算 (44)立柱配筋计算 (47)主拱圈配筋计算 (48)支座计算 (52)桥台计算 (53)1.方案比选桥梁设计原则1)．适用性：满足车辆个人群的通行，即要满足基本的交通量问题。
此外，除桥面交通量，桥下如果有过水量，桥下通行高度、通行量要求是，设计也需要考虑。
并要求考虑到长久发展问题，即将未来交通量的增长考虑进去，保证增长后的交通量，持续发展还包括桥梁的修理、维护保养，设计都需要考虑到。
2).安全与舒适性：在满足交通量的同时，还需要保证车辆、人群通行的舒适问题。
桥面的竖向、横向震动要得到控制。
安全问题在所有设计中都应放在第一位，桥面系需要有足够的承载力安全保障，桥下支撑结构同样需要验算各种受力问题。
3).经济性：经济性包括施工难以程度，桥梁材料的消耗，建成后的后期维修、保养费用，在设计中都需要考虑到。
4).先进性：桥梁设计施工等都应劲量优先使用先进的设计、施工技术和理念。
便于施工、架设。
运用先进的施工技术还能够有效的减短施工周期，保证在短时间完成最优、最安全的设计工程。
5).美观：建筑发展中美观也是一个必不可少的因素，桥梁设计需要考虑与周围景色的协调，保证整体的美观效果。
方案设计方案一：双塔三跨式斜拉桥①桥梁整体布置：9+32+9，全长50m，布置图见图。
②上部结构布置：桥面净宽+2×加上的人行道护栏，桥面横坡为双向2%。
③下部构造：采用钻孔灌注桩做主塔基础，每个主塔采用4根钻孔桩。
拱桥的计算
Rg
l1 0
g x dx
m2 2 ln(m
1 m2
1)
g d l0
k
'g
g d l0
(0.527
~
0.981) g d l0
拱圈各截面轴力： N H g / cos
kg , k 'g 可从《拱桥（上）》第580页表（III）-4查得。
（1）不考虑弹性压缩的结构自重内力—空腹式拱
空腹式悬链线无铰拱的拱轴线与压力线均有偏离，计算时 分为两部分相叠加：
在 y1/4 =0.25至 y1/4 =0.18的范围内，以0.005为级差，编制了
f0
f0
悬链线拱轴坐标的表格，拱轴系数m 和
y1/ 4
共分14档,两者
一一对应，由于
y1/ 4 f0
f0
取成了定数，拱轴系数m
就成了另数。
11.1.3 拱轴系数的确定
（1）实腹式拱桥拱轴系数的确定
gd 1hd 2d
五点弯矩为零的条件：
#1、拱顶弯矩为零：
M d 0, Qd 0 ，只有轴力 H g
#2、拱脚弯矩为零：
Hg
Ma f0
#3、1/4点弯矩为零：
Hg
M1/ 4 y1/ 4
#4、 得到：
Ma
M1/ 4
f0
y1/ 4
#5、 主拱圈恒载下的
M1/4 ,
Ma,
y1/ 4 f0
可由《拱桥（上）》第988页附录III表(III)-19查得
k ln(m m2 1)
拱轴线各点水平倾角只与 f0 /l0 和 m 有关，该值可 从《拱桥（上）》第577页表（III）-2查得。
11.1.5 基本结构与弹性中心 计算无铰拱内力时，为简化计算常利用弹性中心的特点；将 无铰拱基本结构取为悬臂曲梁和简支曲梁。
桥梁工程-拱桥计算1 - 其它内力计算分享
用GQJS程序计算某拱桥的模型图
裸拱模型图,不考虑拱上建筑联合作用 将腹拱圈与主拱一起建模，考虑拱上建筑联合作用
三、拱桥内力计算
（一）解析法计算主拱圈内力 （二）有限元法计算简介 （三）主拱附加内力计算 （四）主拱在横向力及偏心荷载作用下的计算 （五）拱上建筑的计算 （六）连拱计算简介 （七）拱桥动力及抗震计算要点 （八）主拱内力调整 （九）考虑几何非线性的主拱内力计算简介 （十）主拱圈结构验算
(二)有限元方法计算简介
等截面悬链线拱的附加内力计算
超静定拱中，温度变化、混凝土收缩变形和拱脚变位都会产 生附加内力。
我国许多地区温度变化大，温度引起的附加内力不容忽视。 混凝土收缩徐变引起拱桥开裂。 拱桥墩台变位的影响突出。据统计分析，两拱脚相对水平位
移超过L/1200时，拱桥的承载力就会大大降低，甚至破坏。
✓ 温度变化内力计算 ✓ 混凝土收缩变形影响 ✓ 拱脚变位引起的内力计算 ✓ 水浮力引起的内力计算
Ht
lt
' 22
lt '
22
(升温，t为正，反之，为负 )
升温时，轴力为正，在拱顶，
M t Ht y Ht ( y1 ys ) M为负，拱脚M为正，与该
Nt Ht cos
两截面的控制弯矩方向正好 相反，对拱圈受力有利。
Qt Ht sin
降温时，轴力为负，拱顶拱 脚的弯矩与控制弯矩方向相 同，对拱圈不利。
《公路圬工桥涵设计规范》（JTG D61-2005）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1）拱顶弯矩为零条件： M d 0 , Q d 0 ，只有轴力 H g
（2）拱脚弯矩为零： H
g
M f
j
（3）1/4点弯矩为零：H
（4）
M f
j
g
M
1/ 4
y1 / 4
M
1/ 4
y1 / 4
1/ 4
主拱圈恒载的 M
, M
j
可由《拱桥（上）》
第988页附录III表(III)-19查得。
j
)
gd
1hd 2 d
1 , 2 , 3 分别为拱顶填料、主拱圈和拱腹填料的容重；
hd , d , h,
j
分别为拱顶填料厚度、主拱圈厚度、拱脚拱 腹填料厚度及拱脚处拱轴线水平倾角。
1）确定拱轴系数的步骤： （1） 假定m （ 2 ） 从 《 拱 桥 （ 上 ） 》 第 1000 页 附 录 III 表 (III)-20查 cos j （3）由公式计算新的m′ （4）若计算的m′ 和假定m 相差较远，则再 次计算m′ 值 （5）直到前后两次计算接近(相差半级)为止。
拱桥计算
一、拱轴线的选择与确定
二、确定拱轴系数
三、主拱圈弹性中心及弹性压缩系数计算
四、主拱圈截面内力计算
五、主拱圈正截面强度验算
六、主拱圈稳定性验算
七、主拱圈裸拱强度和稳定性验算 八、主拱圈应力调整
2.3.3 主拱圈弹性中心及弹性压缩系数计算
1 悬链线无铰拱的弹性中心
采用恒载压力线作为拱轴线，在恒载作用下不
悬链线作拱轴线，使压力线同拱轴线在两拱脚、拱顶三点重合，
允许在L/4点略有偏离，而在全拱范围内压力线同拱轴线更加接
近。 目前大、中跨径的拱桥都普遍采用悬链线拱轴线形，采用悬 链线拱轴线对空腹式拱桥主拱受力是有利的。
拱轴线和恒载压力线
悬链线方程：
y1 f m 1 ( chk 1 )
拱的跨径和矢高确定后，拱轴线坐标取
2、空腹式拱桥拱轴系数的确定
拱轴线变化：空腹式拱桥跨结构恒 载分为两部分：分布恒载和集中恒载。 恒载压力线不是悬链线，也不是一条 光滑曲线。 五点重合法：使悬链线拱轴线接近 其恒载压力线，即要求拱轴线在全拱 有5点（拱顶、拱脚和1/4点）与其三 铰拱恒载压力线重合。
1） 五点弯矩为零的条件：
②悬链线曲边三角形部分重量
P= l1 f1 （shkξ0-kξ0）γ4
（m-1）k
f1=f- yi（1/cosφj-1）
4、各块恒载对拱脚及拱跨1/4截面的力矩
∑Mj= ∑pidi
∑M1/4= ∑pidi p：各块恒载重量KN； d：各块恒载对拱脚或1/4截面的力臂。
（3）确定拱轴系数 m
由前计算可得： ∑M1/4/∑Mj= m′
第三节
拱桥计算
一、拱轴线的选择与确定
二、确定拱轴系数
三、主拱圈弹性中心及弹性压缩系数计算
四、主拱圈截面内力计算
五、主拱圈正截面强度验算
比较计算所得m ′值和假定的m值对应y1/4/f
值相近（相差半级）时，即可确定拱轴系数为
假定的m值，若两者相差较大，则应以计算出
的m ′值为假定的m值，代回重新计算。
拱轴线水平倾角：tgφ
拱轴线上各点水平倾角tgφ只与f/l和m有
关，该值可从《拱桥》 （上册）第577页表 （III）-2查得。
第三节
考虑拱圈变形的影响时，拱圈各截面均只有轴向压 它在恒载产生的轴向压力作用下会产生弹性压缩， 使拱轴长度缩短，这种现象称为拱的弹性压缩。由 会在拱中产生内力，在设计中为了计算方便将恒载 压力分为两个部分，即：不考虑弹性压缩引起的内 力与弹性压缩引起的内力。两者相加，得到恒载作
力，此时拱圈处于纯压状态。但是拱圈材料有弹性，
4、悬链线
（1）实腹式拱桥的恒载集度由拱顶到拱脚是 连续分布、逐渐增大的，其恒载压力线是一 条悬链线。
（2）空腹式拱桥恒载的变化不是连续的函数，
如果要与压力线重合，则拱轴线非常复杂。
（3）悬链线方程为：
y1 f m 1 ( chk 1)
五点重合法：使拱轴线和恒载压力线在两拱脚、拱顶和两
（2）已知f、l时，利用 上述关系计算各种几 何量。
圆弧形拱轴线是对应于同一 深度静水压力下的压力线， 与实际的恒载压力线有偏离。
3、抛物线
（1）在均匀荷载作用下，拱的合理拱轴线是 二次抛物线，适宜于恒载分布比较均匀的 4 f 拱桥，拱轴线方程为： y x
2 1
l
2
（2）在一些大跨径拱桥中，也采用高次抛物 线作为拱轴线。
2、拱上空腹段恒载计算 ①腹孔上部计算 腹拱圈外弧跨径：l外′=l′+2d′Sinφ0 腹拱圈内弧半径：R0=Rl′ 腹拱圈重量：Pa=S (R0+d′/2) d′γS 腹拱侧墙护拱重量：Pb=0.11889(R0+d′) 2γ2 三个系数R、S、0.11889分别查《拱桥》上册表。 填料及路面重量：Pc= l外′hdγ1 两腹拱之间起拱线以上部分重量：
选择原则：尽可能降低荷载弯矩值 三种拱轴线形： （1）圆弧线----15m-20m石拱桥、拱式腹拱 （2）抛物线----轻型拱桥或中承式拱桥
（3）悬链线----最常用的拱轴线
2、圆弧线 （1）圆弧线拱轴线线 形简单，全拱曲率相 同，施工方便：
x
2
y 1 2 Ry 1 0
2
x R sin y 1 R (1 cos ) l 1 R f /l 2 4 f /l
2
2 fk l ( m 1)
shk
k ln( m
m 1)
拱轴线各点水平倾角只与f/l和m有关，该值可从 《拱桥》 （上）第577页表（III）-2查得。
5）拱轴系数的计算
（1）拟定上部结构尺寸
1、计算主拱圈几何尺寸
①截面几何特性计算
截面高度：d
主拱圈横桥向取1米单位宽度计算： 横截面面积：A 截面惯性矩：I 截面抵抗矩：W
1/4点重合来选择悬链线拱轴线的方法。 由于空腹式拱桥恒载的变化不是连续的，即使做到拱轴线 和恒载压力线五点重合,也不能保证其余各点重合.通常压力线在 L/8处偏低,在3L/8处偏高,偏离的绝对值以L/8附近较大。为使恒
载压力线同拱轴线吻合度更好，可调整拱上结构重力及其分布
状况，充分注意减少空腹段恒载的离散度；或者另外选择一条
Pd=(b-x′)y′γ3+[f′+d′-y′)γ2+hdγ1](b-2x′)
得到一个腹拱重量：P=Pa+Pb+Pc+Pd
②腹孔下部计算 计算各道横墙、立柱、柱座、盖梁重：Pi ③集中力计算 各腹拱墩中心处恒载之和：P=P腹拱重+P横墙重 若为梁式腹孔：P=P一孔恒载重+P盖梁重+P立柱重+P柱座重 3、拱上实腹段恒载计算 ①拱顶填料及桥面重（等厚部分） P=lxhdγ1 其中：lx=ξl1 lx：实腹段长度 l1=L /2（ L ：计算跨径）
四、主拱圈截面内力计算
五、主拱圈正截面强度验算 六、主拱圈稳定性验算 七、主拱圈裸拱强度和稳定性验算 八、主拱圈应力调整
2.3.1拱轴线的选择与确定 •拱轴线的形状直接影响主拱截面内力大小与分布。 1、相关概念： •压力线：荷载作用下拱截面上弯矩为零（全截面受压） 的截面合内力作用点的连线； •恒载压力线：恒载作用下截面弯矩为零的截面合内力 作用点的连线； •各种荷载压力线：各种荷载作用下截面弯矩为零的截 面合内力作用点的连线； •理想拱轴线：与各种荷载压力线重合的拱轴线； •合理拱轴线：拱圈截面上各点均为受压应力，尽量趋 于均匀分布，能充分发挥圬工材料良好的抗压性能； •选择拱轴线的原则：尽量降低荷载弯矩值；考虑拱轴 线外形与施工简便等因素。
截面回转半径：rw
②计算跨径和计算矢高 计算跨径：L
计算矢高：f
Sinφj、cosφj根据假定的拱轴系数ｍ和矢跨
比f／ L查《拱桥》 手册表（III）-2０（８）
查得。
③拱脚截面投影
水平投影：x=d· Sinφj
竖向投影：y=d· cosφj
④主拱圈坐标计算
将主拱圈沿跨径划分为24、48等分，求
2 ） 拱轴系数的确定步骤：
（1）假定拱轴系数m
（2）布臵拱上建筑，求出 M
1 2 f y1 / 4
1/ 4
, M
j
（3）利用（1-2-24）和（1-2-27）联立解出m为
m ( 2) 1
2
（4）若计算m与假定m不符，则以计算m作为
假定值m重新计算，直到两者接近(相差半级)为止。
2.3.2 拱轴系数的确定 1、实腹式拱桥拱轴系数的确定
拱顶 g d 1 h d 2 d
拱脚
g
j
1hd
d
2
cos
2
3hh f
j
d 2
d 2 cos
j
拱轴系数
m
g
1hd
j
d cos
j
3( f
d 2
d 2 cos
每等分长 L ；
以拱顶截面形心为坐标原点，拱轴线上
各截面纵坐标的计算：拱轴线竖坐标y1、拱背
竖坐标y1′、拱腹竖坐标y1″；
2、拱上构造尺寸计算
①腹拱圈
根据矢跨：Sinφ0、cosφ0；
计算水平投影：X′= d′ Sinφ0
计算竖向投影：Y′＝d′ cosφ0
于无铰拱是超静定结构，弹性压缩引起拱轴的缩短，
用下的总内力。
主拱圈弹性中心 ys的求解： 计算无铰拱内力时，为简化计算常利用弹 性中心的特点；将无铰拱基本结构取为悬臂曲 梁和简支曲梁。