《MATLAB及应用》实验报告2
MATLAB实验报告
MATLAB实验报告实验报告课程名称 MATLAB基础及应用专业班级电子xxxx姓名学号电气与信息学院实验二 MATLAB 数值计算（一）一实验目的：1．掌握数组的创建与运算方法；2. 掌握矩阵的创建与运算方法；3. 掌握数组的运算方法和矩阵运算方法的区别；4．掌握线性方程的求解方法二实验装置：计算机三实验内容：1．数组的创建和运算创建两个含5个元素的一维数组，并求这两个数组的四则运算。
2．矩阵的创建和运算（1）创建两个3×3的矩阵，并求这两个矩阵的四则运算。
（2）创建一个4×4的矩阵，并求这个矩阵的行列式值。
（3）线性方程的求解解方程组=6613753467294x 。
四实验要求:写出实验程序与仿真结果。
1. >> a=linspace(2,10,5) a =2 4 6 8 10>> b=linspace(1,9,5) b =1 3 5 7 9>> a+bans =3 7 11 15 19>> a-bans =1 1 1 1 1>> a.*bans =2 12 30 56 90>> a./bans =2.0000 1.3333 1.2000 1.1429 1.1111 >> a.\b ans =0.5000 0.7500 0.8333 0.8750 0.9000 2.(1) >> a=[1 1 1;2 2 2;3 3 3];>> b=[4 4 4;5 5 5;6 6 6];>> a+bans =5 5 57 7 79 9 9>> a-bans =-3 -3 -3-3 -3 -3-3 -3 -3>> a*bans =15 15 1530 30 3045 45 45>> a/bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNNaN NaN NaN>> a\bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNInf Inf Inf(2).>> a=[1 1 1 1;2 2 2 2;3 3 3 3;4 4 4 4];>> det(a)ans =(3).>> a=[4 9 2;7 6 4;3 5 7];>> b=[13;6;6];>> x=inv(a)*bx =-0.53081.7109-0.1374实验三 MATLAB数值计算（二）一实验目的：1．掌握多项式的创建与运算方法；2. 掌握基本的数据分析方法；二实验装置：计算机三实验内容：1．多项式创建输入系数矢量，创建多项式x^3-2*x^2+5*x+3。
MATLAB语言及其应用实验报告.doc
MATLAB语言及其应用实验报告.doc一、实验目的1、熟悉MATLAB语言及其基本操作；2、掌握利用MATLAB进行数据分析和可视化的方法；3、掌握MATLAB应用于科学计算的基本方法。
二、实验环境MATLAB R2018a三、实验内容及方法3.1 实验内容1、打开MATLAB环境；2、读入数据文件，并对数据进行分析和处理；3、通过MATLAB绘制图表，对数据进行可视化。
四、实验细节及流程4.1 读入数据文件本实验使用的数据文件为sales.xlsx，其中包括2018年各个季度的销售数据。
首先，通过以下命令导入数据：data=xlsread('sales.xlsx');4.2 数据分析和处理1、计算各季度销售总额通过以下代码计算每个季度的销售额并求和，得到每年的销售总额：Q1=data(:,2);TotalSales=sum([Q1 Q2 Q3 Q4],2);2、计算增长率根据每年的销售总额，计算出每年的增长率。
具体代码如下：GrowthRate(1)=0;for i=2:length(TotalSales)GrowthRate(i)=((TotalSales(i)-TotalSales(i-1))/TotalSales(i-1))*100; endSalesGrowth=[TotalSales GrowthRate];3、计算每个季度的均值和标准差meanQ1=mean(Q1);stdQ1=std(Q1);4、计算出每年第一个季度的销售额所占比例首先，我们将第一个季度的销售额单独提出来，具体代码如下：4.3 数据可视化1、柱形图对于销售总额，使用柱形图进行可视化，具体代码如下：结果如下图所示：图1 销售总额2、线性图3、箱形图boxplot([Q1 Q2 Q3 Q4],{'Q1','Q2','Q3','Q4'});图3 每个季度的销售额4、饼图pie(FirstQSalesRatio(:,1));五、结论本实验通过对销售数据的分析和可视化，得出以下结论：1、2018年销售总额呈逐年上升趋势，其中2017年到2018年的增长率最高；2、每年第一个季度的销售额所占比例在40%至45%之间，与其他季度相比，显著高于其他季度；3、2018年第二季度的销售额经过调整后，表现出了相对较高的波动。
matlab实验报告
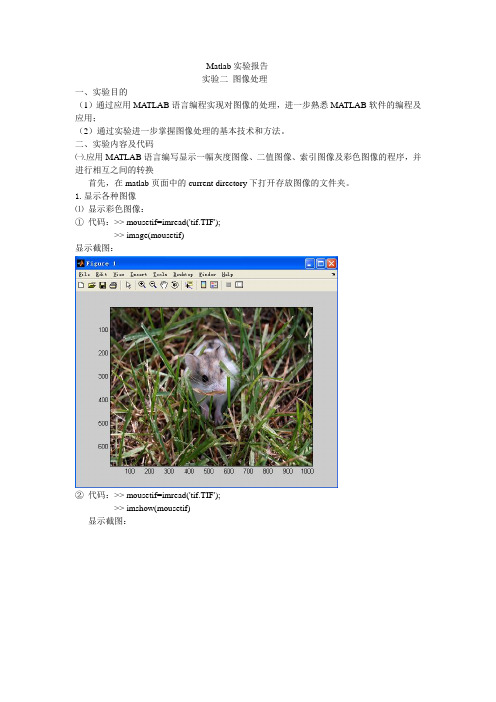
Matlab实验报告实验二图像处理一、实验目的（1）通过应用MA TLAB语言编程实现对图像的处理，进一步熟悉MATLAB软件的编程及应用；（2）通过实验进一步掌握图像处理的基本技术和方法。
二、实验内容及代码㈠.应用MA TLAB语言编写显示一幅灰度图像、二值图像、索引图像及彩色图像的程序，并进行相互之间的转换首先，在matlab页面中的current directory下打开存放图像的文件夹。
1.显示各种图像⑴显示彩色图像：①代码：>> mousetif=imread('tif.TIF');>> image(mousetif)显示截图：②代码：>> mousetif=imread('tif.TIF');>> imshow(mousetif)显示截图：③代码：mousetif=imread('tif.TIF');subimage(mousetif)显示截图：显示截图：⑵显示二值图像①代码：>> I=imread('单色bmp.bmp');>> imagesc(I,[0 2])显示截图：②代码：>> I=imread('单色bmp.bmp');>> imshow(I,2)显示截图：③代码：>> I=imread('单色bmp.bmp');>> subimage(I)显示截图：⑶显示灰度图像①代码：>> I1=imread('256bmp.bmp');>> imagesc(I1,[0,256])显示截图：代码：>> I1=imread('256bmp.bmp');>> colormap(gray);>> subplot(1,2,1);>> imagesc(I1,[0,256]);>> title('灰度级为[0 256]的mouse.bmp图');>> subplot(1,2,2);>> imagesc(I1,[0,64]);>> colormap(gray);>> title('灰度级为[0 64]的mouse.bmp图');显示截图：⑷显示索引图像代码：>> mousetif=imread('tif.TIF');>> [x,map]=rgb2ind(mousetif,0.7);>> subplot(1,2,1);>> imshow(mousetif);>> title('彩色图像');>> subplot(1,2,2);>> imshow(x,map);>> title('索引图');截图显示：彩色图像索引图2.图像之间的转换⑴索引图像转灰度图像代码：>> II1=ind2gray(x,map);>> imshow(x,map);>> title('索引图像');>> imshow(II1);>> title('灰度图像');截图显示：索引图像灰度图像⑵ 索引图像转彩色图像⑶ 索引图像转二值图像⑷ 灰度图像转索引图像代码：>> I1=imread('256bmp.bmp');>> subplot(1,2,1);>> imagesc(I1,[0,256]); >> colormap(gray); >> title('灰度图');>> [x,map]=gray2ind(I1,256); >> subplot(1,2,2); >> image(x);>> colormap(map); >> title('索引图')；显示截图：灰度图2004006008001000100200300400500600索引图2004006008001000100200300400500600⑸灰度图像转彩色图像⑹灰度图像转二值图像⑺彩色图像转灰度图像⑻彩色图像转索引图像代码：>> mousetif=imread('tif.TIF');>> [x,map]=rgb2ind(mousetif,0.7);>> subplot(1,2,1);>> imshow(mousetif);>> title('彩色图像');>> subplot(1,2,2);>> imshow(x,map);>> title('索引图');显示截图：彩色图像索引图⑼彩色图像转二值图像⑽二值图像转索引图像⑾二值图像转彩色图像⑿二值图像转灰度图像㈡应用MA TLAB工具箱演示一幅图像的傅里叶变换、离散余弦变换，观察其频谱图。
MATLAB实验报告(打印版)
MATLAB实验报告班别：09电气3班姓名：李嘉明学号：200924122301实验一/二 MATLAB的基础操作3．自定义一个变量，然后分别用8种不同的数字显示格式显示查看。
>> a=[1.1,1.2,1.3;1.4,1.5,1.6;1.7,1.8,1.9]a =1.1000 1.2000 1.30001.4000 1.5000 1.60001.7000 1.8000 1.9000>> format long>> aa =1.100000000000000 1.200000000000000 1.3000000000000001.400000000000000 1.500000000000000 1.6000000000000001.700000000000000 1.800000000000000 1.900000000000000>> format short e>> aa =1.1000e+000 1.2000e+000 1.3000e+0001.4000e+000 1.5000e+000 1.6000e+0001.7000e+000 1.8000e+000 1.9000e+000>> format long e>> aa =1.100000000000000e+000 1.200000000000000e+000 1.300000000000000e+0001.400000000000000e+000 1.500000000000000e+000 1.600000000000000e+0001.700000000000000e+000 1.800000000000000e+000 1.900000000000000e+000 >> format hex>> aa =3ff199999999999a 3ff3333333333333 3ff4cccccccccccd3ff6666666666666 3ff8000000000000 3ff999999999999a3ffb333333333333 3ffccccccccccccd 3ffe666666666666>> format +>> aa =+++++++++>> format rat>> aa =11/10 6/5 13/107/5 3/2 8/517/10 9/5 19/10>> format short>> aa =1.1000 1.2000 1.30001.4000 1.5000 1.60001.7000 1.8000 1.90005、己举例比较给矩阵的全行赋值，取出矩阵中某一个或几个元素，然后组成一个新的矩阵。
Matlab实验报告
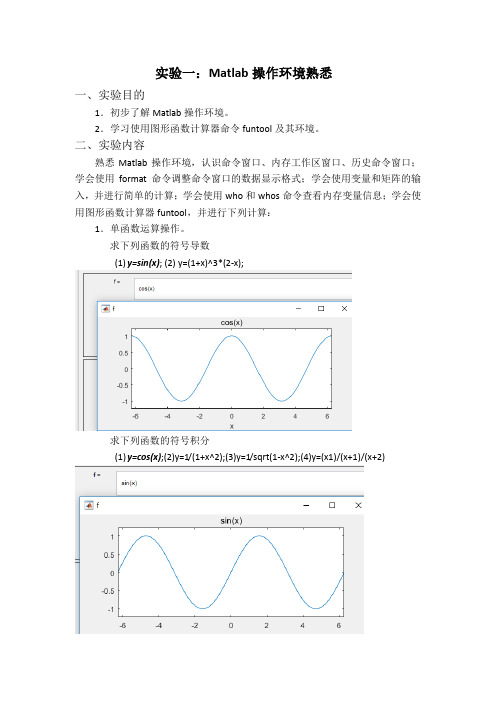
实验一：Matlab操作环境熟悉一、实验目的1．初步了解Matlab操作环境。
2．学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境，认识命令窗口、内存工作区窗口、历史命令窗口；学会使用format命令调整命令窗口的数据显示格式；学会使用变量和矩阵的输入，并进行简单的计算；学会使用who和whos命令查看内存变量信息；学会使用图形函数计算器funtool，并进行下列计算：1．单函数运算操作。
求下列函数的符号导数(1)y=sin(x); (2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1-x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x); (3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x-4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x-3*cos(x)+4*x*sin(x);2．函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2) y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6)y6=x^2/23．两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(-x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x-1)/(x-2);求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二：MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab程序设计与应用(第二版) 刘卫国 课后实验报告
0 0
0 0
4.0000 0
0 9.0000
A,H,Trace,Rank,Norm 结果 H = -3.2509e+004 Trace =33 Rank =5 Norm =25.3208 4、 A=[-29,6,18;20,5,12;-8,8,5]; [V,D]=eig(A); 结果 A = -29 20 -8 5、 5 8 6 18 12 5
0 0 2、 H=hilb(5); P=pascal(5); Hh=det(H); Hp=det(P); Th=cond(H); Tp=cond(P); H,P,Hh,Hp,Th,Tp 结果 Hh = 3.7493e-012 Hp =1 Th = 4.7661e+005 Tp =8.5175e+003 3、 A=fix(10*rand(5)); H=det(A); Trace=trace(A); Rank=rank(A); Norm=norm(A);
b=?1 ans =1 x1 =0.6180 r10 =0.6180 r20 =-1.6180 4、 for i=1:100 if i==1 f(i)=1; elseif i==2 f(i)=0; elseif i==3 f(i)=1; else f(i)=f(i-1)-2*f(i-2)+f(i-3); end end a=max(f); b=min(f); c=sum(f); disp(['最大值',num2str(a)]); disp(['最小值',num2str(b)]); disp(['各数之和',num2str(c)]); zhengshu=length(find(f>0)); zeroshu=length(find(f==0)); fushu=length(find(f<0)); 结果 最大值；4.377633e+011 最小值：-8.994121e+011 各数之和：-7.427456e+011 zhengshu =49 zeroshu = 2 fushu =49 5、 s=0;
MATLAB 语言及其应用 实验报告
《MATLAB 语言及其应用》实验报告目录实验一Matlab 使用方法和程序设计........................实验二控制系统的模型及其转换.............................实验三控制系统的时域、频域和根轨迹分析...........实验四动态仿真集成环境-Simulink.........................实验一Matlab使用方法和程序设计一、实验目的1、掌握Matlab软件使用的基本方法；2、熟悉Matlab的数据表示、基本运算和程序控制语句3、熟悉Matlab绘图命令及基本绘图控制4、熟悉Matlab程序设计的基本方法二、实验内容：1、帮助命令使用help命令，查找 sqrt（开方）函数的使用方法；答：help sqrt2、矩阵运算（1）矩阵的乘法已知A=[1 2;3 4]; B=[5 5;7 8];求A^2*B解：>> A=[1 2;3 4];B=[5 5;7 8];A^2*Bans =105 115229 251（2）矩阵除法已知 A=[1 2 3;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];A\B,A/B解：>> A=[1 2 3;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];>> A\Bans =1.0e+016 *-0.4504 1.8014 -1.35110.9007 -3.6029 2.7022-0.4504 1.8014 -1.3511>> A/Bans =1.0000 1.0000 1.00004.0000 2.5000 2.00007.0000 4.0000 3.0000（3）矩阵的转置及共轭转置已知A=[5+i,2-i,1;6*i,4,9-i];求A.', A'解：>> A=[5+i,2-i,1;6*i,4,9-i];>> A.'ans =5.0000 + 1.0000i 0 +6.0000i2.0000 - 1.0000i 4.00001.0000 9.0000 - 1.0000i>> A'ans =5.0000 - 1.0000i 0 -6.0000i2.0000 + 1.0000i 4.00001.0000 9.0000 + 1.0000i（4）使用冒号表达式选出指定元素已知： A=[1 2 3;4 5 6;7 8 9];求A中第3列前2个元素；A中所有列第2，3行的元素；>> A=[1 2 3;4 5 6;7 8 9];>> B=A(1:2,3)B =36>> B1=A(2:3,:)B1 =4 5 67 8 9用magic函数生成一个4阶魔术矩阵，删除该矩阵的第四列>> A=magic(4)A =16 2 3 135 11 10 89 7 6 124 14 15 1>> B=A(:,1:3)B =16 2 35 11 109 7 64 14 153、多项式（1）求多项式4xxp的根2=x)(3-->> p=[1 0 -2 -4];>> r=roots(p)r =2.0000-1.0000 + 1.0000i-1.0000 - 1.0000i（2）已知A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4] ，求矩阵A的特征多项式;>> A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4] ;>> p=poly(A)p =1.0000 -6.9000 -77.2600 -86.1300 604.5500把矩阵A作为未知数代入到多项式中；>> A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4] ;>> syms x;P=x^3-2*x-4;>> P1=subs(P,x,A)P1 =-4.6720 17.0000 111.0000 -5.0710111.0000 -2.4870 111.0000 200.000017.0000 707.0000 -4.0000 -5.0000-5.0000 0 17.0000 52.00004、基本绘图命令（1）绘制余弦曲线 y=cos(t)，t∈[0，2π]（2）在同一坐标系中绘制余弦曲线y=cos(t-0.25)和正弦曲线y=sin(t-0.5)，t∈[0，2π]解：（1）程序为：t=[0:0.05:2*pi];y=cos(t);plot(t,y)（2）程序如下：x=[0:0.05:2*pi];y1=cos(x-0.25);y2=sin(x-0.5);plot(x,y1,x,y2)绘制曲线如下：5、基本绘图控制绘制[0，4π]区间上的x1=10sint曲线，并要求：（1）线形为点划线、颜色为红色、数据点标记为加号；（2）坐标轴控制：显示范围、刻度线、比例、网络线（3）标注控制：坐标轴名称、标题、相应文本；程序为：>> t=[0:0.05:4*pi];x1=10*sin(t);plot(t,x1,'r-.+')grid on;axis([0,15,-10,10]);title('曲线x1=10sint');xlabel('T轴');ylabel('X1轴');set(gca,'xminortick','on');set(gca,'yminortick','on');6、基本程序设计（1）编写命令文件：计算1+2+…+n<2000 时的最大n值；>> s=1;n=1;while(s<2000-n),n=n+1;s=s+n;end,[s,n]ans =1953 62（2）编写函数文件：分别用for和while循环结构编写程序，求2的0到n次幂的和。
matlab实验报告
实验二特殊函数与图形
一、实验目的及意义
掌握用Matlab软件绘制简单曲线、曲面图形，并通过绘制一些特殊函数的图形，更加深入地理解相关函数的性质，了解函数的性态。
二、实验内容
平面作图、空间作图，比较数值作图与符号作图的异同。
三、实验步骤
1.在D盘建立一个自己的文件夹;
2.开启软件平台——MATLAB，将你建立的文件夹加入到MA TLAB的搜索路径中。
3.利用帮助了解函数plot, surf, ezmesh，ezsurf等的功能和用法。
4.开启MATLAB编辑窗口,键入你编写的M文件（命令文件或函数文件）；
5.保存文件（注意将文件存入你自己的文件夹）并运行；
6.若出现错误，修改、运行直到输出正确结果；
7.写出实验报告，并浅谈学习心得体会。
四、实验要求与任务
根据实验内容和步骤，完成以下具体实验，按要求写出实验报告。
1．作出下图所示的三维图形：
图1
提示：图形为圆环面和球面的组合.
2．作出下图所示的墨西哥帽子及其剪裁图形：
图2
3．画出椭球面、双叶双曲面、单叶双曲面．
4．若要求田螺线的一条轴截面的曲边是一条抛物线：0=y 时25x z =．试重新设计田螺线的参数方程，并画出该田螺线．
5．作出下图所示的马鞍面（颜色为灰色，并有一个标题：“马鞍面”）：
图3
6．绘制黎曼函数的图形，要求分母的最大值n 的数值由键盘输入（提示：使用
input 语句）．。
南华大学《MATLAB及应用》实验报告2
核科学技术学院实验报告实验项目名称MATLAB符号计算所属课程名称MATLAB及应用实验类型上机实验实验日期12月日指导教师谢芹班级学号姓名成绩一、实验名称MATLAB符号计算二、实验目的（1）掌握定义符号对象的方法（2）掌握符号表达式的运算法则以及符号矩阵运算（3）掌握求符号函数极限及导数的方法（4）掌握求符号函数定积分和不定积分的方法三、实验原理1. 函数极限及导数的方法（1）函数极限：limit(F,x,a) 求符号函数f(x)的极限值。
即计算当变量x趋近于常数a时，f(x)函数的极限值。
（2）limit(f)：求符号函数f(x)的极限值。
符号函数f(x)的变量为函数findsym(f)确定的默认变量；没有指定变量的目标值时，系统默认变量趋近于0，即a=0的情况。
（3）limit(f,x,a,'right')：求符号函数f的极限值。
'right'表示变量x从右边趋近于a。
（4）limit(f,x,a,‘left’)：求符号函数f的极限值。
‘left’表示变量x从左边趋近于a。
2. 微分：diff(s)：没有指定变量和导数阶数，则系统按findsym函数指示的默认变量对符号表达式s求一阶导数。
diff(s,'v')：以v为自变量，对符号表达式s求一阶导数。
diff(s,n)：按findsym函数指示的默认变量对符号表达式s求n阶导数，n为正整数。
diff(s,'v',n)：以v为自变量，对符号表达式s求n阶导数。
3. 函数定积分和不定积分的方法：int(s)：没有指定积分变量和积分阶数时，系统按findsym函数指示的默认变量对被积函数或符号表达式s求不定积分。
int(s,v)：以v为自变量，对被积函数或符号表达式s求不定积分。
int(s,v,a,b)：求定积分运算。
a,b分别表示定积分的下限和上限。
梯形法：trapz(x,y)：x为分割点构成的向量，y为被积函数在分割点上的函数值构成的向量；抛物线法：quad(f,a,b,tol)，f 是被积函数，[a,b]是积分区间，tol 是精度。
matlab仿真实验报告,Matlab仿真及其应用实验报告.doc
matlab仿真实验报告,Matlab仿真及其应⽤实验报告.doc Matlab仿真及其应⽤ 实验报告温州⼤学物理与电⼦信息⼯程学院Matlab仿真及其应⽤ 实验报告课程名称：Matlab仿真及其应⽤班 级：10电信姓名：吴** 学号：1011000****实验地点：5B305⽇期：12.25实验⼆ Matlab 基本编程基础[实验⽬的和要求]熟悉MATLAB环境与⼯作空间熟悉变量与矩阵的输⼊、矩阵的运算熟悉M⽂件与M函数的编写与应⽤熟悉MATLAB控制语句与逻辑运算掌握if语句、switch语句、try语句的使⽤。
掌握利⽤for语句、while语句实现循环结构的⽅法。
[实验内容]1⾏100列的Fibonacc 数组a，a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),⽤for循环指令来寻求该数组中第⼀个⼤于10000的元素，并之处其位置i。
编写M函数表⽰曲线以及它的包络线，并从命令窗⼝输⼊命令语句绘制曲线。
t的取值范围是[0，4π]。
设，编写⼀个M函数⽂件，使得调⽤f(x)时，x可⽤矩阵代⼊，得出的f(x)为同阶矩阵。
根据，求时的最⼤n值；与(1)的n值对应的y值。
已知求中，最⼤值、最⼩值、各数之和，以及正数、零、负数的个数。
输⼊⼀个百分制成绩，要求输出成绩等级A,B,C,D,E。
其中，90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下为E。
求分段函数的值。
⽤if语句实现输出x=-5.0, -3.0, 1.0, 2.0, 2.5, 3.0, 5.0时的y值。
编写⼀M函数，实现近似计算指数，其中x为函数参数输⼊，当n+1步与n步的结果误差⼩于0.00001时停⽌。
编写⼀M函数，a和x作为M函数参数输⼊，函数⾥⾯分别⽤if结构实现函数表⽰实验结果及分析：1.a=ones(1,100); %定义数组for i=3:100a(i)=a(i-1)+a(i-2);if(a(i)>10000)a(i),break;endend ,i2.function y=ff(t)y1=exp(-t/3);y2=exp(-t/3).*sin(3*t); y=[y1;y2]3.function y=f(x);a=input('输⼊a值：');x=input('输⼊x值：');if(x<=-a)y=-1;elseif(x-a)y=x/a;elsey=1;endend4.for n=1:100f(n)=1./(2*n-1);y=sum(f)if y>=3my=y-f(n)breakendendmy5.f(1)=1,f(2)=0,f(3)=1; for n=4:100f(n)=f(n-1)-2*f(n-2)+f(n-3);enda=sum(f);b=max(f);c=min(f);p=f==0,d=sum(p);%p等于f为0的个数p1=f>0,e=sum(p1);p2=f<0,f=sum(p2);a,b,c,d,e,f6.clear;n=input('输⼊成绩：');m=floor(n/10);%取整switch mcase num2cell(9:10)disp('A'); %显⽰在控制框case 8disp('B');case 7disp('C');case 6disp('D');case num2cell(0:5)disp('E');otherwisedisp('error')end7.function y=ex3_4(x)for i=1:length(x)if (x(i)<0)&(x(i)~=-3)y(i)=x(i)^2+x(i)-6elseif (x(i)>=0)&(x(i)<5)&(x(i)~=2)&(x(i)~=3) y(i)=x(i)^2-5*x(i)+6else y(i)=x(i)^2-x(i)-1 endendy8.function t=ex3_4(x) n=0;t=1;y=1;x=input(‘’);while y>=0.00001n=n+1;y=x^n/factorial(n);t=t+y;endn9.function y=f(x);a=input('输⼊a值：'); x=input('输⼊x值：'); if。
《Matlab基础及应用》实验报告
组号
成员
班级
姓名
学号
实验日期
实验成绩
01
主要问题叙述
一、用MATLAB命令计算下列极限（10分）
1. 2.
二、用Matlab命令计算不定积分 ，并验证其正确性（10分）
三、绘图题（20分）
在同一个图中绘制两个函数，这两个函数分别是：y=e(-t/3)y0=e(-t/3)*sin(3t)，其中y是用红色的细实线，而y0是用兰色的虚线绘制，t的区间是[0:4?]，t的步长为?/50，t轴和y轴分别给出标识，图中有网格表示。
四、求方程 的根.（10分）
五、求方程 的近似根.（10分）
六、求下面线性方程组的解，并求系数矩阵的特征值（20分）
七、程序设计题（20分）
若一个数等于它的各个真因子之和，则称该数为完数，如6=1+2+3，所以6是完数。求[1,500]之间的全部完数.
实验所用软件及版本
实验过程及
结论
实验过程记录（含基本步骤、主要程序清单及异常情况记录等）：
实验总结与课程体会实验总 Nhomakorabea与课程体会：
教师评语
注：每项大小请自行添减.
matlab实验报告
matlab实验报告实验报告：Matlab实验分析1. 实验目的本实验旨在通过Matlab软件完成一系列数值计算和数据分析的任务，包括绘制曲线、解方程、矩阵运算等，以加深对Matlab软件的理解和掌握。
2. 实验内容2.1 绘制函数曲线首先，我们通过在Matlab中输入函数的表达式来绘制函数曲线。
例如，我们可以输入y = sin(x)来绘制正弦函数的曲线。
另外，我们还可以设置曲线的颜色、线型和坐标轴范围等。
2.2 解方程接下来，我们使用Matlab来解方程。
对于一元方程，我们可以使用solve函数来求出方程的解。
例如，我们输入syms x; solve(x^2 - 2*x - 8)来解方程x^2 - 2x - 8 = 0。
而对于多元方程组，我们可以使用solve函数的向量输入形式来求解。
例如，我们输入syms x y; solve(x^2 + y^2 - 1, x - y - 1)来求解方程组x^2 + y^2 - 1 = 0和x - y - 1 = 0的解。
2.3 矩阵运算Matlab也可以进行矩阵运算。
我们可以使用矩阵相乘、相加和取逆等运算。
例如，我们可以输入A = [1 2; 3 4]和B = [5 6;7 8]来定义两个矩阵，然后使用A * B来计算它们的乘积。
3. 实验结果与分析在本实验中，我们成功完成了绘制函数曲线、解方程和矩阵运算等任务。
通过Matlab软件，我们可以快速、准确地进行数值计算和数据分析。
使用Matlab的高级函数和工具箱，我们可以更方便地处理复杂的数值计算和数据分析问题。
4. 实验总结通过本次实验，我们进一步加深了对Matlab软件的理解和掌握。
Matlab提供了丰富的函数库和工具箱，适用于各种不同的数值计算和数据分析任务。
在日常科研和工程实践中，Matlab是一个非常强大和方便的工具，可以帮助我们更高效地完成任务。
实验2 MATLAB的基本数据类型
数学与软件科学学院实验报告学期：至第学期 201年月日课程名称:MATLAB程序设计及应用专业:信息与计算机科学实验编号：实验项目：MATLAB的基本数据类型指导教师：班级：级班学号：姓名：实验成绩：一、实验目的及要求(1) 熟悉MATLAB提供的常用数据类型：数值：numeric字符：char逻辑：logical单元：cell结构：struct(2) 掌握每种数据类型标识符、范围以及不同数据类型之间的转换方式；(3) 熟悉MATLAB提供的运算符；(4)熟练掌握MATLAB常用函数的用法二、实验内容(1) 利用MATLAB简单计算的功能完成第二章课后习题；(1) 利用MATLAB简单计算的功能完成第二章课后习题；一、判断下面语句的运算结果：(1)4<20(2)4<=20(3)4==20(4)4~=20(5)'b'<'B'二、设a=39，b=58，c=3，d=7，判断下面表达式的值：(1)a>b(2)a<c(3)a>b && b>c(4)a==d(5)a|b>c(6)~~d(2) 利用class()函数测已知变量的数据类型；(3) 熟练掌握不同数据类型之间转换的两种格式，分别将已知变量的数据类型转换成int16,double类型；(4) 利用函数测实数及整数的范围；(5) 通过两种方式创建下列复数，并测试所创建的数是否为复数：100+24i、10-23.567i、20(6) 熟悉逻辑数组的创建、使用方法；。
matlab实验报告
matlab实验报告《matlab 实验报告》一、实验目的通过本次实验，熟悉 MATLAB 软件的基本操作和功能，掌握使用MATLAB 进行数学计算、数据处理、图形绘制等方面的方法和技巧，提高运用 MATLAB 解决实际问题的能力。
二、实验环境1、计算机：＿____2、操作系统：＿____3、 MATLAB 版本：＿____三、实验内容及步骤（一）矩阵运算1、创建矩阵在 MATLAB 中，可以通过直接输入元素的方式创建矩阵，例如：｀A ＝ 1 2 3; 4 5 6; 7 8 9`，创建了一个 3 行 3 列的矩阵 A。
还可以使用函数来创建特定类型的矩阵，如全零矩阵`zeros(m,n)｀、全 1 矩阵`ones(m,n)｀、单位矩阵`eye(n)｀等。
2、矩阵的基本运算加法和减法：两个矩阵相加或相减，要求它们的维度相同，对应元素进行运算。
乘法：矩阵乘法需要满足前一个矩阵的列数等于后一个矩阵的行数。
转置：使用`A'｀来获取矩阵 A 的转置。
（二）函数的使用1、自定义函数可以在 MATLAB 中自定义函数，例如定义一个计算两个数之和的函数：｀｀｀matlabfunction s ＝ add_numbers(a,b)s ＝ a ＋ b;end｀｀｀2、调用函数在命令窗口中输入`add_numbers(3,5)｀即可得到结果 8。
（三）数据的读取和写入1、读取数据使用`load`函数可以读取数据文件，例如`load(＇datatxt'）｀。
2、写入数据使用`save`函数可以将数据保存到文件中，例如`save(＇resulttxt'，A)｀，将矩阵 A 保存到`resulttxt`文件中。
（四）图形绘制1、二维图形绘制折线图：使用`plot(x,y)｀函数，其中 x 和 y 分别是横坐标和纵坐标的数据。
绘制柱状图：使用`bar(x,y)｀函数。
2、三维图形绘制三维曲线：使用`plot3(x,y,z)｀函数。
matlab 实验报告
matlab 实验报告Matlab实验报告引言：Matlab是一种强大的数值计算和可视化软件，广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一：矩阵运算在这个实验中，我使用Matlab进行了矩阵运算。
首先，我创建了一个3x3的矩阵A和一个3x1的矩阵B，并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*，我得到了一个3x1的结果矩阵C。
接着，我对矩阵C进行了转置操作，得到了一个1x3的矩阵D。
最后，我计算了矩阵C和矩阵D的点积，并将结果输出。
实验二：数据可视化在这个实验中，我使用Matlab进行了数据可视化。
我选择了一组实验数据，包括时间和温度两个变量。
首先，我将数据存储在一个矩阵中，并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着，我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后，我使用Matlab的legend函数添加了图例，以便更好地理解图表。
实验三：数值积分在这个实验中，我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先，我使用Matlab的syms函数定义了符号变量x，并定义了函数f(x)。
接着，我使用Matlab的int函数对函数f(x)进行积分计算，并将结果输出。
为了验证结果的准确性，我还使用了Matlab的diff函数对积分结果进行了求导操作，并与原函数f(x)进行了比较。
实验四：信号处理在这个实验中，我使用Matlab进行了信号处理。
我选择了一个音频文件，并使用Matlab的audioread函数读取了该文件。
接着，我使用Matlab的fft函数对音频信号进行了傅里叶变换，并将结果绘制成频谱图。
为了进一步分析信号的特征，我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察，我可以更好地理解信号的频率和时域特性。
MATLAB实验报告
实验一MATLAB环境的熟悉与基本运算一、实验目的及要求1．熟悉MATLAB 的开发环境；2．掌握MATLAB 的一些常用命令；3．掌握矩阵、变量、表达式的输入方法及各种基本运算。
二、实验内容1.熟悉MATLAB 的开发环境：①MATLAB 的各种窗口：命令窗口、命令历史窗口、工作空间窗口、当前路径窗口。
②路径的设置：?建立自己的文件夹，加入到MATLAB 路径中，并保存。
?设置当前路径，以方便文件管理。
2.学习使用clc 、clear ，了解其功能和作用。
3.矩阵运算：已知:A=[1 2;3 4]; B=[5 5;7 8];求:A*B 、A.*B ，并比较结果。
4.使用冒号选出指定元素:已知:A=[1 2 3;4 5 6;7 8 9];求:A 中第3列前2个元素；A 中所有列第2，3行的元素；5.在MATLAB 的命令窗口计算:1))2sin(2) 5.4)4.05589(6.关系及逻辑运算1)已知:a=[5:1:15]; b=[1 2 8 8 7 10 12 11 13 14 15]，求:y=a==b ，并分析结果2)已知:X=[0 1;1 0]; Y=[0 0;1 0]，求:x&y+x>y ，并分析结果7.文件操作1)将0到1000的所有整数，写入到D 盘下的data.txt 文件2)读入D 盘下的data.txt 文件，并赋给变量num 8.符号运算1)对表达式f=x 3-1进行因式分解2)对表达式f=（2x 2*(x+3)-10)*t ，分别将自变量x 和t 的同类项合并3）求3(1)xdzz 三、实验报告要求完成实验内容的3、4、5、6、7、8，写出相应的程序、结果实验二MATLAB语言的程序设计一、实验目的1、熟悉MATLAB 程序编辑与设计环境2、掌握各种编程语句语法规则及程序设计方法3、函数文件的编写和设计4、了解和熟悉变量传递和赋值二、实验内容1．编写程序，计算1+3+5+7+…+(2n+1)的值（用input 语句输入n 值）。
matlab实验报告实验二
matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件，广泛应用于科学研究和工程实践中。
在实验二中，我们将探索Matlab的图像处理功能，并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程，其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中，我们可以利用各种函数和工具箱来实现图像处理的各种任务，如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中，我们可以使用imread函数读取图像文件，并使用imshow函数将图像显示在屏幕上。
例如，我们可以读取一张名为"lena.jpg"的图像，并显示出来：```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中，我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如，我们可以将上一步读取的图像转换为灰度图像：```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程，其中只包含黑色和白色两种颜色。
在Matlab中，我们可以使用imbinarize函数将灰度图像二值化。
例如，我们可以将上一步得到的灰度图像二值化：```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节，使得图像更加平滑和清晰。
在Matlab 中，我们可以使用imfilter函数对图像进行平滑处理。
例如，我们可以对上一步得到的二值图像进行平滑处理：```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程，常用于目标检测和图像分割。
MATLAB原理及应用实验报告第二章
《MATLAB原理及应用》实验报告实验二数组（矩阵）及其运算一．实验目的1、掌握MATLAB软件环境下进行的数值数组（矩阵）的创建和访问的基本方法。
2、掌握数值数组(矩阵)的算术运算、逻辑运算二．实验设备计算机、MATLAB软件三．实验内容1.矩阵的创建(1)矩阵的创建方法1：输入元素列表①矩阵行中的元素以空格()或逗号(,)间隔②矩阵行之间用分号(;)或回车（enter）间隔③整个元素列表用方括号([])括起来>> a=[1 2 3;4 5 6;7 8 9]>> a=[1:3;4:6;7:9];a1=1:6%用冒号(:)可以操作简便方法2：利用MATLAB内部函数产生矩阵>>b=eye(3)>>c=ones(2,5)>>d=zeros(3,2)>>e=linspace(-3,6,10)>>f=logspace(0,4,5)>>r=rand(1,6) %产生[0,1]之间均匀分布的随机向量R(1×6)(2)矩阵元素的提取与替换在MATLAB中，矩阵中元素可以通过其在矩阵中的行标和列标来确定。
对矩阵中的元素进行提取与替换，也可以按行标和列表进行。
【实验2-1】在命令窗口输入：>>A=[1,2,3;4,5,6]运行后显示：A =1 2 34 5 6在命令窗口输入：>>b=A(1,2)运行后显示：b =2在命令窗口输入：>>A(2,3)=-3运行后显示：A =1 2 34 5 -3(3)矩阵的操作>>A=[1,2,3;4,5,6;7,8,9]>>B=diag(A)%X为矩阵时，V=diag(X,k)得到列向量V，它取自X的第K个对角线的元素， %k=0，表示主对角线，等同于V=diag(X）>>C=diag(B) %产生对角阵>>D=rot90(A) %将矩阵A逆时针旋转90度。
matlab实验报告
《MATLAB及其工程应用》实验报告专业：班级：学号：姓名：指导老师：实验一实验名称：Practice how to initialize/save/load the MATLAB实验时间：第六周周三7-8节 实验目的：1、熟练的掌握MATLAB 变量的使用规则，学会创建变量。
2、熟练的掌握数组的相关知识并能加以运用。
实验要求：1、熟练命名合法的变量名。
2、能够应对关于数组的相关问题，如：数组的大小，子数组等。
实验步骤：1.4 假设u=1和v=3,用MATLAB 语句编写下列语句 a. v u 34 b.22)(2v u v +- c.333u v v - d.234v π 解：打开matlab7.0程序，新建一个M-file ，M-file 中输入：u=1;v=3;a=4*u/(3*v);b=2*v^(-2)/(u+v)^2;c=v^3/(v^3-u^3);d=4*pi*v^2/3;abcd然后点击运行，将得到以下结果：a =0.4444b =0.0139c =1.0385d =37.6991实验二实验名称：Practice how to use the MATLAB operators.实验时间：第七周周三7-8节实验目的：1、熟练的掌握数组和矩阵的使用规则。
2、熟练的掌握数组和矩阵的相关知识并能加以运用。
实验要求：1、熟练命名合法的变量名。
2、能够应对关于数组和矩阵的相关问题。
实验步骤：2.1看下面的数组回答有关问题⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0.01.10.01.54.13.14.03.01.01.24.38.26.61.10.00.65.31.20.01.11array a. array1的大小是多少?b. array1(4,1)的值是多少?c. array1(:,1:2)的大小和值为多少?d. array1([1 3],end)的大小和值为多少?解：打开matlab7.0程序，新建一个M-file ，M-file 中输入：array1=[1.1,0.0,2.1,-3.5,6.0;0.0,1.1,-6.6,2.8,3.4;2.1,0.1,0.3,-0.4,1.3;-1.4,5.1,0.0,1.1,0.0];size(array1) %2.11aarray1(4,1) %2.1barray1(:,1:2) %2.1csize(array1(:,1:2)) %2.1carray1([1 3],end) %2.1dsize(array1([1 3],end)) %2.1d然后点击运行，将得到以下结果：ans =4 5ans =-1.4000ans =1.1000 00 1.10002.1000 0.1000-1.4000 5.1000ans =4 2ans =6.00001.3000ans =2 12.3 写出下面的数组的大小和内容.注意后面的数组可能根据前面数组的定义.a. a=1:2:5;b. b=[a' a' a'];c. c=b(1:2:3,1:2:3);d. d=a+b(2,:);e. w=[zeros(1,3) ones(3,1)' 3:5'];f. b([1 3],2)=b([3 1],2);解：>> a=1:2:5a =1 3 5>> size(a)ans =1 3>> b=[a' a' a']b =1 1 13 3 35 5 5>> size(b)ans =3 3>> c=b(1:2:3,1:2:3)c =1 15 5>> size(c)ans =2 2>> d=a+b(2,:)d =4 6 8>> size(d)ans =1 3>> w=[zeros(1,3) ones(3,1)' 3:5'w =0 0 0 1 1 1 3 4 5>> size(w)ans =1 9>> b([1 3],2)=b([3,1],2)b =1 5 13 3 35 1 5>> size(b)ans =3 32.4数组定义如下,写下面的子数组的内容⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0.01.10.01.54.13.14.03.01.01.24.38.26.61.10.00.65.31.20.01.11array a. array1(3,:)b. array1(:,3)c. array1(1:2:3,[3 3 4])d. array1([1 1],:)解：>> array1=[1.1 0.0 2.1 -3.5 6.0;0.0 1.1 -6.6 2.8 3.4;2.1 0.1 0.3 -0.4 1.3 ;-1.45.1 0.0 1.1 0.0]array1 =1.1 02.1 -3.5 60 1.1 -6.6 2.8 3.42.1 0.1 0.3 -0.4 1.3-1.4 5.1 0 1.1 0>> array1(3,:)ans =2.1 0.1 0.3 -0.4 1.3>> array1(:,3)ans =2.1-6.60.3>> array1(1:2:3,[3 3 4])ans =2.1 2.1 -3.50.3 0.3 -0.4>> array1([1 1],:)ans =1.1 02.1 -3.5 61.1 02.1 -3.5 6实验三实验名称：Practice MATLAB display and plotting functions.实验时间：第九周周三7-8节实验目的：1、掌握三种常见函数：disp ，fprintf ，plot2、掌握画图函数的使用方法实验要求：1、熟练掌握plot 函数的使用方法2、能运用画图函数画一些较简单的图形实验步骤：2.10 球的位置和速度.如果一静止小球在离地h 0的地方以初速度v 0做垂直运动，其等等式为o o h t v gt t h ++=221)( (2.10) o v gt t v +=)( (2.11)其中g 为重力加速度(9.81m/(s*s)),h (t )代表在t 时刻小球的高度.v (t )代表在时刻t 小球的速度.编写一个MATLAB 程序,计算出每一秒钟的速度和高度,并打印出h ,v 关于时间t 的函数.确保在你的图中有合适的标签.解：v0=input('v0=');h0=input('h0=');t=-10:0.01:10;h=0.5.*(-9.81).*t.^2+v0.*t+h0;v=(-9.81).*t+v0;plot(t,h,'r--',t,v,'g');axis([-10,10,-50,50]);xlabel('t');ylabel('h and v');legend('h','v')结果：v0=10h0=102.13双曲余弦.双曲余弦的定义如下2cosh xx e e x -+=编写一个程序,计算出用户指定的x 的值对应的双曲余弦值.用这个程序计算3.0的双曲余弦值.和MATLAB 中的内建函数cosh(x)得到的值是否完全相同.用MATLAB 打印出这个函数的图象.当x 为何值时,这个函数有最小值?最小值为多少?解：注：以下结果均为x=3.0时的值。
matlab实验报告
matlab实验报告引言：Matlab（矩阵实验室）是一款功能强大的数值计算和科学计算软件，广泛应用于工程、科学和经济等领域。
本实验报告将探讨我在使用Matlab进行实验过程中的心得体会和实验结果。
实验一：图像处理在这个实验中，我使用Matlab对一张图像进行了处理，并应用了各种图像处理算法。
这包括图像增强、边缘检测和图像分割等技术。
通过Matlab的图像处理工具箱，我能够轻松调用各种算法函数，并对图像进行快速处理。
实验结果表明，Matlab图像处理工具箱提供了丰富的函数和算法，极大地方便了我们的图像处理工作。
实验二：模拟信号处理模拟信号处理是Matlab中的一个重要应用领域。
在这个实验中，我模拟了一个带噪声的正弦信号，并使用Matlab进行了噪声滤波和频谱分析。
通过使用Matlab的滤波函数，我能够有效地去除信号中的噪声，并还原出原始信号。
同时，Matlab提供了功能强大的频谱分析工具，我可以轻松地对信号的频率特性进行分析和可视化。
实验三：数据分析与统计数据分析与统计是Matlab的另一个重要应用领域。
在这个实验中，我使用Matlab对一组实验数据进行了分析和统计。
通过使用Matlab的统计函数和工具，我能够计算出数据的均值、方差、标准差等统计指标，并绘制出数据的直方图和散点图。
这些统计分析结果对我的实验研究提供了有力的支持，并帮助我更好地理解实验数据。
实验四：数值计算与优化数值计算与优化是Matlab的核心功能之一。
在这个实验中，我使用Matlab进行了一组数值计算和优化实验。
通过使用Matlab的数值计算函数和优化工具箱，我能够快速计算出复杂的数学问题，并找到最优解。
同时，在进行优化实验时，我可以设置各种约束条件和目标函数，从而得到最优解的参数值。
这些数值计算和优化工具极大地提高了我的研究效率和准确度。
结论：通过这些实验，我深刻认识到Matlab的强大功能和广泛应用领域。
无论是图像处理、信号处理、数据分析还是数值计算与优化，Matlab都提供了丰富的函数和工具，让我们能够快速高效地完成实验和研究工作。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
核科学技术学院实验报告实验项目名称MATLAB符号计算所属课程名称MATLAB及应用实验类型上机实验实验日期12月日指导教师谢芹班级学号姓名成绩一、实验名称MATLAB符号计算二、实验目的（1）掌握定义符号对象的方法（2）掌握符号表达式的运算法则以及符号矩阵运算（3）掌握求符号函数极限及导数的方法（4）掌握求符号函数定积分和不定积分的方法三、实验原理1. 函数极限及导数的方法（1）函数极限：limit(F,x,a) 求符号函数f(x)的极限值。
即计算当变量x趋近于常数a时，f(x)函数的极限值。
（2）limit(f)：求符号函数f(x)的极限值。
符号函数f(x)的变量为函数findsym(f)确定的默认变量；没有指定变量的目标值时，系统默认变量趋近于0，即a=0的情况。
（3）limit(f,x,a,'right')：求符号函数f的极限值。
'right'表示变量x从右边趋近于a。
（4）limit(f,x,a,‘left’)：求符号函数f的极限值。
‘left’表示变量x从左边趋近于a。
2. 微分：diff(s)：没有指定变量和导数阶数，则系统按findsym函数指示的默认变量对符号表达式s求一阶导数。
diff(s,'v')：以v为自变量，对符号表达式s求一阶导数。
diff(s,n)：按findsym函数指示的默认变量对符号表达式s求n阶导数，n为正整数。
diff(s,'v',n)：以v为自变量，对符号表达式s求n阶导数。
3. 函数定积分和不定积分的方法：int(s)：没有指定积分变量和积分阶数时，系统按findsym函数指示的默认变量对被积函数或符号表达式s求不定积分。
int(s,v)：以v为自变量，对被积函数或符号表达式s求不定积分。
int(s,v,a,b)：求定积分运算。
a,b分别表示定积分的下限和上限。
梯形法：trapz(x,y)：x为分割点构成的向量，y为被积函数在分割点上的函数值构成的向量；抛物线法：quad(f,a,b,tol)，f是被积函数，[a,b]是积分区间，tol是精度。
4. 求和及泰勒级数展开的方法：（1）求和symsum(s,v,n,m) 其中s 表示一个级数的通项，是一个符号表达式。
v 是求和变量，v 省略时使用系统的默认变量。
n 和m 是求和的开始项和末项。
（2）泰勒级数展开 taylor(f,v,n,a) 该函数将函数f 按变量v 展开为泰勒级数，展开到第n 项(即变量v 的n-1次幂)为止，n 的缺省值为6。
v 的缺省值与diff 函数相同。
参数a 指定将函数f 在自变量v=a 处展开，a 的缺省值是0。
四、实验内容1. 求下列极限： 求极限前先定义符号变量（1） 10arctan lim x x F x→= （2）1201lim()1x x x F x →+=- （3）320ln(1)limsin x x x F x →+= （4）43111lim()11x F x x→=--- （5）552lim(1)x x t F ax →∞=+ 2. 求下列函数的导数：（1） 3cos cos3y x x =- （2）1sin ln y x x x = （3）21sin x xe y x-= （4）3cos x y e x = （5） 2sin y x x = （6） 3cos ln x ae t x f t x x ⎡⎤=⎢⎥⎣⎦，求df dx ，22d f dt ，2d f dtdx 3. 求下列函数的积分（1） sin sin sin ax bx cxdx ⎰ （2）(53)4x x x dx +-⎰ （3）120(1)x xe dx x +⎰ （4）[0,1][0,1]1Dx dxdy D xy =⨯+⎰⎰ （5） V zdxdydz ⎰⎰⎰ 由曲面22y xz +=，1=z ，2=z 所围成（6） 21cos x bx dx x e x ⎡⎤⎢⎥⎢⎥⎣⎦⎰ 4. 解下列方程组。
（1）123123123257543232615x x x x x x x x x -+-=-⎧⎪+-=⎨⎪++=⎩（2）1122125sin 4cos 05cos 4sin 0x x x x x x --=⎧⎨-+=⎩ （3）()5()()()()5()dx t x t y t dt dy t y t x t dt⎧=-+⎪⎪⎨⎪=-+⎪⎩ 5. 求下列级数的和（1） 11212n n n I ∞=-=∑ （2）211(21)n I n n ∞==+∑ 6. 泰勒级数展开将函数21()53f x x x =+-展开成2-x 的幂级数 五、实验过程及结果（含源代码）（此处按题号顺序写上所写的程序语句内容以及matlab 中出现的程序运行结果） 1.syms x;f1='arctan(x)/x'F1=limit(f1,x,0)f2='((1+x)/(1-x))^(1/x)'F2=limit(f2,x,0)f3='(x*ln(1+x))/(sin(x^2))'F3=limit(f3,x,0)f4='(1/(1-x))-(1/(1-x^3))'F4=limit(f4,x,1)f5='(1+((2*t)/(a*x)))^(5*x)'F5=limit(f5,x,inf)f1 =arctan(x)/xF1 =1f2 =((1+x)/(1-x))^(1/x)F2 =exp(2)f3 =(x*ln(1+x))/(sin(x^2))F3 =1f4 =(1/(1-x))-(1/(1-x^3))F4 =NaNf5 =(1+((2*t)/(a*x)))^(5*x)F5 =exp((10*t)/a)2.syms x ln(x) cos(x) sin(x) t a; y1=(cos(x))^3-cos(3*x)Y1=diff(y1)y2=x*sin(x)*ln(x)Y2=diff(y2)y3=(x*exp(x)-1)/sin(x)Y3=diff(y3)y4=exp(x)*cos(x)Y4=diff(y4)y5=(x^2)*sin(x)Y5=diff(y5)y6=[a*exp(x) (t^3)*x;t*cos(x) ln(x) ]Y6=diff(x)Y7=diff(x,2)y1 =cos(x)^3 - cos(3*x)Y1 =3*cos(x)^2*diff(cos(x), x) - 3*D(cos)(3*x)y2 =x*ln(x)*sin(x)Y2 =ln(x)*sin(x) + x*ln(x)*diff(sin(x), x) + x*sin(x)*diff(ln(x), x)y3 =(x*exp(x) - 1)/sin(x)Y3 =(exp(x) + x*exp(x))/sin(x) - ((x*exp(x) - 1)*diff(sin(x), x))/sin(x)^2 y4 =exp(x)*cos(x)Y4 =exp(x)*cos(x) + exp(x)*diff(cos(x), x)y5 =x^2*sin(x)Y5 =2*x*sin(x) + x^2*diff(sin(x), x)y6 =[ a*exp(x), t^3*x][ t*cos(x), ln(x)]Y6 =1Y7 =3.syms x y z ;f1='sin(a*x)*sin(b*x)*sin(c*x)';f2='x^5+x^3-(x^(1/2))/4';f3='x*(exp(x))/(1+x^2)';f4='x/(1+x*y)';f='x^2+y^2';f6=sym('[1/x,b*x^2;exp(x),cos(x)]'); int(f1,x)int(f2,x)int(f3,x,0,1)int(int(f4,x,0,1),y,0,1)int(int(int(f,x),y),z,1,2)int(f6,x)ans =(a*b^2*cos(a*x)*sin(b*x)*sin(c*x) - b^3*cos(b*x)*sin(a*x)*sin(c*x) - c^3*cos(c*x)*sin(a*x)*sin(b*x) - a^3*cos(a*x)*sin(b*x)*sin(c*x) +a^2*b*cos(b*x)*sin(a*x)*sin(c*x) + a*c^2*cos(a*x)*sin(b*x)*sin(c*x) + a^2*c*cos(c*x)*sin(a*x)*sin(b*x) + b*c^2*cos(b*x)*sin(a*x)*sin(c*x) + b^2*c*cos(c*x)*sin(a*x)*sin(b*x) +2*a*b*c*cos(a*x)*cos(b*x)*cos(c*x))/(a^4 - 2*a^2*b^2 - 2*a^2*c^2 + b^4 - 2*b^2*c^2 + c^4)ans =x^4/4 - x^(3/2)/6 + x^6/6ans =- (ei(-i)*exp(i))/2 - (ei(i)*exp(-i))/2 + (ei(1 - i)*exp(i))/2 + (ei(1 + i)*exp(-i))/2ans =log(4) - 1ans =(x*y*(x^2 + y^2))/3ans =[ log(x), (b*x^3)/3][ exp(x), sin(x)]4.[x,y,z]=solve('-2*x+5*y-7*z=5','4*x+5*y-2*z=3','2*x+y+6*z=15') [x,y]=solve('x-5*sin(x)-4*cos(y)=0','y-5*cos(x)+4*sin(y)=0') [x,y]=dsolve('Dx=-5*x+y','Dy=-y+5*x')x =-212/81y =307/81z =74/27x =1.8207539129496562592168622750749y =-3.8552617061181725539710730412911x =C2/5 - C1*exp(-6*t)y =C2 + C1*exp(-6*t)5.syms nf1='(2*n-1)/2^n';f2='1/(n*(2*n+1))';I1=symsum(f1,n,1,inf)I2=symsum(f2,n,1,inf)I1 =3I2 =2 - 2*log(2)6.syms xtaylor('1/(x^2+5*x-3)',x,2)ans =(70*(x - 2)^2)/1331 - (9*x)/121 - (531*(x - 2)^3)/14641 + (4009*(x - 2)^4)/161051 - (30240*(x - 2)^5)/1771561 + 29/121六、实验总结通过本次的matlab上机实验，使我了解了符号对象定义的方法，可以较为熟练地运用计算法则以及对符号助阵的求解。