大学物理运动守恒定律1
合集下载
大学物理(上册)_动量 动量守恒定律(1)

mi ai
i
M
或
adm M
质心加速度是各质点加速度的加权平均
vc , ac
也可以写成分量式。
3.质点系动量的时间变化率
质心运动定理
内力——质点系内质点间的相互作用力 外力——质点系外的物体对系内任一质点的作用力
F外 Fi外
i
F1外
F12
m1
F13
i
M
;
yc
m y
i i 1
N
i
M
; zc
m zi 1N源自i iM质量连续分布的质点系
z
dm x , y , z
体分布
dm dV
dm dS dm dl
r
M
面分布
线分布
x o
y
dm:宏观小,微观大
xc
rc r dm M
xdm
M
yc zc
(英)I . Newton
《自然哲学的数学原理》
1642-1727
1687年出版
结构框图 质量 动 量
动量的时 间变化率
速度
动量 定理
动量守恒 定律
牛顿运动定律 以动量及其守恒定律为主线,从动量时间变化率引 入牛顿运动定律,并在中学基础上扩展其应用范围。 恒力,质点,惯性系 变力,质点系,非惯性系
?
第二篇 实物的运动规律 第四章 动量 动量守恒定律
本章共2讲
运动学(第三章 运动的描述)
第四章: 动量 动量守恒定律
动力学
第五章: 角动量 角动量守恒定律
(运动的度量)
第六章: 能量 能量守恒定律 特点:以守恒量和守恒定律为中心。
大学物理-运动定律与力学中的守恒定律

二、质点系的动量定理
n1 第i个质点受到的合力为 Fi外 f ji j 1
Fi外
f ji
mi
mj f ij
F j外
对第i个质点 t f ji dt mi vi 2 i i1 运用动量定理有:t Fi外 j 1 n n n1 n n t t Fi外 dt t f ij dt mi vi 2 mi vi1 t i 1 i 1 i 1 i 1 j 1
2、惯性系与非惯性系 问 题 a=0时人和小球的状态符合牛顿定律 a≠0时人和小球的状态为什麽不符合牛顿定律? 结论:牛顿定律成立的参照系称为惯性系。相对惯性 系作加速运动的参照系是非惯性系。而相对惯性系作 匀速直线运动的参照系也是惯性系。 根据天文观察,以太阳系作为参照系研究行星运动时发现 行星运动遵守牛顿定律,所以太阳系是一个惯性系。
y
O
v2 30o
I F 6.14N t
6.14 10 2 Ns
45o x
v1
n
mv 2 F t sin sin 105
F
51.86 tsin 0.7866
v1 v1
v2
51.86 45 6.86
x
例:质量 m1 0.25kg 的小球,静止在光滑水平面上, 受到另一质量 m2 0.30kg ,速度 v20 0.5m / s 的小球斜碰。设碰后小球 m2 的速度v2 0.3m / s 运动方向与原方向成 30 ,求小球 m1 碰撞后 速度的大小和方向。 v 2 解:把两球看作一 v20 x m2 m2 个系统,系统 m1 v10 0 不受外力, 故动量守恒: v1
大学物理 动量和动量守恒定律

解得
于是滑槽在水平面上移动的距离 S Vdt
0
t
m R M+m
22
大学 物理学
小
微分形式
结
积分形式
t1
•冲量
t2 I = Fdt
•质点的动量定理
dP F dt
I Fdt= P
t1
t2
•质点系的动量定理 F外 d Nhomakorabea dt
I 外= F外dt P
解:取车和人作为系统,该 系统水平方向动量守恒。设 人和车相对于地面的速度分 别为v 和 V,则
0 mv MV
mvdt MVdt mx MX M
0 0
t
t
xX L
L
x
M m
m X L Mm
大学 物理学
例2.13如图所示,在一个水平面上,炮车发射炮弹。 炮身质量为M,仰角为 ,炮弹质量为m。炮弹刚 出口时,相对于炮身的速度为u。不计地面摩擦, 求炮弹刚出口时炮车的速度。 解:取炮车和炮弹为系统。 u 系统所受的外力是重力和 支持力,都沿竖直方向, 所以水平方向动量守恒。 炮弹速度的水平分量为
t1
t2
•动量守恒定律
n 若F外 0, 则P= mi v i 恒 矢 量
i 1
惯性系
若f内 F外 , 则P= mi vi 恒矢量
i 1 n
n
若F外x 0, 则Px= mi vix 恒量
i 1
大学 物理学
§2-3 功 动能 势能 机械能守恒定律
F
大学 物理学
3. 严格不受外力或外力矢量和为零的系统 是很少见的,但 a.当外力<<内力 且作用时间极短时 (如碰撞),
角动量 角动量守恒定律大学物理

对定轴转动的刚体 Miin 0 ,合外力矩
M
Miex
d dt
(
mi
ri
2
)
d(J
dt
)
d( J )
dL
M
dt dt
第3章 守恒定律
12
大学物
理学
第二版
t2 t1
Mdt
L2
L1
t2 t1
Mdt
L2
L1
当转轴给定时,作用在物体上的冲量 矩等于角动量的增量.——定轴转动的角 动量定理
第3章 守恒定律
然长度处以
垂直于弹簧运动,当
弹簧与初始位置垂直时,弹簧长度
v
求此时滑块的速度.
v0
第3章 守恒定律
图 3.4
大学物 理学
第二版
【解】 由角动量和机械能守恒
结论:对于有心力问题,系统对力心处的 角动量守恒.
第3章 守恒定律
大学物
理学
第二版
三、角动量守恒定律的应用
(1)常平架回转仪(陀螺仪) (2)直升飞机尾翼
质点角动量定理的推导
L r p r mv
dL
d
(r
p)
r
dp
dr
p
dt dt dr v,v p 0
dt dL
dt
r
dp
r
F
dt
dt
dt
第3章 守恒定律
4
大学物
理学
第二版
dL
M
dt
作用于质点的合外力对参考点 O 的力 矩,等于质点对该点 O 的角动量随时间的 变化率.
13
大学物
理学
第二版
对定轴转动的刚体,受合外力矩M,
大学物理 动量 动量守恒定律汇总

Fdt (m dm)v (mv dm 0) vdm vkdt
F k v 200 4 8 10
2
N
12
3-9 一小船质量M=100kg,船头到船尾长度l=3.6m。现 有一质量m=50kg的人从船尾走到船头时,船头将移动多 少距离?假定水的阻力不计。
Fi外
Fij
j
i
内力-----是质点系内各质点间的作用力; 外力------是质点系外物体对质点系内质点的力。
由牛顿第三定律,内力必定是成对出现,且每对内力 都沿两质点连线的方向。
3
i质点合力
t2
t1
( Fi外 f ji )dt mi vi 2 mi vi1
j 1
n 1
F i外 f
9
n
例2.5 一弹性球,质量m=0.20kg,速度 v=5m/s, 与墙碰撞后弹回.设弹回时速度大小不变,碰撞前后的 运动方向和墙的法线所夹的角都是α,设球和墙碰撞 的时间Δt=0.05s,α=60°,求在碰撞时间内,球和 墙的平均相互作用力. 解:以球为研究对象.设墙对 球的平均作用力为 f ,球在 碰撞前后的速度为 v1和 v 2 , 由动量定理可得
2
t1 t2
Fx dt mv2 x mv1x
Iy Iz
t1 t2
Fy dt mv2 y mv1 y Fz dt mv2 z mv1z
2
t1
3
二 质点系的动量定理
如果研究的对象为多个质 点,则称为质点系 对质点系,受力可分为 “内力”和“外力”。
质点系
Fj外
Fji
§2.2 动量 动量守恒定律
力对时间的累积效应
大学物理动量守恒定律和能量守恒定律

04
动量守恒定律和能量守恒定 律的意义与影响
在物理学中的地位
基础定律
动量守恒定律和能量守恒定律是物理学中的两个基础定律,它们 在理论物理学和实验物理学中都占据着重要的地位。
理论基石
这两个定律为物理学理论体系提供了基石,许多物理理论和公式都 是基于这两个定律推导出来的。
验证实验
许多实验通过验证动量守恒定律和能量守恒定律的正确性,来检验 实验的准确性和可靠性。
适用条件
系统不受外力或外力合力为零
动量守恒定律只有在系统不受外力或外力合力为零的情况下才成立。如果系统受到外力作 用,则总动量将发生变化。
系统内力的作用相互抵消
系统内力的作用只会改变系统内各物体的速度,而不会改变系统的总动量。如果系统内力 的作用相互抵消,则总动量保持不变。
理想气体和刚体的动量守恒
未来能源利用的发展需要解决环 境问题和能源短缺问题,动量守 恒定律和能量守恒定律将在新能 源技术、节能技术等领域发挥关
键作用。
感谢您的观看
THANKS
在理想气体和刚体的研究中,由于气体分子之间的相互作用力和刚体之间的碰撞力都可以 忽略不计,因此它们的动量守恒。
实例分析
弹性碰撞
当两个小球发生弹性碰撞时,根据动量守恒定律,它们碰撞后 的速度满足m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'。由于弹性碰撞中能 量没有损失,因此碰撞前后两小球的速度变化量相等。
动量与能量的关系
动量是质量与速度的乘积,表 示物体的运动状态;能量是物 体运动状态的度量,包括动能
和势能。
动量和能量都是矢量,具有 方向性,遵循矢量合成法则。
动量和能量可以相互转化,但 总量保持不变,这是动量守恒 和能量守恒定律的内在联系。
大学物理—运动守恒定律

由质点动能定理: A E k 2 E k 1 E k
质点系动能定理:系统的外力和内力作功的总和等 于系统动能的增量。
Ae A i
(2m
i
1
i
v
2 i2
1 2
m iv ) E k 2 E k1 E k
2 i1
二、质点系功能原理
Work-energy principle of particle system 1、系统的机械能 mechanical energy of system
x
1 2
kx
2
选弹簧原长为弹性势能零点
/\/\/\/\/\/\/\
E
p
1 2
k ( y0 y )
2
k o
其中 ky 0 mg
y0
mg k
m
y
选弹簧系统平衡位置为弹性势能零点
E
p
1 2
ky
2
C
E
p0
1 2
1 2
ky
2 0
2 0
C 0
1 2 ky
2
C
1 2
ky
2 0
与与路径有关。
b
A
a ( L)
F cos ds F dr
a ( L)
b
b
( F dx F dy F dz )
x y z a ( L)
• 2、保守力 conservative force :作功的大小只与物体的
始末位置有关,而与所经历的路径无关,这种力叫做保守 力。重力、万有引力,弹性力及静电力都是保守力。没有 这种性质的力称为非保守力nonconservative force (耗散 力 dissipative force),如摩擦力。
大学物理 守恒定律(一)
F
解:A
1 2
mv32
1 2
mv12
0
所有外力的功
AF
F ds
F
dsdt dt
Fvdt v Fdt
vI 4 201 40 125.6(J )
2
20 10
0 12 3 t
弹簧k,一端固定,水平面光滑,A、B间轻绳相连。恒 力F使 m2自平衡位置由静止开始运动。则
a) A、B系统所受合外力为0时的速度
0
Fdx
1 2
mv02
即子弹到深度x=0.02m时速度还没有减为0
A
0.02
0
105
xdx
xm
0.02
2
103
dx
0
1 2
mv02
xm
0.21m
桌面光滑, m与挡板摩擦系数为μ,求m一端进另端出的过 程中A摩
解:A
2
F
1
dr
Ek
1 mv 2 2
1 2
mv
2 0
1 2
mv
2 0
(e
2
1)
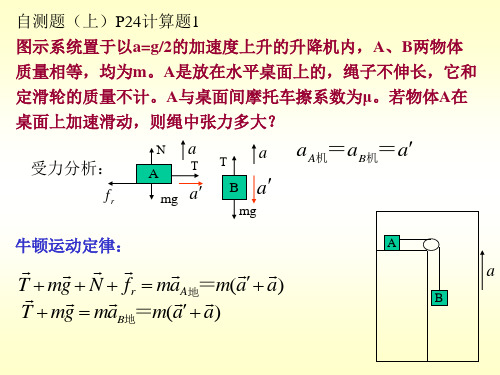
ma
ma
x
A
T fr ma
a
N mg ma 0 T 3mg(1 )
B
T mg ma ma
4
fr N
[教材P45:1-18] 物体m1下落时,带动绳子从细圆柱m2的 中心细孔中加速上升。若m2相对绳子的加速度为a, 求m1、m2相对地面的加速度a1 、a2。
解: m1:以地面为参照系 m1g T m1a 1 ①
vmM 0 v0
vmM末 0
(mg
m2 g
M )SmM
1 2
mv
