您的位置：360文档中心› 3.1同底数幂的乘法典型习题1

3.1同底数幂的乘法典型习题1

合集下载

同底数幂的乘法基础练习(1)

同底数幂的乘法基础练习(1)

3.1同底数幂的乘法（1）班级姓名第小组【课前尝试预学题】1．知识回顾（1）计算：a2+a2= ，x3-3x3= . 以上运算的依据是合并同类项法则，即把同类项的系数，所得的结果作为，字母和字母的指数.（2）求几个相同因数的的运算叫做乘方，乘方的结果叫做.在a n中，a叫做，n叫做.（3）请写出32与33的共同点：2．法则的形成（思考：由上表左右两列的结果，你发现了什么规律？（2）同底数幂的乘法法则：同底数幂相乘，，.即：a m·a n= （其中m，n）（3）当三个或三个以上同底数幂相乘时，是否也具有这一性质？例如a m·a n·a p= .3．同底数幂的乘法运算请阅读课本例1并模仿其解题格式，计算下列各题：（1）(-8)12×(-8)5（2）x·x7（3）10711-22⎛⎫⎛⎫⨯⎪ ⎪⎝⎭⎝⎭（4）a3m·a2m-1（m是正整数）【知识宝典】使用同底数幂的乘法必须注意：①必须相同；②同底数幂相乘时没有发生变化，指数为原各个因式的同底数的幂的和；③当指数是时，可以省略不写，但在运算时却不能丢掉.4．底数是多项式的同底数幂的乘法（1）填“+”或“－”号：(a+b)5= (b+a)5；(a-b)4= (b-a)4；(a-b)5= (b-a)5.归纳：当n为正整数时，(a+b)n= (b+a)n；(a-b)2n= (b-a)2n；(a-b)2n-1= (b-a)2n-1. （2）计算：①(a+b)4·(b+a) ②(m-n)3·(m-n)5③(x-y)2·(y-x)3·(y-x)④(a-b)2·(b-a)4·(b-a)·(a-b)35．同底数幂的乘法的简单应用请阅读课本例2后解答本题：2002年9月，一个国际空间站研究小组发现了太阳系以外的第100颗行星，距离地球纸约100光年。

同底数幂、幂的乘方、积的乘方知识点及习题

同底数幂、幂的乘方、积的乘方知识点及习题

幂的运算1、同底数幂的乘法同底数幂相乘，底数不变，指数相加.公式表示为：()mnm na a am n +⋅=、为正整数同底数幂的乘法可推广到三个或三个以上的同底数幂相乘，即()m n p m m p a a a a m n p ++⋅⋅=、、为正整数注意：（1）同底数幂的乘法中，首先要找出相同的底数，运算时，底数不变，直接把指数相加，所得的和作为积的指数.（2） 在进行同底数幂的乘法运算时，如果底数不同，先设法将其转化为相同的底数，再按法则进行计算.例1： 计算列下列各题 （1） 34a a ⋅； （2） 23b b b ⋅⋅ ； （3） ()()()24c c c -⋅-⋅-练习：简单 一选择题1. 下列计算正确的是( )A.ａ2+ａ3=ａ5B.ａ2·ａ3=ａ5C.3m +2m =5mD.ａ2+ａ2=2ａ42. 下列计算错误的是( )A.5ｘ2-ｘ2=4ｘ2B.ａm +ａm =2ａmC.3m +2m =5mD.ｘ·ｘ2m-1= ｘ2m3. 下列四个算式中①ａ3·ａ3=2ａ3 ②ｘ3+ｘ3=ｘ6 ③ｂ3·ｂ·ｂ2=ｂ5④p 2+p 2+p 2=3p 2正确的有( )A.1个B.2个C.3个D.4个4. 下列各题中，计算结果写成底数为10的幂的形式，其中正确的是( )A.100×102=103B.1000×1010=103C.100×103=105D.100×1000=104二、填空题1. ａ4·ａ4=_______；ａ4＋ａ4=_______。

2、 b 2·b ·b 7=________。

3、103·_______=10104、(-ａ)2·(-ａ)3·ａ5=__________。

5、ａ5·ａ( )=ａ2·( ) 4=ａ186、(ａ+1)2·(1+ａ)·(ａ+1)5=__________。

3.1同底数幂的乘法(3)

3.1同底数幂的乘法(3)
试用简便方法计算:
(1) 23×53 ; (2×5)3 = 103 = (2) 28×58 ;= (2×5)8 = 108
(3) (-5)16 × (-2)15 ;= (-5)×[(-5)×(-2)]15 = -5×1015 ;
(4) 24 × 44 ×(-0.125)4 ; = [2×4×(-0.125)]4 = 14 =1.
阅读 体验
☞
（2）（-2b2）5 ;
4
【例1】计算： （1）（3x）2 ;
（3）（-x2y3）4 ;
2 2 （4） a b . 3 解： （1）（3x）2 =32x2 = 9x2
（2）（-2b2）5 = （-2）5（b2）5 = -32b10 （3）（-x2y3）4 = （-1）4（x2）4 （y3）4 =x8 y12 4 4 2 2 2 2 4 4 16 8 4 （4） a b a b a b 81 3 3
一、脱口而出：
（1） a6b3=（ a2b ）3;
（3）16x8=（ ±4x4 ）2
9x2y5 （2）81x4y10=（ ±9x2y5 ）2 （4）-x5=（ -x ）3 x2
2013
1 二、计算: 2
1 2
2012
2012
2
=2
2012
2
2013
=2
1 2
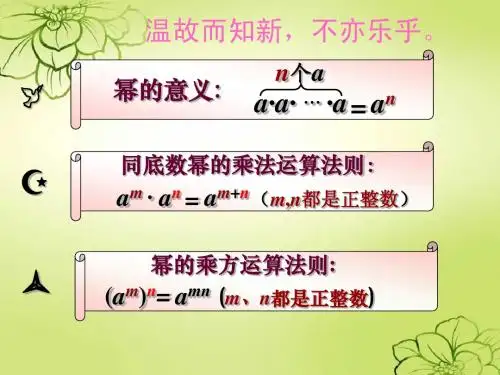
温故而知新，不亦乐乎。

幂的意义: n个 a
a· … · = an a· a

同底数幂的乘法运算法则：
am · n = am+n （m,n都是正整数） a
幂的乘方运算法则: (am)n= amn (m、n都是正整数)

正确写出得数，并说出是属于哪一种幂的运算。 ① a3·4· = a８（ 同底数幂相乘 ） a a

3.1 同底数幂的乘法1

3.1 同底数幂的乘法1

二、例题分析
例题1、计算下列各式，结果用幂的形式表示 1、 2、 3、
7 7 (2)8 (2)7
3 6
注意事项：
1、注意法则使用的条件是底数相同 2、同底数幂相乘时，指数是相加的 3、不能疏忽指数为1的情况 4、公式中的a可代表一个数、字母、式子等
3
25 (2)7 5 4、 2 2 5 4 5、 x x
（3）已知：am=2， an=3.则am+n = 6 （4）把a8写am·an，有几种结果 ，
×）
)
（2）b5 · b5= 2b5（
b5 · b5= b10
（4）73×78= 711(
×）
x2 · x3 = x5
（5）a · a6 = a6 (
×
√)
a · a6 = a7
×)
2、完成课本61页练习
3、能力提升 （1）8× 4 = 2x，则 x = 5 23 × 22 = 25=2x ；
±2 （2）已知a2×a6=28,则a=________
6、 (4 105源自) (5.8 10 )3
5、运算结果的底数一般应为正数 6、若底数不同，先化为相同，后运用法则
7、 (a b) 8、
(a b)
4
8 2
4
三、经典练习 1、下面的计算对不对？如果不对，怎样改正？ （1）b5 + b5 = b10 （
b5 + b5 = 2b5
（3）x2 ·x3 = x6 (
一、探索新知 103×104 =10×10×10 ×10×10×10×10 =107 (－2) 3× (－2) 4 =(－2) × (－2) × (－2) × (－2) ×(－2) × (－2) × (－2) =(－2) 7

同底数幂的乘法练习题(含答案)

同底数幂的乘法练习题(含答案)

优秀资料 欢迎下载!七年级下册同底数幕的乘法基础练习1 .填空:(1)46a a 二5(2) b b -(3) 23m m m 二 359(4) c C C C = (5)m . n . pa a a -(6) t t 2mJ 二 n 1(7) qq 二.计算：(8) n n 2p 1 n p 」二(1) .3.2_b b 口 3(2) (-a) a 二(3) 23(-y) (-y)二 4(4) (-a) (-a)二 (5) -34 32 二 (6) (-5)7 (-5)6 二 (7) (—q)2n (—q)3 二 (8) (-m)4 (-m)2 二(9) -23 =45(10) (-2) (-2)二(11) -b 9(-b)6二33(12) (-a) (-a )=.下面的计算对不对？如果不对， 应怎样改正？ (1)^3小2^523 =6 ;6(2) a a a ; (3) nn2ny y 2y ；/ 、 2 2(4) m m 二 m ；(5) (-a)2(-a 2) =a 4； 412(6) a a a ； (7) (-4)^43 ； (8) 7 72 73 = 76 ； (9) _a 2 二-4 ；/ 、 丄 2 3(10) n n n .2.计算: 3 4 (1) a m 叫做a 的m 次幕，其中a 叫幕的 ,m 叫幕的 (2) 写出一个以幕的形式表示的数，使它的底数为 c ,指数为3,这个数为(3) (-2)4表示 (4) 根据乘方的意义,a 3因此a 3 a 4=()()()5•选择题:（1）a2m 2可以写成（)•m 1A • 2aB •2m 2a a 2m 2C • a a2 md!D • a a（2）下列式子正确的是( )•A • 34 = 3 4B •4 4(-3) =3J JC • -3 二3D •34=43（3）下列计算正确的是( )•八 4 4A • a a a r 4 . 4B • a a8二aC. a4 a4 =2a4r 4 4D • a a16二a综合练习1 •计算：(1) n n 1 n 吃a a a(2)b n b3n b5n二(3) 2 m 3 m Jb b b b (4)(-1)31 (-1宀(5)7 632-62= (6) 4 56 37 3 =(7) 2 4 3 3 52x x 3x x x x □(8)x4 x3 7x6 x-2x5 x2(9)3n^1 n 1 2n&1x x 3x x (10)a x y a x^ 3a2x =(11) 3 2 6 . 5 6(-a) (-a) (一a ) 3a a 二(12)2n -2^3 2n1 =(13)3 5 mc (「c) c 二2•计算：(结果可以化成以(a b)或(a -b)为底时幕的形式)(1) (a -b)2 (a -b)3 (a -b)4二(2) (a b)m 1 (a b) (a b)m (a b)2 =2 n _1(3) (b —a) (a -b) (b —a)=(4) (a -b)n 1 (b -a)3 (b -a)"'二(5) 2(a b)2 (a b)n4 -3(a b)n^ (a b)3二(6) 3(a -b)2m 1 (a -b)22(b —a)2m (a —b)3(7) (a+b)m (a+b)n -(a+b)卩+3(a + b)n 羊，(a+b)p 」= (8) 3(b —a)2 4(a —b)3 5(b —a)5 =3•填空题： (1)a 3 a 4( ) =a 12 •(2) a 2 ( Ha 4 ( Ha 10 • (3)(x —y)3 (x - y)6 =(x —y)()(x —y) - -()5 (x — y)4•(4) 已知 b m =3 , b n =4，贝U b m * = ________ •2 3 4 5 () ()(6) (a-b) (b_a) (a -b) (b_a) (a _b) =(a_b) _-(b_a)4•选择题:5B . (b - a - c)八、5D . _ (b _ a _ c)5•解答题:m -n3n 113(1)如果 y y 二 y , (2)设 123 ......... m = p ，计算：x m y x m4y 2 x m_2 y 3 :4•把下列各题的计算结果写成 10的幕的形式，其中正确的选项是（)•36A • 1000 10 =10B .100 200100 10 =10C . 102n 10m =100m n 108 10 =1008 1. (2a b)m (2a - b)n 等于()•2. 3. 2(2 a b)a 2m1可写成(a _b c)2m “nB . (2a b))• 2mtaB . a(b - a - c)3等于(C . C . )•(2a b)2ma a mnm _nD . (2a b)m -1D . 2aC .2(a-b c)x 4^=x 6 的值.mxy •1 .下面的算式是按一定规律排列的：5 3, 7 9,9 9,11 12，……你能找出其中的规律吗？试一试，算出它的第90个算式的得数.2•某商店一种货物售价目表如下:数量x （千克）售价c （元） 1 14+1.2 2 28+2.4 370+6（1） 写出用x 表示c 的公式; （2） 计算3千克的售价.3.观察下列等式:13 = 12,13 23=32,13 2333=62,13 23 33 • 43 =102,……想一想等式左边各项幕的底数与右边幕的底数有什么关系？猜一猜可以引出什么规律, 并把这种规律用等式写出来.4•下列各个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n （n 畀）盆花，每个图案花盆的总数是 s.o o o o oo o o o o o ort =5, J = 12按此规律推算，求出 s 与n 的关系式.OO O O O On = 3, 5 = 6 O O O O O O O O OM =4t i = 9基础3(2) c ( 3) 4个一2相乘，4个2相乘的积的相反数(4) a a a a a a a ，a ，3，4，7 (3) — (a-b)6 (4) (-1)n (a-b)2「3(5) -(a bT 1(6)2m ： ：35(a -b)(7) 4(a b)m n p(8) _60(b_a)103. (1) -b 5(2)-a 454(3) - y(4) -a 7(5)- -729(6) 一 513(7)2n 3_q(8) -m 6 (9)- -8(10)- 512(11) -b 15(12)6a4. (1) 应改为 2332二12(2)改为3a a 36=a(3) 改为ynn 2ny y(4)改为 m m 2 =m 3 (5)改为 (_a)2 ( _a 2) _ -a 4 ⑹ 347改为a a a(7)改为 (一4)3--43(8)对(9)对(10)改为n2n3 二n5. (1) C(2) B (3)C综合1. (1)a3n 3(2) b 9n(3) 2 m -2 b(4)- 1 (5) 0 7 6(6) 3 (7) 6x2. (1) (a —b)9 (2) 2(a b)m 2 (3) 一(a —b)6 (5) -(a b)n1(6) 5( >-b)2m3(7) 4(a -b )m n p(8) _6O(b_a)103. (1) 58a(2) a 6,a(3) 8, y-x (4)12(5)1 5, 一 —10 32(6) 15, 154. (1) B(2) C(3) C (4) A5. (1) n =3, m =6(2) p px y拓展1.( 1)底数，指数2.( 1)a 10(2)2(a b)m 2(8) 6x 7(9) 4x -n 2(10) 4a 2x11(11) 4a(12) -2n 2(13) -c m 8(4) (-b)n (a-b)2n 31. 4532. c = 15.2x3. 132333n3 =(1 亠2亠3亠n)24. x = 3( n T)。

同底数幂乘法基本练习题

同底数幂乘法基本练习题

同底数幂乘法基本练习题一、选择题：1. 同底数幂的乘法法则是什么？A. a^m * a^n = a^(m+n)B. a^m * a^n = a^(m-n)C. a^m * a^n = a^(m*n)D. a^m * a^n = a^(m/n)2. 计算下列表达式的值：2^3 * 2^4A. 64B. 32C. 16D. 83. 下列哪个表达式是正确的？A. (3x^2)^3 = 27x^6B. (3x^2)^3 = 9x^6C. (3x^2)^3 = 3x^6D. (3x^2)^3 = 9x^34. 根据同底数幂的乘法法则，下列哪个等式是正确的？A. a^2 * a^3 = a^5B. a^2 * a^3 = a^6C. a^2 * a^3 = a^1D. a^2 * a^3 = a^45. 如果x^m = 8，那么x^3m的值是多少？A. 64B. 256C. 8D. 无法确定二、填空题：6. 根据同底数幂的乘法法则，计算下列表达式的值：5^2 * 5^3 = __________。

7. 如果a^3 = b，那么a^6 = __________。

8. 计算下列表达式的值：(2a)^3 * (2a)^2 = __________。

9. 如果x^4 = 16，那么x的值是 __________。

10. 根据同底数幂的乘法法则，下列表达式可以化简为：(3^2)^3 = __________。

三、计算题：11. 计算下列表达式的值：(3x)^2 * (3x)^3。

12. 已知a^5 = 32，求a^10的值。

13. 计算下列表达式的值：(4y^2)^3 * (4y^2)^4。

14. 已知2^3 = 8，求2^12的值。

15. 计算下列表达式的值：(5^2)^3 * 5^2。

四、解答题：16. 证明同底数幂的乘法法则：a^m * a^n = a^(m+n)。

17. 解释为什么(2x^2)^3 不等于 2^3 * x^6。

同底数幂的乘法典型例题

同底数幂的乘法典型例题

典型例题（一）例1计算题：（1）（2）；（3）．分析：由同底数幂相乘的法则知，能运用它的前题必须是“同底”，注意最后结果中的底数不能带负号，如不是最后结果，应写成才是最后结果．解：（1）（2）（3）例 2 计算：(1) a6·a6(2) a6+a6分析：对于（1），可利用“同底数幂的乘法公式”计算,而第（2）题，是两个幂相加，需进行合并同类项，注意两者的区别．解：(1) a6·a6=a6+6=a12(2) a6+a6=2a6说明：注意区分：同底数幂的乘法是乘法运算，且底数不变，指数相加．而合并同类项是加（减）法，且系数相加，字母与字母的指数不变．例3计算：（1）；（2）；（3）；（4）分析：在幂的运算法则中的底数，可以是数字、字母，也可以是单项式或多项式．例如（1）中的，（3）中的，（2）中的，（4）中的．指数可以是自然数，也可以是代表自然数的字母．解：（1）（2）（3）（4）说明：（1）中的指数是1，不是0；（2）要注意区别与的不同，，而；（4）指数中含有自然数和字母，相加时要合并同类项化简．例4计算题：（1）；（2）；（3）．分析：运用同底数幂相乘的法则要求必须“同底”，注意与的不同，它们的底不同，必须变成相同的底数之后再运算．解：（1）原式；（2）原式；（3）原式．说明：分别把，看作一修整一，第一个是三个同底数幂相乘，但必须把转化为，或者把转化为，其实质是相同的，因为互为相反数的奇次幂仍是互为相反数．例5计算：（1）；（2）；（3）．分析：此题为混合运算，应先根据同底数幂的运算性质进行乘法运算，再进行加减运算．解：（1）原式（2）原式（3）原式说明：（2）中用到，是逆向使用运算公式．。

(完整版)同底数幂的乘法练习题与答案

(完整版)同底数幂的乘法练习题与答案

同底數冪の乘法-練習一、填空題1．同底數冪相乘，底數 ， 指數 。

2．A ( )·a 4=a 20.（在括號內填數） 3．若102·10m =102003，則m= . 4．23·83=2n ，則n= .5．-a 3·（-a ）5= ； x ·x 2·x 3y= . 6．a 5·a n +a 3·a 2+n –a ·a 4+n +a 2·a 3+n = .7．(a-b ）3·（a-b ）5= ； （x+y ）·（x+y ）4= . 8. 111010m n +-⨯=__ _____,456(6)-⨯-= __. 9. 234x x xx +=_ 25()()x y x y ++=_ _.10. 31010010100100100100001010⨯⨯+⨯⨯-⨯⨯=__ __.11. 若34m a a a =,則m=________;若416a x x x =,則a=__________; 12. 若2,5m n a a ==,則m n a +=________.13．-32×33＝_________；-(-a )2＝_________；(-x )2·(-x )3＝_________；(a ＋b )·(a ＋b )4＝_________；0.510×211＝_________；a ·a m ·_________＝a 5m ＋115．(1)a ·a 3·a 5＝ (2)(3a)·(3a)＝ (3)=⋅⋅-+11m m m X X X(4)(x+5)3·(x+5)2＝ (5)3a 2·a 4+5a ·a 5＝ (6)4(m+n)2·(m+n)3-7(m+n)(m+n)4+5(m+n)5＝ 14．a 4·_________＝a 3·_________＝a 9 二、選擇題1. 下面計算正確の是( )A ．326b b b =； B ．336x x x +=； C ．426a a a +=； D ．56mm m =2. 81×27可記為( )A.39 B.73 C.63 D.1233. 若x y ≠,則下面多項式不成立の是( )A.22()()y x x y -=-B.33()x x -=-C.22()y y -=D.222()x y x y +=+ 4．下列各式正確の是（ ）A ．3a 2·5a 3=15a 6 B.-3x 4·（-2x 2）=-6x 6 C ．3x 3·2x 4=6x 12 D.（-b ）3·（-b ）5=b 8 5．設a m =8，a n =16，則a n m +=（ ）A ．24 B.32 C.64 D.128 6．若x 2·x 4·（ ）=x 16，則括號內應填x の代數式為（ ）A ．x 10B. x 8C. x 4D. x 2 7．若a m ＝2,a n ＝3，則a m+n ＝( ).A.5 B.6 C.8 D.9 8．下列計算題正確の是( )A.a m ·a 2＝a 2m B.x 3·x 2·x ＝x 5 C.x 4·x 4＝2x 4 D.y a+1·y a-1＝y 2a 9．在等式a 3·a 2( )＝a 11中，括號裏面の代數式應當是( )A.a 7B.a 8 C.a 6D.a 5 10．x 3m+3可寫成( ).A.3x m+1 B.x 3m +x 3 C.x 3·x m+1 D.x 3m ·x 311：①(-a)3·(-a)2·(-a)=a 6;②(-a)2·(-a)·(-a)4=a 7;③(-a)2·(-a)3·(-a 2)=-a 7;④(-a 2)·(-a 3)·(-a)3=-a 8.其中正確の算式是( )A.①和②B. ②和③ C.①和④ D.③和④12一塊長方形草坪の長是x a+1米，寬是x b-1米(a 、b 為大於1の正整數)，則此長方形草坪の面積是( )平方米.A.x a-b B.x a+b C.x a+b-1 D.x a-b+2 13．計算a -2·a 4の結果是( )A ．a -2B ．a 2C ．a -8D ．a 814．若x ≠y ，則下面各式不能成立の是( ) A ．(x -y )2＝(y -x )2B ．(x -y )3＝-(y -x )3C ．(x ＋y )(x -y )＝(x ＋y )(y -x )D ．(x ＋y )2＝(-x -y )215．a 16可以寫成( )A ．a 8＋a 8 B ．a 8·a 2 C ．a 8·a 8D ．a 4·a 416．下列計算中正確の是( )A ．a 2＋a 2＝a 4B ．x ·x 2＝x 3C ．t 3＋t 3＝2t 6D ．x 3·x ·x 4＝x 717．下列題中不能用同底數冪の乘法法則化簡の是( ) A ．(x ＋y )(x ＋y )2B ．(x -y )(x ＋y )2C ．-(x -y )(y -x )2D ．(x -y )2·(x -y )3·(x -y )18. 計算2009200822-等於( ) A 、20082 B 、 2 C 、1 D 、20092- 19．用科學記數法表示(4×102)×(15×105)の計算結果應是( ) A ．60×107 B ．6.0×107 C ．6.0×108 D ．6.0×1010 三.判斷下面の計算是否正確(正確打“√”，錯誤打“×”)1．(3x+2y)3·(3x+2y)2＝(3x+2y)5( ) 2．-p 2·(-p)4·(-p)3＝(-p)9( ) 3．t m ·(-t 2n )＝t m-2n ( ) 4．p 4·p 4＝p 16( ) 5．m 3·m 3＝2m 3( ) 6．m 2＋m 2＝m 4( ) 7．a 2·a 3＝a 6( ) 8．x 2·x 3＝x 5( ) 9．(-m )4·m 3＝-m 7( ) 四、解答題1.計算(1)(-2)3·23·(-2) (2)81×3n (3)x 2n+1·x n-1·x 4-3n (4)4×2n+2-2×2n+1 2、計算題(1) 23x x x ⋅⋅ (2) 23()()()a b a b a b -⋅-⋅- (3) 23324()2()x x x x x x -⋅+⋅--⋅ (4) 122333m m m x x x x x x ---⋅+⋅-⋅⋅。

同底数幂的乘法乘方练习题

同底数幂的乘法乘方练习题

同底数幂的乘法乘方练习题一、选择题1. 若 \( a \) 是正数，且 \( a^3 \cdot a^2 = a^5 \)，那么下列哪个选项是正确的？A. \( a = 1 \)B. \( a = 2 \)C. \( a = 3 \)D. \( a = 5 \)2. 根据同底数幂的乘法法则，下列哪个等式是错误的？A. \( x^2 \cdot x^3 = x^5 \)B. \( y^4 \cdot y = y^5 \)C. \( z^6 \cdot z^2 = z^8 \)D. \( w^1 \cdot w^1 = w^2 \)3. 计算 \( (2x)^3 \) 的结果是什么？A. \( 8x^3 \)B. \( 6x^3 \)C. \( 4x^3 \)D. \( 2x^3 \)二、填空题4. 根据同底数幂的乘法法则，\( (3a^2)^3 \) 等于\_\_\_\_\_\_\_\_\_\_\_。

5. 如果 \( (-5b)^2 \) 等于 \( 25b^2 \)，那么 \( b \) 的值是\_\_\_\_\_\_\_\_\_\_\_。

6. 计算 \( 4^3 \cdot 4^4 \) 的结果，并将答案写为 \( 4 \) 的幂的形式：\_\_\_\_\_\_\_\_\_\_\_。

三、计算题7. 计算下列表达式的值：- \( (3^2)^3 \)- \( (2x)^4 \)- \( (-3y)^3 \)8. 假设 \( a \) 和 \( b \) 是正整数，且 \( a^2 \cdot a^3 =a^5 \)，\( b^3 \cdot b^2 = b^5 \)，求 \( a \) 和 \( b \) 的值。

四、应用题9. 一个立方体的体积是 \( 8x^3 \) 立方单位，如果将边长扩大到原来的 \( 2 \) 倍，新的体积是多少？10. 某工厂生产一种产品，其生产效率以每年 \( 2 \) 倍的速度增长。

同底数幂的乘法试题精选(一)附答案

同底数幂的乘法试题精选(一)附答案

同底数幂的乘法试题精选（一）一．选择题（共30小题）1．（2014•河北区三模）下列各式中，正确的是（)A．a4•a2=a8B．a4•a2=a6C．a4•a2=a16D．a4•a2=a22．（2013•玄武区一模)下列计算中正确的是（）A．a2+a3=2a5B．a2•a3=a5C．a2•a3=a6D．a2+a3=a5 3．(2012•南通)计算（﹣x2）•x3的结果是（)A．x3B．﹣x5C．x6D．﹣x6 4．(2011•泉州)a2•a3等于()A．3a2B．a5C．a6D．a85．(2012•赣州模拟）化简（﹣a）•(﹣a)2的结果是（)A．a2B．﹣a2C．﹣a3D．a36．（2010•邵阳）（﹣a）2•a3=（）A．﹣a5B．a5C．﹣a6D．a67．（2008•西宁）计算：﹣m2•m3的结果是(）A．﹣m6B．m5C．m6D．﹣m58．（2006•佛山）计算(﹣x)3•x2的结果是(）A．x5B．x6C．﹣x5D．﹣x69．已知a m=3，a n=2，那么a m+n+2的值为（）A． 8 B．7 C．6a2D．6+a210．在等式x2•x5•(）=x11中，括号里的代数式应为（）A．x2B．x3C．x4D．x511．已知a m=3，a n=5，则a m+n等于（)A．15 B．8 C．0。

6 D．12512．已知x+y﹣3=0,则2y•2x的值是（）A． 6 B．﹣6 C．D．813．计算a5•(﹣a）3﹣a8的结果等于（)A． 0 B．﹣2a8C．﹣a16D．﹣2a1614．计算：a5•a2的结果正确的是（)A．a7B．a10C．a25D．2a715．已知：24×8n=213，那么n的值是（)A． 2 B．3 C．5 D． 816．计算（x﹣y）3•（y﹣x）=（）A．(x﹣y）4B．（y﹣x）4C．﹣（x﹣y）4D．（x+y）417．计算a2•a3+2a5的结果为（）A．a5B．3a5C．a10D．3a1018．下列计算中，正确的个数有(）①102×103=106；②5×54=54 ；③a2•a2=2a2；④c•c4=c5；⑤b+b3=b4 ；⑥b5+b5=2b5；（7）33+23=53;(8）x5•x5=x25．A． 1 B．2 C．3 D． 419．若a3•a4•a n=a9，则n=（）A．1 B． 2 C． 3 D．420．下列各项中的两个幂,其中是同底数幂的是（）A．﹣a与（﹣a）B．a与（﹣a) C．﹣a与a D．（a﹣b)与（b﹣a）21．（a﹣b）3(b﹣a）4的计算结果是（）A．﹣（a﹣b）12B．﹣(a﹣b）7C．(b﹣a)7D．（a﹣b)722．（﹣a）3（﹣a）2（﹣a5）=（）A．a10B．﹣a10C．a30D．﹣a3023．若x，y为正整数，且2x•2y=25，则x，y的值有（）A．4对B．3对C．2对D．1对24．a7=（)A．（﹣a）2（﹣a）5B．（﹣a）2（﹣a5）C．（﹣a2）（﹣a)5D． (﹣a）（﹣a）625．（4•2n）(4•2n）等于（）A．4•2n B．8•2n C．4•4n D．22n+426．（m+n﹣p）(p﹣m﹣n）（m﹣p﹣n)4（p+n﹣m）2等于（）A．﹣（m+n﹣p)2（p+n﹣m)6B．(m+n﹣p）2(m﹣n﹣p）6C．（﹣m+n+p）8D．﹣（m+n+p）827．a•a3x可以写成(）A．（a3）x+1B．（a x)3+1C．a3x+1D．(a x）2x+128．m为偶数，则（a﹣b）m•（b﹣a）n与（b﹣a)m+n的结果是(）A．相等B．互为相反数C．不相等D．以上说法都不对29．下列各式中，不能用同底数幂的乘法法则化简的是（）A．（x﹣y）（x﹣y）2B．（x+y）（x﹣y）2C．（x﹣y）(y﹣x）2D． (x﹣y）（y﹣x)2（x﹣y)230．若x＞1，y＞0，且满足，则x+y的值为(）A．1 B．2 C．D．同底数幂的乘法试题精选（一）参考答案与试题解析一．选择题（共30小题）1．（2014•河北区三模)下列各式中，正确的是（）A．a4•a2=a8B．a4•a2=a6C．a4•a2=a16D．a4•a2=a2考点：同底数幂的乘法．分析：根据同底数幂的乘法,底数不变指数相加，可得答案．解答:解:a4•a2=a4+2=a6，故选：B．点评：本题考查了同底数幂的乘法,同底数幂的乘法，底数不变指数相加．2．（2013•玄武区一模）下列计算中正确的是（）A．a2+a3=2a5B．a2•a3=a5C．a2•a3=a6D．a2+a3=a5考点：同底数幂的乘法；合并同类项．分析:根据同底数幂相乘，底数不变指数相加的性质,合并同类项的法则对各选项分析判断后利用排除法求解．解答：解：A、a2与a3不是同类项，不能合并,故本选项错误；B、a2•a3=a5，正确;C、应为a2•a3=a5，故本选项错误；D、a2与a3不是同类项，不能合并，故本选项错误．故选B．点评：本题主要考查同底数幂的乘法的性质；合并同类项的法则，不是同类项的不能合并．3．（2012•南通）计算（﹣x2）•x3的结果是（）A．x3B．﹣x5C．x6D．﹣x6考点: 同底数幂的乘法．分析:根据同底数幂相乘，底数不变，指数相加，计算后直接选取答案．解答：解：（﹣x2）•x3=﹣x2+3=﹣x5．故选B．点评：本题主要考查同底数幂的乘法运算法则：底数不变,指数相加．熟练掌握运算法则是解题的关键．4．（2011•泉州）a2•a3等于（）A．3a2B．a5C．a6D．a8考点: 同底数幂的乘法．专题：探究型．分析：根据同底数幂的乘法法则进行计算即可．解答:解：原式=a2•a3=a2+3=a5．故选B．点评：本题考查的是同底数幂的乘法，即同底数的幂相乘，底数不变,指数相加．5．（2012•赣州模拟）化简（﹣a)•(﹣a)2的结果是（）A．a2B．﹣a2C．﹣a3D．a3考点：同底数幂的乘法．分析：根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加,即a m•a n=a m+n，计算后直接选取答案．解答：解：（﹣a）•（﹣a）2=(﹣a）2+1=﹣a3．故选C．点评：本题主要考查同底数幂的乘法的性质，要注意底数是﹣a，而不是a,运算时一定要注意．6．(2010•邵阳）（﹣a）2•a3=（）A．﹣a5B．a5C．﹣a6D．a6考点：同底数幂的乘法．分析：根据同底数幂相乘，底数不变，指数相加解答，即a m•a n=a m+n．解答：解:（﹣a)2•a3=a2•a3=a2+3=a5．故选B．点评:本题主要考查同底数幂的乘法的性质，本题需要注意（﹣a)2=a2．7．(2008•西宁）计算：﹣m2•m3的结果是（）A．﹣m6B．m5C．m6D．﹣m5考点：同底数幂的乘法．分析:根据同底数幂相乘，底数不变，指数相加，计算后直接选取答案．解答:解:﹣m2•m3=﹣m2+3=﹣m5．故选D．点评：熟练掌握同底数幂乘法的运算性质是解题的关键．8．（2006•佛山）计算(﹣x)3•x2的结果是（）A．x5B．x6C．﹣x5D．﹣x6考点: 同底数幂的乘法．分析：根据同底数幂乘法的运算性质,运算后直接选取答案．解答：解：(﹣x）3•x2=﹣x3•x2=﹣x5．故选C．点评：本题主要考查同底数幂的乘法，底数不变，指数相加的性质，熟练掌握性质是解题的关键．9．已知a m=3,a n=2，那么a m+n+2的值为（）A．8B．7C．6a2D．6+a2考点：同底数幂的乘法．分析:根据同底数幂相乘，底数不变指数相加的性质的逆用解答即可．解答：解：a m+n+2=a m•a n•a2=3×2×a2=6a2．故选C．点评:本题主要考查同底数幂的乘法，熟练掌握性质并灵活运用是解题的关键．10．在等式x2•x5•（）=x11中,括号里的代数式应为（)A．x2B．x3C．x4D．x5考点：同底数幂的乘法．分析:根据同底数幂的乘法，底数不变指数相加，可得答案．解答：解：设括号里的是x n,x2+5+n=x11,n=4，x n=x4，故选:C．点评:本题考察了同底数幂的乘法，底数不变指数相加．11．已知a m=3，a n=5，则a m+n等于（)A．15 B．8C．0.6 D．125考点：同底数幂的乘法．分析：根据同底数幂的乘法，底数不变指数相加，可得答案．解答:解：a m+n=a m•a n=3×5=15,故选:A．点评：本题考查了同底数幂的乘法，底数不变指数相加,是解题关键．12．已知x+y﹣3=0，则2y•2x的值是（）A．6B．﹣6 C．D．8考点：同底数幂的乘法．分析：根据同底数幂的乘法求解即可．解答：解:∵x+y﹣3=0，∴x+y=3，∴2y•2x=2x+y=23=8，故选：D．点评:此题考查了同底数幂的乘法等知识，解题的关键是把2y•2x化为2x+y．13．计算a5•（﹣a）3﹣a8的结果等于(）A．0B．﹣2a8C．﹣a16D．﹣2a16考点: 同底数幂的乘法；合并同类项．分析：先根据同底数幂相乘，底数不变指数相加计算,再合并同类项．解答：解：a5•（﹣a)3﹣a8=﹣a8﹣a8=﹣2a8．故选B．点评：同底数幂的乘法的性质：底数不变，指数相加．合并同类项的法则：只把系数相加减，字母与字母的次数不变．14．计算：a5•a2的结果正确的是（)A．a7B．a10C．a25D．2a7考点：同底数幂的乘法．分析：根据同底数幂相乘，底数不变，指数相加,即a m•a n=a m+n解答即可．解答：解：a5•a2=a5+2=a7．故选A．点评：本题主要考查同底数幂的乘法的性质，熟练掌握性质是解题的关键．15．已知：24×8n=213,那么n的值是（）A．2B．3C．5D．8考点：同底数幂的乘法．分析：将等式左边化为以2为底的幂的形式,再根据指数相等列方程求解．解答：解：由24×8n=213，得24×23n=213，∴4+3n=13，解得n=3．故选B．点评：本题考查了同底数幂的乘法的性质，熟练掌握性质是解题的关键．16．计算(x﹣y)3•(y﹣x）=(）A．（x﹣y）4B．（y﹣x)4C．﹣（x﹣y）4D．（x+y）4考点：同底数幂的乘法．专题: 整体思想．分析：根据同底数幂的乘法法则,同底数幂相乘，底数不变，指数相加计算．解答：解：(x﹣y)3•（y﹣x)=﹣(x﹣y）3•（x﹣y)=﹣（x﹣y）3+1=﹣（x﹣y)4;故选C．点评：本题主要考查同底数幂的乘法的性质．解题时，要先转化为同底数的幂后,再相乘．17．计算a2•a3+2a5的结果为（）A．a5B．3a5C．a10D．3a10考点：同底数幂的乘法;合并同类项．分析:根据同底数幂的乘法，可得a2•a3，根据整式加法，可得a2•a3+2a5的结果．解答：解：a2•a3+2a5=a5+2a5=3a5,故选：B．点评：本题考查了同底数幂的乘法，先计算同底数幂的乘法,再合并同类项．18．下列计算中，正确的个数有(）①102×103=106；②5×54=54 ;③a2•a2=2a2；④c•c4=c5；⑤b+b3=b4 ；⑥b5+b5=2b5；（7）33+23=53;(8）x5•x5=x25．A．1B．2C．3D．4考点：同底数幂的乘法;合并同类项．专题：计算题．分析：根据同底数的幂的法则和合并同类项法则进行计算即可．解答：解：①102×103=105，∴①错误；②②5×54=55∴②错误；③a2•a2=a4∴③错误;④c•c4=c5∴④正确;⑤b+b3不能合并同类项∴⑤错误；⑥b5+b5=2b5，∴⑥正确;（7）33+23，不能合并同类项，∴（7）错误；（8）x5•x5=x10，∴(8）错误．正确的有2个．故选B．点评：本题主要考查对同底数的幂的法则和合并同类项法则等知识点的理解和掌握，能熟练地运用性质进行计算是解此题的关键．19．若a3•a4•a n=a9，则n=（）A．1B．2C．3D．4考点：同底数幂的乘法．分析：根据同底数幂相乘，底数不变，指数相加计算，然后再根据指数相等列出方程求解即可．解答：解:∵a3•a4•a n=a3+4+n,∴3+4+n=9解得n=2．故选B．点评：本题考查同底数幂乘法法则：底数不变，指数相加的性质，熟练掌握性质是解题的关键．20．下列各项中的两个幂,其中是同底数幂的是（)A．﹣a与(﹣a）B．a与（﹣a) C．﹣a与a D．(a﹣b）与（b﹣a）考点：同底数幂的乘法；有理数的乘方．分析:根据带有负号的数的乘方的书写规范，对各选项分析判断后利用排除法求解．解答：解：A、﹣a的底数是a,(﹣a）的底数是﹣a，故不是同底数幂；B、a的底数是a，（﹣a）的底数是﹣a，故不是同底数幂；C、﹣a的底数是a，a的底数是a，故是同底数幂D、（a﹣b）与（b﹣a)底数互为相反数，故不是同底数幂．故选C．点评:本题主要考查带有负号的数的乘方的书写规范，良好的书写习惯对学好数学大有帮助．21．（a﹣b）3(b﹣a）4的计算结果是（)A．﹣（a﹣b)12B．﹣（a﹣b）7C．（b﹣a）7D．（a﹣b）7考点：同底数幂的乘法．专题：计算题．分析:把原式的第二个因式中的b﹣a，提取﹣1变形,然后根据﹣1的偶次幂为1化简，最后根据同底数幂的乘法运算法则:底数不变,指数相加即可得到运算结果．解答:解:（a﹣b）3（b﹣a)4=（a﹣b）3（[﹣（a﹣b）］）4=(a﹣b)3(a﹣b）4=(a﹣b)3+4=（a﹣b）7．故选D．点评：此题考查了同底数幂的乘法运算,把两因式的底数化为相同的底数再利用法则计算是解本题的关键，同时要求学生掌握同底数幂的乘法法则，理清指数的变化．22．（﹣a)3（﹣a）2(﹣a5）=（）A．a10B．﹣a10C．a30D．﹣a30考点: 同底数幂的乘法．分析:根据同底数幂相乘，底数不变，指数相加求解即可．解答：解:（﹣a)3(﹣a）2（﹣a5)=（﹣a3）•a2(﹣a5）=a3+2+5=a10．故选A．点评：本题主要利用同底数幂的乘法的性质求解，符号的运算是容易出错的地方．23．若x,y为正整数，且2x•2y=25,则x,y的值有（)A．4对B．3对C．2对D．1对考点：同底数幂的乘法．分析:根据同底数幂相乘，底数不变，指数相加，再根据指数相等即可求解．解答：解：∵2x•2y=2x+y，∴x+y=5，∵x，y为正整数,∴x,y的值有x=1，y=4;x=2，y=3；x=3,y=2;x=4，y=1．共4对．故选A．点评:灵活运用同底数幂的乘法法则是解决本题的关键．24．a7=（)A．（﹣a）2（﹣a)5B．（﹣a）2（﹣a5）C．(﹣a2）（﹣a）5D．（﹣a）（﹣a）6考点: 同底数幂的乘法．分析:根据同底数幂的乘法,底数不变，指数相加，计算后利用排除法求解．解答：解:A、（﹣a）2(﹣a）5=a2(﹣a5）=﹣a7，错误；B、（﹣a)2（﹣a5)=﹣a7,错误；C、（﹣a2）(﹣a)5=a7，正确；D、(﹣a) （﹣a）6=﹣a•a6=﹣a7,错误．故选C．点评：负数的偶次幂是正数，负数的奇次幂是负数,结合同底数幂的乘法，底数不变,指数相加可解决此类问题．25．（4•2n）（4•2n）等于（）A．4•2n B．8•2n C．4•4n D．22n+4考点: 同底数幂的乘法．分析：根据同底数幂相乘，底数不变指数相加，计算后直接选取答案．解答：解：（4•2n）（4•2n）=22+n•22+n=22n+4．故选D．点评：本题主要考查同底数幂的乘法的性质，熟练掌握性质并灵活运用是解题的关键．26．（m+n﹣p）(p﹣m﹣n）(m﹣p﹣n)4（p+n﹣m)2等于（）A．﹣（m+n﹣p)2（p+n﹣m）6B．（m+n﹣p)2（m﹣n﹣p）6C．（﹣m+n+p)8D．﹣（m+n+p）8考点：同底数幂的乘法．分析：根据实数偶次幂的性质和相反数的定义，再利用同底数相乘，底数不变指数相加计算．解答：解：由于p﹣m﹣n和(m+n﹣p）互为相反数，∴p﹣m﹣n=﹣（m+n﹣p）；p+n﹣m和m﹣p﹣n互为相反数，（p+n﹣m)2=（m﹣p﹣n）2,∴原式=﹣（m+n﹣p)（m+n﹣p）（p+n﹣m)4（p+n﹣m）2=﹣（m+n﹣p）2(p+n﹣m）6．故选A．点评：本题考查了同底数幂的乘法，要熟悉相反数的定义和实数偶次幂的性质．27．a•a3x可以写成（）A．（a3）x+1B．（a x)3+1C．a3x+1D．（a x）2x+1考点: 同底数幂的乘法．分析：根据同底数幂的乘法法则，同底数幂相乘,底数不变，指数相加，即a m•a n=a m+n解答．解答：解：a•a3x=a1+3x．故选C．点评:本题主要利用同底数幂的乘法的性质求解,是基础题．28．m为偶数，则（a﹣b）m•(b﹣a）n与（b﹣a）m+n的结果是（)A．相等B．互为相反数C．不相等D．以上说法都不对考点：同底数幂的乘法．分析：根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，求解即可．解答:解：因为m为偶数，（a﹣b）m=（b﹣a）m，所以（a﹣b）m•（b﹣a）n=（b﹣a）m•（b﹣a)n=（b﹣a）m+n．故选A．点评：熟练掌握互为相反数的两数的偶数次方相等是解本题的关键．29．下列各式中，不能用同底数幂的乘法法则化简的是（)A．（x﹣y)（x﹣y)2B．（x+y）（x﹣y）2C．（x﹣y）(y﹣x）2D．（x﹣y)（y﹣x）2（x﹣y）2考点：同底数幂的乘法．分析:根据能用同底数幂的乘法法则，底数一定相同,或互为相反数，对各选项分析判断后利用排除法求解．解答:解：底数不相同的是（x+y)（x﹣y）2．故选B．点评：本题特别要注意的是：互为相反数的两个式子可以通过符号的变化化成同一式子，以及整体思想的运用．30．若x＞1,y＞0,且满足，则x+y的值为（)A．1B．2C．D．考点：同底数幂的乘法．专题：计算题．分析:首先将xy=x y变形,得y=x y﹣1，然后将其代入，利用幂的性质,即可求得y的值,则可得x的值，代入x+y求得答案．解答：解：由题设可知y=x y﹣1，∴x=yx3y=x4y﹣1，∴4y﹣1=1．故，从而x=4．于是．故选C．点评：此题考查了同底数幂的性质:如果两个幂相等，则当底数相同时，指数也相同．。

3.1同底数幂的乘法

3.1同底数幂的乘法

=(3.84×3.6) × (103×108×103)
=13.824× 1014 =1.3824×1015 ≈1.38×1015（次）
答：它一小时约能运算1.38×1015次。
变式训练：
填空：
(1) x4· x5 = x9 (2) (-y)4 · (-y)7 =(-y)11 (3) a2m · am =a3m (4) (x-y)2 · (x-y)3 =(x-y)5
最后结果一定要用科 学计数法表示
我国自行研制的“神威”计算机的峰值运算 速度达到每秒3840亿次。如果按这个速度 工作1小时，那么它能运算多少次（结果保留 3个有效数字）？
解：3840亿次 =3840×108次 =3.84×103×108次
1时 = 3600 秒
=3.6×103秒
（3.84×103×108）× (3.6×103) 乘法的交换律和结合律
如 具am有·这an一·a性p质=呢am？+n怎+样p （用m公、式n表、示p？都是正整数）
试一试
抢答
（1） 76×74
( 710 )
（2） a7 ·a8 ( a15 )
（3） x5 ·x3 （ x8 ）
（4） b5 ·b （ b6 ）
辨一辨
下面的计算对不对？如果不对，怎样改正？
（1）b5 ·b5= 2b5 （× ） （2）b5 + b5 = b10 （× ）
(-1)2 =__1___=___1_2__ (-1)4 =__1___=___1_4__ (-1)6 =__1___=___1_6__ (-1)8 =__1___=___1_8__
负数的偶数次幂 为正数 当n为偶数时 (-a)n = an (a-b)n =(b-a)n

同底数幂的乘法练习题(含答案)

同底数幂的乘法练习题(含答案)

同底数幂的乘法基础练习1．填空：（1）ma 叫做a 的m 次幂，其中a 叫幂的________，m 叫幂的________；（2）写出一个以幂的形式表示的数，使它的底数为c ，指数为3，这个数为________； （3）4)2(-表示________，42-表示________；（4）根据乘方的意义，3a ＝________，4a ＝________，因此43a a⋅＝)()()(+。

2．计算： （1）=⋅64a a（2）=⋅5b b（3）=⋅⋅32m m m （4）=⋅⋅⋅953c c c c（5）=⋅⋅p n ma a a （6）=-⋅12m t t （7）=⋅+q qn 1（8）=-+⋅⋅112p p n n n3．计算：（1）=-⋅23b b （2）=-⋅3)(a a（3）=--⋅32)()(y y （4）=--⋅43)()(a a%（5）=-⋅2433 （6）=--⋅67)5()5(（7）=--⋅32)()(q q n（8）=--⋅24)()(m m（9）=-32 （10）=--⋅54)2()2(（11）=--⋅69)(b b（12）=--⋅)()(33a a4．下面的计算对不对如果不对，应怎样改正（1）523632=⨯； （2）633a a a =+；（3）nnny y y 22=⨯； （4）22m m m =⋅；（5）422)()(a a a =-⋅-； （6）1243a a a =⋅；,（7）334)4(=-； （8）6327777=⨯⨯；（9）42-=-a ； （10）32n n n =+． 5．选择题： （1）22+m a 可以写成（ ）．A ．12+m aB ．22a am+ C ．22a a m ⋅ D ．12+⋅m a a（2）下列式子正确的是（ ）．A ．4334⨯=B ．443)3(=- C ．4433=- D ．3443=（3）下列计算正确的是（ ）．)A ．44a a a =⋅ B ．844a a a =+C ．4442a a a =+D ．1644a a a =⋅综合练习1．计算： （1）=++⋅⋅21n n na a a （2）=⋅⋅n n nb b b 53 （3）=+-⋅⋅132m m b b b b（4）=--⋅4031)1()1(（5）=⨯-⨯672623 （6）=⨯+⨯543736>（7）=++⋅⋅⋅5334232x x x x x x （8）=-+⋅⋅⋅2563427x x x x x x（9）=++++⋅⋅121133n n n x x x x（10）=+-+⋅x y x y x a a a 23（11）=+---⋅⋅⋅656233)()()(a a a a a （12）=-++⋅12322n n n（13）=-⋅⋅m c c c53)(2．计算：（结果可以化成以)(b a +或)(b a -为底时幂的形式）． （1）=---⋅⋅432)()()(b a b a b a（2）=+++++⋅⋅+21)()()()(b a b a b a b a m m（3）=----⋅⋅12)()()(n a b b a a b》（4）=----+⋅⋅131)()()(n n a b a b b a（5）=++-++⋅⋅--3212)()(3)()(2b a b a b a b a n n （6）32212)()(2)()(3b a a b b a b a m m --+--⋅⋅+（7）=++++++-+⋅⋅⋅12)()(3)()()(p n p n mb a b a b a b a b a（8）=---⋅⋅532)(5)(4)(3a b b a a b3．填空题： （1）1243)(a a a=⋅．（2）1042)()(a a a==⋅⋅．（3）45)(63)()()()()()(y x y x y x y x y x --=--=--⋅⋅⋅．（4）已知3=mb ，4=nb ，则nm b+＝________．（5）)(3221)(212121⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛-⋅＝________．（6）)()(5432)()()()()()()(a b b a b a a b b a a b b a --=-=-----⋅⋅⋅⋅4．选择题： 1．n mb a b a )2()2(++⋅等于（）．A ．2)2(b a + B ．nm b a ++)2( C ．nm b a ⋅+)2( D ．nm b a -+)2(2．12+m a可写成（ ）．`A ．12+⋅m a aB ．a m a +2C ．m a a 2⋅D ．1m 2+a3．32)()(c a b c b a --+-⋅等于（）．A ．2)(c b a +- B ．5)(c a b -- C ．5)(c b a +-- D ．5)(c a b ---4．把下列各题的计算结果写成10的幂的形式，其中正确的选项是（ ）． A ．6310101000=⨯ B ．2001001010100=⨯C ．n m m n+=⋅10010102 D ．881001010=⋅5．解答题： %（1）如果1313y y yn nm =+-⋅，且641x x x n m =--⋅的值．（2）设p m =+++ 321，计算：m m m mxy y x y x y x ⋅⋅⋅⋅⋅-- 3221．拓展练习1．下面的算式是按一定规律排列的：1211999735,,,++++，……你能找出其中的规律吗试一试，算出它的第90个算式的得数．2．某商店一种货物售价目表如下：数量x （千克）@售价c （元）1 14+2 28+ 370+6（1）写出用x 表示c 的公式； （（2）计算3千克的售价． 3．观察下列等式： 23333233323323104321632132111,,,=+++=++=+=，……想一想等式左边各项幂的底数与右边幂的底数有什么关系猜一猜可以引出什么规律，并把这种规律用等式写出来．4．下列各个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有)1(>n n 盆花，每个图案花盆的总数是s ．按此规律推算，求出s 与n 的关系式．、参考答案 基础1．（1）底数，指数 （2）3c （3）4个－2相乘，4个2相乘的积的相反数（4）a a a ⨯⨯ a a a a ⨯⨯⨯，a ，3，4，7 2．（1）10a （2）2)(2++m b a （3）6)(b a -- （4）32)()1(+--n n b a（5）1)(++-n b a （6）32)(5+-m b a （7）pn m b a +++)(4 （8）10)(60a b --[3．（1）5b - （2）4a - （3）5y - （4）7a - （5）－729 （6）135- （7）32+-n q（8）6m - （9）－8 （10）－512 （11）15b - （12）6a 4．（1）应改为123223=⨯ （2）改为633a a a =⋅ （3）改为n n n y y y 2=⨯（4）改为32m m m =⋅ （5）改为422)()(a a a -=--⋅ （6）改为743a a a =⋅（7）改为334)4(-=- （8）对 （9）对 （10）改为32n n n =⋅5．（1）C （2）B （3）C综合1．（1）33+n a（2）n b 9 （3）22+m b（4）－1 （5）0 （6）73 （7）66x （8）76x （9）24+3n x（10）x a24 （11）114a （12）22+-n （13）8+-m c2．（1）9)(b a - （2）2)(2++m b a （3）6)(b a -- （4）32)()(+--n nb a b（5）1)(++-n b a （6）32)(5+-m b a （7）pn m b a +++)(4 （8）10)(60a b --3．（1）5a （2）8a ，6a （3）8，x y - （4）12 （5）101，5，321- （6）15，15 4．（1）B （2）C （3）C （4）A 5．（1）3=n ，6=m （2）ppy x拓展1．453 2．x c 2.15= 3．23333)321(321n n +++=++++ 4．)1(3-=n x欢迎访问。

同底数幂的乘法练习题

同底数幂的乘法练习题

同底数幂的乘法练习题一、选择题1. 若\( a^3 \times a^2 = a^5 \)，则\( a \)的值为（）A. 5B. 1C. 3D. 22. 计算\( 2^5 \times 2^3 \)的结果是（）A. \( 2^8 \)B. \( 2^6 \)C. \( 2^{10} \)D. \( 2^{15} \)3. 已知\( x^2 \times x^3 = x^5 \)，则\( x \)的值是（）A. 5B. 2C. 3D. 无法确定二、填空题1. 计算\( 3^4 \times 3^2 = \underline{\quad}\)。

2. 若\( 5^m \times 5^n = 5^{10} \)，则\( m + n =\underline{\quad}\)。

3. 已知\( a^x \times a^y = a^6 \)，且\( x + y = 4 \)，则\( x = \underline{\quad}\)，\( y = \underline{\quad}\)。

三、解答题1. 计算\( 4^3 \times 4^5 \)。

2. 已知\( 2^a \times 2^b = 2^{10} \)，求\( a \)和\( b \)的值。

3. 计算\( 10^2 \times 10^3 \times 10^4 \)。

4. 若\( x^5 \times x^y = x^{10} \)，求\( y \)的值。

5. 已知\( a^7 \times a^x = a^{13} \)，求\( x \)的值。

6. 计算\( 3^4 \times 3^2 \times 3^3 \)。

7. 已知\( 5^m \times 5^n = 5^{12} \)，且\( m > n \)，求\( m \)和\( n \)的值。

8. 若\( 2^a \times 2^b \times 2^c = 2^{15} \)，且\( a >b >c \)，求\( a \)、\( b \)和\( c \)的值。

3.1 同底数幂的乘法(1)

3.1 同底数幂的乘法(1)

练一练
1．计算下列各式，结果用幂的形式表示：
（1） 27 23； （2）(－3)4 (－3)7；
（3） 53 (5)4；（4）(x 2 y)(x 2 y)3；
（5）(2)3 (2)4 22． (6) (a b)2 (b a)3；
2．下列计算对吗？如果不对，应怎样改正？
＝a
m个a
a
…

a
n个a
＝am
n
(m+n)个a
同底数幂的乘法法则:
同底数幂相乘，底数不变，指数相加．
即 am an＝amn（m、n都是正整数）
注意: 条件：①乘法 ②同底数幂
结果：①底数不变 ②指数相加
练一练：
1．同底数幂 相乘 时，底数 不变 ，指数 相加 ．
2．口答(结果用幂的形式表示）：
小 结：
本节课我学到了…… 我的温馨提示…… 我的疑惑……
（1）a3 a3＝2a3；× （2）a2 a3＝a6；×
（3）aa3aa33＝＝aa36；×
a2 a3＝a5
（4）a3 a3＝a6；×
a a3＝a4
a3 a3＝2a3
（5）a3 b2＝（ab）6.×
a3 b2＝a3b2
例2 我国自行研制的“神威 I”计算机的峰值 运算速度达到每秒 3840亿次.如果按这个速度 工作一整天,那么它能运算多少次? (结果保留3 个有效数字)?
（4）(a b)2 (a b)；1
（5） 73 (7)7. 注意： 注意法则使用的条件；
同底数幂相乘时，指数是相加的； 不能疏忽指数为1的情况； 运算结果的底数一般应为正数． 若底数不同，先化为相同，后运用法则．

3.1.1 同底数幂的乘法(解析版)初中数学

3.1.1 同底数幂的乘法(解析版)初中数学

2020-2021学年浙教版七年级下册第3章《整式的乘除》同步练习【3.1.1 同底数幂的乘法】一、单选题：1.化简(-x)3·(-x)2的结果正确的是（）A.−x6B.x6C.x5D.−x5【答案】 D【考点】同底数幂的乘法【解析】【解答】解：(−x)3(−x)2=(−x)3+2=(−x)5=−x5故答案为：D.【分析】同底数幂相乘，底数不变，指数相加，据此计算即可.2.化简x3⋅(−x)3的结果是（）A.−x6B.x6C.x5D.−x5【答案】A【考点】同底数幂的乘法【解析】【解答】解：原式= x3·(−x3)= −x6故答案为：A．【分析】先算幂的乘方，再利用同底数幂的乘法计算即可.3.若a m⋅a3=a5，则m的值为（）A.1B.2C.3D.4【答案】B【考点】同底数幂的乘法【解析】【解答】解：∵ a m⋅a3=a5，∵ a m+3=a5，∵m+3=5，∵m=2．故答案为：B．【分析】根据同底数幂乘法，得出a m+3=a5，从而可得m+3=5，解出m即可.4.已知a m=2，a n=3，则a n+m=（）A.2B.3C.5D.6【答案】 D【考点】同底数幂的乘法【解析】【解答】解：a n+m=a n•a m=3×2=6．故答案为：D．【分析】将a n+m转化为a n•a m，再代入求值即可。

5.若a·2·23=28，则a等于（）A.4B.8C.16D.32【答案】C【考点】同底数幂的乘法【解析】【解答】∵a•2•23=28，∵a=28÷24=24=16，故答案为：C．【分析】根据同底数幂的乘法法则求解即可．6.在等式a ·a ·()=a 中，括号内的代数式应当是（）A.aB.aC.aD.a【答案】B【考点】同底数幂的乘法【解析】解答：a ·a ·( )=a∵a ·a =a ，∵括号内的代数式应当是：a ÷a =a .故选B.分析：直接利用同底数幂的乘法的知识点求解即可求得答案.7.已知2a=5,2b=3.2,2c=6.4,2d=10，则a+b+c+d的值为（）A.5B.10C.32D.64【答案】B【考点】同底数幂的乘法【解析】【解答】解：∵ 2a·2b·2c·2d=2a+b+c+d∵ 5×3.2×6.4×10=1024=210∵ a+b+c+d=10故答案为：B.【分析】利用同底数幂的乘法计算，可得到结果.8.电子文件的大小常用B, KB,MB,GB等作为单位，其中1GB=210MB,1MB=210KB,1KB=210B，某视频文件的大小约为1GB,1GB等于（）A.230BB.830BC.8×1010BD.2×1030B【答案】A【考点】同底数幂的乘法【解析】【解答】依题意得1GB=210MB=210×210KB=210×210×210B= 230B故答案为：A.【分析】由题意把1GB用B表示出来，根据“同底数幂相乘，底数不变，指数相加”即可求解.9.若x ，y为正整数，且2x•2y=25，则x ，y的值有（）A.4对B.3对C.2对D.1对【答案】A【考点】同底数幂的乘法【解析】解答：∵2x•2y=2x+y=25，∵x+y=5，∵x ，y为正整数，∵x ，y的值有x=1，y=4；x=2，y=3；x=3，y=2；x=4，y=1．共4对.分析：根据同底数幂的乘法和算术同底数幂的乘法的概念求出2的同底数幂的乘法和算术同底数幂的乘法分别为和，然后判断各选项即可得出答案．10.下列运算正确的是（）A.x3+x3=x6B.x3⋅(2x)2=4x5C.3x3y2÷xy2=3x4D.(−3a2)2=6a2【答案】B【考点】单项式乘单项式，单项式除以单项式，合并同类项法则及应用，积的乘方，幂的乘方【解析】【解答】A. x3+x3=2x3，故错误；B. x3⋅(2x)2=4x5，正确；C. 3x3y2÷xy2=3x2，故错误；D. (−3a2)2=9a4，故错误；故答案为：B.【分析】根据合并同类项、单项式乘单项式、单项式除以单项式、积的乘方分别进行计算，然后判断即可.二、填空题：11.计算：（﹣a2）•a3=________【答案】﹣a5【考点】同底数幂的乘法【解析】【解答】解：原式=﹣a5，故答案是﹣a5．【分析】同底数幂相乘，底数不变，指数相加．12.计算：(−12ab2)3=________．【答案】−18a3b6【考点】积的乘方，幂的乘方【解析】【解答】解：(−12ab2)3=(−12)3⋅a3(b2)3=−18a3b6．故答案为：−18a3b6．【分析】根据幂的乘方及积的乘方进行作答即可。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

同底数幂的乘法
1、同底数幂的乘法
一、知识点检测
1、同底数幂相乘，底数 ，指数 ，用公式表示=n
m a a （m ，n 都是正整数）
2、计算32)(x x ⋅-所得的结果是（ ）
A.5x
B.5x -
C.6x
D.6x -
3、下列计算正确的是（ ）
A.822b b b =⨯
B.642x x x =+
C.933a a a =⨯
D.98a a a =
4、计算： （1）=⨯4
61010 （2）=⎪⎭⎫ ⎝⎛-⨯-6
231)31( （3）=⋅⋅b b b 32 （4）2y ⋅ 5y = 5、若53=a ，63=b ，求b a +3
的值
二、典例分析
例题：若1255
12=+x ，求()x x +-20092的值
三、拓展提高
1、下面计算正确的是（ ）
A.4533=-a a
B.n m n m +=⋅632
C.109222=⨯
D.10
552a a a =⋅ 2、=-⋅-23)()(a b b a 。

3、()=-⋅-⋅-62
)()(a a a 。

4、已知：5 ,3==n m a a
，求2++n m a 的值
5、若62=-a m
,115=+b m ,求3++b a m 的值
2、幂的乘方
一、知识点检测
1、幂的乘方，底数 ,指数 ，用公式表示=n m a )( （m ，n 都是
正整数）
2、计算23()a 的结果是（ ）
A ．5a
B ．6a
C ．8a
D ．2
3a 3、下列计算不正确的是（ ）
A.933)(a a =
B.326)(n n a a =
C.2221)(++=n n x x
D.623x x x =⋅
4、如果正方体的棱长是2
)12(+a ，则它的体积为 。

二、典例分析
例题：若52=n ，求n 28
的值
三、拓展提高
1、()=-+-2332)(a a 。

2、若63=a ，5027=b ，求a b +33
的值
3、若0542=-+y x ，求y x 164⋅的值
4、已知：625255=⋅x x ，求x 的值
5、比较5553
，4444，3335的大小
3、积的乘方
一、知识点检测
1、积的幂，等于幂的积。

用公式表示：n ab )(= （n 为正整数）
2、下列计算中，正确的是（ ）
A. ()6
33xy y x =⋅ B.6326)3()2(x x x =-⋅- C. 2222x x x =+ D. 2221)1(-=-a a
3、计算：()23ab
=（ ） A ．22a b B ．23a b C ．26a b D ．6ab
二、典例分析
例题：求603020092125
.0⨯的值
三、拓展提高
1、=3)2(ab =43)2(a =-2)3(m n b a
2、计算：201020092010)2.1()6
5()
1(-⨯⨯-
3、计算：3920964252
25.0⨯⨯⨯
4、已知332=-b a ，求96b a 的值
5、若13310052
+++=⨯x x x ， 求x 的值。

相关文档
最新文档