6第六讲(实心圆杆扭转)解析
第6章 扭转

观察变形
应变分布
应力分布
静力方程
应力公式 ①变形几何方面 等直圆杆横截面应力 ②物理关系方面 ③静力学方面源自171、等直圆杆扭转实验观察
(1)实验前: ①绘纵向线,圆周线; ②施加一对外力偶 m。 (2)实验后: ①圆周线不变; ②纵向线变成斜直线。
18
(3)实验结论: ①圆筒表面的各圆周线的形状、
的边缘各点处,即该轴最大切应力为 τmax=71.3MPa。
30
[例题6.3]
实心圆轴与空心圆轴通过牙嵌式离合器相联,并传
递功率,如图所示。已知轴的转速n=100r/min,传递 的功率P=7.5kW。实心圆轴的直径d1=45mm;空心圆轴 的内、外直径之比(d2/D2)=0.5,D2=46mm。试确定实 心轴与空心圆轴横截面上的最大剪应力。
9
5、
扭矩图的意义
① 反映出扭矩沿截面位置变化关系,较直观; ② 确定出最大扭矩的数值及其所在横截面的位置, 即确定危险截面位置,为强度计算提供依据。
10
[例6.1]已知:一传动轴, n =300r/min,主动轮1输入功率
NK1=500kW,从动轮2、3、4输出 功率分别为NK2=150kW, NK3=150kW,NK4=200kW,试绘制扭矩图。 解:①计算外力偶矩
T2
T3
T1 n
T4
N K1 T1 9.55 n 2 3 1 500 9.55 15.93(kN m) 300 NK2 150 T2 T3 9.55 9.55 4.78 (kN m) n 300 NK4 200 T4 9.55 9.55 6.37 (kN m) n 300
4
工程中的扭转问题
6第六讲(实心圆杆扭转)

等直圆杆扭转应力
D
Ip
2 d A
2 d
2π 3
d
A
2
( ( π D4 d 4 πD4 1 4
32
32
其中 d
D
( ( W p D I/ p 2 π D 1 4 D d 6 4 π 1 D 31 6 4
( 注意:对于空心圆截面,Wp
πD3 16
13
。
三峡大学 工程力学系
圆截面扭转参数
力的绝对值最大;
45 m ax 45 m in
三峡大学 工程力学系
扭转斜截面上的应力
材料力学教案
等直圆杆扭转第三应章力扭转
强度条件
max[]
此处[]为材料的许用切应力。对于等直圆轴亦即 Tmax [ ]
Wp 铸铁等脆性材料制成的等直圆杆扭转时虽沿斜截面因 拉伸而发生脆性断裂,但因斜截面上的拉应力与横截面上 的切应力有固定关系,故仍可以切应力和许用切应力来表 达强度条件。
三峡大学 工程力学系
扭转强度条件
材料力学教案
等直圆杆扭转第三应章力扭转
例题 图示阶梯状圆轴,AB段直径d1=120 mm,BC段直径 d2=100 mm。扭转力偶矩MA =22 kN·m,MB =36 kN·m,MC
=14 kN·m,材料的许用切应力[ ]80 MPa。试校核该轴的强
度。
三峡大学 工程力学系
可见,在横截面的同一半径 的圆周上各点处的切 应力 均相同,其值 与 成正比,其方向垂直于半径。
三峡大学 工程力学系
扭转应力推导—本构关系
材料力学教案
等直圆杆扭转应力
静力学方面
AdAT
即
G d d xA2dAT
其中 2 A
6.圆轴扭转PPT课件

A
B O
A
BO
Me
Me
扭转角():任意两截面绕轴线转动而发生的角位移。
剪应变():直角的改变量。
2021/3/9
授课:XXX
3
二、传动轴的外力偶矩
传递轴的传递功率、转速与外力偶矩的关系:
m954P9(Nm) 其中:P — 功率,千瓦(kW)
n
n — 转速,转/分(rpm)
m702P4(Nm) n
2021/3/9
授课:XXX
1
§6–1 圆轴扭转的概念与实例 扭矩与扭矩图
一、概念与实例
1. 丝锥杆发生扭转变形。
2. 方向盘操纵杆
2021/3/9
授主要变形的构件。 如:机器中的传动轴、 石油钻机中的钻杆等。
扭转:外力的合力为一力偶,且力偶的作用面与直杆的轴线 垂直,杆发生的变形为扭转变形。
(实心截面)
(空心截面)
工程上采用空心截面构件:
提高强度,节约材料,重量轻,结构轻便,应用广泛。
2021/3/9
授课:XXX
19
⑤ 确定最大剪应力:
由
T
Ip
知:当 Rd2, max
ma xTIpd 2IpTd 2W TP (令 WIp
d) 2
max
T max WP
Wp — 抗扭截面系数(抗扭截面模量), 几何量,单位:mm3或m3。
圆轴扭转的概念不实例扭矩不扭矩图62圆轴扭转时的应力不强度计算63圆轴扭转时的变形不刚度计算第六章圆轴扭转第六章圆轴扭转圆轴扭转的概念不实例扭矩不扭矩图圆轴扭转的概念不实例扭矩不扭矩图丝锥杆发生扭转变形
第六章 圆轴扭转
§6–1 圆轴扭转的概念与实例 扭矩与扭矩图 §6.2 圆轴扭转时的应力与强度计算 §6.3 圆轴扭转时的变形与刚度计算
材料力学第6章扭转.doc
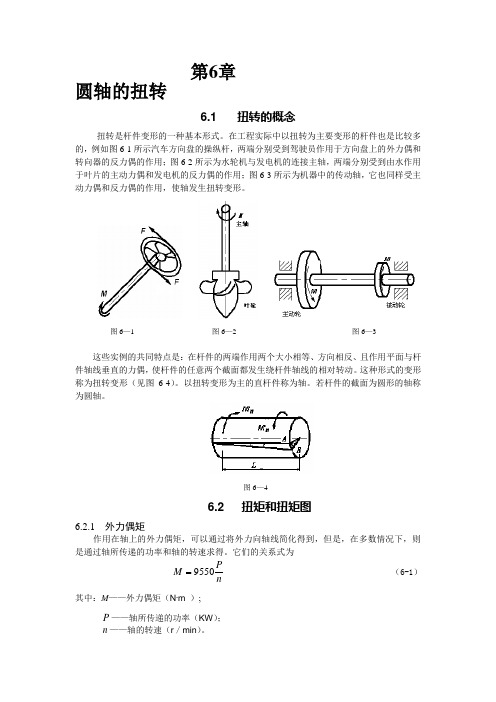
第6章圆轴的扭转6.1 扭转的概念扭转是杆件变形的一种基本形式。
在工程实际中以扭转为主要变形的杆件也是比较多的,例如图6-1所示汽车方向盘的操纵杆,两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图6-2所示为水轮机与发电机的连接主轴,两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用;图6-3所示为机器中的传动轴,它也同样受主动力偶和反力偶的作用,使轴发生扭转变形。
图6—1 图6—2 图6—3这些实例的共同特点是:在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的任意两个截面都发生绕杆件轴线的相对转动。
这种形式的变形称为扭转变形(见图6-4)。
以扭转变形为主的直杆件称为轴。
若杆件的截面为圆形的轴称为圆轴。
图6—46.2 扭矩和扭矩图6.2.1 外力偶矩作用在轴上的外力偶矩,可以通过将外力向轴线简化得到,但是,在多数情况下,则是通过轴所传递的功率和轴的转速求得。
它们的关系式为nPM 9550 (6-1) 其中:M ——外力偶矩(N ·m ); P ——轴所传递的功率(KW ); n ——轴的转速(r /min )。
外力偶的方向可根据下列原则确定:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。
6.2.2 扭矩圆轴在外力偶的作用下,其横截面上将产生连续分布内力。
根据截面法,这一分布内力应组成一作用在横截面内的合力偶,从而与作用在垂直于轴线平面内的外力偶相平衡。
由分布内力组成的合力偶的力偶矩,称为扭矩,用n M 表示。
扭矩的量纲和外力偶矩的量纲相同,均为N·m 或kN·m 。
当作用在轴上的外力偶矩确定之后,应用截面法可以很方便地求得轴上的各横截面内的扭矩。
如图6-5(a )所示的杆,在其两端有一对大小相等、转向相反,其矩为M 的外力偶作用。
为求杆任一截面m-m 的扭矩,可假想地将杆沿截面m-m 切开分成两段,考察其中任一部分的平衡,例如图6-5(b )中所示的左端。
工程力学(静力学与材料力学)-6-圆轴扭转

圆轴扭转时横截面上的 剪应力分析与强度设计
第6章 圆轴扭转
返回
第6章 圆轴扭转
School of Life and Environmental Science
圆轴扭转时横截面上的剪应力分析与强度设
计
应用平衡方法可以确定圆杆扭转时横截面上的内力分量 ——扭矩,但是不能确定横截面上各点剪应力的大小。为了 确定横截面上各点的剪应力,在确定了扭矩后,还必须知道 横截面上的剪应力是怎样分布的。
dz dx
第6章 圆轴扭转
School of Life and Environmental Science
剪应力互等定理 y
剪切胡克定律
剪应力成对定理
dy
x
dz dx
在两个互相垂直的平面 上,剪应力必然成对存在 , 且数值相等,两者都垂直于 两个平面的交线 ,方向则共 同指向或共同背离这一交线 ,这就是 剪应力成对定理 ( pairing principle of shear stresses)。
计
dA M
A
x
d G G dx
d M x dx GI P
式中 GIP—扭转刚度;
I P 2 dA
A
IP—横截面的极惯性矩。
第6章 圆轴扭转
School of Life and Environmental Science
第6章 圆轴扭转
School of Life and Environmental Science
圆轴扭转时横截面上的剪应力分析与强度设
计
确定横截面上剪应力 的方法与过程
平面假定
变 形 应变分布
物性关系
工程力学第6章 扭转

T 2 A0
6.2.2 切应力互等定理
从薄壁圆筒中包括横截 面取出一个单元体
将(d)图投影到铅垂坐标平面,得到一个平面单元
根据力偶平衡理论
y
(dydz )dx ( dxdz)dy
dy
dz
在相互垂直的两个平面 上,切应力必成对出现, 两切应力的数值相等, 方向均垂直于该平面的 x 交线,且同时指向或背 离其交线。
对于各向同性材料,在弹性变形范围内,切变 模量G 、弹性模量E 和泊松比之间有下列关系:
G
E (1 ) 2
6-3 实心圆轴扭转时的应力和强度条件
6.3.1 、 扭转剪应力在横截面上的分布规律
Ⅰ. 横截面上的应力 表面 变形 情况 推断 横截面 的变形 情况 横截面 上应变 应力-应变关系
两互相垂直截面上在其相交处的剪应力 成对存在,且数值相等、符号相反,这称为 剪应力互等定理。
例题 3
试根据切应力互等定理,判断图中所示的各 单元体上的切应力是否正确。
10 kN
30 kN 50 kN
10 kN
20 kN
50 kN 30 kN
20 kN
30 kN
6.2.3 剪切胡克定律(Hooke’s law in shear) Me Me
n
主轴
主动轮 叶片
本章研究杆件发生除扭转变形外,其它变形可忽略的 情况,并且以圆截面(实心圆截面或空心圆截面)杆为主要
研究对象。此外,所研究的问题限于杆在线弹性范围内工
作的情况。
6-1 概述
1. 扭转的概念 4种基本变形(轴向拉压、剪切、扭转、弯曲)之一 特点: 圆截面轴(实心、空心)
第6章 扭转
3)变形几何关系 将圆轴看成由无数个同心薄壁圆筒组成,然后,再想象从 圆轴的dx微段中,取出一半径为 厚度为d 的薄壁圆筒 1 2
B o o
max
A
1
A B
d
d
B B
d
d
dx
2
dx
max
AA R d dx dx
BB d dx dx
17
三、剪应力互等定理
1、薄壁圆筒扭转时的切应力与变形
为了解决圆轴的扭转应力计算,我们先 讨论比较简单的薄壁圆筒的扭转问题。
t R0
R0 (t ) 10
t
R0
18
m
n
γ
m
n
Me
Me
19
t
R0
m0
m0
变形现象
试 验 观 察
①
各圆周线形状、大小、间距不变。
② 各纵向线倾斜相同角度,由矩形 变成平行四边形。
3.计算内力 4.强度计算
max
Me
T 572940 N m
T 572940 T 3 Wt 0.3 4 4 3 D 1 0.55 1 16 0.55 16 19.24 MPa
50
以上公式只对等直圆杆成立。 对截面变化比较缓慢的圆截面直杆近似成立。 此外,max应小于剪切比例极限。
40
4、极惯性矩和抗扭截面系数的计算
(1) 实心圆轴
Ip d A
2 A
取距离圆心为,厚度 为d的环形面积为dA 于是,
2 A
dA 2d
d /2 0
I p dA
杆的扭转定理和公式
圆截面杆的扭转外力与内力 || 圆杆扭转切应力与强度条件 || 圆杆扭转变形与刚度条件 || 圆杆的非弹性扭转1.外力与内力杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶(图2·2-1a),其变形特点是在任意两个截面绕轴线发生相对转动。
轴类构件常有扭转变形发生。
作用在传动轴上的外力偶矩m通常是根据轴所传递的功率N和转速n(r/min)来计算。
当N的单位为千瓦(kW)时当N的单位为马力(HP)时扭转时的内力为扭矩T,用截面法求得。
画出的内力图称为扭矩图(或T图),如图2·2-1b所示图2·2-1 圆杆的扭转2.圆杆扭转切应力与强度条件当应力不超过材料的剪切比例极限r p时,某横截面上任意C点(图2·2-2)的切应力公式为式中T——C 点所在横截面上的扭矩p——C点至圆心的距离L p——横截面对圆心的极惯性矩,见表2-2-1 等直杆扭转时的截面几何性质。
图2·2-2 切应力分布圆杆横截面上的切应力r沿半径呈线性分布,其方向垂直于半径(图2·3-2)。
模截面上的最大切应力在圆周各点上,其计算公式为等截面杆的最大切应力发生在T max截面(危险截面)的圆周各点(危险点)上。
其强度条件为式中,[τ]为许用扭转切应力,与许用拉应力[σ]的关系为:[τ]=(0.5~0.6)[σ] (塑性材料)或[τ]=(0.5~0.6)[σ](脆性材料)3.圆杆扭转变形与刚度条件在比弹性范围内,圆杆在扭矩T作用下,相中为L的两截面间相对扭转角为或式中G——材料的切变模量单位扭转角公式为或式中GL p——抗扭刚度圆杆上与杆轴距离为p外(图2·2-2)的切应变r为圆杆表面处的最大切应变为式中,r——圆杆的半径等截面圆杆的最大单位扭转角,发生在T max一段内,其刚度条件为式中,[θ]为圆杆的许用单位扭转角(°)/m4.圆杆的非弹性扭转讨论圆杆扭转时切应力超过材料的比例极限并进入塑性状态的情况。
第6讲 Chapter3-1第三章 扭转1
第三章扭转(一)Torsion(Part 1)第六讲教学内容§3-1扭转的概念§3-2 薄壁圆筒的扭转§3-3 传动轴的外力偶矩扭矩扭矩图§3-4 等直圆杆扭转时的应力23§3-1扭转的概念及实例扳手螺丝刀汽车传动轴4电动机轴/传动轴56打稻机受力特征:杆受一对大小相等、方向相反的力偶,力偶作用面垂直于轴线。
7§3-2 薄壁圆筒的扭转薄壁圆筒δ≤r0/10δr0一、薄壁圆筒的扭转应力分析等厚度的圆筒,平均半径为r, 壁厚为δ89扭转试验机10扭转试样扭转试验现象观察试验前试验后观察到如下现象:(1)圆周线的形状、大小及圆周线之间的距离没有改变;(2)纵向线均倾斜了同一微小角度γ。
1112(1)圆筒横截面上没有正应力,只有切应力;(2)沿圆周各点的切应力数值上相等,方向垂直于半径。
根据以上实验现象,可得结论:TeM TTTT T 由实验可观察到:TTdxdxTTlr17上式关系称为剪切胡克定律。
G 称为材料的切变模量(剪变模量)。
G 的量纲与弹性模量E 相同ML -1T -2; 单位(国际单位制):N/m 2(Pa);钢材的切变模量约为G =80GPaG τγ=18桥梁板式橡胶支座是由多层橡胶片与薄钢板硫化、粘合而成, 板式橡胶支座有足够的竖向钢度,能将上部构造的载荷可靠地传递给墩台。
有良好的弹性,以适应梁端的转动,又有较大的剪切变形能力,以满足上部构造所需的水平位移。
E =G+)1(2υ§3-3 传动轴的外力偶矩扭矩扭矩图20I、外力偶矩的计算设某轮所传递的功率是P( 单位:kW)轴的转速是n(单位:rpm或r/m-revolution per minute)2122(kW)P 的功率相当于每分钟作功:1)(60(J)1000=1××P W 所作的功:外力偶矩e M 2)( (J) 2= e 2n M W π⋅(1)=(2) 得e 100060=2 P M nπ⋅××外力偶矩的计算:24主动轮从动轮从动轮外力偶矩的方向提供动力的轮主动轮上的外力偶矩的方向与轴的转动方向相同;从动轮上的外力偶矩的方向与轴的转动方向相反;截面法II、扭矩和扭矩图M eM e eT M=eT M'=M eT M eT’2526将扭矩按右手螺旋法则用力偶矢来表示,则当力偶矢的指向离开截面扭矩为正,反之为负M eTM eT T (+)T(-)扭矩的正负号规定:29M BM CM AM D112233M BT 11351N mBT M =-=-⋅M BM CT 22()702N mB C T M M =-+=-⋅T 3M D3468N mDT M ==⋅1170N mA M =⋅351N mB C M M ==⋅468N mD M =⋅§3-4 等直圆杆扭转时的应力强度条件一、横截面上的应力MM从三方面考虑几何关系物理关系静力学关系3132观察到下列现象:(1)各圆周线的形状、大小以及两圆周线间的距离没有变化;(2)纵向线仍近似为直线, 但都倾斜了同一角度。
建筑力学 扭转
T
扭矩
内力偶矩T称为 扭矩(Torsional moment )
扭矩的单位: N m 或
kN m
扭矩符号规定 (为了表达方便,按变形特点规定符号)
右手螺旋法则: (扭矩矢量指离截面为 + ,指向截面为 -)
Me
I
m m
T
T
m
II
Me
m
扭矩图
扭矩图意义:为了表达杆件各个截面的扭矩与 截面位置之间的关系。 画例题6-1和6-2的扭矩图
Ip R
Wp
max
T Wp
式中Wp称为扭转截面系数,其单位为m3。
应力公式
1)横截面上任意点:
扭转
T T:横截面上的扭矩 I p :点到截面形心的距离
Tr T 2)横截面边缘点: max I p Wt
T d/2 ρ O O
其中: Wp
T D/2 d/2
Ip r
抗扭截面模量
m ax
m ax
实心圆
d 4 W d Ip p
32
3
空心圆
16
Ip
D 32
4
d
4
D 4
32
(1 )
4
Wp
D 3
16
(1 4 )
强度计算
等直圆轴在扭转时,杆内各点均处于纯剪切状态,其强 度条件是最大工作剪应力不大于材料的许用剪应力。
即:
杆轴线始终保持直线,这种变形形式称为扭转变形。
扭转
m A'
g
m B j B'
A
外力偶作用平面和杆件横截面平行
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等直圆杆扭转应力
G G
d dx
可见,在横截面的同一半径 的圆周上各点处的切 应力 均相同,其值 与 成正比,其方向垂直于半径。
三峡大学 工程力学系
扭x
等直圆杆扭转应力
A
O2
d
a O1
GG ρ tan ρ EG d dx
b
即
G
D D'
d/2
A
E
O2 d G'
d ρ dx
扭转应力推导—应变特征
三峡大学 工程力学系
材料力学教案 横截面上一点处的切应变
a T b
等直圆杆扭转应力
d ρ dx
d 式中 ——相对扭转角 dx
I p 2 d A 2π 3 d
A 4 π π D D4 d 4 1 4 32 32 d 其中 D D 2 d 2
等直圆杆扭转应力
(
(
π D4 d 4 πD 3 Wp 1 4 D/2 16D 16 Ip
(
(
πD 3 1 3 。 注意:对于空心圆截面,Wp 16 三峡大学 工程力学系
扭转应力推导—静力方程
材料力学教案 横截面上应力分布规律 T max
等直圆杆扭转应力
T Ip
max
T
横截面周边上各点处( r)的最大
d
切应力为
max
d
max
Tr T T I p I p Wp r
max
D
式中Wp称为扭转截面系数,其单
材料力学教案
等直圆杆扭转应力
上一讲我们学到:
(1)认识了扭转基本变形。 ( 2 ) 薄壁圆筒扭转变形特征、 内力、应力、变形的计算。
三峡大学 工程力学系
材料力学教案
等直圆杆扭转应力
第六讲
等直圆杆扭转应力和强度问题
三峡大学 工程力学系
材料力学教案 扭转变形特征
等直圆杆扭转应力
1)轴向线仍为直线,且长度不变. 2)横截面仍为平面且与轴线垂直。 3)径向线保持为直线,只是绕轴线旋转。 平面假设: 变形前为平面的横截面 , 变形后仍保持为平面。
c
x
z
单元体及切应力互等
材料力学教案 斜截面上的应力
等直圆杆扭转应力
现分析单元体内垂直于前、后两平面的任一斜截面
ef (如图)上的应力。
三峡大学 工程力学系
扭转斜截面上的应力
材料力学教案
分离体上作用力的平衡方程为
等直圆杆扭转应力
d A ( d A cos sin ( d A sin cos 0
dA T
A
2 dA T
其中A 2 d A 称为横截面的极惯性矩Ip, 它是横截面的几何性质。 以 I p d A 代入上式得:
2 A
d T d x GI p
从而得等直圆杆在线弹性范围内扭转时,横截面上任一点 处切应力计算公式
T T ρ G GI I p p 三峡大学 工程力学系
扭转强度条件
材料力学教案
第三章 扭转 等直圆杆扭转应力
例题 图示阶梯状圆轴,AB段直径d1=120 mm,BC段直径 d2=100 mm。扭转力偶矩MA =22 kN· m,MB =36 kN· m , MC =14 kN· m,材料的许用切应力[ ]80 MPa。试校核该轴的强 度。
F 0, F 0,
d A ( d A cos cos ( d A sin sin 0
利用 ',经整理得
sin 2 , cos2
三峡大学 工程力学系
扭转斜截面上的应力
材料力学教案
由此可知:
等直圆杆扭转应力
sin 2 , cos2
(1) 单元体的四个侧面( = 0°和 = 90°)上切应力的
绝对值最大;
(2) =-45°和 =+45°截面上切应力为零,而正应
力的绝对值最大;
45 max
45 min
三峡大学 工程力学系
三峡大学 工程力学系
扭转应力推导--扭转变形特征
材料力学教案 横截面上应力分布规律
等直圆杆扭转应力
与薄壁圆筒相似,在小变形条件下,等直圆杆在扭转时横
截面上也只有切应力。
三峡大学 工程力学系
扭转应力推导—应力分布规律
材料力学教案 横截面上一点处的切应变
等直圆杆扭转应力
a T
b
A
E
O1
T
G D G' D' dx dx
位为 m3。
扭转应力推导—计算公式
三峡大学 工程力学系
材料力学教案
等直圆杆扭转应力
圆截面的极惯性矩Ip和扭转截面系数Wp
实心圆截面:
Ip 2 d A
A
d 2 0
4 π d 2π 3 d 32
πd 3 Wp d / 2 16
Ip
三峡大学 工程力学系
圆截面扭转参数
材料力学教案 空心圆截面:
A
E
O1
T
G D G' D' dx
O2
d
a
沿杆长的变化率,常用' 来
表示,对于给定的横截面为常 量。
b
可见,在横截面的同一半径 的圆周上各点处的切应变
均相同; 与 成正比,且发生在与半径垂直的平面内。
三峡大学 工程力学系
扭转应力推导--扭转应变特征
材料力学教案 物理方面(本构关系)
扭转斜截面上的应力
材料力学教案
第三章 扭转 等直圆杆扭转应力
强度条件
max [ ]
此处[]为材料的许用切应力。对于等直圆轴亦即
Tmax [ ] Wp
铸铁等脆性材料制成的等直圆杆扭转时虽沿斜截面因 拉伸而发生脆性断裂,但因斜截面上的拉应力与横截面上 的切应力有固定关系,故仍可以切应力和许用切应力来表 达强度条件。 三峡大学 工程力学系
(
圆截面扭转参数
材料力学教案
等直圆杆扭转应力
单元体· 切应力互等定理
以横截面、径向截面以及与表面平行的面(切向截面)从
受扭的薄壁圆筒或等直圆杆内任一点处截取一微小的正六面
体——单元体。
y
dy
单元体两个相互垂直平面上
a
dx
b
d
的剪应力同时存在,且大小
相等,都指向(或背离)该 两平面的交线。 三峡大学 工程力学系
