八年级数学一次月考Microsoft Word 文档
八年级(下)学期 第一次月考数学试题含答案

八年级(下)学期 第一次月考数学试题含答案一、选择题1.下列计算正确的是( )A =B .2=C .(26=D==2.下列计算正确的是( )A 1BCD ±3. )A B .C .D .4.x 的取值可以是( )A B .0C .12-D .-15.下列各式中,运算正确的是( )A =﹣2B +C 4D .=26.下列式子中,属于最简二次根式的是( )A BC D 7.下列各式计算正确的是( )A =B 6=C .3+=D 2=-8.m 能取的最小整数值是( ) A .m = 0B .m = 1C .m = 2D .m = 3 9.下列运算正确的是( )A .52223-=y yB .428x x x ⋅=C .(-a-b )2=a 2-2ab+b 2D =10.已知m 、n m ,n )为( ) A .(2,5)B .(8,20)C .(2,5),(8,20)D .以上都不是11.已知226a b ab +=,且a>b>0,则a ba b+-的值为( )A B C .2D .±212.如果关于x的不等式组0,222 3x mxx-⎧>⎪⎪⎨-⎪-<-⎪⎩的解集为2x>,且式子3m-的值是整数,则符合条件的所有整数m的个数是().A.5 B.4 C.3 D.2二、填空题13.观察下列等式:第1个等式:a1=2112=-+,第2个等式:a2=3223=-+,第3个等式:a3=32+=2-3,第4个等式:a4=5225=-+,…按上述规律,回答以下问题:(1)请写出第n个等式:a n=__________.(2)a1+a2+a3+…+a n=_________14.对于任意实数a,b,定义一种运算“◇”如下:a◇b=a(a-b)+b(a+b),如:3◇2=3×(3-2)+2×(3+2)=13,那么3◇2=_____.15.将一组数2,2,6,22,10,…,251按图中的方法排列:若2的位置记为(2,3),7的位置记为(3,2),则这组数中最大数的位置记为______.16.11122323-=11113-23438⎛⎫=⎪⎝⎭11114-345415⎛⎫=⎪⎝⎭据上述各等式反映的规律,请写出第5个等式:___________________________.17.2m1-1343m--mn=________.18.2121=-+3232=+4343=+++……=___________.19.x 的取值范围是_____.20.x 的取值范围是_____三、解答题21.小明在解决问题:已知a2a 2-8a +1的值,他是这样分析与解答的:因为a=2,所以a -2所以(a -2)2=3,即a 2-4a +4=3. 所以a 2-4a =-1.所以2a 2-8a +1=2(a 2-4a)+1=2×(-1)+1=-1. 请你根据小明的分析过程,解决如下问题: (1)计算:= - . (2)… (3)若a,求4a 2-8a +1的值.【答案】 ,1;(2) 9;(3) 5 【分析】(11==;(2)根据例题可得:对每个式子的分子和分母中同时乘以与分母中的式子相乘符合平方差公式的根式,去掉分母,然后合并同类项二次根式即可求解; (3)首先化简a ,然后把所求的式子化成()2413a --代入求解即可. 【详解】(1)计算:1=; (2)原式)1...11019=++++==-=;(3)1a ===,则原式()()224213413a a a =-+-=--,当1a =时,原式2435=⨯-=.【点睛】本题考查了二次根式的化简求值,正确读懂例题,对根式进行化简是关键.22.计算:10099+【答案】910【解析】 【分析】先对代数式的每一部分分母有理化,然后再进行运算 【详解】10099++10099+++=991-++-=1- =1110- =910【点睛】本题看似计算繁杂,但只要找到分母有理化这个突破口,就会化难为易。
八年级数学(下)第一次月考.doc

八年级数学(下)第一次月考试卷一、填空题:(每空2分,共28分)a b1、若则x-2 y~2; 3 V 9 则3a 3a(填“<、>或=”号)2、*的5倍与12的差不小于6,用不等式表示为; 是非负数用不等式表示为3、分解因式:x3y-2x2y2 +xy34、如果奴y +9y2是一个完全平方式,那么k的值是3 — 2、5、当y 时,代数式4 的值是负数,不等式6 —IZxvO的解集是________________________ O6、不等式5(x- l)<3(x + l)的正整数解为:。
7、若一次函数' =2* — 6 ,当时,y > °8、不等式一3vl — 2xV5的解集为它的非负整数解为9、已知X2+3X =7 ,贝!|代数式2X2+6X-3的值为二、选择题:(每小题3分,共计30分)10、不等式2X+1V8最大整数解是()A、4B、3C、2D、1[2x < 31 1、不等式组I】+ * < 2x的解集是( )3, 3■< —、 1 V X V —A 、2 B、工 > : C 2 D、x > 21 2.下列变形是分解因式的是()A 。
之一4。
/? + 4/?2 = (Q-2Z?)2 B6x2y2= 3xy • 2xyr(x + 2)(x +1) = x2 + 3x + 2 n x2 -9-6x = (x + 3)(x — 3)-6x 13、已知两个不等式的解集在数轴上如图表示,[x>bYx < a 且a 手b ,如果这个不等式组无实数解,那么 D 、a < b < 0 16、不等式_x, ITT ^3-2 4 0 1那么这个解集为( ) A 、* 2 -1B 、x > 1C 、-3<x<-lD 、1>-3 14. 下列多项式的分解因式,正确的是() A 、 12xyz —9JV 2J ^2 = 3jvyz(4 — 3xyz}B 3々2y — 3ay + 6y = 3y(a 2 —a + 2)C _ 乂2 + jcy _ xz ——工(乂2 + y _ N)D ci 2b + 5ab — b = bia 1 + 5a)15. 把多项式m\a-2) + m(2-a)分解因式等于() A (o-2)(麻+秫) B~ 2X^2 —m) C 、m(々一2Xm — l)D 、M ^A ~ + 1) 与“、人的关系是( ) \、a > b B 、"V 。
八年级数学第二学期第一次月考.doc
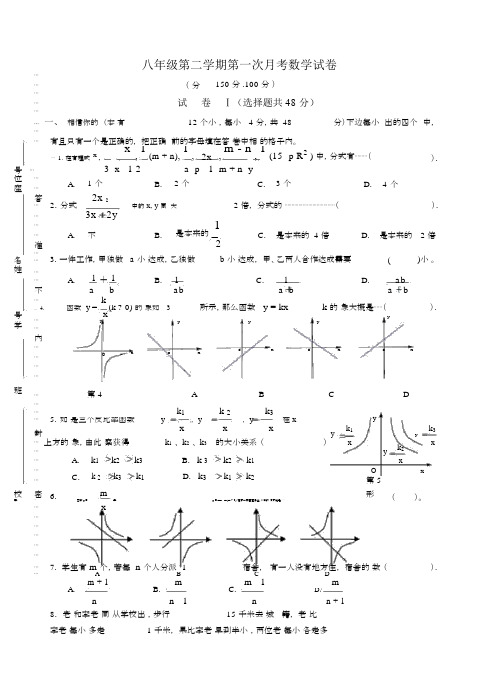
八年级第二学期第一次月考数学试卷⋯ ( 分150 分 .100 分 )⋯ ⋯ 试 卷 Ⅰ(选择题共48 分)⋯⋯12 个小 ,每小 4 分,共 48⋯ 一、相信你的 (本 有分)下边每小 出的四个 中,⋯ 有且只有一个是正确的, 把正确 前的字母填在答 卷中相 的格子内。
⋯x , 1 (m + n), 1 , 2x , m - n , 1(15- p R 2) 中,分式有⋯⋯⋯(⋯ 1.在有理式 x,).号 ⋯ 3 x - 1 2 a p - 1 m + n y位 ⋯ A. 1 个 B. 2 个 C. 3 个 D. 4 个座 ⋯2x 2答 2.分式 2 倍, 分式的 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(). ⋯ 3x 中的 x, y 同 大⋯ 2y⋯ 是本来的 1⋯ A. 不B. C. 是本来的 4 倍 D. 是本来的 2 倍 准 2名 ⋯ 3. 一件工作,甲独做 a 小 达成,乙独做 b 小 达成, 甲、乙两人合作达成需要( )小 。
⋯姓 ⋯ 1 + 1 1 1 abA.B.C.D.⋯ 不 a b ab a b a b⋯ k 所示,那么函数 y = kx - k 的 象大概是⋯⋯(). 号 ⋯ 4.函数 y = (k ? 0) 的 象如 3 ⋯ y x y y y y 学⋯内⋯Oxoxoxoxox⋯⋯⋯班⋯ 第 4ABCD⋯ k 1 k 2 k 3⋯y⋯5.如 是三个反比率函数yx, yx, y在 x封xyk 1k 3k 1 、 k 2 、 k 3xy⋯ 上方的 象,由此 察获得 的大小关系 ()k 2x⋯A. k 1 k 2k 3B. k 3 k 2k 1yx⋯⋯C. k 2 k 3k 1D. k 3k 1k 2Ox⋯第 5m校 密 6.形()。
学⋯ 函数 y =与 y = mx - m(m ? 0) 在同一平面直角坐 系中的 像可能是⋯⋯⋯⋯ x⋯ ⋯ ⋯ ⋯ ⋯⋯ 7. 学生有 m 个,若每 n 个人分派 1宿舍, 有一人没有地方住, 宿舍的 数 ().⋯ABCDA.m + 1B.mC.m - 1mnn - 1nD.n + 18. 老 和李老 同 从学校出 ,步行 15 千米去 城 籍, 老 比李老 每小 多走1 千米, 果比李老 早到半小 ,两位老 每小 各走多少千米? 李老 每小 走x 千米,依 意, 获得的方程是 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A.15 -15=1 B. 15 -15 =1C.15 -15=1 D. 15 -15 = 1x + 1 x 2x x + 1 2x - 1 x 2x x - 1 29.已知1- 1=3, 5x + xy - 5y 的 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()x yx - xy - yA.-7B.7 C.2 D.―2227710. 若分式方程1 + 1 =2 有增根 , 增根可能是⋯⋯⋯⋯⋯⋯()x - a x - b ( x - a )( x - b )A. aB.bC.a 和 bD. a 或 b11 .已知 ab = 1, M =1 + 1 , N = a + b, M 与 N 的大小关系 ⋯⋯ ().1+ a 1+ b 1+ a 1+ bA. M>NB.M=NC. M<ND. 不可以确立12. 学校 划将 120 名学生均匀分红若干个学 小 ,若每个小 比原 划多一个人,要比原划少分出 6 个小 ,那么原 划要分红的小 数是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯()A . 40B . 30C . 24D .20号1 2 3 4 5 6 7 8 9 10 11 12答案试 卷 Ⅱ(非选择题共 102 分)二、填空题 (本 有8 个小 ,每小 4 分,共32 分)13. ①在分式x - 2 中,当 x =,分式无心 .x 2 + 5x - 14②在分式a 2 - a - 12 中,当 a = ,分式的 零 .2a 2 - 5a - 12a -b 13a 2 - 5ab + 2b 2 的 是a -b=14. ①若= ,2a 2 + 3ab - 5b 2,②化b2a -bab15.人体中成熟的胞的均匀直径 0.0000077m , 用 科 学数 法 可 表 示mm .16. 不改 分式的 ,1- a - a 2①使它的分子与分母中最高次 的系数都 正数, 2 + 5a - a 3=. ②使它的分子与分母中各 系数都化 整数,0.2m + 0.9n =.0.1m - 0.7n17. 已知函数 y =( m - 1) xm2-5是反比率函数,且它的 象在第一、三象限,那么m =18. 已知圆柱的侧面积是 6 πcm 2 ,若圆柱的底面圆的半径为x ( cm ),高为 y ( cm ),则 y 与 x 的函数关系式是1PP19. 已知函数 y =-在第一象限的图象如图 8 所示,点为图象上的随意一点,过作⊥xPA x轴于 A ,PB ⊥y 轴于 B ,则△APB 的面积为.20. 如图,一次函数 y = kx + b 与反比率函数 y = -m的图象交于A (-2 , 1 )、B ( 1 ,n )两点,x依据图象能够知道:一次函数的值大于反比率函数的值的X 的取值范围是三、计算题 (本大题共 18 分)a 2 +b 2 -a -b 2ab2 ,而后请选择一组你喜爱的 a,b 21 .(此题 10 分)先化简代数式 ( 2 - b 2 ) ? (a - b)(a + b)a a +b 的值代入求值.22 .(此题 8 分)解方程:x + 1-4 = 1.x - 1x 2 - 1四、拓广探究(本大 共 12 分)23 .(本 12 分)小明在 算 1?11,1?1 1 , 1?11 ,⋯1=1-1,1=1-1,2363 4 124 520623123 4111=-,⋯20 45( 1)用式子表示 一 化 律;( 2)利用 一 律 算:22+22( x +1)( x + 3) ++ +.( x + 3)( x + 5)( x + 5)( x + 7)(x + 2005)( x + 2007)五.解答题:(本大题共 4 小题,共 40 分。
八上第一次月考Microsoft Word 文档 (4)
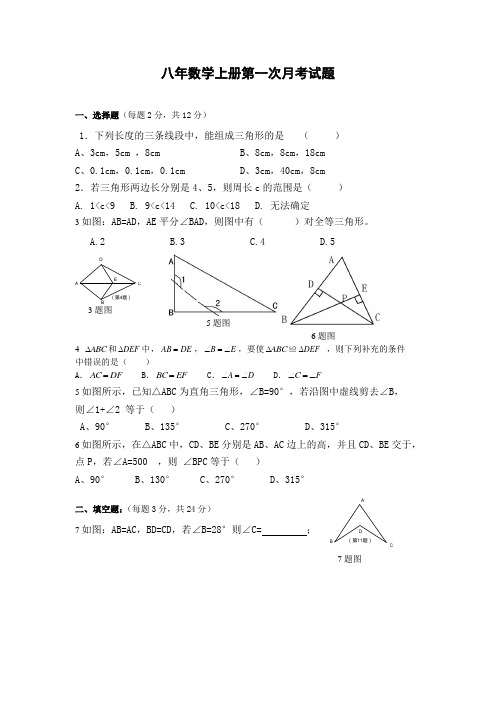
八年数学上册第一次月考试题一、选择题(每题2分,共12分)1.下列长度的三条线段中,能组成三角形的是 ( )A 、3cm ,5cm ,8cmB 、8cm ,8cm ,18cmC 、0.1cm ,0.1cm ,0.1cmD 、3cm ,40cm ,8cm 2.若三角形两边长分别是4、5,则周长c 的范围是( ) A. 1<c<9 B. 9<c<14 C. 10<c<18 D. 无法确定3如图:AB=AD ,AE 平分∠BAD ,则图中有( )对全等三角形。
A.2B.3C.4D.53题图5题图6题图4 ABC ∆和DEF ∆中,DE AB =,E B ∠=∠,要使ABC ∆≌DEF ∆ ,则下列补充的条件 中错误的是( )A .DF AC =B .EF BC = C .D A ∠=∠ D .F C ∠=∠5如图所示,已知△ABC 为直角三角形,∠B=90°,若沿图中虚线剪去∠B ,则∠1+∠2 等于( )A 、90°B 、135°C 、270°D 、315°6如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于,点P ,若∠A=500 ,则 ∠BPC 等于( )A 、90°B 、130°C 、270°D 、315°二、填空题:(每题3分,共24分)7如图:AB=AC ,BD=CD ,若∠B=28°则∠C= ;7题图(第4题)EDCBA (第11题)D CBA8 若一个等腰三角形的两边长分别是3 cm 和5 cm ,则它的周长是 cm 。
9 如图:在△ABC 中,AD=AE ,BD=EC ,∠ADB=∠AEC=105°,∠B=40°,则∠CAE= ;9题图 10题图 12题图10 如图:AB ,CD 相交于点O ,AD =CB ,请你补充一个条件,使得 △AOD ≌△COB ,你补充的条件是 ;11.已知a 、b 、c 是三角形的三边长,化简:|a -b +c|+|a -b-c|=___________ 12为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做 的道理是 。
八年级第二学期 第一次月考数学试题含答案

一、选择题1.已知2a =,2b =的值为( ) A .4B .5C .6D .72的倒数是( ) AB.2C. D.2-3.a b =--则( ) A .0a b +=B .0a b -=C .0ab =D .220a b +=4.下列说法错误的个数是( )a =;④数轴上的点都表示有理数 A .1个B .2个C .3个D .4个5.设ab21b a-的值为() A1+B1+C1D16.当4x =-的值为( )A .1BC .2D .37.下列计算或判断:(1)±3是27的立方根;(2;(32;(4;(5) A .1个B .2个C .3个D .4个8.下列各组二次根式中,能合并的一组是() AB和CD9.如果实数x ,y=-(),x y 在( ) A .第一象限 B .第二象限C .第一象限或坐标轴上D .第二象限或坐标轴上10.的值应在( ) A .1和2之间B .3和4之间C .4和5之间D .5和6之间二、填空题11.已知实数,x y 满足()()22200820082008x x y y ----=,则2232332007x y x y -+--的值为______.12.能力拓展:1:2121A -=+;2:3232A -=+;3:4343A -=+;4:54A -=________.…n A :________.()1请观察1A ,2A ,3A 的规律,按照规律完成填空.()2比较大小1A 和2A∵32+________21+∴32+________21+ ∴32-________21-()3同理,我们可以比较出以下代数式的大小:43-________32-;76-________54-;1n n +-________1n n --13.已知x=3+1,y=3-1,则x 2+xy +y 2=_____.14.实数a 、b 满足22a -4a 436-12a a 10-b 4-b-2+++=+,则22a b +的最大值为_________.15.已知120654010144152118+++可写成235a b c ++的形式(,,a b c 为正整数),则abc =______.16.若613-的整数部分为x ,小数部分为y ,则(213)x y +的值是___.17.将1、2、3、6按右侧方式排列.若规定(m ,n )表示第m 排从左向右第n 个数,则(5,4)与(9,4)表示的两数之积是______.18.2,26,210,…,51若2的位置记为(2,3),7的位置记为(3,2),则这组数中最大数的位置记为______. 19.计算:200820092+323⋅-=_________.20.4102541025-+++=_______.三、解答题21.我国南宋时期有个著名的数学家秦九韶提出了一个利用三角形的三边求三角形的面积的公式,若三角形三边为a b c 、、,则此三角形的面积为:2222221122a b c S a b ⎛⎫+-=- ⎪⎝⎭同样古希腊有个几何学家海伦也提出了一个三角形面积公式:2()()()S p p a p b p c =---2a b cp ++=(1)在ABC 中,若4AB =,5BC =,6AC =,用其中一个公式求ABC 的面积. (2)请证明:12S S【答案】(11572) 证明见解析 【分析】(1)将4AB =,5BC =,6AC =代入2222221122a b c S a b ⎛⎫+-=- ⎪⎝⎭(2)对1S 和2S 分别平方,再进行整理化简得出2212S S =,即可得出12S S .【详解】解:(1)将4AB =,5BC =,6AC =代入2222221122a b c S a b ⎛⎫+-=- ⎪⎝⎭得: 222222145615745224S ⎛⎫+--=⎪⎝⎭⨯= (2)222222211[()]24a b a S c b +-=-=222222)1(22(4)a b c a b c ab ab +-+--+=2222()2(21)4c a c a b b +⋅---⋅ =()(1()()16)c a b c a b a b c a b c +-++-++- 22()()()S p p a p b p c =---∵2a b cp ++=, ∴22()(2)(222)S a a b c a b c a b c a b c b c +++++++-+=-- =2222a b c b c a a c b a b c +++-+-+-⋅⋅⋅ =1()()()()16a b c b c a a c b a b c +++-+-+- ∴2212S S =∵10S >,20S >, ∴12S S .【点睛】本题考查了二次根式的运算,解题的关键是理解题中给出的公式,灵活运用二次根式的运算性质进行运算.22.阅读下列材料,然后回答问题:1== . 以上这种化简过程叫做分母有理化.1===. (1)请用其中一种方法化简;(2+99+【答案】(2) 3 1. 【分析】(1)运用了第二种方法求解,即将4(2)先把每一个加数进行分母有理化,再找出规律,即后面的第二项可以和前面的第一项抵消,然后即可得出答案.【详解】 (1)原式==;(2)原式=+++…=﹣1+﹣+﹣+…﹣=﹣1=3﹣1【点睛】本题主要考查了分母有理化,找准有理化的因式是解题的关键.23.1524-45-656 【分析】先化为最简二次根式,再将被开方数相同的二次根式进行合并. 【详解】 151024-45-6552526-35-6 525-3526-6 6. 【点睛】本题考查了二次根式的加减运算,在进行此类运算时,先把二次根式化为最简二次根式的形式后再运算.24.先观察下列等式,再回答下列问题: 2211111111121112++=+-=+; 2211111111232216++=+-=+ 22111111113433112++=+-=+ (1)2211145++ (2)请你按照上面各等式反映的规律,用含n 的等式表示(n 为正整数).【答案】(1)1120(2)()111n n++(n为正整数)【解析】试题分析:(1)从三个式子中可以发现,第一个加数都是1,第二个加数是个分数,设分母为n,第三个分数的分母就是n+1,结果是一个带分数,整数部分是1,分数部分的分子也是1,分母是前项分数的分母的积.所以由此可计算给的式子;(2)根据(1)找的规律写出表示这个规律的式子.试题解析:(1)=1+14−141+=1120,1 1 20(2)1n−1n1+=1+()1n n1+ (n为正整数).a=,也考查了二次根式的运算.此题是一道阅读题目,通过阅读找出题目隐含的条件.总结:找规律的题目,都要通过仔细观察找出和数之间的关系,并用关系式表示出来.25.观察下列一组等式,然后解答后面的问题1)1=,1=,1=,1=⋯⋯(1)观察以上规律,请写出第n个等式:(n为正整数).(2(3【答案】(1)1=;(2)9;(3【分析】(1)根据规律直接写出,(2)先找出规律,分母有理化,再化简计算.(3)先对两个式子变形,分子有理化,变为分子为1,再比大小.【详解】解:(1)根据题意得:第n个等式为1=;故答案为1=;(2)原式111019==-=;(3-==,<∴>.【点睛】本题是一道利用规律进行求解的题目,解题的关键是掌握平方差公式.26.2020(1)- 【答案】1 【分析】先计算乘方,再化简二次根式求解即可. 【详解】2020(1)-=1 =1. 【点睛】本题考查了二次根式的混合运算,先把二次根式化为最简二次根式,再合并即可.27.先化简,再求值:221()a ba b a b b a-÷-+-,其中a =2b =- 【答案】1a b -+,12-. 【分析】先把分式进行化简,得到最简分式,然后把a 、b 的值代入计算,即可得到答案. 【详解】 解:原式1()()a b a b aa b a b b a b b--=⨯-⨯+-+()()a b a b a b b a b -=--++()b bb a =-+1a b=-+,当a =2b =原式12==-.【点睛】本题考查了二次根式的混合运算,分式的化简求值,分式的混合运算,解题的关键是熟练掌握运算法则进行解题.28.(1)计算)(2201113-⎛⎫--•- ⎪⎝⎭(2)已知,,a b c为实数且2c =2c ab-的值【答案】(1)13;(2)12-【分析】(1)利用完全平方公式、负整数指数幂、零指数幂分别计算再合并即可; (2)先依据二次根式有意义的条件,求得a 、b 、c 的值,然后再代入计算即可. 【详解】(1))(2201113-⎛⎫--•- ⎪⎝⎭31=+⨯=4+9=13;(2)根据二次根式有意义的条件可得:∵()2303010a a b ⎧-≥⎪⎪-≥⎨⎪-+≥⎪⎩, ∴3a =,1b =-, ∴2c =∴(()2223112c ab -=-⨯-=-【点睛】本题主要考查了二次根式的混合运算,二次根式有意义的条件以及二次根式的化简求值,熟练掌握二次根式有意义的条件是解题的关键.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B解析:B 【分析】根据二次根式的混合运算和完全平方公式进行计算,即可得到结果. 【详解】解:∵2a =,2b =, ∴227a b ++2252527 55454745425=∴255故选:B . 【点睛】本题主要考查了二次根式的混合运算和完全平方公式,熟悉相关运算法则是解题的关键2.B解析:B 【分析】根据倒数的定义,即可得到答案. 【详解】2,; 故选:B. 【点睛】本题考查了倒数的定义和化为最简二次根式,解题的关键是熟记倒数的定义进行解题.3.C解析:C 【分析】直接利用二次根式的性质 ,将已知等式左边化简,可以得到a 与b 中至少有一个为0,进而分析得出答案即可. 【详解】解:∵a b =--, ∴a-b=-a-b , 或b-a=-a-b∴a= -a ,或b=-b, ∴a=0,或b=0, ∴ab=0, ∴0ab =. 故选:C . 【点睛】本题考查了二次根式的性质与化简,正确掌握二次根式的性质是解题的关键.4.C解析:C【分析】根据无理数定义判断①;根据平方根的算法判断②;利用二次根式的性质化简判断③;根据数轴的特点,判断④.【详解】无限不循环小数才是无理数,①错误;=,3的平方根是②正确;3=,③错误;a数轴上的点可以表示所有有理数和无理数,④错误故选:C.【点睛】本题考查无理数的定义、平方根的计算、二次根式的性质以及数轴表示数,紧抓相关定义是解题关键.5.B解析:B【分析】首先分别化简所给的两个二次根式,分别求出a、b对应的小数部分,然后化简、运算、求值,即可解决问题.【详解】∴a,∴b,∴21b a-,故选:B.【点睛】该题主要考查了二次根式的化简与求值问题;解题的关键是灵活运用二次根式的运算法则来分析、判断、解答.6.A解析:A【分析】根据分式的运算法则以及二次根式的性质即可求出答案.【详解】解:原式2223232323x xx x112323x x将4x=代入得,原式11423423221113133113133131131=.故选:A.【点睛】本题考查分式的运算以及二次根式的性质,解题的关键是熟练运用分式的运算法则以及观察出分母可以开根号,本题属于较难题型.7.B解析:B【解析】根据立方根的意义,可知27的立方根是3,故(1a=正确,故(2)正=8,可知其平方根为±,故(3)不正确;根据算术平方根的意义,可知=,故=,故(48(5)正确.故选B.8.B解析:B【分析】先化简,再根据同类二次根式的定义解答即可.【详解】解:A、是最简二次根式,被开方数不同,不是同类二次根式;B是同类二次根式;3CD故选B.【点睛】本题考查的知识点是同类二次根式的定义,解题关键是熟记同类二次根式的定义.9.D解析:D【分析】先判断出点的横纵坐标的符号,进而判断点所在的象限或坐标轴.【详解】=-∴x、y异号,且y>0,∴x<0,或者x、y中有一个为0或均为0.,x y在第二象限或坐标轴上.∴那么点()故选:D.【点睛】根据二次根式的意义,确定被开方数的取值范围,进而确定a、b的取值范围,从而确定点的坐标位置.10.B解析:B【分析】原式利用多项式除以单项式法则计算,估算确定出范围即可.【详解】=∵1<2<4,∴1<2,即3<<4,则原式的值应在3和4之间.故选:B.【点睛】本题考查了二次根式的混合运算,以及无理数的估算,解题的关键是熟练掌握运算法则进行解题.二、填空题11.1【分析】设a=,b=,得出x,y及a,b的关系,再代入代数式求值.【详解】解:设a=,b=,则x2−a2=y2−b2=2008,∴(x+a)(x−a)=(y+b)(y−b)=2008……解析:1【分析】设x,y及a,b的关系,再代入代数式求值.【详解】解:设x2−a2=y2−b2=2008,∴(x+a)(x−a)=(y+b)(y−b)=2008……①∵(x−a)(y−b)=2008……②∴由①②得:x+a=y−b,x−a=y+b∴x=y,a+b=0,∴,∴x2=y2=2008,∴3x2﹣2y2+3x﹣3y﹣2007=3×2008−2×2008+3(x−y)−2007=2008+3×0−2007=1.故答案为1.【点睛】本题主要考查了二次根式的化简求值,解题的关键是求出x,y及a,b的关系. 12.(1)、;(2);(3)【解析】【分析】(1)观察A1,A2,A3的规律可知将等式的右边乘以分母的有理化分式,即可得到左边的代数式;(2)先根据不等式的性质等式的两边同时加上或減去一个数,等解析:(1)=;(2),,><<;(3) ,,<<< 【解析】【分析】(1)观察A 1,A 2,A 3的规律可知将等式的右边乘以分母的有理化分式,即可得到左边的代数式;(2)先根据不等式的性质等式的两边同时加上或減去一个数,等式仍成立,求得>1)的结论解答;(3)利用(2)的结论进行填空.【详解】解:(1)观察A 1,A 2,A 3的规律可知,将等式右边的分式分母有理化,即得等式左边的代数式,所以=,(2>1>>,<<(3)由(1)、(2<,故答案为:=;(2),,><<;(3),,<<< 【点睛】 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.13.10【解析】根据完全平方式的特点,可得x2+xy+y2=(x+y )2﹣xy=(2)2﹣(+1)(﹣1)=12﹣2=10.故答案为10.解析:10【解析】根据完全平方式的特点,可得x 2+xy+y 2=(x+y )2﹣xy=(2﹣1)=12﹣2=10.故答案为10.14.【分析】首先化简,可得|a-2|+|a-6|+|b+4|+|b-2|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a ,b 的取值范围,即可求出的最大值.【详解】解析:【分析】10-b 4-b-2=+,可得|a-2|+|a-6|+|b+4|+|b-2|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a ,b 的取值范围,即可求出22a b +的最大值.【详解】10-b 4-b-2=+,1042b b =-+--, ∴261042a a b b -+-=-+--, ∴264210a a b b -+-+++-=,∵264a a -+-≥,426b b ++-≥,∴ 264a a -+-=,42=6b b ++-,∴2≤a≤6,-4≤b≤2,∴22a b +的最大值为()226452+-=,故答案为52.【点睛】本题考查了二次根式的性质与化简,绝对值的意义,算术平方根的性质.解题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2. 15.【解析】【分析】根据题意,可得到=,利用平方关系把根号去掉,根据、、的系数相等的关系得到关于a ,b ,c 的三元方程组,解方程组即可.【详解】∵=∴,即.解得.【点睛】本题考查了解析:【解析】【分析】a ,b ,c 的三元方程组,解方程组即可.【详解】∴(22118=,即2222118235a b c =+++++. 2222352118,2120,2540,2144,a b c ab ac bc ⎧++=⎪=⎪∴⎨=⎪⎪=⎩ 解得15,4,18.a b c =⎧⎪=⎨⎪=⎩154181080abc ∴=⨯⨯=.【点睛】本题考查了二次根式的加减,解本题的关键是将等式平方去根号,利用等量关系中等式左、.16.3【分析】先估算,再估算,根据6-的整数部分为x,小数部分为y,可得: x=2, y=,然后再代入计算即可求解.【详解】因为,所以,因为6-的整数部分为x,小数部分为y,所以x=2,解析:3【分析】先估算34<<,再估算263<<,根据6x ,小数部分为y ,可得: x =2, y=4然后再代入计算即可求解.【详解】因为34<,所以263<-<,因为6x ,小数部分为y ,所以x =2, y=4-,所以(2x y =(4416133=-=, 故答案为:3.【点睛】本题主要考查无理数整数部分和小数部分,解决本题的关键是要熟练掌握无理数估算方法和无理数整数和小数部分的求解方法. 17.【解析】试题解析:(5,4)表示第5排从左向右第4个数是:,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1, 第9排是奇数排,最中间的也就是这排的第5个数是1,那么第解析:【解析】试题解析:(5,4)表示第5排从左向右第4,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1,第9排是奇数排,最中间的也就是这排的第5个数是1,那么第4,∴(5,4)与(9,4)故答案为18.(17,6)【解析】观察、分析这组数据可发现:第一个数是的积;第二个数是的积;第三个数是的积,的积.∵这组数据中最大的数:,∴是这组数据中的第102个数.∵每一行排列了6个数,而∴是第1解析:(17,6)【解析】的积,.∵这组数据中最大的数: ∴102个数.∵每一行排列了6个数,而1026=17÷ ∴17行第6个数,∴这组数据中最大的一个数应记为(17,6).点睛:(1)这组数据组中的第n 2)该组数据是按从左到右,从小到大,每行6个数进行排列的;(3)6n ÷6n ÷的余数是所在的列数.19.【解析】原式==20.【分析】设,将等式的两边平方,然后根据完全平方公式和二次根式的性质化简即可得出结论.【详解】解:设,由算术平方根的非负性可得t≥0,则.故答案为:.【点睛】此题考查的是二【分析】t =,将等式的两边平方,然后根据完全平方公式和二次根式的性质化简即可得出结论.【详解】t=,由算术平方根的非负性可得t≥0,则244t=+=+8=+8=+81)=+62=1)∴=.1t.【点睛】此题考查的是二次根式的化简,掌握完全平方公式和二次根式的性质是解题关键.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无。
2020-2021学年河南郑州七中八年级(上)第一次月考数学试卷(Word+答案)

2020-2021学年河南郑州七中八年级(上)第一次月考数学试卷
一.选择题
1.(3分)在实数:﹣,3.1415926,π,,3.15,,中,无理数的个数为()A.2个B.3个C.4个D.5个
2.(3分)下列各组数中,分别以它们为边长能构成直角三角形的是()
A.3,4,5B.,,C.D.32,42,52
3.(3分)△ABC的三边长分别为a,b,c.下列条件,其中能判断△ABC是直角三角形的个数有()
①∠A=∠B﹣∠C
②a2=(b+c)(b﹣c)
③∠A:∠B:∠C=3:4:5
④a:b:c=5:12:13
A.1个B.2个C.3个D.4个
4.(3分)下列运算中错误的有()
①=4,②=±,③=﹣3,④±=3.
A.4个B.3个C.2个D.1个
5.(3分)如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为()
A.2B.C.D.
6.(3分)如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm的B处的食物,则蚂蚁经过的最短距离为()
第1页(共13页)。
人教数学八年级下册初二年级第一次月考.docx
初中数学试卷马鸣风萧萧2014——2015初二年级第一次月考时间:120分钟满分:100分命题人:张丹一、选择题(每小题3分,共30分)1、下列根式中,属于最简二次根式的是()A.27B.12+x C.21D.ba22、如果a是任意实数,下列各式中一定有意义的是()A.aB.21aC.12+a D.2a-3、实数a、b在数轴上的位置如图所示,则化简222)(baba---的结果是()A.b2- B.a2- C.)(2ab- D.04、在ABC∆中,︒=∠90BAC,3=AB,4=AC.AD平分BAC∠交BC于点D,则BD的长为()A.715B.512C.720D.521(第4题图)(第7题图)(第8题图)(第9题图)5、已知三角形的三边长之比为2:1:1,则此三角形一定是()A.锐角三角形B.钝角三角形C.等边三角形D.等腰直角三角形6、甲、乙两艘客轮同时离开港口,航行的速度都是min/40m,甲客轮用min15到达A,乙客轮用min20到达B。
若A,B两点的直线距离为m1000,甲客轮沿着北偏东︒30的方向航行,则乙客轮的航行方向可能是()A.北偏西︒30 B.南偏西︒30 C.南偏东︒60 D.南偏西︒607、如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC的中点,则下列式子中一定成立的是()A.OEAC2= B.OEBC2= C.OEAD= D.OEOB=8、如图,在A B C ∆中,BC AD ⊥于点D ,17=AB ,15=BD ,6=DC ,则AC 的长为 ( )A.11B.10C.9D.89、如图,在平行四边形ABCD 中,5=AD ,3=AB ,AE 平分BAD ∠交BC 于点E ,则线段BE ,EC 的长度分别为 ( ) A.2和3 B.3和2 C.4和1 D.1和410、如图,把矩形ABCD 沿直线EF 折叠,若︒=∠201,则=∠2 ( ) A.︒80 B.︒70 C.︒40 D.︒20(第10题图) (第13题图) (第14题图) (第15题图) 二、填空题(每小题3分,共15分) 11、已知直角三角形的周长为62+,斜边长为2,则它的面积为12、215- 21.(填“>”“<”或“=”) 13、如图所示,在平行四边形ABCD 中,AD CM ⊥于点M ,AB CN ⊥于点N ,若︒=∠50B ,则=∠MCN 14、如图所示,在ABC ∆,M 是BC 边的中点,AD 平分BAC ∠,AD BD ⊥于D ,12=AB ,20=AC ,则MD 的长为15、如图,直线l 过正方形ABCD 的顶点B 、点A 、C 到直线l 的距离分别是1和2,则正方形的边长是 三、解答题(共55分)16、计算(每小题3分,总分12分)(1)311227+-; (2)311)7548(⨯- (3)2)1(96----; (4)2327)3()3(3302-+-++-π17、(7分)17.已知a 、b 为直角三角形两条边长,且a 、b 满足4623+-+-=a a b ,求此三角形的周长。
完整word版,人教版八年级数学下册第一次月考测试题附答案
大布初级中学第二学期八年级第一次月考试卷出卷人:薛兵燕一、填空题( 3×10=30 )1. 数 3 的平方根是 ,算术平方根是; 2.4 的平方根是 , a 2 的算数平方根是;3. 若 2a + 3 存心义,则 a 的取值范围是 ;4. ( 3)2= , (3)2 =, 32=, 32=;5.aa 3a 5 =;6. 已知 a+b =- 3, ab=2, 则 a 2 b 2 2ab =;7. 若 aa 存心义,则 ( 2)a = ;8. 等式 a 1a 1a 2 1 建立的条件是;9. 若 16 a 是整数,则非负整数 a=, 16 a 的值为 ;10. 在一个半径为 2m 的圆形纸片上截出一个面积最大的正方形,则这个正方形的边长是.二 . 选择题( 3×8=24)11. 在 x 2 存心义的范围内,二次根式能表示的最小实数是( )A . 0B. 2C. 2D. 不存在12. 对于 12 的以下说法中错误的选项是( )A . 12 是无理数 B. 3< 12 <4 C. 12 是 12 的算数平方根D. 12 不可以化简13. 已知 20a 是整数,则知足条件的最小正整数a 的值是( ) A . 2B. 3C. 4D . 514. 若 (x 1)2 1 x ,则 x 的取值范围是()A . x ≤ 1B. x ≥ 1C. x <1D. x > 115. 以下各数中,与 2 3 的积为有理数的是()A . 3B. 2 3C. 2 3D. 2316. 若 a ≤ 0, 化简 a a 2的结果是()A . 0B. 2aC.- 2a D . 2a 或 - 2a17. 化简 x1 ,正确的结论是()xA .xB .-xC.xD.-x18. 以下计算中:①9 93,②b 1 b ,③ 2 1 21 12 ,④ 4y2 3y25255a a 44227x 2 9x完整正确的个数是()A . 2B. 1C. 4D . 3三 . 解答题(共 66 分)191 计算:(1) 2 27 3 12 6(2) 22050解:解:(3) ( 2 21)2(4) x 2 6x 94解:解:20. ( 5 分)化简求值: 2a( a+b )- (a+b )2,此中 a=2008 , b= 2009 ;21. ( 24 分)化最简二次根式:( 1) 2.5(2) 2 23解:解:( 3)b 2 ( 4) a 2 x 2abx b 2 x20a解:解:11 (6) 12( 75 31 (5)(6)(24)48)82322. ( 10 分)计算:(1) ( 3 2)( 32)(2) ( 5 2)2 (2 5)223. ( 6 分)解方程3( x2) x 124.(5分)74325. ( 5 分)若 8-11 的整数部分是a, 小数部分是b,求 2ab- b2的值 .答案:一. 填空题1.3, 3;2.2 , a ;3. a ≥ 3 ;4. 3,3, 3,-3;5. a 4 a ;6. 1;7. 1;8. a ≥21; 9. 0, 7, 12, 15, 16; 4, 310.2 m.二. 选择题11.A ; 12. D ; 13.D ; 14. C ; 15. B ;16. C ;17.B ;18. A.三. 解答题19. ( 1) 108 3 ; ( 2) 105 2 ; (3)9; ( 4) x 3 ;20.2a( a+b )- (a+b) 2=( a+b ) (2a-a-b )=a 2-b 2,-1;21. (1) 10 ;(2)2 6;( 3)b5a ;2310a( 4) a + b x ;( 5)6212;( )2622. (1)1;(2) 8 5 ;23. 3 23 6 1x2;24. 解: 7 4 3 4 4 3 322 43 (3)2 (2 3) 22 3 23 .25. ∵ a=4,∴ b=8- 11 - 4=4 - 11 , 故 2ab- b 2=b(2a-b)=( 4 - 11 )( 8- 4+ 11 )=5.。
湖南长沙湘郡培粹实验中学度初二数学第一次月考试题(Word版,无答案)
湖南长沙湘郡培粹实验中学度初二数学第一次月考试题(Word 版,无答案)第一次月考数学问卷时间:120 分钟 满分:120 分一、选择题(共 10 小题,满分 30 分)1.下列图形中,不是轴对称图形的是( ) .A . B. C. D.2.下列运算正确的是( ).A . a 2 + a 3 = a 5B . a 2 a 3 = a 5C . (a 2 )3 = a 5D . a 10 ÷ a 2 = a 53.下列各式由左边到右边的变形中,是分化因式的是( ).A . a ( x + y ) = ax + ayB . x 2 - 4x + 4 = x ( x - 4) + 4C .10x 2 - 5x = 5x (2x - 1)D . 2x 3 - 4x 2 + 2x = 2x ( x 2 - 2x + 1)4.已知 x m = 6, x n = 3 ,则 x 2 m - n 的值为().A . 9.B .34C . 12D .435.如 ( x + m ) 与 ( x + 3) 的乘积中不含x 的一次项,则 m 的值为( ).A . -3B . 3C . 0D .1 6.若分式242x x --的值为 0,则 x 的值是( ).A . -2B . 2C . ±2D .不能确定7.如图所示,在边长为 a 的正方形中,剪去一个边长为 b 的小正方形( a > b ),将余下部分拼成 一个梯形,根据两个图形阴影部分面积的干系,得到一个关于 a , b 的恒等式为( ).A . (a - b )2 = a 2 - 2ab + b 2B . (a + b )2 = a 2 + 2ab + b 2C . a 2 - b 2 = (a + b )(a - b )D . a 2 + ab = a (a + b )8.如图,在 ABC , AC = 4cm ,线段 AB 的垂直中分线交 AC 于点 N , BCN 的周长为 7cm , 则 BC 的长为().A . 1cmB . 2cmC . 3cmD .4cm 第 8 题 第 9 题 第 12 题9.如图,D 为 AB 上的一点,E 为 BC 上的一点,且AC = CD = BD = BE , A = 50︒ , 则 ∠CDE 的度数为(). A . 50︒B . 51︒C . 51.5︒D . 52.5︒ 10.要是分式2()xy x y +中的 x 和 y 都扩大 2 倍,则分式的值是( ). A .扩大 4 倍 B .扩大 2 倍 C .不变D .缩小 2 倍 11.要是12x x +=,则221=x x+ A . 4 B . 2 C . 0 D .612.如图, A , C , B 三点在联合条直线上, DAC 和 EBC 都是等边三角形, AE , BD 分 别与 CD , CE 交于点 M , N ,有如下结论:① ACE ≌ DCB ;② CM = CN ;③ AC = CN 此中正确结论的个数是( )A .3 个B .2 个C .1 个D .0 个二、填空题(共 6 小题,每小题 3 分,共 18 分)13.一个等腰三角形的双方长分别是 2cm 、 5cm ,则它的周长为 cm .14.如图, Rt ABC 中, ACB = 90︒ , A = 50︒ ,将其折叠,使点 A 落在边 CB 上 A 2 处,折痕 为 CD ,则 A 2DB 为 .15.若 a - b = 1 ,则代数式 a 2 - b 2 - 2b 的值为 .16.谋略2018201952()(2)125⋅= 17.在实数范畴内因式分化: 2x 2 - 4 = .18.若 x 2 + 2 ( m - 3) x + 16 是关于 x 的完全平方法,则 m =. 三、解答题(共 8 小题)19.谋略:⑴ ( 2a )3 · b 4 ÷12a 3b 2 ⑵ (-3x + 3 y + 2) (3x + 3 y - 2)20.因式分化:⑴ 4mx 3 - 24mx 2 + 36mx ⑵25 + 10 ( m + n ) + ( m + n )221.谋略:22. △ABC 在平面直角坐标系中的位置如图所示.⑴在图画中画出 △ABC 与关于 y 轴对称的图形△A 1 B 1C 1 ,并求出 △ABC 的面积;⑵若将线段 A 1C 1 平移后得到线段 A 2C 2 ,且A 2(a ,2) , C 2(-2, b ) ,求 a , b 的值. 23.已知 x 2 + 2x - 5 = 0 ,求代数式 ( x - 3)2- ( 2x + y ) ( 2x - y ) - y 2 的值.24.如图,已知△ABC 为等边三角形, D 为 BC 延长线上的一点,CE 中分 ACD ,CE = BD , 求证:△ADE 为等边三角形.25.如图,在△ABC 中,ABC = 45︒,CD ⊥AB 于点D ,BE 中分∠ABC ,且BE ⊥AC 于点E,与CD 相交于点F ,H 是边BC 的中点,相连DH 与BE 相交于点G .⑴求证:BF =AC ;⑵若CE = 3 ,求GE 的长.26.已知等边△ABC⑴如图①,若点M 在线段AB 上,点N 在线段BC 上,AN ,CM 交于点P ,且AM =BN ,则∠CPN 的度数是.⑵如图②,点M 在AB 的延长线上,点N 在BC 的延长线上,且AM =BN ,直线CM 交直线AN于点P .①求CPN 的度数;② 作MG ⊥BC 于点G ,若GNnBG=,求点M 在运动历程中,使△CPN 为等腰三角形时n 的值.27 .在平面直角坐标系中,A点的坐标为(a,0),B点的坐标为(0, b),且a,b满足a2 - 2ab + 2b2 - 24b +144 = 0 ,将△OAB 沿直线AB 翻折得到△ABM .⑴求证:∠OAB =∠OBA ;⑵如图①,将OA 绕点A 旋转到AF 处,相连OF ,过点B 作BC ⊥OF 于点C ,过点A 作AD ⊥OF 于点D .① 求证:△BOC≌△OAD ;② 作AN 中分∠MAF 交OF 于点N ,相连BN ,求∠ANB 的度数;⑶如图②,若D (0, 4),E 为BM 上一点,且满足EAD = 45︒,试求线段EB 的长度.。
八年级数学第一次月考测试题.docx
八年级数学第一次考试试卷时间:120分钟总分:150分一、选择题(每小题4分,共40分,请将答案写在题后的答题卡内)1.若0 V6ZV1,则点M (a —1卫)在()A.第一象限B.第二象限C.第三象限D.第四象限2.己知点P的坐标为(3,4),则下列说法止确的是()A.点P到x轴的距离是3B.点P到y轴的距离是4C.点P到x轴的距离是4D.以上说法都正确3.一次函数『=伙-2)x + 3的图象如图1所示,则k的取值范围的()4.己知一次函数y = /a+b的图象经过第一、二、三象限,则方的值可以是()A.・2B.・1C. 0D. 25.直线y = kx + 2与两坐标轴围成的三角形面积是1,则£值为()2 3 3A. -B. -C. ±2D. ±-3 2 26.将直线y = 2兀向右平移1个单位后所得图象对应的函数解析式为()A. y = 2x-1B. y = 2x-2C. y = 2x + lD. y = 2x + 27.函数y =(加-2)#z +加+ 1是关于兀的一次函数,则加的值为()A.・2B. 2C. ±2D.不等于2的实数8.已知点(-4, y) , (2, %)都在直线》=-* + 2上,则X,旳的大小关系是()A. > y2B. y f = y2C.< y2D.不能比较9.函数工中,自变量兀的取值范围是()x-1A. x 1B. x>-2C.・2 < %< 1D. x> -2.且xHl10.关于无的一次函数y = d + f+ 1的图象可能正确的是()二、填空题(每小题4分,共20分)11.把P(3,-2)沿兀轴向左平移1个单位,得到的点人的坐标是_____ ,再将A沿y轴向上平移2个单位,得到的点/的坐标是_________ ・12.若点(4-/卫一1)在y轴负半轴上,贝ljd= _________ •13.设P (3,加),Q(彼2)都在函数y = x + b的图象上,贝0 m + n = __ .14.已知y与兀+1成正比例,且当x = l时,y = 4 ,则y = 5时,x= _________ .15.一个y关于兀的函数同时满足两个条件:①图象过(2,1)点;②当兀>0时,y随兀的增大而减小•这个函数解析式为____________ (写出一个即可).三、解答题16.(8分)已知:A(a-2,5)和出(1, b-1)关于x轴对称,求(^ + /?)2012的值.17.写出下列各题中因变量与自变量Z间的关系式,并判断因变量是否为自变量的一次函数?(每小题5分,共25分)(1)正方体的表面积y与棱长兀之间的关系;⑵ 某汽车加油站油库的库容量为80000升,售岀的汽油为无(升),则油库中剩余的汽油y (升)与售出的汽油兀(升)之间的关系;⑶ 长方体的高为12cm ,宽为11cm ,体积V ( cm 3)与长兀(cm )之间的关系;⑷ 圆的底面半径为厂(cm ),圆的面积S ( cm 2 )与半径为厂(cm ) Z 间的关系;⑸一箱苹果质量为10千克,售价为56元,苹果的售价y (元)与质量兀(千克)之间 的关系.18. (8分)如图2,等腰梯形ABCD 的上底为4,下底为6, 坐标系,并写出各个顶点的坐标. 19. (13分)已知三角形ABC 的顶点C 的坐标为(0,5), A 、B 两点的坐标恰好满足: x 2 + y 2-25| + (3x-4y)2=0,且A 点在第一象限,求:(1)4、B 两点的坐标;⑵在平面直角坐标系中画出三角形ABC,并求出它的面积.20. (10 分)已知函数 y = (a + T )x + 3/ _ 12.高为3,建立适当的直角4 R图2(1) G为何值时,这个函数是关于自变量兀的一次函数?⑵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定远中学秋季八年级数学第一次月考
时间:100分钟 满分120分
一、选择题。
(每题3分,共30分)
1.下列图形中,不是轴对称图形的是 ( )
A
B 。
C 。
D 。
2、和点P (-3,2)关于y 轴对称的点是( )
A.(3, 2)
B.(-3,2)
C. (3,-2)
D.(-3,-2)
3.若x 2
+2(m -3)x+16是完全平方式,则m 的值等于( )
A .1或5
B .5
C .7
D .7或-1
4.圆、正方形、长方形、等腰梯形中有唯一条对称轴的是 ( )
(A)圆 (B)正方形 (C)长方形 (D)等腰梯形
5、一个多项式分解因式的结果是,那么这个多项式是(
)
A 、
B 、
C 、
D 、
6.下列长度的三条线段,能组成等腰三角形的是 ( )
(A) 1,1,2 (B) 2,2,5 (C) 3,3,5 (D) 3,4,5
7、分解因式得(
) A 、
B 、
C 、
D 、
8.已知∠AOB=45°,点P 在∠AOB 内部,P 1与P 关于OB 对称,P 2与P
关于OA 对称,则P 1,O,P 2三点构成的三角形是
)2)(2(3
3
b b -+46-b 64b -46+b 46--b 14
-x )1)(1(2
2-+x x 2
2
)1()1(-+x x )1)(1)(1(2
++-x x x 3
)1)(1(+-x x
D C
B
A
( )
(A)直角三角形 (B)等腰三角形 (C)等边三角形 (D)等
腰直角三角形
9.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )(A)锐角三角形.(B)直角三角形.(C)钝角三角形.(D)不能确定.
10、如图,如果直线m是多边形ABCDE的对称轴,
其中∠A=130°,∠B=110°,
那么,∠BCD的度数等于()A、40° B、50°
C、60°
D、70°
二.填空题(每题3分,共30分)
1、多项式分解因式的结果是
2、()()3.在△ABC中,已知AD是角平分线,∠B=
∠BAD=________。
4.小丽从镜子中看到的电子表的读数是
读数________.
5、若
6简便计算:
7.如图,中,,AD平分,BC=10cm,BD=6cm,
则点D到AB的距离为。
8.如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,
则△
2
3ab
a-
+
2
49x=
+4
16y2。
=
,
,则b
a
b
b
a=
=
+
-
+
-0
1
2
22。
-=
2
271
.2
29
.7
ABC
∆
90
=
∠C BAC
∠
D
E
D
A
B C
第8题
第7题
9、一个等腰三角形有两边分别为5和8厘米,则周长是___ _______厘米. 10.若∠AOB=2∠AOC,则OC是∠AOB的角平分线。
___________(填对或错)
三、作图题(5分)
如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)(5分)
四、将下列各式分解因式(每小题4分,共16分) (1)
(2)
-ma²+2mab -mb²
(3)
(4)3x³+6x²y+3xy²
五、
解答题及证明题(共39分)
1已知,求
的值。
(7分) 2、大正方形的周长比小正方形的周长长96厘米,它们的面积相差960平
3
123x x -2
2
4520bxy bx a -22==+ab b a ,32232
1
21ab b a b a ++
方厘米。
求这两个正方形的边长。
(5分)
3、如图,△ABC 中,DE 是AC 的垂直平分线,AE=4cm ,△ABD 的周长为13cm ,求△ABC 的周长。
(7分)
4.如图,AD ⊥BC,BD=DC,点C 在AE 的垂直平分线上,AB+BD 与DE 的长度有什么关系?并加以证明.(6分)
5、如图,点P 为∠AOB 内一点,分别作出P 点关于OA 、OB 的对称点P 1,P 2,连接P 1P 2交OA 于M,B 于N ,P 1P 2=15,求△PMN 的周长。
(7分)
6、如图,在△ABC 中,∠ACB =90°,DE 是AB ︰∠EAB =4︰1.求∠B 的度数.(7分)
选作题:已知是△ABC 的三边的长,且满足,试判断此三角形的形状。
(10分)
A
B
E
C
D
c b a 、、0)(22222=+-++c a b c b a A B
C
E
D
答案:
一、选择题
1、C
2、A
3、D
4、D
5、B
6、C
7、C
8、D
9、B 10、C
二、填空题
1、a(a+b)(a-b)
2、+56xy² 7x±4y²
3、30º
4、12:01
5、21
6、45.874cm、
8、18cm、9、18或21 10、错
三、作图题:运用点的对称性,作图省略
四、将下列各式分解因式(每小题4分,共16分)
1、3x(1+2x) (1-2x) 2 、-m(a-b)²
3、5bx(2a+3y) (2a-3y) 4 、 3x(x+y)²
五、解答题及证明题(共39分)
1、4
2、22cm 38cm
3、21cm
4、AB+BD=DE
5、15
6、18°
选作题:
此三角形的形状为等边三角形。
