9-5 电场强度与电势梯度的关系
袁艳红主编大学物理学第九章课后习题答案

----------专业最好文档,专业为你服务,急你所急,供你所需-------------文档下载最佳的地方第9章 静电场习 题一 选择题9-1 两个带有电量为2q 等量异号电荷,形状相同的金属小球A 和B 相互作用力为f ,它们之间的距离R 远大于小球本身的直径,现在用一个带有绝缘柄的原来不带电的相同的金属小球C 去和小球A 接触,再和B 接触,然后移去,则球A 和球B 之间的作用力变为[ ](A)4f (B) 8f (C) 38f (D) 16f答案:B解析:经过碰撞后,球A 、B 带电量为2q,根据库伦定律12204q q F r πε=,可知球A 、B 间的作用力变为8f。
9-2关于电场强度定义式/F E =0q ,下列说法中哪个是正确的?[ ] (A) 电场场强E 的大小与试验电荷0q 的大小成反比 (B) 对场中某点,试验电荷受力F 与0q 的比值不因0q 而变 (C) 试验电荷受力F 的方向就是电场强度E 的方向 (D) 若场中某点不放试验电荷0q ,则0=F ,从而0=E 答案:B解析:根据电场强度的定义,E 的大小与试验电荷无关,方向为试验电荷为正电荷时的受力方向。
因而正确答案(B )习题9-3图(B) 穿过S 面的电场强度通量改变,O 点的场强大小改变 (C) 穿过S 面的电场强度通量不变,O 点的场强大小改变 (D) 穿过S 面的电场强度通量不变,O 点的场强大小不变 答案:D解析:根据高斯定理,穿过闭合曲面的电场强度通量正比于面内电荷量的代数和,曲面S 内电荷量没变,因而电场强度通量不变。
O 点电场强度大小与所有电荷有关,由点电荷电场强度大小的计算公式204q E rπε=,移动电荷后,由于OP =OT ,即r 没有变化,q 没有变化,因而电场强度大小不变。
因而正确答案(D )9-4 在边长为a 的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为 [ ](A) q /ε0 (B) q /2ε0 (C) q /4ε0 (D) q /6ε0 答案:D解析:根据电场的高斯定理,通过该立方体的电场强度通量为q /ε0,并且电荷位于正立方体中心,因此通过立方体六个面的电场强度通量大小相等。
9-5 电场强度与电势梯度的关系

q V 4πε0 ( x 2 R 2 )1 2
R
o
x
P
x
例、在x-y平面上,各点的电势满足下 面的式子:
式中的x、y为任一点的坐标,a、b为常 数。求任一点电场强度的Ex和Ey分量。
U Ex x
U y
2
U Ez z
U a 2ax bx Ex 2 2 2 2 2 2 2 3/ 2 x x y (x y ) (x y )
dV El dl
电场强度与电势梯度
即:电场强度沿某一方向的分量等于沿该方向 电势的变化率(方向导数)的负值
dV El dl
一般
V V ( x , y , z)
V V V Ex Ez Ey x z y E Ex i E y j Ez k
电荷沿等势面移动时,电场力做功为零, 等势面与电力线处处正交;
电力线指向电势降落的方向 . 课堂练习: a、b点的场强大小和方向 已知: V1 V2 V2 V3 0
V
Ea Eb
b
a
V3
V2
二
E dl E cos dl El dl dV 得:E在 dl方向上的分量
V
El
n
dl
a
b
E
En cos
电势梯度是一个矢量,它的大小为电势变化率的最大值 (沿等势面法线方向,电势的变化率最大, ),它的方向 沿等势面法线方向且指向电势增大的方向。
电场强度等于电势梯度的负值
V V V E ( i j k ) gradV V x y z
9-5. 电场强度与电势梯度的关系 一 等势面
电场强度和梯度

r 化率的负值。
e r 电场强度的单位也用V/m。 V e 2 电势梯度
显然电势沿不同方向 V V
的单位长度增量是不同的,
rt
dl A
r
r dln
n
现讨论两个特殊方向上的
E低高
情况:切向和法向。
电电 势势
⑴
沿切向
Et
dV dlt
Q dV 0 Et 0
⑵ 沿法向
En
dV dln
V
Q
dV dln
电子在分子电偶极子电场中所受的力为
F
eE
2e
4 0
p x3
2 1.60 1019 6.2 1030 1.431010 N
4 8.851012 (51010 )3
a
F m
1.431010 9.111031
m s2
1.57 1020 m s2
vat 1.57 1020 1014 m s-1 1.57 106 m s-1
r E
(V
r i
V
r j
V
r k ) gradV
x y z
电场强度与电势梯度关系的物理意义
① 空间某点电场强度的大小取决于该点领域内
电势V的空间变化率。
② 电场强度的方向恒指向电势降落的方向。
讨论
⑴ 电场弱的地方电势低;电场强的地方电势高吗?
r
⑵ V=0地方, E 0 吗?
r
r
⑶ E 相等的地方,V一定相等吗?等势面上 E一定
(4x2 (x2
y )2 1/ 2 y2 )2
A点在电偶极矩的延长线上时:
2p 1 y0 E
4 0 x3
A点在电偶极矩的中垂线上时:
电势梯度和电场强度的关系

电势梯度和电场强度的关系
电势梯度和电场强度是电学中两个非常重要的概念,它们之间存在着密切的关系。
电势梯度是指电势在空间中的变化率,而电场强度则是指单位电荷在电场中所受到的力的大小。
在电学中,电势梯度和电场强度的关系是非常紧密的,它们之间的关系可以用以下公式来表示:
E = -∇V
其中,E表示电场强度,V表示电势,∇表示梯度运算符。
这个公式告诉我们,电场强度的大小与电势梯度的大小成反比。
也就是说,当电势梯度越大时,电场强度就越小;反之,当电势梯度越小时,电场强度就越大。
这个公式的意义可以通过一个简单的例子来说明。
假设我们有一个电荷为Q的点电荷,它在空间中产生了一个电势场。
如果我们想知道在某一点P处的电场强度,我们可以通过以下步骤来计算:
1. 首先,我们需要计算出点P处的电势V。
2. 然后,我们需要计算出点P处的电势梯度∇V。
3. 最后,我们可以通过公式E = -∇V来计算出点P处的电场强度E。
这个例子告诉我们,电势梯度和电场强度之间的关系是非常密切的。
在电学中,我们经常使用这个公式来计算电场强度,从而更好地理解电场的性质和行为。
电势梯度和电场强度是电学中两个非常重要的概念,它们之间存在着密切的关系。
电场强度的大小与电势梯度的大小成反比,这个关系可以用公式E = -∇V来表示。
在电学中,我们可以通过这个公式来计算电场强度,从而更好地理解电场的性质和行为。
8.5电场强度与电势梯度的关系

E
ds
等势面——规定、性质、梯度
gradU
U n
n
三、 q、E、U 三者关系网
1、 q E
E
1
4 0
dq r3
r
sE
ds
1
0
vdv
2、 q U
U
1
4 0
dq r
U LE dl
3 E U
U LE dl
势面2,电场力做功
dA qE dl
qEdl cos
en
1
2
P1
en P2
P3
qEdn
V V+dV
上页 下页 返回 退出
电场力做功等于电势能的减少量 dA q dU
E dU dn
场强也与等势面垂直,但指向电势降低的方向。
E Een 写成矢量形式
E
第一章 真空中静电场小结
一、理论体系:
出发点
:叠 库加 仑原 定理 律
高斯定理 环路定理
电场为有源场 电场是有势场
二、内容:
1、一个定律 : 2、两个定理 :
F
q1q2
4 0
r r3
E
ds
1
dv
s
0 v
l E dl 0
上页 下页 返回 退出
则 dn dl cos
dU dU cos
dl dn
2
P1
en P2
P3
U U+dU
上页 下页 返回 退出
定义电势梯度
1.6 电场强度与电势的微分关系
V E n
V E en n
V
V+dV
E与 V 的关系
V E 大小: n 方向:沿V 减小方向
V 大小:
V n
dln
e n
Q
q
dl
P
方向:沿V增大方向
E
V E e n gradV V n
E V
V V lim n n 0 n
U E
两方向微商的关系:
V V cos l n
P n l
Q R
U U
V V V V V lim lim lim cos cos l l 0 l n0 n / cos n0 n n
V Q 4 0 R 2 x 2
小
计算电势的方法
1、点电荷场的电势及叠加原理
结
计算场强的方法
1、点电荷场的场强及叠加原理
V
i
4 0 ri (分立)
qi
E
i
V
dq 4 0 r
Q
(连续)
E
2、可有
r dq (连续) Q 4 r 3 0
qi r 4 0 ri3 (分立)
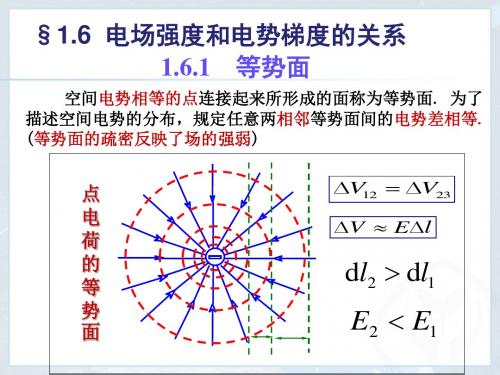
§1.6 电场强度和电势梯度的关系 1.6.1 等势面
空间电势相等的点连接起来所形成的面称为等势面. 为了 描述空间电势的分布,规定任意两相邻等势面间的电势差相等. (等势面的疏密反映了场的强弱)
点 电 荷 的 等 势 面
V12 V23
V El
dl2 dl1
E2 E1
两平行带电平板的电场线和等势面
三.同一问题中能否选取不同的电势零点 例:均匀外电场 E0 中置入一点电荷 q 求空间任意一点的电势 .p 解:把坐标原点选取在点电荷所
电势梯度和电场强度的关系

电势梯度和电场强度的关系电势梯度与电场强度是电学中两个重要的概念,它们之间存在着密切的联系和相互依赖关系。
本文将从电势梯度和电场强度的定义、计算方法以及它们之间的关系等方面展开阐述。
我们来了解一下电势梯度和电场强度的定义。
电势梯度是指电势在空间中变化的快慢程度,表示为电势的变化率。
电场强度是指单位正电荷所受的力的大小和方向,表示为电场力的大小。
电势梯度的计算方法是通过对电势函数沿着某一方向求偏导数,即电势梯度等于电势函数在某一方向上的偏导数。
电场强度的计算方法是通过库仑定律得到的,即电场强度等于单位正电荷所受力的大小。
接下来,我们来探讨电势梯度和电场强度之间的关系。
根据定义可知,电场强度是电势梯度的负梯度,即电场强度与电势梯度具有相反的方向。
这是因为电势梯度表示电势的变化率,而电场强度表示单位正电荷所受的力的大小和方向,二者之间存在着直接的关系。
进一步地,我们可以通过电势梯度和电场强度的性质来理解它们之间的关系。
首先,电势梯度的方向指向电势变化率最快的方向,而电场强度的方向指向力的作用方向。
由于力的方向是电势下降最快的方向,所以电势梯度的方向与电场强度的方向相反。
电势梯度的大小与电场强度的大小成正比。
根据电势梯度的定义可知,电势梯度的大小等于电势函数在某一方向上的偏导数。
而根据电场强度的定义可知,电场强度的大小等于单位正电荷所受力的大小。
由于电场力与电势梯度具有相反的方向,所以电场强度的大小与电势梯度的大小成正比。
我们可以通过具体的例子来进一步说明电势梯度和电场强度之间的关系。
假设有一个点电荷位于原点,我们要计算该点电荷在距离原点某一点的电场强度。
首先,我们可以通过库仑定律计算出该点电荷在距离原点某一点的电势。
然后,我们可以通过计算电势在该点的梯度得到该点电荷在该点的电场强度。
根据电势梯度和电场强度的关系可知,电场强度的大小与电势梯度的大小成正比,方向与电势梯度的方向相反。
电势梯度和电场强度之间存在着密切的关系。
高二物理竞赛课件电场强度与电势梯度

荷系。因此任意点电荷系的电场力所做的功,等于
组成此点电荷系的各点电荷的电场力所做功的代数
和:
E Ei
i
W
q0
E dl
l
i
q0 l Ei dl
结论:静电场力做功与路径无关,与始末位置有关.
10.4.2 静电场的环路定理
q0 E dl q0 E dl
ABC
ADC
q0( E dl E dl ) 0
r
dl
rdl
cos
rdr
B
rB
dl
dr
E
r
dW
q0 E
dl
qq0
4π 0r3
r
dl
q rA q0
A
W qq0
4 π0
rB dr r rA 2
qq0 ( 1 1 )
4 π0 rA rB
结果: A 仅与 q0 的始末
位置有关,与路径无关.
任意带电体都可看成由许多点电荷组成的点电
电场强度与电势梯度
电场强度与电势梯度 等势面 电场中电势相等的点所构成的面,叫做等势面。
相邻两个等势面间电势差等于常量。
点电荷的电场线与等势面
一对等量异号点电荷的电 场线和等势面
-
-
+
两平行带电平板的电场线和等势面
++++++++++++
等势面的性质: (1)等势面与电力线处处垂直,电力线的方向是 电势降落的方向。 (2)等势面的疏密反映了场强的强弱。等势面较 密的地方场强大,较疏的地方场强小。
i
j
k
x y z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
qE dl q[U (U dU)] qdU 即: E dl dU
ˆ) (dxi ˆ) ˆ Ey ˆ ˆ dyˆ E dl ( Exi j Ez k j dzk
Ex dx Ey dy Ez dz
又因电势是空间坐标的函数U=U(x,y,z),因此,对 电势的微分可表示为:
课堂练习:利用场强与电势梯度的关系,计 算均匀带电圆盘中心轴线上的场强。
dr
R
r
o
x
P
x
Up
R
2rdr
4 0
0
2 2 [ R x x] 2 2 2 0 r x
U Ex x
U Ey y
U Ez z
U x Ex [1 ] 2 2 x 2 0 R x
例、在x-y平面上,各点的电势满足下 面的式子:
ax b U 2 2 2 2 x y (x y )
式中的x、y为任一点的坐标,a、b为常 数。求任一点电场强度的Ex和Ey分量。
U Ex x
U Ey y
2
U Ez z
U a 2ax bx Ex 2 2 2 2 2 2 2 3/ 2 x x y (x y ) (x y )
U ˆ U ˆ U ˆ 在数学上,我们将 ( i j k) x y z
定义为电势U的梯度,用gradU或U表示,即:
U ˆ U ˆ U ˆ gradU U i j k x y z
“梯度”是指一个物理量的空间变化率,电 势梯度当然就是指电势的空间变化率。注意: 电势梯度是矢量,其大小等于电势变化最快 的方向上的电势变化率,方向与等势面正交 且指向电势升高的方向。
例.利用场强与电势梯度的关系, 计算均匀带 电细圆环轴线上一点的场强。
dq
y
r
R
x
p x z
Up (q ຫໍສະໝຸດ 2R)dl 4 0 R 2 x 2
q 4 0 R 2 x 2
U Ex x
U Ey y
U Ez z
U qx Ex 2 2 3/ 2 x 4 0 ( R x )
将上述两式代入: E dl dU
U U U dU dx dy dz x y z
可得:
U U U Ex dx E y dy Ez dz ( dx dy dz) x y z
由于dx、dy、dz为任意,故两边它们的系数应分 别相等,即:
9-5 电场强度与电势梯度的关系 一、 等势面
等势面 : 电场中电势相等的点所构成的曲面。
下面我们来看几种典型的等势面。
正点电荷的等势面
+
负点电荷的等势面
-
电偶极子的等势面
+
等势面的性质
(1)等势面与电场线处处正交, 电场线指向电势降落
的方向,即沿着场强的方向电势降落。因此,在等势面
上移动电荷时,电场力不作功,电荷的电势能不变。 (2)规定:电场中任意两相邻等势面间的电势差必须 相等,由于场强大的地方产生相同的电势差所需的距离
U Ex x
U Ey y
U Ez z
这样,场强E就可表示为:
U ˆ U ˆ U ˆ E ( i j k) x y z
U dU
U
a
dn
n
dl
b
E
从图中可以看出,在两等势面之间,由a点出发沿不同的方向 电势变化率显然不同。其中沿着与等势面正交的方向 n ,电势 的变化率最大,即沿着此方向电势变化得最快。我们通常就将 沿着与等势面正交且指向电势升高的方向的电势变化率定义为 电势梯度,即沿着电势变化最快的方向的电势变化率。
U 2axy by Ey 2 2 2 2 2 3/ 2 y ( x y ) ( x y )
小,而场强小的地方产生相同的电势差所需的距离大,
这样就会形成场强大的地方等势面密集,而场强小的地 方等势面稀疏。
二、场强与电势梯度的关系
如图所示,在电场取两个靠的 很近的等势面,电势分别为U 和U+dU,场强方向和等势面的 法线方向如图所示。
U dU
U
n
dl
E l qa
b
q
E
现在我们将一正电荷q从 a到 b,由于两等势面靠的很 近,因此,可近似认为从a到b的过程中,场强不变, 这样电场力所作的功:
这样就有:
U ˆ U ˆ U ˆ E ( i j k ) gradU U x y z
即电场任意一点的场强等于该点电势梯度的负值。
总结:
(1)电势梯度是一个矢量,它的大小为电势 沿等势面法线方向的变化率,它的方向沿等 势面法线方向且指向电势增大的方向。
(2)电场中任意一点的电场强度等于该点 电势梯度的负值。
