电场强度与梯度
电场强度和梯度

r 化率的负值。
e r 电场强度的单位也用V/m。 V e 2 电势梯度
显然电势沿不同方向 V V
的单位长度增量是不同的,
rt
dl A
r
r dln
n
现讨论两个特殊方向上的
E低高
情况:切向和法向。
电电 势势
⑴
沿切向
Et
dV dlt
Q dV 0 Et 0
⑵ 沿法向
En
dV dln
V
Q
dV dln
电子在分子电偶极子电场中所受的力为
F
eE
2e
4 0
p x3
2 1.60 1019 6.2 1030 1.431010 N
4 8.851012 (51010 )3
a
F m
1.431010 9.111031
m s2
1.57 1020 m s2
vat 1.57 1020 1014 m s-1 1.57 106 m s-1
r E
(V
r i
V
r j
V
r k ) gradV
x y z
电场强度与电势梯度关系的物理意义
① 空间某点电场强度的大小取决于该点领域内
电势V的空间变化率。
② 电场强度的方向恒指向电势降落的方向。
讨论
⑴ 电场弱的地方电势低;电场强的地方电势高吗?
r
⑵ V=0地方, E 0 吗?
r
r
⑶ E 相等的地方,V一定相等吗?等势面上 E一定
(4x2 (x2
y )2 1/ 2 y2 )2
A点在电偶极矩的延长线上时:
2p 1 y0 E
4 0 x3
A点在电偶极矩的中垂线上时:
电学中的电场分布

电学中的电场分布在电学领域中,电场是一个重要的概念,它描述了电荷周围的电力场分布。
本文将探讨电学中的电场分布及其相关性质。
一、电场的定义和基本性质电场是指电荷所产生的影响其他电荷的空间区域。
根据库仑定律,电荷之间的相互作用力与它们之间的电荷量成正比,与它们之间的距离的平方成反比。
电场的表达式可以用公式E=KQ/r^2表示,其中E表示电场强度,K为库仑常数,Q为电荷量,r为与电荷之间的距离。
1.1 电场强度的方向与性质电场强度的方向由正电荷朝向负电荷,且它的性质具有以下特点:首先,电场强度是一个矢量量,并具有大小和方向。
电荷为正时,电场强度指向外部;电荷为负时,电场强度指向内部。
其次,电场强度在空间中的大小与电荷之间的距离成反比。
电荷和距离之间的关系遵循反比例关系,即电荷增大,电场的强度减小;同样,距离增大,电场强度减小。
最后,电场强度受到电荷的影响。
当有多个电荷时,它们对一个点的电场强度的效果将叠加,取决于它们的位置和电荷量。
1.2 电场线的描述和分布为了更直观地表示电场分布情况,人们通常使用电场线进行描述。
电场线是沿着电场方向的曲线,在空间中将电场的分布进行了可视化。
电场线有一系列重要的特性:首先,电场线趋向于从正电荷流向负电荷。
这表示电荷之间会相互吸引,而不是相互推开。
其次,电场线不会相交。
如果相交,将会形成多个方向冲突的电场强度,这在物理上无法解释。
最后,电场线的密度表示电场强度的大小。
密集的电场线表示电场强度较大,而稀疏的电场线表示电场强度较小。
二、几种常见电场分布的模型根据不同的电荷分布情况,可以得到一些常见的电场分布模型。
下面将介绍一些常见的电场分布情况:2.1 点电荷电场分布点电荷是一种理想化的电场分布模型,即电荷集中在一个点上。
该模型下,电场强度的表达式为E=KQ/r^2。
点电荷的电场在空间中是球对称分布的,电场线以点电荷为中心向外辐射。
2.2 均匀带电平面电场分布均匀带电平面是一种常见的电场分布模型,例如平行板电容器的电场分布。
8.5电场强度与电势梯度的关系

E
ds
等势面——规定、性质、梯度
gradU
U n
n
三、 q、E、U 三者关系网
1、 q E
E
1
4 0
dq r3
r
sE
ds
1
0
vdv
2、 q U
U
1
4 0
dq r
U LE dl
3 E U
U LE dl
势面2,电场力做功
dA qE dl
qEdl cos
en
1
2
P1
en P2
P3
qEdn
V V+dV
上页 下页 返回 退出
电场力做功等于电势能的减少量 dA q dU
E dU dn
场强也与等势面垂直,但指向电势降低的方向。
E Een 写成矢量形式
E
第一章 真空中静电场小结
一、理论体系:
出发点
:叠 库加 仑原 定理 律
高斯定理 环路定理
电场为有源场 电场是有势场
二、内容:
1、一个定律 : 2、两个定理 :
F
q1q2
4 0
r r3
E
ds
1
dv
s
0 v
l E dl 0
上页 下页 返回 退出
则 dn dl cos
dU dU cos
dl dn
2
P1
en P2
P3
U U+dU
上页 下页 返回 退出
定义电势梯度
高二物理竞赛课件:电场强度与电势梯度

40a(a l )
Q
Q a l
(2)球在 x 处电势 V 4 0 x
ln 40 a
2
电场强度和电势梯度 d V:两等位面电势之差。
E
dl
nˆ
d l:两等位面间在P1点处的最短距离。 P1
P2
(等位面间在P1点处的法向距离)
nˆ :P1点处法线方向上的单位矢量,
V V dV
指向电势升高的方向。
r
dr
2 0
4 0
(
R2
r2
)
0
外电场对电偶极子的力矩和取向作用
解:电偶极子受 力偶的作用
F qE F qE
合力: F F F
电矩
0
p ql
l
F
q
q
F E
故偶极子不平动。 合力矩:
M 的方向
M
M
2F
P
l 2
sin qEl
E
M使 p
sin
转向
E
pE
sin
2
电荷在外电场中的静电势能 任何电荷在静电场中都具有势能,叫的静电势能。
E R2
若令V= 0 则
rR V
R2
E dl
r
2 0 r
r
R2 dr 2 0 r
ln 电势发散,无意义!
20 r
R
只能取有限远处电势为零。
r
若令柱面 处 VR=0,则
r > R:V R R2 dr R2 ln R 0
r 20r
20 r
r
r < R:V
R r
W q0 (Vb Va )
2
例、长为L 的均匀带电导线,电荷线密度为 。
1.6 电场强度与电势的微分关系
V E n
V E en n
V
V+dV
E与 V 的关系
V E 大小: n 方向:沿V 减小方向
V 大小:
V n
dln
e n
Q
q
dl
P
方向:沿V增大方向
E
V E e n gradV V n
E V
V V lim n n 0 n
U E
两方向微商的关系:
V V cos l n
P n l
Q R
U U
V V V V V lim lim lim cos cos l l 0 l n0 n / cos n0 n n
V Q 4 0 R 2 x 2
小
计算电势的方法
1、点电荷场的电势及叠加原理
结
计算场强的方法
1、点电荷场的场强及叠加原理
V
i
4 0 ri (分立)
qi
E
i
V
dq 4 0 r
Q
(连续)
E
2、可有
r dq (连续) Q 4 r 3 0
qi r 4 0 ri3 (分立)
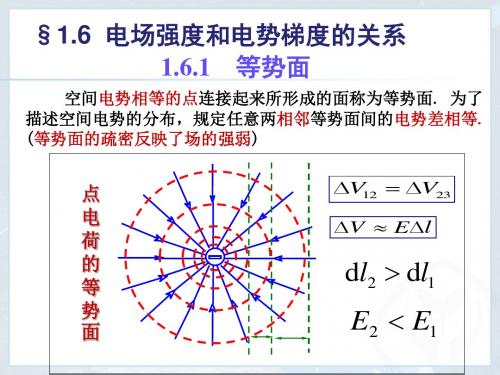
§1.6 电场强度和电势梯度的关系 1.6.1 等势面
空间电势相等的点连接起来所形成的面称为等势面. 为了 描述空间电势的分布,规定任意两相邻等势面间的电势差相等. (等势面的疏密反映了场的强弱)
点 电 荷 的 等 势 面
V12 V23
V El
dl2 dl1
E2 E1
两平行带电平板的电场线和等势面
三.同一问题中能否选取不同的电势零点 例:均匀外电场 E0 中置入一点电荷 q 求空间任意一点的电势 .p 解:把坐标原点选取在点电荷所
求电场强度的几种特殊方法解读

求电场强度的几种特殊方法解读一、高斯定律:高斯定律是求解电场强度的一种常用方法。
该定律表明,电场强度的大小与电场线通过一个封闭曲面的总电通量成正比,而与曲面的形状和大小无关。
具体而言,高斯定律可以表示为:∮E·dA=Q/ε₀其中,∮E·dA表示电场强度E与曲面元dA的点乘积之和,Q表示曲面内的总电量,ε₀是真空中的电介质常量。
通过高斯定律,可以在适当选择曲面和利用对称性的条件下,简化求解电场强度的问题。
例如,对于具有球对称性的电荷分布,可以选择一个球面作为高斯面,从而简化计算。
二、电势:电场强度可以通过电势概念来解释和计算。
电势是一种物理量,表示单位正电荷在电场中所具有的势能。
对于电场中的一点,电势的大小与从该点出发的单位正电荷移动到无穷远的位置所需做的功成反比。
具体而言,电场强度E与电势V之间存在以下关系:E=-∇V其中,∇表示向量算符的梯度运算。
即,电场强度是电势的负梯度。
通过求解电势,可以间接得到电场强度。
一般情况下,电势可以通过求解电场线积分或者通过泊松方程来计算。
三、能量方法:电场强度还可以通过能量方法来解读。
根据电场的定义,电场对单位电荷所作的功等于单位电荷从一个位置移动到另一个位置时,电场的势能变化。
具体而言,单位电荷在电场中的势能变化可以表示为:ΔU = -∫E·dr其中,ΔU表示势能的变化,E表示电场强度,dr表示路径的微元。
通过能量方法,可以求解电场强度在空间中的分布规律。
例如,可以通过比较不同路径上的势能变化来确定电场强度的大小和方向。
四、李纳准则:李纳准则是一种用于确定电场强度分布的方法,特别适用于导体表面的电势分布问题。
该准则认为,在导体表面上,电场强度的切线方向与导体表面上的等势线相切。
利用李纳准则,可以确定导体表面的电场强度分布,进而求解导体内部的电场强度。
总结:以上是几种特殊方法来解读电场强度的常用方法,包括高斯定律、电势、能量方法和李纳准则。
电场强度知识点总结
电场强度知识点总结电场是物理学中的一个重要概念,它描述了电荷之间相互作用的力。
而电场强度则是描述这种相互作用力的大小和方向的量。
本篇文章将以电场强度为主题,结合相关理论和实例,总结电场强度的知识点。
一、电场强度的概念电场强度(Electric Field Intensity)表示在某一点单位正电荷所受到的力的大小和方向。
它是一个矢量量,通常用E表示。
电场强度的方向指向力所作用的方向,大小与力的大小成正比。
二、电场强度的计算公式电场强度的计算公式为E=F/q,其中F表示受力的大小,q表示单位正电荷的电荷量。
该公式表明,电场强度和受力的比值是恒定的,即电场强度与单位电荷受到的力成正比。
三、电场强度的单位电场强度的单位通常有N/C或V/m,其中N代表牛顿,C代表库仑,V代表伏特,m代表米。
这些单位可以互相转换,具体转换方式可以根据公式进行计算。
四、电场强度的叠加原理当有多个电荷同时存在时,每个电荷产生的电场强度可以叠加。
根据叠加原理,可以通过将每个电荷产生的电场强度向量相加,得到整个系统的总电场强度。
五、均匀带点直线上的电场强度考虑一个长度为L的均匀带电直线,电荷线密度为λ,那么该直线在距离直线上一点的电场强度可由公式E=λ/2πε0r计算得出,其中r表示距离直线的垂直距离,ε0为真空中的介电常数。
六、均匀带点圆环上的电场强度考虑一个半径为R的均匀带电圆环,电荷线密度为λ,那么该圆环在距离圆环垂直中轴线的一点的电场强度可由公式E=λR/4πε0(r²+R²)^(3/2)计算得出,其中r表示距离圆环中心的距离。
七、电偶极子产生的电场强度电偶极子是由两个电荷大小相等但符号相反的点电荷组成。
电偶极子在与两点电荷连线垂直的轴线上的电场强度可由公式E=kp/r³计算得出,其中p为电偶极矩的大小,k为库仑常数,r为距离两点电荷连线的垂直距离。
八、电场强度与电势的关系电势是电场能量在单位电荷处的分布情况。
9-5 电场强度与电势梯度的关系
qE dl q[U (U dU)] qdU 即: E dl dU
ˆ) (dxi ˆ) ˆ Ey ˆ ˆ dyˆ E dl ( Exi j Ez k j dzk
Ex dx Ey dy Ez dz
又因电势是空间坐标的函数U=U(x,y,z),因此,对 电势的微分可表示为:
课堂练习:利用场强与电势梯度的关系,计 算均匀带电圆盘中心轴线上的场强。
dr
R
r
o
x
P
x
Up
R
2rdr
4 0
0
2 2 [ R x x] 2 2 2 0 r x
U Ex x
U Ey y
U Ez z
U x Ex [1 ] 2 2 x 2 0 R x
例、在x-y平面上,各点的电势满足下 面的式子:
ax b U 2 2 2 2 x y (x y )
式中的x、y为任一点的坐标,a、b为常 数。求任一点电场强度的Ex和Ey分量。
U Ex x
U Ey y
2
U Ez z
U a 2ax bx Ex 2 2 2 2 2 2 2 3/ 2 x x y (x y ) (x y )
U ˆ U ˆ U ˆ 在数学上,我们将 ( i j k) x y z
定义为电势U的梯度,用gradU或U表示,即:
U ˆ U ˆ U ˆ gradU U i j k x y z
“梯度”是指一个物理量的空间变化率,电 势梯度当然就是指电势的空间变化率。注意: 电势梯度是矢量,其大小等于电势变化最快 的方向上的电势变化率,方向与等势面正交 且指向电势升高的方向。
5-5 电场强度与电势梯度的关系
2
2
P 2 2 4 x y 4 0 ( x 2 y 2 ) 2
P(0,y) y E -q
-L/2
讨论:
1. 在X轴上,y=0,则
Ex P 20 x 3 P 40 y
Ey 0
3
2. 在Y轴上,x=0,则
Ex
+q
O
L/2
P(x,0)
Ey 0
E
x
与用叠加原理得到的结果一致。
1 1
E
en
P2
P1
P3
V
V+dV
例1 试由电偶极子的电势分布求其的电场强度。 解: 在直角坐标系中先写出电势的表达式,
1 q 1 q q r r V 40 r 40 r 40 r r
L cos P cos 2 2 40 r 4 0 r Px 40 ( x 2 y 2 ) 3 / 2 q
P3
V
则 dn dl cos
V+dV
定义电势梯度
dV grad V en dn
单位:V/m
其量值为该点电势增加率的最大值。 方向与等势面垂直,并指向电势升高的方向。 电势梯度与电场强度的关系 2
en
电荷q从等势面1移动到等 势面2,电场力做功
1
en P1
dA qE dl qE dl cos qE den
例2 将半径为R2 的圆盘在盘心处挖去半径为R1的小孔,并 使盘均匀带电.试通过用电势梯度求电场强度的方法,计算这 个中空带电圆盘轴线上任一点P处的电场强度.
解:设圆盘上的电荷 面密度为 轴线上任一点p 到中空圆盘的 距离为x,在圆 盘上取半径为r 宽为dr的圆环 ,环上所带电 z 荷为
两个电场强度公式的比较
两个电场强度公式的比较在物理学中,电场强度是描述电场属性的量,它表示一个电荷对周围空间内其他电荷施加的力。
电场强度可通过不同的公式来计算,其中最常用的是库仑定律和电场中位移法(也称为电势梯度)。
库仑定律是描述两个点电荷之间电场力的公式,它由法国物理学家库仑在18世纪末提出。
库仑定律表达式为:F=k*(q1*q2)/r²其中,F表示电场力的大小,q1和q2是两个电荷的大小,r是两个电荷之间的距离,k是库仑常数。
通过库仑定律,我们可以计算两个点电荷之间的电场力大小,并且可以根据所加电场力的方向来确定电场强度的方向。
然而,库仑定律只适用于点电荷之间的电场力计算,对于电荷连续分布情况下电场强度的计算并不适用。
在这种情况下,我们可以使用电场中位移法来计算电场强度。
电场中位移法是一种基于电势概念的计算电场强度的方法。
电场中位移法的基本思想是利用电势梯度来计算电场强度。
电场强度的计算公式为:E=-∇V其中,E表示电场强度,V表示电势,∇表示梯度算子。
通过梯度算子的运算,我们可以得到电势梯度,从而计算电场强度的大小和方向。
电场中位移法适用于各种电荷分布情况,包括点电荷、连续电荷分布和电荷面上。
与库仑定律相比,电场中位移法更加灵活和普适。
它可以应用于更复杂的电荷分布情况,包括连续电荷分布和电荷面上。
另外,电场中位移法还可以与电势概念结合,使得问题的求解更加简便。
通过计算电势梯度,我们可以直接获得电场强度的数值和方向,而无需考虑具体的电场力计算过程。
然而,电场中位移法也存在一些局限性。
由于电势的概念是建立在电场强度上的,而电场强度又是由电势梯度计算得到的,因此在具体问题中,我们需要先计算出电势,然后再计算电势梯度,最终得到电场强度。
这个过程相对复杂,不如直接使用库仑定律进行计算直观和简单。
另外,电场中位移法的数学运算也相对复杂,可能需要较高水平的数学知识才能理解和应用。
综合来看,库仑定律和电场中位移法是计算电场强度的常用方法,它们各有优劣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p Ep = −eV = − 4π ε 0 r 2
e = 1.60 ×10−19 C
e
o
H H
r p A
1.60 ×10−19 6.2 ×10−30 = 3.57 ×10−20 J Ep = 4π × 8.85 ×10−12 (5 ×10−10 ) 2
与气体分子热运动能量比较
Ep 3.57 ×10−20 = K = 2.59 ×103 K T= k 1.38 × 10−23
y q 解 QV = 4πε 0 ( x 2 + R 2 )1 2 r R q E = −∇V o ∂V ∴ E = Ex = − z ∂x ∂ 1 q =− 2 2 12 ∂x 4πε 0 ( x + R )
r
θ
P
x
x
qx = 4πε 0 ( x 2 + R 2 )3 2
1
的电势和电场强度。 例2 求电偶极子电场中任意一点V的电势和电场强度。 解 V = +
Q r0 << r ∴ r− − r+ ≈ r0 cos θ
q 4π ε 0 r+ 1 q V− = − 4π ε 0 r− V = V+ + V− q r− − r+ = 4π ε 0 r+ r− 1
y
r−
θ
A
r+ r
−q o r +q x
θ=
π
2
r0
V =0
写成: 用A点的坐标x,y写成:
x V= 4π ε 0 ( x 2 + y 2 )3 / 2
p
y
r−
θ
A
∂V p y2 − 2x2 Ex = − =− ∂x 4π ε 0 ( x 2 + y 2 )5 / 2
r+ r
∂V p 3xy Ey = − = ∂y 4π ε 0 ( x 2 + y 2 )5 / 2
b
r r q0 ≠ 0 E ≠ 0 dl ≠ 0
r r ∴ E ⊥dl
等势面密集的地方电场强度大, ② 等势面密集的地方电场强度大,稀疏的地方电 场强度小。 场强度小。 2 几种电荷分布的电场线 与等势面 ⑴ 点电荷的电场线与等势面
+q
⑵ 一对等量异号点电荷的电场线和等势面
−q
+q
⑶ 两平行带电平板的电场线和等势面
r e
r e
高 电 势
沿
向
dV Et = − dlt
Q dV = 0
∴ Et = 0
dV ⑵ 沿法向 En = − V rt dln n dV dl A Q < 0 时E > 0 V +∆V θ r dln dln r r ∴ E 的方向总是由高电 高 低 r E 电 电 势指向低电势,即 E 与 r r 势 r 向 势 dV e En = − en d ln n r dV e 电势 电的电势 , n d ln r dV e grad V = d ln n
电子在分子电偶极子电场中所受的力为
p F = eE = 4π ε 0 x 3 2 ×1.60 ×10−19 6.2 ×10−30 = = 1.43 ×10−10 N 4π × 8.85 ×10−12 (5 ×10−10 )3 2e
F 1.43 × 10−10 a= = m ⋅ s −2 = 1.57 × 1020 m ⋅ s −2 −31 m 9.11× 10
△l→0时有 →0时有
r B ∆l r
A
V
∆V dV El = − lim =− ∆l →0 ∆l dl
电场中某一点的电场强度沿某一方向的分量, 电场中某一点的电场强度沿某一方向的分量, 等于这一点的电势沿该方向单位长度上电势变 化率的负值。 化率的负值。 rt 电场强度的单位也用V/m。 V dl A n 2 电势梯度 V +∆V θ r 显然电势沿不同方向 dln r 不同的, 的单位长度 量 不同的, 低 E 电 方向上的 势 向。 向 向。
r+ r
−q o r +q x
r0
r− r+ ≈ r
2
q r− − r+ q r0 cos θ ≈ V= 4π ε 0 r 2 4π ε 0 r+ r− 1 p cos θ = 4π ε 0 r 2
y
r−
θ
A
p cosθ 即V≈ 4πε0 r2 1
p θ =0 V ≈ 4π ε 0 r 2 1 p θ =π V ≈ − 4π ε 0 r 2 1
⑵ 直角坐标系中
∂V ∂V ∂V Ex = − Ey = − Ez = − ∂x ∂y ∂z r ∂V r ∂V r ∂V r E=− ( i+ j+ k ) = −gradV ∂x ∂y ∂z
ቤተ መጻሕፍቲ ባይዱ
电场强度与电势梯度关系的物理意义 ① 空间某点电场强度的大小取决于该点领域内 电势V的空间变化率。 电势V的空间变化率。 电场强度的方向恒指向电势降落的方向。 ② 电场强度的方向恒指向电势降落的方向。
r−
r
θ
r+
x=0
−q o r +q x
r0
如图所示, 例3 如图所示,水分子可以近似看作为电偶极矩 p=6.2×10-30C·m 的电偶极子。有一电子放在电 m 的电偶极子。 偶极矩的延长线、距电偶极矩中心O 偶极矩的延长线、距电偶极矩中心O为5×10-10m 的点A 的点A上。求电子的势能和作用在电子上的力。 求电子的势能和作用在电子上的力。 解 电子在A点的电势能为 电子在A
+ + + + + + + + + + + + + + + +
二 电场强度与电势梯度 1 电势沿任意方向的增加率
r r El θ U AB = − VB − VA) E ⋅ ∆l ( = r = E ∆l cos θ E Q E cos θ = El ∆V = VB − VA V +∆V ∆V ∴ − ∆V = El ∆l 即 El = − ∆l
r e
r e
3 电场强度与电势梯度的关系
r r dV r r r r Q E = En + Et Et = 0 ∴ E = En − en dln
可见:电场强度大小等于电势梯度的负值, 可见:电场强度大小等于电势梯度的负值, 方向由高电势指向第电势处。 方向由高电势指向第电势处。
dV 电场强度沿任意方向的分量: ⑴ 电场强度沿任意方向的分量:El = − r r dl El = E cos( E , l ) = E cos θ = −( gradV )l = − dV cos θ dln Qdl > dln ∴ En > El
8-8 一
电场强度与电势梯度
等势面(电势图示法) 等势面(电势图示法) 电场中由电势相等的点组成的面叫等势面。 电场中由电势相等的点组成的面叫等势面。 为了描述空间电势的分布, 为了描述空间电势的分布,规定任意两相邻等 势面间的电势差相等。 则等势面越密的地方, 势面间的电势差相等。 则等势面越密的地方, 电场强度越大。 电场强度越大。
−q o r +q x
r0
p (4 x 2 + y 2 )1/ 2 ∴ E = Ex2 + E y2 = 4π ε 0 ( x 2 + y 2 ) 2
A点在电偶极矩的延长线上时: 点在电偶极矩的延长线上时:
y
A
y=0
2p 1 E= 4π ε 0 x 3 1 E= 4π ε 0 y 3 p
A点在电偶极矩的中垂线上时: 点在电偶极矩的中垂线上时:
讨论 电场弱的地方电势低;电场强的地方电势高吗? ⑴ 电场弱的地方电势低;电场强的地方电势高吗?
r r 相等的地方, 一定相等吗? ⑶ E 相等的地方,V一定相等吗?等势面上 E一定
相等吗? 相等吗?
r =0地方 地方, ⑵ V=0地方, E = 0 吗?
求一均匀带电细圆环轴线上任一点的电场强度。 例1 求一均匀带电细圆环轴线上任一点的电场强度。
1 等势面基本性质 在静电场中,电场强度与等势面处出正交, ① 在静电场中,电场强度与等势面处出正交,且 指向电势降落的方向。 指向电势降落的方向。
静电场中电荷沿等势面移动时, 静电场中电荷沿等势面移动时,电场力作功
r r W ab = q 0 (Va −Vb ) = ∫a q 0 E ⋅d l = 0
v = at = 1.57 ×1020 ×10−14 m ⋅ s-1 = 1.57 × 106 m ⋅ s-1
