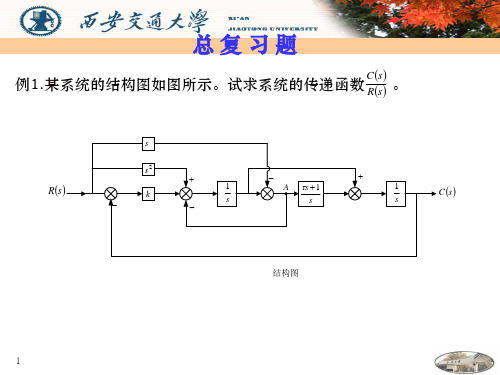
例1某系统的结构图如图所示试求系统的传递函数
例1某系统的结构图如图所示试求系统的传递函数
有
24
3s 2 12s 8 0
s1 3.155 不在根轨迹上,舍去。 s2 0.845 是分离点, s1,2 2 1.155,
分离角为 90 。 根据幅值条件可求出分离点处的增益
k2 s2 s2 2 s2 4 3.1
④ 根轨迹与虚轴的交点 特征方程为 劳斯表为
2. 解: 因为
k1k 2 Y s 2 Rs s as k 2
k1k 2 k1k 2 1 Y s 2 Rs 2 s as k 2 s as k 2 s
所以
k1k 2 1 y lim yt lim s 2 k1 2 t s 0 s as k 2 s
于是,渐近线与实轴交点为 2, 0 。 ,
180 2k 1 a 3
当k 0 时 当 k 1时
a 180
a 60
Qs ss 2s 4 代入方程 ③ 求分离点:由开环传递函数知 Ps 1 ,
Ps Qs Ps Qs 0
A
s 1
s
1 s
C s
结构图
1
1.解:
Rs
s
s2
k
1 s
A
s 1
s
1 s
C s
结构图
s
s2
Rs
k
B
1 s
s 1
s
A
1 s
C s
2
(a)
s
s2
Rs
k
B
第二章传递函数案例

解:
系统的结构图为
3. 结构图化简 (结构图的等效变换)
化简目的:
将结构图化简为一个方块,即传递函数。
化简原则:
保证化简前后的代数等价关系不变
等效变换法则
环节串联
环节并联
反馈回路化简
负反馈
正反馈
相加点移动
分支点移动
前移
后移
信号的分支点与相加点不可以互换
例:化简结构图,求取传递函数
阶跃响应曲线
七、比例积分环节 (P-I)
定义:环节输出正比于输入信号和它对时间的积分。
微分方程
1 c( t ) K r t Ti
0 r t dt
t
传递函数
1 G( s) K 1 T s i
阶跃响应曲线
八 、延迟环节
四、惯性环节
定义:环节的输出不能立即复现输入,而是经过 一定时间后才能复现输入的变化。
微分方程 传递函数
dc( t ) T c( t ) Kr ( t ) dt
K G( s) Ts 1
运算放大器
1 1 Rf Rf Cf s Cf s U 2 ( s) U1 ( s ) R1 Rf R1 K Rf Cf s 1 Ts 1
dr ( t ) c( t ) K r ( t ) TD d t
微分方程
传递函数
G( s)
c s r s
K 1 TD s
在放大器上加以 RC 网 络 反 馈 , 当 增益K足够大时
U 2 ( s) U1 ( s ) K 1 1 K RCs 1 K RCs 1 RCs 1 K RCs 1 RC 1 s 1 K K RCs 1 s1
中国计量大学801自动控制原理1-2015--2019年考研初试真题
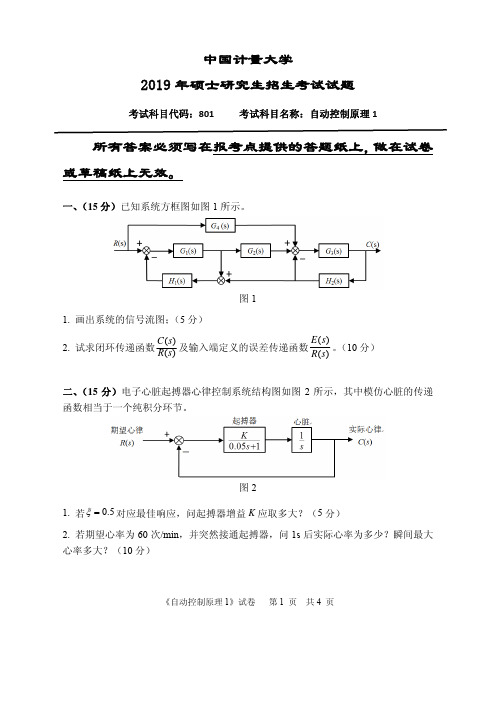
《自动控制原理1》试卷 第1 页 共4 页中国计量大学2019年硕士研究生招生考试试题考试科目代码:801 考试科目名称:自动控制原理1所有答案必须写在报考点提供的答题纸上,做在试卷或草稿纸上无效。
一、(15分)已知系统方框图如图1所示。
图11. 画出系统的信号流图;(5分)2. 试求闭环传递函数)()(s R s C 及输入端定义的误差传递函数)()(s R s E 。
(10分)二、(15分)电子心脏起搏器心律控制系统结构图如图2所示,其中模仿心脏的传递函数相当于一个纯积分环节。
图21. 若5.0=ξ对应最佳响应,问起搏器增益K 应取多大?(5分)2. 若期望心率为60次/min ,并突然接通起搏器,问1s 后实际心率为多少?瞬间最大心率多大?(10分)《自动控制原理1》试卷 第2 页 共4 页三、(15分)系统结构图如图3所示,[]()()()e t r t b t =−。
图31. 已知G 1(s )的单位阶跃响应为21e t −−,试求G 1(s );(5分) 2. 利用求出的G 1(s ),当r (t )=10·1(t )时,试求:①系统的稳态输出;②系统的超调量、调节时间和稳态误差。
(10分)四、(15分)已知系统结构图如图4所示:图41. 绘出K *从0→+∞变化时系统的根轨迹;(8分)2. 确定系统处于欠阻尼条件下的K *范围;(4分)3. 确定系统稳定时的最小阻尼比。
(3分)五、(15分)已知系统传递函数为)52)(2()(2+++=s s s K s G ,1. 画出奈奎斯特图;(10分) 2. 当K =52,利用奈奎斯特稳定判据判断其闭环系统的稳定性。
(5分)六、(15分)已知最小相位开环系统的渐近对数幅频特性如图5所示,试求: 1. 系统的开环传递函数;(4分) 2. 截止频率c ω和相角裕量γ;(8分)3. 若使截止频率s rad c /10=ω,其放大倍数应取多少?(3分)《自动控制原理1》试卷 第3 页 共4 页七、(20分)已知采样系统结构如图6所示,其中采样周期s T 4.0=。
自动控制
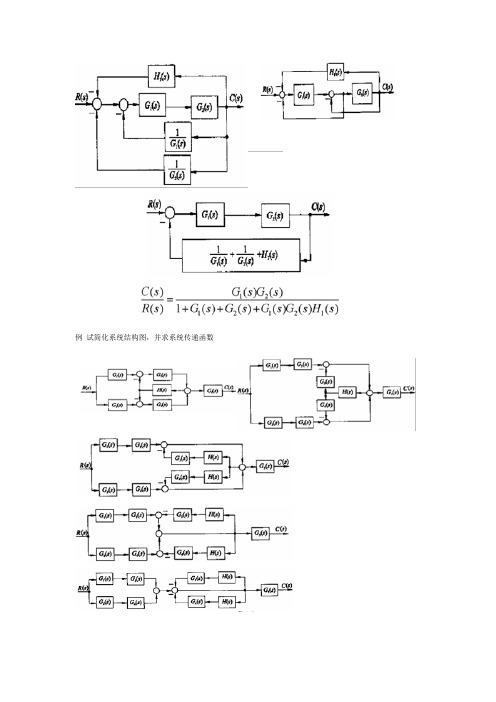
例试简化系统结构图,并求系统传递函数3、信号流图的组成及性质(1)、信号流图的组成:由节点和支路组成的一种信号传递网络。
A、节点:即变量,用小圆圈表示,为流向该节点的信号的代数和。
B、支路:定向线段,标支路增益,相当于乘法器,表因果关系。
(2)、信号流图的性质A、节点标志系统的变量;B、支路相当于乘法器;C、信号沿箭头单向传递;D、系统的信号流图不是惟一的。
下图为典型的信号流图(3)、常用术语源节点(或输入节点):只有输出支路而没有输入支路的节点,如图中的节点X1 。
阱节点(或输出节点):只有输出支路而没有输入支路的节点,如图中的节点X5 。
混合节点:既有输入支路又有输出支路的节点,如图中的节点X2X3X4X5。
前向通路:信号从输入节点到输出节点传递时,每个节点只通过一次的通路。
从源节点X1到阱节点X5,共有两条前向通路:一条是X1->X2->X3->X4->X5,其前向通路总增益P1=abc;另一条是X1->X2->X5,其前向通路总增益P2=d。
回路:起点和终点在同一节点,而且信号通过每一节点不多于一次的闭合通路。
X2->X3->X2,其回路增益L1=ae,X3->X4->X3其回路增益L2=bf;X5->X5 的自回路,其回路增益是g。
不接触回路:回路之间没有公共节点时,这种回路叫做不接触回路。
一对X5->X5 是和X2->X3->X2;另一对是X5->X5和X3->X4->X3。
4、信号流图的绘制(1)由系统微分方程绘制信号流图微分方程先拉氏变换,指定系统变量,按因果关系排列,连成信号流图。
下面结合示例说明:例试绘制RC无源网络的信号流图。
设电容初始电压为U1(0)。
解由基尔霍夫定律,列写微分方程式如下:各微分方程式进行拉氏变换,则有对变量Ui(s),Ui(s)-U0(s),I1(s),I2(s),I(s),U0(s)及U1(0)分别设置七个节点;然后,用相应增益的支路将个节点连接起来,便得到RC无源网络的信号流图。
第一学期《自动控制原理》考卷A卷答案

安徽大学2009 —2010学年第 一学期《 自动控制理论》(A 卷)考试试题参考答案及评分标准一、系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
解:图中有2条前向通路,5个回路,,,,112321211=∆==∆=G P G G P,,,,,22135342132212121H G H G L G L G G L H G G L H G L =-=-=-=-=,)(154321L L L L L ++++-=∆则有∆∆+∆=2211)()(P P s R s C 2213321221123211H G H G G G G H G G H G G G G -+++++=二、(1)闭环传递函数为 21132223211()75007500()234.675007500n n n n s K s K s s s s K s s s K ωζωωω++Φ==++++++ 特征方程为321()34.6750075000D s s s s K =+++= 列劳斯表如下:321s s s s 11134.634.67500750034.67500K K ⨯- 1750075000K 根据劳斯判据得到:1034.6K <<时,系统稳定。
(2)令s=s 1-1代入到原特征方程,得到新的特征方程:321111()(1)34.6(1)7500(1)75000D s s s s K =-+-+-+=整理得:321111()34.67433.875007466.40D s s s s K =+++-=()列劳斯表如下:321s s s s 11131.631.67433.875007466.431.675007466.4K K ⨯---() 17433.875007466.40K - 根据劳斯判据得到:1032.3K <<时,闭环系统的极点全部位于s=-1垂线之左。
(3)31()R s s =, 单位反馈系统的误差传递函数()1()e s s Φ=-Φ故2321(34.6)()34.675007500s s e s s s s K +Φ=+++2332001320111(34.6)()lim ()()lim 34.675007500(34.6)34.61lim 7500375034.675007500s s s s s E s sR s e s s s s s s K s K s s s K →→→+=Φ=++++===+++三、1.绘制根轨迹的典型步骤如下:(1) 开环极点为0,-1,-2,见图,它们是根轨迹各分支上的起点。
机械工程控制基础期末试卷+答案3

机械控制工程基础期末考试试卷课程名称: 机械控制工程基础1;试卷编号:卷;考试时间:120分钟;考试形式:闭卷一、填空( 每小题4分,共20分)得分 评卷人复查人1、某系统传递函数为21s,在输入t t r 3sin 2)( 作用下,输出稳态分量的幅值为 。
2、谐波输入下,系统的 响应称为频率响应。
3、已知某系统开环传递函数的零点都在左半S 平面,其开环频率特性曲线如图1.5所示,则该系统位于右半S 平面的极点数有 个。
4、控制系统的基本要求主要有: , , 。
5、Nyquist 图上以原点为圆心的单位圆对应于Bode 图上 的 线。
二、选择题( 每小题3分,共30分 )1、关于反馈的说法,正确的是( )A .反馈实质上就是信号的并联B .反馈都是人为加入的C .正反馈就是输入信号与反馈相加D .反馈就是输出以不同方式作用于系统 2、关于系统模型的说法,正确的是( )A .每个系统只有一种数据模型B .动态模型在一定条件下可简化为静态模型C .动态模型比静态模型好D .静态模型比动态模型好 3、某环节的传递函数为s 1,则该环节为( )A. 惯性环节B. 积分环节 C .微分环节 D .比例环节 4、系统的传递函数( )学院 专业班级 年级姓名 学号 装订线(答题不得超过此线)A .与外界无关B .反映了系统、输出、输入三者之间的关系C .完全反映了系统的动态特性 D. 与系统的初始状态有关 5、二阶欠阻尼系统的上升时间为( )A .阶跃响应曲线第一次达到稳定值的98%的时间B .阶跃响应曲线达到稳定值的时间C .阶跃响应曲线第一次达到稳定值的时间D .阶跃响应曲线达到稳定值的98%的时间 6、关于线性系统时间响应,说法正确的是( )A .时间响应就是系统输出的稳态值B .由单位阶跃响应和单位脉冲响应组成C .由强迫响应和自由响应组成D .与系统初始状态无关 7、系统的单位脉冲响应函数为te t w 2.03)(-=,则系统的传递函数为( )A .2.03)(+=S s G B. 32.0)(+=S s GC .2.06.0)(+=S s G D .36.0)(+=S s G8、以下系统中,属于最小相位系统的是( ) A .s s G 01.011)(-= B .s s G 01.011)(+=C .101.01)(-=s s G D .)1.01(1)(s s s G -=9、一个线性系统稳定与否取决于( )A .系统的结构和参数B .系统的输入C .系统的干扰D .系统的初始状态 10、一个系统稳定的充要条件是( )A .系统的全部极点都在[S]平面的右半平面内B .系统的全部极点都在[S]平面的上半平面内C .系统的全部极点都在[S]平面的左半平面内D .系统的全部极点都在[S]平面的下半平面内三、系统结构图如下图所示,求)()(s R s Y (15分)四、系统在静止平衡状态下,加入输入信号t t r +=1)(,测得响应为9.09.0)(10+-=-tet t C试求系统的传递函数。
自动控制原理期末试卷及答案
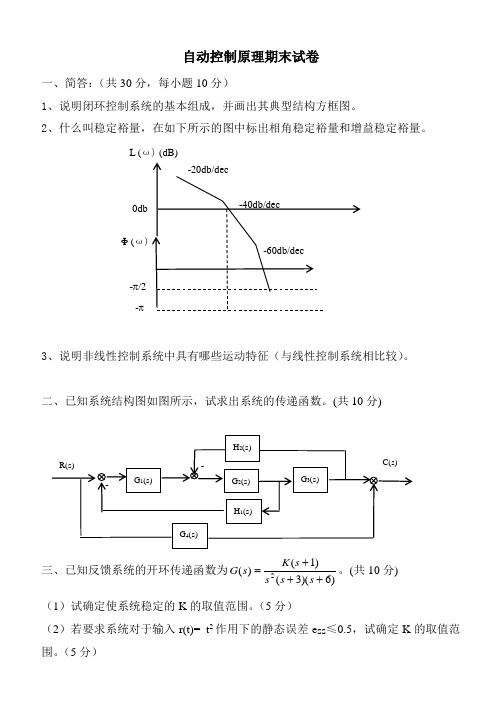
自动控制原理期末试卷一、简答:(共30分,每小题10分)1、说明闭环控制系统的基本组成,并画出其典型结构方框图。
2、什么叫稳定裕量,在如下所示的图中标出相角稳定裕量和增益稳定裕量。
3、说明非线性控制系统中具有哪些运动特征(与线性控制系统相比较)。
二、已知系统结构图如图所示,试求出系统的传递函数。
(共10分)三、已知反馈系统的开环传递函数为)6)(3()1()(2+++=s s s s K s G 。
(共10分) (1)试确定使系统稳定的K 的取值范围。
(5分)(2)若要求系统对于输入r(t)= t 2作用下的静态误差e SS ≤0.5,试确定K 的取值范围。
(5分)四、已知最小相位系统开环对数幅頻特性图如图所示,写出相应的传递函数。
(共10分)五、已知单位负反馈系统的开环传递函数为 )1)(1()(21++=s T s T s Ks G 。
(共10分)(1)试概略画出G (s )对应的Nyquist 图。
(5分) (2)由Nyquist 稳定判据给出闭环系统稳定的条件。
(5分) 六、已知系统的开环传递函数为)1()3(2)(+++=s s s s K s G )(绘制负反馈的根轨迹图,并确定使系统处于欠阻尼的K 值范围。
(共15分) 七、某采样控制系统的结构如图所示,已知τ=1,求: (1)求系统的脉冲传递函数。
(10分) (2)求系统稳定的K 值范围。
(5分)答案一、 简答:(共30分,每小题10分)1、答案:闭环控制系统的基本组成:检测元件、比较元件、放大元件、执行元件、给定元件、校正元件及被控对象。
(共6分,除被控对象外,每一个元件给1分)典型结构方框图(4分,可以没有局部反馈)2、答案:稳定裕量是系统距离稳定 的边界所具有的余量(5分)。
相角稳定裕量(3分)。
增益稳定裕量(2分)。
3、答案:与线性控制系统相比非线性控制系统表现出如下的特征: (1)非线性控制系统的运动不满足态的迭加原理。
《 自动控制原理 》典型考试试题
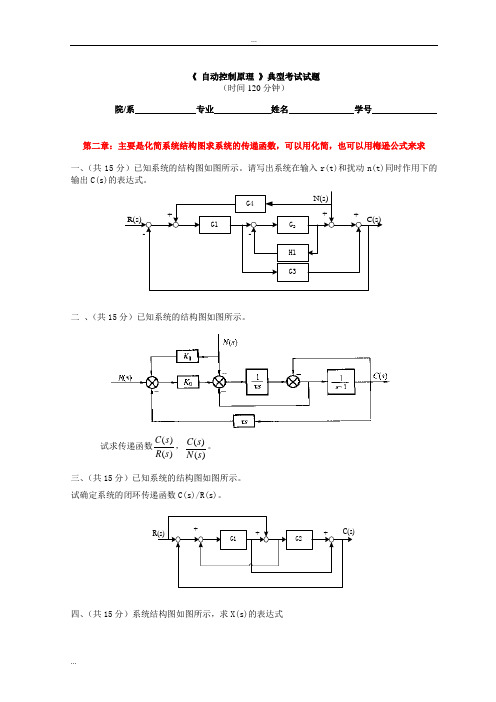
《 自动控制原理》典型考试试题(时间120分钟)院/系 专业 姓名 学号第二章:主要是化简系统结构图求系统的传递函数,可以用化简,也可以用梅逊公式来求一、(共15分)已知系统的结构图如图所示。
请写出系统在输入r(t)和扰动n(t)同时作用下的输出C(s)的表达式。
G4H1G3G1G 2N(s)C(s)R(s)--+++二 、(共15分)已知系统的结构图如图所示。
试求传递函数)()(s R s C ,)()(s N s C 。
三、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
G1G2R(s)-++C(s)-+四、(共15分)系统结构图如图所示,求X(s)的表达式G4(s)G6(s)G5(s)G1(s)G2(s)N(s)C(s)R(s)--G3(s)X(s)五、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)和C(s)/D(s)。
G1G2R(s)-++C(s)-+D(s)G3G4六、(共15分)系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
七、(15分)试用结构图等效化简求题图所示各系统的传递函数)()(s R s C一、(共15分)某控制系统的方框图如图所示,欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为ss e =0.25,试确定系统参数K 、τ。
二、(共10分)设图(a )所示系统的单位阶跃响应如图(b )所示。
试确定系统参数,1K 2K 和a 。
三、(共15分)已知系统结构图如下所示。
求系统在输入r(t)=t 和扰动信号d(t)=1(t)作用下的稳态误差和稳态输出)(∞C2/(1+0.1s)R(s)-C(s)4/s(s+2)E(s) D(s)四、(共10分)已知单位负反馈系统的开环传递函数为:2()(2)(4)(625)KG s s s s s =++++试确定引起闭环系统等幅振荡时的K 值和相应的振荡频率ω五、(15分)设单位反馈系统的开环传递函数为12 )1()(23++++=s s s s K s G α若系统以2rad/s 频率持续振荡,试确定相应的K 和α值第三章:主要包括稳、准、快3个方面稳定性有2题,绝对稳定性判断,主要是用劳斯判据,特别是临界稳定中出现全零行问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以 则Gs 分母的常数项应为零。
设 则闭环系统传递函数为
Gs
k s as2 bs c
ห้องสมุดไป่ตู้
s
Gs k 3 1 Gs as bs2 cs k
14
特征方程式为
as3 bs2 cs k s 3 4s 2 6s 10 0
1 s
C s
2
(a)
s
s2
Rs
k
B
1 s
s 1
s
A
1 s
C s
(a)
s
s 1
s
s2
Rs
k
1 s
s 1
s
1 s
C s
k
3
(b)
s
s 1
s
s2
Rs
k
1 s
s 1
s
1 s
C s
k
(b)
s 1
总复习题
C s 例1.某系统的结构图如图所示。试求系统的传递函数 Rs
。
s
s2
Rs
k
1 s
A
s 1
s
1 s
C s
结构图
1
1.解:
Rs
s
s2
k
1 s
A
s 1
s
1 s
C s
结构图
s
s2
Rs
k
B
1 s
s 1
s
A
图a。下例的变换也是这个思路,碰到这类分支点和相加点需要相互移动的题目,
6
例2. 图(a)为系统结构图,图(b)为某典型单位阶跃响应。试确定 k1 , k 2 和 a 的值。
Rs
k1
k2 ss a
Y s
yt
2.18 2.0
(a)
0
0.8
(b)
t
7
(a)系统结构图
(b)阶跃响应曲线
a 1 , b 4 , c 6 , k 10
比较系数得
即
10 G s s s 2 4s 6
15
例5. 某单位反馈随动系统的开环传递函数为
Gs 20000 ss 5s 500
s
s2
Rs
k
1 s 1
1
s 1
s
1 s
C s
k
4
(c)
s 1
s
s2
Rs
k
1 s 1
1
s 1
s
1 s
C s
k
(c)
s 1
Rs
s2 s k
1s 1 s s 1
1 s
C s
k 1s 1 ss 1
5
(d)
Rs
1
C s
(e)
所以
G s
C s 1 Rs
提示:本题用等效变换法做较复杂。主要困难可能出现在分支点和相加点互相 移动时(本例中的第一步变换),其移动的思路大致是:(参考图a)当原图 的反馈点(即分支点)A前移到 A 点时, A点的反馈值比在A点反馈少了s Rs , 为了保证变换的等效性,需在相加点 B 处加以补偿,大小为s Rs ,于是有了 可用梅逊公式求解较为简单。
E s
Rs
G s
Y s
系统结构图
13
4. 解:由单位阶跃引起的误差为
1 Rs s E s 1 G s 1 G s
由题意知稳态误差为
1 s ess lim s 0 s 0 1 G s
lim G s
2s 4 2 2s 1s 1s j s j 0 这样特征方程可写为
s 2s 1s 1s j s j 0
s j, 可见,系统在S右半平面有一个根 s 1,在虚轴上有两个根 s j, 在S左半平面有两个根 s 1 ,s 2 。
提示:该例显示了用劳斯判据是系统稳定性的方法。讨论了两种特殊情况 (劳斯阵某行元素全为零和第一列某元素为零)下劳斯阵的组成方法。
12
例4.闭环控制系统的结构图如图所示。试求满足下列两个条件的三阶开环传递函 数 Gs ,应满足的条件: (1)由单位阶跃函数输入引起的稳态误差为零; (2) 闭环系统的特征方程为 s 3 4s 2 6s 10 0 。
n k2 Gs ss a ss 2 n
2
又因为 所以
n 2 k 2 2 n a
8
据题意知
解得
2.18 2 % 100% 9% e 2 0.608
1 2
t p 0.8
解得 故
n 1 2
2. 解: 因为
k1k 2 Y s 2 Rs s as k 2
k1k 2 k1k 2 1 Y s 2 Rs 2 s as k 2 s as k 2 s
所以
k1k 2 1 y lim yt lim s 2 k1 2 t s 0 s as k 2 s
Rs
1 s2 s
1 s2 s
2
Y s
系统结构图
10
3. 解:系统的闭环传递函数为 系统的特征方程为
s
2 s 5 2s 4 s 2
s 5 2s 4 s 2 0
s5 s4 s3 s2 s1 s
0
看出特征方程的系数不全为正,所以系统是不稳定的。为了求出S右半平面 的极点数,列劳斯阵如下:
n 4.946rad s
k 2 2 24.463
a 2 n 2 0.608 4.946 6.014
提示:该例显示了由动态性能指标求系统参数的方法。
9
例3. 系统的结构图如图所示,试判别系统的稳定性。若不稳定求在S右半 平面的极点数。
s 1
1 s
s
1 2 0 0 0 0 1 2
8 0
16 2 0 2 0
第三行元素全为零,对辅助方程
11
2s 4 2 0
8s 3 0
求导得
可用8,0替换第三行0,0;第四行第一列元素为零;用小正数 替换0, 继续排列劳斯阵。 劳斯阵第一列元素变号一次,说明特征方程有一个正根。劳斯阵有一行 元素全为零,说明可能有大小相等、符号相反的实根;或一对共轭虚根;或 , 对称于虚轴的两对共轭复根。解辅助方程得:
