(北师大版七年级数学上册) 一元一次方程:水箱变高了练习题
北师大版数学七年级上册:5.3 应用一元一次方程——水箱变高了 同步练习(附答案)

3 应用一元一次方程——水箱变高了1.把一个用铁丝围成的长方形改制成一个正方形,则这个正方形与原来的长方形相比( )A .面积与周长都不变化B .面积相等但周长发生变化C .周长相等但面积发生变化D .面积与周长都发生变化2.根据图中给出的信息,可得正确的方程是( )A .π×(82)2×x =π×(62)2×(x +5) B .π×82×x =π×62×5C .π×(82)2×x =π×(62)2×(x -5) D .π×82×x =π×62×(x -5)3.有一个底面半径为10 cm ,高为30 cm 的圆柱形大杯中存满了水,把水倒入一个底面直径为10 cm 的圆柱形小杯中,刚好倒满12杯,则小杯的高为( )A .6 cmB .8 cmC .10 cmD .12 cm4.要锻造直径为16 cm 、高为5 cm 的圆柱形毛坯,设需截取横截面边长为6 cm 的方钢(横截面为正方形的钢材)x cm ,则可得方程为 .5.一个长方体合金底面长为80 mm 、宽为60 mm 、高为100 mm ,现要锻压成新的长方体合金,其底面是边长为40 mm 的正方形,则新长方体合金的高为 .6.将一个底面半径为6 cm 、高为40 cm 的“瘦长”圆柱形钢材锻压成底面半径为12 cm 的“矮胖”圆柱形零件毛坯,请问毛坯的高是多少?7.在“爱护环境,建我家乡”的活动中,七(1)班学生回收饮料瓶共10 kg ,男生回收的重量是女生的4倍,设女生回收饮料瓶x kg ,根据题意,可列方程为( )A .4(10-x)=xB .x +14x =10 C .4x =10+x D .4x =10-x8.七、八年级学生分别到雷锋、毛泽东纪念馆参观,共589人,到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍多55人.设到雷锋纪念馆的人数为x 人,可列方程为 .9.李明和他父亲年龄的和为55岁,又知父亲的年龄比他年龄的3倍少1岁,求李明和他父亲的年龄分别为多少岁?10.有一根钢管长12米,要锯成两段,使第一段比第二段短2米,求每段长各多少米?11.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有女子善织,日自倍,五日织五尺.问日织几何?译文:一位善于织布的妇女,每天织的布都是前一天的2倍,她5天共织了5尺布,问在这5天里她每天各织布多少尺?设她第一天织布为x尺,以下列出的方程正确的是( )A.x+2x=5 B.x+2x+4x+6x+8x=5C.x+2x+4x+8x+16x=5 D.x+2x+4x+16x+32x=512.用长为1米、直径为50毫米的圆钢可以拉成直径为1毫米的钢丝米.13.一个两位数,个位数字与十位数字的和是9.若将个位数字与十位数字对调后所得的新数比原数小9,则原来的两位数为.14.如图,一个酒瓶的容积为500毫升,瓶子内还剩有一些黄酒.当瓶子正放时,瓶内黄酒的高度为12厘米,倒放时,空余部分的高度为8厘米,则瓶子的底面积为平方厘米.(1毫升=1立方厘米)15.用长为10 m的铁丝沿墙围成一个长方形(墙的一面为长方形的长,不用铁丝),长方形的长比宽多1 m,求长方形的面积.16.在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6 cm,高为10 cm的圆柱形玻璃杯中,能否完全装下?若装不下,则瓶内水还剩多高?若未能装满,求杯内水面离杯口的距离.17.如图,长方形ABCD 中有6个形状、大小相同的小长方形,根据图中所标尺寸,则图中阴影部分的面积之和为 .18.我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的23,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?1.C2.A3.C4.(162)2π×5=62·x . 5.300_mm .6.解:设毛坯的高为x cm ,根据题意,得π×62×40=π×122·x.解得x =10.答:毛坯的高是10 cm.7.D8.2x +55=589-x .9.解:设李明的年龄为x 岁,则他父亲的年龄为(3x -1)岁,可列方程为 3x -1+x =55,解得x =14.则3x -1=41.答:李明的年龄为14岁,他父亲的年龄为41岁.10.解:设第二段长为x 米,则第一段长为(x -2)米.根据题意,得x +(x -2)=12.解得x =7.答:第一段长为5米,第二段长为7米.11.C12.2_500.13.54.14.25.15.解:设宽为x m,则长为(x+1)m.根据题意,得2x+(x+1)=10.解得x=3.所以x+1=4.故长方形的面积为3×4=12(m2).答:长方形的面积为12 m316.解:设圆柱形瓶内的水倒入玻璃杯中水的高度为x cm.由题意,得(52)2π×18=(62)2πx.解得x=12.5.因为12.5>10,所以不能完全装下.设瓶内水还剩y cm高.由题意,得(52)2π×18=(52)2πy+(62)2π×10.解得y=3.6.答:瓶内水还剩3.6 cm 高.17.44_cm 2.18.解:设这批书共有3x 本.根据题意,得 2x -4016=x +409.解得x =500.所以3x =1 500.答:这批书共有1 500本.。
北师大版七年级数学上册《应用一元一次方程——水箱变高了》同步练习2-精品

应用一元一次方程—水箱变高了
一、选择题
1.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆柱钢长( )
A .10厘米
B .20厘米
C .30厘米
D .40厘米
2.一个长方形的周长是40 cm ,若将长减少8 cm ,宽增加2 cm ,长方形就变成了正方形,则正方形的边长为( )
A. 6 cm
B.7 cm
C.8 cm
D.9 cm
3.请根据图中给出的信息,可得正确的方程是( ) A. ()5262822+∙⎪⎭
⎫ ⎝⎛∙=⎪⎭⎫ ⎝⎛∙x x ππ
B.
()5262822-∙⎪⎭⎫ ⎝⎛∙=⎪⎭⎫ ⎝⎛∙x x ππ C. ()56822+∙∙=∙x x ππ
D. 56822∙∙=∙ππx
二、填空题
1.一块长、宽、高分别为4cm,3cm,2cm 的长方体橡皮泥,要用它来捏一个底面半径为2
3cm 的圆柱,若圆柱的高是xcm,则可列方程 .
2.把一个半径为3的铁球融化后,能铸造________个半径为1的小铁球.(球体积公式为:334r V π=)
三、解答题
如图,一个盛有水的圆柱形玻璃容器的内底面半径为10cm,原容器内水的高度为12cm,把一根半径为2cm 的玻璃棒垂直插入水中后,问容器内的水将升高多少cm?
5.3应用一元一次方程—水箱变高了
一、选择题
1.D
2.B
3. A
二、填空题 1.24232=∙⎪⎭⎫ ⎝⎛∙x π 2. 27
三、解答题
1.解:设容器内的水将升高xcm ()()x x +∙=+∙+⨯∙12101221210222πππ 解得:2
3=x 答:容器内的水将升高23cm。
2017-2018学年七年级北师大版数学上册练习(PDF版):5.3 应用一元一次方程——水箱变高了
找不准等量ห้องสมุดไป่ตู้系 .
( 凉山州中 考 ) 根 据 图 中 给 出 的 信 息, 解答下列问 1 3. ( ) 放入一个大 放入一个小 球 水 面 升 高 2 c m, 1 球水面升高 3 c m; 各多少个 ? 题.
8 0
国庆节要到了 , 小新所在的班准备做直角边分别为 7.
老师派小新 0. 4 米和 0. 3 米的三角形小旗共 6 4 面. 去买长1. 宽1. 那么小新应 6米、 2 米的长方形红纸 , 买这种尺寸的红纸 A. 1张 B. 2张
7 9 — — 水箱变高了 5 . 3 应用一元一次方程 —
如金 等体积变形 : 同一物体的外形发生了变化 , 但变化前后的 体 积 不 变 , 1.
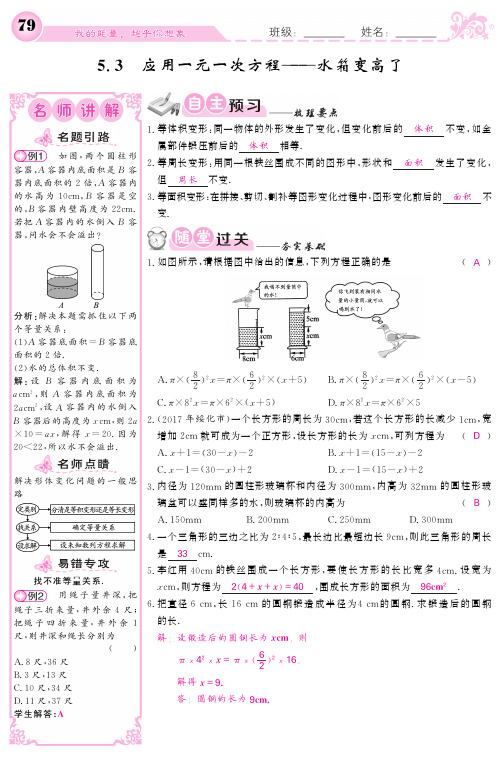
两个圆柱形 如 图, 等周长变形 : 用同一根铁丝围成不同的图形中 , 形状和 面 积 发 生 了 变 化 , 2. 容器 , A 容器内 底 面 积 是 B 容 但 周长 不变 . 器内 底 面 积 的 2 倍 , A 容器内 的水 高 为 1 等面积变形: 在拼接、 剪切、 割补等图形变化过程中, 图形变化前后的 面积 不 0 c m, B 容 器 是 空 3. 的, 2 c m. B 容器内壁高度为2 变. 若把 A 容 器 内 的 水 倒 入 B 容 器, 问水会不会溢出 ?
π×8x= π×6 × x+5 D. π×8x= π×6 ×5 C. 2 设A 容器内的水倒入 2 a c m, ( 一个长方形的周长为 3 若这个长方形的长减少 1 宽 2 0 1 7 年绥化市 ) 0 c m, c m, 则2 B 容器后 的 高 度 为x c m, a 2. 解 得 x=2 因为 ×1 0=a x, 0. (D ) 可列方程为 增加 2 设长方形的长为 x c m, c m 就可成为一个正方形 , , 所以水不会溢出 2 0<2 2 .
北师大版数学七年级上册3 应用一元一次方程——水箱变高了同步练习含答案

的长条,如果两次剪下的长条面积正好相等,则原正方形的边长是( )
A.20 B.24 C.48 D.144 6.如图,一个装有半瓶饮料的饮料瓶中,饮料的高度为 20 cm,把饮料瓶倒过来放置,饮料瓶空余部分的 高度为 5 cm.已知饮料瓶的容积为 30 立方分米,则瓶内现有饮料________立方分米.
答案:
Байду номын сангаас
2020 年最新
解得:x=900,x-21000=40. 答:这批服装的订货任务是 900 套,原计划 40 天完成 10. 设火车提速后的速度为 x 千米/小时, 则提速前的速度为(x-200)千米/小时,则4600x=2(x-200). 解得 x=300,即火车提速后的速度为 300 千米/时 11. 设应从乙处调 x 人到甲处, 依题意得:196-x=31(272+x), 解得 x=79. 答:应从乙处调 79 人到甲处 12. 64π×5=36x
原计划几天完成任务?
2020 年最新
10.连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的 2 小时缩短为 40 分钟, 其速度每小时将提高 200 km.求提速后的火车速度.
11.在甲处工作的有 272 人,在乙处工作的有 196 人,要使乙处工作的人数是甲处工作人数的13,则应从 乙处调多少人到甲处?
圆柱,高变成了多少?
2020 年最新
17.用长为 16 m 的铁丝沿墙围成一个长方形(墙的一面为长方形的长,不用铁丝),长方形的长比宽长 1 m, 求长方形的面积.
18.如图所示,一个长方体容器里装满了果汁,长方体的长为 12 cm,宽为 8 cm,高为 24 cm.把果汁倒满 旁边的圆柱形的玻璃杯,杯子的内径为 6 cm,高为 18 cm,这时原装的果汁容器内的果汁高度是多少?(π 取 3.14,结果精确到 0.01 cm)
北师大版七年级上册5.3 应用一元一次方程——水箱变高了同步测试

应用一元一次方程——水箱变高了(含答案)一.选择题:(四个选项中只有一个是正确的,选出正确选项填在题目的括号内)1.直径为80mm 、高为60mm 的圆柱的体积是直径为40mm 、高为x (mm )的圆柱的体积的5倍,则所列方程正确的是( )A .2240805()()6022x π⨯⋅=π⋅⨯B .2280540()602x π⋅⋅=π⋅⨯ C .2280405()602x π⋅⋅=π⋅⨯ D .224080()5()6022x π⨯⋅=π⋅⨯ 2.用长为30米的铁丝围成一个长方形方框,使长为7.8米、宽为x 米,则可列方程为( )A .27.830x +⨯=B .7.830x +=C .27.830x +=D .2(7.8)30x +=3.要修一块周长为140m 的长方形绿地,并且长比宽多10m ,设绿地的宽为x (m );根据题意,正面列出的方程正确的是( )A .2(10)140x -=B .[]2(10)140x x +-=C .2(10)140x +=D .[]2(10)140x x ++=4.已知长方形的长是宽的3倍,如果宽增加4米,而长减少5米,那么面积增加15米2,设长方形原来的宽为x 米,则可列方程( )A .2(4)(35)153x x x +-+=B .2(4)(35)153x x x +--=C .2(4)(35)153x x x -+-=D .2(4)(35)153x x x -++=5.要锻造一个直径为10cm ,高为6cm 的圆柱形毛坯,至少要截取直径为5cm 的圆钢( )A .10cmB .20cmC .24cmD .30cm6.在周长为10米的长方形窗户钉上一块宽为1米的长方形遮阳布,使透光部分正好是正方形,则钉好后透光面积为( )A .4米2B .9米2C .16米2D .25米27.内径为200mm 、内高为360mm 的圆柱形玻璃杯内盛满水,倒入内径为240mm 的圆柱形玻璃杯,刚好倒满,则内径为240mm 的玻璃杯的内高是( )A .240mmB .250mmC .260mmD .270mm8.用一根长为48cm 的铁丝围成一个长与宽的比是5:1的长方形,则长方形的面积是( )A .50cm 2B .80cm 2C .100cm 2D .200cm 29.有甲、乙、丙三个圆柱形容器,甲的内径(指直径)为10cm ,高为40cm ,乙的内径(指直径)为20cm ,高为40cm ,甲、乙容器都装满了水,把甲、乙容器的水都倒入内径(指直径)为40cm 的丙容器中,而使水不溢出,则丙容器至少要高( )cmA .12.5B .20C .25D .3010.一个长方形的长比宽多4cm ,若把它的长、宽分别增加4cm 后,面积增加了48cm 2,则原来的长方形的长、宽分别是( )A .4cm ,2cmB .6cm ,2cmC .6cm ,4cmD .8cm ,4cm 二.填空题:(将正确答案填在题目的横线上)11.将一个底面直径为50cm ,高为36cm 的圆柱锻压成底面直径为30cm 的圆柱,高变成了多少?设_____________________________,填表:由题意,可列方程:____________________________;12.将一个底面直径为10cm,高为40cm的圆柱锻压成一个底面直径为20cm的圆柱,求它的高;若设高为xcm,则所列的方程为___________________________;13.钢锭的截面是正方形,其边长是40厘米,要锻造成长、宽、高分别为50厘米,20厘米,10厘米的长方体,应截取这种钢锭的长度为________厘米;14.如图,“目”字形木窗框的木条总长是7.2米,窗的高比宽多0.6米,则窗的宽是_______米;15.有一个底面半径为20cm,高为20 cm的圆柱形大杯中存满了水,把它里边的水倒入一个底面半径为5 cm的圆柱形小杯中,刚好倒满20杯,则小杯的高为__________cm;三.解答题:(写出必要的说明过程,解答步骤)16.用一根绳子可以围成一个边长是16cm的正方形,若用这根绳子围成一个长比宽多2cm 的长方形,求长方形的面积;17.将一个底面直径为20cm,高为60cm的圆柱锻压成一个底面直径为40cm的圆柱,高缩短了多少?18.如图,由6个正方形拼成一个大长方形,如果中间最小的的正方形边长为5cm,求拼成的长方形的面积;第14题图19.如图,宽为50cm的长方形由10个全等的小长方形拼成,求小长方形的面积;20.一个长方形的养鸡场的长边靠墙,墙长16.5米,其他三边用竹篱笆围成,现有长为41米的竹篱笆,甲打算用它围成一个养鸡场,其中长比宽多5米;乙也打算用它围成一个养鸡场,其中长比宽多3.5米;谁的设计符合实际?按照他的设计,养鸡场的面积是多少?5.3应用一元一次方程——水箱变高了参考答案:1~10 ADDBC ABBAB11.高变成了xcm ,可列方程:22536π⋅⨯=215x π⋅⋅;12.221020()40()22x π⋅⨯=π⋅⋅; 13.6.25; 14.1.34; 15.16; 16.设长方形的宽为xcm ,则长为(x +2)cm ,由题意得:2[x +(x +2)]=16 解得:x=3,∴x +2=5∴长方形的面积为:3×5=15(cm 2)17.设锻压后的圆柱高为xcm , 由题意得:222040()60()22x π⋅⨯=π⋅⋅ 解得:x=15 又60-15=45 ∴锻压后的圆柱的高缩短了45cm ;18.设右下角的两个小正方形的边长为xcm ,由图可得:长方形的宽为:(5)(10)215x x x +++=+长方形的长为:(5)x x x +++ 或表示为:(10)(105)x x +++ ∴(5)(10)(15)x x x x x +++=+++ 解得:20x =∴长方形的长为:65,宽为55;∴长方形的面积为:65×55=3575(cm 2);19.设小长方形的宽为xcm ,由图可得:小长方形的长为:50252= 由42550x += 得:254x = ∴ 小长方形的面积为: 22525156.25()4cm ⨯=; 20.甲的设计方案:设长方形的宽为x 米,则长为(x +5)米根据题意,得2x +(x +5)=41 解得x =12∴甲设计的长为x +5=12+5=17(米)而墙的长度只有16.5米,∴甲的设计不符合实际;乙的设计方案:设宽为y 米,则长为(y +3.5)米根据题意,得:2y +(y +3.5)=41 解得x =12.5∴乙设计的长为:x +3.5=12.5+3.5=16(米)而墙的长度是16.5米,∴乙的设计符合要求此时,养鸡场的面积为12.5×16=200 (米2)答:乙的设计符合要求,按他的设计养鸡场的面积是200米2;。
七年级上应用一元一次方程水箱变高了训练题有解析北师大版

适用精选文件资料分享七年级上应用一元一次方程- 水箱变高了训练题(有解析北师大版)七年级上应用一元一次方程 - 水箱变高了训练题(有解析北师大版)(30 分钟 50 分) 一、选择题( 每题 4 分, 共 12 分) 1. 小明在一次登山活动中捡到一块矿石 , 回家后 , 他使用一把刻度尺 , 一只圆柱形的玻璃杯和足量的水 , 就丈量出了这块矿石的体积 . 假如他量出玻璃杯的内直径是 d, 把矿石完满吞没在水中 , 测出杯中水面上涨的高度为h, 则小明的这块矿石体积是() A. d2h B. d2h C. π d2h πd2h 2. 小明用长 250cm的铁丝围成一个长方形 , 而且长方形的长比宽多 25cm,设这个长方形的长为 x cm,则 x 等于请依据图中给出的信息 , 可得正确的方程是( ) A. π?( )2x= π?( )2?(x+5) B. π?( )2x= π?( )2?(x -5) C.π?82x=π? 62(x+5) D.π?82x=π?62×5 二、填空题 ( 每题 4 分,共12 分) 4. 一根内径为3cm的圆柱形长试管中装满了水, 现把试管中的水逐渐滴入一个内径为 8cm、高为 1.8cm 的圆柱形玻璃杯中 , 当玻璃杯装满水时 , 试管中的水的高度降落了cm. 5. 用直径为4cm的圆钢 , 锻造三个直径为 2cm,高为 16cm的圆柱形部件 , 则需要截取的圆钢长cm. 6. 用 5 个相同大小的小长方形恰好可以拼成以以下列图的大长方形 , 若大长方形的周长是14, 则小长方形的长是, 宽是.三、解答题(共26分) 7.(8分)将一个底面半径是 5 厘米 , 高为 10 厘米的圆柱体冰淇淋盒改造成一个直径为20 厘米的圆柱体 , 若体积不变 , 高为多少 ? 8.(8 分) 长方形纸片的长是15cm,长、宽上各剪去 1 个宽为 3cm的长条 , 剩下的面积是原面积的 . 求原面积 . 【拓展延伸】 9.(10 分) 一个长方形的鸡场的长边靠墙 , 墙长14 米, 其余三边用篱笆笆围成 , 现有长为 35 米的篱笆笆 , 小王打算用它围成一个鸡场 , 此中长比宽多 5 米; 小赵也打算用它围成一个鸡场 , 此中长比宽多 2 米, 你以为谁的设计切合实质 ?依据他的设计 , 鸡场的面积是多少 ?答案解析 1. 【解析】选 A. 依据圆柱的体积公式可得这块矿石的体积为: d2h. 2. 【解析】选 A. 依据题意得 : 2(x+x-25)=250, 解得 :x=75.3.【解析】选 A. 依据圆柱的体积公式求得大批筒中的水的体积为: π×( )2x.小量筒中的水的体积为:π×( )2×(x+5).依据等量适用精选文件资料分享关系列方程得 : π×( )2x= π×( )2(x+5). 4.【解析】设试管中的水的高度降落了 xcm, 依据题意得 : π?1.52?x= π?42×1.8,解方程得:x=12.8.答案:12.8 5.【解析】设截取的圆钢长xcm. 依据题意得: π×( )2x=3 ×π×( )2 ×16, 解方程得 :x=12. 答案: 12 6. 【解析】设小长方形的宽为 x, 则长为 2x, 由题意得 :(5x+2x) ×2=14, 解方程得 x=1, 即小长方形的宽为 1, 长为 2. 答案: 2 1 7. 【解析】设圆柱体的高为 x 厘米 . 依据题意得 :25 π×10=1 00 πx, 解得:x=2.5. 答: 高为 2.5 厘米 . 8. 【解析】设长方形纸片的宽是 xcm,原面积是 15xcm2, 长、宽上各剪去 1 个宽为 3cm的长条 , 剩下的面积是12(x-3)cm2, 由题意得:15x ×=12(x -3), 所以9x=12(x-3), 解方程得x=12, 12×15=180(cm2), 所以原面积是180cm2. 9. 【解析】依据小王的设计可以设宽为 x 米, 则长为 (x+5) 米, 依据题意得:2x+(x+5)=35, 解方程得 :x=10. 所以小王设计的长为x+5=10+5=15(米), 而墙的长度只有 14 米, 故小王的设计不切合实质 . 依据小赵的设计可以设宽为 y 米, 则长为 (y+2) 米, 依据题意得2y+(y+2)=35, 解方程得 :y=11. 所以小赵设计的长为y+2=11+2=13(米), 而墙的长度为 14 米, 明显小赵的设计切合实质 , 此时鸡场的面积为13×11=143(平方米 ).。
北师大版七年级数学上册应用一元一次方程——水箱变高了测试题

5.3 应用一元一次方程——水箱变高了一、选择题(每小题4分,共12分)1.小明在一次登山活动中捡到一块矿石,回家后,他使用一把刻度尺,一只圆柱形的玻璃杯和足量的水,就测量出了这块矿石的体积.如果他量出玻璃杯的内直径是d,把矿石完全浸没在水中,测出杯中水面上升的高度为h,则小明的这块矿石体积是( )A.d2hB.d2hC.πd2hD.4πd2h2.小明用长250cm的铁丝围成一个长方形,并且长方形的长比宽多25cm,设这个长方形的长为x cm,则x等于( )A.75 cmB.50 cmC.137.5 cmD.112.5 cm3.请根据图中给出的信息,可得正确的方程是( )A.π·()2x=π·()2·(x+5)B.π·()2x=π·()2·(x-5)C.π·82x=π·62(x+5)D.π·82x=π·62×5二、填空题(每小题4分,共12分)4.一根内径为3cm的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8cm、高为1.8cm的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了cm.5.用直径为4cm的圆钢,铸造三个直径为2cm,高为16cm的圆柱形零件,则需要截取的圆钢长cm.6.用5个一样大小的小长方形恰好可以拼成如图所示的大长方形,若大长方形的周长是14,则小长方形的长是,宽是.答案解析1.【解析】选A.根据圆柱的体积公式可得这块矿石的体积为:d2h.2.【解析】选A.根据题意得:2(x+x-25)=250,解得:x=75.3.【解析】选A.根据圆柱的体积公式求得大量筒中的水的体积为:π×()2x. 小量筒中的水的体积为:π×()2×(x+5).根据等量关系列方程得:π×()2x=π×()2(x+5).4.【解析】设试管中的水的高度下降了xcm,根据题意得:π·1.52·x=π·42×1.8,解方程得:x=12.8.答案:12.85.【解析】设截取的圆钢长xcm.根据题意得:π×()2x=3×π×()2×16,解方程得:x=12.答案:126.【解析】设小长方形的宽为x,则长为2x,由题意得:(5x+2x)×2=14,解方程得x=1,即小长方形的宽为1,长为2.答案:2 1掌握的三个数学答题方法树枝答题法关注数学题的解题过程2014年上海市中考状元徐瑜卿认为,数学是一门思维学科,并不是平时做题多就一定会拿高分。
北师大版初中数学七年级上册《5.3 应用一元一次方程——水箱变高了》同步练习卷

北师大新版七年级上学期《5.3 应用一元一次方程——水箱变高了》同步练习卷一.选择题(共41小题)1.某商场一种品牌的服装标价为每件1000元,为了参与市场竞争,商场按标价的8.5折(即标价的85%)再让利40元销售,结果每件服装仍可获利进价的20%.若设这种服装每件的进价是x元,请列出关于x的方程是()A.1000×85%﹣40=20%xB.(1000﹣40)×85%﹣x=20%xC.1000×85%﹣40﹣x=20%×1000D.1000×85%﹣40=(1+20%)x2.2018年宁波市中考新增英语口语听力自动化考试,考试需要耳麦,已知甲耳麦比乙耳麦贵20元,某校购买了甲耳麦40个、乙耳麦60个,共花费了6000元,假设甲耳麦每个x 元,由题意得()A.40x+60(x﹣20)=6000B.40x+60(x+20)=6000C.60x+40(x﹣20)=6000D.60x+40(x+20)=60003.游泳池中有一批小朋友,男生戴蓝色游泳帽,女生戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍.设男孩有x 人,则可列方程()A.x=2(x﹣2)B.x﹣1=2(x﹣2)C.x=2(x﹣1)D.x﹣1=2x4.某班分两组志愿者去社区服务,第一组20人,第二组26人.现第一组发现人手不够,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程()A.20=2(26﹣x)B.20+x=2×26C.2(20+x)=26﹣x D.20+x=2(26﹣x)5.甲、乙两人从学校到博物馆去,甲每小时走4km,乙每小时走5km,甲先出发0.1h,结果乙还比甲早到0.1h.设学校到博物馆的距离为xkm,则以下方程正确的是()A.B.C.D.4x﹣0.1=5x+0.16.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x天,由题意得方程()A.+=1B.+=1C.+=1D.+=17.轮船在静水中的速度为20km/h,水流速度为4km/h,从甲码头顺流航行到乙码头,再返回甲码头,共用5h(不计停留时间),求甲、乙两码头间的距离.设甲、乙两码头间的距离为x km/h,则列出的方程正确的是()A.20x+4x=5B.(20+4)x+(20﹣4)x=5C.D.8.10月31日是王阳明先生诞辰日,为纪念王阳明先生诞辰545周年,某校在余姚阳明文化周期间组织了阳明文化节,某班有42名同学报名参加了阳明心学讲坛或阳明书画社活动,已知参加阳明心学讲坛的人数比参加阳明书画社的人数多4人,两个活动都参加的有22人,问参加阳明心学讲坛的有多少名同学?设参加阳明心学讲坛的有x名同学,根据题意,可列方程为()A.x+x+4﹣22=42B.x+x﹣4﹣22=42C.x+x+4+22=42D.x+x﹣4+22=429.某市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完,设原有树苗x棵,则根据题意列出方程正确的是()A.5(x+21﹣1)=6(x﹣1)B.5(x+21)=6(x﹣1)C.5(x+21﹣1)=6x D.5(x+21)=6x10.杭州市用水收费规定如下:若每户每月的用水量不超过18立方米,则每立方米水价按2.9元收费,若用水量在18﹣25(含)立方米之间,则超过18立方米部分每立方米按3.85元收费,已知小静家1月份共交水费67.6元.若设小静家1月份用了x立方米的水,根据题意列出关于x的方程,正确的是()A.3.85x=67.6B.18×2.9+3.85(x﹣18)=67.6C.18×2.9+3.85x=67.6D.18×2.9+3.85(25﹣x)=67.611.在一次革命传统教育活动中,有n位师生乘坐m辆客车.若每辆客车乘60人,则还有10人不能上车,若每辆客车乘62人,则最后一辆车空了8个座位.在下列四个方程①60m+10=62m﹣8;②60m+10=62m+8;③;④中,其中正确的有()A.①③B.②④C.①④D.②③12.“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是()A.3x+1=4x﹣2B.3x﹣1=4x+2C.D.13.有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43人,则只有1人不能上车,有下列四个等式:①40m+10=43m﹣1;②;③;④40m+10=43m+1,其中正确的是()A.①②B.②④C.②③D.③④14.某村原有林地54公顷,旱地108公顷,为保护环境,需把一部分旱地改造为林地,使旱地占林地面积的20%,设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108B.54﹣x=20%×(108+x)C.54+x=20%×162D.108﹣x=20%(54+x)15.用铝片做听装饮料瓶,现有150张铝片,每张铝片可制瓶身16张或制瓶底43张,一个瓶身和两个瓶底可配成一套,设用x张铝片制瓶身,则下面所列方程正确的是()A.2×16x=43(150﹣x)B.16x=43(150﹣x)C.16x=2×43(150﹣x)D.16x=43(75﹣x)16.一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:①4×3(2x+3)=0.5×0.5×504;②2×3(2x+6)+2×3x=0.5×0.5×504;③(x+6)(2x+6)﹣2x•x=0.5×0.5×504,其中正确的是()A.②B.③C.②③D.①②③17.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是()A.18(42﹣x)=12x B.2×18(42﹣x)=12xC.18(42﹣x)=2×12x D.18(21﹣x)=12x18.某区今年暑假选派了180名教师担任G20交通引导志愿者、80名教师担任安全维护志愿者,现要把一部分安全维护志愿者调到交通引导志愿者队伍中,使安全维护志愿者人数占交通引导志愿者人数的30%,设把x名安全维护志愿者调到交通引导志愿者队伍中,则可列方程()A.80﹣x=30%×(180+x)B.80﹣x=30%×180C.180+x=30%×(80﹣x)D.80﹣x=30%×26019.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价为200元,按标价的五折销售,仍可获利10%,设这件商品的标价为x元,根据题意列出方程()A.0.5x﹣200=10%×200B.0.5x﹣200=10%×0.5xC.200=(1﹣10%)×0.5x D.0.5x=(1﹣10%)×20020.若m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则只有1人不能上车,有下列四个等式:(1)40m+10=43m+1;(2)=;(3)=;(4)40m﹣10=43m﹣1,其中正确的是()A.(1)(2)B.(2)(4)C.(1)(3)D.(3)(4)21.七年级1班学生参加净化校园劳动,其中参加打扫操场的有28人,参加清洗教室的有20人,现根据需要,从参加清洗教室的同学中抽调部分去打扫操场,使参加打扫操场的人数是参加清洗教室人数的2倍,问应从参加清洗教室的同学中抽调多少人去打扫操场?设应抽调x人去打扫操场,可得正确方程是()A.28﹣x=2(20﹣x)B.28+x=2(20+x)C.28+x=2(20﹣x)D.28﹣x=2(20+x)22.包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42﹣x)名工人生产圆形铁片,则下列所列方程正确的是()A.120x=2×80(42﹣x)B.80x=120(42﹣x)C.2×80x=120(42﹣x)D.23.甲、乙两人从学校到博物馆去,甲每小时走4km,乙每小时走6km,甲先出发1h,结果乙还比甲早到1h.设学校到博物馆的距离为S,则以下方程正确的是()A.B.C.D.4S﹣1=6S+1 24.某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可赢利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程,正确的是()A.(1+50%)x×80%﹣x=8B.50%x×80%﹣x=8C.(1+50%)x×80%=8D.(1+50%)x﹣x=825.某学生从家到学校时,每小时行5千米;按原路返回家时,每小时行4千米,结果返回的时间比去学校的时间多花10分钟.设去学校所用时间为x小时,则可列方程得()A.B.C.D.26.有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则还多出2个座位,有下列四个等式:①40m+10=43m﹣2;②=;③=;④40m﹣10=43m+2.其中正确的是()A.①②B.②④C.①③D.③④27.小红去水果店买苹果,店内一欧四种苹果,各品种的单价如下表所示:回家后,小红根据买的情况看列了一个方程50﹣12.4x﹣9(4﹣x)=3.8(设购买B品种的苹果x千克),像考考妈妈,下列说法与实际购买信息不符合的是()A.一共买了4千克苹果B.(4﹣x)表示买C品种苹果的千克数C.没有买A,D品种的苹果D.本次购买苹果共支出50元28.“实现五水共治,绿化美丽东吴”,东吴镇计划把某一河岸的一侧全部载上杨柳树,要求岸边的两端各载上一棵,并且每两棵树的间隔相等,如果每隔4米栽1棵,则树苗缺25棵;如果每隔5米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是()A.4(x+25)=5x B.4(x+25)=5(x﹣1)C.4(x+25﹣1)=5x D.4(x+25﹣1)=5(x﹣1)29.洪峰到来前,120名战士奉命加固堤坝,已知5人运沙袋3人堆垒沙袋,正好运来的沙袋能及时用上且不窝工,为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是()A.=x B.120﹣x=xC.x=(120﹣x)D.3x+2x=12030.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是()A.5x+4(x+2)=44B.5x+4(x﹣2)=44C.9(x+2)=44D.9(x+2)﹣4×2=4431.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为()A.518=2(106+x)B.518﹣x=2×106C.518﹣x=2(106+x)D.518+x=2(106﹣x)32.为了参加社区“畅响G20”文艺演出,某校组建了46人的合唱队和30人的舞蹈队,现根据演出需要,从舞蹈队中抽调了部分同学参加合唱队,使合唱队的人数恰好是舞蹈队人数的3倍,设从舞蹈队中抽调了x人参加合唱队,可得正确的方程是()A.3(46﹣x)=30+x B.46+x=3(30﹣x)C.46﹣3x=30+x D.46﹣x=3(30﹣x)33.甲、乙两班共有98人,若从甲班调3人到乙班,那么两班人数正好相等.设甲班原有人数是x人,可列出方程()A.98+x=x﹣3B.98﹣x=x﹣3C.(98﹣x)+3=x D.(98﹣x)+3=x﹣334.一队师生共328人,乘车外出旅行,已有校车可乘64人,如果租用客车,每辆可乘44人,那么还要租用多少辆客车?如果设还要租x辆客车,可列方程为()A.44x﹣328=64B.44x+64=328C.328+44x=64D.328+64=44x 35.有一批画册,若3人合看一本,则多余2本;若2人合看一本,就有9人没有,设人数为x,则列出的方程是()A.3x+2=2x﹣9B.﹣2=C.+2=D.+2=﹣9 36.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108B.54﹣x=20%(108+x)C.54+x=20%×162D.108﹣x=20%(54+x)37.汽车队运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,求这个车队有多少辆车?设这个车队有x辆车,可列方程为()A.4x﹣8=4.5x B.4x+8=4.5xC.4(x﹣8)=4.5x D.4(x+8)=4.5x38.2013年“地球停电一小时”活动的某地区烛光晚餐中,设座位有x排,每排坐30人,则有8人无座位;每排坐31人,则空26个座位.则下列方程正确的是()A.30x+8=31x﹣26B.30x+8=31x+26C.30x﹣8=31x﹣26D.30x﹣8=31x+2639.某人以每小时5千米的速度从家步行到单位上班,下班时以每小时4千米的速度按原路返回,结果下班时比上班时多用10分钟,如果设上班时所用的时间为x小时,则下列根据题意所列方程正确的是()A.5x=4(x﹣10)B.C.D.40.种一批树,如果每人种10棵,则剩6棵未种;如果每人种12棵,则缺6棵,设有x 棵树,则根据题意列出方程正确的是()A.10x﹣6=12x+6B.=C.10x+6=12x﹣6D.=41.某车间有26名工人,每人每天能生产螺栓12个或螺母18个.若要使每天生产的螺栓和螺母按1:2配套,则分配几人生产螺栓?设分配x名工人生产螺栓,其他工人生产螺母,所列方程正确的是()A.12x=18(26﹣x)B.18x=12(26﹣x)C.2×18x=12(26﹣x)D.2×12x=18(26﹣x)二.填空题(共9小题)42.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/小时,设A港和B港相距x千米,则根据题意列出的方程是.43.整理一批图书,由一个人做要40小时完成,现计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?设先安排x人工作,可列方程:.44.如图,天平左边放着3个乒乓球,右边放5.4g的砝码和1个乒乓球,天平恰好平衡.如果设1个乒乓球的质量为x(g),请你列出一个含有未知数x的方程.45.某村原有林地108公顷,旱地54公公顷,为保护环境,需把一部分旱地改造为林地,使旱地占林地面积的20%.设把x公顷旱地改为林地,则为可列方程为.46.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成了任务,而且还多生产了60件,设原计划每小时生产y个零件,可列方程为.47.某厂10月份的产值是125万元,比3月份的产值的3倍少13万元,若设3月份的产值为x万元,则可列出的方程为.48.从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲乙两地相距x千米,则列方程为.49.一个数的3倍比它的2倍多10,若设这个数为x,可得到方程.50.一轮船从甲港顺流驶到乙港,比从乙港返回甲港少用了2.5小时,若船速为26千米/时,水速为2千米/时,求甲港和乙港相距多少千米?设甲港和乙港相距x千米,根据题意,可列出的方程是.北师大新版七年级上学期《5.3 应用一元一次方程——水箱变高了》2019年同步练习卷参考答案与试题解析一.选择题(共41小题)1.某商场一种品牌的服装标价为每件1000元,为了参与市场竞争,商场按标价的8.5折(即标价的85%)再让利40元销售,结果每件服装仍可获利进价的20%.若设这种服装每件的进价是x元,请列出关于x的方程是()A.1000×85%﹣40=20%xB.(1000﹣40)×85%﹣x=20%xC.1000×85%﹣40﹣x=20%×1000D.1000×85%﹣40=(1+20%)x【分析】根据题意可以列出相应的方程,从而可以解答本题.【解答】解:由题意可得,100×85%﹣40=x(1+20%),故选:D.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.2.2018年宁波市中考新增英语口语听力自动化考试,考试需要耳麦,已知甲耳麦比乙耳麦贵20元,某校购买了甲耳麦40个、乙耳麦60个,共花费了6000元,假设甲耳麦每个x 元,由题意得()A.40x+60(x﹣20)=6000B.40x+60(x+20)=6000C.60x+40(x﹣20)=6000D.60x+40(x+20)=6000【分析】根据题意可以列出相应的方程,从而可以解答本题.【解答】解:由题意可得,40x+60(x﹣20)=6000,故选:A.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.3.游泳池中有一批小朋友,男生戴蓝色游泳帽,女生戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍.设男孩有x 人,则可列方程()A.x=2(x﹣2)B.x﹣1=2(x﹣2)C.x=2(x﹣1)D.x﹣1=2x【分析】设男孩有x人则女孩有(x﹣1)人,根据题意可得等量关系:男孩人数=2×(女孩人数﹣1),根据等量关系列出方程即可.【解答】解:设男孩有x人则女孩有(x﹣1)人,由题意得:x=2(x﹣2),故选:A.【点评】此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,找出题目中的等量关系,列出方程.4.某班分两组志愿者去社区服务,第一组20人,第二组26人.现第一组发现人手不够,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程()A.20=2(26﹣x)B.20+x=2×26C.2(20+x)=26﹣x D.20+x=2(26﹣x)【分析】设抽调x人,则调后一组有(20+x)人,第二组有(26﹣x)人,根据关键语句:使第一组的人数是第二组的2倍列出方程即可.【解答】解:设抽调x人,由题意得:20+x=2(26﹣x),故选:D.【点评】本题主要考查由实际问题抽象出一元一次方程,解题的关键是理解题意,确定相等关系,并据此列出方程.5.甲、乙两人从学校到博物馆去,甲每小时走4km,乙每小时走5km,甲先出发0.1h,结果乙还比甲早到0.1h.设学校到博物馆的距离为xkm,则以下方程正确的是()A.B.C.D.4x﹣0.1=5x+0.1【分析】根据题意可以列出相应的方程,本题得以解决.【解答】解:由题意可得,,故选:B.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.6.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x天,由题意得方程()A.+=1B.+=1C.+=1D.+=1【分析】直接利用总工作量为1,分别表示出两人完成的工作量进而得出等式即可.【解答】解:设乙独做x天,由题意得方程:+=1.故选:B.【点评】此题主要考查了由实际问题抽象出一元一次方程,正确表示出两人完成的工作量是解题关键.7.轮船在静水中的速度为20km/h,水流速度为4km/h,从甲码头顺流航行到乙码头,再返回甲码头,共用5h(不计停留时间),求甲、乙两码头间的距离.设甲、乙两码头间的距离为x km/h,则列出的方程正确的是()A.20x+4x=5B.(20+4)x+(20﹣4)x=5C.D.【分析】首先理解题意找出题中存在的等量关系:顺水从甲到乙的时间+逆水从乙到甲的时间=5小时,根据此等式列方程即可.【解答】解:设两码头间的距离为x km,则船在顺流航行时的速度是:24km/时,逆水航行的速度是16km/时.根据等量关系列方程得:.故选:D.【点评】考查了由实际问题抽象出一元一次方程.列方程解应用题的关键是找出题目中的相等关系,注对于此类题目要意审题.8.10月31日是王阳明先生诞辰日,为纪念王阳明先生诞辰545周年,某校在余姚阳明文化周期间组织了阳明文化节,某班有42名同学报名参加了阳明心学讲坛或阳明书画社活动,已知参加阳明心学讲坛的人数比参加阳明书画社的人数多4人,两个活动都参加的有22人,问参加阳明心学讲坛的有多少名同学?设参加阳明心学讲坛的有x名同学,根据题意,可列方程为()A.x+x+4﹣22=42B.x+x﹣4﹣22=42C.x+x+4+22=42D.x+x﹣4+22=42【分析】设参加阳明心学讲坛的有x名同学,根据参加阳明心学讲坛的人数+参加阳明书画社的人数﹣两个活动都参加的有22人=42列出方程.【解答】解:设参加阳明心学讲坛的有x名同学,根据题意,可列方程为x+x﹣4﹣22=42.故选:B.【点评】考查了由实际问题抽象出一元一次方程.解题的关键是读懂题意,找到等量关系,列出方程.9.某市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完,设原有树苗x棵,则根据题意列出方程正确的是()A.5(x+21﹣1)=6(x﹣1)B.5(x+21)=6(x﹣1)C.5(x+21﹣1)=6x D.5(x+21)=6x【分析】根据题意可以列出相应的方程,从而可以解答本题.【解答】解:由题意可得,5(x+21﹣1)=6(x﹣1),故选:A.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程,注意要求路的两端各栽一棵.10.杭州市用水收费规定如下:若每户每月的用水量不超过18立方米,则每立方米水价按2.9元收费,若用水量在18﹣25(含)立方米之间,则超过18立方米部分每立方米按3.85元收费,已知小静家1月份共交水费67.6元.若设小静家1月份用了x立方米的水,根据题意列出关于x的方程,正确的是()A.3.85x=67.6B.18×2.9+3.85(x﹣18)=67.6C.18×2.9+3.85x=67.6D.18×2.9+3.85(25﹣x)=67.6【分析】根据水费是由两部分费用组成,不超过18立方米的费用和超过18立方米的费用相加即可.【解答】解:设小静家1月份用了x立方米的水,不超过18立方米收费为18×2.9,超过18立方米的水费为3.85×(x﹣18),即18×2.9+3.85(x﹣18)=67.6,故选:B.【点评】本题考查了由实际问题抽象出一元一次方程,解题的关键是理解水费的收费标准.11.在一次革命传统教育活动中,有n位师生乘坐m辆客车.若每辆客车乘60人,则还有10人不能上车,若每辆客车乘62人,则最后一辆车空了8个座位.在下列四个方程①60m+10=62m﹣8;②60m+10=62m+8;③;④中,其中正确的有()A.①③B.②④C.①④D.②③【分析】首先要理解清楚题意,知道总的客车数量及总的人数不变,然后采用排除法进行分析从而得到正确答案.【解答】解:根据总人数列方程,应是60m+10=62m﹣8,根据客车数列方程,应该为:=,故选:A.【点评】此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,能够根据不同的等量关系列方程.12.“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是()A.3x+1=4x﹣2B.3x﹣1=4x+2C.D.【分析】根据苹果总个数不变,结合每个小朋友分3个则剩1个;每个小朋友分4个则少2个,分别表示苹果数量进而得出等式即可.【解答】解:∵设共有x个苹果,∴每个小朋友分3个则剩1个时,小朋友的人数是;,若每个小朋友分4个则少2个时,小朋友的人数是;,∴,故选:C.【点评】此题主要考查了用一元一次方程解决实际问题,列方程解应用题的关键是找出题目中的相等关系,此题从分体现了数学与实际生活的密切联系.13.有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车,若每辆客车乘43人,则只有1人不能上车,有下列四个等式:①40m+10=43m﹣1;②;③;④40m+10=43m+1,其中正确的是()A.①②B.②④C.②③D.③④【分析】首先要理解清楚题意,知道总的客车数量及总的人数不变,然后采用排除法进行分析从而得到正确答案.【解答】解:根据总人数列方程,应是40m+10=43m+1,①错误,④正确;根据客车数列方程,应该为,②错误,③正确;所以正确的是③④.故选:D.【点评】此题的关键是能够根据不同的等量关系列方程.14.某村原有林地54公顷,旱地108公顷,为保护环境,需把一部分旱地改造为林地,使旱地占林地面积的20%,设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108B.54﹣x=20%×(108+x)C.54+x=20%×162D.108﹣x=20%(54+x)【分析】设把x公顷旱地改为林地,根据旱地面积占林地面积的20%列出方程即可.【解答】解:设把x公顷旱地改为林地,根据题意可得方程:108﹣x=20%(54+x).故选:D.【点评】本题考查一元一次方程的应用,关键是设出未知数以以改造后的旱地与林地的关系为等量关系列出方程.15.用铝片做听装饮料瓶,现有150张铝片,每张铝片可制瓶身16张或制瓶底43张,一个瓶身和两个瓶底可配成一套,设用x张铝片制瓶身,则下面所列方程正确的是()A.2×16x=43(150﹣x)B.16x=43(150﹣x)C.16x=2×43(150﹣x)D.16x=43(75﹣x)【分析】由一个瓶身与两个瓶底才能配成一套,可知瓶底的个数是瓶身个数的2倍;根据这一数量关系列方程解答即可.【解答】解:设用x张制瓶身,则用(150﹣x)张制瓶底才能正好制成整套的饮料瓶,根据题意列方程得,2×16x=43(150﹣x),故选:A.【点评】此题考查一元一次方程的问题,解答此题抓住“一个瓶身与两个瓶底才能配成一套”,理清数量关系,列出方程解决问题.16.一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:①4×3(2x+3)=0.5×0.5×504;②2×3(2x+6)+2×3x=0.5×0.5×504;③(x+6)(2x+6)﹣2x•x=0.5×0.5×504,其中正确的是()A.②B.③C.②③D.①②③【分析】根据题意表示出长方形框的面积进而分别得出答案.【解答】解:设此标志性建筑底面长方形的宽为x米,给出下列方程:①4×3(2x+3)=0.5×0.5×504,错误;②2×3(2x+6)+2×3x=0.5×0.5×504,正确;③(x+6)(2x+6)﹣2x•x=0.5×0.5×504,正确.故选:C.【点评】此题主要考查了由实际问题抽象出一元一次方程,正确表示出长方形边框的面积是解题关键.17.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是()A.18(42﹣x)=12x B.2×18(42﹣x)=12xC.18(42﹣x)=2×12x D.18(21﹣x)=12x【分析】根据题意,可以列出相应的方程,从而可以解答本题.【解答】解:由题意可得,12x×2=(42﹣x)×18,故选:C.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,找出题目中的等量关系,列出相应的方程.18.某区今年暑假选派了180名教师担任G20交通引导志愿者、80名教师担任安全维护志愿者,现要把一部分安全维护志愿者调到交通引导志愿者队伍中,使安全维护志愿者人数占交通引导志愿者人数的30%,设把x名安全维护志愿者调到交通引导志愿者队伍中,则可列方程()A.80﹣x=30%×(180+x)B.80﹣x=30%×180C.180+x=30%×(80﹣x)D.80﹣x=30%×260【分析】根据题意可以列出相应的方程,从而可以解答本题.【解答】解:由题意可得,80﹣x=30%×(180+x),故选:A.【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.19.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价为200元,按标价的五折销售,仍可获利10%,设这件商品的标价为x元,根据题意列出方程()A.0.5x﹣200=10%×200B.0.5x﹣200=10%×0.5xC.200=(1﹣10%)×0.5x D.0.5x=(1﹣10%)×200【分析】根据题意可得等量关系:标价×打折﹣进价=利润率×进价,根据等量关系可得方程.【解答】解:设这件商品的标价为x元,根据题意得:0.5x﹣200=10%×200,故选:A.【点评】此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,掌握售价、进价、利润之间的关系.20.若m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则只有1人不能上车,有下列四个等式:(1)40m+10=43m+1;(2)=;(3)=;(4)40m﹣10=43m﹣1,其中正确的是()A.(1)(2)B.(2)(4)C.(1)(3)D.(3)(4)【分析】首先要理解清楚题意,知道总的客车数量及总的人数不变,然后采用排除法进行分析从而得到正确答案.【解答】解:根据总人数列方程,应是40m+10=43m+1,(4)错误,(1)正确;根据客车数列方程,应该为)=;(2)错误,(3)正确;所以正确的是(1)(3).故选:C.【点评】此题考查了由实际问题抽象出一元一次方程的知识,解题的关键是能够根据不同的等量关系列方程.21.七年级1班学生参加净化校园劳动,其中参加打扫操场的有28人,参加清洗教室的有20人,现根据需要,从参加清洗教室的同学中抽调部分去打扫操场,使参加打扫操场的人数是参加清洗教室人数的2倍,问应从参加清洗教室的同学中抽调多少人去打扫操场?设应抽调x人去打扫操场,可得正确方程是()A.28﹣x=2(20﹣x)B.28+x=2(20+x)C.28+x=2(20﹣x)D.28﹣x=2(20+x)【分析】设应抽调x人去打扫操场,根据参加打扫操场的人数是参加清洗教室人数的2倍列出方程即可.【解答】解:设应抽调x人去打扫操场,根据题意列出方程为:28+x=2(20﹣x),故选:C.【点评】本题考查一元一次方程的应用,关键是根据参加打扫操场的人数是参加清洗教室人数的2倍列出方程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元一次方程应用题水箱变高了
一、水箱变高了:圆柱的体积=2π⨯⨯半径高
例1:某居民楼顶有一个底面直径和高均为4m 的圆柱形储水箱。
现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m 减少为3.2m 。
那么在容积不变的前提下,水箱的高度将由原先的4m 增高为多少米?
等量关系:旧水箱的容积=新水箱的容积
根据等量关系,列出方程: ()()224x ππ⨯⨯=⨯⨯
解得:x=
答:
变式练习:将一个底面直径是20厘米,高为9厘米的“矮胖”形圆柱锻压成底面直径是10厘米的“瘦长”形圆柱,
高变成了多少?
这个问题中的等量关系是:
解:
例2:用一根长为10m 的铁丝围成一个长方形.
(1)使得该长方形的长比宽多1.4m ,此时长方形的长、宽各为多少米?
(2)使得该长方形的长比宽多0.8m ,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比、面积有什么变化?
(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
例3:(1)小明的爸爸想用10米铁线在墙边围成一个鸡棚,使长比宽大4米,问小明要帮他爸爸围成的鸡棚的长和宽各是多少呢?
(2)若小明用10米铁线在墙边围成一个长方形鸡棚,使长比宽大5米,但在宽的一边有一扇1米宽的门,那么,请问小明围成的鸡棚的长和宽又是多少呢?
课后练习:
1、用直径为40mm 、长为1m 的圆钢,能拉成直径为4mm 、长为_______m 的钢丝。
2、用一根铁丝可围成一个长24厘米、宽12厘米的长方形。
若将它围成一个正方形,则这个 正方形的面积是( )
A 、81cm²
B 、18cm²
C 、324cm²
D 、326cm²
3、将底面直径为12厘米,高为30厘米的圆柱水桶装满水,倒人一个长方体水箱中,水只占水箱容积的32,设水箱容积为x 立方厘米,则可列方程_________________.
4、将一个底面直径是10厘米,高为40厘米的圆柱锻压成底面直径为l5厘米的圆柱,求它的高?若设高为x 厘米,则所列的方程为_____________.
5、把一块长、宽、高分别为5cm 、3cm 、3cm 的长方体铁块,浸入半径为4cm 的圆柱形水杯中(盛有水),水面将增高多少?(不外溢)
3.填空:
长方形的周长=_________. 面积=__________ .
长方体的体积=_________. 正方体的体积=__________.
圆的周长=___________. 面积=_______________.
圆柱的体积=_______________.
解决以下问题:
1.将一个底面直径是20厘米、高为9厘米的“矮胖”形圆柱锻压成底面直径为l0厘米的“瘦长”
形圆柱,高变成了多少?
假设在锻压过程中圆柱的体积保持不变,那么在这个问题中有如下的等量关系:锻压前的体积=锻压后的体积.
解:设锻压后圆柱的高为x米,填写下表:
根据等量关系,列出方程:___________________________________________.
解得
x_______________.
答:高变成了__________厘米.
2.用一根长为l0米的铁丝围成一个长方形.
(1)使得该长方形的长比宽多1.4米,此时长方形的长为________米,宽为_________米.
(2)使得该长方形的长比宽多0.8米,此时长方形的长为_______米,宽为_____米,它所围成的长方形与(1)中所围长方形相比,面积有什么变化?
(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是______米,它所围成的面积与(2)中相比又有什么变化?
二:典例讲练
例1.请根据图5—3—2中给出的信息,可得正确的方程是( )
【跟踪练习】
1.长方形的长是宽的3倍,如果宽增加了4 m,而长减少了5 m,那么面积增加15㎡,设长方形原来的宽为x m,则所列方程是( )
2.一块矩形草坪的长比宽多l0米,它的周长是132米,求宽x.所列的方程是( )
3.如图5—3—3,把一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积.
解:设正方形A的边长为x厘米,则
99
x
正方形B的边长为________厘米;
正方形C的边长为________厘米;
正方形D的边长为________厘米;
正方形E的边长为________厘米.
由题意可得方程:______________________.
解得x= ________,答:长方形的面积为___________平方厘米.
【当堂达标】
7.用直径为120 mm的圆钢铸造成5.9㎏的工件,已知每立方厘米的圆钢重7.8g,这样需截取圆钢的长是多少㎜?解题时,设需要截圆钢的长为x mm,那么下面列方程正确的是( )
8.为了做一个试管架,在长为a cm(a>6 cm)的木板上钻3个小孔(如图5—3—4),每个小孔的直径为2cm,则x等于( )
9.已知一个三角形三条边长的比为2:4:5,最长边比最短边长6㎝,则这个三角形的周长为( ) A.21㎝B.22㎝C.23㎝D.24㎝
10.墙上钉着用一根彩绳围成的梯形形状的饰物,如图5—3—8实线所示.小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图5—3—8虚线所示.小颖所钉长方形的长、宽各为
___________________厘米?
11.要锻造直径为16厘米、高为5厘米的圆柱形毛坯.设需截取边长为6厘米的方钢x厘米,可得方程为___________________________.
12.(2012.山西)图5—3—5是边长为30 cm的正方形纸板,裁掉阴影部分后将其折叠成如图5—3—5所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是________.
13·一个底面半径为4㎝,高为10㎝的圆柱形烧杯中装1 cm高的水.把烧杯中的水倒入底面半径为1㎝的圆柱形试管中,刚好倒满试管.问试管的高为多少㎝?
三:巩固练习
一、选择题
1.周长为68的长方形ABCD被分成7个全等的长方形,如图5—3—6所示,则长方形ABCD的面积为( )
A .98
B .196
C .280
D .284
2.用长为20米的铁丝围成一个长方形方框,使长为6.2
米,宽为x 米,则可列方程为 ( )
3.一个长方形的周长是40 cm ,若将长减少8 cm ,宽增加
2 cm ,长方形就变成了正方形,则正方形的边长为( )
A .6 cm
B .7 cm
C .8 cm
D .9 cm
4.有一个底面半径为10 cm ,高为30 cm 的圆柱形大杯中存满了水,把水倒人一一个底面直径为lo cm 的圆柱形小杯中,刚好倒满12杯,则小杯的高为 ( )
A .6 cm
B .8 cm
C .10 cm
D .12 cm
二、填空题
5.三角形三边长之比为7:5:4,若中等长度的一边长的两倍比其它两边长的和少3 cm ,则三角形的周长为_________________________.
6.将底面直径为12厘米,高为30厘米的圆柱水桶装满水,倒人一个长方体水箱中,水只占水箱容积的3
2,设水箱容积为x 立方厘米,则可列方程_________________. 7.将一个底面直径是10厘米,高为40厘米的圆柱锻压成底面直径为l5厘米的圆柱,求它的高?若设高为x 厘米,则所列的方程为_____________.
8.三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:㎝)如图5—3—7所示.则三个几何体的体积和为_____________3cm .(计算结果保留π)
三、解答题
9.将一个底面直径是10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖’’形圆柱,高变成了多少?
四、拓展应用
10.从两块分别重10千克和15千克且含铜的百分比不同的合金上各切下重量相等的一块,再把切下的每一块与另一块切后剩余的部分合在一起,熔炼后两者含铜的百分比恰好相等,则切下的一块重量是多少?。
