第4篇载波恢复和时钟恢复
理解载波恢复
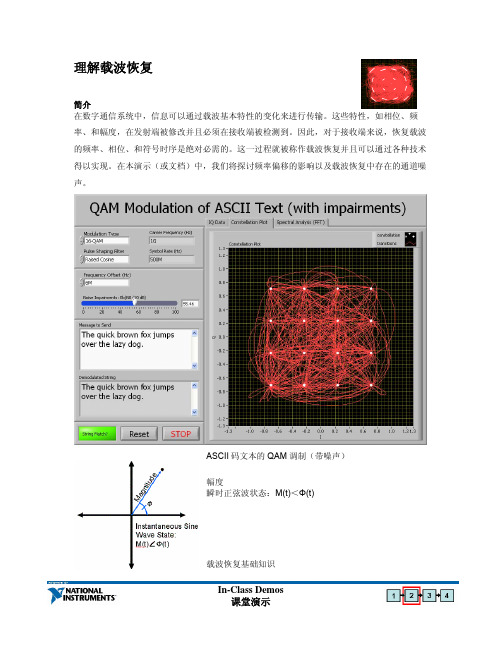
理解载波恢复简介在数字通信系统中，信息可以通过载波基本特性的变化来进行传输。
这些特性，如相位、频率、和幅度，在发射端被修改并且必须在接收端被检测到。
因此，对于接收端来说，恢复载波的频率、相位、和符号时序是绝对必需的。
这一过程就被称作载波恢复并且可以通过各种技术得以实现。
在本演示（或文档）中，我们将探讨频率偏移的影响以及载波恢复中存在的通道噪声。
ASCII 码文本的QAM 调制（带噪声）幅度瞬时正弦波状态：M(t)＜Φ(t)载波恢复基础知识In-Class Demos一个QAM 发送端使用特定的相位和幅度来调制载波信号，而另一方面，如果接收器能够确定原始信号的相位和频率，那它就能准确地检测到这个信号。
因此，两者之间的同步是必需的。
在理想情况下，发送端和接收端将会完美地同步工作。
换句话说，两者将会以同样的方式解释信号的相位和频率。
然而，实际的硬件并不是完美的，而且即使利用某种纠错机制，接收端也不可能精确地锁定到与发送端完全相同的相位和频率。
为了弥补这些不尽完美的特性，采用锁相环或PLL 来匹配接收端和发送端之间的频率（1）。
利用星座图，我们可以表示出每个符号的幅度和相位。
此外，每个符号覆盖在另一个符号之上是为了说明与我们所能恢复载波的相位和幅度之间的一致性。
理想情况下，当接收端的PLL 能够恢复载波，那么每个符号就会在星座图上清楚地分布。
然而，当载波由于通道噪声或频率误差的原因而无法恢复时，星座图也能表示来了。
在右边，我们示出了一幅符号出现在正确幅度处，但其相位正持续变化的星座图。
因为：Frequency = d Θ / dt频率= d Θ / dt所以，当星座图的相位持续变化时，我们能够确定频率估计是错误的。
在这个特定的实例中，我们已经通过在系统中引入足够的噪声来仿真频率误差，从而得以干扰PLL ，甚至将噪声去除之后，PLL 仍然可能无法锁定正确的频率。
载波恢复步骤解决这个载波恢复问题的方法有两个部分，它们可以粗略地分为以下两个部分：频率恢复和符号时序（相位）恢复。
第4篇载波恢复和时钟恢复.
平方差分SD算法及锁相环PLL算法都要求对接收信号 进行预处理。
能否有算法不做预处理？
第10章 载波恢复
思路： 1. 对接收信号r(kTs)=s(kTs) cos(2πf0kTs + 2 Φ)下 变换到 基带 即：LPF {r(kTs) cos(2πf0kTs + 2 θ)} 2. 再对变换的信号平方 （LPF {r(kTs) cos(2πf0kTs + 2 θ)}）2
第10章 载波恢复
此时的性能 函数为： JC(θ )= avg（LPF {r(kTs) cos(2πf0kTs + 2 θ)}）2 选择合适的低通滤波器的截止频率
JC(θ )= avg[1/2s(kTs)cos( θ- Φ)]2
=1/4avg[s 2(kTs)cos( θ- Φ)2 ]
故当代价函数极值化时，可得θ= Φ+n π
梯度算法方程为：
dJ SD ( ) [k 1] [k ] | [ k ] d
第10章 载波恢复
10.2 平方差分环路
dJSD ( ) davg[e 2 ( , k )] d [e 2 ( , k )] avg d d d d [e( , k )] 2avg{e( , k )} d avg{[ rp (kTs) cos(4f 0 kTs 2 )]sin(4f 0 kTs 2 )}
第10ቤተ መጻሕፍቲ ባይዱ 载波恢复
将r2 (kTs)通过以2f0为中心的窄带带通滤波器则 rp(kTs) = (1/2)s2 avgcos(4πf0kTs + 2Φ + φ) 其中φ为中心窄带带通滤波器的相位偏移
程序示例：pllpreprocess.m
第10章 载波恢复
载波恢复详解
为解调抑制载波相位键控(PSK)信号而设计的该相干载波恢复电路，涉及到多种权衡和性能考虑。
虽然有很多的方法是可用的，但本文将把焦点集中在一个多用途PSK解调器上，该解调器不需要改变任何结构，就能适用于不同的调制方案中的不同数据率。
这种解调器对卫星地面站接收来自具有不同有效载荷特性的各种遥感卫星的数据是很理想的。
图1展示了一个PSK解调器的简化结构。
它由一个输入自动增益控制(AGC)放大器、相干载波恢复电路和相干检波器组成。
中频(IF)信号加上噪声经带通滤波AGC放大器放大后,并行加到载波恢复电路和相干数据检波器上。
载波恢复电路再生了加到相干数据检波器的解调相干基准。
相干数据检波器提取了同相(I)和正交(Q)数据流,该数据流经低通滤波后，送到相应的位同步插件和信号调节器(BSSC)单元。
该BSSC单元恢复了用来使数据与符号时钟同步的相干符号时序。
在这种情况下，BSSC单元还提供串行数据和时钟输出。
利用如下的三种载波恢复电路之一，就能满足大多数应用场合：增倍环(像BPSK的平方环)、科斯塔斯(Costas)环和再调制环。
其它类型的载波恢复方案都是这些技术的延伸或改进。
例如，用于MPSK的增倍环(图2)是利用了先用带通滤波器滤除调制的第M阶非线性平方律函数。
一个传统的PLL，工作频率为M×f c，M是谐波乘数，f c是载波频率，锁定在非线性输出的第M谐波分量，而压控振荡器(VOC)除以M，以得到要求到的基准载波频率。
在BPSK Costas环(图3)中，通过将附加噪声的输入压缩载波分别与VCO的输出和经90度相移后的VCO输出信号相乘，对这两个乘积的结果进行滤波，并用这两个滤波后的信号的乘积去控制VCO信号的相位和频率。
当在I和Q臂的滤波器由积分陡落(integrate-and-dump)电路控制时,这个环叫做带有源滤波器的Costas环。
最佳的相位评估器需要在I路滤波器之后的双曲正切[tanh(KE b/N O)]非线性特性。
载波恢复技术(带图)
载波恢复技术及其相关算法4.1 载波恢复的基本原理在数字传输系统中，接收端解调部分通常采用相干解调(同步解调)的方法，因为相干解调无论在误码率、检测门限还是在输出信噪比等方面较非相干解调都具有明显优势。
相干解调要求在接收端必须产生一个与载波同频同相的相干载波。
从接收信号中产生相干载波就称为载波恢复。
相干解调的优越性是以接收端拥有准确相位的参考载波为前提的，如果频率有误差，解调就不能正常工作，如果相位有误差，解调的性能就会下降。
因为星座点数多的QAM(如64QAM,256QAM)对载波相位抖动非常敏感，所以对DVB-C 系统的QAM 调制方式来说，在接收端取得精确频率和相位的相关载波尤为重要。
在数字传输系统中，由于收发端的本振时钟不精确相等或者信道特性的快速变化使得信号偏离中心频谱，都会导致下变频后的基带信号中心频率偏离零点，从而产生一个变化的频偏，同时，信号的相位在传输中也会受到影响，引起信号的相位抖动。
为了消除因此产生的载波频偏Δf 和相偏Δθ，在数字传输系统接收端的QAM 解调器中需要通过载波恢复(Carrier recovery)环路来计算出信号中载波频偏与相偏，并将载波频偏与相偏的值反馈回混频器来消除载波频偏与相偏。
本文论述采用特殊的锁相环来获得相干载波的方法，其基本思想是：对于经过了下变频、滤波器、定时恢复和均衡之后的信号，应用盲载波恢复，通过利用锁相环，提取出频偏并且跟踪相偏。
4.2 载波恢复的具体方法以下介绍从抑制载波的己调信号中恢复相干载波的常用的方法：四次方环法、同相正交环法、逆调制环法、判决反馈环法。
4.2.1 四次方环四次方环[6]的基本方法是将接收信号进行四次方运算，然后用选频回路选出4c f 分量，再进行四分频，取得频率为c f 的相干载波。
具体的四次方环载波恢复框图如图4-1所示。
图4-1中接收到的射频信号与本地振荡器混频，在中频处理阶段进行滤波和自动增益控制后，升为四次幂，送入锁相环。
《面向400G的光通信的时钟与数据恢复电路设计》
《面向400G的光通信的时钟与数据恢复电路设计》面向400G光通信的时钟与数据恢复电路设计一、引言随着互联网的迅猛发展，对高速、大容量的光通信技术需求日益增长。
其中，400G光通信技术以其高速率和高效能的优势，成为了现代通信网络的关键技术之一。
在400G光通信系统中，时钟与数据恢复电路的设计显得尤为重要。
本文将探讨面向400G 光通信的时钟与数据恢复电路设计，以提高系统性能和可靠性。
二、时钟与数据恢复电路的重要性在光通信系统中，时钟与数据恢复电路是关键组成部分。
它负责从接收到的光信号中提取时钟信号和数据信息，以保证信号传输的同步性和准确性。
时钟与数据恢复电路的性能直接影响整个系统的传输速率、误码率和可靠性。
因此，优化设计时钟与数据恢复电路是提高400G光通信系统性能的关键。
三、设计要求与挑战在面向400G光通信的时钟与数据恢复电路设计中，需要满足以下要求：1. 高速度：电路必须能够处理高达400Gbps的数据速率，以满足高速传输的需求。
2. 低抖动：时钟信号的抖动必须尽可能小，以保证信号传输的稳定性和准确性。
3. 抗干扰能力强：电路应具备较好的抗电磁干扰和光噪声干扰能力，以保证在复杂电磁环境下的性能稳定性。
4. 低功耗：在保证性能的前提下，应尽量降低电路功耗，以延长设备使用寿命和降低运营成本。
然而，在实际设计中，面临诸多挑战。
例如，如何在高速传输中保持低抖动、如何提高电路的抗干扰能力以及如何在保证性能的同时降低功耗等。
这些挑战要求设计者具备深厚的电子工程知识和丰富的实践经验。
四、设计思路与方法为了满足上述设计要求，可以采取以下设计思路与方法：1. 采用先进的电路技术：如采用高速、低抖动的时钟恢复电路和高速、高灵敏度的数据恢复电路，以提高电路的性能和稳定性。
2. 优化电路结构：通过优化电路布局和参数设计，降低电路功耗，提高抗干扰能力。
3. 引入先进算法：如采用锁相环、自适应滤波等算法，实现时钟与数据的同步恢复和优化处理。
细说盲扫
细说”盲扫■刘广山《卫星电视与宽带多媒体》2006年第10期科普知识-技术实践卫星数字接收机的盲扫功能是非常有用的，在无法预知卫星信号的频率、符号率、前向纠错的收缩率等一系列参数的情况下，具备盲扫功能的接收机可以自动搜索到未知的信号参数，是非常方便和实用的功能。
普通的免费机加上这项功能之后，对于产品是一种功能上的升级。
有了这个功能，可以经常对卫星上的信号做一个扫描，发现新的信号，及时更新参数，信号的搜索会变得非常方便，同时也非常有趣。
配置盲扫功能的接收机，不仅可以扫描免费开放的一些信号，同时也可以检测一些加密传输信号，可以帮助我们更好的了解到这些信号的相关参数。
如何打开接收机的盲扫选项，在此前的很多文章中已经有很多的讨论和论述，在此不多讲，笔者下面仅仅就接收机如何找到卫星信号参数，实现盲扫功能的一些原理谈谈自己的一些观点。
QPSK的调制解调和盲扫的原理卫星接收机实现正确解调所需要的信号参数包括下面几项：极化方式、下行频率、符号率和前向纠错系数（卷积码的收缩率）等，其中的极化方式在线极化传输中无非是水平极化和垂直极化两种，接收机内部的CPU和控制电路配合就可以实现两种极化的倒换和接收，比较容易实现，也很容易理解，不会构成盲扫的门槛。
接收部分的解调电路和CPU配合需要识别和解出的参数主要是三项：下行频率、符号率和前向纠错系数。
这三个参数的识别和解码是在QPSK解调的部分完成的，目前经常用到的一些芯片，如STV0399、MT312C、ZL10312等都可以实现上述参数的盲扫。
现在生产的接收机比较倾向于使用板载的高频头，可以比较方便在接收机的线路板上看到这些芯片。
其它采用一体化高频头的机器，芯片位于高频头内，需要解体高频头才可以看到芯片。
本文在前半部分先对于上面提到的三个参数的盲扫机理做分析和讨论，后半部分将结合STV0399芯片对具体的集成电路芯片做一些探讨。
1、下行频率的盲扫卫星传输中采用的调制方式是QPSK，采用这种方式是和卫星传输距离远、信号衰减大、传输环境恶劣的传输特点相对应的，QPSK的调制和解调如图1和图2。
一种缓存控制的自适应时钟恢复的改进算法
一种缓存控制的自适应时钟恢复的改进算法刘秋明;江雷婧【摘要】文章介绍了TDMoIP(TDM over IP)技术中的一种基于去抖动缓存区自适应时钟恢复的改进算法,该算法将原算法的按固定周期长度调整接收端时钟频率改进为变长调整周期,通过改进算法和原算法的仿真对比,可以看出改进后的算法克服了原算法中的矛盾现象.最后对改进算法的性能进行分析,从理论上进一步验证了改进算法的优越性.【期刊名称】《光通信研究》【年(卷),期】2011(000)003【总页数】3页(P17-19)【关键词】TDM over IP;抖动缓存;时钟恢复算法【作者】刘秋明;江雷婧【作者单位】江西理工大学,南昌校区信息工程系,江西,南昌,330013;江西信息应用职业技术学院,江西,南昌,330043【正文语种】中文【中图分类】TN9150 引言TDMoIP(TDM over IP)技术是在时分复用(TDM)和互联网基础上发展起来的一种新的传输技术[1]，能够在IP网络上透明传输TDM业务，并可保证TDM业务的服务质量。
它是在网络接入口通过适配和封装TDM业务，将TDM同步比特流打成包，再加上IP头，封装成IP数据包，然后通过IP网络把这些数据包传输到目的地。
在目的地去掉数据包中的IP头，并重新生成同步时钟信号，把剩下的数据转化成TDM同步比特流发送出去。
本文研究了一种基于去抖动缓存区的自适应时钟恢复的改进算法，将原算法中的固定周期长度调整接收端时钟频率改进为变长调整周期，改进算法克服了固定周期长度调整算法的矛盾现象。
1 算法介绍在TDMoIP技术中，发送端按照固定比特长度封装TDM信息，在分组交换网上透明传输。
采用文献[2]中对TDMoIP的封装技术，用p(j)表示所产生的数据包，j 表示第j个数据包。
在接收端，用p(i)表示接收的数据包，i表示第i个数据包。
网络传输的抖动为q(i)=T(i)-T。
缓存大小函数为φ(k)，k表示第k个数据包接收完毕的时刻。
相位处理载波恢复算法研究
信 息 与 电 子 工 程
p( k ) = mod( ϕ k + θ k + nθ ( k ))
p( k + 1 ) = mod( ϕ k +1 + θ k +1 + nθ ( k + 1 ))
第1卷
两式相减，得
V ( k ) = mod( p( k + 1 ) − p( k )) %θ ( k )) = mod( ∆ϕ k + Ω + n %θ ( k ) = mod( nθ ( k + 1 ) − nθ ( k )) 其中： ∆ϕ k = mod( ϕ k +1 − ϕ k ) ， n
由式（5）计算 W(k)
判决
ˆk ∆ϕ
p(k)
由式（4）计算 Ω
k
估计算法
ˆ Ω k
图3
载波频率估计算法结构图
ˆ 的算法。 下面推导估计 Ω k +1
a) 统计平均法 假定在一段时间长度 NT 的观测区间内，已知载波频差 Ω 的 N 个观测值 Ω k − N +1 ,Ω k − N +2 ,L ,Ω k , 求估计值
第1卷 第2期 2003 年 6 月
信
息
与
电
子
工
程
INFORMATION AND ELECTRONIC ENGINEERING
Vol.1， No.2 Jun.,2003
文章编号：1672-2892(2003)02-0036-05
相位处理载波恢复算法研究
袁清升 1，刘 文2
(1.上海交通大学，上海 200030； 2. 哈尔滨工程大学, 黑龙江 哈尔滨 150001)
《面向400G的光通信的时钟与数据恢复电路设计》
《面向400G的光通信的时钟与数据恢复电路设计》面向400G光通信的时钟与数据恢复电路设计一、引言随着互联网技术的飞速发展，光通信技术作为信息传输的主要手段，正面临前所未有的挑战与机遇。
在众多光通信技术中，400G光通信以其高带宽、低延迟的特点，已成为现代通信网络的重要组成部分。
然而，随着数据传输速率的提升，时钟与数据恢复电路设计也面临更高的技术要求。
本文旨在探讨面向400G光通信的时钟与数据恢复电路设计的核心技术和关键方法。
二、时钟与数据恢复电路的基本原理时钟与数据恢复电路是光通信系统中的重要组成部分，主要负责从接收到的光信号中提取出时钟信号和数据进行恢复。
时钟信号用于同步数字电路的工作，而数据恢复则是将接收到的光信号转换为可用的电信号。
在400G光通信系统中，由于数据传输速率极高，因此对时钟与数据恢复电路的精度和稳定性要求也极高。
三、面向400G光通信的时钟电路设计1. 高速时钟提取技术：在400G光通信系统中，需要采用高速时钟提取技术从接收到的光信号中提取出高精度的时钟信号。
目前常用的高速时钟提取技术包括基于相位锁相环（PLL）的技术和基于锁频环（FLL）的技术。
这些技术可以根据接收到的光信号的特性进行选择和优化。
2. 抖动抑制技术：抖动是影响时钟信号稳定性的重要因素。
在400G光通信系统中，需要采用先进的抖动抑制技术来降低时钟信号的抖动，保证时钟信号的稳定性。
四、面向400G光通信的数据恢复电路设计1. 前置放大与滤波：接收到的光信号需要进行前置放大和滤波处理，以提高信号的信噪比和抗干扰能力。
这可以通过使用高性能的放大器和滤波器来实现。
2. 时钟数据恢复联合设计：在数据恢复电路中，需要同时考虑时钟信号和数据信号的恢复。
通过联合设计时钟与数据的恢复电路，可以实现更高的恢复精度和更低的误码率。
3. 均衡与解码：在数据传输过程中，由于信道的不完全匹配和干扰等因素，可能会导致接收到的数据信号发生失真和衰减。
数字载波调制实验报告(3篇)
第1篇一、实验目的1. 理解数字载波调制的基本原理和过程。
2. 掌握常见的数字调制方式，如振幅键控（ASK）、频移键控（FSK）和相移键控（PSK）。
3. 学习数字调制信号的生成和解调方法。
4. 通过实验，加深对数字调制技术在实际通信系统中的应用理解。
二、实验原理数字载波调制是数字通信中一种常见的信号处理技术，它通过改变载波的某些参数（如幅度、频率或相位）来携带数字信息。
常见的数字调制方式包括：1. 振幅键控（ASK）：通过改变载波的幅度来表示数字信息，通常用高电平表示“1”，低电平表示“0”。
2. 频移键控（FSK）：通过改变载波的频率来表示数字信息，通常用不同的频率分别表示“1”和“0”。
3. 相移键控（PSK）：通过改变载波的相位来表示数字信息，通常用不同的相位来表示不同的数字符号。
数字调制信号可以通过以下步骤生成：1. 基带信号生成：将数字信息转换成基带信号，通常为二进制序列。
2. 调制：将基带信号与载波信号相乘，得到已调信号。
3. 滤波：对已调信号进行滤波，去除不必要的频率分量。
数字调制信号的解调过程如下：1. 载波恢复：从已调信号中恢复出载波信号。
2. 解调：将恢复的载波信号与已调信号相乘，得到基带信号。
3. 判决：根据基带信号的幅度或频率，判断原始数字信息。
三、实验器材1. 数字信号发生器2. 数字示波器3. 数字信号分析仪4. 信号源5. 连接线四、实验步骤1. 实验一：ASK调制和解调- 使用数字信号发生器生成二进制序列。
- 将基带信号与载波信号相乘，得到ASK调制信号。
- 使用数字示波器观察ASK调制信号的波形。
- 将ASK调制信号与恢复的载波信号相乘，得到解调信号。
- 使用数字示波器观察解调信号的波形。
2. 实验二：FSK调制和解调- 使用数字信号发生器生成二进制序列。
- 将基带信号与两个不同频率的载波信号相乘，得到FSK调制信号。
- 使用数字示波器观察FSK调制信号的波形。
【精品】-一种时钟恢复算法的FPGA实现
2010年第08期，第43卷 通 信 技 术 Vol.43，No.08,2010 总第224期 Communications Technology No.224,Totally一种时钟恢复算法的FPGA实现王黎明①，苗 东②，何奎龙②(①海军装备部驻重庆地区军事代表局，重庆 400042；②四川九洲电器集团责任有限公司，四川 绵阳 621000)【摘 要】给出一种基于全数字接收机的加德纳时钟恢复算法的FPGA实现方法。
首先分析了该算法的系统结构及论述各个模块的作用，然后简要给出每个模块的硬件实现方法，其次用MATLAB对该算法进行仿真并给出仿真结果，结果表明该算法是可行的，最后在ISE9.1环境下编写Verilog HDL代码和测试激励，用ModelSim对该算法进行硬件仿真验证。
结果表明这种算法时钟抖动小，同步时间快，定时精度高，硬件实现比较简单。
该成果已经成功运用在某项目中。
【关键词】时钟恢复；现场可编程门阵列；法罗结构；加德纳算法【中图分类号】TN914【文献标识码】A【文章编号】1002-0802(2010)08-0067-03 FPGA-based Implementation of Timing Recover AlgorithmWANG Li-ming②， MIAO Dong②， HE Kui-long②(①Equipment Department, Chongqing Navy Military Representative Office, Chongqin 400042, China;②Sichuan Jiuzhou Electronic Group Co. Ltd., Chengdu Sichuan 621000, China)【Abstract】A FPGA-based implementation of Gardner timing recover algorithm in all-digital receiver is proposed. This paper first analyzes the system structure of the algorithm and discusses the role of each module, then briefly describes the hardware implementation of each module, including the algorithm simulation and simulation results with MATLAB, the results show that the algorithm is feasible practicable. Finally, Verilog HDL code is written and test incentive is done in ISE9.1 environment. Hardware simulation of the algorithm indicates that this algorithm is small in clock jitter, fast in synchronization time, precise in timing relatively simple in hardware implementation. Now the research result is successfully applied in certain project.【Key words】timing recover; FPGA; Farrow structure; Gardner algorithm0 引言接收机的时钟应该与输入信号的符号周期同步，才能准确采样接收的信号。
空间通信中GMSK信号的载波恢复与时钟同步
中应用最为广泛的两种环路。在环路设计中，环路捕获带宽和 环路锁定精度是相互矛盾的。尤其在空间通信中，接收信号往 往存在较大的多普勒频移和多普勒变化率，如火星探测任务中 多普勒频移最大可以达到 ９０ｋＨｚ左右，多普勒变化率最大达 到 １０００Ｈｚ／ｓ［７］。如果想要提高捕获范围大小，就意味着增加 环路噪声带宽，在低信噪比下增加环路噪声带宽会造成锁定精 度下降。因此，在实际应用中需要寻找折中的办法来达到工程 所需求的性能。与此同时自动频率控制环路同样可以完成某 些调制信号的载 波 恢 复 和 频 偏 估 计 ［８，９］，通 常 应 用 突 发 通 信， 载波恢复速度很快，在信噪比低的情况下往往锁定精度达不到 要求。
在实现载波恢复与频偏估计的工程应用中，文献［１０，１１］ 中提出使用通用数字环路对 ＧＭＳＫ调制信号进行载波恢复， 但是由于鉴相器具有正弦鉴相特性，在较大误差信号下，鉴相 曲线并非呈现线性特性。文献［１２］中提出基于 ＦＰＧＡ线性鉴 相全 数 字 锁 相 环，采 用 数 字 计 算 机 算 法 （ｃｏｏｒｄｉｎａｔｅｒｏｔａｔｉｏｎ ｄｉｇｉｔａｌｃｏｍｐｕｔｅｒ，ＣＯＲＤＩＣ）实 现 线 性 鉴 相 范 围 的 扩 展。 而 针 对 空间通信 中 出 现 的 大 多 普 勒 频 移。 文 献 ［１３］提 出 一 种 基 于
ＣａｒｒｉｅｒｒｅｃｏｖｅｒｙａｎｄｃｌｏｃｋｓｙｎｃｈｒｏｎｉｚａｔｉｏｎｏｆＧＭＳＫｓｉｇｎａｌｓｉｎ ｓｐａｃｅｃｏｍｍｕｎｉｃａｔｉｏｎｓ
ＴａｎｇＺｈｉｌｉｎｇ，ＺｏｕＸｉｎ，ＬｉＳｉｍｉｎ
（ＧｕａｎｇｘｉＫｅｙＬａｂｏｒａｔｏｒｙｏｆＷｉｒｅｌｅｓｓＢｒｏａｄｂａｎｄＣｏｍｍｕｎｉｃａｔｉｏｎ＆ ＳｉｇｎａｌＰｒｏｃｅｓｓｉｎｇ， ＧｕｉｌｉｎＵｎｉｖｅｒｓｉｔｙｏｆＥｌｅｃｔｒｏｎｉｃＴｅｃｈｎｏｌｏｇｙ， Ｇｕｉｌｉｎ Ｇｕａｎｇｘｉ５４１００４，Ｃｈｉｎａ）
相干检测载波恢复算法的概述
相干检测载波恢复算法的概述摘要：随着互联网流量的日益增长，部署更高数据速率和大容量的光传输系统已成为势在必行。
然而，偏振模色散和信道内的非线性效应使信号质量明显变差，基于直接检测系统将不再满足高质量的接收性能要求。
前瞻性的研究进展明确指出，与数字信号处理(DSP)技术的结合将使相干检测技术更加具有吸引力。
在相干检测DSP算法中，载波恢复是必不可少的。
对调相信号,载波与本振间的频率和相位偏移会使信号产生较大的相位失真,为了保证信息的可靠传输，对载波频率偏移和相位偏移估计方法的研究与改进具有重要意义。
关键词：偏振模色散；光传输；相干检测；DSP；载波恢复1、前言在当今的信息化、网络化时代，随着社会科技水平的进步和人们生活水平的提高，人们对通信业务的需求及通信质量的要求越来越高。
第四代移动通信系统（4G）在全球范围内已经广泛应用，它是一种能够提供多种类型、高质量的多媒体业务，可以实现全球无缝隙覆盖，具有全球漫游能力，并且与固定网络相互兼容，用终端设备可以在任何时候、任何地点与任何人进行任何形式通信的移动通信系统。
然而随着技术的不断发展和用户对新业务的需求的不断提升，更高速、更高质量和超大容量成为了通信领域发展所追求的主要目标。
目前，电信正以惊人的速度在发展，而光纤通信是电信中发展最快、最具有活力的部分之一。
在当前的通信网络构架中，光通信系统，特别是光纤通信系统在容量、速率和传输距离方面表现出强大的优势，使其逐渐占据了通信舞台的主角地位。
在20世纪80年代末期和90年代初期，相干系统曾经是重要的技术，但在20世纪90年代末期，由于光放大器的出现，对相干系统的研究出现了停滞。
近年来，随着数字信号处理(Digital Signal Processing,DSP)技术的发展和低成本器件的出现，使得相干接收技术的研究又开始火热起来，这主要是因为相干系统可在高数据速率条件下降低对接收机的要求以及相干接收所具有的一些独特优势。
载波恢复的基本原理
载波同步技术平方法 抑制载波的双边带信号中插入导频科斯塔斯环 残留边带信号中插入导频 时域插入导频法 性能指标 两种载波同步方法的比较提取载波的方法一般分为两类：一类是不专门发送导频，而在接收端直接从发送信号中提取载波，这类方法称为直接法，也称为自同步法；另一类是在发送有用信号的同时，在适当的频率位置上，插入一个（或多个）称作导频的正弦波，接收端就利用导频提取出载波，这类方法称为插入导频法，也称为外同步法。
直接法（自同步法）有些信号（如抑制载波的双边带信号等）虽然本身不包含载波分量，但对该信号进行某些非线性变换以后，就可以直接从中提取出载波分量来，这就是直接法提取同步载波的基本原理。
下面介绍几种直接提取载波的方法。
设调制信号为()m t ，()m t 中无直流分量，则抑制载波的双边带信号为()()cos c s t m t t ω= （7-1）接收端将该信号进行平方变换，即经过一个平方律部件后就得到2222()1()()cos ()cos 222c c m t e t m t t m t t ωω==+（7-2）由式（7-2）可以看出，虽然前面假设()m t 中无直流分量，但2()m t 却一定有直流分量，这是因为2()m t 必为大于等于0的数，因此，2()m t 的均值必大于0，而这个均值就是2()m t 的直流分量，这样e (t )的第二项中就包含2c f 频率的分量。
例如，对于2PSK 信号，()m t 为双极性矩形脉冲序列，设()m t 为±1，那么2()m t =1，这样经过平方率部件后可以得到2211()()cos cos 222c c e t m t t t ωω==+（7-3）由式（7-3）可知，通过2c f 窄带滤波器从 ()e t 中很容易取出2c f 频率分量。
经过一个二分频器就可以得到c f 的频率成分，这就是所需要的同步载波。
因而，利用图7-1所示的方框图就可以提取出载波。
高速数据传输中的载波恢复和位同步技术研究
目录摘要 (i)ABSTRACT (ii)第一章绪论 (1)1.1 研究背景和意义 (1)1.2 国内外发展现状 (2)1.2.1 小卫星数据传输系统的发展 (2)1.2.2 载波恢复技术 (3)1.2.3 位同步技术 (3)1.3 论文研究内容 (4)第二章星载高速调制解调方法研究 (5)2.1 数字调制解调技术的基本原理 (5)2.2 调制解调方式的选择 (6)2.2.1 功率有效性和恒包络调制 (6)2.2.2 频带利用率 (6)2.3 QPSK调制解调原理 (7)2.3.1 QPSK调制原理 (7)2.3.2 QPSK解调原理 (12)2.4 数字锁相环原理 (13)2.5 本章小结 (16)第三章QPSK高速载波恢复技术 (17)3.1 载波恢复简述 (17)3.2 QPSK载波恢复算法 (17)3.2.1 M次方环法 (17)3.2.2 逆调制环 (18)3.2.3 Costas环法 (19)3.3 载波恢复性能仿真 (22)3.3.1 载波恢复性能指标 (22)3.3.2 参数设定和仿真 (23)3.4 本章小结 (26)第四章QPSK高速位同步技术研究 (27)4.1 位同步技术概述 (27)4.2 Gardner位同步算法 (28)4.2.1 定时误差检测器 (28)4.2.2 插值控制器 (29)4.2.3 插值滤波器 (30)4.3 位同步性能仿真 (33)4.3.1 环路滤波器阶数对同步性能的影响 (34)4.3.2 插值滤波器的类型对同步性能影响 (36)4.3.3 信噪比对同步性能影响 (38)4.3.4 位同步误差检测的载波独立性验证 (39)4.4.1 系统性能指标 (42)4.4.2 仿真性能和分析 (43)4.5 本章小结 (44)第五章基于软件无线电的宽带数据收发实验平台设计 (45)5.1 实验平台简介 (45)5.1.1 硬件平台 (45)5.1.2 软件平台 (50)5.2 实验算法 (50)5.2.1 调制算法实现 (50)5.2.2 解调算法实现 (52)5.3 实验结果 (53)5.4 本章小结 (55)第六章总结与展望 (56)6.1 论文总结 (56)6.2 下一步工作展望 (56)致谢 (58)参考文献 (59)作者在学期间取得的学术成果 (63)附录A 实验算法源代码 (64)A.1 载波恢复锁相环部分程序 (64)A.2 位同步部分程序 (65)表2.1 几种调制方式的性能比较 (7)表2.2 QPSK调制编码 (8)表3.1 载波恢复仿真结果 (26)表4.1 立方插值法的Farrow结构系数 (33)表4.2 分段抛物线法的Farrow结构系数 (33)表5.1 AD9125主要参数 (46)表5.2 AD9361主要参数 (47)表5.3 Artix-7系列FPGA的资源 (48)图2.1 QPSK调制信号矢量图 (8)图2.2 QPSK调制原理图 (9)图2.3 升余弦滚降滤波器特性曲线 (11)图2.4 QPSK信号成型滤波前后频谱 (12)图2.5 高速并行相干解调原理图 (13)图2.6 QPSK解调原理 (13)图2.7 锁相环基本结构 (14)图2.8 数字锁相环的相位模型 (14)图2.9一阶数字环路滤波器的原理框图 (15)图3.1四次方环原理结构图 (18)图3.2 逆调制环 (19)图3.3 QPSK的基础Costas环 (19)图3.4 硬判决型Costas环 (21)图3.5 四相松尾环 (21)图3.6不同Costas环的鉴相特性曲线 (22)图3.7 QPSK载波恢复性能仿真 (25)图4.1前馈型数字位同步原理图 (27)图4.2反馈型数字位同步原理图 (27)图4.3 Gardner环路框图 (28)图4.4 Gardner位定时关系 (29)图4.5 NCO关系图 (30)图4.6 Farrow结构图 (32)图4.7 线性插值滤波器结构 (33)图4.8 一阶位同步环路性能 (35)图4.9 二阶位同步环路性能 (36)图4.10 线性插值滤波器的位同步性能 (37)图4.11 SNR=5时位同步误差性能 (38)图4.12 信噪比对位同步性能的影响 (39)图4.13 载波相差对位同步的影响 (40)图4.14 载波频差对位同步的影响 (41)图4.15 QPSK载波恢复和位同步模块耦合框图 (42)图4.16 系统误比特率曲线 (43)图5.2 AD9125调制实现 (46)图5.3 平台发送链路实物图 (49)图5.4 平台接收链路实物图 (49)图5.5 收发实验平台实物图 (49)图5.6 发送链路硬件实现结构 (51)图5.7 QPSK调制硬件实现结构 (51)图5.8 接收链路程序流程图 (52)图5.9 接收链路硬件实现结构 (52)图5.10调制信号频谱 (53)图5.11 实验平台的载波恢复结果 (54)图5.12实验平台的位同步结果 (54)图5.13解调过程中的信号 (54)摘要小卫星的蓬勃发展推动了卫星数据服务业的繁荣，随着卫星载荷分辨率的提高，下行数据量随之增长，而软件定义卫星的兴起也对小卫星的数据上注能力也提出了更高的要求。
超高速数码信号传输中的时钟恢复技术研究
超高速数码信号传输中的时钟恢复技术研究引言随着数字通信技术的进步和智能设备的不断出现，对于高速数据传输的需求也越来越大。
超高速数码信号传输中的时钟恢复技术是实现高速数据传输的关键技术之一。
本文将从时钟恢复技术的基本概念、原理和分类，时钟恢复技术在超高速数码信号传输中的应用以及研究进展等方面进行阐述和分析。
第一章时钟恢复技术的基本概念、原理和分类1.1 什么是时钟恢复技术时钟恢复技术是将接收机收到的信息进行采样，并根据采样的结果恢复出原信号的时钟信息，以保证正确的解析数据。
由于信号的传输存在着很多的不确定性，如信号失真、抖动、滞后……等，因此，时钟恢复技术在实际通信中显得十分重要，也是一项非常复杂的技术。
1.2 时钟恢复技术的原理对于高速信号，在信号传输过程中，由于存在着噪声、失真、抖动等因素，经过传输的信号时钟可能与原信号时钟有一定偏移，采样时钟与信号时钟之间也有可能存在较大的相位偏移。
因此，正确恢复原信号时钟信息是非常关键的。
时钟恢复技术的实现原理主要有两种方法：基于锁相环（PLL）的时钟恢复和基于延迟锁定环（DLL）的时钟恢复。
基于PLL的时钟恢复主要利用自适应滤波器将误差信号反馈到VCO来调整与发射时钟的相位，从而实现时钟的恢复。
而基于DLL的时钟恢复则是将接收到的信号和本地时钟进行延时，并将两路信号进行比较，通过调节延时量来实现时钟的恢复。
两种方式具有不同的优缺点，具体的应用需根据具体情况选择。
1.3 时钟恢复技术的分类时钟恢复技术根据采样时钟和数据时钟的关系，一般可分为三类：边沿对齐、符号同步和自适应时钟恢复。
边沿对齐主要是将参考时钟与接收到的时钟进行相位对齐，当接收到的时钟存在相位偏移，需要根据已知的速率调整时钟相位。
符号同步是指通过接收机对已传输数据的边界进行识别，并根据此对时钟相位进行调节。
自适应时钟恢复则是通过自适应算法将参考时钟与接收到的时钟进行相位同步。
第二章时钟恢复技术在超高速数码信号传输中的应用时钟恢复技术在高速通信中广泛应用于多种领域，特别是在超高速网络、高速存储系统、视频传输等领域中则有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第10章 载波恢复
科斯塔斯环的梯度算法方程为： dJ C ( ) [k 1] [k ] | [ k ] d
dJC ( ) avg d dLPF{rp (kTs) cos(2f 0 kTs 2 )}2 d dLPF{rp (kTs) cos(2f 0 kTs 2 )}
第12章 时钟恢复
符号定时理想时，τ=0；采样间隔时间为M=1T 此时综合信道的冲激响应为奈奎斯特脉冲
符号定时非理想时，输出
第12章 时钟恢复
考虑三种情况 1）τ=0 2）τ〉0 3）τ<0 τ=0
第12章 时钟恢复
τ=0 x[k]=s[k-1],系统为纯有两个非零点h(τ0), h(T+τ0) 。 冲激响应的采样值为
f [k 1] f [k ]
第10章 载波恢复
图10-17 频率估计算法开始收敛，但过一段时间 后，估测值与预期值越离越远。 讨论其代价函数： 1 1 J ( f ) LPF{1 cos(4f 0t ) cos(4ft ) 2 2 cos[4 ( f 0 f )t ] cos[4 ( f 0 f )t ]}
习题： P149: 由P149页的dullplls.m程序，试写程序来恢复载 波频率大小？ 第10章习题，提交电子文档。zhongjun55@ 邮件题目：姓名第10章习题。 如：王东第10章习题
第11章 脉冲成形与滤波
脉冲及脉冲幅度调制的频谱 眼图 奈奎斯特脉冲 匹配滤波器 传输和接收匹配滤波器
第10章 载波恢复
将r2 (kTs)通过以2f0为中心的窄带带通滤波器则 rp(kTs) = (1/2)s2 avgcos(4πf0kTs + 2Φ + φ) 其中φ为中心窄带带通滤波器的相位偏移
程序示例：pllpreprocess.m
第10章 载波恢复
10.2 平方差分环路 经预处理的信号为： rp(kTs) = (1/2)s2 avgcos(4πf0kTs + 2Φ + φ) 现理想化方程 rp(t)=cos(4πf0kTs + 2θ) 并选择代价函数为： Jsd(θ)=avg{e2 (θ,k)} =1/4{(rp(kTs) - avgcos(4πf0kTs + 2 θ)} 2
第10章 载波恢复
10.6 频率跟踪 10.6.1 直接频率估测 设接收信号
1 r (t ) LPF r (t ) cos( 2ft 2
f f [k ]
利用梯度算法：
dJ ( f ) f [k 1] f [k ] df
LPF 2kTs r (kTs cos(2kTs f [k ]) sin(2kTs f [k ])
第10章 载波恢复
科斯塔斯环相位跟踪算法程序示例： costasloop.m
第10章 载波恢复
10.5 直接判决相位跟踪 x(t)=2LPF{s(t) cos(2πf0kTs + Φ ) cos(2πf0kTs + θ)
此时的性能 函数为：
JDD(θ )=1/4 avg{(Q(x[k])-x[k])2]}
[k 1] [k ] avg{[rp (kTs) cos(4f 0 kTs 2b)]sin(4f 0 kTs 2 )}
第10章 载波恢复
程序示例：pllsd
平方差相位跟踪算法的框图
第10章 载波恢复
10.3 锁相环路
利用已知频率为2f0,相位为2Φ + φ的余弦信号，调制 预处理的rp(t)，并通过低通滤波器。
第11章 脉冲成形与滤波
11.3眼图：
第11章 脉冲成形与滤波
11.3不同汉明窗宽度所对应的眼图：
第11章 脉冲成形与滤波
11.4奈奎斯特脉冲：一个脉冲与另一个脉冲在以T间 隔的采样时间内不发生混叠。
宽度小于T的矩形脉冲是奈奎斯特脉冲
第11章 脉冲成形与滤波
SINC脉冲
1. 2. 3. 4.
第12章 时钟恢复
τ <0 在冲激响应的采样点中有两个非零点h(2T+τ0), h(T+τ0) 。 冲激响应的采样值为
d d{rp (kTs) cos(2f 0 kTs 2 )} d
2avgLPF{rp (kTs) cos(2f 0 kTs 2 )}
2avgLPF{rp (kTs) cos(2f 0 kTs 2 )}LPF
第10章 载波恢复
科斯塔斯环的梯度算法方程为：
2avgLPF {rp (kTs) cos(2f0kTs 2 )}LPF{rp (kTs) sin(2f0kTs 2 )}
第10章 载波恢复
梯度算法方程为：
dJ PLL ( ) [k 1] [k ] | [ k ] d
dLPF{rp (kTs) cos(4f 0 kTs 2 } dJPLL ( ) | [ k ] | [ k ] d d LPF d{rp (kTs) cos(4f 0 kTs 2 } d | [ k ]
JPLL(θ )=1/2LPF{r(kTs) cos(4πf0kTs + 2θ + ψ)} =1/2LPF{cos(4πf0kTs + 2Φ + φ) cos(4πf0kTs + 2θ + ψ)} = 1/4LPF{cos(2Φ - 2θ )cos(8πf0kTs + 2Φ +2θ +2 φ)} = 1/4cos(2Φ - 2θ ) 故当代价函数极值化时，可得θ= Φ
第10章 载波恢复
载波恢复 对于大载波条件下的AM调制. 应用FFT来恢复载波与相位，（想一想，为什么?） 对于抑制载波条件下的AM调制. 应用FFT来恢复载波与相位时，不能恢复相位偏移 量，且频谱最大值经常不出现在载波频率上 ，（想 一想，为什么?）
第10章 载波恢复
对于抑制载波条件下的AM调制可采用预处理方法 r2(kTs) = (1/2)s2(kTs)[1 + cos(4πf0kTs + 2 Φ)] 将s2(t)用平均值和偏移量的和来表示 s2 (kTs) = s2avg + v(kTs) r2 (kTs) =1/2s2 (kTs)[1 + cos(4πf0kTs + 2 Φ)]= (1/2)[s2avg +v(kTs)+s2avgcos(4πf0kTs +2 Φ) +v(kTs)cos(4πf0kTs + 2 Φ)]
第10章 载波恢复
相位跟踪 平方差分 锁相环 科斯塔斯环 直接判决相位 频域跟踪
第10章 载波恢复
第10章 载波恢复
接收机的载波不同步时：当只有相位不同步
第10章 载波恢复
接收机的载波不同步时：当只有频率不同步
第10章 载波恢复
自适应方法 找到代价函数 检查调整参数是否达到最优 应用梯度算法，其中最关键的是计算更新因子 检查性能
第11章 脉冲成形与滤波
第11章 脉冲成形与滤波
11.1脉冲的频谱： 当上变频与下变频准确执行时。 可以下述基带模型来描述。
第11章 脉冲成形与滤波
发送端离散序列转换成模拟脉冲串。
成形滤波器的输出：
第11章 脉冲成形与滤波
汉明窗的时域图形：
第11章 脉冲成形与滤波
汉明窗的频域图形：
第11章 脉冲成形与滤波
经脉冲成形后的输出： （汉明窗宽度等于符号周期，过采样率M=10)
第11章 脉冲成形与滤波
11.2码间干扰： 脉冲宽度大于符号周期。 存在多径干扰。 示例：过宽脉冲引起的码间干扰
第11章 脉冲成形与滤波
汉明窗宽度是符号周期的3倍宽时：
第11章 脉冲成形与滤波
汉明窗宽度是符号周期的3倍宽时，4PAM信号的输出：
平方差分SD算法及锁相环PLL算法都要求对接收信号 进行预处理。
能否有算法不做预处理？
第10章 载波恢复
思路： 1. 对接收信号r(kTs)=s(kTs) cos(2πf0kTs + 2 Φ)下 变换到 基带 即：LPF {r(kTs) cos(2πf0kTs + 2 θ)} 2. 再对变换的信号平方 （LPF {r(kTs) cos(2πf0kTs + 2 θ)}）2
LPF{rp (kTs) sin(4f0kTs 2[k ] )}
第10章 载波恢复
梯度算法方程为：
[k 1] [k ] LPF{rp (kTs) sin(4f0kTs 2[k ] )}
程序示例：pllconverge.m
第10章 载波恢复
10.4 科斯塔斯环
第10章 载波恢复
此时的性能 函数为： JC(θ )= avg（LPF {r(kTs) cos(2πf0kTs + 2 θ)}）2 选择合适的低通滤波器的截止频率
JC(θ )= avg[1/2s(kTs)cos( θ- Φ)]2
=1/4avg[s 2(kTs)cos( θ- Φ)2 ]
故当代价函数极值化时，可得θ= Φ+n π
J ( f ) 1 LPF{cos[2 ( f0 f )t}
第10章 载波恢复
10.6.2 间接频率估测
第10章 载波恢复
10.6.2 间接频率估测
第一支路的锁相环： 1 (t ) 2 ( f 0 f c )t b
第二支路振荡器输出 ：
sin(4ft 21 (t ) 22 (t )) sin(4f 0t 2b 22 (t ))
直接判决相位跟踪算法方程为：
dJ DD ( ) [k 1] [k ] | [ k ] d