圆弧过渡
小砖块铺装道路转角圆弧过度的施工方法

小砖块铺装道路转角圆弧过度的施工方法
小砖块铺装道路转角圆弧过度的施工方法一般可以分为以下几个步骤:
1. 准备工作:确定转角圆弧的位置和尺寸,并在该位置清理好地面,去除杂物和积土。
确定好砖块的颜色和种类,准备好所需的工具和材料。
2. 检测地面水平:使用水平仪或尺具检测转角圆弧所在地面的水平度,确保其平整度,必要时进行调整。
3. 制作圆弧模板:根据转角圆弧的半径和弧度,制作一个木质或金属模板,用于指导铺设砖块的位置和角度。
模板应该与转角圆弧的形状相匹配。
4. 铺设砖块:根据模板的指引,逐个铺设砖块。
在开始铺设之前,可以先在地面上涂一层薄薄的水泥浆,以增加砖块的粘性和稳定性。
将砖块逐层紧密铺设,确保它们与模板的形状和角度相符。
使用橡胶锤和水平仪来调整砖块的位置和水平度。
5. 填充缝隙:完成砖块的铺设后,使用沙子或砂浆填充砖缝。
将砂浆或沙子均匀地填入砖缝中,使用拓宽刀或扫帚清除多余的沙子,使整个铺装表面平整、美观。
6. 整理边缘:最后,对转角圆弧的边缘进行整理和修整。
使用锤子和凿子,将砖块的边缘打磨成圆弧形状,使其与转角圆弧相吻合。
检查铺装质量和均匀性。
请注意,施工方法可能因具体情况而有所不同,建议在进行转角圆弧过渡铺装之前,先咨询专业人士或就地方进行详细分析和规划。
阶梯型变幅杆圆弧过渡动力学分析

【 摘
要】 阶梯型变幅杆 由于加工简单, 易修正, 放大比大等优点 , 用较广, 应 然而由于大小端过渡
处 的应 力、 位移 分布 比较 复杂 , 而导致谐 振频 率 小于理论 频 率 , 从 一直 制约 着其在 实际生产 中的运 用 。 本 文通过 A ss 限元 分析 软件 对 阶梯 形 变幅杆 大 小端 突 变处添加 不 同的过 渡 圆弧 , ny 有 综合 比较 、 分析
将 () 带人() 可得 : 7式 6式
S tn L + ,a k 0 ,a k 5 tn L
() 7
( 8)
为了进一步研究 阶梯型变幅杆在相同放大 比时 ,大端直径 对频率和应力的影响 , 我们又对大端半径为 2 mm,5 m的阶梯 0 1r a 型变幅杆进行 了有限元分析 , 结合半径 为 2mm, 8 其频率 、 应力分 析结果 的做了, 如图 3 所示 。
小端的位移分布 :
() 2ok+ 2i xO x L ) csxB s k ( < < 2 n _ _ () 6
变幅杆 大端位移为换能器输出最大值 ,小端理论上为输 出 端最大值 , 渡段初步认 为位移和应力是连续的 , 且过 可得边界条 件:
( 。 ( ) ; () ( ) 。0 () ) L -  ̄o - " o; o。 s () z 0
Z ENG n a W ANG h-y n LV n Fa -fn. S i i g. Mi g
( iu n Unv ri f c n lg , iest f n n Tay a ies yo Te h oo y Unv ri o ig& T c n lg , ay a 3 0 4, ia t y Mi e h oo y T iu n0 0 2 Chn )
零件过渡圆弧的切点坐标计算参数化

零件过渡圆弧的切点坐标计算参数化摘要:台阶轴类零件,大多在台阶的过渡区采用圆弧加斜面的过渡结构,该类零件如果选用数控车床加工,在编制加工程序时,需要计算出过渡圆弧与接触面的切点坐标值,计算过程较为复杂,有时因计算错误而造成零件报废,且效率较低。
通过对该种零件的结构进行分析,利用excell的一些特有功能,将计算参数化,可视化,大大提高了计算的准确率和效率。
关键词: 过渡圆弧切点坐标 excel 参数化一.引言在机械加工行业中,经常会遇到一些台阶轴类零件,在台阶的过渡区,大多采用圆弧加斜面的过渡结构,如果选用数控车床加工,在编制加工程序时,需要计算出过渡圆弧与接触面的切点坐标值,常规计算方法大多采用公式和计算器计算的方法,也有采用AutoCAD软件进行一比一比例作图,然后利用软件本身的测量功能进行实际测量,依据实际测量结果确定切坐标值。
并且每项产品、每项产品的每个过渡区均需要计算或制图,但不管哪种方法,都有因人为因素犯错而造成零件报废,且效率较低。
通过对该类种零件的结构进行分析,找出共同特征,利用excell软件的一些独特功能,实现输入参数而迅速得出想要计算结果的功能,从而避免人为计算的错误,还大幅提高了工作效率。
二.台阶轴类零件圆弧过渡结构特点分析1.台阶轴类零件圆弧过渡结构的特点在生产实际中,经常会遇到台阶轴类零件,为了增加该类零件的强度,台阶过渡区大多采用圆弧加斜面的过渡结构。
如图1所示。
图1 台阶轴类零件结构图该类零件通常存在以下几个方面的特点:1)该类零件各外圆间存在阶差。
2)台阶过渡区有斜面和圆弧过渡。
3)不同的零件或同一零件的不同部位过渡区的圆弧半径R值不同。
4)不同的零件或同一零件的不同部位过渡区的斜面角度α值不同。
5)圆弧与两面的交点(切点)坐标尺寸在制造图纸中均未给出。
2.数控车编程时所需要的参数及常规计算方法1)数控车编程时所需要的参数目前,很多机械加工厂家大多还采用手工编程的方法,所以对零件中的一些参数必须提前确定好,并计算出结果,以便于接下来的编程及加工。
高速加工轨迹拐角速度平滑处理讲解

弓高误差
1 42 l2
2
V l 2 2 ( )2
TT
max为共建允许的最大弓高误差,2 VF )
V2 T
2 ( max)2
(2 T
2 ( max)2 VF )
弓高误差约束法——直接近似法
式中,VF 为数控程序段中的进给速度;
题目:高速加工轨迹拐角速度平滑处理
高速加工过程中,要求数控系统确保机床运 动的平稳性, 防止较大冲击载荷影响零件的加工质 量, 并保护机床的进给系统,需要在加工轨迹拐角 处进行速度的平滑处理,本文将运用直接转接法、 圆弧过渡法和弓高误差约束法对高速数控加工轨 迹的拐角进行速度平滑处理。
高速加工理论是由德国物理学家萨洛蒙于 1931年提出的,当其切削速度达到一定数值后, 切削力、切削温度以及切削变形会迅速变小,加 工表面质量也会得到极大提高,甚至无需光整加 工。且实践证明,高速加工可以成倍提高生产效 率。
Thank you !
a
t
2V2
sin
2
(
)
直接转接法
式中,t 为机床数控系统的插补周期 T ,amax为机 床数控系统设置的最大加速度,是一个确定值,建立 约束条件
0 a amax
V2
T
amax
2 s in
2
圆弧过渡法
圆弧过渡法是在程序间用圆弧来处理拐角的速度。 通过限制小圆弧的最大法向加速度来限制拐角的速 度,同时考虑精度影响。根据运动学的有关公式, 圆周运动的进给法向加速度为
高速加工同时也给数控系统带来一定的挑战, 若再加工区域中存在尖锐的拐角或是高曲率路径时, 由于高速加工的进给速度都比较高,很容易产生过 切、拐角处表面质量不好等情况。因此,对加工轨 迹中的拐角进行平滑处理是很有必要的,在本文中 将运用直接转接法、圆弧过渡法和弓高误差约束法 对加工轨迹中的拐角进行平滑处理。
基于圆弧过渡的五段S型加减速算法

文章编号
Modular Machine Tool & Automatic Manufacturing Technique
D01 : 10.13462/j. cnki. mmtamt. 2017. 03.002
组合机床与自动化加工技术
No. 3 Mar. 2017
: 1001 -2265(2017)03 -0006 - 04
〇 引言
在复杂曲面的高速加工中, 通常根据允许误差、 机 床动力学等约 束 条件使用 CAD/ CAM 把复杂曲面离散 成一系列连续微小线段。有很多因素影响微小线段间 的加工效率和加工质量, 例如在离散过程中并未充分 考虑微小线段间的平滑过渡等。因此在高速高精数控 加工中, 如果数控系统严格执行编程指令, 对相邻微小 线段间的轨迹和转接速度不做平滑过渡处理, 可能会 引起系统的频繁启停, Xt机床造成很大的冲击, 并且难 以在保证加工质量的前提下, 提高加工效率[1]。 目前常用的加减速控制算法有直线加减速算 法 [7]、 S 型加减速算法[84°]、 多项式加减速算法[11]。直 线加减速算法的加速度在启停及加减速结束时存在突 *
prove the efficiency of processing and reduce the impact on machine as the same time. Experimental results show that the algorithm enables the machine drive in higher speed between the switching, extending the life of the machine tools, improving flexibility of the system.
浅议数控车削中刀尖圆弧过渡刃对车削圆弧的影响
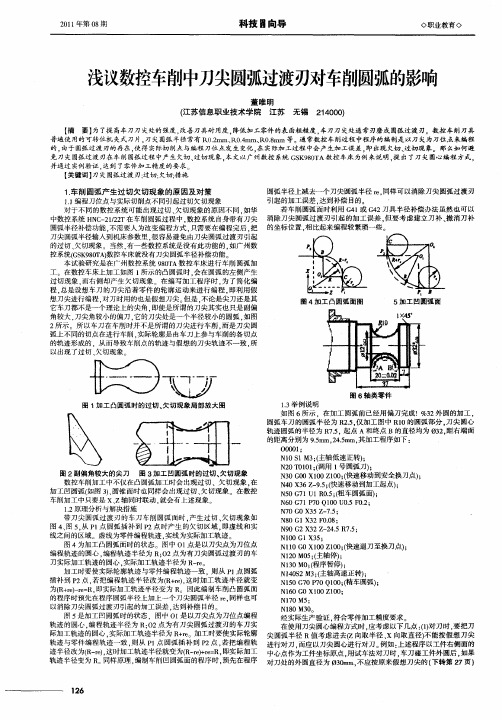
普遍使 用的可转位机 夹式刀片, 刀尖 圆弧半径 常有 R02 .mm、 .mr、 . K04 n R08 mm 等。通常数控 车削过程 中程序的编制是 以刀尖为刀住点来编程 的. 由于圆弧过渡刃的存在 . 使得 实际切削点与编程刀位点发生变化 . 实际加工过程 中会产生加工误 差. 在 即出现 欠切、 过切现象。那么如何避 免刀尖圆弧过渡刃在车削圆弧过程 中产生欠切 、 过切现象 . 本文以广州数控 系统 GS 9 0 A数控 车床 为例 来说 明. 出 了刀尖圆心编程 方式. K 8T 提 并 通过 实例 验证 . 达到 了零 件 加 工 精度 的要 求 【 键 词 】 尖 圆弧 过 渡 刃 ; 切 : 关 刀 过 欠切 : 施 措 圆弧半径上减去一个刀尖圆弧半径 r . e 同样 可以消 除刀尖 圆弧过渡刃 引起的加工误差 , 达到补偿 目的。 1】 . 编程 刀位点 与实际切削点不 同引起过切欠 切现象 若车削圆弧面时利用 G 或 G 2刀具半径补偿 办法虽然也可 以 41 4 对于不同的数控系统可 能出现过切 、 欠切现象 的原 因不 同 . 如华 但要考虑建 立刀补、 撤消刀补 中数控系统 H C 2 / T N 一 1 2 在车削 圆弧过程 中. 2 数控系统 自身带有刀尖 消除刀尖 圆弧过渡刃引起 的加工误差 , 相 圆弧半径补偿功能. 不需要人为改变 编程方式 , 只需要在编程完后 , 把 的坐标位置 , 比起来编程较繁琐一些 。 刀尖 圆弧半径输人 到机床参数里 . 容易避免 由刀尖 圆弧过渡刃引起 很 的过切 、 欠切现象 。当然 . 有一些数控系统是没有此功能的 , 如广州数 控系统(S 9 0 A数控车床就没有刀尖圆弧半 径补偿功能 G K 8T ) 本 试 验 研 究 是 在 广 州 数 控 系 统 90 A数 控 车 床 进 行 车 削 圆 弧 加 8T 工 。在数控车床上加工如图 1 所示 的凸圆弧时 . 会在圆弧 的左侧产生 过切现象 , 而右侧却产生欠 切现象 。在编写加工程序 时 . 了简化编 为 程, 总是设想车刀 的刀尖沿着零件 的轮廓运动来进行编程 . 即利用假 想刀尖进行编程 . 对刀时用的也是假想刀尖 但是 . 不论是尖刀还是其 图 4m - 凸 圆弧 面 图 r 5加 工 凹 圆 弧面 它车刀都不是一个理论上的尖角 . 即使是所谓的刀尖其实也只是副偏 角较大 , 刀尖角较小 的偏刀 . 它的刀尖处是一个半径较小的圆弧 . 如图 2所示 所 以车刀在车削时并不是所谓的刀尖进 行车削 . 而是刀尖圆 弧上不同的切点在进行车削 . 实际轮廓是 由车刀上参与车削的各切点 的轨迹形成的.从而导致车削点 的轨迹与假想的刀尖轨迹不一致 . 所 以出现了过切、 欠切现象
数车过渡圆弧的计算公式
数车过渡圆弧的计算公式在道路设计和交通工程中,过渡圆弧是一种常见的道路曲线设计元素。
它被用来连接两个不同半径的圆弧或直线,以平稳地过渡车辆的行驶轨迹,减少车辆的颠簸和转向压力。
因此,正确计算过渡圆弧的长度和半径对于确保道路的安全和舒适性至关重要。
本文将介绍数车过渡圆弧的计算公式,并讨论其在道路设计中的应用。
首先,我们需要了解几个基本参数,以便计算过渡圆弧的长度和半径。
这些参数包括,初始半径R1、终点半径R2、过渡圆弧的长度L、过渡圆弧的半径R、过渡圆弧的曲率K。
其中,初始半径R1和终点半径R2是已知的道路曲线参数,而过渡圆弧的长度L、半径R和曲率K则需要根据设计要求进行计算。
过渡圆弧的长度L可以通过以下公式进行计算:L = (R2 R1) / K。
其中,R1和R2分别为初始半径和终点半径,K为过渡圆弧的曲率。
根据这个公式,我们可以通过已知的初始半径和终点半径,以及设计要求的曲率,计算出过渡圆弧的长度。
过渡圆弧的半径R可以通过以下公式进行计算:R = (R1 + R2) / 2 + (L^2 K) / 8。
其中,R1和R2分别为初始半径和终点半径,L为过渡圆弧的长度,K为过渡圆弧的曲率。
通过这个公式,我们可以根据已知的初始半径和终点半径,以及设计要求的过渡圆弧长度和曲率,计算出过渡圆弧的半径。
过渡圆弧的曲率K可以通过以下公式进行计算:K = (R2 R1) / L。
其中,R1和R2分别为初始半径和终点半径,L为过渡圆弧的长度。
通过这个公式,我们可以根据已知的初始半径和终点半径,以及设计要求的过渡圆弧长度,计算出过渡圆弧的曲率。
以上三个公式为计算过渡圆弧的长度、半径和曲率提供了基本的数学工具。
在实际的道路设计中,工程师可以根据道路的实际情况和设计要求,利用这些公式进行计算,从而确定过渡圆弧的几何参数,确保道路的安全和舒适性。
除了基本的计算公式外,还有一些其他因素需要考虑在内,以确保过渡圆弧的设计符合实际需要。
新代系统圆弧过渡代码
新代系统圆弧过渡代码新代系统圆弧过渡的代码取决于具体的编程语言和系统以及所用的设备等等因素,下面是一些常见的实现方式,供您参考:1. 在Windows平台的C/C++中,可以使用函数ArcTo()来实现圆弧过渡效果,示例代码如下:```void DrawArcTo(HWND hwnd, HDC hdc, int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4){// 创建一个圆弧路径BeginPath(hdc);ArcTo(hdc, x1, y1, x2, y2, x3, y3, x4, y4);EndPath(hdc);// 调用SelectObject()函数选择画刷和画笔来填充路径HBRUSH hBrush = CreateSolidBrush(RGB(255, 0, 0)); // 红色画刷HBRUSH hOldBrush = SelectObject(hdc, hBrush);HPEN hPen = CreatePen(PS_SOLID, 1, RGB(0, 0, 255)); // 蓝色画笔HPEN hOldPen = SelectObject(hdc, hPen);FillPath(hdc);StrokePath(hdc);// 清除选择的画刷和画笔,释放资源SelectObject(hdc, hOldBrush);DeleteObject(hBrush);SelectObject(hdc, hOldPen);DeleteObject(hPen);}```2. 在Android平台的Java语言中,可以使用类Path的arcTo()方法来实现圆弧过渡效果,示例代码如下:```Path path = new Path();path.arcTo(new RectF(x1, y1, x2, y2), startAngle, sweepAngle, true);Paint paint = new Paint();paint.setStyle(Paint.Style.FILL_AND_STROKE);paint.setColor(Color.RED);canvas.drawPath(path, paint);```3. 在Web开发中,可以使用HTML5和CSS3来实现圆弧过渡效果,示例代码如下:HTML部分:```<div class="my-progress"><div class="bar"></div></div>```CSS部分:```.my-progress {width: 200px;height: 200px;position: relative;margin: 50px auto;border-radius: 50%;background-color: #eee;overflow: hidden;}.bar {position: absolute;width: 100%;height: 100%;border-radius: 50%;background-color: #f00;clip: rect(0, 100px, 200px, 0);}```JavaScript部分:```var bar = document.querySelector('.bar');var progress = 0;setInterval(function() {progress++;bar.style.clip = "rect(0, " + progress + "px, 200px, 0)"; }, 10);```。
环形刀宽行加工圆弧过渡区域算法的研究
2 0 1 4年 第 1期
机 械 工ቤተ መጻሕፍቲ ባይዱ程 与 自 动 化
效 率 较 球 头 刀提 高 了 5倍 。 关 键 词 :环 形 刀 ;广 域 曲率 吻 合 ; 圆弧 过 渡 中 图分 类 号 :T P 3 9 1 . 7 文 献 标 识 码 :A
0 引 言
圆弧 过渡 曲面 常用 于组合 曲面之 间 的光 滑 过渡 连 接, 广泛 出现在 航空 发动 机机 匣 、 涡轮 叶 片等关键 零件 的设 计 中 。这类 零 件结 构复杂 、 精 度要 求 高 、 加工 难度 大, 其 加工 程序 的好 坏 直 接关 系 到整 机 的加 工 质量 和 生产 效率 。传统 中 , 对 于 圆 弧过 渡 面 的加 工 主 要通 过 靠 刀 法[ 1 来 实现 , 但频 繁 的 换 刀 带来 了 成本 高 , 工 作 效 率低 且 质量不 稳 定 等 问题 。 因此 , 这 种 方 法 已逐 渐
图 2所 示 。
针对 上述 问题 , 本 文 的 研究 内容 主 要 集 中在两 个 方面 : ①设计 一 种具 有复 杂母线 的环形 刀具 模型 , 利用 母 线上 的不 同部 位加 工 零 件 曲面 结 构 的不 同部 位 , 解
* 国 家 自然 科 学 基 金 资助 项 目 ( 5 1 0 7 5 0 2 1 )
环 形 刀宽 行 加 工 圆弧过 渡 区域 算 法 的研 究举
王 小 文
( 北 京 航 空 航 天 大 学 机 械 工 程 及 自动 化 学 院 ,北 京 1 O O 1 9 1 )
摘 要 :基 于广 域 曲率 吻 合 原 则 ,研 究 了利 用 环 形 刀 侧 铣 加 工 组 合 曲 面 圆弧 过 渡 区域 的 新 方 法 。 首先 建 立 环 形 刀 的 几何 模 型 , 通 过 调 整 刀 具 姿 态 角 ,使 刀 具 表 面和 工 件 表 面 在 不 发 生 干 涉 的条 件 下 实 现 密切 接 触 。通 过 迭
曲线过渡圆弧过渡
4.点裁剪 【功能】 利用点(通常是屏幕点)作为剪刀, 对曲线进行裁剪。 【说明】 点裁剪具有曲线延伸功能,用户可以利用本功能实现曲线的延伸。
图4-4点裁剪示例图 (1)、单击 按钮,在立即菜单中选择“点裁剪”。 (2)、拾取被裁剪的线(选取保留的段),该曲线变红。 (3)、拾取剪刀点,点裁剪完成。 【注意】 在拾取了被裁剪曲线之后, 利用点工具菜单输入一个剪刀点,系统对曲 线在离剪刀点最近处施行裁剪。
1.快速裁剪 【功能】 快速裁剪是指系统对曲线修剪具有指哪裁哪的快速反映。 快速裁剪的方式:正常裁剪和投影裁剪。正常裁剪适用于裁剪同一平面上的曲 线,投影裁剪适用于裁剪不共面的曲线。 【说明】 在操作过程中,拾取同一曲线的不同位置将产生不同的裁剪结果。
(a)拾取操作 (b)裁剪结果 (c)拾取操作 (d)裁剪结果 图4-1快速裁剪示例图 图4-2快速裁剪示例图 1、单击按钮,在立即菜单中选择快速裁剪和正常裁剪(或投影裁剪)。 2、拾取被裁剪线(选取被裁掉的段),快速裁剪完成。 【注意】 1、当系统中的复杂曲线极多的时候,建议不用快速裁剪。因为在大量复杂曲 线处理过程中,系统计算速度较慢,从而将影响用户的工作效率。 2、在快速裁剪操作中,拾取同一曲线的不同位置,将产生不同的裁剪结果。
4.3 曲线打断 【功能】 曲线打断用于把拾取到的一条曲线在指定点处打断,形成两条曲线。 (a) 打断直线 (b) 打断圆弧 1、单击主菜单“造型”,指向“曲线编辑”,然后单击“曲线打断”,或者直 接单击 按钮。 2、拾取被打断的曲线,拾取打断点,曲线打断完成。 【注意】 在拾取曲线的打断点时,可使用点工具捕捉特征点,方便操作。
3. 倒角过渡 【功能】 倒角过渡用于在给定的两直线之间进行过渡, 过渡后在两直线之间有一条按 给定角度和长度的直线。 【说明】 倒角过渡后, 两直线可以被倒角线裁剪,也可以不被裁剪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a)过渡前 (b) 过渡后 圆弧过渡图(1)19.mp4
任务四:举一反三
① ②
(a)过渡前 (b) 过渡后 圆弧过渡图(2)15.mp4
① ②
(a)过渡前 (b) 过渡后 圆弧过渡图(3)16.mp4
① ②
(a)过渡前 (b) 过渡后 圆弧过渡图(4)
任务五:小结
圆弧过渡: 分为曲线剪裁与不曲线剪裁两类 ① 单击 按钮 在立即菜单中选择“圆弧过渡”方式,输入半径, 选择是否裁剪曲线1和曲线2。
项目:曲线过渡之圆弧过渡
任务清单:
一、找找
二、摸一摸
三、小试牛刀 四、举一反三
五、小结
六、大显身手
任务一:看一看
思考:
外观最大的不同?
边角处
(a )
(b)
任务二:摸一摸
圆弧过渡:
用于在两条曲线之间进行给定半 径的圆弧光滑过渡。
作用:
1、感触:舒适
2、审美:美观
3、力学:减少应力集中
任务三:小试牛刀
② 拾取第1条曲线、第2条曲线,圆弧过渡完成。
注意:曲线的选择顺序。
√
圆弧过渡
√ ?
圆弧过渡图(5)
√
任务六:大显身手
项目:曲线过渡之圆弧过渡
任务清单:
一、找一找
二、摸一摸
三、小试牛刀 四、举一反三
五、小结
六、大显身手
