第二章 结构图的等效变换求系统的传递函数 (1)
结构图变换举例 (1)

五
举例说明(例2)
例2:系统动态结构图如下图所示,试求 系统传递函数C(s)/R(s)。
H 2 ( s)
R(s )
-
-
G1 ( s )
G2 ( s )
-
G3 ( s ) H 3 ( s)
C (s )
G4 ( s )
H1 ( s)
五
举例说明(例2)
例2:系统动态结构图如下图所示,试求 系统传递函数C(s)/R(s)。
G4 ( s )
C(s)
H3 (s)
H1 ( s)
例2 (解题方法一之步骤5)
内反馈环节等效变换结果
R(s)
1
3
G1 (s)
-
G2 ( s )
-
G3 ( s ) 1 G2 ( s )G3 ( s ) H 2 ( s )
H 3 ( s)
C(s)
G4 (s)
H1 ( s)
例2 (解题方法一之步骤6)
1
-
3
B
C
G1 ( s )
- 2
G2 ( s )
-
G3 ( s )
A
G4 ( s )
C (s )
H 3 ( s)
H1 ( s)
例2 (解题方法一之步骤2)
R(s)
1
3
-
?
G3 ( s ) G4 ( s )
C(s)
H 3 ( s)
G1 ( s )
-
G2 ( s )
2
H1 ( s)
例2 (解题方法一之步骤3)
C (s )
H 3 ( s)
H1 ( s)
例2 (解题方法四)
第二章传递函数案例

解:
系统的结构图为
3. 结构图化简 (结构图的等效变换)
化简目的:
将结构图化简为一个方块,即传递函数。
化简原则:
保证化简前后的代数等价关系不变
等效变换法则
环节串联
环节并联
反馈回路化简
负反馈
正反馈
相加点移动
分支点移动
前移
后移
信号的分支点与相加点不可以互换
例:化简结构图,求取传递函数
阶跃响应曲线
七、比例积分环节 (P-I)
定义:环节输出正比于输入信号和它对时间的积分。
微分方程
1 c( t ) K r t Ti
0 r t dt
t
传递函数
1 G( s) K 1 T s i
阶跃响应曲线
八 、延迟环节
四、惯性环节
定义:环节的输出不能立即复现输入,而是经过 一定时间后才能复现输入的变化。
微分方程 传递函数
dc( t ) T c( t ) Kr ( t ) dt
K G( s) Ts 1
运算放大器
1 1 Rf Rf Cf s Cf s U 2 ( s) U1 ( s ) R1 Rf R1 K Rf Cf s 1 Ts 1
dr ( t ) c( t ) K r ( t ) TD d t
微分方程
传递函数
G( s)
c s r s
K 1 TD s
在放大器上加以 RC 网 络 反 馈 , 当 增益K足够大时
U 2 ( s) U1 ( s ) K 1 1 K RCs 1 K RCs 1 RCs 1 K RCs 1 RC 1 s 1 K K RCs 1 s1
第二章习题解答

第二章2-3 设系统传递函数为342)(2++=s s s G 初始条件0/)0(,1)0(=-=dt dc c 。
求单位阶跃输入r (t)=1(t)时,系统的输出响应c (t)。
【解】系统传递函数与微分方程是一一对应的,故通过传递函数先求出微分方程,然后通过拉氏变换的方法求解微分方程。
系统对应的微分方程为 4()3()2()c c t c t r t ++= 在给定的非零初始条件下,进行拉氏变换22(43)()(0)(0)4(0)s s C s sc c c s++---=整理后2221()(43)(43)s C s s s s s s +=-++++部分分式展开后,拉氏反变换111223242/35/25/6()[()][][](43)(43)13255326t t s c t L C s L L s s s s s s s s e e -----+==-=-+++++++=-+2-4 在图2-48中,已知G (s) 和H (s)两方框对应的微分方程分别为()2()5()4()3()6()c t c t e t b t b t c t +=+=图2-48 习题2-4系统结构框图且初始条件为零,试求传递函数C (s)/R (s)。
【解】求出每个方框的传递函数,利用反馈等效的方法求C(s)/R(s)。
根据定义可得 5()2G s s =+,6()43H s s =+ 255()5()25(43)10075(2)56()1()()(2)(43)30411361(2)(43)C s G s s s s R s G s H s s s s s s s +++====+++++++++2-5 图2-49是由电阻、电容和运算法放大器组成的无源网络和有源网络,试列写以V in (t)为输入量,V out (t)为输出量的传递函数。
(a) (b )(c) (d)图2-49 习题2-5电路图【解】(a) 1211211,1RZ R Z C s RC s C s===+ 22112121211()1()11Z C s RC s G s R Z Z R C C s RC s C s +===+++++(b ) 21122211R Z R Z R Cs R Cs ===+ 2222111211()1R Z R Cs R G s Z R R R Cs +=-==-+ (c) 32321123232321()(1)1()1()1R R R R Cs Cs Z R Z R R Cs R R Cs R R Cs++==+==++++ 323232211132(1)()11()()1R R Cs R R Cs R Z R Cs G s Z R R R R Cs ++++=-=-=-++ (d)本题和(b)、(c)做法图通,因为反馈通路有接地的部分。
中国计量大学801自动控制原理1-2015--2017考研专业课真题

(5 分)
(2) 求相稳定裕度 γ 和剪切频率 wc ;(6 分)
(3) 判断系统的稳定性。
(4 分)
db
……
…… ………....…
26
-40
-20 20 40
w
1 2 4 wc
-40d B/dec
图3
七、(20 分)已知一采样系统如图 4 所示,其中采样时间 T=1s。试求:
(1)
开环脉冲传递函数 C(z) ; E(z)
1 T
C
0
1
0
,
U
u w
(1) 判断系统能控性;(10 分) (2) 求系统在路面 w=10cm 阶跃输入时的超调量; (5 分) (3) 求系统调整时间(稳态误差 2%)。 (5 分)
【完】
《自动控制原理 1》试卷 第 3 页 共 3 页
一、(15 分)分别用下列方法求图 1 所示系统的传递函数。 (1)结构图等效变换;(7 分) (2)梅森公式。(8 分)
R(s)
T0s +1
+-
10K1 s(s + 5)(s + 20)
N(s) + C(s) +
图3
《自动控制原理 1》试卷 第 1 页 共 3 页
四、(15 分)设单位负反馈控制系统的开环传递函数为:G(s)H (s) =
K
s(s + 2)(s + 7)
(1)绘制系统的根轨迹图;(8 分) (2)确定系统稳定时 K 的最大值;(4 分)
(2 分)
《自动控制原理 1》试卷 第 1 页 共 3 页
五、(15
分)画出
第二章习题解题过程和参考答案

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ,位移)(t x 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),μ(阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解:2-1(a) 取质量m 为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m 上的力有外力f(t),重力mg ,这两个力向下,为正。
有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ,这两个力向上,为负。
其中,0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。
根据牛顿第二定理F ma ∑=,有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中:0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式:22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成:22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。
2-1(b) 如图,取A 点为辅助质点,设该点位移为()Ax t ,方向如图。
再取B 点也为辅助质点,则该点位移即为输出量()y t ,方向如图A 点力平衡方程:1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程:2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得:21()()()Akx t x t y t k=-二边微分:21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②:221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式:1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成:()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。
第二章-系统的传递函数方框图及其简化.

系统闭环传递函数
GB (s)
X o (s) Xi (s)
由图可知
X i (s) E(s) G(s)
B(s)
H (s)
X o (s)
E(s) Xi (s) B(s) Xi (s) Xo(s)H (s) Xo(s) G(s)E(s) G(s)[Xi (s) Xo(s)H (s)]
G(s)Xi (s) G(s)Xo(s)H (s) 由此可得:
GK (s) G(s)H (s) E(s)
无量纲.
系统闭环传递函数
GB (s)
X o (s) Xi (s)
注意:我们所指的前向通道的传递函数、反馈回路的
传递函数和开环传递函数都是针对一个闭环系统而
言的。它们都是闭环系统的一部分。系统闭环传递
函数是闭环系统的传递函数。看一个传递函数是什
么具体类型,要从定义出发,而不能只看其符号。
8.分支点和相加点之间等效规则
X1(s)
X1(s) X2(s)
X 2 (s)
X1(s) X2(s)
X1(s)
X 2 (s)
X1(s) X2(s)
X1(s) X2(s)
X 2 (s)
一般应避免分支点和相加点之间的相互移动
三、方框图简化的一般方法 (法1)
1.确定系统的输入量和输出量.若作用在系统上的输 入量或输出量有多个,则必须分别对每一输入量,逐个 进行方框图的简化,以求得各自的传递函数. 2.若方框图中有交叉连接,则利用分支点或相加点的 移动规则,将交叉消除,简化成无交叉的多回路方框图 的形式.(大回路套小回路) 3.对多回路方框图,按照先里后外的顺序依次对各个 回路进行简化. 4.写出系统的传递函数.
Ua (s) 0
《自动控制原理》第二章传递函数
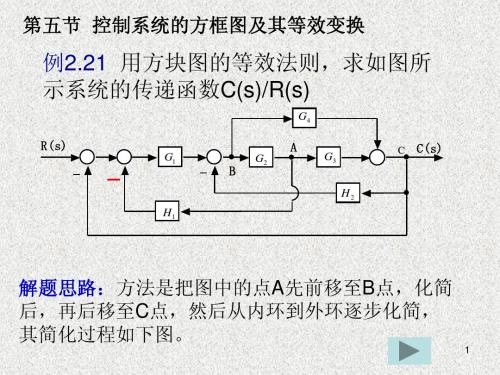
G2 ( s ) N ( s) 1 + G1 ( s)G 2 ( s) H ( s)
∑ C ( s ) = Φ ( s) R( s) + Φ ( s) N ( s) =
G2 ( s )[G1 ( s) R ( s) + N ( s )] 1 + G1 ( s)G 2 ( s ) H ( s)
20
N ( s)
14
例2.23
R(s)
G4 G1 A G3 H2 H1
C
p1 = G1G2G3
_
-
B
G2
C (s)
∆1 = 1
L1 = −G1 G 2 H 1
p2 = G1G4
∆2 = 1
L2 = − G 2 G 3 H 2 L3 = −G 1 G 2 G3
L4 = − G 4 H 2
注意:回路 注意: 找不全是最 大的问题
5
1 R 1 G1 -1 1 G2 -1 1 G3 -1 K C
1
-1
•前向通路:开始于输入节点,沿支路箭头方向,每个节点 前向通路:开始于输入节点,沿支路箭头方向, 前向通路 只经过一次,最终到达输出节点的通路称之前向通路。 只经过一次,最终到达输出节点的通路称之前向通路。 •回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路 •回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益 •不接触回路:回路之间没有公共节点时, 不接触回路:回路之间没有公共节点时, 不接触回路 不接触回路。 这种回路叫做 不接触回路。 •在信号流图中,可以有两个或两个以上不接触回路。 在信号流图中, 在信号流图中 可以有两个或两个以上不接触回路。
自动控制原理课后习题答案解析
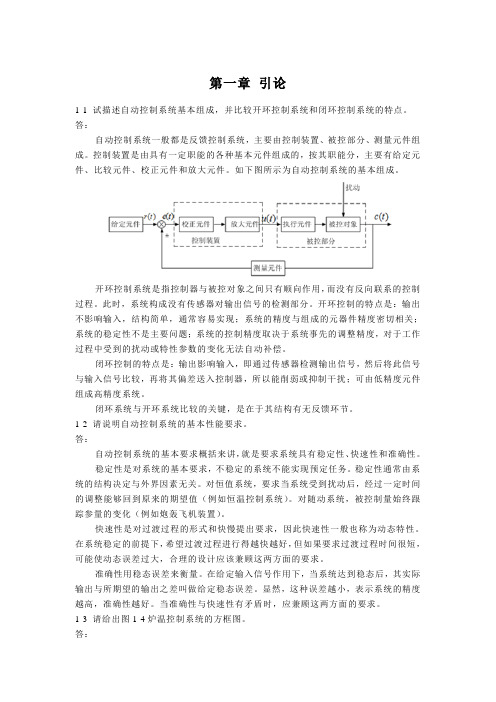
第一章引论1-1 试描述自动控制系统基本组成,并比较开环控制系统和闭环控制系统的特点。
答:自动控制系统一般都是反馈控制系统,主要由控制装置、被控部分、测量元件组成。
控制装置是由具有一定职能的各种基本元件组成的,按其职能分,主要有给定元件、比较元件、校正元件和放大元件。
如下图所示为自动控制系统的基本组成。
开环控制系统是指控制器与被控对象之间只有顺向作用,而没有反向联系的控制过程。
此时,系统构成没有传感器对输出信号的检测部分。
开环控制的特点是:输出不影响输入,结构简单,通常容易实现;系统的精度与组成的元器件精度密切相关;系统的稳定性不是主要问题;系统的控制精度取决于系统事先的调整精度,对于工作过程中受到的扰动或特性参数的变化无法自动补偿。
闭环控制的特点是:输出影响输入,即通过传感器检测输出信号,然后将此信号与输入信号比较,再将其偏差送入控制器,所以能削弱或抑制干扰;可由低精度元件组成高精度系统。
闭环系统与开环系统比较的关键,是在于其结构有无反馈环节。
1-2 请说明自动控制系统的基本性能要求。
答:自动控制系统的基本要求概括来讲,就是要求系统具有稳定性、快速性和准确性。
稳定性是对系统的基本要求,不稳定的系统不能实现预定任务。
稳定性通常由系统的结构决定与外界因素无关。
对恒值系统,要求当系统受到扰动后,经过一定时间的调整能够回到原来的期望值(例如恒温控制系统)。
对随动系统,被控制量始终跟踪参量的变化(例如炮轰飞机装置)。
快速性是对过渡过程的形式和快慢提出要求,因此快速性一般也称为动态特性。
在系统稳定的前提下,希望过渡过程进行得越快越好,但如果要求过渡过程时间很短,可能使动态误差过大,合理的设计应该兼顾这两方面的要求。
准确性用稳态误差来衡量。
在给定输入信号作用下,当系统达到稳态后,其实际输出与所期望的输出之差叫做给定稳态误差。
显然,这种误差越小,表示系统的精度越高,准确性越好。
当准确性与快速性有矛盾时,应兼顾这两方面的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L1L4=(–G1H1)(–G4G3)=G1G3G4H1
G3(s) R(s) R(s) R(s) R(s)
梅逊公式求E(s)
N(s) N(s) N(s)
G2(s) C(s) C(s) C(s)
P2= - G3G2H3 △2= 1 P2△2=?
G3 (s) E(S)G(s) G33(s) E(S) E(S) E(S) GG (s) 1 (s) G(s)
综合点移动
G3
G1
G2
向同类移动 无用功
错!
G2
H1
G3 G1
G1
G2
H1
G4 G1 G2
作用分解
G3
H1
G4 G1 G2
H3
G3
H1 H1
H3 H3
R(s)
G1A Cຫໍສະໝຸດ DG2BC(s)
当比较点和引出点出现相交叉的情况时,如上 图所示系统,比较点A因为引取出点C、D的存 在,引出点因为比较点A、B的存在不能前后 移动,不能用方框图化简的方法来求传递函数, 而必须借助梅森(Mason)增益公式。
引出点移动
H3(s) G1(s)
G 2G 3G 4G 3 (s)G 4 (s) G2(s) G3(s) G4(s) 1+G 3 (s)G 4 1+G 2 G 3H 2 +G 3G 4 H 3 (s)H3 (s)
H2(s)
1 G 4 (s)
H1(s)
G1G 2 G 3G 4 1+G1G 2 G 3G 4 H1 +G 2 G 3 H 2 +G 3G 4 H3
1 1
G2(s) G22(s) G (s) HH (s) 2 (s) H(s) 2 2
HH (s) 1 (s) H(s) 1 1
H3(s)
H3(s) H33(s) H (s)
C(s)
G1(s)
R(s) E(S) P1= –G2H3 P1=1 H1(s)
△△1= 1 2HH2(s)P1△1= ? 1=1+G 2
C(s) G1(s) =?
G4(s)
△2=1+G1H1
G2(s) G3(s) 试着写出答案,如何? G3(s)
P2= G4G3
L4= – G4G3
P1=G1G2G3
L1= –G1 H1 L2= – G3 H3 L5 = – G1G2G3
L3= – G1G2G3H3H1
L1L2= (–G1H1) (–G3H3) = G1G3H1H3
△k称为第k条前向通路的余子式 △k求法: 去掉第k条前向通路后所求的△ △k=1-∑LA+ ∑LBLC- ∑LDLELF+…
R(s)
a b
c
G4(s) G (s) G11(s) H1(s)
d e
梅逊公式例R-C
G22(s) G (s)
f
G33(s) G (s)
g H3(s)
h
C(s)
△1=1
R(s)
E(s)=
R(s)[ (1+G2H2) + (- G3G2H3) ] + (–G2H3) N(s)
1 - G1H1 + G2H2
+ G1G2H3 -G1H1G2 H2
梅逊公式介绍
R-C :
C(s) = R(s)
∑Pk△k △
其中:
△称为系统特征式 △= 1 - ∑La + ∑LbLc -∑LdLeLf+…
所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和
— ∑L
a
Pk—从R(s)到C(s)的第k条前向通路传递函数
