国外计算机科学教材系列 离散数学(第4版)-3
离散数学第3章 函数
显然fC不是函数。可见如果一个函数不是双射的, 它的逆就不是函数。
软件学院
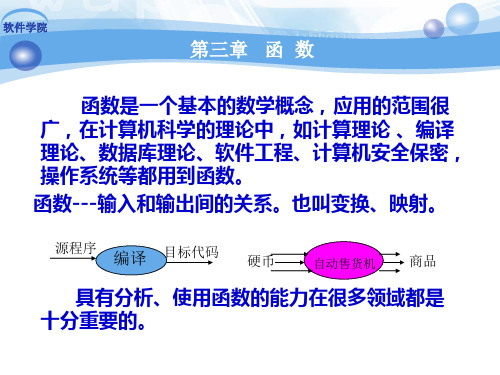
第三章 函 数 2.自变元与函数值(像源与映像) :
f:XY, 如果<x,y>∈f,称x是自变元(像源),称 y是x 的函数值(x的映像) 。
<x,y>∈f y=f(x) f:XY 3.定义域、值域 :f:XY, f的定义域,记作Df 即
Df ={x|x∈X,y(y∈Y,<x,y>f)} =X
注意:这里把g写在f的左边了.所以叫左复合. g f :XZ,即 g f 是X到Z的函数.这样写是为了
照顾数学习惯: g f(x)=g(f(x))
复合函数的计算方法同复合关系的计算.
软件学院
复合函数
例1 f:XY, g:YZ X={1,2,3} Y={1,2,3,4,} Z={1,2,3,4,5,} f= {<1,2>,<2,4>,<3,1>} g={ <1,3>,<2,5>,<3,2>,<4,1> } g f={ <1,3>,<2,5>,<3,2>,<4,1> } {<1,2>,<2,4>,<3,1>} ={<1,5>,<2,1>,3,3>} g f g 用有向图复合: f X Z X Y X 。 1 。 。 。 1 。 1 1 1 。 2 。 2 。 。 2 。 2。 3 。 2 3 。 。 3。 4 。 4 3。 3 。 。 5 。 5
《离散数学》,屈婉玲、耿素云-KefeiChen陈克非

离散数学课程介绍
• 研究对象:离散量(自然数、真假值、字母 表等)
• 研究内容:离散量的结构与关系(数理逻
辑、集合论、图论、代数系统、组合计数、初 等数论、离散概率、有限自动机、图灵机等)
• 预修课程:线性代数(高等代数) • 后继课程:数据结构、数据库等
5
教材与参考书
• 教材:《离散数学》,屈婉玲、耿素云、张立昂 编,清华大学出版社, 2013年第三版;
12
包含与相等
包含(子集) A B x (xA xB) 不包含 A ⊈ B x (xA xB) 相等 A=BABBA 不相等 ABA⊈BB⊈A 真包含(真子集) A B A B A B 例如, A={1,2,3}, B={ x | xR|x|1 }, C={ x | xRx2=1 }, D={-1,1}, C B, C B, C ⊈ A, A ⊈ B, B ⊈ A, C = D 性质 (1) A A (2) A B B C A C
离 散 数 学
Discrete Mathematics
陈克非 杭州师范大学理学院 kfchen@
https:///s/1mXVWVKfYtUnjaiZUhmNulQ
为什么要离散数学
不离散化就无法 跟上时代步伐
• 工业革命时代以微积分为代表的连续数学占主流的地 位已经发生了变化 • 信息时代离散数学的重要性逐渐被人们认识。离散数 学的思想和方法,广泛地体现在计算机科学技术及相 关专业的诸领域
3
四色问题
计算机的作用不仅 仅是计算,还有逻 辑推演、决策、AI
• 离散数学也可以说是计算机科学的基础核心学科 • 离散数学中的有一个著名的典型例子-四色定理又称四 色猜想,这是世界近代三大数学难题之一,它是在 1852年,由英国的一名绘图员弗南西斯· 格思里提出的
离散数学第四版课后答案(第4章)

第4章 习题解答4.1 A :⑤; B :③; C :①; D :⑧; E :⑩4.2 A :②; B :③; C :⑤; D :⑩; E :⑦4.3 A :②; B :⑦; C :⑤; D :⑧; E :④分析 题4.1-4.3 都涉及到关系的表示。
先根据题意将关系表示成集合表达式,然后再进行相应的计算或解答,例如,题4.1中的}2,2,1,2,2,1,1,1{},2,2,1,1{><><><><=><><=s s E I};2,2,2,1,1,1{><><><=s I而题4.2中的}.1,4,4,3,1,2,4,1,1,1{><><><><><=R为得到题4.3中的R 须求解方程123=+y x ,最终得到}.1,9,2,6,3,3{><><><=R求R R 有三种方法,即集合表达式、关系矩阵和关系图的主法。
下面由题4.2的关系分别加以说明。
1°集合表达式法将ranR ran domR domR,, 的元素列出来,如图4.3所示。
然后检查R 的每个有序对,若R y x >∈<,,则从domR 中的x 到ranR 中的y 画一个箭头。
若danR 中的x 经过2步有向路径到达ranR 中的y ,则R R y x >∈<,。
由图4.3可知}.1,3,4,2,1,2,4,4,1,44,1,1,1{><><><><>><<><=R R如果求G F ,则将对应于G 中的有序对的箭头画在左边,而将对应于F 中的有序对的箭头画在右边。
对应的三个集合分别为ranF domF ran domG ,, ,然后,同样地寻找domG 到ranF 的2步长的有向路径即可。
(完整版)离散数学电子教材1(可编辑修改word版)

(完整版)离散数学电子教材1(可编辑修改word版)第1 章命题逻辑逻辑是研究人的思维的科学,包括辩证逻辑和形式逻辑。
辩证逻辑是研究反映客观世界辩证发展过程的人类思维的形态的。
形式逻辑是研究思维的形式结构和规律的科学,它撇开具体的、个别的思维内容,从形式结构方面研究概念、判断和推理及其正确联系的规律。
数理逻辑是用数学方法研究推理的形式结构和推理的规律的数学学科。
所谓的数学方法也就是用一套有严格定义的符号,即建立一套形式语言来研究。
因此数理逻辑也称为符号逻辑。
数理逻辑的基础部分是命题逻辑和谓词逻辑。
本章主要讲述命题逻辑,谓词逻辑将在第2 章进行讨论。
1.1命题及其表示1.1.1命题的基本概念数理逻辑研究的中心问题是推理(Inference),而推理就必然包含前提和结论,前提和结论都是表达判断的陈述句,因而表达判断的陈述句就成为推理的基本要素。
在数理逻辑中,将能够判断真假的陈述句称为命题。
因此命题就成为推理的基本单位。
在命题逻辑中,对命题的组成部分不再进一步细分。
定义1.1.1 能够判断真假的陈述句称为命题(Proposition)。
命题的判断结果称为命题的真值,常用T(True)(或1)表示真,F(False)(或0)表示假。
真值为真的命题称为真命题,真值为假的命题称为假命题。
从上述的定义可知,判定一个句子是否为命题要分为两步:一是判定是否为陈述句,二是能否判定真假,二者缺一不可。
例1.1.1 判断下列句子是否为命题(1)北京是中国的首都。
(2)请勿吸烟!(3)雪是黑的。
(4)明天开会吗?(5)x+y=5。
(6)我正在说谎。
(7)9+5≤12 。
(8)1+101=110 。
(9)今天天气多好啊!(10)别的星球上有生物。
解在上述的十个句子中,(2)、(9)为祈使句,(4)为疑问句,(5)、(6)虽然是陈述句,但(5)没有确定的真值,其真假随x、y 取值的不同而有改变,(6)是悖论(Paradox)(即由真能推出假,由假也能推出真),因而(2)、(4)、(5)、(6)、(9)均不是命题。
离散数学.第1章

例4
设P:我们去看电影。Q:房间里有十张桌子。则
P ∧ Q表示“我们去看电影并且房间里有十张桌子。”
10
3. 析取“∨”(相容或)[讲解教材P3-5关于或]
4. 定义1.3
由命题P和Q利用“∨”组成的复合命题,称 为析取式复合命题,记作“P∨Q”(读作“P或Q”)。 当且仅当P和Q至少有一个取值为真时,P∨Q取值为真。
练习1-1
1. 判断下列语句哪些是命题,若是命题,则指出其真值。
(1) (2) 只有小孩才爱哭。 X+6=Y ( 是 假 ) ( 不是 ) (是 真) ( 不是 )
(3)
银是白的。
(4) 起来吧,我的朋友。 2. 将下列命题符号化
(1) 我看见的既不是小张也不是老李。 解 令P:我看见的是小张;Q:我看见的是老李。 则该命题可表示为¬ P∧¬ Q (2) 如果晚上做完了作业并且没有其它的事,他就会 看电视或听音乐。 解 令 P:他晚上做完了作业;Q:他晚上有其它的事; R:他看电视; S:他听音乐。 则该命题可表示为(P∧¬ Q)→(R∨S)
28
1.3 等值演算
• 定义1.10 设A和B是两个命题公式, 若等价式A↔B 是重言式,则称公式A 和B等值,记为A B,称 AB为等 值式。
• 注意: (1)符号“”与“↔”的区别与联系 “”不是联结词,AB不表示一个公式, 它表示两个公式间的一种关系,即等值关系。 “↔”是联结词,A↔B是一个公式。 AB 当且仅当 A↔B 是永真公式。
1 0 1 0 1 0 1 0
0 0 1 1 1 1 1 1
0 0 0 1 0 0 0 1
1 1 0 1 0 0 0 1
离散数学北美教材

离散数学北美教材
在北美地区,离散数学是计算机科学和数学专业的重要课程之一。
以下是一些常见的北美离散数学教材:
《Discrete Mathematics and Its Applications》(离散数学及其应用)- Kenneth H. Rosen:这本教材是离散数学领域的经典教材之一。
它涵盖了离散数学的各个主题,包括集合论、图论、逻辑、证明技巧、组合数学等。
该教材以清晰的讲解和丰富的例子,帮助学生理解离散数学的基本概念和应用。
《Concrete Mathematics: A Foundation for Computer Science》(具体数学:计算机科学基础)- Ronald L. Graham, Donald E. Knuth, Oren Patashnik:这本教材是计算机科学领域的经典之作,它将离散数学与计算机科学的应用紧密结合。
该教材涵盖了离散数学的各个主题,包括递归、生成函数、离散概率等。
它以严谨的数学推导和实际的计算机科学问题,帮助学生培养数学建模和问题解决的能力。
《Discrete Mathematics: An Open Introduction》(离散数学:开放式导论)- Oscar Levin:这本教材是一本开放式教材,可以免费在线获取。
它涵盖了离散数学的基本概念和技巧,包括集合论、图论、逻辑、证明技巧等。
该教材以易懂的语言和丰富的练习题,帮助学生掌握离散数学的核心概念。
这些教材都是离散数学领域的经典教材,被广泛使用于北美的大学和学院。
具体选择教材时,可以根据个人的学习风格和教师的推荐来决定。
另外,还可以参考课程教材清单或与教师咨询,以获取更准确的教材推荐。
离散数学完整版课件全套ppt教学教程最全整套电子讲义幻灯片(最新)

1.1 命题及联结词
定义1.5双条件:当p与q值相同时,pq为1,不同 为0。 称p当且仅当q
“普通老师赚了100万当且仅当他 中了100万的彩票”, 普通老师赚了100万 普通老师买彩票中了100万大奖
故pq为0
1.1 命题及联结词
定义1.4条件式当p是1 ,q是0时,pq为0,即 10为0,其他情况为1。 p称为前件,q称为后件
(1)当p为1即“我期终考了年级前10”
q为0即“我老妈没有奖励1000元” 这时老妈的话为假,即pq为0 (2)当p为1即“我期终考了年级前10” q为1即“我老妈奖励1000元” 这时妈妈的话就对了,即pq为1
由于所有内容(整数,实数,字符,汉字,图片,声 音,视频,网页,……)进入电脑后,全是01组成的字 符串,从而都可以用布尔运算即逻辑运算实现,命题逻 辑成为计算机的基础。
命题逻辑将数学由连续变到离散,由高数进入离散。
Google采用逻辑运算进行搜索:数字之美 吴军 杨圣洪 000100010001110000 两者对应位置与运算。 离散数学 100100000000100001
陈述句(6)的正确性,到2018年12月时能确定的,若届 时建成了则它是对的、为真命题,否为假命题。
1.1 命题及联结词
对错确定的陈述语句称为命题。如:
(7) x与y之和为100,其中x为整数,y为整数 (8)1加1等于10 (7)的对错不确定。当x为50、y为50时是对的,当x为 51、y为52时是错的。 (8)的对错是不确定的,为二进制时正确,当为八进制、 十进制时是错的,因此这两个陈述句不是命题。 (9)青枫峡的红叶真美呀! (10)动作快点! (11)你是杨老师吗? 这三个语句不是陈述语句,因此不是命题。
计算机国外著名教材列表

作者:
作者:Kip R. Irvine
其他影印版图书
C++ Network Programming, Volume 1: Mastering Complexity with ACE and Patterns C++网络编程, 卷1: 运 用ACE和模式消除复杂 性 ISBN:7-302-07644-8 作者:Douglas C. Schmidt Stephen D. Huston 定价:29.00元 Computing Concepts 新概念计算机英语 ISBN:7-302-07357-0 作者:Stephen Haag Maeve Cummings Alan I Rea, Jr 定价:52.00元 C++ Network Programming, Volume 2: Systematic Reuse with ACE and Frameworks C++网络编程,卷2: 基 于ACE和框架的系统 化复用 ISBN:7-302-07964-1 作者:Douglas C. Schmidt Stephen D. Huston 定价:34.00元
Reference, Fourth Edition C++完全参考手册(第 4版) 作者:Herbert Schildt ISBN 7-302-10157-4 定价:96.00元 Parallel Programming: in C with MPI and OpenMP 并行程序设计: C、MPI 与OpenMP 作者:Michael J. Qiunn ISBN 7-302定价:元 Fundamentals of Algorithmics 算法基础 作者:Gilles Brassard, Paul Bratley ISBN 7-302定价:元 Business Data Communications, 5E 事务数据通信(第5 版) 作者:William Stallings ISBN 7-302定价:元 即将出版 Classic and Contemporary Cryptology 经典密码学与现代密码 学 作者:Richard J. Spillman Object-Oriented Programming in C++, 2E C++面向对象程序设计 (第2版) 作者:Richard Johnsonbaugh, Martin Kalin Assembly Language for Intel-Based Computers, 4E Intel汇编语言程序设计 (第4版)
