实验10 二叉树的基本操作
二叉树的基本操作

二叉树的基本操作二叉树是一种常见的数据结构,它由节点组成,每个节点最多有两个子节点。
二叉树在计算机领域中得到广泛应用,它的基本操作包括插入、删除、查找、遍历等。
1.插入操作:二叉树的插入操作是将一个新的节点添加到已有的二叉树中的过程。
插入操作会按照一定规则将新节点放置在正确的位置上。
插入操作的具体步骤如下:-首先,从根节点开始,比较新节点的值与当前节点的值的大小关系。
-如果新节点的值小于当前节点的值,则将新节点插入到当前节点的左子树中。
-如果新节点的值大于当前节点的值,则将新节点插入到当前节点的右子树中。
-如果当前节点的左子树或右子树为空,则直接将新节点插入到该位置上。
-如果当前节点的左子树和右子树都不为空,则递归地对左子树或右子树进行插入操作。
2.删除操作:二叉树的删除操作是将指定节点从二叉树中删除的过程。
删除操作有以下几种情况需要考虑:-如果待删除节点是叶子节点,则直接将其从二叉树中删除即可。
-如果待删除节点只有一个子节点,则将其子节点替换为待删除节点的位置即可。
-如果待删除节点有两个子节点,则需要找到其左子树或右子树中的最大节点或最小节点,将其值替换为待删除节点的值,然后再删除最大节点或最小节点。
3.查找操作:二叉树的查找操作是在二叉树中查找指定值的节点的过程。
查找操作的具体步骤如下:-从根节点开始,将待查找值与当前节点的值进行比较。
-如果待查找值等于当前节点的值,则返回该节点。
-如果待查找值小于当前节点的值,则在当前节点的左子树中继续查找。
-如果待查找值大于当前节点的值,则在当前节点的右子树中继续查找。
-如果左子树或右子树为空,则说明在二叉树中找不到该值。
4.遍历操作:二叉树的遍历操作是按照一定规则依次访问二叉树中的每个节点。
有三种常用的遍历方式:- 前序遍历(Preorder Traversal):先访问根节点,然后递归地前序遍历左子树和右子树。
- 中序遍历(Inorder Traversal):先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
完整word版二叉树基本操作 实验报告

一、实验目的实验报告 1、 熟悉二叉树树的基本操作。
2、 掌握二叉树的实现以及实际应用。
3、 加深二叉树的理解,逐步培养解决实际问题的编程能力。
二、实验环境 1 台 WINDOWS 环境的 PC 机,装有 Visual C++ 6.0。
三、实验内容【问题描述】现需要编写一套二叉树的操作函数, 以便用户能够方便的利用这些函数来实现自己的应用。
其中操作函数包括: 创建二叉树CreateBTNode(*b,*str):根据二叉树括号表示法的字符串*str 生成对应的链 式存储结构。
输出二叉树 DispBTNode(*b):以括号表示法输出一棵二叉树。
查找结点FindNode(*b,x):在二叉树b 中寻找data 域值为x 的结点,并返回指向该结点 的指针。
求高度BTNodeDepth(*b):求二叉树b 的高度。
若二叉树为空,则其高度为0;否则,其 高度等于左子树与右子树中的最大高度加 求二叉树的结点个数 先序遍历的递归算法: 中序遍历的递归算法: 后序遍历递归算法: 1> 2> 3> 4>5> 6>7> 8>9> NodesCou nt(BTNode *b) void P reOrder(BTNode *b) void In Order(BTNode *b) void P ostOrder(BTNode *b) 层次遍历算法 void LevelOrder(BTNode *b) 【基本要求】实现以上9个函数。
主函数中实现以下功能: 创建下图中的树b 输出二叉树b 找到''节点,输出其左右孩子值 输出b 的高度输出b 的节点个数A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))程序:#in elude <stdio.h>#in elude <malloc.h> #defi ne MaxSize 100 typ edef char ElemT ype;typ edef struct node{ElemT ype data; structnode *lchild; struct node*rchild;} BTNode; /*数据元素*/ /*指向左孩子*/ /*指向右孩子*/void CreateBTNode(BTNode *&b,char *str);// 创建 BTNode *Fi ndNode(BTNode *b,ElemTy pe x);// 查找节点 int BTNodeHeight(BTNode *b);// 求高度void Dis pBTNode(BTNode *b);// 输出int NodesCount(BTNode *b);// 二叉树的结点个数void PreOrder(BTNode *b);// 先序遍历递归void InOrder(BTNode *b);// 中序遍历递归void PostOrder(BTNode *b);// 后序遍历递归void LevelOrder(BTNode *b);// 层次遍历〃创建void CreateBTNode(BTNode *&b,char *str){BTNode *St[MaxSize],* p=NULL;int top=-1,k,j=O;char ch;输出b 的四种遍历顺序 上图转 叉树括号表示法为b=NULL;ch=str[j];while(ch!='\0'){switch(ch){case '(':t op++;St[t op]=p ;k=1;break;case ')':t op--;break;case ',':k=2;break;default: p=(BTNode *)malloc(sizeof(BTNode)); p->data=ch; p->lchild=p-> rchild=NULL; if(b==NULL) b=p;else{switch(k){case 1:St[t op]->lchild=p ;break;case 2:St[t op]->rchild=p ;break;}}} j++;ch=str[j];}}//输出void Dis pBTNode(BTNode *b){if(b!=NULL){prin tf("%c",b->data);if(b->lchild!=NULL||b->rchild!=NULL){prin tf("(");Dis pBTNode(b->lchild); if(b->rchild!=NULL)prin tf(",");Dis pBTNode(b->rchild); prin tf(")");〃查找节点BTNode *Fin dNode(BTNode *b,ElemTy pe x){BTNode *p;if(b==NULL)return b;else if(b->data==x)return b;else{p=Fi ndNode(b->lchild,x);if(p !=NULL)return p;elseretur n Fin dNode(b->rchild,x);//求高度int BTNodeHeight(BTNode *b){ int lchildh,rchildh; if(b==NULL)return (0);else{lchildh=BTNodeHeight(b->lchild); rchildh=BTNodeHeight(b->rchild); return(lchildh>rchildh)?(lchildh+1):(rchildh+1);〃二叉树的结点个数int NodesCou nt(BTNode *b){ if(b==NULL)return 0;elsereturn NodesCou nt(b->lchild)+NodesCou nt(b->rchild)+1;//先序遍历递归void P reOrder(BTNode *b){ if(b!=NULL){prin tf("%c",b->data); PreOrder(b->lchild); PreOrder(b->rchild);〃中序遍历递归void InO rder(BTNode *b){ if(b!=NULL){InO rder(b->lchild); prin tf("%c",b->data); InO rder(b->rchild);}}//后序遍历递归void P ostOrder(BTNode*b){ if(b!=NULL){P ostOrder(b->lchild);P ostOrder(b->rchild); prin tf("%c",b->data);}}//层次遍历void LevelOrder(BTNode *b){BTNode *p;BTNode *qu[MaxSize];int fron t,rear;fron t=rear=-1;rear++;qu[rear]=b;while(fro nt!=rear){fron t=(fro nt+1)%MaxSize;p=qu[fron t];prin tf("%c", p->data);if(p->lchild!=NULL){rear=(rear+1)%MaxSize; qu[rear]=p->lchild;}if(p->rchild!=NULL){ rear=(rear+1)%MaxSize; qu[rear]=p-> rchild; void mai n()BTNode *b,* p, *l p,*rp;char str[]="A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,l)))";// 根据树形图改写成的〃二叉树括号表示法的字符串 *str//char str[100];sca nf("%s",& str);// 自行输入括号表示的二叉树CreateBTNode(b,str); // 创建树 b prin tf("\n");printf (”输出二叉树:");//输出二叉树bDis pBTNode(b);prin tf("\n");printf("'H'结点:");//找到'H'节点,输出其左右孩子值 p=Fi ndNode(b,'H');prin tf("\n");if (p !=NULL){printf("左孩子节点的值");prin tf("%c", p->lchild->data); prin tf("\n");printf("右孩子节点的值");prin tf("%c", p->rchild->data); prin tf("\n");//此处输出p 的左右孩子节点的值}prin tf("\n");printf (” 二叉树 b 的深度:%d\n",BTNodeHeight(b));// 输出 b 的高度 printf (”二叉树b 的结点个数:%d\n",NodesCount(b));//输出b 的节点个数 prin tf("\n");先序遍历序列:\n");//输出b 的四种遍历顺序算法:");PreOrder(b);printf("\n"); 中序遍历序列:\n"); 算法:");InOrder(b);printf("\n"); 后序遍历序列:\n"); 算法:");PostOrder(b);printf("\n"); 层次遍历序列:\n"); 算法:”);LevelOrder(b); printf("\n");printf (”printf (”printf (”printf (”printf (”printf (”printf (”四、实验心得与小结通过实验,我熟悉二叉树树的基本操作,掌握二叉树的实现以及实际应用。
二叉树的基本操作课件浙教版(2019)高中信息技术选修1(24张PPT)

A
B
D
C
E
F
G
头指针
二叉树的list实现
二叉树节点可以看成是一个三元组,元素是左、右子树和本节点数据。
Python的list可以用于组合这样的三个元素。
下面介绍用list构造二叉树的方法。
(1)空树用None表示。
(2)非空二叉树用包含三个元素的列表[d,l,r]表示,其中:d表示根节点的元素,l和r是两棵子树,采用与整个二叉树同样结构的list表示。
二叉树的遍历
在完成二叉树的建立操作后,就可以对二叉树的各个节点进行访问,即遍历操作。二叉树的遍历,是指按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。按照不同的遍历方式对节点进行访问,其处理效率不完全相同。二叉树的遍历方式有很多,主要有前序遍历、中序遍历和后序遍历等。
1.数组实现
用数组来表示二叉树时,分为以下两种情况。
(1)完全二叉树从二叉树的根节点开始,按从上而下、自左向右的顺序对n个节点进行编号,根节点的编号为0,最后一个节点的编号为n-1。然后依次将二叉树的节点用一组连续的数组元素来表示,节点编号与数组的下标一一对应。如下图中图甲所示的完全二叉树所对应的一维数组表示如图乙所示。
A
B
C
A
B
C
甲 原二叉树
乙 补全后的二叉树
0
1
2
3
4
5
6
7
丙 数组实现示意图
A
B
C
对于完全二叉树而言,一维数组的表示方式既简单又节省存储空间。但对于一般的二叉树来说,采用一维数组表示时,结构虽然简单,却容易造成存储空间的浪费。
二叉树的定义及基本操作

(所输入的数据及相应的运行结果,运行结果要有提示信息,运行结果采用截图 方式给出。)
2
① 输入界面
②输出结果
③测试式子 6*((5+(2+)*8)+3)
六、总结与体会
(调试程序的心得与体会,若实验课上未完成调试,要认真找出错误并分析原因 等。)
每次的实验,总是很受打击。不过,在这过程中,能让我发现自己的 不足,逐渐改善,这是做实验给我最大的收获。 七、程序清单(包含注释)
四、实验记录
(调试过程及调试中遇到的问题及解决办法,其他算法的存在与实践等。) ① 调试过程老是出现访问冲突的错问,通过上网查找访问冲突方面的消息,才
知道应该是指针指错地址,经过调试,最终解决了问题。 ②
调试过程中还出现了这个问题,Status CreateBiTree(BiTree T),当这样定 义时,问题就出现了,但是 Status CreateBiTree(BiTree &T)这样定义就没问题 了,这个想不通。
-
+
/
1.中缀表达式(中序遍历): a+(b*(c-d))-(e/f)
a
*e
2.前缀表达式/波兰式(前序遍历):
f
-+a*b-cd/ef
b-
3.后缀表达式/逆波兰式(后序遍历): abcd-*+ef/-
《《《《《
《 《《《《
C《《《 《 P129
cd
表达式二叉树
1
三、实验所涉及的知识点 递归函数 二叉树
输入说明
***\n"); printf("*** 请按先序输入表达式,当结点的左子树或者右
子树为空时输入‘#‘***\n");
(完整版)C++二叉树基本操作实验报告

一、实验目的选择二叉链式存储结构作为二叉树的存储结构,设计一个程序实现二叉树的基本操作(包括建立、输出、前序遍历、中序遍历、后序遍历、求树高、统计叶子总数等)二、实验开发环境Windows 8.1 中文版Microsoft Visual Studio 6.0三、实验内容程序的菜单功能项如下:1------建立一棵二叉树2------前序遍历递归算法3------前序遍历非递归算法4------中序遍历递归算法5------中序遍历非递归算法6------后序遍历递归算法7------后序遍历非递归算法8------求树高9------求叶子总数10-----输出二叉树11-----退出四、实验分析1、建立一棵二叉树2、输入二叉树各节点数据cout<<"请按正确顺序输入二叉树的数据:";cin.getline(t,1000); //先把输入的数据输入到一个t数组3、递归前序遍历void BL1(ECS_data *t){if(NULL!=t){cout<<t->data<<",";BL1(t->l);BL1(t->r);}}4、非递归前序遍历void preOrder2(ECS_data *t){stack<ECS_data*> s;ECS_data *p=t;while(p!=NULL||!s.empty()){while(p!=NULL){cout<<p->data<<" ";s.push(p);p=p->l;}if(!s.empty()){p=s.top();s.pop();p=p->r;}}}5、递归中序遍历void BL2(ECS_data *t){if(NULL!=t){BL2(t->l);cout<<t->data<<",";BL2(t->r);}}6、非递归中序遍历void inOrder2(ECS_data *t) //非递归中序遍历{stack<ECS_data*> s;ECS_data *p=t;while(p!=NULL||!s.empty()){while(p!=NULL){s.push(p);p=p->l;}if(!s.empty()){p=s.top();cout<<p->data<<" ";s.pop();p=p->r;}}}7、递归后序遍历void BL3(ECS_data *t){if(NULL!=t){BL3(t->l);BL3(t->r);cout<<t->data<<",";}}8、非递归后序遍历void postOrder3(ECS_data *t){stack<ECS_data*> s;ECS_data *cur; //当前结点ECS_data *pre=NULL; //前一次访问的结点s.push(t);while(!s.empty()){cur=s.top();if((cur->l==NULL&&cur->r==NULL)||(pre!=NULL&&(pre==cur->l||pre==cur->r))){cout<<cur->data<<" "; //如果当前结点没有孩子结点或者孩子节点都已被访问过s.pop();pre=cur;}else{if(cur->r!=NULL)s.push(cur->r);if(cur->l!=NULL)s.push(cur->l);}}}9、求树高int Height (ECS_data *t){if(t==NULL) return 0;else{int m = Height ( t->l );int n = Height(t->r);return (m > n) ? (m+1) : (n+1);}}10、求叶子总数int CountLeaf(ECS_data *t){static int LeafNum=0;//叶子初始数目为0,使用静态变量if(t)//树非空{if(t->l==NULL&&t->r==NULL)//为叶子结点LeafNum++;//叶子数目加1else//不为叶子结点{CountLeaf(t->l);//递归统计左子树叶子数目CountLeaf(t->r);//递归统计右子树叶子数目}}return LeafNum;}五、运行结果附:完整程序源代码://二叉树链式存储的实现#include<iostream>#include<cstring>#include <stack>using namespace std;struct ECS_data //先定义好一个数据的结构{char data;ECS_data *l;ECS_data *r;};class ECS{private://int level; //树高int n; //表示有多少个节点数int n1; //表示的是数组的总长度值,(包括#),因为后面要进行删除判断ECS_data *temp[1000];public:ECS_data *root;ECS() //初始化{ECS_data *p;char t[1000];int i;int front=0,rear=1; //front表示有多少个节点,rear表示当前插入的点的父母cout<<"请按正确顺序输入二叉树的数据:";cin.getline(t,1000); //先把输入的数据输入到一个t数组//cout<<t<<" "<<endl;int n1=strlen(t); //测量数据的长度n=0;for(i=0;i<n1;i++){if(t[i]!='#'){p=NULL;if(t[i]!=',') //满足条件并开辟内存{n++;p=new ECS_data;p->data=t[i];p->l=NULL;p->r=NULL;}front++;temp[front]=p;if(1 == front){root=p;}else{if((p!=NULL)&&(0==front%2)){temp[rear]->l=p;//刚开始把这里写成了==}if((p!=NULL)&&(1==front%2)){temp[rear]->r=p;}if(1==front%2)rear++; //就当前的数据找这个数据的父母}}}}~ECS() //释放内存{int i;for(i=1;i<=n;i++)if(temp[i]!=NULL)delete temp[i];}void JS() //记录节点的个数{int s;s=n;cout<<"该二叉树的节点数为:"<<s<<endl;}void BL1(ECS_data *t)//递归前序遍历{if(NULL!=t){cout<<t->data<<",";BL1(t->l);BL1(t->r);}}void preOrder2(ECS_data *t) //非递归前序遍历{stack<ECS_data*> s;ECS_data *p=t;while(p!=NULL||!s.empty()){while(p!=NULL){cout<<p->data<<" ";s.push(p);p=p->l;}if(!s.empty()){p=s.top();s.pop();p=p->r;}}}void BL2(ECS_data *t)//递归中序遍历{if(NULL!=t){BL2(t->l);cout<<t->data<<",";BL2(t->r);}}void inOrder2(ECS_data *t) //非递归中序遍历{stack<ECS_data*> s;ECS_data *p=t;while(p!=NULL||!s.empty()){while(p!=NULL){s.push(p);p=p->l;}if(!s.empty()){p=s.top();cout<<p->data<<" ";s.pop();p=p->r;}}}void BL3(ECS_data *t)//递归后序遍历{if(NULL!=t){BL3(t->l);BL3(t->r);cout<<t->data<<",";}}void postOrder3(ECS_data *t) //非递归后序遍历{stack<ECS_data*> s;ECS_data *cur; //当前结点ECS_data *pre=NULL; //前一次访问的结点s.push(t);while(!s.empty()){cur=s.top();if((cur->l==NULL&&cur->r==NULL)||(pre!=NULL&&(pre==cur->l||pre==cur->r))){cout<<cur->data<<" "; //如果当前结点没有孩子结点或者孩子节点都已被访问过s.pop();pre=cur;}else{if(cur->r!=NULL)s.push(cur->r);if(cur->l!=NULL)s.push(cur->l);}}}int Height (ECS_data *t) //求树高{if(t==NULL) return 0;else{int m = Height ( t->l );int n = Height(t->r);return (m > n) ? (m+1) : (n+1);}}int CountLeaf(ECS_data *t) //求叶子总数{static int LeafNum=0;//叶子初始数目为0,使用静态变量if(t)//树非空{if(t->l==NULL&&t->r==NULL)//为叶子结点LeafNum++;//叶子数目加1else//不为叶子结点{CountLeaf(t->l);//递归统计左子树叶子数目CountLeaf(t->r);//递归统计右子树叶子数目}}return LeafNum;}};int main(){ECS a;a.JS();cout<<"递归前序遍历:";a.BL1(a.root);cout<<endl;cout<<"非递归前序遍历:";a.preOrder2(a.root);cout<<endl;cout<<"递归中序遍历:";a.BL2(a.root);cout<<endl;cout<<"非递归中序遍历:";a.inOrder2(a.root);cout<<endl;cout<<"递归后序遍历:";a.BL3(a.root);cout<<endl;cout<<"非递归后序遍历:";a.postOrder3(a.root);cout<<endl;cout<<"树高为:"<<a.Height(a.root)<<endl;cout<<"叶子总数为:"<<a.CountLeaf(a.root)<<endl;return 0;}。
二叉树的基本操作

二叉树的基本操作公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]浙江大学城市学院实验报告课程名称数据结构基础实验项目名称实验十二叉树的基本操作学生姓名吴奇专业班级信管1204 学号实验成绩指导老师(签名)日期一. 实验目的和要求1、掌握二叉树的链式存储结构。
2、掌握在二叉链表上的二叉树操作的实现原理与方法。
3、进一步掌握递归算法的设计方法。
二. 实验内容1、按照下面二叉树二叉链表的存储表示,编写头文件,实现二叉链表的定义与基本操作实现函数;编写主函数文件,验证头文件中各个操作。
二叉树二叉链表存储表示如下:struct BTreeNode {ElemType data; 函数的功能说明及算法思路struct BtreeNode{elemtype data; 实验结果与分析五. 心得体会通过这次实验,我掌握了二叉树的基本操作,对非线性储存结构有了一定的了解,相对于之前的线性储存结构来说,非线性储存结构确实是比较抽象、困难的,在接下来的时间里,要好好对非线性储存结构了解一番。
【附录----源程序】struct BtreeNode{elemtype data; //结点值域BtreeNode *lchild; //定义左孩子指针BtreeNode *rchild; //定义右孩子指针};struct lnode{ //定义队列结点结构用于二叉树层遍历BtreeNode *data1;lnode *next;};struct Queue{ //定义队列首尾指针lnode *front;lnode *back;};void initQueue(Queue &Q) //初始化队列{==NULL;}void insertQueue(Queue &Q,BtreeNode *item) //元素入队列{lnode *newptr=new lnode;newptr->data1=item;newptr->next=NULL;if==NULL)==newptr;else=>next=newptr;}BtreeNode *deleteQueue(Queue &Q) //队首元素出队列{BtreeNode *temp=>data1;lnode *p=;=p->next;if==NULL)=NULL;delete p;return temp;}bool emptyQueue(Queue Q) //判断队列是否为空{return ==NULL;}void initBtree(BtreeNode *&BT) //二叉树的初始化{BT=NULL;}void insertBtree(BtreeNode *&BT) //创建二叉树{elemtype ch;ch=getchar();if(ch=='$') //判断是不是结束标志BT=NULL;else{BT=new BtreeNode; //创建结点BT->data=ch; //赋值insertBtree(BT->lchild); //左子叶递归insertBtree(BT->rchild); //右子叶递归}}bool emptyBtree(BtreeNode *BT) //判断二叉树是否为空{return BT==NULL;}int depthBtree(BtreeNode *BT) //求二叉树的深度{if(emptyBtree(BT))return 0;else{int dep1=depthBtree(BT->lchild); //左子叶递归int dep2=depthBtree(BT->rchild); //右子叶递归return dep1>dep2dep1+1:dep2+1; //判断哪个子叶的深度最大//树的深度为左右子叶的最大深度加上1}}void preorder(BtreeNode *BT) //前序遍历{if(!emptyBtree(BT)){cout<<BT->data<<" "; //输出结点值preorder(BT->lchild); //左子叶递归preorder(BT->rchild); //右子叶递归}}void midorder(BtreeNode *BT) //中序遍历{if(!emptyBtree(BT)){midorder(BT->lchild); //左子叶递归cout<<BT->data<<" "; //输出结点值midorder(BT->rchild); //右子叶递归}}void laterorder(BtreeNode *BT) //后序遍历{if(!emptyBtree(BT)){laterorder(BT->lchild); //左子叶递归laterorder(BT->rchild); //右子叶递归cout<<BT->data<<" "; //输出结点值}}bool findBtree(BtreeNode *BT,elemtype x) //查找二叉树中结点元素为x值的结点{if(emptyBtree(BT)) //空树,返回false return false;else{if(BT->data==x) //找到,返回truereturn true;else{if(findBtree(BT->lchild,x)) //左子叶递归查找return true;if(findBtree(BT->rchild,x)) //右子叶递归查找return true;return false;}}}void levelorder(BtreeNode *BT) //按层遍历二叉树{Queue queue; //用于存放二叉树结点的队列initQueue(queue);BtreeNode *P;if(!emptyBtree(BT)) //二叉树不为空,根节点入队insertQueue(queue,BT);while(!emptyQueue(queue)){ //当队列不为空时,队首元素出队列P=deleteQueue(queue);cout<<P->data<<" "; //输出出队元素值if(P->lchild!=NULL) //当左右子叶不为空时,递归insertQueue(queue,P->lchild);if(P->rchild!=NULL)insertQueue(queue,P->rchild);}}int Get_Sub_Depth(BtreeNode *BT,elemtype x)//求二叉树中以元素值为x的结点为根的子树的深度{int m,n;if(!emptyBtree(BT)){ //二叉树非空if(BT->data==x) //找到,返回其深度return depthBtree(BT);else{m=Get_Sub_Depth(BT->lchild,x); //左右子叶递归,返回深度n=Get_Sub_Depth(BT->rchild,x);return m>nm:n;}}elsereturn 0;}void printBtree(BtreeNode *BT,int n) //打印二叉树{int i;if(emptyBtree(BT)) //二叉树为空,返回return;printBtree(BT->rchild,n+1); //先递归输出右子树for(i=0;i<n;i++)cout<<" "; //前导空格,表示层次cout<<"---";cout<<BT->data; //结点的值cout<<endl;printBtree(BT->lchild,n+1); //再递归输出右子树}void PrintBtree(BtreeNode *BT) //二叉树的广义表打印{if(!emptyBtree(BT)){cout<<BT->data;if(!emptyBtree(BT->lchild)||!emptyBtree(BT->rchild)){cout<<"(";PrintBtree(BT->lchild);if(!emptyBtree(BT->rchild))cout<<",";PrintBtree(BT->rchild);cout<<")";}}}#include<>#include<>#include<>typedef char elemtype;#include""void main(){BtreeNode *Btree;initBtree(Btree);elemtype a,b;cout<<"请严格按照先序顺序输入二叉树中的数据,以“$”为每个结点的结束标志"<<endl;insertBtree(Btree);cout<<"二叉树的深度为:"<<depthBtree(Btree)<<endl;cout<<"先序遍历二叉树:";preorder(Btree);cout<<endl;cout<<"中序遍历二叉树:";cout<<endl;cout<<"后序遍历二叉树:";laterorder(Btree);cout<<endl;cout<<"层序遍历二叉树:";levelorder(Btree);cout<<endl;cout<<"请输入需查找字符:";cin>>a;if(findBtree(Btree,a))cout<<"查找字符"<<a<<"成功!"<<endl;elsecout<<"查找失败,没有该字符!"<<endl;cout<<"请输入以元素值为x的结点为根的子树的深度的x的值:";cin>>b;if(Get_Sub_Depth(Btree,b)==0)cout<<"未查询到该结点!!"<<endl;elsecout<<"结点元素值为x的深度为:"<<Get_Sub_Depth(Btree,b)<<endl;cout<<"二叉树的广义表打印如下图:"<<endl;cout<<endl;cout<<"二叉树打印如下图:"<<endl;printBtree(Btree,depthBtree(Btree)); }。
二叉树的基本操作实验报告

二叉树的基本操作实验报告学号姓名实验日期 2012-12-26实验室计算机软件技术实验指导教师设备编号 401实验内容二叉树的基本操作一实验题目实现二叉树的基本操作的代码实现二实验目的1、掌握二叉树的基本特性2、掌握二叉树的先序、中序、后序的递归遍历算法3、通过求二叉树的深度、度为2的结点数和叶子结点数等算法三实习要求(1)认真阅读书上给出的算法(2)编写程序并独立调试四、给出二叉树的抽象数据类型ADT BinaryTree{//数据对象D:D是具有相同特性的数据元素的集合。
//数据关系R:// 若D=Φ,则R=Φ,称BinaryTree为空二叉树;// 若D?Φ,则R={H},H是如下二元关系;// (1)在D中存在惟一的称为根的数据元素root,它在关系H下无前驱; // (2)若D-{root}?Φ,则存在D-{root}={D1,Dr},且D1?Dr =Φ; // (3)若D1?Φ,则D1中存在惟一的元素x1,<root,x1>?H,且存在D1上的关系H1 ?H;若Dr?Φ,则Dr中存在惟一的元素xr,<root,xr>?H,且存在上的关系Hr ?H;H={<root,x1>,<root,xr>,H1,Hr};// (4)(D1,{H1})是一棵符合本定义的二叉树,称为根的左子树;(Dr,{Hr})是一棵符合本定义的二叉树,称为根的右子树。
//基本操作:CreateBiTree( &T, definition ) // 初始条件:definition给出二叉树T的定义。
// 操作结果:按definiton构造二叉树T。
BiTreeDepth( T )// 初始条件:二叉树T存在。
// 操作结果:返回T的深度。
PreOrderTraverse( T, visit() ) // 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
二叉树的基础操作
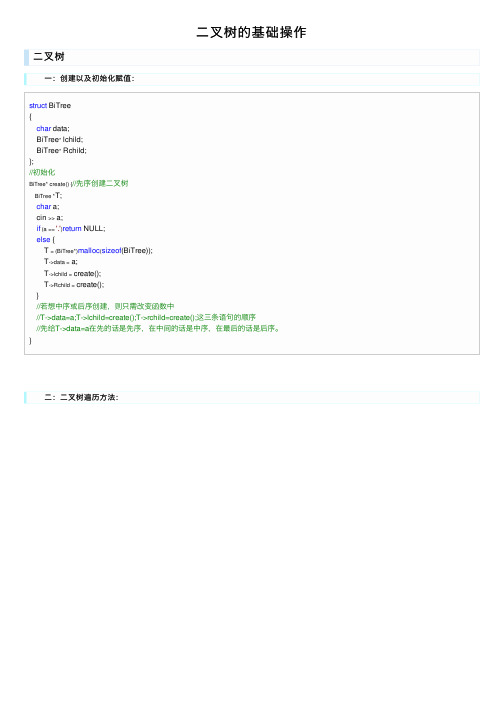
⼆叉树的基础操作⼆叉树 ⼀:创建以及初始化赋值:struct BiTree{char data;BiTree* lchild;BiTree* Rchild;};//初始化BiTree* create() {//先序创建⼆叉树BiTree *T;char a;cin >> a;if (a == '.')return NULL;else {T = (BiTree*)malloc(sizeof(BiTree));T->data = a;T->lchild = create();T->Rchild = create();}//若想中序或后序创建,则只需改变函数中//T->data=a;T->lchild=create();T->rchild=create();这三条语句的顺序//先给T->data=a在先的话是先序,在中间的话是中序,在最后的话是后序。
} ⼆:⼆叉树遍历⽅法:/*先序的遍历顺序是根节点->左⼦树->右⼦树。
中序的遍历顺序是左⼦树->根节点->右⼦树。
后序的遍历顺序是右⼦树->根节点->左⼦树。
层序的遍历顺序是按层顺次遍历。
先序、中序、后序的代码基本相同*/void pre(BiTree *root) {BiTree* p = root;if (p) {cout << p->data;pre(p->lchild);pre(p->Rchild);}}void mid(BiTree* root) {BiTree* p = root;if (root) {mid(p->lchild);cout << p->data;mid(p->Rchild);}}void post(BiTree* root) {BiTree* p = root;if (p) {post(p->Rchild);post(p->lchild);cout << p->data;}} 三:⼆叉树插⼊操作://插⼊操作,没有重复的元素//插⼊法1:BiTree* BSTInsert(BiTree* L, int key) {if (!L) {//若是⼀个空表,那么就创建最开始的L = (BiTree*)malloc(sizeof(BiTree));L->data = key;L->lchild = L->Rchild = NULL;}else {//若不是空表就按照⼆叉树组成规则遍历插⼊if (L->data < key)L->Rchild = BSTInsert(L->Rchild, key);else if (L->data > key)L->lchild = BSTInsert(L->lchild, key);}return L;}//插⼊法2:整列树的插⼊//int data[9]={8,3,10,13,14,1,6,7,4};BiTree* Insert(BiTree* L, int data[], int n) {int i;for (int i = 0; i < n; i++) {L = BSTInsert(L, data[i]);}return L;} 四:⼆叉树查询://查询元素位置:/*查询法1:寻找最⼩、最⼤元素的⽅法是相同的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江大学城市学院实验报告课程名称数据结构基础实验项目名称实验十二叉树的基本操作学生姓名专业班级学号实验成绩指导老师(签名)日期2014-12-18一.实验目的和要求1、掌握二叉树的链式存储结构。
2、掌握在二叉链表上的二叉树操作的实现原理与方法。
3、进一步掌握递归算法的设计方法。
二.实验内容1、按照下面二叉树二叉链表的存储表示,编写头文件binary_tree.h,实现二叉链表的定义与基本操作实现函数;编写主函数文件test4_1.cpp,验证头文件中各个操作。
二叉树二叉链表存储表示如下:struct BTreeNode {ElemType data; // 结点值域BTreeNode *lchild , *rchild ; // 定义左右孩子指针} ;基本操作如下:①void InitBTree( BTreeNode *&BT );//初始化二叉树BT②void CreateBTree( BTreeNode *&BT, char *a );//根据字符串a所给出的广义表表示的二叉树建立二叉链表存储结构③int EmptyBTree( BTreeNode *BT);//检查二叉树BT是否为空,空返回1,否则返回0④int DepthBTree( BTreeNode *BT);//求二叉树BT的深度并返回该值⑤int FindBTree( BTreeNode *BT, ElemType x);//查找二叉树BT中值为x的结点,若查找成功返回1,否则返回0⑥void PreOrder( BTreeNode *BT);//先序遍历二叉树BT⑦void InOrder( BTreeNode *BT);//中序遍历二叉树BT⑧void PostOrder( BTreeNode *BT);//后序遍历二叉树BT⑨void PrintBTree( BTreeNode *BT );//输出二叉树BT⑩void ClearBTree( BTreeNode *&BT );//清除二叉树BT2、选做:实现以下说明的操作函数,要求把函数添加到头文件binary_tree.h 中,并在主函数文件test4_1.cpp中添加相应语句进行测试。
①void LevelOrder( BTreeNode *BT )//二叉树的层序遍历②int Get_Sub_Depth( BTreeNode *T , ElemType x)//求二叉树中以元素值为x的结点为根的子树的深度3、填写实验报告,实验报告文件取名为report10.doc。
4、上传实验报告文件report10.doc、源程序文件test4_1.cpp及binary_tree.h 到Ftp服务器上自己的文件夹下。
三. 函数的功能说明及算法思路(包括每个函数的功能说明,及一些重要函数的算法实现思路)ADT GeneralTree isData:二元组 ( D , R )D是具有相同特性的数据元素的集合。
数据关系R为:当 n > 0(非空树)时,满足下列条件:①有且仅有一个结点没有前驱,此结点称为根。
②除根以外,其余结点有且仅有一个前驱结点。
③所有结点可以有任意多个(含0个)后继。
Operations:void InitBTree( BTreeNode *&BT ); //初始化二叉树BTvoid CreateBTree( BTreeNode *&BT, char *a ); //根据字符串a所给出的广义表表示的二叉树建立二叉链表存储结构int EmptyBTree( BTreeNode *BT); //检查二叉树BT是否为空,空返回1,否则返回0int DepthBTree( BTreeNode *BT);//求二叉树BT的深度并返回该值int FindBTree( BTreeNode *BT, ElemType x); //查找二叉树BT中值为x的结点,若查找成功返回1,否则返回0void PreOrder( BTreeNode *BT);//先序遍历二叉树BTvoid InOrder( BTreeNode *BT);//中序遍历二叉树BTvoid PostOrder( BTreeNode *BT); //后序遍历二叉树BTvoid PrintBTree( BTreeNode *BT ); //输出二叉树BTvoid ClearBTree( BTreeNode *&BT ); //清除二叉树BTend GeneralTree四. 实验结果与分析(包括运行结果截图、结果分析等)五. 心得体会(记录实验感受、上机过程中遇到的困难及解决办法、遗留的问题、意见和建议等。
)【附录----源程序】test4_1.cpp:#include<stdio.h>#include<iostream.h>#include<stdlib.h>typedef char ElemType;#include "binary_tree.h"void main(){BTreeNode* BT;InitBTree(BT);char b[50];cout<<"输入二叉树广义表字符串:"<<endl;cin.getline(b,sizeof(b));CreateBTree(BT,b);cout<<"前序遍历:";PreOrder(BT); cout<<endl;cout<<"中序遍历:";InOrder(BT); cout<<endl;cout<<"后序遍历:";PostOrder(BT); cout<<endl;cout<<"广义表形式遍历:";PrintBTree(BT); cout<<endl;cout<<"按层遍历:";LevelOrder(BT); cout<<endl;ElemType x,y;cout<<"输入一个需要查找的字符:";cin>>x;if(FindBTree(BT,x)){cout<<"查找字符"<<x<<"成功!"<<endl;cout<<"该字符的深度为:";cout<<DepthBTree(BT)<<endl;}elsecout<<"查找字符"<<x<<"失败,该字符不存在!"<<endl;cout<<"输入一个元素(以该元素的结点为根):";cin>>y;cout<<"以"<<y<<"的结点为根的子树的深度为:";cout<<Get_Sub_Depth(BT,y)<<endl;ClearBTree(BT);}binary_tree.h:struct BTreeNode {ElemType data; // 结点值域BTreeNode *lchild , *rchild ; // 定义左右孩子指针} ;void InitBTree( BTreeNode *&BT ){//初始化二叉树BTBT=NULL;}void CreateBTree( BTreeNode *&BT, char *a ){//根据字符串a所给出的广义表表示的二叉树建立二叉链表存储结构const int MaxSize=10; //栈数组长度>=二叉树的深度减1 BTreeNode* s[MaxSize]; //s数组作为存储根结点指针的栈使用int top=-1; //top为栈顶指针,表示栈空BTreeNode *p; //二叉树结点指针int k,i=0; //k=1时处理左子树,k=2处理右子树while(a[i]){switch(a[i]){case ' ':break;case '(':if(top==MaxSize-1){cout<<"栈空间太小,请增加MaxSize的值!"<<endl;exit(1);}top++;s[top]=p; k=1;break;case ')':if(top==-1){cout<<"二叉树广义表字符串错!"<<endl;exit(1);}top--;break;case ',':k=2;break;default:p=new BTreeNode;p->data=a[i];p->lchild=p->rchild=NULL;if(BT==NULL)BT=p;else{if(k==1) s[top]->lchild=p;else s[top]->rchild=p;}}i++;}}int EmptyBTree( BTreeNode *BT){//检查二叉树BT是否为空,空返回1,否则返回0return BT==NULL;}int DepthBTree( BTreeNode *BT){//求二叉树BT的深度并返回该值if (BT==NULL)return 0;else{int dep1 = DepthBTree(BT->lchild);int dep2 = DepthBTree(BT->rchild);if (dep1>dep2)return dep1+1;elsereturn dep2+1;}}int FindBTree( BTreeNode *BT, ElemType x){//查找二叉树BT中值为x的结点,若查找成功返回1,否则返回0 if(BT==NULL) return 0;else{if (BT->data==x) //先与根结点相比,若不同再去左右子树查找 return 1;else{if (FindBTree(BT->lchild, x)) return 1;if (FindBTree(BT->rchild, x)) return 1;return 0;}}}void PreOrder( BTreeNode *BT){//先序遍历二叉树BTif(BT!=NULL){cout<<BT->data<<' ';PreOrder(BT->lchild);PreOrder(BT->rchild);}}void InOrder( BTreeNode *BT){//中序遍历二叉树BTif(BT!=NULL){InOrder(BT->lchild);cout<<BT->data<<' ';InOrder(BT->rchild);}}void PostOrder( BTreeNode *BT){//后序遍历二叉树BTif(BT!=NULL){PostOrder(BT->lchild);PostOrder(BT->rchild);cout<<BT->data<<' ';}}void PrintBTree( BTreeNode *BT ){//输出二叉树BTif(BT!=NULL){cout<<BT->data; //输出根结点if (BT->lchild!=NULL || BT->rchild!=NULL){//若非叶子结点,则递归调用输出左右子树cout<<'(';PrintBTree(BT->lchild);if(BT->rchild!=NULL){cout<<',';PrintBTree(BT->rchild);}cout<<')';}}}void ClearBTree(BTreeNode *&BT){//清除二叉树BTif(BT!=NULL){ClearBTree(BT->lchild);ClearBTree(BT->rchild);free(BT);BT=NULL;}}void LevelOrder( BTreeNode *BT ){//二叉树的层序遍历const int MaxSize=30; //定义用于存储队列的数组长度BTreeNode* q[MaxSize]; //数组空间int front=0,rear=0;BTreeNode* p;if(BT!=NULL){ //根指针进队rear=(rear+1)%MaxSize;q[rear]=BT;}while(front!=rear){front=(front+1)%MaxSize;p=q[front];cout<<p->data<<' ';if(p->lchild!=NULL){ //左孩子存在则左结点指针进队rear=(rear+1)%MaxSize;q[rear]=p->lchild;}if(p->rchild!=NULL){ //右孩子存在则右结点指针进队rear=(rear+1)%MaxSize;q[rear]=p->rchild;}}}int Get_Sub_Depth( BTreeNode *T , ElemType x){//求二叉树中以元素值为x的结点为根的子树的深度if(T){if(T->data==x)return DepthBTree(T);else{int dep1=Get_Sub_Depth(T->lchild,x);int dep2=Get_Sub_Depth(T->rchild,x);if(dep1>dep2) return dep1;else return dep2;}}else return 0;}。
