双电层模型
双电层及其结构模型

组织工程
双电层结构在组织工程领 域的应用主要涉及仿生细 胞外基质的设计,以促进 细胞生长和功能化。
生物传感器
双电层理论在生物传感器 设计中发挥关键作用,能 够提高传感器的灵敏度和 选择性。
06
结论与展望
研究结论
总结了双电层的形成机制和影响因素,包括电解质 浓度、表面活性剂和胶体颗粒的存在等。
分析了双电层的结构和性质,包括电位分布、电荷 密度和电导率等,揭示了其与物质传递和化学反应 过程的关系。
实验与理论相结合
应用导向的研究
双电层的研究将更加注重实际应用, 解决能源、环境、生物医学等领域中 的实际问题,推动科技成果转化和应 用。
未来的研究将更加注重实验与理论的 结合,通过实验验证理论预测,同时 通过理论指导实验设计和解释。
双电层研究的挑战与机遇
挑战
双电层的行为和性质受到多种因素的影响,如表面电荷分布、溶液组成、离子 浓度等,如何全面理解和掌握这些因素对双电层的影响是当前研究的难点。
03
双电层的结构模型
结构模型的种类
物理模型
通过物理手段模拟双电层的形成和结构,如电泳、 电聚焦等。
数学模型
通过建立数学方程来描述双电层的性质和行为,如 电位分布、离子浓度等。
计算机模拟模型
利用计算机技术模拟双电层的结构和行为,如分子 动力学模拟、蒙特卡洛模拟等。
结构模型的建立方法
80%
实验测量
深入研究双电层在生物医学领 域的应用,如药物传递、基因 治疗和组织工程等,以提高治 疗效果和降低副作用。
深入研究双电层在生物医学领 域的应用,如药物传递、基因 治疗和组织工程等,以提高治 疗效果和降低副作用。
THANK YOU
感谢聆听
双电层理论(共8张PPT)

在Stern模型中,带有溶剂化层的滑移界面与溶液之间的电位差称为 电势。 S固te体rn与对液扩体散总双的电电层位模差型即作等进于一热步力修学正电。势 0 ,在双电层内,热力学电势呈直线下降。
比Stern层略右的曲线表示。 构这成模的 型平过面于称简为单,Ste由rn于平离面子。热运动,不可能形成平板电容器
H构e成lm的ho平ltz面双称电为层S模te型rn平面。 他 在认电为场吸 作附 用在 下固 ,体 带表 电面 质的点紧 和密 反层 离约 子有 分一 别、 向二 相个 反分 方子 向层 运的 动厚 。度,后被称为Stern层; 这在模Ste型rn过模于型简中单,,带由有于溶离剂子化热层运的动滑,移不界可面能与形溶成液平之板间电的容电器位差称为 电势。 固构体成与 的液平体面总称的为电Ste位rn差平即面等。于热力学电势 0 ,在双电层内,热力学电势呈直线下降。 SHteelmrnh对o扩ltz散双双电电层层模模型型作进一步修正。 在电场作用下,带电质点和反离子分别向相反方向运动。 只电有势在 总带是电比质热点力移学动电时势才低显,示外出加电解电质势会,使所以电它势又变被小称甚为至电改动变电符势号。。 在S电te场rn作模用型下中,,带带电有质溶点剂和化反层离的子滑分移别界向面相与反溶方液向之运间动的。电位差称为 电势。
这模型过于简单,由于离子热 运动,不可能形成平板电容器
扩散双电层模型
Gouy和Chapman认为,由于正、负离子静电吸引 和热运动两种效应的结果,溶液中的反离子只有一部 分紧密地排在固体表面附近,相距约一、二个离子厚 度称为紧密层;
另一部分离子按一定的浓 度梯度扩散到本体溶液中,离 子的分布可用Boltzmann公式表
Stern双电层模型
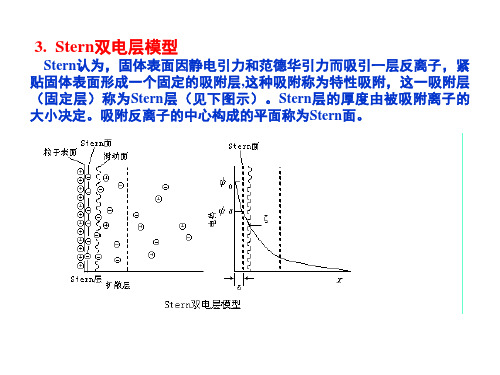
Grahame进一步将Stern层分成两部分。特性吸附离子不水合,因而比 Stern层更接近表面。特性吸附离子所在部位称为内Helmholtz面,而扩 散层起始的面称为外Helmholtz面。阴离子特性吸附在负电荷表面时离 子相应电势的分布如下图示。
这里ψ2相当于ψδ(扩散层)。在H-层中,电势呈线性变化。ζ Nhomakorabea0
ε δ
'
(ψ 0 ψ δ )
σ0为胶粒表面电荷密度。它与Stern层表面电荷密度σ1和扩散层表面电 荷密度σ2和关系为 σ0 +σ1 +σ2 =0 整个双电层为电中性。 假设Stern层中反离子的吸附服从Langmuir吸附等温式,
θ Kn
0 0
1 Kn
ζ ζ
0 s0
于是有,
(ψ 0 ψ ) δ
由于stern层中的反离子与扩散层中的反离子处于平衡状态若在高浓度的电解质溶液中便会有更多的反离子进入stern层导致电势的降低此时电势与高价反离子或大的反离子如表面活性剂离子不仅与质点表面间有强烈的静电吸引力还有较强的范德华力引力质点对它们发生很强烈的的选择性吸附这就是特性吸附而进入stern层导致号电势也随之反号
在稀溶液中,扩散层相当厚,而质点表面所束缚的溶剂化层厚度通常 与分子大小的数量级相同,因此,ψδ≌ζ。由于Stern层中的反离子与扩 散层中的反离子处于平衡状态,若在高浓度的电解质溶液中,便会有 更多的反离子进入Stern层导致ζ电势的降低,此时ζ电势与ψδ的差值加 大。 高价反离子或大的反离子(如表面活性剂离子)不仅与质点表面 间有强烈的静电吸引力,还有较强的范德华力引力,质点对它们发生 很强烈的的选择性吸附(这就是特性吸附)而进入Stern层,导致ψδ反 号,ζ电势也随之反号。 同号大离子由于与质点间有很强的范德华力引力,当范德华力引 力克服静电斥力时,便进入Stern层而使Stern层的|ψδ|升高甚至超过表 面电势ψ0 。另外,由于同号大离子的体积较大会使Stern层的δ增大。 见上图示。 由此可见Stern模型比Gouy-Chapman模型能更好的解释电动现象。 但是,发生离子特性吸附的Stern面与扩散层起始平面的吻合仍然引起 了混乱。
双电层模型(精)

2. 胶体粒子的双电层结构
粒子的相反电荷离子是由紧密层 和扩散层两部分组成。
电 势
+ +
+++++++++
(设粒子荷负电)
+Leabharlann +扩散层紧密层中的反号离子被束缚在胶
体粒子周围, 扩散层中的反号离子虽受胶体粒 子的静电引力的影响,但可脱离 胶体粒子而移动。
紧密层
双电层示意图
电 势
+ +
+
+++++++++
+
0
0 :固体表面和液体内部的总
的电位差
紧密层
扩散层
动电位(电势): 紧密层的外界面与本体溶液之间的电 势差。 电势决定着胶体粒子在电场中的运动速度。
d
电势对其它离子十分敏
感,外加电解质的变化会引起 电势的显著变化。因为外加 电解质浓度加大时,会使进入 紧密层的反号离子增加,使得 粒子外界面与溶液本体的电 势差减小,即 电势下降, 从而使双电层变薄。
AgI
碘化银胶团示意图(KI过量)
(AgI) m nI (n x)K xK 扩散层 紧密层 胶核
胶粒 胶团
x
(1)整个胶团是电中性的。 (2)胶粒电荷的符号取决于被吸附离子的符号,胶粒带电 的多少由被吸附离子与紧密层反号离子电荷之差(n - x)来决 定。
d
0 ´
b'
b
电解质对电势的影响
当电解质浓度增加到一定程度时,扩散厚度变零, 电势 也变为零。这就是胶体电泳的速度会随着电解质浓度的加大而 变小,甚至变为零的原因。
电化学基础(ⅲ)——双电层模型及其发展

电化学基础(ⅲ)——双电层模型及其发展引言电化学是研究电与化学相互作用的学科,它的核心是电极上的电荷转移过程。
而双电层模型是电化学研究中的重要理论模型之一,它描述了电极表面与电解质溶液之间形成的一层电荷分布现象。
本文将介绍双电层模型的基本概念、发展历程以及在电化学研究中的应用。
一、双电层模型的基本概念双电层模型是由德国物理学家赫尔曼·赫尔姆霍兹于19世纪末提出的。
它认为在电极表面与电解质溶液之间存在一个电荷分布层,该层由两层电荷组成:靠近电极表面的一层是吸附在电极上的电荷,称为内层电荷;远离电极表面的一层是溶液中的离子,称为外层电荷。
这两层电荷之间形成了一个电势差,称为电极电势。
二、双电层模型的发展随着科学技术的不断发展,双电层模型逐渐得到了完善。
20世纪初,瑞典物理学家古斯塔夫·奥斯特瓦尔德提出了电解质溶液中的离子在电场作用下会发生移动的理论,即电解质溶液中的离子迁移现象。
这一理论为双电层模型提供了更加准确的解释。
在古斯塔夫·奥斯特瓦尔德的基础上,英国化学家彼得·迪拜和美国化学家约翰·纽曼进一步发展了双电层模型。
他们发现,双电层模型中的电荷分布不仅与离子的吸附有关,还与电解质溶液中的离子浓度、温度、电极材料等因素有关。
近年来,随着纳米技术的发展,双电层模型在纳米材料研究中得到了广泛应用。
研究人员发现,纳米材料的比表面积较大,因此它们与电解质溶液之间形成的双电层效应更加显著。
这为纳米材料的电化学应用提供了理论支持。
三、双电层模型在电化学研究中的应用双电层模型在电化学研究中有着广泛的应用。
首先,它可以用于解释电解质溶液中的离子迁移现象。
通过研究双电层模型,可以揭示离子在电场作用下的迁移规律,从而优化电解质溶液的组成,提高电化学反应的效率。
双电层模型还可以应用于电化学传感器的设计与制备。
电化学传感器是一种利用电化学原理进行物质检测的装置,它通常由电极、电解质溶液和检测物质组成。
电化学双电层理论和模型

双电层双电层的形成:当两相接触时,如果电子或离子等荷电粒子在两相中具有不同的电化学位,荷电粒子就会在两相之间发生转移或交换,界面两侧便形成符号相反的两层电荷,人们把界面上的这两个荷电层称为双电层。
如金属、溶液界面(M/L)两侧,若μM+>μM+(L),则荷电粒子发生转移,金属表面荷负点;反之,则金属表面荷正,这种双电层常称为离子双层。
尽管有时上述的离子双层并不存在,但金属与溶液界面间仍然会存在着电位差,无论是金属表面,还是溶液表面,都存在着偶极层。
由于偶极子正负电荷分隔开而形成的双电层,称为偶极双电层。
对任何一种金属而言,由于金属的电子会“溢出”金属表面形成双极子。
所以即使溶液一侧不存在偶极子层,但对金属与溶液的界面来说,这种偶极双层总是存在的。
此外,溶液中某一种离子有可能被吸附于电极与溶液界面上,形成一层电荷。
这层电荷又借助静电作用吸引溶液中同等数量的带相反电荷的离子而形成双电层,可称之为吸附双层。
这里应当注意:界面上第一层电荷的出现,靠的是静电力以外的其他化学与物理作用,而第二层电荷则是由第一层电荷的静电力引起的。
如果界面上有了吸附双层,当然也会产生一定大小的电位差。
金属与溶液界面的电位差系由上述的三种类型电位差的一部分或全部组成,但其中对电极反应速度有重大影响的,则主要是离子双层的电位差。
离子双层的形成有两种可能的情况。
一是在电极与溶液一旦接触后的瞬间自发形成的。
另一种情况,是在外电源作用下强制形成的双电层。
因为有的时候,当金属与溶液接触时,并不能自发地形成双电层。
如将纯汞(Hg)放入Kill溶液的界面上常常不能自发的形成双电层。
但是,如果将Hg电极与外电源负极连接,外电源就向Hg电极供应电子,在其电位达到K+还原电位之前,电极上不会发生电化学反应,因而此时Hg电极上有了多余的电子而带上负电。
这层负电荷吸引溶液中相同数量的正电荷(如K+),形成双电层。
双电层的结构模型:金属电极和溶液之间界面上形成的双电层,从结构上可以有离子双电层、表面偶极双电层和吸附双电层等三种类型。
扩散双电层模型

(-) 2Cl-(a1) —→ Cl2 (P) +2e (+) Cl2 (P) +2e —→ 2Cl-(a2) 总:2Cl-(a1) —→2 Cl-(a2)
aCl
a H
a
a1/ 2
E RT Ln (a )2 RT Ln a1 F (a )1 2F a2
15
b)压差:
③ (-) Pt, H2(P1)│HCl(a)│H2(P2), Pt (+)
阻碍作用
4
金属附近所带的电荷与金属本身所带电荷
相反,形成双电层
与金属表面最接近的一层为 紧密层,其厚度 d < 10-8cm 扩散到溶液中的称为扩散层 其厚度δ= 10-8~10-4cm
双电层:紧密层和扩散层 是由静电吸引和热
运动达平衡产生的
双电层电荷相反, 存在一定的界面电位差
5
当然也可能是溶液中的负离子被电极所吸
2
c) 电动势 E =φ+-φ-= - 0.424V
E < 0,电池反应不能自发进行,书写应为
(-)Pt, H2(P1)|H+(aH+=0.01)‖Cu2+(aCu2+=0.1)| Cu (+)
d)ΔGm= -nFE=81.832KJ/mol
ΔGm > 0,不能自发进行
3
五、电极电势产生的原因
1. 金属―溶液间的电势――绝对电极电势
盐桥:①固体电解质:扩散速度相同
②浓度很大 由于不同电解质间连接了盐桥,界面就不
产生液接电势
2. 液接电势的计算
El 很难测量和计算,推导近似公式
(-)Pt, H2(P)│HCl(a1)│HCl(a2)│H2(P), Pt(+)
简述斯特恩扩散双电层模型的要点

简述斯特恩扩散双电层模型的要点斯特恩扩散双电层模型是电化学领域中一个重要的理论模型,它描述了电解质溶液中带电粒子在固体电极表面的吸附现象。
本文将简述斯特恩扩散双电层模型的要点,帮助读者更好地理解这一理论。
一、斯特恩扩散双电层模型的背景在电解质溶液中,带电粒子(如离子)会在固体电极表面形成一个电荷层,这一现象被称为电双层。
斯特恩扩散双电层模型是在电双层理论基础上发展起来的,它考虑了电解质溶液中带电粒子的扩散作用,为研究电极表面的电荷分布和电化学反应提供了重要依据。
二、斯特恩扩散双电层模型的要点1.电极表面的电荷层斯特恩扩散双电层模型认为,电极表面存在一个紧密排列的电荷层,称为斯特恩层。
该层中的电荷密度较大,与电解质溶液中的电荷密度相差较大。
斯特恩层中的电荷主要来源于电解质溶液中离子的吸附。
2.扩散层在斯特恩层外侧,电解质溶液中的带电粒子会因浓度梯度而发生扩散运动,形成一个较宽的扩散层。
扩散层中的电荷密度逐渐减小,直至与溶液中的电荷密度相等。
3.电荷分布斯特恩扩散双电层模型中,电极表面的电荷分布呈阶梯状。
斯特恩层与扩散层之间的电荷密度差异导致电势差,称为斯特恩电势。
电解质溶液中的电荷密度与斯特恩层电荷密度之间的电势差称为扩散电势。
4.双电层厚度斯特恩扩散双电层模型的另一个重要要点是双电层厚度的估算。
双电层厚度取决于电解质溶液的浓度、离子价数以及电极表面的特性。
斯特恩层和扩散层的厚度之和即为双电层厚度。
5.电化学反应的影响斯特恩扩散双电层模型考虑了电解质溶液中带电粒子的扩散作用对电化学反应的影响。
在电极反应过程中,带电粒子的扩散速率会影响反应速率和电极表面的电荷分布。
三、总结斯特恩扩散双电层模型是研究电解质溶液中带电粒子在固体电极表面吸附现象的重要理论模型。
通过阐述电极表面的电荷层、扩散层、电荷分布、双电层厚度以及电化学反应的影响,该模型为我们理解电化学过程提供了有力支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AgI
碘化银胶团示意图(KI过量)
(AgI) m ⋅ nI − ⋅ (n − x)K + ⋅xK + 胶核 扩散层 紧密层
胶粒 胶团
x−
(1)整个胶团是电中性的。 ) (2)胶粒电荷的符号取决于被吸附离子的符号,胶粒带电 )胶粒电荷的符号取决于被吸附离子的符号, 的多少由被吸附离子与紧密层反号离子电荷之差( 被吸附离子与紧密层反号离子电荷之差 的多少由被吸附离子与紧密层反号离子电荷之差(n - x)来决 ) 定。
对于双电层的具体结构, 对于双电层的具体结构, 最早于1879年Helmholtz提出平板模型; 年 提出平板模型 最早于 提出平板模型; 1910年Gouy和1913年Chapman修正了平板模型,提出 年 修正了平板模型, 和 年 修正了平板模型 了扩散双电层模型; 扩散双电层模型; 后来1924年Stern又提出了 年 又提出了Stern模型。 模型。 后来 又提出了 模型
1. 溶胶粒子的结构
以AgI的水溶胶为例。 固体粒子AgI称为“胶 核”。若稳定剂是 KI ,则胶核 吸附I-带负电,反号离子 K+一部分进入紧密层,另 一部分在扩散层。胶核与 紧密层的反号离子构成 “ 胶粒 ”。溶胶中的独立运 溶胶中的独立运 动单位是胶粒,胶粒与扩 动单位是胶粒 散层离子构成“胶团”。可用下式 表示:
胶体微粒受电解质的影响使双电层变薄的理论称为 双电层压缩理论。 双电层压缩理论。 根据这一理论, 根据这一理论,可以解释为何在河流与海洋交界的 河口地区有大量的泥沙沉积。 河口地区有大量的泥沙沉积。
甚至胶体粒子有时会由于某种电 解质的加入而改变电泳方向, 解质的加入而改变电泳方向,即ζ 电 势改变符号。此时, 势改变符号。此时,进入紧密层的 反号离子电荷除中和固体表面的电 荷外还有剩余。 荷外还有剩余。
+
ϕ0
ϕ0 :固体表面和液体内部的总
的电位差
紧密层
扩散层
电位 ζ电 差 ζ 电
: 紧密层的 体面 电来自体 的液的电
d
ζ 电势对其它离子十分敏
感,外加电解质的变化会引起 ζ 电势的显著变化。因为外加 电势的显著变化。 电解质浓度加大时, 电解质浓度加大时,会使进入 紧密层的反号离子增加, 紧密层的反号离子增加,使得 粒子外界面与溶液本体的电 电势下降, 势差减小,即 ζ 电势下降, 势差减小, 从而使双电层变薄 双电层变薄。 从而使双电层变薄。
+ζ -ζ
ϕ0
ζ 电势改变符号是由于胶体粒子
表面对某种反号离子具有很强的吸附 能力,从而吸附了过多的反号离子。 能力,从而吸附了过多的反号离子。
例如, 使胶体 使胶体SiO2聚沉是一个典型例子: 聚沉是一个典型例子: 例如,Fe使胶体 利用粒子的光散射测定Fe 加入SiO2后的聚沉作用表明, 后的聚沉作用表明, 利用粒子的光散射测定 3+加入 约为5时 胶体SiO2表面有负电荷,Fe的主要形态为 表面有负电荷, 的主要形态为 在pH约为 时,胶体 约为 Fe(OH)2+,Fe(OH)2+及多聚配合物 x(OH)y(H2O)z3x-y。 及多聚配合物Fe 在log[Fe3+]=-5.26时,突然发生聚沉, 时 突然发生聚沉, 而在log[Fe3+]= -4.48时,胶体悬浮体又重新建立。 而在 时 胶体悬浮体又重新建立。
二、双电层模型
由于胶粒表面带某种电荷, 由于胶粒表面带某种电荷,则固液两相分别带有不 同符号的电荷(整个胶体溶液是电中性的),在界面上 同符号的电荷(整个胶体溶液是电中性的),在界面上 ), 形成了双电层结构。 形成了双电层结构。 双电层结构 所以胶体溶液表现出各种电学性质(电泳、电渗、 所以胶体溶液表现出各种电学性质(电泳、电渗、流动 电势、沉降电势等)。 电势、沉降电势等)。
电 势
+ + + +
扩散层
+++++++++
2. 胶体粒子的双电层结构 粒子的相反电荷离子是由紧密层 和扩散层两部分组成。 紧密层中的反号离子被束缚在胶 体粒子周围, 扩散层中的反号离子虽受胶体粒 子的静电引力的影响,但可脱离 胶体粒子而移动。
(设粒子荷负电)
紧密层
双电层
电 势
+ +
ζ +
+++++++++
d′
ϕ0 ζ´ ζ
b'
b
电解质对ζ电势的影响
当电解质浓度增加到一定程度时,扩散厚度变零,ζ 电势 也变为零。这就是胶体电泳的速度会随着电解质浓度的加大而 变小,甚至变为零的原因。
如果ζ 电势降到不足以排斥胶体微粒相互碰撞时的分 子间作用力,则微粒会聚集变大,而在重力作用下沉降。 子间作用力,则微粒会聚集变大,而在重力作用下沉降。 电势,称作临界电位。 胶体微粒开始明显聚集的ζ 电势,称作临界电位。 临界电位 电势绝对值在0.07V时,胶体微粒在溶液中 大约ζ 电势绝对值在 时 相当稳定,引入电解质到足够的浓度, 相当稳定,引入电解质到足够的浓度, ζ 电势绝对值 变化到大约是0.03V时,胶体微粒就会开始明显聚集, 变化到大约是 时 胶体微粒就会开始明显聚集, 而且电解质中影响的离子价数越高, 而且电解质中影响的离子价数越高,所起的凝聚作用越 强。
