八年级数学竞赛例题专题:几何变换

八年级数学竞赛例题专题
整体与完形
阅读与思考
许多几何问题,常因图形复杂、不规则而给解题带来困难,这些复杂、不规则的图形,从整体考虑,可看作某种图形的一部分,如果将它们补充完整,就可得到常见的特殊图形,那么就能利用特殊图形的特殊性质转化问题,这就是解几何问题的补形法,常见的补形方法有:
1.将原图形补形为最能体现相关定理、推论、公理的基本图形;
2.将原图形补形为等腰三角形、等边三角形、直角三角形等特殊三角形;
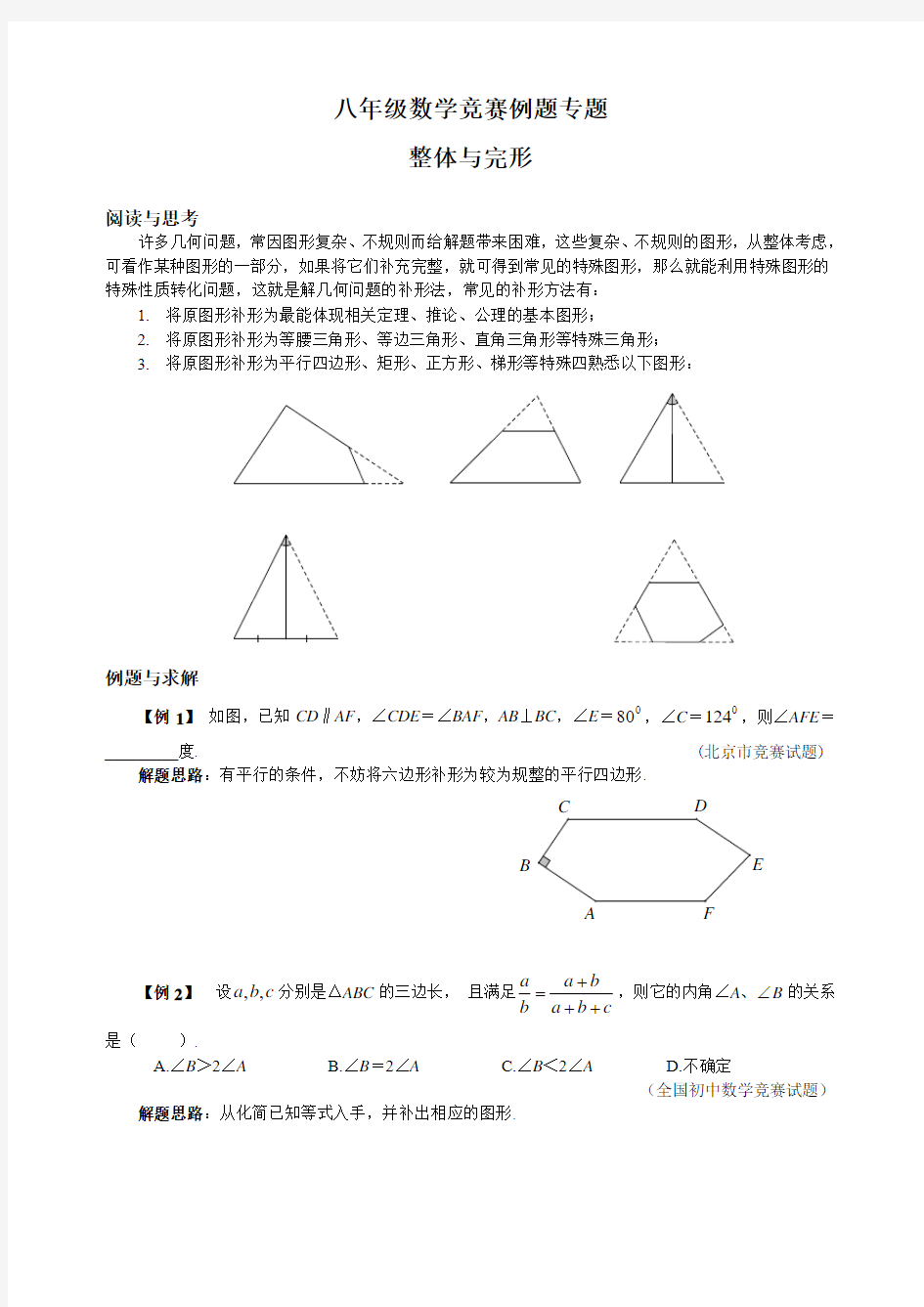
3.将原图形补形为平行四边形、矩形、正方形、梯形等特殊四熟悉以下图形:
例题与求解
【例1】如图,已知CD∥AF,∠CDE=∠BAF,AB⊥BC,∠E=0
80,∠C=0
124,则∠AFE=_________度. (北京市竞赛试题) 解题思路:有平行的条件,不妨将六边形补形为较为规整的平行四边形.
B
【例2】设,,
a b c分别是△ABC的三边长,且满足
a a b
b a b c
+
=
++
,则它的内角∠A、∠B的关系
是().
A.∠B>2∠A
B.∠B=2∠A
C.∠B<2∠A
D.不确定
(全国初中数学竞赛试题)解题思路:从化简已知等式入手,并补出相应的图形.
高中数学竞赛讲义(16)平面几何
高中数学竞赛讲义(十六) ──平面几何 一、常用定理(仅给出定理,证明请读者完成) 梅涅劳斯定理设分别是ΔABC的三边BC,CA,AB或其延长线上的点,若三点共线,则 梅涅劳斯定理的逆定理条件同上,若 则三点共线。 塞瓦定理设分别是ΔABC的三边BC,CA,AB或其延长线上的点,若三线平行或共点, 则 塞瓦定理的逆定理设分别是ΔABC的三边 BC,CA,AB或其延长线上的点,若则三线共点或互相平行。 角元形式的塞瓦定理分别是ΔABC的三边BC,CA,AB所在直线上的点,则平行或共点 的充要条件是 广义托勒密定理设ABCD为任意凸四边形,则AB?CD+BC?AD≥AC?BD,当且仅当A,B,C,D四点共圆时取等号。
斯特瓦特定理设P为ΔABC的边BC上任意一点,P不同于B,C,则有 AP2=AB2?+AC2?-BP?PC. 西姆松定理过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。 西姆松定理的逆定理若一点在三角形三边所在直线上的射影共线,则该点在三角形的外接圆上。 九点圆定理三角形三条高的垂足、三边的中点以及垂心与顶点的三条连线段的中点,这九点共圆。 蒙日定理三条根轴交于一点或互相平行。(到两圆的幂(即切线长)相等的点构成集合为一条直线,这条直线称根轴)欧拉定理ΔABC的外心O,垂心H,重心G三点共线,且 二、方法与例题 1.同一法。即不直接去证明,而是作出满足条件的图形或点,然后证明它与已知图形或点重合。 例1 在ΔABC中,∠ABC=700,∠ACB=300,P,Q为ΔABC内部两点,∠QBC=∠QCB=100,∠PBQ=∠PCB=200,求证:A,P,Q三点共线。 [证明] 设直线CP交AQ于P1,直线BP交AQ于P2,因为∠ACP= ∠PCQ=100,所以,①在ΔABP,ΔBPQ,ΔABC中由正弦定理有
高中数学竞赛平面几何中的几个重要定理
平面几何中几个重要定理及其证明 一、 塞瓦定理 1.塞瓦定理及其证明 定理:在?ABC 内一点P ,该点与?ABC 的三个顶点相连所在的三条直线分别交?ABC 三边AB 、BC 、CA 于点D 、E 、F ,且D 、E 、F 三点均不是?ABC 的顶点,则有 1AD BE CF DB EC FA ??=. 证明:运用面积比可得ADC ADP BDP BDC S S AD DB S S ????==. 根据等比定理有 ADC ADC ADP APC ADP BDP BDC BDC BDP BPC S S S S S S S S S S ??????????-=== -, 所以APC BPC S AD DB S ??=.同理可得APB APC S BE EC S ??=,BPC APB S CF FA S ??=. 三式相乘得 1AD BE CF DB EC FA ??=. 注:在运用三角形的面积比时,要把握住两个三角形是“等高” A B C D F P
还是“等底”,这样就可以产生出“边之比”. 2.塞瓦定理的逆定理及其证明 定理:在?ABC 三边AB 、BC 、CA 上各有一点D 、E 、F ,且D 、 E 、 F 均不是?ABC 的顶点,若1AD BE CF DB EC FA ??=,那么直线CD 、AE 、BF 三线共点. 证明:设直线AE 与直线BF 交于点P ,直线CP 交AB 于点D /,则据塞瓦定理有 / / 1AD BE CF D B EC FA ??=. 因为 1AD BE CF DB EC FA ??=,所以有/ /AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线. 注:利用唯一性,采用同一法,用上塞瓦定理使命题顺利获证. 二、 梅涅劳斯定理 A B C D E F P D /
人教版八年级数学几何专题
八年级数学下册期末专题复习和训练:几何计算题、证明题 一、题型特点:四边形(五种常见的)、三角形的中位线、矩形的推论穿插其中,…… 二、常见新型题型:动点、折纸、开放(条件、结论开放)、探索性(数量关系、位置关系),…… 三、图形搭建:三角形中搭建四边形、四边形中搭建三角形、组合图形,…… 下面我根据图形搭建结构特征进行分类,列举一部分和本期几何部分(主要是平行四边形)的计算题、证明题,让我们共同来探究、解析. 一、以平行四边形搭建起来的图形 例1.ABCD Y 中,AB=4cm ,AD=7cm, ∠ABC 的平分线交AD 于E,交CO 的延长线于F,求DF 的长? 分析: 本题要求的DF 长的途径有两条:其一.DF CF CD =-;其二. DF DE AD AE ==-. 采取第一途径可以少一些环节,根据平行四边形的性质和角的平分线的定义可以 比较容易得出BCF V 是等腰三角形,即CF CB =;由于平行四边形 的对边相等可以得出:,CD AB 4cm CB AD 7cm ====.故DF 743cm =-= 例2.△ABC 、△ADE 都是正三角形,CD=BF. (1)、求证:△ACD ≌△CBF (2)、当D 运动至BC 边上的何处时,四边形CDEF 为平行四边形,且∠DEF=30°, 并证明你的结论 . 分析: ⑴.证明△ACD ≌△CBF 已经有了CD=BF ,而△ABC 、△ADE 都是正三角形又可以给我们提供 ,CA CB ACD CBF 60=∠=∠=o 条件,根据“SAS ”判定方法可 以证得△ACD ≌△CBF. ⑵.根据⑴问的△ACD ≌△CBF 得出AD CF =,又△ADE 是正三角形的DE CF =,所以CF DE =;要使四边形CDEF 为平行四边形可以证CF DE P . 若四边形CDEF 为平行四边形,则FCD DEF 30∠=∠=o ;当EDB 30∠=o 时,就有FCD EDB ∠=∠,此时就能证得CF DE P .由正△ADE 可以得出ADE 60∠=o ,则 ADB 603090∠=+=o o o ,AD BC ⊥;由于等腰三角形具有“三线合一”的特征,所以当D 运动至BC 边上中点时,四边形CDEF 为平行四边形. 练习: 1.如图,在□ABCD 中,AE ⊥BC,AF ⊥CD,∠EAF=60°,则∠B=( ); 2.□ABCD 的周长为60cm,对角线AC 、BD 交于点O,△AOB 的周 长比△BOC 的周长多10cm,则AD=( ),DC=( ); 3.□ABCD 中,∠ABC 的平分线BE 交AD 于E 点,若∠ABE=25°CD=5cm,BC=7cm,那么∠ABE=( ),∠BED=( ),AE=( ). 4. 已知□ABCD ,BE=AB,BF =BD. 求证:CD=CM 5. △ABC 是正三角形,AE=BD,DF ∥CE,EF ∥CD. 求证: △AGF ≌△EAC 6.以△ABC 的三边在BC 的同侧做等边△EBC 、等边△FBA 、等边△DAC. ⑴.判断四边形FADE 的形状? ⑵.当∠BAC 为多少度时,四边形FADE 为矩形? ⑶.当∠BAC 为多少度时,四边形FADE 不存在? 7. 有一块如图的玻璃,不小心把DEF 部分打碎,现在只测得AB=60cm,BC=80cm ,∠ A=120°,∠B=60°,∠C=150°,你能根据测得的数据计算AD 的长? 二、以矩形搭建起来的图形 例1.D 为□ABCD 外一点,∠APC=∠BPD=90°.求证: □ABCD 为矩形 分析:判定矩形的方法主要有三种.但在已知了四边形ABCD 是平行 四边形的情况下,要判定ABCD Y 是矩形的途径有两条:其一、找 一内角是直角;其二、找出对角线相等,即找出AC BD =. 由于本题的另一主要条件是∠APC=∠BPD=90°,要根据题中条件和图形位置转换成四边形的内角为90°比较困难,所以本题我们先想办法找出对角线相等,即找出AC BD =. 我们发现本题在APC Rt V 和BPD Rt V 的两斜边的交点O 恰好是平行四边形对角线的交点,根据平行四边形对角线互相平分可知:O 同时是AC BD 、的中点;所以自然联想到连结PO 这条两直角三角形公共的中线(见图).根据以上条件,在APC Rt V 和BPD Rt V 中就有:AC 2PO = BD 2PO =,故AC BD =,由对角线相等的平行四边形是矩形,可判定ABCD Y 是矩形. 例2. 矩形ABCD 中,AB=3,AD=4,PE ⊥AC ,PF ⊥BD , ⑴.求PE+PF 的值? ⑵.若点P 是AD 上的一动点(不与A D 、重合),还是作PE ⊥AC ,PF ⊥BD ,则PE+PF 的值是否会发生变化?为什么? 分析:求线段的和或差我们会联想到证明中的“截长补短”法,但本题不具备这方面的条件. 本题从面积入手可以破题:如图连结PO ,只要我们能求出APO V 和DPO V 的面积之和问题便可以获得解决. 略解:⑴.∵四边形ABCD 是矩形 M C D F B A E F D B C A D F E B C A A B C D P E F O F A B F E D A C
数学竞赛平面几何重要知识点绝对精华
数学竞赛平面几何重要知识点 梅涅劳斯定理: 设D 、E 、F 分别是ABC ?三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=??EA CE FC BF DB AD 。 斯德瓦特定理:设P 是ABC ?的边BC 边上的任一点,则 BC PC BP AP BC AB PC AC BP ??+?=?+?222 西摩松定理: 设P 是ABC ?外接圆上任一点,过P 向ABC ?的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
6、共角定理:设ABC ?和C B A '''?中有一个角相等或互补(不妨设A=A ')则 C A B A AC AB S S C B A ABC ' '?''?='''?? 与圆有关的重要定理 4.四点共圆的主要判定定理 (1)若∠1=∠2,则A 、B 、C 、D 四点共圆; (2)若∠EAB=∠BCD ,则A 、B 、C 、D 四点共圆; (3)若PA ?PC=PB ?PD ,则A 、B 、C 、D 四点共圆; 三角形的五心 三角形的三条中线共点,三条角平分线共点,三条高线共点,三条中垂线共点。三角形的垂心、重心、外心共线(欧拉线),并且重心把连结垂心和外心的线段分成2∶1的两段。三角形的外心和内心的距离)2(r R R d -=。此公式称为欧拉式,由此还得到r R 2≥。当且仅当△ABC 为正三角形时,d=0,此时R=2r.其中R 和r 分别是三角形外接圆半径和内切圆半径。 与△的一边及另两边的延长线均相切的圆称为△的旁切圆,旁切圆的圆心称为旁心。
重要例题 例1.设M 是任意ABC ?的边BC 上的中点,在AB 、AC 上分别取点E 、F,连EF 与AM 交于N ,求证:)(21AF AC AE AB AN AM +=(1978年辽宁省中学数学竞赛) 例 2. 已知点O 在ABC ?内部,022=++OC OB OA .OCB ABC ??与的面积之比为_________________. 例3. 如图①,P 为△ABC 内一点,连接P A 、PB 、PC ,在△P AB 、△PBC 和△P AC 中,如果存在一个三角形与△ABC 相似,那么就称P 为△ABC 的自相似点. ⑴如图②,已知Rt △ABC 中,∠ACB =90°,∠ACB >∠A ,CD 是AB 上的中线,过点B 作BE ⊥CD ,垂足为E ,试说明E 是△ABC 的自相似点. ⑵在△ABC 中,∠A <∠B <∠C . ①如图③,利用尺规作出△ABC 的自相似点P (写出作法并保留作图痕迹); ②若△ABC 的内心P 是该三角形的自相似点,求该三角形三个内角的度数.
初中数学竞赛辅导几何变换(旋转)
第2讲几何变换——旋转 典型例题 【例1】C是线段AE上的点,以AC、CE为边在线段AE的同侧作等边三角形ABC、CDE, △是等设AD的中点是M,BE的中点是N,连结MN、MC、NC,求证:CMN 边三角形.Array【例2】如图,两个正方形ABCD和AKLM有一个公共点A.求证:这两个正方形的中心以 及线段BM,DK的中点是某正方形的顶点. L
【例3】 已知:如图,ABC △、CDE △、EHK △都在等边三角形,且A 、D 、K 共线, AD DK =.求证:HBD △也是等边三角形. 【例4】 ABC △是等边三角形,P 是AB 边的中点,Q 是AC 边的中点,R 为BC 边的中点, M 为RC 上任意一点,且PMS △是等边三角形,S 与Q 在PM 的同侧,求证: RM QS =. E C H D B A Q ? S M P C B A R
【例5】 ABCD 是正方形,P 是ABCD 内一点,1PA =,3PB = ,PD =求正方形ABCD 的面积. 【例6】 P 是等边三角形ABC 内的一点,6PA =,8PB =,10PC =.求ABC △的边长. D
【例7】 设O 是等边ABC △内一点,已知115AOB ?∠=,125BOC ?∠=,求以线段OA 、OB 、 OC 为边所构成的三角形的各内角大小. 【例8】 如图,在ABC △中,90ACB ?∠=,AC BC =,P 是ABC △内一点,3PA =,1PB =, 2PC =,求BPC ∠. A P C
如图,已知ABC △中,90A =,AB AC =,D 为BC 上一点,求证:2222BD DC AD +=. 【例9】 如图,在等腰直角ABC △中,90ACB ?∠=,CA CB =,P 、Q 在斜边AB 上,且 45PCQ ?∠=,求证:222PQ AP BQ =+. A D C B A Q B C P
人教版八年级数学几何专题
人教版八年级数学几何 专题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
2 八年级数学下册期末专题复习和训练:几何计算题、证明题 一、题型特点:四边形(五种常见的)、三角形的中位线、矩形的推论穿插其中,…… 二、常见新型题型:动点、折纸、开放(条件、结论开放)、探索性(数量关系、位置关系),…… 三、图形搭建:三角形中搭建四边形、四边形中搭建三角形、组合图形,…… 下面我根据图形搭建结构特征进行分类,列举一部分和本期几何部分(主要是平行四边形)的计算题、证明题,让我们共同来探究、解析. 一、以平行四边形搭建起来的图形 例1. ABCD 中,AB=4cm ,AD=7cm, ∠ABC 的平分线交AD 于E,交CO 的延长线于F, 求DF 的长? 分析: 本题要求的DF 长的途径有两条:其一.DF CF CD =-;其二. DF DE AD AE ==-. 比较容易得出BCF 是等腰三角形,即CF CB =的对边相等可以得出:,CD AB 4cm CB AD 7cm ====.故DF 743cm =-= 例2.△ABC 、△ADE 都是正三角形,CD=BF. (1)、求证:△ACD ≌△CBF (边上的何处时,四边形CDEF 为平行四边形,且∠DEF=30°, 分析: ⑴.证明△ACD ≌△CBF 已经有了CD=BF ,而△ABC 、△ADE 都是正三角形又可以给我们提供 ,CA CB ACD CBF 60=∠=∠=条件,根据“SAS ”判定方法可以证得△ACD ≌△CBF. ⑵.根据⑴问的△ACD ≌△CBF 得出AD CF =,又△ADE 是正三角形的DE CF =,所以CF DE =;要使四边形CDEF 为平行四边形可以证CF DE . 若四边形CDEF 为平行四边形,则FCD DEF 30∠=∠=;当EDB 30∠=时,就有FCD EDB ∠=∠,此时就能证得CF DE .由正△ADE 可以得出ADE 60∠=,则 ADB 603090∠=+=,AD BC ⊥;由于等腰三角形具有“三线合一”的特征,所以当D 运动至BC 边上中点时,四边形CDEF 为平行四边形. 练习: 1.如图,在□ABCD 中,AE ⊥BC,AF ⊥CD,∠EAF=60°,则∠B=( 2.□ABCD 的周长为60cm,对角线AC 、BD 交于点O,△AOB 的周 长比△BOC 的周长多10cm,则AD=( ),DC=( ); 3.□ABCD 中,∠ABC 的平分线BE 交AD 于E 点,若∠ABE=25°CD=5cm,BC=7cm,那么 ∠ABE=( ),∠BED=( ),AE=( )4. 已知□ABCD ,BE=AB,BF =BD. 求证:5. △ABC 是正三角形,AE=BD,DF ∥CE,EF ∥CD. 求证: △AGF ≌△EAC 6.以△ABC 的三边在BC 的同侧做等边△EBC 、等边△FBA
高中数学竞赛题之平面几何
第一讲 注意添加平行线证题 在同一平面,不相交的两条直线叫平行线.平行线是初中平面几何最基本的,也是非常重要的图形.在证明某些平面几何问题时,若能依据证题的需要,添加恰当的平行线,则能使证明顺畅、简洁. 添加平行线证题,一般有如下四种情况. 1 为了改变角的位置 大家知道,两条平行直线被第三条直线所截,同位角相等,错角相等,同旁角互补.利用这些 性质,常可通过添加平行线,将某些角的位置改变,以满足求解的需要. 例1 设P 、Q 为线段BC 上两点,且BP =CQ ,A 为BC 外一动点(如图1).当点A 运动到使 ∠BAP =∠CAQ 时,△ABC 是什么三角形?试证明你的结论. 答: 当点A 运动到使∠BAP =∠CAQ 时,△ABC 为等腰三角形. 证明:如图1,分别过点P 、B 作AC 、AQ 的平行线得交点D .连结DA . 在△DBP =∠AQC 中,显然 ∠DBP =∠AQC ,∠DPB =∠C . 由BP =CQ ,可知 △DBP ≌△AQC . 有DP =AC ,∠BDP =∠QAC . 于是,DA ∥BP ,∠BAP =∠BDP . 则A 、D 、B 、P 四点共圆,且四边形ADBP 为等腰梯形.故AB =DP . 所以AB =AC . 这里,通过作平行线,将∠QAC “平推”到∠BDP 的位置.由于A 、D 、B 、P 四点共圆,使证明很顺畅. 例2 如图2,四边形ABCD 为平行四边形,∠BAF =∠BCE .求证:∠EBA =∠ADE . 证明:如图2,分别过点A 、B 作ED 、EC 的平行线,得交点P ,连PE . 由AB CD ,易知△PBA ≌△ECD .有PA =ED ,PB =EC . ∥= A D B P Q 图1 P E D G A B F C 图2
高中复习数学竞赛基础平面几何知识点总结
高中数学竞赛平面几何知识点基础 1、相似三角形的判定及性质 相似三角形的判定: (1)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似; (2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为:两边对应成比例且夹角相等,两个三角形相似.); (3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(简叙为:三边对应成比例,两个三角形相似.); (4)如果两个三角形的两个角分别对应相等(或三个角分别对应相等),则有两个三角形相似(简叙为两角对应相等,两个三角形相似.). 直角三角形相似的判定定理: (1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似; (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 常见模型: 相似三角形的性质: (1)相似三角形对应角相等 (2)相似三角形对应边的比值相等,都等于相似比 (3)相似三角形对应边上的高、角平分线、中线的比值都等于相似比 (4)相似三角形的周长比等于相似比 (5)相似三角形的面积比等于相似比的平方 2、内、外角平分线定理及其逆定理 内角平分线定理及其逆定理: 三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例。 如图所示,若AM平分∠BAC,则AB AC =BM MC 该命题有逆定理: 如果三角形一边上的某个点与这条边所成的两条线段与这条边的对角的两边对应成比例,那么该点与对角顶点的连
线是三角形的一条角平分线 外角平分线定理: 三角形任一外角平分线外分对边成两线段,这两条线段和夹相应的内角的两边成比例。 如图所示,AD平分△ABC的外角∠CAE,则BD DC =AB AC 其逆定理也成立:若D是△ABC的BC边延长线上的一点, 且满足BD DC =AB AC ,则AD是∠A的外角的平分线 内外角平分线定理相结合: 如图所示,AD平分∠BAC,AE平分∠BAC的外角 ∠CAE,则BD DC =AB AC =BE EC 3、射影定理 在Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,则有射 影定理如下: BD2=AD·CD AB2=AC·AD BC2=CD·AC 对于一般三角形: 在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,则有 a=bcosC+ccosB b=ccosA+acosC c=acosB+bcosA 4、旋转相似 当一对相似三角形有公共定点且其边不重合时,则会产生另 一对相似三角形,寻找方法:连接对应点,找对应点连线和 一组对应边所成的三角形,可以得到一组角相等和一组对应 边成比例,如图中若△ABC∽△AED,则△ACD∽△ABE 5、张角定理 在△ABC中D为BC边上一点,则 sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD 6、圆内有关角度的定理 圆周角定理及其推论: (1)圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半(2)同弧所对的圆周角相等 (3)直径所对的圆周角是直角,直角所对的弦是直径
-初中数学竞赛——几何变换——旋转
第2讲 几何变换——旋转 典型例题 【例1】 C 是线段AE 上的点,以AC 、CE 为边在线段AE 的同侧作等边三角形ABC 、CDE ,设AD 的中点是M ,BE 的中点是N ,连结MN 、MC 、NC ,求证:CMN △是等边三角形. 【例2】 如图,两个正方形ABCD 和AKLM 有一个公共点A .求证:这两个正方形的中心以及线段BM , DK 的中点是某正方形的顶点. 【例3】 已知:如图,ABC △、CDE △、EHK △都在等边三角形,且A 、D 、K 共线,AD DK . 求证:HBD △也是等边三角形. K E C H D B A L
【例4】 ABC △是等边三角形,P 是AB 边的中点,Q 是AC 边的中点,R 为BC 边的中点,M 为RC 上任意一点,且PMS △是等边三角形,S 与Q 在PM 的同侧,求证:RM QS =. 【例5】 ABCD 是正方形,P 是ABCD 内一点,1PA =,3PB = ,PD =ABCD 的面积. 【例6】 P 是等边三角形ABC 内的一点,6PA =,8PB =,10PC =.求ABC △的边长. Q ? S M P C B A R D
【例7】 设O 是等边ABC △内一点,已知115AOB ?∠=,125BOC ?∠=,求以线段OA 、OB 、OC 为 边所构成的三角形的各内角大小. 【例8】 如图,在ABC △中,90ACB ?∠=,AC BC =,P 是ABC △内一点,3PA =,1PB =,2PC =, 求BPC ∠. 【例9】 如图,已知ABC △中,90A = ,AB AC =,D 为BC 上一点,求证:2222BD DC AD +=. A P C B A D C B
初二数学几何图形题
几何图形题 常见辅助线的作法有以下几种: 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”. 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠” 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、以等边三角形为基础 1.已知:如图1,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F.(1)求证:AN=BM; (2)求证:△CEF为等边三角形; (3)将△ACM绕点C按逆时针方向旋转90 O,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明). 2.如图,△ABC为等边三角形,AB=6cm,O为AB上的任意一点(与B点不重合),OD⊥BC于D;DE⊥AC于E;EP⊥AB于P。问:当OB的长等于多少时,点P与点O重合?
二、以等腰直角三角形为基础 3.如图1图2图3,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90o, (1)在图1中,AC与BD相等吗,有怎样的位置关系?请说明理由。 (2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗,还具有那种位置关系吗?为什么? (3)若△COD绕点O顺时针旋转一定角度后,到达图3的位置,请问AC与BD还相等吗?还具有上问中的位置关系吗?为什么? 4.如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.
高中数学竞赛题之平面几何
第一讲 注意添加平行线证题 在同一平面内,不相交的两条直线叫平行线.平行线是初中平面几何最基本的,也是非常重要的图形.在证明某些平面几何问题时,若能依据证题的需要,添加恰当的平行线,则能使证明顺畅、简洁. 添加平行线证题,一般有如下四种情况. 1 为了改变角的位置 大家知道,两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.利 用这些性质,常可通过添加平行线,将某些角的位置改变,以满足求解的需要. 例1 设P 、Q 为线段BC 上两点,且BP =CQ ,A 为BC 外一动点(如图1).当点A 运动到使 ∠BAP =∠CAQ 时,△ABC 是什么三角形?试证明你的结论. 答: 当点A 运动到使∠BAP =∠CAQ 时,△ABC 为等腰三角形. 证明:如图1,分别过点P 、B 作AC 、AQ 的平行线得交点D .连结DA . 在△DBP =∠AQC 中,显然 ∠DBP =∠AQC ,∠DPB =∠C . 由BP =CQ ,可知 △DBP ≌△AQC . 有DP =AC ,∠BDP =∠QAC . 于是,DA ∥BP ,∠BAP =∠BDP . 则A 、D 、B 、P 四点共圆,且四边形ADBP 为等腰梯形.故AB =DP . 所以AB =AC . 这里,通过作平行线,将∠QAC “平推”到∠BDP 的位置.由于A 、D 、B 、P 四点共圆,使证明很顺畅. 例2 如图2,四边形ABCD 为平行四边形,∠BAF =∠BCE .求证:∠EBA =∠ADE . 证明:如图2,分别过点A 、B 作ED 、EC 的平行线,得交点P ,连PE . 由AB CD ,易知△PBA ≌△ECD .有PA =ED ,PB =EC . 显然,四边形PBCE 、PADE 均为平行四边形.有 ∠BCE =∠BPE ,∠APE =∠ADE . 由∠BAF =∠BCE ,可知 ∠BAF =∠BPE . 有P 、B 、A 、E 四点共圆. 于是,∠EBA =∠APE . 所以,∠EBA =∠ADE . 这里,通过添加平行线,使已知与未知中的四个角通过P 、B 、A 、E 四点共圆,紧密联系起来.∠APE 成为∠EBA 与∠ADE 相等的媒介,证法很巧妙. 2 欲“送”线段到当处 利用“平行线间距离相等”、“夹在平行线间的平行线段相等”这两条,常可通过添加平行线,将某些线段“送”到恰当位置,以证题. 例3 在△ABC 中,BD 、CE 为角平分线,P 为ED 上任意一点.过P 分别作AC 、AB 、BC 的垂线,M 、N 、Q 为垂足.求证:PM +PN =PQ . 证明:如图3,过点P 作AB 的平行线交BD 于F ,过点F 作BC 的平行线分别交PQ 、AC 于K 、G ,连PG . 由BD 平行∠ABC ,可知点F 到AB 、BC 两边距离相等.有KQ =PN . 显然,PD EP =FD EF =GD CG ,可知PG ∥EC . 由CE 平分∠BCA ,知GP 平分∠FGA .有PK =PM .于是, PM +PN =PK +KQ =PQ . 这里,通过添加平行线,将PQ “掐开”成两段,证得PM =PK ,就有PM +PN =PQ .证法非常简捷. 3 为了线段比的转化 ∥= A D B P Q 图1P E D G A B F C 图2 A N E B Q K G C D M F P 图3
八年级数学几何板块专题复习
八年级数学 几何板块专题复习 一、考点、热点回顾 一、三角形 1. 三角形基本概念 1. 定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形,用符号“?” 表示,顶点是C B A ,,的三角形记作“ABC ?” ,读作“三角形ABC ”。 2. 三角形分类: ①三角形按边的关系分类 ②三角形按角的关系分类 3. 三角形三边关系定理:三角形的两边之和大于第三边.(根据两点之间线段最短可得) 推论:三角形两边之差小于第三边. 4. 三角形内角和定理:三角形三个内角和等于ο180。 推论:直角三角形的两个锐角互余。 5. 三角形的外角及其性质:1、三角形的一个外角等于和它不相邻的两个内角的和。 2、三角形的一个外角大于任何一个和它不相邻的内角。 6. 三角形的三条重要线段 (1)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。注意:①是一个三角形有三条角平分线,并且相交于三角形内部一点,我们把这一点叫做三角形的内心;②是三角形的角平分线是一条线段,而角的平分线是一条射线。 (2)在三角形中,连结一个顶点和它对边的中点的线段叫做三角形的中线。注意:①一个三角形有三条中线,并且相交于三角形内部一点,我们把这个点叫做三角形的重心;②三角形的重心把中线的长度按2:1的比例分开。 (3)从三角形一个顶点向它对边画垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。注意:①三角形的高是线段,而垂线是直线。②锐角三角形的三条高都在三角形内部;直角三角形的两条高与直角边重合,另一条高在三角形内部;钝角三角形的两条高在外部,一条高在内部。 2.全等三角形 1. 定义:能够完全重合的两个三角形叫做全等三角形。 2. 表示方法:△ABC 全等于△DEF,或△ABC≌△DEF。 3. 全等三角形的性质:全等三角形的对应边相等 全等三角形的对应角相等 4.三角形全等的判定 三边对应相等的两个三角形全等。 两角和它们的夹边对应相等的两个三角形全等。 (5) 斜边、直角边 .):斜边和直角边对应相等的两个直角三角形全等。 注:角角角、边边角不能判定两三角形全等。 【经典例题】 1.下列命题正确的是( )
人教版九年级数学竞赛专题:平面几何的定值问题(含答案)
人教版九年级数学竞赛专题:平面几何的定值问题(含答案) 【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧上任意一点.求证:为定值. AD ⌒ PA PC PB P A B C D 【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦 CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变 C.等分 D.随C 点的移动而移动 DB ⌒ A
【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂 线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角. B 【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是上异于A ,B 的动点,过点C AB ⌒ 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形; (2)当点C 在上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段AB ⌒ 的长度; (3)求证:CD 2+3CH 2是定值. B O A C E H G D 【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8.
小学数学竞赛几何题集锦
小学数学竞赛几何图形集锦 第一部分基础题 1、(06年清华附中考题) 如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13 AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积. 2、(06年西城实验考题) 四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米,大正方形面积是5平方米,那麽直角三角形中,最短的直角边长度是______米. 3、(05年101中学考题) 一块三角形草坪前,工人王师傅正在用剪草机剪草坪.一看到小灵通,王师傅热情地招呼,说:“小灵通,听说你很会动脑筋,我也想问问你,这块草坪我把它分成东、西、南、北四部分(如图).修剪西部、东部、南部各需10分钟,16分钟,20分钟.请你想一想修 4、(05年三帆中学考题) 右图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE 的面积是平方厘米. 5、 (06年北大附中考题)
三角形ABC 中,C 是直角,已知AC =2,CD =2,CB=3,AM=BM ,那么三角形AMN (阴影部分)的面积为多少? 6、(★★)如右图所示,已知三角形ABC 面积为1,延长AB 至D ,使BD=AB ;延长BC 至E ,使CE=2BC ;延长CA 至F ,使AF=3AC , 求三角形DEF 的面积。 7、(★★)右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为15、18、30公顷,问图中阴影部分的面积是多少? 8、正方形ABFD 的面积为100平方厘米,直角三角形ABC 的面 积,比直角三角形(CDE 的面积大30平方厘米,求DE 的长是多少? 9、(★★★)如下图,已知D 是BC 的中点,E 是CD 的中点,F 是AC 的中点,且ADG ?的 面积比EFG ?的面积大6平方厘米。?的面积是多少平方厘米 ABC ? A B C D E F G 10、(★★)长方形ABCD 的面积为36平方厘米,E 、F 、G 分别为边AB 、BC 、CD 的中点,H 为AD 边上的任一点。求图中阴影部分的面积是多少?
高中数学竞赛讲座 08几何变换
竞赛专题讲座08 -几何变换 【竞赛知识点拨】 一、平移变换 1.定义设是一条给定的有向线段,T是平面上的一个变换,它把平面图形F 上任一点X变到X‘,使得=,则T叫做沿有向线段的平移变换。记为X X’,图形F F‘ 。 2.主要性质在平移变换下,对应线段平行且相等,直线变为直线,三角形变为三角形,圆变为圆。两对应点连线段与给定的有向线段平行(共线)且相等。 二、轴对称变换 1.定义设l是一条给定的直线,S是平面上的一个变换,它把平面图形F上任一点X变到X’,使得X与X‘关于直线l对称,则S叫做以l为对称轴的轴对称变 换。记为X X’,图形F F‘ 。 2.主要性质在轴对称变换下,对应线段相等,对应直线(段)或者平行,或者交于对称轴,且这两条直线的夹角被对称轴平分。 三、旋转变换 1.定义设α是一个定角,O是一个定点,R是平面上的一个变换,它把点O 仍变到O(不动点),而把平面图形F上任一点X变到X’,使得OX‘=OX,且 ∠XOX’=α,则R叫做绕中心O,旋转角为α的旋转变换。记为X X‘, 图形F F’ 。 其中α<0时,表示∠XOX‘的始边OX到终边OX’的旋转方向为顺时针方向;α>0时,为逆时针方向。 2.主要性质在旋转变换下,对应线段相等,对应直线的夹角等于旋转角。 四、位似变换
1.定义设O是一个定点,H是平面上的一个变换,它把平面图形F上任一点X 变到X‘,使得=k·,则H叫 做以O为位似中心,k为位似比的位似 变换。记为X X’,图形 F F‘ 。 其中k>0时,X’在射线OX上,此时的位似变换叫做外位似;k<0时, X‘在射线OX 的反向延长线上,此时的位似变换叫做内位似。 2.主要性质在位似变换下,一对位似对应点与位似中心共线;一条线上的点变到一条线上,且保持顺序,即共线点变为共线点,共点线变为共点线;对应线段的比等于位似比的绝对值,对应图形面积的比等于位似比的平方;不经过位似中心的对应线段平行,即一直线变为与它平行的直线;任何两条直线的平行、相交位置关系保持不变;圆变为圆,且两圆心为对应点;两对应圆相切时切点为位似中心。 【竞赛例题剖析】 【例1】P是平行四边形ABCD内一点,且∠PAB=∠PCB。 求证:∠PBA=∠PDA。 【分析】作变换△ABP△DCP’, 则△ABP≌△DCP‘,∠1=∠5,∠3=∠6。由PP’AD BC,ADPP‘、PP’CB都是平行四边形,知∠2=∠8,∠4=∠7。由已知∠1=∠2,得∠5=∠8。 ∴P、D、P‘、C四点共圆。故∠6=∠7,即∠3=∠4。 【例2】“风平三角形”中,AA’=BB‘=CC’=2,∠AOB‘=∠BOC’=60°。
(完整版)人教版八年级下册数学几何题训练含答案
八年级习题练习 四、证明题:(每个5分,共10分) 1、在平行四边形ABCD 中,AE ⊥BC 于E ,CF ⊥AD 于F ,求证:BE = DF 。 2、在平行四边形DECF 中,B 是CE 延长线上一点,A 是CF 延长线上一点,连结AB 恰过点D ,求证:AD ·BE =DB ·EC 五、综合题(本题10分) 3.如图,直线y=x+b (b ≠0)交坐标轴于A 、B 两点,交双曲线y=x 2 于点D , 过D 作两坐标轴的垂线DC 、DE ,连接OD . (1)求证:AD 平分∠CDE ; (2)对任意的实数b (b ≠0),求证AD ·BD 为定值; (3)是否存在直线AB ,使得四边形OBCD 为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由. F E D C B A F E D C B A
4. 如图,四边形ABCD 中,AB=2,CD=1 ,∠A=60度,∠D=∠B=90度,求四边形ABCD 的面积S 5.如图,梯形ABCD 中,AD//BC,AB=DC. 如果P 是BC 上任意一点(中点除外),PE//AB ,PF//DC ,那么AB=PE+PF 成立吗?如果成立,请证明,如果不成立,说明理由。 参考答案 证明题 1、证△ABE ≌△CDF ; 2、 ??? ?∠=∠?∠=∠?A BDE AC DE B ADF BC DF △ADF ∽△DBE BE DF DB AD =? 综合题 1.(1)证:由y=x +b 得 A (b ,0),B (0,-b ). ∴∠DAC=∠OAB=45 o 又DC ⊥x 轴,DE ⊥y 轴 ∴∠ACD=∠CDE=90o ∴∠ADC=45o 即AD 平分∠CDE.
初中数学竞赛 几何专题:点共线问题(含答案)
初中数学竞赛 几何专题:点共线问题(含答案) 1. 锐角三角形ABC 中,45BAC ∠=?,BE 、CF 是两条高,H 为ABC △的垂心,M 、K 分别是BC 、 AH 的中点.证明:MK 、EF 和OH 共点,这里O 为ABC △的外心. 解析 如图,由条件45BAE ∠=?,可知AEB △和AFC △都是等腰直角三角形,而O 为AB 、BC 的中垂线上的点,故EO AB ⊥,FO AC ⊥,于是EO CF ∥,FO BE ∥,从而四边形EOFH 为平行四边形.故EF 与OH 的交点为EF 的中点. 另一方面,M 、K 为BC 、AH 的中点,结合直角三角形斜边上的中线等于斜边的一半,可知 12EM MF BC ==,1 2 EK KF AH ==.即四边形EKFM 为菱形,所以EF 与KM 的交点亦是EF 的中点. 从而命题获证. 2. 四边形SPNM 与PFET 都是正方形,且点S 、P 、T 共线,点N 、P 、F 共线,连结MT 、SE , 点S 在MT 上的射影是点A ,点T 在SE 上的射影是点B ,求证:点A 、P 、B 共线. 解析 设AB 与ST 交于点P ',又设ATS α∠=,TSE β∠=.于是由180ASB ATB ∠+∠=?,有 tan cot ASB ATB S SP AS BS P T S AT BT αβ'?===?'?△△ MS ST MS SP ST TE TE PT = ?== , 即点P 与点P '重合. 3. 在矩形ABCD 的边AB 、BC 、CD 、DA 上分别取异于顶点的K 、L 、M 、N ,已知KL MN ∥.证明KM 与LN 的交点O 在矩形的对角线BD 上. 解析 连结OB 、OD . B M N A S P T F E D M C N O L A K B
(完整版)八年级数学几何经典题【含答案】
F 八年级数学几何经典题【含答案】 1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长 线交MN 于E 、F . 求证:∠DEN =∠F . 2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG , 点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半. 3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF . . 4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF . B
5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF . 6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE =CF .求证:∠DPA =∠DPC . 7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。 求证:EF=FD 。 8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。 9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EF D F E P C B A F P D E C B A
