第9章统计实验统计实验(对应分析)
多元统计分析(聚类分析,判别分析,对应分析)

h
11
对应分析
概述
对应分析的重要输出结果之一在于,把变量与样品同时反映到相同 坐标轴(因子轴)的一张图形上,结合计算结果,在绘出的图形上能 够直观地观察变量之间的关系、样品之间的关系以及变量与样品 之间的对应关系。为此也有人认为,对应分析的实质是将变量、 样品的交叉表变换成为一张散点图,从而将表格中包含的变量、 样品的关联信息用各散点空间位置关系的形式表现出来。
(5)画谱系聚类图; (6)决定总类的个数及各类的成员。
h
聚类分析 6
结果分析
返回
h
判别分析 7
概述
判别分析是用于判断个体所属类别的一种统计方法。根据已知观 测对象的分类和若干表明观测对象特征的变量值,建立判别函数和判 别准则,并使其错判率最小,对于一个未知分类的样本,将所测指标 代入判别方程,从而判断它来自哪个总体。当然,这种准则在某种意 义上是最优的,如错判概率最小或错判损失最小等。其前提是总体均 值有显著差异,否则错分率大,判别分析无意义。
h
目录 3 h
聚类分析 4 定义 聚类分析是统计学中研究“物以类聚”问题的多元统计分析方法。聚
类分析又称群分析,它是研究对样品或指标进行分类的一种多元统计 方法。所谓的“类”,通俗地说就是相似元素的集合。
h
聚类分析 5
基本步骤
(1)计算n个样品两两间的距离,得样品间的距离矩阵 。类与类之间的距 离本文应用的是类平均法。所谓类平均法就是:两类样品两两之间平方距 离的平均作为类之间的距离,即: 采用这种类间距离的聚 类方法,称为 类平均法。
(2) 初始(第一步:i=1)n个样本各自构成一类,类的个数k=n,第t类 (t=1,2···,n)。此时类间的距离就是样品间的距离(即 )。
第九章统计决策

(2)最小期望损失值决策法 这是与最大期望收益相对应的另外一种决策方法,
即根据损失值进行决策,将期望损失值最小的方 案作为最优方案。 决策步骤: A首先列出决策的损失矩阵表(形式同表9-5), B以决策的损失矩阵表为基础,根据各种自然状 态的概率计算出不同方案的期望损失值, C然后从期望值中选择最小的值所对应的方案作 为最优方案。 最小期望损失值决策方法的计算公式是:
称为先验概率
利用附加信息对先验概率进行修正后得到的概率 为后验概率。
由于后验概率的计算方法是著名的贝叶斯定理, 所以利用补充信息,根据概率计算中的贝叶斯公 式来估计后验概率,并在此基础上对备选方案进 行评价和选择的决策方法,被称之为贝叶斯决策 方法。
设某种状态θj的先验概率为P(θj),通过调查获得的补充信息为 ek ,θj给定时,ek的条件概率(似然度)为P(ek/θj),则在给 定信息ek的条件下, 可用贝叶斯公式计算θj的条件概率即后验概 率:
例9.7
四.折衷决策法 折衷决策准则是对“乐观”和“悲观”决策准则
进行折衷处理而得到的一种新的决策准则,也称 作“系数”收益决策准则或赫威兹准则。
决策者在决策时,既不支持极端冒险的乐观态度, 也不持极端保守的悲观态度,而是持一种折衷的 温和态度,这种折衷的态度通过对未来情况赋予 一个乐观系数来体现。
最大最大决策法又叫乐观法,其决策原则是“大 中取大”。
选择方案的标准是:“大中取大收益,小中取小 损失”。
A决策者总是假定未来是最理想的自然状态占优 势,因此,先选出各自然状态下每个方案的最大 收益值,然后再从这些最大收益值中选出最大者, 与最大收益值对应的方案就是合适的方案;B如 果方案的付酬值是用亏损或支付额估计的,则先 选出各自然状态下每个方案的最小亏损值,然后 从这些最小亏损值中选出最小值,与最小亏损值 对应的方案就是合适的方案。
多元统计分析-对应分析

03
列联表检验的零假设是两变量 X和Y 相互独立,计算一个卡方统计量,与列联表中频数取值 和零假设下期望取值之差有关,当卡方 很大时否定零假设。
BA
患慢性支 未患慢性 气管炎 支气管炎
吸烟
43
162
不吸烟
13
121
为了探讨吸烟与慢性支气管炎有无关系, 调查了339人,情况如表所示:
设想有两个随机变量A,B:A:1表示吸 烟,
对应分析
对应分析基本步骤: 建立列联表
利用对应图解释结 果。
1
2
3
一.获取对应分析 数据 确定研究目的, 选择对应分析 所需数据,应 该包括的背景 资料。
对应分析
4
5
二、对应分析 的原理
01
由于R型因子分析和 02
设原始数据矩阵为:
Q型因子分析是反映
一个整体的不同侧面,
R型因子分析是从列
来讨论(对变量),
k
特征根。
Zu k
设 1 2…
三、对应图u 1u 11u 21 A和l(0Bu <的p 1 i<非m零in特(n征,p根)),为其矩相阵应 u 2u 12u 22 的特征u p 向2量为
v 1 v 1 1v 2 1 v n 1 v 2 v 1 2 v 2 2 v n 2
我们知道因子载荷矩阵的含义是原始变量与公共因子之间的 相关系数,所以如果我们构造一个平面直角坐标系,将第一 公共因子的载荷与第二个公共因子的载荷看成平面上的点, 在坐标系中绘制散点图,则构成对应图。
Q型因子分析是从行
来讨论(对样品),
因此 在的
他们之
联 x系1。1
间
存在
x12
内
高考数学总复习(一轮)(人教A)教学课件第九章 统计、成对数据的统计分析第3节 成对数据的统计分析

(xn,yn)(n≥2,x1,x2,…,xn互不相等) 的散点图中,若所有样本点
(xi,yi)(i=1,2,…,n)都在直线y= x-5上,则这组样本数据的样本
相关系数为(
A.-
)
B.
C.-1
√
D.1
解析:(2)由题意可知,所有样本点(xi,yi)(i=1,2,…,n)都在直线
y= x-5上,则这组样本数据完全正相关,且相关系数为1.故选D.
解:(2)由(1)得 =
=
∑ -
=
=
^
=0.67,
^
=- =75-0.67×30=54.9,
^
所以 y 关于 x 的经验回归方程为 =0.67x+54.9.
^
将 x=130 代入 =0.67x+54.9,
^
得 =0.67×130+54.9=142,
)
√
解析:对于A,残差与观测时间有线性关系,故A错误;对于B,残差
的方差不是一个常数,随着观测时间变大而变小,故B错误;对于
C,残差与观测时间是非线性关系,故C错误;对于D,残差比较均
匀地分布在以取值为0的横轴为对称轴的水平带状区域内,故D
正确.故选D.
5.已知P(χ2≥6.635)=0.01,P(χ2≥10.828)=0.001.在检验30岁以
则r 与r 的大小关系是 r1>r2 .
1
2
解析:(2)因为Y与X之间正相关,所以r1>0;因为V与U之间负相关,
所以r2<0,因此r1>0>r2.
考点二
回归模型及其应用
高考数学总复习(一轮)(人教A)教学课件第九章 统计、成对数据的统计分析第2节 用样本估计总体

6
10
9
8
7
则该校学生开展志愿者活动时长的第40百分位数是
8.5
.
解析:(2)40×40%=16,故第40百分位数是第16个数和第17个数的平
均数, 即
+
=8.5.
考点二
总体集中趋势的估计
[例3] (多选题)某学校共有2 000名男生,为了了解这部分学生的身
体发育情况,学校抽查了100名男生的体重情况.根据所得数据绘制
=0.01.
(2)根据频率分布直方图,估计样本数据的15%和85%分位数.
解 :(2)由 图 可 知 ,[20,40)内 的 比 例 为 10%,[40,60)内 的 比 例 为
20%,[60,80)内的比例为40%,[80,100]内的比例为30%.
因此,15%分位数一定位于[40,60),85%分位数一定位于[80,100],
直方图如图所示:
得分 [20,40) [40,60) [60,80) [80,100]
人数
6
a
24
18
(1)求a,b的值;
解:(1)由频率分布直方图可知,
得分在[20,40)的频率为0.005×20=0.1,
故抽取的学生答卷数为6÷0.1=60,由6+a+24+18=60,得a=12.
所以 b=
[针对训练] (2023·全国乙卷)某厂为比较甲乙两种工艺对橡胶产品伸缩率
的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产
品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡
胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为
第九章-对应分析

pp i r i cD c 1r i c
i 1
2
总 惯 量 jq 1 p ji p 1p ij p p ji p i jq 1 p jc j r D r 1c j r
其中
2
ricD c 1ricq j1
pij
pipj pj
称为第i 行轮廓 r i 到行轮廓中心c 的卡方( 2 )距离, 它可看作是一个加权的平方欧氏距离。同样,
❖ 将表9.1.3中的数据除以,得到对应矩阵,列于表
9.1.4中。表9.1.4给出的行密度和列密度向量为
0.185
r0.363, c0.305,0.173,0.231,0.160,0.131
0.218 0.186 0.235 0.117 0.068
RDr1P00..331029
pp2
p p p p
❖ 其中 D r d ia gp 1 ,p 2 , ,p p 。
p1q
p1
p2q p2
p pq
p p
列轮廓矩阵
p11 p1
p12 p2
C PDc1 c1,c2 ,
p21
,cq p1
p22 p2
p p1 p p2
p1
p2
❖ 其中 D c d ia gp 1 ,p 2 , ,p q。
和c 的元素有时称为行和列密度(masses)。
三、行、列轮廓
❖ 第 i 行轮廓:
ri p p ii1 ,p p ii2 , ,p p iiq n n ii1 ,n n ii2 , ,n n iiq
其各元素之和等于1 ,即 r i1 1 , i 1 ,2 , ,p 。 ❖ 第 j 列轮廓:
cj p p1 jj,p p2 jj, ,p ppjj n n1 jj,n n2 jj, ,n npjj
(09)第9章 一元线性回归(2011年)

变量之间是否存在关系? 如果存在,它们之间是什么样的关系? 变量之间的关系强度如何? 样本所反映的变量之间的关系能否代表总体 变量之间的关系?
9-9 *
9.1 变量间的关系 9.1.1 变量间是什么样的关系?
统计学 STATIS TICS
函数关系
(第四版) 1. 是一一对应的确定关系 2. 设有两个变量 x 和 y ,变量 y y 随变量 x 一起变化,并完 全依赖于 x ,当变量 x 取某 个数值时, y 依确定的关系 取相应的值,则称 y 是 x 的 函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量 x 3. 各观测点落在一条线上
y 是 x 的线性函数(部分)加上误差项 线性部分反映了由于 x 的变化而引起的 y 的变化 误差项 是随机变量 反映了除 x 和 y 之间的线性关系之外的随机因素 对 y 的影响 是不能由 x 和 y 之间的线性关系所解释的变异性 0 和 1 称为模型的参数
9 - 30 *
统 计 学 数据分析 (方法与案例)
作者 贾俊平
统计学 STATIS TICS
(第四版)
统计名言
不要过于教条地对待研究的结果, 尤其当数据的质量受到怀疑时。
——Damodar N.Gujarati
9-2 *
第 9 章 一元线性回归
9.1 9.2 9.3 9.4 变量间关系的度量 一元线性回归的估计和检验 利用回归方程进行预测 用残差检验模型的假定
9-7
*
第 9 章 一元线性回归
9.1 变量间的关系
9.1.1 变量间是什么样的关系? 9.1.2 用散点图描述相关关系 9.1.3 用相关系数度量关系强度
应用统计学对应分析等
重庆交通大学管理学院
22:22:28
1、什么是典型相关分析? 典型相关分析是研究两组变量之间相关关系 的多元统计分析方法.它借用主成分分析降维的 思想,分别对两组变量提取主成分,且使两组变 量提取的主成分之间的相关程度达到最大,而从 同一组内部提取的各主成分之间互不相关,用从 两组之间分别提取的主成分的相关性来描述两组 变量整体的线性相关关系.
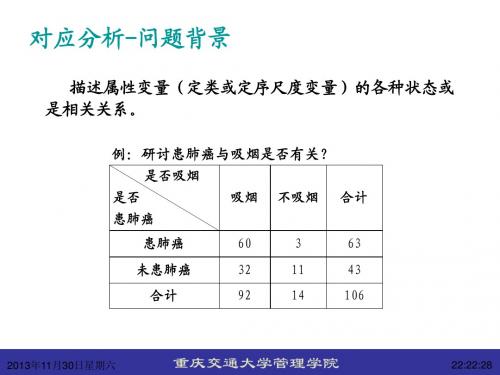
对应分析-问题背景
描述属性变量(定类或定序尺度变量)的各种状态或 是相关关系。
例:研讨患肺癌与吸烟是否有关?
是否吸烟 是否 患肺癌 患肺癌 未患肺癌 合计 60 32 92 3 11 14 63 日星期六
重庆交通大学管理学院
22:22:28
当属性变量A和B的状态较多时,很难透过列联表作 出判断。 怎样简化列联表的结构? 利用降维的思想。如因子分析和主成分分析。但因 子分析的缺陷是在于无法同时进行R型因子分析和Q 型因子分析。 怎么办?
2013年11月30日星期六
重庆交通大学管理学院
22:22:28
其优点是可以把方差分析和线性模型方法相结合,估 计模型中各个参数,而这些参数值使各个变量的效应和变 量间的交互作用效应得以数量化。
(2)Logistic 模型 是将概率比取对数后,再进行参数化而获得。设因变 量y为二值定性变量,用0和1表示两个不同状态,y=1的概 率p=P(y=1)是研究对象。若有多个因素影响y的取值,这 些因素就是自变量,记为:x1,x2…xk(既可以是定性变量 也可以是定量变量)。 Logistic 线性回归模型:
信度分类
内在信度:调查表中的一组问题(或整个调查表)是否测 量的是同一个概念,也就是这些问题之间的内在一致性 如何。 • 最常用的内在信度系数为克朗巴哈α系数和折半信度。 外在信度:在不同时间进行测量时调查表结果的一致性程 度。最常用的外在信度指标是重测信度,即用同一问卷 在不同时间对同一对象进行重复测量,然后计算一致程 度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五对应分析1.实验目的:本实验讨论利用对应分析从众多变量和样品信息中找出变量间、样品间、变量与样品间的本质联系。
通过该实验,能够起到如下的效果:(1) 理解对应分析的作用、思想、数学基础、方法和步骤;(2) 熟悉如何利用对应分析,提出问题、分析问题、解决问题、得出结论;(3)会调用SAS软件实现对应分析的各个步骤,根据计算的结果进行分析,得出正确的结论,解决实际的问题。
2.知识准备:对应分析是从众多变量和样品信息中找出变量间、样品间、变量与样品间的本质联系。
其思想是:对于某份数据(n份样品、p维数据),其变量点(n维空间的点,坐标为该变量在各个样品处的值)的协差阵和样品点(p维空间的点,坐标为该样品在各个变量处的值)的协差阵有本质的联系,而且有相同的特征值,特征向量也具有某种联系。
利用该联系进行适当的、尽量保留较多信息的降维,就会既反映变量间、样品间的本质联系,又反映变量与样品间的本质联系。
对应分析的步骤大体分为:首先把指标进行正向化;然后计算过渡矩阵,消除原始数据量纲的影响,使样品和变量具有某种意义下的对等性,以便可以在同一坐标轴中进行描述;然后对数据进行R型因子分析,根据过渡矩阵的相关阵的特征根和累计贡献率选取适当的公因子,计算出R型(变量点对应的)因子载荷和Q型(样品点对应的)因子载荷;然后把样品点和变量点根据它们变换后的坐标(R型因子得分或Q型因子的得分),描述到同一坐标轴中;最后根据样品点和变量点间的距离进行分析,得出结论。
3.实验内容:下面表1的数据是2009年广东省城镇居民家庭平均每人全年消费性支出构成的基本数据,其中的单位是百分比,数据来源于《广东省2009统计年鉴》:表1 广东省城镇居民家庭平均每人全年消费性支出构成的基本数据居民经济成份食品衣着居住家庭设备用品医疗保健交通和通讯教育文化娱乐服务其他消费最低收入户52.84 3.64 14.97 4.15 5.53 10.36 6.24 2.27 困难户54.52 3.43 15.24 4.65 5.55 8.63 5.70 2.28 低收入户52.77 4.78 13.03 4.56 4.67 10.29 7.57 2.33 中等偏下户46.92 5.46 11.20 5.69 4.91 13.49 9.68 2.65 中等收入户39.23 6.37 10.26 5.83 5.97 16.72 11.92 3.70 中等偏上户35.55 6.59 9.65 6.36 5.56 18.77 13.46 4.06 高收入户29.56 6.58 12.08 7.04 5.08 20.35 15.39 3.92 最高收入户28.70 7.17 9.86 7.05 5.91 21.10 15.71 4.50 利用对应分析对该数据进行处理,给出R型、Q型因子载荷,并结合该数据,给出适当的结论。
4.实验步骤:SAS程序:1.读入数据:Data consumption;input type X1-X8;cards;1 52.84 3.64 14.97 4.15 5.53 10.36 6.24 2.272 54.52 3.43 15.24 4.65 5.55 8.63 5.70 2.283 52.77 4.78 13.03 4.56 4.67 10.29 7.57 2.334 46.92 5.46 11.20 5.69 4.91 13.49 9.68 2.655 39.23 6.37 10.26 5.83 5.97 16.72 11.92 3.706 35.55 6.59 9.65 6.36 5.56 18.77 13.46 4.067 29.56 6.58 12.08 7.04 5.08 20.35 15.39 3.928 28.70 7.17 9.86 7.05 5.91 21.10 15.71 4.50;run;2.进行对应分析,并画出散点图:Proc corresp data=consumption out=result;var X1-X8;id type;Proc plot data=result;plot dim1*dim2="*"$type/ haxis=-0.06 to 0.1 by 0.02vaxis=-0.35 to 0.35 by 0.1vspace=3hspace=10HREF=0VREF=0;run;语句解释:“Proc corresp”指调用对应分析程序;“var X1-X8;”指变量是“X1-X8”;“id type;”指样品名是变量“type”;“Proc plot”指调用作图程序;“plot dim1*dim2="*"$type”指作以“dim1”为纵坐标、以“dim2”为横坐标的平面坐标图,坐标点用“*”和样品名“type”标出,其中符号“$”指后面变量“type”是字符型;“/ haxis=-0.06 to 0.1 by 0.02 vaxis=-0.35 to 0.35 by 0.1”中“/”指后面的语句是对坐标轴进行补充说明,“haxis=-0.06 to 0.1 by 0.02”指横轴上的刻度是从“-0.06”到“0.1”,每格代表“0.02”,“vaxis=-0.35 to 0.35 by 0.1”指横轴上的刻度是从“-0.35”到“0.35”,每格代表“0.1”;“vspace=3 hspace=10”指定图中纵坐标、横坐标单位格在图中的实际长度;“HREF=0 VREF=0”在横坐标等于“0”、纵坐标等于“0”的地方分别划一条平行与纵轴、横轴的参考线,其它更多的语句参见书【2】。
运行结果及解释:图1中数据“Singular Value”是过渡矩阵的奇异值,“Principal Inertia”是过渡矩阵的奇异值的特征值,“Chi-Square”是卡方检验值,“Percent”是特征值的贡献率,“Cumulative Percent”是特征值的累计贡献率;图1中重点的信息在于“特征值”及其“贡献率”,根据图1的数据知道:第一特征值的贡献率为96.47%,基本上反映了所有的信息,前两个特征值的累计贡献率为98.92%,因此选用前两个公因子就基本上反映了所有的信息;图2是样品点在两个公因子下的载荷,即R型因子载荷,也可以认为是样品点在新坐标系(以Dim1、Dim2为坐标轴)中的坐标;图1惯量和卡方分解图图2样品点的新坐标图3样品点的统计量图4 样品点对公因子贡献图3中数据“Quality”是前两个公因子对样品的共同度(如果保留所有的8个公因子,则共同度应该等于1),“Mass”是原始数据中各行数据之和占总数据之和的比,“Inertia”指各样品对总特征值的贡献率;图3中重点信息在于“Quality”的值。
由图3中数据知道:前两个公因子对每个样品的共同度都达到了0.89以上,基本上反映了每个样品的信息;图4是每个样品对公因子的贡献率,各列之和应该等于1。
由据图4中数据知道:样品1、2、3、7、8(最低收入户、困难户、低收入户、高收入户、最高收入户)对第一个公因子贡献比较大,样品1、2、4、5、7(最低收入户、困难户、中等偏下户、中等收入户、高收入户、最高收入户)对第二个公因子贡献比较大;图5对样品点贡献最大的公因子图5是各样品点的坐标对特征值贡献多少的说明,其中0、1、2分别代表贡献少、中、多;图6样品点余弦平方值图6是前两个公因子各自对样品的贡献率,各行的数值和应该等于图3中“Quality”的数值;根据图6的数据知道:第一个公因子对除4(中等偏下户)外的其他样品的贡献率都达到了0.81以上,基本上反映了除4外的其他样品的信息;图7 变量点的新坐标图8 变量点的统计量图9 变量点对公因子贡献图10 对变量点贡献最大的公因子图11 变量点余弦平方值图7-图11的数据是对变量点情况的说明,类似与图2-图6;根据图11的数据知道:第一个公因子对除X3(居住消费)、X5(医疗保健消费)外的其他变量的贡献率都达到了0.92以上,基本上反映了除X3、X5外的其他变量的信息;又根据图8中“Quality”的数据知道:前两个公因子对X3的共同度达到了0.99以上,基本上反映了X3的信息;图12 散点图实验结论:从图1的数据知道:第一公因子反映了绝大部分信息,前两个公因子基本上反映了所有的信息;而且从图6和图11的数据知道:第一个公因子(Dim1)基本上反映了除4(中等偏下户)、X3(居住消费)、X5(医疗保健消费)外的其他样品及变量的信息;前两个公因子基本上反映了除X5(居住消费)外的其他样品及变量的信息;因此以Dim1为纵轴、以Dim2为横轴的坐标轴基本上能反映样品和变量的信息,特别是纵轴的信息更为重要;从散点图上分析:(1)X1(食品)、X3(居住)纵轴坐标为负,而且X3与1(最低收入户)和2(困难户)距离最近,X1与3(低收入户)和4(中等偏下户)距离最近。
这说明X1和X3是最低端的生活必须品,经济条件差的居民与该消费关系最为密切,政府应该关心低收入人群的食品和居住费用,控制食品的价格,提供价格便宜的廉租房。
(2)X2(衣着)、X4-X8(家庭设备用品、医疗保健、交通和通讯、教育文化娱乐服务、其他消费)纵轴坐标为正,而且X2与5(中等收入户)和6(中等偏上户)距离最近,X4-X8与7(高收入户)和8(最高收入户)距离最近。
这说明衣着消费与中等收入的居民关系密切,中等收入的居民有了一定的生活保证,开始通过购买服装来追求时尚、体现个性。
家庭设备用品、医疗保健、交通和通讯、教育文化娱乐服务、其他消费是属于相对高端的消费,只有高收入的人群才有较大的消费比重。
(3)从上面的分析可以看到,目前收入中等偏上的居民主要的消费还只是与衣着消费密切,交通和通讯、教育文化娱乐服务等还属于高收入人群的消费。
这说明虽然广东省的人民生活水平步入了小康阶段,但与发达国家相比还是有不少的差距,有待提高。
5. 思考与练习:⑴运用对应分析研究我国近些年的社会消费品零售额的构成。
⑵运用对应分析尝试研究我国各省市国民生产总值的收入和支出的情况,并进行适当的分析。
⑶运用对应分析尝试研究我国各省市住房有关指标的情况,并进行适当的分析。
参考文献【1】于秀林、任雪松(1999):《多元统计分析》,中国统计出版社。
【2】汪远征、徐雅静(2007):《SAS软件与统计应用教程》,机械工业出版社。
【3】林海明:《因子分析模型的改进和应用》,数理统计与管理,28,2009,998-1012。
【4】林海明:《对主成分分析法运用中十个问题的解析》,统计与决策,16,2007,16-18。
