《推荐》月考02第二章综合测试卷(A卷)-2016-2017学年高一数学同步单元双基双测AB卷Word版含解析
江西省上高二中高一上学期第二次月考试题 数学
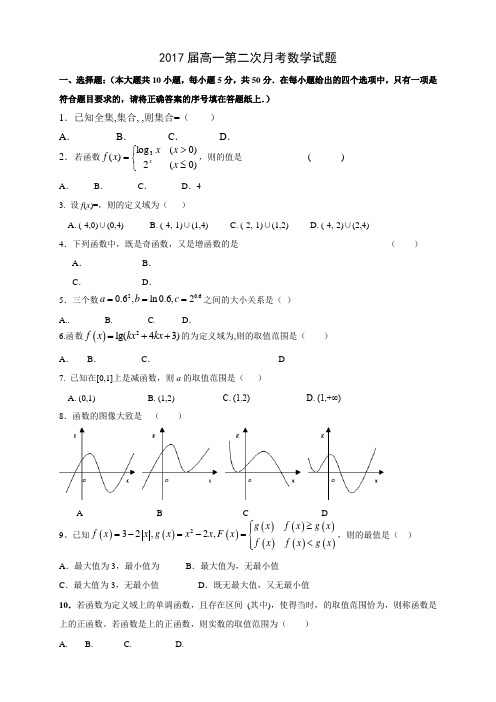
2017届高一第二次月考数学试题一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的序号填在答题纸上.)1.已知全集,集合, ,则集合=( )A .B .C .D .2.若函数⎩⎨⎧≤>=)0(2)0(log )(3x x x x f x ,则的值是 ( )A .B .C .D .43. 设f (x )=,则的定义域为( )A. (-4,0)∪(0,4)B. (-4,-1)∪(1,4)C. (-2,-1)∪(1,2)D. (-4,-2)∪(2,4)4.下列函数中,既是奇函数,又是增函数的是 ( ) A . B . C .D .5.三个数20.60.6,ln 0.6,2a b c ===之间的大小关系是( )A..B. C . D .6.函数()2lg(43)f x kx kx =++的为定义域为,则的取值范围是( )A .B .C .D7. 已知在[0,1]上是减函数,则a 的取值范围是( )A. (0,1)B. (1,2)C. (1.2)D. (1,+∞) 8.函数的图像大致是 ( )A BC D9、已知()()()()()()()()()232,2,g x f x g x f x x g x x x F x f x f x g x ≥⎧⎪=-=-=⎨<⎪⎩,则的最值是( )A .最大值为3,最小值为B .最大值为,无最小值C .最大值为3,无最小值D .既无最大值,又无最小值10.若函数为定义域上的单调函数,且存在区间 (其中),使得当时,的取值范围恰为,则称函数是上的正函数。
若函数是上的正函数,则实数的取值范围为( ) A. B. C. D.二、填空题:(本大题共5小题,每小题5分,共25分。
在答题卡上的相应题目的答题区域内作答). 11. 当x ∈(0,+∞)时,幂函数y =(m 2-m -1)x m 为减函数,则实数m 的值为________. 12.已知是奇函数,且.若,则_______ .13.函数y=() (-3)的值域是 。
青海省西宁市2016-2017学年高一数学下学期第二次月考试题(含解析)

青海省西宁市2016-2017学年⾼⼀数学下学期第⼆次⽉考试题(含解析)西宁市16—17学年第⼆学期第⼆次⽉考试卷⾼⼀数学⼀、选择题:(本⼤题共12⼩题,每⼩题5分,满分60分。
在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的)1. 若aA. a|c|B. abC. a-cD.【答案】C【解析】选项A中c=0时不成⽴;选项B中a≤0时不成⽴;选项D中取a=-2,b=-1,c =1验证,不成⽴,故选C.2. 等⽐数列x,3x+3,6x+6,…的第四项等于( )A. -24B. 0C. 12D. 24【答案】A【解析】由x,3x+3,6x+6成等⽐数列得选A.考点:该题主要考查等⽐数列的概念和通项公式,考查计算能⼒.3. 当x>1时,不等式x+≥a恒成⽴,则实数a的取值范围是( )A. (-∞,2]B.【答案】D考点:基本不等式.4. 等差数列{a n}满⾜,则其前10项之和为( )A. -9B. -15C. 15D. ±15【答案】D【解析】由已知(a4+a7)2=9,所以a4+a7=±3,从⽽a1+a10=±3.所以S10=×10=±15.故选D.5. 已知△ABC中,三内⾓A、B、C成等差数列,边a、b、c依次成等⽐数列,则△ABC是( )A. 直⾓三⾓形B. 等边三⾓形C. 锐⾓三⾓形D. 钝⾓三⾓形【答案】B【解析】∵△ABC中,三内⾓的度数成等差数列,∴,⼜,∴°.⼜边依次成等⽐数列,∴,在△ABC中,由余弦定理得:,∴,∴,∴,∴,⼜,∴为等边三⾓形。
故选B.6. 设变量x,y满⾜约束条件,则Z=x+2y的最⼤值为( )A. 1B. 2C. 6D. 7【答案】A【解析】作出⼀组平⾏线的,这⼀组平⾏线与平⾯区域有公共点时,且直线在y轴的截距最⼤,则最⼤.由图可知,当经过直线和的交点B(3,2)时,最⼤.最⼤值为=7.故选D.点睛:本题是常规的线性规划问题,线性规划问题常出现的形式有:①直线型,转化成斜截式⽐较截距,要注意前⾯的系数为负时,截距越⼤,值越⼩;②分式型,其⼏何意义是已知点与未知点的斜率;③平⽅型,其⼏何意义是距离,尤其要注意的是最终结果应该是距离的平⽅;④绝对值型,转化后其⼏何意义是点到直线的距离.7. 已知数列{a n}满⾜(n+2)a n+1=(n+1)a n,且a2=,则a n等于( )A. B. C. D.【答案】A【解析】因为(n+2)·a n+1=(n+1)a n,所以,⼜当n=1时,3a2=2a1,所以a1=a2=.所以.故选A.8. 已知,则f(x)>-1的解集为( )A. (-∞,-1)∪(0,+∞)B. (-∞,-1)∪(0,1)∪(1,+∞)C. (-1,0)∪(1,+∞)D. (-1,0)∪(0,1)【答案】B【解析】依题意,若,则x>0且x≠1;若>-1,则x<-1,综上所述.故选B.9. 在平⾯直⾓坐标系中,已知第⼀象限的点(a,b)在直线2x+3y-1=0上,则的最⼩值为()A. 24B. 2 5C. 26D. 27【答案】A【解析】∵第⼀象限的点在直线上,∴,且,即,∴.当且仅当,即时,的最⼩值为,故选B.点睛:在⽤基本不等式求最值时,应具备三个条件:⼀正⼆定三相等.①⼀正:关系式中,各项均为正数;②⼆定:关系式中,含变量的各项的和或积必须有⼀个为定值;③三相等:含变量的各项均相等,取得最值.10. 执⾏如图所⽰的程序框图,如果输出S=132,则判断框中应填()A. i≥10?B. i≥11?C. i≥12?D. i≤11?【答案】C【解析】程序执⾏过程中的数据变化如下:,,,,不成⽴,输出.故选:B.11. 已知等⽐数列{a n}满⾜=,,则=( )A. 2B. 1C.D.【答案】B【解析】试题分析:设等⽐数列{a n}的公⽐为q,则由已知得:,即:,解得:,因此,故选C.考点:等⽐数列.12. 设是等差数列{a n}的前项和,若,则()A. B. C. D.【答案】D【解析】试题分析:由等差数列的性质可得,,,仍成等差数列,∵,∴,∴,∴,,∴两式相加可得,∴,∴,故选A.考点:等差数列的前项和.⼆、填空题:(本⼤题共4⼩题,每⼩题5分,共20分)13. 在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM=,则sin∠BAC=________.【答案】【解析】因为,所以.如图,在△ABM中,利⽤正弦定理,得,所以.在Rt△ACM中,有.由题意知BM=CM,所以.化简,得.所以,解.再结合,∠BAC为锐⾓可解得=.14. 在等差数列{a n}中,若a3+a4+a5+a6+a7=25,则a2+a8=________.【答案】10【解析】试题分析:据等差数列的性质可知,项数之和相等的两项之和相等,化简已知的等式即可求出a5的值,然后把所求的式⼦也利⽤等差数列的性质化简后,将a5的值代⼊即可求出值.解:由a3+a4+a5+a6+a7=(a3+a7)+(a4+a6)+a5=5a5=450,得到a5=90,则a2+a8=2a5=180.故答案为:180.考点:等差数列的性质.15. ⽤秦九韶算法求多项式f(x)=6+5+4+3+2+x当x=2时的值时,=________.【答案】【解析】. 当x=2时的值时,点评:利⽤秦九韶算法求多项式的值⾸先要将多项式改写为每个括号内为关于x的⼀次式的形式,由内层括号到外层括号依次为.16. 不等式(a-2)+2(a-2) x-4<0对⼀切x R恒成⽴,则实数的取值范围是________.【答案】3【解析】试题分析:当时恒成⽴,当时,利⽤⼆次函数图象知,所以答案应填:.考点:含参⼆次不等式恒成⽴.【思路点晴】本题主要考查是含参数⼆次不等式的恒成⽴问题,属于中档题.解题时⼀定注意对的分类讨论,不能忘记的情况,同时,要结合⼆次函数图象及⽅程根的情况,应该开⼝向下,判别式⼩于零,列出满⾜的条件求解.三、解答题:(本⼤题共6⼩题,共70分)17. 设△ABC的内⾓A,B,C的对边分别为a,b,c,a=b tan A,且B为钝⾓.(1)证明:B-A=;(2)求sin A+sin C的取值范围.【答案】(1)见解析;(2).【解析】试题分析:(Ⅰ)运⽤正弦定理将化简变形,再解三⾓⽅程即可获解;(Ⅱ)将⾓⽤表⽰,换元法求函数的值域即可.试题解析:(Ⅰ)由及正弦定理,得,∴,即,⼜为钝⾓,因此,故,即;(Ⅱ)由(1)知,,∴,于是,∵,∴,因此,由此可知的取值范围是.考点:正弦定理、三⾓变换,⼆次函数的有关知识和公式的应⽤.18. 公差不为零的等差数列{a n}中,a3=7,且a2,a4,a9成等⽐数列.(1)求数列{a n}的通项公式;(2)设b n=2a n,求数列{b n}的前n项和S n.【答案】(1)a n=3n-2;(2).【解析】试题分析:(1)设数列的公差为d,根据a3=7,⼜a2,a4,a9成等⽐数列,可得(7+d)2=(7-d)(7+6d),从⽽可得d=3,进⽽可求数列{a n}的通项公式;(2)先确定数列{b n}是等⽐数列,进⽽可求数列{b n}的前n项和S n.试题解析:(1)由数列{a n}为公差不为零的等差数列,设其公差为d,且d≠0.因为a2,a4,a9成等⽐数列,所以a=a2·a9,即(a1+3d)2=(a1+d)(a1+8d),整理得d2=3a1d.因为d≠0,所以d=3a1.①因为a3=7,所以a1+2d=7.②由①②解得a1=1,d=3,所以a n=1+(n-1)×3=3n-2.故数列{a n}的通项公式是a n=3n-2.(2)由(1)知b n=23n-2,因为==8,所以{b n}是等⽐数列,且公⽐为8,⾸项b1=2,所以S n==.19. 已知函数f(x)=x2-2x-8,g(x)=2x2-4x-16.(1)求不等式g(x)<0的解集;(2)若对⼀切x>2,均有f(x)≥(m+2)x-m-15成⽴,求实数m的取值范围.【答案】(1){x|-2【解析】试题分析:(1)通过分解因式法进⾏求解;(2)作差,分离常数,将问题转化为求最值问题,再利⽤基本不等式求最值.试题解析:(1)g(x)=2x2-4x-16<0,∴(2x+4)(x-4)<0,∴-2<x<4,∴不等式g(x)<0的解集为{x|-2<x<4}.(2)∵f(x)=x2-2x-8.当x>2时,f(x)≥(m+2)x-m-15恒成⽴,∴x2-2x-8≥(m+2)x-m-15,即x2-4x+7≥m(x-1).∴对⼀切x>2,均有不等式成⽴.⽽=(x-1)+-2≥2-2=2(当且仅当x=3时等号成⽴),∴实数m的取值范围是(-∞,2].考点:1.⼀元⼆次不等式的解法;2.基本不等式.【⽅法点睛】本题考查⼀元⼆次不等式的解法、基本不等式的应⽤以及含参数的不等式恒成⽴问题,属于中档题;在处理含参数的不等式恒成⽴问题时,往往利⽤“分离参数法”将参数进⾏分离,使不等式恒成⽴问题转化为求函数的最值问题,如本题中将“对于恒成⽴”转化为“对于恒成⽴”,即求的最⼩值.20. 设数列{a n}的前n项和为S n=2n2,{b n}为等⽐数列,且a1=b1,b2(a2-a1)=b1.(1)求数列{a n}和{b n}的通项公式;(2)设c n=,求数列{c n}的前n项和T n.【答案】(1)a n=4n-2,;(2)T n=.【解析】略21. 在锐⾓△ABC中,三个内⾓A,B,C所对的边分别为a,b,c,且ac sin C=(a2+c2-b2)·sin B.(1)若C=,求A的⼤⼩;(2)若a≠b,求的取值范围.【答案】(1);(2).【解析】试题分析:(1)将已知等式变形,整理得, 可得,由此可得C=2B或C+2B=π,最后结合三⾓形内⾓和定理和∠C, 即可算出∠A的⼤⼩.(2)根据三⾓形为⾮等腰三⾓形,结合(1)中化简的结果可得C=2B,利⽤△ABC是锐⾓三⾓形,得到B 的范围,⼜即可得范围.试题解析:(1)因为ac sin C=(a2+c2-b2)sin B,所以==2=2cos B,所以sin C=sin 2B,所以C=2B或C+2B=π.若C=2B,C=,则A= (舍去).若C+2B=π,C=,则A=.故A=.(2)若三⾓形为⾮等腰三⾓形,则C=2B且A=π-B-C=π-3B,⼜因为三⾓形为锐⾓三⾓形,因为0<2B<,0<π-3B<,故<B<.⽽==2cos B,所以∈(,).22. 某⼯⼚建造⼀间地⾯⾯积为12的背⾯靠墙的矩形⼩房,房屋正⾯的造价为1200元,房屋侧⾯的造价为800元,屋顶的造价为5800元.若墙⾼为3,且不计房屋背⾯的费⽤,则建造此⼩房的最低总造价是多少元?【答案】当|AB|=3 m,|BC|=4 m时,能使整个框架⽤材料最少.【解析】试题分析:试题解析:设总造价为Z元,则有.∴.当时,即时,Z有最⼩值34600,此时答:长4m,宽3m.最低总造价为34600元点睛:在⽤基本不等式求最值时,应具备三个条件:⼀正⼆定三相等.①⼀正:关系式中,各项均为正数;②⼆定:关系式中,含变量的各项的和或积必须有⼀个为定值;③三相等:含变量的各项均相等,取得最值.。
2016年12月份月考数学试题(必修2第一章+第二章)

高一上学期12月份月考数学试题(试卷满分:120分 考试时间:100分钟)一、选择题(每小题4分,共40分)1、线段AB 在平面α内,则直线AB 与平面α的位置关系是()A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对 2、下列说法正确的是()A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点 3、垂直于同一条直线的两条直线一定()A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A BC D -中,下列几种说法正确的是()A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45 角D 、11AC 与1BC成60 角 5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是()A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点 6、下列命题中:(1)、平行于同一直线的两个平面平行; (2)、平行于同一平面的两个平面平行; (3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行。
其中正确的个数有()A 、1B 、2C 、3D 、47、在空间四边形A B C D 各边AB BC CD DA 、、、上分别取E F GH 、、、四点,如果与EF GH 、能相交于点P ,那么()A 、点必P 在直线AC 上B 、点P 必在直线BD 上C 、点P 必在平面ABD 内 D 、点P 必在平面ABC 外 8、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有() A 、0个 B 、1个 C 、2个 D 、3个B 1C 1A1D 1BACD9、如右图所示的直观图,其平面图形的面积为()A . 3B .C . 6D .. 310、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为()A 、2V B 、3V C 、4V D 、5V 二、填空题(每小题4分,共20分)11、已知圆锥的母线长为2,高为3,则该圆锥的侧面积是________12、右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是13、正方体1111ABCD A BC D -中,平面11AB D 和平面1BC D 的位置关系为 14、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,则平行四边形ABCD 一定是 .15、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件_________时,有A 1B ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)三、解答题(共60分,要求写出主要的证明、解答过程)16、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(12分)2232QPC'B'A'C BA俯视图 正(主)视图 侧(左)视图2 32 217、若E 、F 、G 、H 为空间四边形ABCD 边AB 、BC 、CD 、DA 上的点,且EH∥FG. 求证:EH ∥BD . (12分)18、在三棱锥V —ABC 中,V A=VB=AC=BC=2,AB=2 3,VC=1,求二面角V —AB —C 的大小. (12分)19、已知正方体1111ABCD A BC D -,O 是底ABCD 对角线的交点. 求证:(1)O C 1∥面11AB D ; (2 )1AC ⊥面11AB D . (12分) D 1C 1B 1A 1H G F ED BAC20、B为ACD所在平面外一点,M、N、G分别为ABC、ABD、BCD的重心,(1)求证:平面MNG//平面ACD;高一上学期12月份月考数学参考答案一、选择题(每小题4分,共40分)ACDDD BCBCB二、填空题(每小题4分,共20分)11、2π12. 12π13、平行14、菱形15、1111AC B D 对角线与互相垂直 三、解答题(共60分,要求写出主要的证明、解答过程)16、解:设圆台的母线长为l ,则 1分圆台的上底面面积为224S ππ=⋅=上 3分圆台的上底面面积为2525S ππ=⋅=下 5分 所以圆台的底面面积为29S S S π=+=下上 6分 又圆台的侧面积(25)7S l l ππ=+=侧 8分于是725l ππ= 9分 即297l =为所求. 10分 17、证明:,EH FG EH ⊄ 面BCD ,FG ⊂面BCDEH ∴ 面BCD 6分又EH ⊂ 面BCD ,面BCD 面ABD BD =,EH BD ∴ 12分18、解:取AB 的中点O ,连接VO ,CO-----------1分 因为△V AB 为等腰三角形∴VO ⊥AB---------2分 又因为△CAB 为等腰三角形∴CO ⊥AB------------3分 则∠VOC 为二面角V —AB —C 的平面角-------5分 ∵AB=2 3,∴AO= 3------- 6分又V A=2 则在Rt △VOA 中,VO=1------------8分 同理可求:CO=1---------------10分又已知VC=1 ,则△VOC 为等边三角形,∴∠VOC=60゜ ∴二面角V —AB —C 为60゜.------------------------------------------12分 6019、证明:(1)连结11AC ,设11111AC B D O =连结1AO , 1111ABCD A B C D -是正方体11A ACC ∴是平行四边形11AC AC ∴ 且11AC AC = 2分又1,O O 分别是11,AC AC 的中点,11O C AO ∴ 且11O C AO =11AOC O ∴是平行四边形 4分 111,C O AO AO ∴⊂ 面11AB D ,1C O ⊄面11AB D∴1C O 面11AB D 6分(2)1CC ⊥ 面1111A B C D 11!CC B D ∴⊥ 7分又1111AC B D ⊥ ,1111B D AC C ∴⊥面8分111AC B D ⊥即9分 同理可证11AC AB ⊥, 10分 又1111D B AB B =∴1AC ⊥面11AB D 12分 20、证明:连结BM 、BN 、BG 并延长交AC 、AD 、CD 分别于P 、F 、H 。
高一数学(人教A版)必修2第二章综合素能检测【推荐】

第二章综合素能检测时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )A.3 B.4C.5 D.6[答案] C[解析] AB与CC1为异面直线,故棱中不存在同时与两者平行的直线,因此只有两类:第一类与AB平行与CC1相交的有:CD、C1D1与CC1平行且与AB相交的有:BB1、AA1,第二类与两者都相交的只有BC,故共有5条.2.室内有一直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在的直线( )A.异面B.相交C.平行D.垂直[答案] D[解析] 当直尺与地面垂直时,地面上的任意一条直线都和直尺所在的直线垂直;当直尺所在的直线与地面不垂直时,过直尺所在的直线作一与地面垂直的平面,此平面与地面的交线设为a,则地面内任一与交线a垂直的直线都与直尺所在的直线垂直.3.如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l 与棱AB,AD,AA1所成的角都相等,这样的直线l可以作( )A.1条B.2条C.3条D.4条[答案] D[解析] 连接AC1,则AC1与棱AB,AD,AA1所成的角都相等;过点A分别作正方体的另外三条体对角线的平行线,则它们与棱AB,AD,AA1所在的角也相等,故这样的直线l可以作4条.4.设P是△ABC所在平面α外一点,H是P在α内的射影,且PA,PB,PC与α所成的角相等,则H是△ABC的( )A.内心B.外心C.垂心D.重心[答案] B[解析] 由题意知Rt△PHA≌Rt△PHB≌Rt△PHC,得HA=HB=HC,所以H是△ABC的外接圆圆心.5.已知二面角α-l-β的大小为60°,m,n为异面直线,且m⊥α,n⊥β,则m,n所成的角为( )A.30° B.60°C.90° D.120°[答案] B[解析] 易知m,n所成的角与二面角的大小相等,故选B.6.下面四个命题:①若直线a,b异面,b,c异面,则a,c异面;②若直线a,b相交,b,c相交,则a,c相交;③若a∥b,则a,b与c所成的角相等;④若a⊥b,b⊥c,则a∥c.其中真命题的个数为( )A.4 B.3C.2 D.1[答案] D[解析] 异面、相交关系在空间中不能传递,故①②错;根据等角定理,可知③正确;对于④,在平面内,a∥c,而在空间中,a与c可以平行,可以相交,也可以异面,故④错误.7.在正方体ABCD-A1B1C1D1中,E,F分别是线段A1B1,B1C1上的不与端点重合的动点,如果A1E=B1F,有下面四个结论:①EF⊥AA1;②EF∥AC;③EF与AC异面;④EF∥平面ABCD.其中一定正确的有( )A.①②B.②③C.②④D.①④[答案] D[解析] 如图所示.由于AA1⊥平面A1B1C1D1,EF⊂平面A1B1C1D1,则EF⊥AA1,所以①正确;当E,F分别是线段A1B1,B1C1的中点时,EF ∥A1C1,又AC∥A1C1,则EF∥AC,所以③不正确;当E,F分别不是线段A1B1,B1C1的中点时,EF与AC异面,所以②不正确;由于平面A1B1C1D1∥平面ABCD,EF⊂平面A1B1C1D1,所以EF∥平面ABCD,所以④正确.8.设a,b为两条不重合的直线,α,β为两个不重合的平面,下列命题中为真命题的是( )A.若a,b与α所成的角相等,则a∥bB.若a∥α,b∥β,α∥β,则a∥bC.若a⊂α,b⊂β,a∥b,则α∥βD.若a⊥α,b⊥β,α⊥β,则a⊥b[答案] D[解析] 选项A 中,a ,b 还可能相交或异面,所以A 是假命题;选项B 中,a ,b 还可能相交或异面,所以B 是假命题;选项C 中,α,β还可能相交,所以C 是假命题;选项D 中,由于a ⊥α,α⊥β,则a ∥β或a ⊂β,则β内存在直线l ∥a ,又b ⊥β,则b ⊥l ,所以a ⊥b .9.(2012·大纲版数学(文科))已知正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为BB 1、CC 1的中点,那么直线AE 与D 1F 所成角的余弦值为( )A .-45D.35 C.34D .-35[命题意图] 本试题考查了正方体中异面直线的所成角的求解的运用.[答案] D[解析] 首先根据已知条件,连接DF ,然后则∠DFD 1即为异面直线所成的角,设边长为2,则可以求解得到5=DF =D 1F ,DD 1=2,结合余弦定理得到结论.10.如图,在三棱柱ABC -A ′B ′C ′中,点E ,F ,H ,K 分别为AC ′,CB ′,A ′B ,B ′C ′的中点,G 为△ABC 的重心,从K ,H ,G ,B ′中取一点作为P ,使得该三棱柱恰有2条棱与平面PEF 平行,则点P 为( )A.K B.HC.G D.B′[答案] C[解析] 应用验证法:选G点为P时,EF∥A′B′且EF∥AB,此时恰有A′B′和AB平行于平面PEF,故选C.11.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD .平面ADC ⊥平面ABC [答案] D[解析] 由平面图形易知∠BDC =90°.∵平面ABD ⊥平面BCD ,CD ⊥BD ,∴CD ⊥平面ABD .∴CD ⊥AB .又AB ⊥AD ,CD ∩AD =D ,∴AB ⊥平面ADC .又AB ⊂平面ABC ,∴平面ADC ⊥平面ABC .12.(2013·全国卷)已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,则CD 与平面BDC 1所成角的正弦值等于( )A.23B.33C.23D.13[答案] A[解析] 如图,连接AC 交BD 于点O ,连接C 1O ,过C 作CH ⊥C 1O 于点H ,⎭⎪⎬⎪⎫BD ⊥ACAA 1⊥BD AC ∩AA 1=A ⇒⎭⎪⎬⎪⎫BD ⊥面ACC 1A 1CH ⊂面ACC 1A 1⇒⎭⎪⎬⎪⎫BD ⊥HCOC 1⊥HC BD ∩OC 1=0⇒CH ⊥面BDC 1,∴∠HDC 为CD 与面BDC 1所成的角, 设AA 1=2AB =2,OC =22,CC 1=2,OC 1=322,CH =OC ·CC 1OG =23,∴sin ∠HDC =CH CD =23,故选A.二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)13.直线l与平面α所成角为30°,l∩α=A,m⊂α,A∉m,则m与l所成角的取值范围是________.[答案] [30°,90°][解析] 直线l与平面α所成的30°的角为m与l所成角的最小值,当m在α内适当旋转就可以得到l⊥m,即m与l所成角的最大值为90°.14.正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于________.[答案] 45°[解析] 如图所示,正方体ABCD-A1B1C1D1中,由于BC⊥AB,BC1⊥AB,则∠C1BC是二面角C1-AB-C的平面角.又△BCC1是等腰直角三角形,则∠C1BC=45°.15.设平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD 交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=________.[答案] 9[解析] 如下图所示,连接AC,BD,则直线AB ,CD 确定一个平面ACBD . ∵α∥β,∴AC ∥BD ,则AS SB =CS SD ,∴86=12SD,解得SD =9. 16.(2013·高考安徽卷)如图正方体ABCD -A 1B 1C 1D 1,棱长为1,P 为BC 中点,Q 为线段CC 1上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是________.(写出所有正确命题的编号)①当0<CQ <12时,S 为四边形②当CQ =12时,S 为等腰梯形③当CQ =34时,S 与C 1D 1交点R 满足C 1R 1=13④当34<CQ <1时,S 为六边形⑤当CQ =1时,S 的面积为62.[答案] ①②③⑤[解析] 设截面与DD 1相交于T ,则AT ∥PQ ,且AT =2PQ ⇒DT =2CQ . 对于①,当0<CQ <12时,则0<DT <1,所以截面S 为四边形,且S为梯形,所以为真.对于②,当CQ =12时,DT =1,T 与D 重合,截面S 为四边形APQO 1,所以AP =D 1Q ,截面为等腰梯形,所以为真.对于③,当CQ =34,QC 1=14,DT =2,D 1T =12,利用三角形相似解得,C 1R 1=13,所以为真.对于④,当34<CQ <1时,32<DT <2,截面S 与线段A 1D 1,D 1C 1相交,所以四边形S 为五边形,所以为假.对于⑤,当CQ =1时,Q 与C 1重合,截面S 与线段A 1D 1相交于中点G ,即即为菱形APC 1G ,对角线长度为2和3,S 的面积为62,所以为真,综上,选①②③⑤.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)如右图,在三棱柱ABC-A1B1C1中,△ABC 与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.求证:(1)平面AB1F1∥平面C1BF;(2)平面AB1F1⊥平面ACC1A1.[分析] 本题可以根据面面平行和面面垂直的判定定理和性质定理,寻找使结论成立的充分条件.[证明] (1)在正三棱柱ABC-A1B1C1中,∵F、F1分别是AC、A1C1的中点,∴B1F1∥BF,AF1∥C1F.又∵B1F1∩AF1=F1,C1F∩BF=F,∴平面AB1F1∥平面C1BF.(2)在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∴B1F1⊥AA1.又B1F1⊥A1C1,A1C1∩AA1=A1,∴B1F1⊥平面ACC1A1,而B1F1⊂平面AB1F1,∴平面AB1F1⊥平面ACC1A1.18.(本小题满分12分)如下图所示,在四棱锥P-ABCD中,PA ⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.(1)证明:CD⊥平面PAE;(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.[解析] (1)如下图所示,连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5.又AD=5,E是CD的中点,所以CD⊥AE.∵PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD.而PA,AE是平面PAE内的两条相交直线,所以CD⊥平面PAE.(2)过点B作BG∥CD,分别与AE,AD相交于F,G,连接PF.由(1)CD ⊥平面PAE 知,BG ⊥平面PAE .于是∠BPF 为直线PB 与平面PAE 所成的角,且BG ⊥AE .由PA ⊥平面ABCD 知,∠PBA 为直线PB 与平面ABCD 所成的角.AB =4,AG =2,BG ⊥AF ,由题意,知∠PBA =∠BPF , 因为sin ∠PBA =PA PB ,sin ∠BPF =BFPB,所以PA =BF .由∠DAB =∠ABC =90°知,AD ∥BC ,又BG ∥CD ,所以四边形BCDG 是平行四边形,故GD =BC =3.于是AG =2.在Rt △BAG 中,AB =4,AG =2,BG ⊥AF ,所以BG =AB 2+AG 2=25,BF =AB 2BG =1625=855.于是PA =BF =855.又梯形ABCD 的面积为S =12×(5+3)×4=16,所以四棱锥P -ABCD 的体积为V =13×S ×PA =13×16×855=128515. 19.(本小题满分12分)如图所示,边长为2的等边△PCD 所在的平面垂直于矩形ABCD 所在的平面,BC =22,M 为BC 的中点.(1)证明:AM ⊥PM ;(2)求二面角P -AM -D 的大小.[解析] (1)证明:如图所示,取CD 的中点E ,连接PE ,EM ,EA ,∵△PCD 为正三角形,∴PE ⊥CD ,PE =PD sin ∠PDE =2sin60°= 3. ∵平面PCD ⊥平面ABCD ,∴PE ⊥平面ABCD ,而AM ⊂平面ABCD ,∴PE ⊥AM . ∵四边形ABCD 是矩形,∴△ADE ,△ECM ,△ABM 均为直角三角形,由勾股定理可求得EM =3,AM =6,AE =3,∴EM 2+AM 2=AE 2.∴AM ⊥EM .又PE ∩EM =E ,∴AM ⊥平面PEM ,∴AM ⊥PM . (2)解:由(1)可知EM ⊥AM ,PM ⊥AM , ∴∠PME 是二面角P -AM -D 的平面角.∴tan ∠PME =PE EM =33=1,∴∠PME =45°.∴二面角P -AM -D 的大小为45°.20.(本小题满分12分)如图,几何体E-ABCD是四棱锥,△ABD 为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.[解析] (1)设BD中点为O,连接OC,OE,如图,则由BC=CD 知,CO⊥BD,又已知CE⊥BD,所以BD⊥平面OCE.所以BD⊥OE,即OE是BD的垂直平分线,所以BE=DE.(2)取AB中点N,连接MN,DN,∵M是AE的中点,∴MN∥BE,∵△ABD是等边三角形,∴DN⊥AB.由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即BC⊥AB,所以ND∥BC,所以平面MND∥平面BEC,故DM∥平面BEC.21.(本小题满分12分)如图,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.(1)证明:平面AB1C⊥平面A1BC1;(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D DC1的值.[解析] (1)因为侧面BCC1B1是菱形,所以B1C⊥BC1,又已知B1C⊥A1B,且A1B∩BC1=B,所以B1C⊥平面A1BC1,又B1C⊂平面AB1C,所以平面AB1C⊥平面A1BC1 .(2)设BC1交B1C于点E,连接DE,则DE是平面A1BC1与平面B1CD 的交线.因为A1B∥平面B1CD,A1B⊂平面A1BC1,平面A1BC1∩平面B1CD=DE,所以A1B∥DE.又E是BC1的中点,所以D为A1C1的中点.即A1D DC1=1.22.(本小题满分12分)(2013·全国新课标卷Ⅰ)如图三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,(1)证明AB ⊥A 1C ;(2)若AC 1=6,AB =CB =2,求三棱柱ABC -A 1B 1C 1的体积S . [命题意图] 本题主要考查空间线面,线线垂直的判定与性质,及体积的计算,考查空间想象能力,逻辑推理论证能力,属容易题.[解析] (1)取AB 中点E ,连接CE ,A 1B ,A 1E , ∵AB =AA 1,∠BAA 1=60°,∴△BAA 1是等边三角形, ∴A 1E ⊥AB ,∵CA =CB ,∴CE ⊥AB , ∵CE ∩A 1E =E ,∴AB ⊥面CEA 1,∴AB ⊥A 1C .(2)由于△CAB 为等边三角形,∴CE =3,S 底面积=12×AB ×CE =12×2×23=23,A 1E ⊥AB ,A 1E ⊥CE ,∴h =A 1E =3,V =Sh =23×3=6.。
安徽省淮北市2016-2017学年高一数学下学期第二次月考试题

安徽省淮北市2016-2017学年高一数学下学期第二次月考试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|4}A x Z x =∈≤,{|1}B x x =>-,则AB =( )A . {0,1}B .(1,2]-C .{0,1,2}D .{1,0,1}- 2.设{A =小于90的角},{B =第一象限角},则A B =( )A .{锐角}B .{小于90的角}C .{第一象限角}D .{|36036090,0}k k k Z k αα<<+∈≤且3.始边与x 轴正半轴重合,终边所在直线与y 轴夹角为6π的角的集合是( ) A .{|,}6k k Z πααπ=±∈ B .{|,}3k k Z πααπ=±∈C .{|2,}6k k Z πααπ=±∈D .{|2,}3k k Z πααπ=±∈4.要使1()3x g x t +=+的图象不经过第二象限,则t 的取值范围为( )A .1t ≤-B .1t <- C. 3t ≤- D .3t ≥- 5.若08πθ-<<,则sin ,cos ,tan θθθ的大小关系( )A .sin cos tan θθθ<<B .sin tan cos θθθ<< C. tan sin cos θθθ<< D .以上都不是6.一个几何体的三视图如图所示,其表面积为6π,则该几何体的体积为( )A .4πB .2π C.113π D .3π 7.设函数()sin()(0,)22f x x ππωϕωϕ=+>-<<的最小正周期为π,且图象关于直线23x π=对称,则它的一个对称中心的坐标是( )A .(,0)12π-B .(,0)12π C. (,0)6π- D .(,0)6π8.函数cos sin y x x x =+的图象大致为( )A .B .C. D .9.已知sin α是方程25760x x --=的根,且α是第三象限角,则233sin()cos()tan ()22cos()sin()22ππααπαππαα----=-+( ) A .916 B .916- C. 34 D .34-10. AOB ∠如图,O 与x 轴的正半轴交点为A ,点,B C 在O 上,且34(,)55B -,点C 在第一象限,AOC α∠=,1BC =,则5cos()6πα-=( )A .45-B .35- C. 35 D .4511.已知函数()y f x =是(1,1)-上的偶函数,且在区间(1,0)-单调递增,,,A B C 是锐角ABC ∆的三个内角,则下列不等式中一定成立的是( )A .(sin )(cos )f A f A >B .(sin )(cos )f A f B > C. (cos )(sin )fC f B >D .(sin )(cos )f C f B >12.已知函数()y f x =是定义域为R 的偶函数,当0x ≥时,5sin(),0142()1()1,14x x x f x x π⎧≤≤⎪⎪=⎨⎪+>⎪⎩,若关于x 的方程2[()]()0(,)f x af x b a b R ++=∈有且仅有6个不同的实数根,则实数a 的取值范围是( ) A .59(,)24-- B .9(,1)4-- C. 59(,)24--9(,1)4-- D .5(,1)2-- 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知cos()6πα+=5cos()6πα-的值为 . 14.函数()f x =的定义域为 . 15.一圆内切于一圆心角为3π,半径为R 的扇形,则该圆的面积该与扇形的面积之比为 . 16.已知函数sin(0)2a y a π=>在区间(0,1)内至少取得两次最小值,且至多取得三次最大值,则a 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (1)已知角α终边上一点(4,3)P -,求cos()sin()2119cos()sin()22παπαππαα+---+的值. (2)设k 为整数,化简sin()cos[(1)]sin[(1)]cos()k k k k παπαπαπα-+--++.18. 如图,四边形ABCD 为矩形,平面ABCD ⊥平面ABE ,BE BC =,F 为CE 上的一点,且BF ⊥平面ACE .(1)求证:AE BE ⊥; (2)求证://AE 平面BFD .19. 若函数2cos sin y x a x b =-+的最大值为0,最小值为-4,试求a 与b 的值,并求使y 取得最大值和最小值时的x 值.20. 设函数()f x 的定义域是(0,)+∞,且对任意的正实数,x y 都有()()()f xy f x f y =+恒成立,已知(2)1f =,且1x >时,()0f x >.(1)求1()2f 的值;(2)判断()y f x =在(0,)+∞上的单调性,并给出你的证明; (3)解不等式2()(86)1f x f x >--. 21. 已知圆22:2430C x y x y ++-+=.(1)若圆C 的切线在x 轴和y 轴上的截距相等,求此切线的方程;(2)从圆C 外一点11(,)P x y 向该圆引一条切线,切点为M ,O 为坐标原点,且有||||PM PO =,求使得||PM 取得最小值的点P 的坐标.22.定义在D 上的函数()f x ,如果满足:对任意x D ∈,存在常数0M >,都有|()|f x M ≤成立,则称()f x 是D 上的有界函数,其中D 称为()f x 的上界,已知函数11()1()()24xxf x a =++.(1)当1a =时,求函数()f x 在(,0)-∞上的值域,并判断函数()f x 在(,0)-∞上是否有上界,请说明理由;(2)若函数()f x 在[0,)+∞上是以3为上界的有界函数,求实数a 的取值范围.淮北一中2016-2017学年高一下学期答案和解析【答案】1.C2.D3.B4.C5.C6.D7.A8.D9.B 10.A 11.C 12.C13. 3-14. [2,)[,)242πππ-- 15.2:3 16. (7,13]17.解:(1)∵角α终边上一点(4,3)P -, ∴4x =-,3y =,||5r OP ==,3sin 5y r α==,4cos 5x r α==-, ∴cos()sin()sin sin sin sin sin 32119sin cos cos 4cos()sin()cos()sin()2222παπααααααππππααααααα+----====---+++. (2)因为()[(1)]2k k k παπαππ-+-+=-,k Z ∈()[(1)]2k k k παπαππ+++-=+,k Z ∈原式=sin()cos[(1)]sin[(1)]cos()k k k k παπαπαπα-+--++sin cos 1sin (cos )αααα==-- 18.解:(1)证明:∵平面ABCD ⊥平面ABE ,平面ABCD 平面ABE AB =,AD AB ⊥,∴AD ⊥平面ABE ,AD AE ⊥. ∵//AD BC ,则BC AE ⊥. 又BF ⊥平面ACE ,则BF AE ⊥. ∵BCBF B=,∴AE ⊥平面BCE ,∴AE BE ⊥.(2)设AC BD G =,连接FG ,易知G 是AC 的中点,∵BF ⊥平面ACE ,则BF CE ⊥. 而BC BE =,∴F 是EC 中点. 在ACE ∆中,//FG AE ,∵AE ⊄平面BFD ,FG ⊂平面BFD ,∴//AE 平面BFD .19.解:2()cos sin f x y x a x b ==-+ 2sin sin 1x a x b =--++22(sin )124a a xb =-++++,令sin t x =,11t -≤≤ ,则22()124a a y tb =-++++,(i )当12a≤-,即2a ≤-时,min max(1)4(1)0y f a b y f b a =-=+=-⎧⎨==-=⎩,解得22a b =-⎧⎨=-⎩,(ii )当102a-<-≤,即02a ≤<时 2max min()1024(1)4a a y f b y f b a ⎧==++=⎪⎨⎪==-=-⎩解得22a b =⎧⎨=-⎩(舍去)或610a b =-⎧⎨=-⎩(舍去)(iii )当012a<-<,即20a -<<时, 2max min()1024(1)4a a y f b y f b a ⎧==++=⎪⎨⎪=-=+=-⎩解得22a b =-⎧⎨=-⎩(舍)或610a b =⎧⎨=-⎩(舍)(iv )当12a-≤-,即2a ≥时, max (1)0y f a b =-=+=,max (1)4y f b a ==-=- 解得22a b =⎧⎨=-⎩,综上,22a b =⎧⎨=-⎩,22a b =-⎧⎨=-⎩∴当2,2a b ==-时,22()cos 2sin 2(sin 1)f x x x x =--=-+ 若2()2x k k Z ππ=+∈时, y 取得最小值;若2()2x k k Z ππ=-+∈时,y 取得最大值.当2,2a b =-=-时, 22()cos 2sin 2(sin 1)f x x x x =+-=-- 若2()2x k k Z ππ=-+∈, y 取得最小值;若2()2x k k Z ππ=+∈时, y 取得最大值.20.解:(1)令1x y ==,则可得(1)0f =, 再令12,2x y ==,得1(1)(2)()2f f f =+,故1()12f =- (2)设120x x <<,则2121()()()x f x f f x x += 即2211()()()x f x f x f x -=, ∵211x x >,故21()0x f x >,即21()()f x f x >,故()f x 在(0,)+∞上为增函数(3)由2()(86)1f x f x >--得211()(86)()[(86)]22f x f x f f x >-+=-,故得243x x >-且860x ->,解得解集为3{|13}4x x x <<>或. 21.解:(1)∵切线在两坐标轴上的截距相等, ∴当截距不为零时,设切线方程为x y a +=, 又∵圆22:(1)(2)2C x y ++-=,∴圆心(1,2)C -,= 解得:1a =-或3a =, 当截距为零时,设y kx =,同理可得2k =+2k =-则所求切线的方程为10x y ++=或30x y +-=或(2y x =+或(2y x =. (2)∵切线PM 与半径CM 垂直, ∴222||||||PM PC CM =-.∴22221111(1)(2)x y x y ++-=+.∴112430x y -+=.∴动点P 的轨迹是直线2430x y -+=.∴||PM 的最小值就是||PO 的最小值.而||PO 的最小值为原点O 到直线2430x y -+=的距离10d =, ∴由2211119202430x y x y ⎧+=⎪⎨⎪-+=⎩,可得1131035x y ⎧=-⎪⎪⎨⎪=⎪⎩故所求点P 的坐标为33(,)105P -. 22.解:(1)当1a =时,11()1()()24xxf x =++, 令1(),12xt t =>,则2213()()1()24f xg t t t t ==++=++, ∵()g t 在(1,)+∞上单调递增,∴()(1)g t g >, 即()f x 在(,0)-∞上的值域为(3,)+∞, 故不存在常数0M >,使|()|f x M ≤成立, 所以函数()f x 在(,1)-∞上不是有界函数. (2)由题意知,|()|3f x ≤在[0,)+∞上恒成立. ∴3()3f x -≤≤,1114()()2()424xxxa --≤≤-,∴1142()22()22xx x x a --≤≤-在[0,)+∞上恒成立,即max min 11[42()][22()]22x x xx a --≤≤-,设2xt =,则1142t a t t t --≤≤-,设1()4h t t t =--,1()2p t t t=-,由[0,)x ∈+∞ 得 1t ≥.设121t t ≤<, 则21121212()(41)()()0t t t t h t h t t t ---=>,12121212()(21)()()0t t t t p t p t t t -+-=<,所以,()h t 在[1,)+∞上递减,()p t 在[1,)+∞上递增,故()h t 在[1,)+∞上的最大值为(1)5h =-,()p t 在[1,)+∞上的最小值为(1)1p =, 所以实数a 的取值范围为[5,1]-.2016-2017学年高一下学期答案和解析【答案】1.C2.D3.B4.C5.C6.D7.A8.D9.B10.A 11.C 12.C13.-14.15.2:316.(7,13]17.解:(1)∵角α终边上一点P(-4,3),∴x=-4,y=3,r=|OP|=5,sinα==,cosα==-,∴====-.(2)因为原式==-118.解:(1)证明:∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,AD⊥AB,∴AD⊥平面ABE,AD⊥AE.∵AD∥BC,则BC⊥AE.(3分)又BF⊥平面ACE,则BF⊥AE.∵BC∩BF=B,∴AE⊥平面BCE,∴AE⊥BE.(7分)(2)设AC∩BD=G,连接FG,易知G是AC的中点,∵BF⊥平面ACE,则BF⊥CE.而BC=BE,∴F是EC中点.(10分)在△ACE中,FG∥AE,∵AE⊄平面BFD,FG⊂平面BFD,∴AE∥平面BFD.(14分)19.解:f(x)=y=cos2x-asinx+b=-sin2x-asinx+b+1=-+令t=sinx,,则y=-(t+)+,(i)当,即时,,解得(ii)当,即0a<2时解得(舍去)或(舍去)(iii)当,即-2<a<0时,解得(iv)当,即时,y max=f(-1)=a+b=0,y min=f(1)=b-a=-4解得,综上,,∴当a=2,b=-2时,f(x)=cos2x-2sinx-2=-(sinx+1)2,若时,y取得最小值;若时,y取得最大值.当a=-2,b=-2时,f(x)=cos2x+2sinx-2=-(sinx-1)2,若,y取得最小值;若时,y取得最大值.20.解:(1)令x=y=1,则可得f(1)=0,再令x=2,y=,得f(1)=f(2)+f(),故f()=-1(2)设0<x1<x2,则f(x1)+f()=f(x2)即f(x2)-f(x1)=f(),∵>1,故f()>0,即f(x2)>f(x1)故f(x)在(0,+∞)上为增函数(3)由f(x2)>f(8x-6)-1得f(x2)>f(8x-6)+f()=f[(8x-6)],故得x2>4x-3且8x-6>0,解得解集为{x|<x<1或x>3}.21.解:(1)∵切线在两坐标轴上的截距相等,∴当截距不为零时,设切线方程为x+y=a,又∵圆C:(x+1)2+(y-2)2=2,∴圆心C(-1,2)到切线的距离等于圆的半径,即,解得:a=-1或a=3,当截距为零时,设y=kx,同理可得或,则所求切线的方程为x+y+1=0或x+y-3=0或或.(2)∵切线PM与半径CM垂直,∴|PM|2=|PC|2-|CM|2.∴(x1+1)2+(y1-2)2-2=x12+y12.∴2x1-4y1+3=0.∴动点P的轨迹是直线2x-4y+3=0.∴|PM|的最小值就是|PO|的最小值.而|PO|的最小值为原点O到直线2x-4y+3=0的距离,∴由,可得故所求点P的坐标为.22.解:(1)当a=1时,f(x)=1++,令t=t>1,则f(x)=g(t)=t2+t+1=+,∵g(t)在(1,+∞)上单调递增,∴g(t)>g(1),即f(x)在(-∞,0)上的值域为(3,+∞),故不存在常数M>0,使|f(x)|≤M成立,所以函数f(x)在(-∞,1)上不是有界函数.(2)由题意知,|f(x)|≤3在[0,+∞)上恒成立.∴-3≤f(x)≤3,-4-≤a•≤2-,∴-4•2x-≤a≤2•2x-在[0,+∞)上恒成立,即[-4•2x-]max≤a≤[2•2x-]min,设2x=t,则-4t-≤a≤2t-,设h(t)=-4t-,p(t)=2t-,由x∈[0,+∞)得t≥1.设1≤t1<t2,则h(t1)-h(t2)=>0,p(t1)-p(t2)=<0,所以,h(t)在[1,+∞)上递减,p(t)在[1,+∞)上递增,故h(t)在[1,+∞)上的最大值为h(1)=-5,p(t)在[1,+∞)上的最小值为p(1)=1,所以,实数a的取值范围为[-5,1]。
月考02 第二章综合测试卷(A卷)-2016-2017学年高一数学同步单元双基双测“AB”卷(解析版)

班级 姓名 学号 分数(测试时间:120分钟 满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知向量(2,1)a =- ,(1,7)b =,则下列结论正确的是( )A .a b ⊥B .//a bC .()a a b ⊥+D .()a a b ⊥-【答案】C 【解析】因)6,3(=+,)8,1(-=-,故066)(=-=+⋅.所以应选C. 2.平面向量a 与b 的夹角为60°,()2,0,1a b == ,则2a b +等于( )A ..4 C .12 D .16 【答案】A 【解析】222224424412cos 6012a b a b a b +=++⋅=++⨯⨯⨯=,因此2a b +=,选A.3.已知向量,a b 的夹角为120°,且2,3a b ==,则向量23a b +在向量2a b +方向上的投影为( )A B C 【答案】A 【解析】4.已知向量()3,2=a ,()2,1-=b ,若b a m 4+与b a 2-共线,则m 的值为( )1.2A .2B 1.2C - .2D - 【答案】D【解析】)83,42(4+-=+m m m ,()1,42-=-,由于m 4+与2-共线,()()834421+=--∴m m ,解得2-=m ,故答案为D.5.已知向量)2,1(),3,2(-==b a ,若n m +与2-共线,则=nm( ) A .21 B .2 C .-21D .2- 【答案】C 【解析】231-2≠,所以a 与b不共线,那么当n m +与2-共线时,21-=n m ,即得21-=n m ,故选C. 6.在平面直角坐标系x y O 中,已知四边形CD AB 是平行四边形,()1,2AB =- ,()D 2,1A =,则D C A ⋅A =( )A .2B .3C .4D .5 【答案】D7.b a ,2,且a b a ⊥+)(,则与的夹角为( ) A .30° B.60° C.120° D.150° 【答案】C【解析】由⊥+)(知,()a b a +⋅ =2a a b +⋅ =0,所以2a b a ⋅=- =-1,所以cos ,a b =||||a b a b ⋅=12-,所以与的夹角为 120,故选C.8.圆O 为△ABC 的外接圆,半径为2,若 AB + AC =2 AO ,且| OA |=| AC |,则向量 BA 在向量BC 方向上的投影为( )A .1 B.2 C.3 D.4 【答案】C【解析】∵ AB + AC =2 AO ,∴O 是BC 的中点,故△ABC 为直角三角形.在△AOC 中,有| OA |=|AC |,∴∠B =30°.由定义,向量 BA 在向量 BC 方向上的投影为| BA |cos ∠B==3.9.已知点()1,3A ,()4,1B -,则与AB同方向的单位向量是( ) A . 34,55⎛⎫-⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭ C . 34,55⎛⎫- ⎪⎝⎭ D . 43,55⎛⎫- ⎪⎝⎭【答案】A.【解析】因为点()1,3A ,()4,1B -,所以)4,3(-=→AB ,5=→AB ,所以与AB同方向的单位向量为)54,53(5)4,3(-=-=→→ABAB ,故应选A. 10.已知向量,a b 的夹角为60︒,且1,2=a a ,则=b ( ) A .1BCD .2【答案】A 【解析】由22222|2|4||4||44||||cos 60||42||||3a b a a b b a b b b b -=-⋅+=-︒+=-+= ,解得||1b =,故选A . 11.已知两个单位向量,a b 的夹角为60,且满足()a a b λ⊥- ,则实数λ的值为( )A .-2B .2 CD .1 【答案】B12.在△ABC 中,E ,F 分别在边AB ,AC 上,D 为BC 的中点,2||||||===AC FA EB ,0=⋅DF DE ,则 cos A = ( ) A .0 B .23 C .43 D .169【答案】D【解析】如图,根据已知条件得:AC AB BE DB DE )(21-=--=+=+=;AB AC CF DC DF )(21-=--=+=+=(--⋅-=⋅0=+⋅+-=;cosA=169.故选D .第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知点O 是边长为1的正三角形ABC 的中心,则OB OC ∙=.【答案】16- 【解析】由正三角形的性质可知,,OB OC <>= 所以21cos 36OB OC π⋅==- .14.已知平面向量1)3(2,a m =+,()2b m=,,且a b ∥,则实数m 的值等于 .【答案】2m =-或3215.已知向量1,-()()16,-4a b ==,.若()a tab ⊥+ ,则实数t 的值为________. 【答案】5- 【解析】()()()()6,4,6,41,12100ta b t t ta b a t t t +=+--+⋅=+--⋅-=+=,解得5t =-16. 已知向量,a b 满足||1a = ,||b = a b += .则cos(,)a b =___________。
(人教版A版)高中数学必修第一册 第二章综合测试试卷02及答案
第二章综合测试一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知,,a b c ÎR ,那么下列命题中正确的是( )A .若a b >,则22ac bc >B .若a bc c>,则a b>C .若33a b >,且0ab <,则11a b >D .若22a b >,且0ab >,则11a b<2.如果a ÎR ,且20a a +<,那么2,,a a a -的大小关系为( )A .2a a a ->>B .2a a a ->>C .2a a a ->>D .2a a a->>3.若函数14(2)2y x x x =+-->,则函数y 有( )A .最大值0B .最小值0C .最大值2-D .最小值2-4.不等式1021x x -+的解集为( )A .1|12x x ìü-íýîþ<≤B .1|12x x ìü-íýîþ≤C .1| 12x x x ìü-íýîþ<或≥D .1|| 12x x x x ìü-íýîþ≤或≥5.若不等式220ax bx ++<的解集为11|| 23x x x x ìü-íýîþ<或>,则a b a -的值为( )A .16B .16-C .56D .56-6.若不等式()(2)3x a x a a --->对任意实数x 都成立,则实数a 的取值范围是( )A .(1,3)-B .(3,1)-C .(2,6)-D .(6,2)-7.若0,0a b >>,且4a b +=,则下列不等式恒成立的是( )A .114ab B .111a b+≤C 2D .228a b +≥8.不等式3112x x--≥的解集是( )A .3|24x x ìüíýîþ≤B .3|24x x ìüíýîþ≤<C .3| 24x x x ìüíýîþ≤或>D .{|2}x x <9.若命题“0x $ÎR ,使得200230x mx m ++-<”为假命题,则实数m 的取值范围是( )A .26m ≤≤B .62m --≤≤C .26m <<D .62m --<<10.若正数,x y 满足35x y xy +=,则34x y +的最小值是( )A .245B .285C .5D .611.已知210a +<,关于x 的不等式22450x ax a -->的解集是( )A .{|5 }x x a x a -<或>B .{|5 }x x a x a ->或<C .{|5}x a x a -<<D .{|5}x a x a -<<12.某厂以x 千克/时的速度匀速生产某种产品(生产条件要求110x ≤≤),每小时可获得的利润是310051x x æö+-ç÷èø元.若使生产该产品2小时获得的利润不低于3 000元,则x 的取值范围为( )A .{|3}x x ≥B .1| 35x x x ìü-íýîþ≤或≥C .{|310}x x ≤≤D .{|13}x x ≤≤二、填空题(本大题共4小题,每小题5分,共20分.把答案写在题中的横线上)13.若1x ->,则当且仅当x =________时,函数111x x y +++=的最小值为________.14.若不等式20x ax b ++<的解集为{}|12x x -<<,则不等式210bx ax ++<的解集为________.15.已知,x y +ÎR ,且满足22x y xy +=,那么34x y +的最小值为________.16.若x ÎR ,不等式224421ax x x ++-+≥恒成立,则实数a 的取值范围是________.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.[10分]已知不等式2340x x --<的解集为A ,不等式260x x --<的解集为B .(1)求A B I ;(2)若不等式20x ax b ++<的解集为A B I ,求,a b 的值.18.[12分]已知命题p :方程210x mx ++=有两个不相等的实根,命题p 是真命题.(1)求实数m 的取值集合M ;(2)设不等式()(2)0x a x a ---<的解集为N ,若x N Î是x M Î的充分条件,求a 的取值范围.19.[12分](1)若0,0x y >>,且281x y+=,求xy 的最小值;(2)已知0,0x y >>满足21x y +=,求11x y+的最小值.20.[12分]要制作一个体积为39m ,高为1m 的有盖长方体容器,已知该容器的底面造价是每平方米10元,侧面造价是每平方米5元,盖的总造价为100元.求该长方体容器的长为多少时总造价最低,最低为多少元?21.[12分]已知,,a b c 均为正实数.求证:(1)()2()4a b ab c abc ++≥;(2)若3a b c ++=+.22.[12分]设2()1g x x mx =-+.(1)若()0g x x对任意0x >恒成立,求实数m 的取值范围;(2)讨论关于x 的不等式()0g x ≥的解集.第二章综合测试答案解析一、1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】A 5.【答案】C 6.【答案】D 7.【答案】D 8.【答案】B 9.【答案】A 10.【答案】C【解析】由35x y xy +=可得13155y x+=,所以139431213131234(34)5555555555x y x y x y y x y x æö+=++=++++=+=ç÷èø,当且仅当31255x yy x =且35x y xy +=,即1x =,12y =时取等号.故34x y +的最小值是5.11.【答案】A【解析】方程22450x ax a --=的两根为,5a a -.1210,,52a a a a +\-\-Q <<>.结合2245y x ax a =--的图像,得原不等式的解集是{|5 }x x a x a -<或>.12.【答案】C【解析】根据题意,得3200513000x x æö+-ç÷èø≥,整理,得35140x x --≥,即251430x x --≥.又110x ≤≤,可解得310x ≤≤.即要使生产该产品2小时获得的利润不低于3000元,x 的取值范围是|310{}x x ≤≤.二、13.【答案】0214.【答案】1| 1 2x x x ìü-íýîþ<或>15.【答案】5+16.【答案】2|3a a ìü-íýîþ≥【解析】不等式224421ax x x ++-+≥恒成立2(2)430a x x Û+++≥恒成立220443(2)0a a +>ìïÛí-´´+ïî≤23a Û-≥,故实数a 的取值范围是2|3a a ìü-íýîþ≥.三、17.【答案】(1)解:{|14},{|23}A x x B x x =-=-<<<<,{|13}A B x x \Ç=-<<.(2)解:Q 不等式20x ax b ++<的解集为{|13}x x -<<,1,3\-为方程20x ax b ++=的两根.10,930,a b a b -+=ì\í++=î2,3.a b =-ì\í=-î18.【答案】(1)解:命题p :方程210x mx ++=有两个不相等的实根,所以240m D =->,解得2m >或2m -<.所以{| 2 2}M m m m =->或<.(2)解:因为x N Î是x M Î的充分条件,所以N M Í.因为{|2}N x a x a =+<<,所以22a +-≤或2a ≥,所以4a -≤或2a ≥.19.【答案】(1)解:0,0x y Q >>且281x y+=,281x y \=+=≥,8,当且仅当82x y =且281x y+=即4x =,16y =时取等号.64xy \≥..故xy 的最小值是64.(2)解:0,0,21x y x y >>+=Q11112(2)1233x y x y x y x y y x æö\+=++=++++=+ç÷èø≥当且仅当x =且21x y +=.即x =,y =.故11x y+的最小值是3+20.【答案】解:设该长方体容器的长为m x ,则宽为9m x.又设该长方体容器的总造价为y 元,则9991021510019010y x x x x æöæö=´++´´+=++ç÷ç÷èøèø.因为96x x +=≥(当且仅当9x x =即3x =时取“=”).所以min 250y =.即该长方体容器的长为3m 时总造价最低,最低为250元.答:该长方体容器的长为3m 时总造价最低,最低为250元.21.【答案】(1)证明:因为,,a b c 均为正实数,由基本不等式得a b +≥,2ab c +≥,两式相乘得()2()4a b ab c abc ++≥,当且仅当a b c ==时取等号.所以()2()4a b ab c abc ++≥..(2)解:因为,,a b c 12322a a +++=,当且仅当12a +=时取等号;12322b b +++=,当且仅当12b +=时取等号;12322c c +++=.当且仅当12c +=时取等号.以上三式相加,得962a b c ++++=≤,当且仅当1a b c ===时取等号.22.【答案】(1)解:由题意,若()0g x x≥对任意0x >恒成立,即为10x m x-+对0x >恒成立,即有1(0)m x x x+≤>的最小值.由12(0)x x x +≥>,可得1x =时,1x x+取得最小值2.所以2m ≤.(2)解:2()1g x x mx =-+对应的一元二次方程为210x mx -+=.当240m D =-≤,即22m -≤≤时,()0g x ≥的解集为R ;当0D >,即2m >或2m -<时,方程的两根为x =可得()0g x ≥的解集为|x x x ìïíïî.。
【数学】高一数学上学期12月月考试题A卷
【关键字】数学莆田第六中2016-2017学年高一12月月考A卷数学试卷(时间120分钟,满分150分)第Ⅰ卷一.选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.角的终边过点P(4,-3),则的值为()A.4 B.-.D.2.的值等于()A.B.-C.D.-3.函数的周期,振幅,初相分别是()A.,2,B.,,C.,2,D.,2,4.若,则等于()A.B.C.D.5.函数的定义域为()A.B.C.D.6.计算的值为()A.B.C.D.7.函数在一个周期内的图象如下,此函数的解析式为()A.B.C.D.8.为得到函数的图象,只需将函数的图像()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度9.方程sinπx=x的解的个数是 ( )A.5 B.C.7 D.810.设,,()A.B.C.D.11.函数的最大值为()A .0B .. D .12.若动直线与函数和的图像分别交于两点,则的最大值为 ( )A .1B .C .D .2第Ⅱ卷二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
).13.若,则= .14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是 .15.已知,则的值为 .16.函数的图象为,如下结论中正确的是 (写出所有正确结论的编号).①②③ ①图象关于直线对称;②图象关于点对称;③函数在区间内是增函数;④由的图象向右平移个单位长度可以得到图象.三.解答题:解答应写出文字说明.证明过程或演算步骤17.(本小题满分10分)已知,求函数的值域.18.(本小题满分10分)已知sin 是方程的根,求的值.解:由sin 是方程的根,可得sin= 或sin=2(舍) ∴ sin= -----------4分原式== ------------10分即所求式子的值为 -------------12分19.(本小题满分12分)在平面直角坐标系xoy 中,以x 轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A,B 两点,已知A,B 的横坐标分别为225,105. (Ⅰ)求tan(αβ+)的值;(Ⅱ)求2αβ+的值.【解析】本小题考查三角函数的定义、两角和的正切、二倍角的正切公式.由条件的225cos ,cos 105αβ==,因为α,β为锐角,所以sin α=725,sin 105β=因此1tan 7,tan 2αβ==(Ⅰ)tan(αβ+)= tan tan 31tan tan αβαβ+=--(Ⅱ) 22tan 4tan 21tan 3βββ==-,所以()tan tan 2tan 211tan tan 2αβαβαβ++==--∵,αβ为锐角,∴3022παβ<+<,∴2αβ+=34π20.(本小题满分12分)已知函数2()2sin ()44f x x ππ=+(Ⅰ)把()f x 解析式化为()sin()f x A x b ωφ=++的形式,并用五点法作出函数()f x 在一个周期上的简图;(Ⅱ)计算(1)(2)(2016)f f f ++⋅⋅⋅+的值.解:(Ⅰ)2()2sin ()1cos()1sin .44222f x x x x πππππ=+=-+=+ ……4 分列表:…………………6分描点画图,如下所示………………8分(Ⅱ)(1)(2)(3)(4)21014f f f f +++=+++=. ………………10分而()y f x =的周期为4,20164504=⨯,(1)(2)(2016)45042016.f f f ∴++⋅⋅⋅+=⨯= ………………12 分21.(本小题满分12分)如图,已知正方形ABCD 在直线MN 的上方,边BC 在直线MN 上,E 是线段BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG ,其中AE=2,记∠FEN=α,△EFC 的面积为S.(Ⅰ)求S 与α之间的函数关系;(Ⅱ)当角α取何值时S 最大?并求S 的最大值.解:(Ⅰ)过点F 作FH MN ⊥,H 为垂足由三角知识可证明EAB FEH α∠=∠=,FH BE = ………2 分在Rt ABE ∆中,sin 2sin EB AE αα==所以2s 2sin EC BC EB co αα=-=-………4 分所以FCE ∆的面积 S 1(2s 2sin )2sin 2co ααα=-⋅ 22sin s 2sin co ααα=- ,其中04πα≤≤ ………………………………………6分(Ⅱ)由(Ⅰ)可知22sin s 2sin S co ααα=-sin 2s 212(sin 2)14co πααα=+-=+- …………………9分 由04πα≤≤,得32444ππαπ≤+≤, ∴ 当1242παπ+=,即8πα=时,21S =最大 …………………11分 因此,当8πα=时,EFC ∆的面积S 21. ……………12 分22.(本小题满分14分)已知函数222π()2sin 3(sin cos )4f x x x x ⎛⎫=++- ⎪⎝⎭,ππ42x ⎡⎤∈⎢⎥⎣⎦,. (Ⅰ)求5π12f ⎛⎫ ⎪⎝⎭的值; (Ⅱ)求()f x 的单调区间;(Ⅲ)若不等式()2f x m -<恒成立,求实数m 的取值范围.解:(1)2225ππ5π5π5π2sin 3sin cos 3124121212f ⎛⎫⎛⎫⎫=+-= ⎪ ⎪⎪⎝⎭⎝⎭⎭. ………………3分 (2)π()1cos 2321sin 2322f x x x x x ⎡⎤⎛⎫=-+=+ ⎪⎢⎥⎝⎭⎣⎦π12sin 23x ⎛⎫=+- ⎪⎝⎭. ………………6分 又 ππ42x ⎡⎤∈⎢⎥⎣⎦,, 所以 ππ2π2633x -≤≤, 当πππ2632x -≤≤时,()f x 单调递增; 当ππ2π2233x -≤≤时,()f x 单调递减,所以()f x 的单调递增区间是π5π412⎡⎤⎢⎥⎣⎦,;()f x 的单调递减区间是5ππ122⎡⎤⎢⎥⎣⎦,. …………9分 (3)由(2)得 π212sin 233x ⎛⎫+- ⎪⎝⎭≤≤, 所以 ()f x 的值域是[23],.…………11分 ()2()2()2f x m f x m f x -<⇔-<<+,ππ42x ⎡⎤∈⎢⎥⎣⎦,.…………12分 所以 max ()2m f x >-且 min ()2m f x <+, …………13分所以 14m <<, 即m 的取值范围是(14),. …………14分此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
中学高一数学2月月考试题(扫描版)(2021学年)
河北省蠡县中学2016-2017学年高一数学2月月考试题(扫描版)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河北省蠡县中学2016-2017学年高一数学2月月考试题(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河北省蠡县中学2016-2017学年高一数学2月月考试题(扫描版)的全部内容。
河北省蠡县中学2016-2017学年高一数学2月月考试题(扫描版)以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the whole content ofthis article,Gorky said: "thebook istheladder of humanprogress." I hope you canmake progress with thehelp of this ladder. Material lifeis extremely rich, science and technology are developing rapidly, all of which gradually change the way of people'sstudy and leisure. Many people are nolongereager to pursue a document,butas long as you stillhave such a small persistence,you will continue togrow and progress. When the complex world leadsus to chase out,reading an article or doing aproblem makes us calmdown andreturn to ourselves. With learning,wecan activate ourimagination and thinking, establish our belief, keep ourpure spiritual worldand re sistthe attack of the external world.。
湖北省枣阳市2016_2017学年高一数学下学期2月月测习题
湖北省枣阳市2016-2017学年高一年级下学期2月月考数学试题★祝考试顺利★时间:120分钟分值150分_第I卷(选择题共60分)一、选择题(本大题12小题,每小题5分,共60分)1.值为()A B C D2)A3()A BC.2 D4)A.5A、1B、-1 C D6AC7( )A8,)AB.2 D .-2 9) A.B.C.D.10) A .1 B .-1 C .2 D.-211.123) AC第II 卷(非选择题)二、填空题(本大题共4个小题,每题5分,满分20分)131415.16三、解答题17.(本题1218.(本题1219.(本题12(1(2的最大值及相应20.(10分) 已知函数f (x )=A sin(ωx +φ),x ∈R(其中A >0,ω>0,0<φ的图象与x 轴的交(1)求A ,ω,φ的值.(2)写出函数f (x )图象的对称中心及单调递增区间. (3)当xf (x )的值域. 21.(本题12地段进行市场开发,拟在该地段的一角建设一个景观,,(1(222.(本小题满分13(1(2答案选择:1_5ACCAA 6_10 CAACD 11_12AA填空:1314.115161718.=sin23,即20.(1(2))3)([-1,2])21.(10αβ<+,即(2)由(1)知,tan4π=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级 姓名 学号 分数
(测试时间:120分钟 满分:150分)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量(2,1)a =-,(1,7)b =,则下列结论正确的是( )
A .a b ⊥
B .//a b
C .()a a b ⊥+
D .()a a b ⊥- 【答案】C 【解析】
因)6,3(=+b a ,)8,1(-=-b a ,故066)(=-=+⋅b a a .所以应选C. 2.平面向量与的夹角为60°,()2,0,1a b ==,则2a b +等于( )
A ..4 C .12 D .16 【答案】A 【解析】
222
224424412cos 6012
a b a b a b +=++⋅=++⨯⨯⨯=,因此
223
a b += A.
3.已知向量,a b 的夹角为120°,且2,3a b ==,则向量23a b +在向量2a b +方向上的投影为( )
A B D 【答案】A 【解析】
4.已知向量()3,2=a ,()2,1-=b ,若b a m 4+与b a 2-共线,则m 的值为( )
1.2A .2B 1
.2
C - .2
D - 【答案】D
【解析】)83,42(4+-=+m m m ,()1,42-=-,由于b a m 4+与b a 2-共线,
()()834421+=--∴m m ,解得2-=m ,故答案为D.
5.已知向量)2,1(),3,2(-==b a ,若b n a m +与b a 2-共线,则 )
A . C ..2- 【答案】C 【解析】
,所以与b 不共线,那么当b n a m +与b a 2-共线时,21-2
n C. 6.在平面直角坐标系x y O 中,已知四边形CD AB 是平行四边形,()1,2AB =-,()D 2,1A =,则D C A ⋅A =( )
A .
B .
C .
D . 【答案】D
7.,2,且⊥+)(,则与的夹角为( ) A .30° B.60° C.120° D.150° 【答案】C
【解析】由⊥+)(知,()a b a +⋅=2
a a
b +⋅=0,所以2
a b a ⋅=-=-1,所以cos ,a b =||||
a b
a b ⋅=12-,
所以与的夹角为
120,故选C.
8.圆O 为△ABC 的外接圆,半径为2,若AB +AC =2AO ,且|OA |=|AC |,则向量BA 在向量BC 方向上的投影为( )
A .1 B.2 C.3 D.4 【答案】C
【解析】∵AB +AC =2AO ,∴O 是BC 的中点,故△ABC 为直角三角形.在△AOC 中,有|OA |=|AC |,∴∠B =30°.由定义,向量BA 在向量BC 方向上的投影为|BA |cos ∠B
==3. 9.已知点()1,3A ,()4,1B -,则与AB 同方向的单位向量是( ) A . 34,55⎛⎫-
⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭ C . 34,55⎛⎫
- ⎪⎝⎭ D . 43,55⎛⎫- ⎪⎝⎭
【答案】A.
【解析】因为点()1,3A ,()4,1B -,所以)4,3(-=→
AB ,5=→
AB ,所以与AB 同方向的单位向量为
)5
4
,53(5)4,3(-=-=
→
→AB
AB ,故应选A. 10.已知向量,a b 的夹角为60︒
,且1,2=-=a a b =b ( ) A .1
B
C
D .2
【答案】A 【解析】
由22222
|2|4||4||44||||cos 60||42||||3a b a a b b a b b b b -=-⋅+=-︒+=-+=,解得||1b =,故选A .
11.已知两个单位向量,a b 的夹角为60,且满足()a a b λ⊥-,则实数λ的值为( )
A .-2
B .2 C
.1 【答案】
B
12.在△ABC 中,E ,F 分别在边AB ,AC 上,D 为BC 的中点,2|
||
||
|==
=
AC FA EB ,0=⋅DF DE ,
则 cos A = ( ) A .0 B .23 C .43 D .16
9
【答案】D
【解析】如图,根据已知条件得:
2
1
6131)(213121-=--=+=
+=;
6
1
2132)(213221--=--=+=
+=; )6121()2161(--⋅-=⋅012
1
9212122=+⋅+-=;
把=带入上式并整理得:cosA=169
.
故选D .
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知点O 是边长为1的正三角形ABC 的中心,则OB OC ∙= . 【答案】16
- 【解析】
由正三角形的性质可知,23,,3OB OC OB OC π<>=
==所以321cos 36
OB OC π⋅==-. 14.已知平面向量1)3(2,a m =+,()2b m =,,且a b ∥,则实数m 的值等于 . 【答案】2m =-或
15.已知向量1,-()()16,-4a b ==,.若()
a ta
b ⊥+,则实数t 的值为________.
【答案】5- 【解析】
()()
()()6,4,6,41,12100ta b t t ta b a t t t +=+--+⋅=+--⋅-=+=,解得5t =-
16. 已知向量,a b 满足||1a =,||3b =,(3,1)a b +=.则cos(,)a b =___________。
【答案】
【解析】因||1a =,||3b =且(3,1)a b +=,故422
2
=+⋅+b b a a ,即02=⋅,所以cos(,)a b =0。
故应填0.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分)△ABC 中,∠A=60°,∠A 的平分线AD 交边BC 于D ,已知AB=3,且
,求AD 的长.
【答案】
18.(本小题12分)如图,2,2,,OC OP AB AC OM mOB ON nOA ====,若.
19.(本小题12分)如图,3
AOB π
∠=
,动点12,A A 与12,B B 分别在射线,OA OB 上,且线段12A A 的长为1,
线段12,B B 的长为2,点,M N 分别是线段1122,A B A B 的中点.
(1)用向量12A A 与12B B 表示向量
MN ; (2)求向量MN 的模.
【答案】(1)12121
()2
MN A A B B =
+;(2. 【解析】(1)1122MN MA A A A N =++,1122MN MB B B B N =++两式相加, 并注意到点,M N 分别是线段11A B 、22A B 的中点,得12121
()2
MN A A B B =+, (2)由已知可得向量12A A 与12B B 的模分别为与,夹角为3
π, 所以12121A A B B ⋅=,由12121
()2
MN A A B B =
+得
222
11()2MN A A B B A A B B A A B B =+=++∙=2
.
20.(本小题12分)已知平面内三个向量:(3,2),(1,2),(4,1).a b c ==-= (Ⅰ)若()//(2)a kc b a +-,求实数的值;
(Ⅱ)设(,)d x y =,且满足()()a b d c +⊥-,||5d c -=,求d .
【答案】(Ⅱ)()6,0d =或()2,2. 【解析】
故()6,0d =或()2,2 .
21.(本小题12分)已知向量()1,2a =,()3,4b =-. (1)求a b +与a b -的夹角; (2)若()
a a
b λ⊥+,求实数λ的值.
【答案】(1(2)1-. 【解析】
(1)因为()1,2a =,()3,4b =-,所以()2,6a b +=-,()4,2a b -=-
(2,6,a b a b -+-=
[],0,a b a b π+-∈3,4
a b a b π
+-=
; (2)当()
a a
b λ⊥+时,()
0a a b λ⋅+=,又()13,24a b λλλ+=-+,所以13480λλ-++=,解得:
1λ=-.
22.(本小题12分)已知点(1,0),(0,1)A B -,点(,)P x y 为直线1y x =-上的一个动点. (1)求证:APB ∠恒为锐角;
(2)若四边形ABPQ 为菱形,求BQ AQ ⋅的值. 【答案】(1)证明见解析;(2)2.。
