中学趣味数学:两枚还是三枚
数学趣味小问题

以下是一些数学趣味小问题:
1. 三个小朋友手里的冰淇淋甜筒形状各不相同,分别是3个一排的、2个一排的和1个一排的。
如果3个小朋友每人都有自己的甜筒排成一排,并且没有重叠,那么最多可以同时有多少个冰淇淋甜筒?
2. 你有一块长度为3厘米的木板,准备将其切成两个相等的长度,且每段长度均为整数厘米。
你可以一次完成切割吗?
3. 有两把钥匙和两把锁,这两把钥匙都能开这两把锁,现在随机匹配出一套钥匙和锁进行使用,那么至少需要尝试几次才能成功配对?
4. 有一些珠子,如果三个三个地数,就会剩下两个;如果五个五个地数,就会剩下三个;如果七个七个地数,就会剩下四个。
那么这些珠子至少有多少个?
5. 有一个正方形,它的边长为x,如果边长增加一厘米后,它的面积增加了y平方厘米。
那么y与x之间的函数关系式是什么?
以上问题都具有一定的趣味性,同时也融入了数学原理和概念,希望这些问题能够激发您的思考能力。
数学趣味题(三)

第一种解法:
12 12 4 4 9 9 1 1 6
8 0 8 3 3 0 8 6 6
5 0 0 5 0 3 3 5 0
第二种解法:
12 12 4 0 8 8 3 3 11 11 6 6
8 0 8 8 0 4 4 8 0 1 1 6
其余的小动物听了小狗欢欢和小猴乐乐的话,一起去狐狸家帮助小兔要回亏了的10元
决定了泊松一生道路的数学趣题
泊松(Poisson S.-D,B.,1781.6.21~1840.4.25)是法国数学家,曾任过欧洲许多国家科学院的院士,在积分理论、微分方程、概率论、级数理论等方面都有过较大的贡献。
据说泊松在青年时代研究过一个有趣的数学游戏:
通则:开局是奇数,先取者必胜;反之,若开局为偶数,则先取者会输。
规则四:限制每次所取的火柴数是1或4(一个奇数,一个偶数)。
分析:如前规则二,若甲先取,则甲每次取时留5的倍数的火柴给乙去取,则甲必胜。此外,若甲留给乙取的火柴数为5之倍数加2时,甲也可赢得游戏,因为玩的时候可以控制每轮所取的火柴数为5(若乙取1,甲则取4;若乙取4,则甲取1),最後剩下2根,那时乙只能取1,甲便可取得最後一根而获胜。
? ? 进入20世纪,电子计算机的高速发展方兴未艾,电子计算机的普及和应用在数学领域中也大显身手,电子计算机绘制出的数学图谱更是广泛应用于工艺美术、建筑装饰和自然科学领域。数学上的20棵树植树问题也随之有了更新的进展。在二十世纪七十年代,两位数学爱好者巧妙地运用电子计算机超越数学大师山姆.劳埃德保持的十八行纪录,成功地绘制出了精湛美丽的二十行图谱,创造了20棵树植树问题新世纪的新纪录并保持至今。
初中经典趣味数学题

初中经典趣味数学题本文没有格式错误,但第4段明显有问题,应删除。
1.有27颗珍珠,其中一颗是假的,但外观和真的一样,只是比真的珍珠轻一点。
问:最少用天平称几次(不用砝码),就一定可以把假的珍珠找出来?解答:3次。
第一次把27颗珍珠分成3等份,取其中2份放天平两端称量,如果天平偏斜,则考虑轻的那9颗珍珠,如果不偏斜,则考虑没有称量的那9颗。
同理,将这9颗珍珠再分成3等份,取其中2份放天平两端称量,再次得到3颗“可疑”的珍珠,取出两颗称量,如果天平偏斜,则轻的是次品,否则没称量的是次品。
2.埃及同中国一样,也是世界上著名的文明古国,古代埃及人处理分数与众不同,他们一般只使用分子为1的分数,例如用1/3+1/15表示2/5,用1/4+1/7+1/28来表示3/7等等。
现在用90个埃及分子1/2,1/3,1/4,1/5,……,1/90,其中是否再取10个数,加上正负号后使它们的和为-1.若存在,请写出这10个数,若不存在,请说明理由。
解答:一解:-1=-1/5-1/6-1/8-1/9-1/10-1/12-1/15-1/18-1/20-1/24.二解:1-1/2+1/2-1/3+1/3-1/4+1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10=1-1/10.所以:1/2+1/6+1/12+1/20+1/30+1/42+1/56+1/72+1/90+1/10=1,即:-1/2-1/6-1/12-1/20-1/30-1/42-1/56-1/72-1/90-1/10=-1.3.下诗出于清朝数学家XXX的著作,请算出诗中有多少僧人?巍巍古寺在云中,不知寺内多少僧。
三百六十四只碗,看看用尽不差争。
三人共食一只碗,四人共吃一碗羹。
请问先生明算者,算来寺内几多僧?解答:三人共食一只碗,则吃饭时一人用三分之一个碗,四人共吃一碗羹,则吃羹时一人用四分之一个碗,两项合计,则每人用1/3+1/4=7/12个碗,设共有和尚X人,依题意得:7/12X=364,解之得,X=624.4.本段有问题,应删除。
初中趣味数学知识点归纳大全

初中趣味数学知识点归纳大全数学作为一门理科学科,常常被认为是一门枯燥、乏味的学科,但其实数学也有很多有趣的知识点。
在初中阶段,我们学习的数学知识也有很多有趣的部分,下面将对一些初中趣味数学知识点进行归纳。
1. 无限小数与无理数我们都知道,有些数是可以用分数的形式表示的,比如1/2、2/3等,这些数被称为有理数。
但还有一些数无法用分数的形式精确表示,比如圆周率π、自然对数的底e等,这些数被称为无理数。
无理数的小数表示是无限不循环的,例如π=3.14159...、e=2.71828...,这些小数的位数是无穷的。
2. 黄金比例黄金比例是一种特殊的比例关系,可以用一个特殊的数值表示,即大约等于1.618。
这个比例在建筑、美术、音乐等多个领域都有应用。
而且有趣的是,黄金比例还与斐波那契数列有密切关系,即相邻两个斐波那契数的比趋近于黄金分割。
3. 数学魔术数学魔术是一种结合了数学知识和魔术技巧的表演形式。
通过巧妙的数学计算和推理,可以实现看似不可能的魔术效果,给人们带来惊喜和快乐。
例如,通过奇偶性的变化、数的排列组合等等,展现出奇妙而不可思议的效果。
4. 计数学计数学是一门研究数数特性和计数方法的学科。
在初中阶段,我们常常会遇到各种有趣的计数问题。
例如,有多少种方法将8本书分成两堆,每堆书的数量相同或者差一本?有多少种不同手势可以用五个手指表示?5. 数码根与数的整除性数的数码根是将这个数的各位上的数字相加,直到最后只剩下一个位数。
例如,123的数码根是1+2+3=6。
有趣的是,如果一个数的数码根能被3整除,那么这个数也能被3整除;如果一个数的数码根能被9整除,那么这个数也能被9整除。
6. 罗列法与排列组合初中阶段,我们学习了罗列法和排列组合的知识,它们可以帮助我们解决很多有趣的问题。
例如,在球队十名队员中,选出一名队长和一名副队长的可能性有多少种?一张5元纸币可以由几张1元和几张2元组成?7. 数学游戏数学游戏是一种结合了数学知识和游戏性质的活动形式。
趣味数学100题_(三)
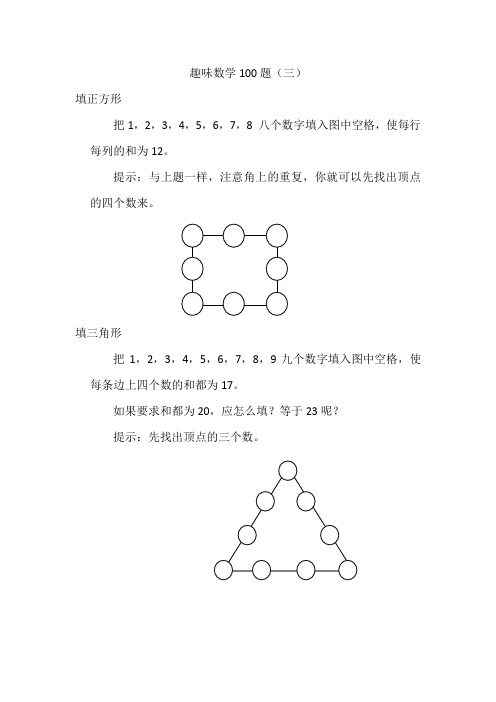
趣味数学100题(三)填正方形把1,2,3,4,5,6,7,8 八个数字填入图中空格,使每行每列的和为12。
提示:与上题一样,注意角上的重复,你就可以先找出顶点的四个数来。
填三角形把1,2,3,4,5,6,7,8,9九个数字填入图中空格,使每条边上四个数的和都为17。
如果要求和都为20,应怎么填?等于23呢?提示:先找出顶点的三个数。
填正六面体把1,2,3,4,5,6,7,8 八个数字填入图中空格,使立方体的任何一个平面上四个数据和都一样。
提示:如果符合题意的话,任何一个平面上的四个数加起来都等于几?花样填数(一)把1,2,3,4,5,6,7,8 八个数字填入图中空格,使每条线(直径或圆周)上的四个数加起来的和都相等。
花样填数(二)把1,2,3,4,5,6,7七个数字填入圆圈,使每条线(半径或圆周)上的三个数加起来的和都相同,有几种可能的填法?乘法填数把1,2,3,4,8,12这六个数字填入圆圈,使每条线上三个数的乘积相等。
填成倍数把1,2,3,4,5,6,7,8,9九个数字填入图中空格。
这样,每一横行的三个数字组成一个三位数。
如果要使第二行的三位数是第一行的两倍,第三行的三位数是第一行的三倍,应怎样填数?有几种填法?把1,2,3,4,5,6填入表格内,要使得每一行右边的数字比左边的数字大,每一列下面的数字比上面的数字大,问有几种填法?51.密码游戏在这张纸上写着一段“密码”。
你要翻译它的话,可以把图上的字抄在方格纸是,再照另一张图画的方框,挖去阴影部分,盖在有字的图上,使箭头向上。
这里你就可以在挖去的方孔里,从左至右,从上至下地念了九个意思连贯的字来。
念完了这九个字,再把纸框顺时针方向转90º,继续念下去,念完再转90º,36个字都念完了,就明白这句“密码”的意思了。
如果你能懂得设计这种纸框和书写“密码”的窍门,当然可以自己另行设计。
52. 24点(四人游戏) 取一副扑克牌,拿去其中J,Q,K,并指定A 代表1。
初中数学趣味数学竞赛课件(共43张)

先考虑两个店主之间的得失,鞋店主先拿假钞去隔壁店主 那里换来两张50元的真钞,后来又赔给隔壁店主100元, 所以双方没得失。所以鞋店主只是损失了一双50元的鞋子 与50元现金。
24.把10个硬币放入三只杯子中,使得每只杯子 中硬币的个数仍都是奇数,请问如何能办得到?
答案:只需要把一个杯子套入另一只杯子之中即可
25. 一辆四轮赛车参加距离比赛,行程18Байду номын сангаас0千米, 轮胎都是新的,每只轮胎在1200千米内有效, 问车上最少应该带几只备用的新轮胎?
答案:2只 当车走了600米时,换下两个轮胎,当走到1200米时, 用之前换下来的两个轮胎去换另外两个轮胎。
26、盒子里有27只球,其中有一只是次品, 这个次品外观上与正品毫无区分,只是分量 略重一些。现在有一架天平,要把次球找出 来,至少要称几次?
答案:后报的取胜
15、请问如何用三根直木棒组成12个直角?
答案:把三根木棒 按东西、南北、上 下三个方位交叉 放置即可组成12个 直角。
16、有一个密封的
长方体水箱(如图)
,如果从里面量得
宽3分米,高5分米,
3
箱内水的高度是4分
米,如果将水箱向
后推倒,以它的后
5
面为底面,这时箱
内水的高度是多少
分米?
答案:先用5升壶装满后倒进6升壶里,在再将 5升壶装满向6升壶里到,使6升壶装满为止, 此时5升壶里还剩4升水将6升壶里的水全部倒 掉,将5升壶里剩下的4升水倒进6升壶里,此 时6升壶里只有4升水再将5升壶装满,向6升壶 里到,使6升壶里装满为止,此时5升壶里就只 剩下3升水了
29、一位老人有17只羊,分给三个儿子:老大 九分之一,老二三分之一,老三二分之一.三个 儿子想:羊又不能宰,这该怎么办?三人各得 多少只羊?
数学 趣味题

数学趣味题1、一个大笼子里关了一些鸡和兔子。
数它们的头,一共有36个;数它们的腿,共100条。
则鸡有多少只,兔有多少只?2、王老师用40元钱买来20枚邮票,全是1元和5元的。
求这两种邮票分别买了多少枚和多少枚。
3、学校派一些学生去搬树苗,如果每人搬6棵,则差4棵,如果每人搬8棵,则差18棵,这批树苗有多少棵。
4、如果整数a能被b整除,那么b就叫做a的一个因数。
例如,1、2、3、4、6都是12的因数。
有一种数,它恰好等于除去它本身以外的一切因数的和,这种数叫做完全数。
例如,6就是最小的一个完全数,因为除6以外的6的因数是1、2、3,而6=1+2+3。
你能在20至30之间找出第二个完全数吗?5、入冬前,妈妈买来了一筐苹果。
清理时,发现这筐苹果2个2个地数,余1个;3个3个地数,余2个;4个4个地数,余3个;5个5个地数,余4个;6个6个地数,余5个。
你知道这筐苹果至少有多少个吗?6、有44枚棋子,要分装在10个小盒中,要求每个小盒中的棋子数互不相同,应该怎样分?7、新年联欢会上,同学们一致要求教数学的王老师出一个节目。
王老师微笑着走到讲台前说:“我给你们表演一个数字魔术吧!”说完,王老师拿出一叠纸条,发给每人一张,并神秘地说:“由于我教你们数学,所以你们脑子里的数也听我的话。
不信,你们每人独立地在纸条上写上任意4个自然数(不重复写),我保证能从你们写的4个数中,找出两个数,它们的差能被3整除。
”王老师的话音一落,同学们就活跃起来。
有的同学还说:“我写的数最调皮,就不听王老师的话。
”不一会儿,同学们都把数写好了,但是当同学们一个个念起自己写的4个数时,奇怪的事果真发生了。
同学们写的数还真听王老师的话,竟没有一个同学写的数例外,都让王老师找出了差能被3整除的两个数。
同学们,你们知道王老师数字小魔术的秘密吗?8、有9个外观完全相同的小球,其中只有一个重量轻一点儿。
现在要求你用一架天平去称,问你至少称几次,才能找出较轻的球?如果是27个球、81个球中只有一个较轻的球,你知道至少称几次才能找出那个较轻的球吗?这里有规律吗?9、晚饭后,爸爸、妈妈和小红三个人决定下一盘跳棋。
初中趣味数学问答题

初中趣味数学问答题初中组:1、一个人花8块钱买了一只鸡,9块钱卖掉了,然后他觉得不划算,花10块钱又买回来了,11块卖给另外一个人。
问他赚了多少?答案:2元2、100-98+96-94+92-90+……+8-6+4-2=()答案:503、小华的爸爸1分钟可以剪好5只自己的指甲。
他在5分钟内可以剪好几只自己的指甲?答案:20只,包括手指甲和脚趾甲4、哪一个月有二十八天? 答案:每个月都有28天5、哪一年正着念和倒着念一样?答案:1961年6、一根绳子两个头,一根半绳子有几个头?答案:4个7、桌子上原有12支点燃的蜡烛,先被风吹灭了3支,不久又被风吹灭了2支,桌子上还剩几支蜡烛呢?答案:12支8、两羊打架,猜一数学名词。
答案:对顶角9、七六五四三二一,猜一数学名词。
答案:倒数10、成绩,猜一数学名词。
答案:分数11、一只猫吃一只老鼠要5分钟吃完,五只猫吃五只老鼠要几分钟吃完?答案:5分钟12、火车由北京到上海需要六个小时,行驶了三个小时后,火车在哪?答案:在铁轨上13、煮一个蛋要4分钟,那么煮8个蛋要多少分钟?答案:4分钟14、按规律填空:2,3,5,7,(),13,17 答案:1115、一张照片上有3个人,但是却有2个爸爸和2个儿子,为什么?答案:照片上的人分别为爷爷、爸爸、儿子16、某公园办展览,老师带了15个男生和12个女生去观看展览,老师应该买几张票?答案:28张17、10个人在玩捉迷藏,已经有4个人被找到,还有几个人没被找到?答案:5个18、观察图形,问号应该是哪个()答案:B19、猩猩最讨厌什么线()答案:B 因为平行线没有相交(香蕉)A中位线 B 平行线 C 角平分线 D 射线20、观察图形,问号应该是()答案:D21、观察图形,问号应该是()答案:D22、一公斤铁和一公斤棉花哪一个轻?()答案:一样轻23、下面哪个图形和其他的不一样?()答案:BA B C D24、假设1=5,2=6,3=7,4=8,那么5=?答案:925、一张方桌据掉一个角,还有几个角?答案:5个26、5只鸡,5天生了5个蛋。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中学趣味数学:两枚还是三枚
有一种硬币游戏,其规那么是:
〔1〕有一堆硬币,共十二枚。
〔2〕双方轮番从中取走两枚或三枚硬币。
〔3〕谁取最后一枚硬币谁输。
Ⅰ.阿曼德和比福德在玩这种游戏,阿曼德残局,比福德随后。
Ⅱ.双方总是尽能够采取能使自己获胜的步骤;假设无法取胜,就尽能够采取能招致和局的步骤。
这两人中能否肯定会有一人赢?假设这样,谁会赢?
〔提示:首先判定当只要一枚硬币要你取的时分,你是处于稳操胜券的位置,还是处于注定要输,或许招致和局的位置;然后,判定当只要两枚硬币要你取的时分,你是处于稳操胜券的位置,还是处于注定要输,或许招致和局的位置;如此停止,直至判定有十二枚硬币要你取的状况。
〕
答案
依据{Ⅱ.双方总是尽能够采取能使自己获胜的步骤;假设无法取胜,就尽能够采取能招致和局的步骤。
},假设有一方可以取胜,那他一定要取胜。
假设一方可以逼和〔假定他不能取胜〕,那他一定要逼和。
依据(2〕和(3〕:
〔a〕当这堆硬币中只要一枚硬币要取的时分、显然游戏只
能以和局告终,由于谁也不能取。
〔b〕当这堆硬币中有两枚硬币要取的时分,取者必输。
这是由于他必需取走这两枚硬币。
〔c〕当这堆硬币中有三枚硬币要取的时分,取者只能采取逼和的战略。
这是由于假设他一下子把三枚硬币全都取走,那他就输了;于是他只取走两枚硬币,这样对方就不能取了。
〔d〕当这堆硬币中有四枚硬币要取的时分,取者可以取走两枚硬币从而获胜,由于这样就使对方堕入了只要两枚硬币要取的必败境地。
假设他取走三枚硬币游戏就以和局告终。
〔e)当这堆硬币中有五枚硬币要取的时分,假设取者可以留下一定枚数的硬币从而使对方陷于必败的境地,那他就赢了。
因此,他取走了三枚硬币,使对方堕入了只要两枚硬币要取的必败境地。
(f〕当这堆硬币中有六枚硬币要取的时分,取者只能采取逼和的战略。
他可以取走三枚硬币,这就形成了有三枚硬币要取的必和局面。
假设他只取走两枚硬币,就把有四枚硬币要取的必胜时机留给了对方。
依照这样的推理,我们可以发现,当这堆硬币中有两枚、七枚或十二枚硬币要取的时分,取者注定要输;当这堆硬币中有四枚、五枚、九枚或十枚硬币要取的时分,取者稳操胜券;这堆硬币中有一枚、三枚、六枚、八枚或十一枚硬币要取的时分,游戏必以和局告终。
以下三表总结了这三类状况区分是怎样注定招致失败、怎样稳步走向成功和怎样以和局告终的。
依据{〔1〕有一堆硬币,共十二枚。
},末尾时有十二枚硬币。
由于十二枚硬币是注定要输的局面,谁残局谁必输。
依据{Ⅰ.阿曼德和比福德在玩这种游戏,阿曼德残局,比福德随后。
},是阿曼德残局,故阿曼德必输。
因此比福德必赢。
