经验分布函数图形的绘制与演示
§6.2 经验分布函数和频率直方图PPT课件

河北 8362
浙江 14655
山西 5460
安徽 5221
内蒙古 6463
福建 12362
辽宁 12041
江西 5221
吉林 7640
山东 10465
黑龙江 9349
河南 5924
湖北 湖南 广东 广西 海南 重庆 四川 贵州 7813 6054 13730 4668 7135 5654 5250 2895
P
fn (x)
p(x)
1
2
E fn (x)
p(x)2
2 2
E fn (x) Efn (x)2 Efn (x) p(x)2
(1)
由于Rn(a,b)~B(n,pk),其中
pk P
X [tk , tk 1)
tk1 p( y)dy Kh
tk
所以当n
时,E
fn (x)
Efn (x)2
用事件{X<x)发生的频率作为其估计即可。这就引出了下面 所谓经验分布函数的概念。
一、经验分布函数 设X1,…,Xn是抽自总体X的一个样本,观察值为x1,…,xn, 次序观测值x(1)≤ …≤x(n),则总体X的经验分布函数定义为
Fn
(x)
样本中小于x的观测值的个数 n
,x
R.
即
0,
Fn
(x)
k
0.032258 0.00000516
频率直方图如下图所示:
初步判断数据是来自什么样的总体? 这个例子中数据量相对来说比较少,一般情况下数据量最好大于100, 分组的个数根据数据量来确定,一般介于[n/10,n/5]之间,最多不能 超过20组。
定理6.2.2 密度函数p(x)在点x[t0,tm)处连续,样本容量为n,且
函数图像绘制技巧与分析

函数图像绘制技巧与分析函数图像是数学中常见的一种形式,它能够直观地展现函数的性质和特点。
在学习和研究函数时,绘制函数图像是一种非常重要的方法。
本文将介绍一些函数图像绘制的技巧,并对函数图像进行一些分析。
一、函数图像绘制的基本步骤绘制函数图像的基本步骤包括确定函数的定义域、确定坐标轴范围、选择合适的点进行绘制、绘制曲线、标注关键点和分析曲线的性质。
首先,确定函数的定义域是绘制函数图像的基础。
函数的定义域是指函数能够取值的范围。
例如,对于函数y = 1/x,其定义域为x ≠ 0。
在确定定义域后,我们可以确定坐标轴的范围,使得函数图像能够在坐标系中完整地展示。
其次,选择合适的点进行绘制。
为了准确地绘制函数图像,我们需要选择一些关键的点来代表函数的特点。
一般来说,选择函数的零点、极值点、拐点等作为绘制的点是比较常见的方法。
通过计算函数在这些点的取值,我们可以得到这些点的坐标,从而绘制出函数图像。
然后,绘制曲线。
通过连接选择的点,我们可以绘制出函数的曲线。
在绘制曲线时,可以使用直线段和曲线段相结合的方式,使得曲线更加平滑和自然。
接下来,标注关键点。
在绘制完曲线后,我们可以通过标注关键点的方式来更好地展示函数的性质。
例如,在函数图像上标注函数的零点、极值点等,有助于读者更加直观地理解函数的特点。
最后,分析曲线的性质。
通过观察函数图像,我们可以分析函数的增减性、奇偶性、周期性等特点。
例如,如果函数图像在某个区间上是递增的,那么我们可以得出函数在该区间上是增函数的结论。
通过对函数图像的分析,我们可以更深入地理解函数的性质。
二、函数图像绘制的技巧在绘制函数图像时,有一些技巧可以帮助我们更加准确和高效地完成任务。
首先,利用对称性。
许多函数具有对称性,例如偶函数和奇函数。
对于偶函数,其函数图像关于y轴对称;对于奇函数,其函数图像关于原点对称。
通过利用对称性,我们可以只绘制函数图像的一部分,然后通过对称性得到整个函数图像。
r语言求经验分布函数

r语言求经验分布函数
经验分布函数(ECDF)是统计学中常用的统计描述性统计方法,用于
表示一个样本集中样本的分布模式和特性,可以将一个离散变量或一组数
据转换为概率密度函数。
它最早由Abraham de Moivre在18th世纪创建,并被用于描述样本的概率分布情况,然后扩展应用到多个统计学领域中去,如贝叶斯统计学。
在R语言中,可以使用ecdf(函数来构造经验分布函数。
ecdf函数的
定义如下:ecdf(x),其中x代表一个离散变量或一组数据,表示输入变
量的值。
这个函数会接受这个输入变量x,然后计算该输入变量x的累积
概率分布函数,即经验分布函数。
下面我们来看一个实际的例子,给定一组x数据,包括:1,2,3,4,5,6,7,8,9,10,我们可以用R语言的ecdf函数来构建经验分布函数:x<-c(1,2,3,4,5,6,7,8,9,10)
ecdf(x)
运行上面的R代码,就可以看到输出的经验分布函数图了,在图中,
x坐标代表样本x的值,y坐标代表样本x的累积概率,它表明当样本x
小于等于其值时,样本x发生的概率。
通过上面的ecdf函数,我们可以
得到x<=1的概率是0.1,x<=2的概率是0.2,x<=3的概率是0.3,依次
类推,x<=10的概率是1.0。
经验分布函数在R语言中也可以用ggplot2包来构建。
波士顿经验曲线(经验学习曲线)
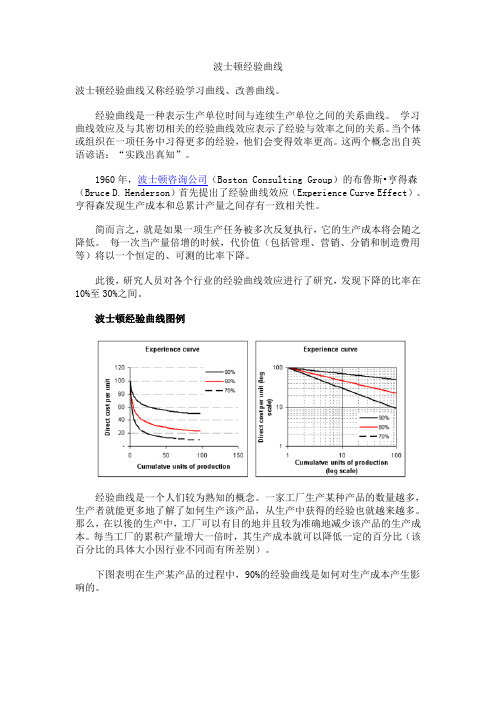
波士顿经验曲线波士顿经验曲线又称经验学习曲线、改善曲线。
经验曲线是一种表示生产单位时间与连续生产单位之间的关系曲线。
学习曲线效应及与其密切相关的经验曲线效应表示了经验与效率之间的关系。
当个体或组织在一项任务中习得更多的经验,他们会变得效率更高。
这两个概念出自英语谚语:“实践出真知”。
1960年,波士顿咨询公司(Boston Consulting Group)的布鲁斯•亨得森(Bruce D. Henderson)首先提出了经验曲线效应(Experience Curve Effect)。
亨得森发现生产成本和总累计产量之间存有一致相关性。
简而言之,就是如果一项生产任务被多次反复执行,它的生产成本将会随之降低。
每一次当产量倍增的时候,代价值(包括管理、营销、分销和制造费用等)将以一个恒定的、可测的比率下降。
此後,研究人员对各个行业的经验曲线效应进行了研究,发现下降的比率在10%至30%之间。
波士顿经验曲线图例经验曲线是一个人们较为熟知的概念。
一家工厂生产某种产品的数量越多,生产者就能更多地了解了如何生产该产品,从生产中获得的经验也就越来越多。
那么,在以後的生产中,工厂可以有目的地并且较为准确地减少该产品的生产成本。
每当工厂的累积产量增大一倍时,其生产成本就可以降低一定的百分比(该百分比的具体大小因行业不同而有所差别)。
下图表明在生产某产品的过程中,90%的经验曲线是如何对生产成本产生影响的。
[编辑]学习曲线效应(The learning curve effect)学习曲线效应指的是越是经常地执行一项任务,每次所需的时间就越少。
这个关系最初在1925年在美国怀特-彼得森空军基地量化,使得航空效率加倍而所需劳动时间下降了10-15%。
随後在其它行业的经验研究得出了不同值:从百分之几到百分之三十。
但在大多数情况下这是一个常量值:它不随行为规模的变化而变化。
学习曲线将学习效果数量化绘制于坐标纸上,横轴代表练习次数(或产量),纵轴代表学习的效果(单位产品所耗时间),这样绘制出的一条曲线,就是学习曲线。
经验分布函数与直方图

直方图与经验分布函数总体X 分布未知samplepopulation直方图(Histogram)总体X 的sample :12,,,n X X X ":()pdf f x 具体步骤:①Sample 观测值12,,,nX X X "min{,1,X X i n =="max{1,,}X X i n =="(1){,}i (){,n i[a,b]m 个小区间(m<n )小区间长度可以不等,设分点为②将[,]分成个小区间,小区间长度可以不等设分点为算数率n bt t t a m =<<<="10③ 计算频数j n 及频率1,,jj f j m n==" ④ 作图:],[1t t −为底边,j f 为高作长方形,面积为f (m 个长方形之和为1)j j jt Δj 用直方图对应的分布函数()jn jf x t Φ=Δ1(,]j j x t t −∈1,,j m ="⎧引进“随机变量”11(,]1,2,,0i j j j x t t i n otherwise ξ−⎪∈⎪⎪==⎨⎪⎪"⎪⎩11{(,]}{1}(1)xxj j j p P x t t P p p ξ−−=∈⇐==−由SLLN(kolmogorov)有1n SLLNjj i i n f E pn ξξ===∑→1j n =jt 11{(,]}()j j j t P x t t f x dx −−=∈=∫()n →∞{lim }1P ==n ⇒→∞{j n f p →∞f 近似代替以)(x f 为曲边的曲边梯形的面积。
j 若∞→n ,j t Δ较小时,可用j f x =Φx x t t jn t Δ)(,近似代替()f ,1(,]j j −∈Example 1:原始数据data=[16,25,19,20,25,33,24,23,20,24,25,17,15,21,22,26,15,23,22,24,20,14,16,11,14,28,18,13,27,31,25,24,16,19,23,26,17,14,30,21,18,16,18,19,2022192218262613211311192318242813112515171820,22,19,22,18,26,26,13,21,13,11,19,23,18,24,28,13,11,25,15,17,18,22,16,13,12,13,11,9,15,18,21,15,12,17,13,14,12,16,10,8,23,18,11,16,28,13,21,22,12,8,15,21,18,16,16,19,28,19,12,14,19,28,28,28,13,21,28,191115182418162819151322141624202818182814132819,11,15,18,24,18,16,28,19,15,13,22,14,16,24,20,28,18,18,28,14,13,28,29,24,28,14,18,18,18,8,21,16,24,32,16,28,19,15,18,18,10,12,16,26,18,19,33,8,11,18,27,23,11,22,22,13,28,14,22,18,26,18,16,32,27,25,24,17,17,283816202832192318281524282916171918]28,38,16,20,28,32,19,23,18,28,15,24,28,29,16,17,19,18]数字特征计算:mean(data) median(data) std(data) var(data) skewness(data) kurtosis(data)195650185000592723513140343125599计算结果19.5650 18.5000 5.9272 35.1314 0.3431 2.5599histfit(data,13)35150经验分布函数(Experience DistributedFunction)经验分布函数(Experience Distributed Function)总体X 的分布函数F 未知,Sample 12,,,()()n n X X X F x F x ⇒⇒"构造()(x F n )方法:12,,,nX X X "(1)(2)()n X X X ≤≤≤"(1)0x X ⎧≤⎪()()(1)()n k k k F x X x X +⎪⎪⎪⎪=<≤⎨⎪1,2,,1k n =−"()1n n x X ⎪⎪⎪>⎪⎩仿真试验固定,()n X F x :表示事件{}X x <在n 次试验中出现的频率,1(){}n i F x x X =−∞落在(,)中的个数n 类似可证:{lim )()}1nP F x F x ==( n →∞Theorem(Glivenko-Cantelli):对任意给定的自然数n ,设12,,,n X X X " 是取自总体X 分布函数)(x F 的一个样本观测值,)(x F n 为其经验 分布函数,记)()({sup x F x F D nx n −=∞<<∞− 则{lim 0}1n n P D →∞==经验分布函数(数据如前例)程序:[h,stats]=cdfplot(data)[h,stats]cdfplot(data) 程序运行结果:Empirical CDF Empirical CDF统计量及分布统计量(St ti ti Sample X X X ",构造statistics ,poplation 统计量(Statistics)Sample 的函数不含参数的函数p 12,,,n ,p p12(,,,)n T T X X X ="Example 7、Sample,statistics:180952809.52i X X n==∑1154.28S ==∑结论:平均(X ),悬殊(S )不大Popalatrion X 的SampleX X X ",则常用的Statistics 1X X = (Mean) p p 12,,,n ①i n∑样本均值()1② S =∑ 样本方差(Sample Variance ) ③ 2S S =样本标准差(Standard Variance )④ 11nkk i i A X n ==∑ 样本k 阶原点矩(Moment )1nkB =−样本⑤1()k i i X X n =∑k 阶中心矩二维两总体X Y 总体的Sample X Y X Y X Y "则有:(,)p 1122(,),(,),,(,)n n ① 121()(ni i S X X Y Y =−− 样本协方差(Covariance )1i n =∑S ②Y x S S 12ˆ=ρ 样本相关系数(Correlation Clefficient )Histogram nn f ii =0x X ⎧⎪≤⎪Experience (1)(1)()()n k k k F x X x X n −⎪⎪⎪⎪=<≤⎨⎪ ()1n x X ⎪⎪⎪>⎪⎪⎩Ordered statistics :Sample X X X"p 12,,,n(1)(2)(1)(2)(),,,n n X X X X X X ≤≤≤⇒"" ()()()()()()1!(1))!()!x F k n k n F x u u du −−⎧⎪⎪=−⎪()(1)0()((1)!(()1(1())k x n x k n k F x F x ⎪−−⎪⎪⎪=−−⎨⎪∫()()(())n n x F x F x ⎪⎪⎪=⎪⎪⎪⎩():'k X k th ordered statistic⇐(1):min X imum ordered statistici d d t ti ti⇐():max n X imum ordered statisticn ()()11!(,)[()][()()][1()](1!(1)!(1)!()!1!i j i j i n j x x f x y F x F y F x F y p i j i n j −−−−=−−−−−−⎧()()2(1)[()()]()()(,)0i n n x x n n F y F x p x p y x y f x y otherwise −⎪−−<⎪⎪=⎨⎪⎪⎪⎩ 11212!()()(,,)n nn n f x f x x x x f x x x ⎧⎪<<<⎪⎪=⎨⎪"""0otherwise⎪⎪⎩X ⎧⎪⎪1()2*()(1)221[]2n n n M X X ++⎪⎪=⎨⎪+⎪⎪⎪⎪⎩ *()(1)n D X X =−反例:..2(,)~i i di X N μσ⇒2111,(),ni X X X μ−∑是1i n σ=Sample二重性Statistic二重性抽样分布2χ分布..22(01)~i i dn=∑"Definition :1()1,,(0,1)~nin i X X N Y Xχ=⇒Theorem1.1(2χ分布addition ):k 个相互独立的r.v. 12,,,k Y Y Y "且2~()j j Y n χ,1,,j k ="Then : 211~()nnj j j j Y Y n χ===∑∑..i i dProof :2=k 推出:If :112121,,,,,,(0,1)~n nnn X X X X X N ++""Then⎪⎪⎫∑∑=+=211122121,n j jn n i jX Y X Y 同分布与同分布与 ⎪⎪⎭⎬∑∑==+121112221n i n j jn j X X Y Y 相互独立与相互独立与又⇓同分布与∑∑∑+===+=++=2112112112221n n j j n i n j j n j X X X Y Y YTheorem1.22~==Theorem1.2X χ⇒① n X n EX 2var ②:的pdf X Where10()0xxe dx ααα∞−−Γ=>∫⎧122210n x n x e x n −−⎪⎪>⎪⎪⎪⎪=()2(20f x otherwise Γ⎨⎪⎪⎪⎪⎪⎪⎩Proof :① ..(0,1)~i i dnii X N X X ⇒∑与同分布1i =且22n nn∑且:111var iii i i i EX E X EXX n=======∑∑()n EX X E X X X ni iiini i∑∑∑===−===1224212])(([var var(var ))时,X t xty y 22121122−−=−②1=n dt e t dye x P x F 022}{)(∫=∫=<=ππn x −−⎧⎪12212101()2()x e x f x ⎪>⎪⎪⎪⎪=Γ⎨ 20otherwise ⎪⎪⎪⎪⎪⎪⎩设:22~(1),~(1),Y n Z Y Z χχ−且与相互独立Then :同分布与Z Y Y +(2χ分布的可加性)11222221102211()()()()11n yy x x Y n f x f y f x y dy ye x y en −−+∞−−−−−∞=−=⋅−−∫∫2(2()22ΓΓ11112221x n −−−−−12()12()2n eyx y dyn −=−Γ∫1x n n 1111222221(1)112n exzz dzn −−−−−=−−ΓΓ∫()(221221n x x e −−=22(2n n ΓB函数duu uB q p 1111−−−=Beta函数q p 0)(),(∫Beta与Gamma关系)()()(),(),(q P q p P q B q p B +ΓΓΓ==t 分布与F 分布Definition设 2~(0,1)~X N Y n X 与Y 相互独立 则(,)()χ~X=()T t n2⎧211()2x X n x f x π−−−⎪⎪⎪=⎪⎪⎪⎪⎧⎪1221()2n n x −−+Γ=22210()2(2n Y y e y n f y ⎪⎪⎨>⎪⎪⎪⎪⎪=⎪⎨Γ⎪⎪⎪⎪⎪()(1)()2T f x n n n π⇒+Γ00x ⎪⎪⎪≤⎪⎪⎩⎪⎩Definition :If 21~()X n χ,22~()Y n χ X 与Y 相互独立, themX 112~(,)n T F n n Y =2ndf为类似可得 ),(21n n F 的pdf 为:⎧1121212122212()20n n n n n n n x n x +⎪+⎪Γ⎪⎪⎪⋅>⎪=12212()()()()220f x n n n x n elsewhere⎨⎪ΓΓ+⎪⎪⎪⎪⎪⎪⎩性质:①),(~1),(~1221n n F n n F F ⇒F②),1(~)(~2n F XY n t X =⇒③1,n n F =),()(12121n n F αα−分位数(quantile).:RV X CDF F X,,给定(){}:()F x P X x CDF F x =<⇒给定的值,要确定X 取什么值? Definition :设X 的,(){}01CDF F X F X P X X ααααα=<=<<为满足 则称αX 为F 的α分为数(点)若X 有pdf )(x f ,则分为数αX 表示αX 以左的一块阴影面积为α。
经验分布函数定义

经验分布函数定义经验分布函数(empirical distribution function,简称EDF)是描述一组随机变量的累积分布函数的一种估计方法。
它通过从这组随机变量中取样得到的观测值的经验累计频率来估计真实的分布函数。
假设我们有一组独立同分布的随机变量X₁,X₂,...,Xn,我们可以将这些随机变量按照大小排列,得到观测值的有序序列:X(1)≤X(2)≤...≤X(n)然后,我们定义经验分布函数F_n(x)为:F_n(x)=(1/n)*Σ(i=1,n)I(X(i)≤x)其中,I(·)是指示函数,当其参数为真时取值为1,否则取值为0。
经验分布函数F_n(x)的值表示小于等于x的观测值所占的比例。
1.F_n(x)是递增函数。
随着x的增加,F_n(x)的值也增加。
2.F_n(x)在每个观测值X(i)处发生跳跃。
当x趋近于一些观测值时,F_n(x)的值在该观测值处跃升。
3.当x趋近于负无穷时,F_n(x)趋近于0;当x趋近于正无穷时,F_n(x)趋近于14.当存在多个相同的观测值时,F_n(x)在这些观测值处的跳跃幅度等于相同观测值的个数除以总观测值的个数。
经验分布函数在统计学中有广泛的应用,特别对于描述数据分布情况和做出推断。
通过经验分布函数,我们可以估计随机变量的各种统计量,比如均值、方差、分位数等。
此外,经验分布函数还可以与其他分布函数进行比较,用来检验数据是否符合一些特定的分布。
在实际应用中,经验分布函数通常会被可视化成经验分布函数图或经验分布函数曲线,用于直观地展示数据的分布情况。
经验分布函数图的横轴表示观测值,纵轴表示累积频率。
通过观察经验分布函数图,我们可以对数据的集中程度、集群情况、异常值等进行初步分析和判断。
总结起来,经验分布函数是一种非参数方法,通过观测值的经验累计频率来估计真实的分布函数。
它在统计数据分析中具有重要的作用,通常用于描述数据分布、做出推断和进行数据分析。
经验累积分布函数图
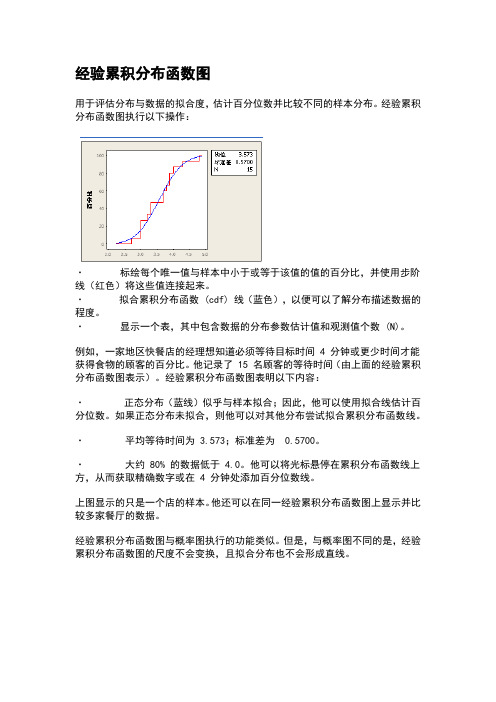
经验累积分布函数图
用于评估分布与数据的拟合度,估计百分位数并比较不同的样本分布。
经验累积分布函数图执行以下操作:
·标绘每个唯一值与样本中小于或等于该值的值的百分比,并使用步阶线(红色)将这些值连接起来。
·拟合累积分布函数 (cdf) 线(蓝色),以便可以了解分布描述数据的程度。
·显示一个表,其中包含数据的分布参数估计值和观测值个数 (N)。
例如,一家地区快餐店的经理想知道必须等待目标时间 4 分钟或更少时间才能获得食物的顾客的百分比。
他记录了 15 名顾客的等待时间(由上面的经验累积分布函数图表示)。
经验累积分布函数图表明以下内容:
·正态分布(蓝线)似乎与样本拟合;因此,他可以使用拟合线估计百分位数。
如果正态分布未拟合,则他可以对其他分布尝试拟合累积分布函数线。
·平均等待时间为 3.573;标准差为0.5700。
·大约 80% 的数据低于 4.0。
他可以将光标悬停在累积分布函数线上方,从而获取精确数字或在 4 分钟处添加百分位数线。
上图显示的只是一个店的样本。
他还可以在同一经验累积分布函数图上显示并比较多家餐厅的数据。
经验累积分布函数图与概率图执行的功能类似。
但是,与概率图不同的是,经验累积分布函数图的尺度不会变换,且拟合分布也不会形成直线。
经验分布函数_概述说明以及解释

经验分布函数概述说明以及解释1. 引言1.1 概述经验分布函数是一种统计工具,用于描述和分析随机变量的分布情况。
它是一种非参数的方法,不需要对概率分布进行假设,因此被广泛应用于各个领域的数据分析中。
通过经验分布函数,我们可以了解到样本数据的累积概率分布,并将其与理论概率分布进行比较。
1.2 文章结构本文将以以下方式呈现关于经验分布函数的研究内容:首先,在第二部分中,我们将对经验分布函数的定义进行详细解释,包括相关的理论介绍、数学表达式以及直观解释。
然后,在第三部分中,我们将探讨经验分布函数在不同领域中的应用场景,例如数据分析与可视化、生物统计学和工程领域等。
接着,在第四部分中,我们将介绍经验分布函数的计算方法和算法实现。
这包括基本思想与步骤、常见的计算方法和公式推导以及算法实现和代码示例。
最后,在第五部分中,我们将给出总结主要观点和研究结果,并对经验分布函数未来发展提出展望和建议。
1.3 目的本文的目的是为读者提供对经验分布函数的全面理解。
通过详细介绍经验分布函数的定义、应用场景以及计算方法,希望能够帮助读者更好地应用经验分布函数进行数据分析,并为未来经验分布函数在各个领域中的发展提供一些启示和建议。
2. 经验分布函数的定义:2.1 理论介绍:经验分布函数是统计学中常用的一种非参数估计方法,用于描述一个随机变量的累积分布函数(CDF)。
该函数基于观测数据样本,通过对每个观测值的累计概率进行排序和求和得到。
它能够直观地展示数据集中数值的分布情况。
2.2 数学表达式:假设我们有一个由n个独立随机观测值组成的样本集合X={x₁, x₂,..., xn},其中每个xi代表一个随机变量。
经验分布函数F(x)在某个特定点x处的取值表示小于或等于x的样本比例。
数学上,经验分布函数可以表示为:F(x) = (1/n) * Σ(i=1 to n) [I(xi ≤x)]其中[ ]表示指示函数,当括号内条件满足时取值为1,否则为0;Σ表示求和运算;i代表索引变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、经验分布函数的作图n=4。
1在Excel中产生一个服从均匀分布U(1,6)的样本容量n=4的随机样本。在单元格A2中输入产生均匀分布U(1,6)的随机数命令“=1+5*RAND()”,再将其拖放填充至A5,就可在单元格区域A2:A5中产生4个样本观测值x1,x2,x3,x4,每按一次F9键,这些随机数就会发生变化,这为我们进行动态显示带来方便。接着我们把样本观测值x1,x2,x3,x4从小到大排序,在单元格B2:B5中分别使用命令“=SMALL($A$2:$A$5,1)”(k=1,2,3,4)得到顺序样本观测值。
实验二经验分布函数图形的绘制与演示
实验序号:2日期:2014年5月29日
班级
数学学院2012级F班
学号
124080Leabharlann 45姓名王信实验名称
经验分布函数图形的绘制与演示
问题的背景和目的:
设X1,X2,…,Xn是取自总体X的随机样本,Fn(x)是总体X的经验分布函数,当n→∞时由格列汶科定理知
该定理说明Fn(x)在整个实数轴上一概率1均匀收敛于F(x)。当样本容量n充分大时,经验分布函数Fn(x)可以作为总体分布函数F(x)的一个良好的近似,这是数理统计学中以样本推断总体的理论依据。
2在单元格C2内输入起始值0,单击【编辑】/【填充】/【系列】,在出现的对话框输入相应选项(如图1所示),就可在单元格区域C2:C702中顺序产生0,0.01,0.02,…,7共703个自变量x的取值序列。
图1
3在D2单元格内输入公式“=IF(C2<$B$2,0,IF(C2<$B$3,1/4,IF(C2<$B$4,2/4,IF(C2<$B$5,3/4,1))))”,再利用拖放填充功能将D2单元格内的计算公式复制到整个单元格区域D2:D702,就自动计算出所有Fn(x)的取值。
图3图4
实验结果总结及实验体会:
实验结果:
经验分布函数作图
正态分布随机数
实验体会:
使用Excel表格,每按一次F9,随机样本观测值发生改变,相应的顺序样本观测值发生相应变化。总体分布函数F(x)和经验分布函数Fn(x)图形也随之发生动态变化。,这给我们留下生动而直观的印象。便于观察总体分布函数和经验分布函数的变化趋势,进行比较。可以加深对经验分布函数的了解。从图可以看出,当样本容量n充分大时经验分布函数可以看做是总体分布函数的一个良好的近似。
教师评语与成绩:
4最后利用单元格区域C2:C702中自变量x的取值和D2:D702中经验分布函数Fn(x)的值画出散点图。单击【插入】/【散点图】。再对所得到的图形进行修饰整理即可得到经验分布函数图(如图2所示)。
图2
2、正态分布随机n=100。N(100,42)
在B2单元格输入公式“=NORMINV(RAND(),10,4)”产生服从正态分布N(100,42)的100个样本观测值x1,x2,...,x100。接着把样本观测值x1,x2,…,x100从小到大排序。在单元格C2中输入公式“=SMALL($B$2:$B$101,A2)”,将C2中的公式拖放填充至C101单元格,得到顺序样本观测值。根据正态分布的3σ原理,在单元格D2中输入起始值-5,单击【编辑】/【填充】/【系列】,在出现的对话框中输入相关选项,这里选择等差数列,序列产生在列,步长值为0.01,终止值为26(如图3所示)。在E2单元格输入公式”=COUNTIF($C$2:$C$101,"<="&$D2)/100”,将其拖放填充至E312单元格得到相应的经验分布函数值Fn(x)。在F2单元格输入公式“=NORMDIST(D2,10,4,1)”将其拖放填充至F312单元格。得到F(x)的值。选中E1:F312单击【插入】/【折线图】,将F(x)和Fn(x)画在同一个图里,对图形进行修饰调整,得到图4.
实验内容:
1、理解经验分布函数的构成,经验分布函数是样本的函数,随着样本观测值的变化而变化。通过实验学习经验分布函数图形的绘制方法和动态演示过程
2、任意产生一组随机样本,对该样本从小到大排序;然后利用排序后的样本作经验分布函数图形;让样本动态发生变化,观察相应的经验分布函数的数值和图形的变化。
实验所用软件及版本:Excel2003
