数学物理方法期末考试试题典型汇总
北京师范大学《数学物理方法》2019-2020学年第一学期期末试卷

北京师范大学《数学物理方法》2019-2020学年第一学期期末试卷2019-2020 学年期末试卷数学物理方法专业:物理学考试时间:120 分钟总分:100 分部分一:选择题(每题 5 分,共 30 分)在数学物理方法中,Green 函数的定义式为:A) G(x, x') = ∫dk e^(ik(x-x')) / (k^2 - k_0^2)B) G(x, x') = ∫dk e^(ik(x-x')) / (k^2 + k_0^2)C) G(x, x') = ∫dk e^(ik(x-x')) / (k^2 - k_0^2 + iε)D) G(x, x') = ∫dk e^(ik(x-x')) / (k^2 + k_0^2 - iε)5 分Legendre 方程的通解为:A) P_n(x) = (1 / 2^n n!) * d^n / dx^n (x^2 - 1)^nB) P_n(x) = (1 / 2^n n!) * d^n / dx^n (x^2 + 1)^nC) P_n(x) = (1 / 2^n n!) * d^n / dx^n (x^2 - 1)^(n+1)D) P_n(x) = (1 / 2^n n!) * d^n / dx^n (x^2 + 1)^(n+1)5 分在球坐标系中,Laplacian 算符的表达式为:A) ∇^2 = ∂^2 / ∂r^2 + (2 / r) ∂ / ∂r + (1 / r^2) ∂^2 / ∂θ^2 + (1 / r^2 sin^2 θ) ∂^2 / ∂φ^2B) ∇^2 = ∂^2 / ∂r^2 + (1 / r) ∂ / ∂r + (1 / r^2) ∂^2 / ∂θ^2 + (1 / r^2 sin^2 θ) ∂^2 / ∂φ^2C) ∇^2 = ∂^2 / ∂r^2 + (3 / r) ∂ / ∂r + (1 / r^2) ∂^2 / ∂θ^2 + (1 / r^2 sin^2 θ) ∂^2 / ∂φ^2D) ∇^2 = ∂^2 / ∂r^2 + (4 / r) ∂ / ∂r + (1 / r^2) ∂^2 / ∂θ^2 + (1 / r^2 sin^2 θ) ∂^2 / ∂φ^25 分在数学物理方法中,Sturm-Liouville 问题的通解为:A) y(x) = c_1 y_1(x) + c_2 y_2(x)B) y(x) = c_1 y_1(x) - c_2 y_2(x)C) y(x) = c_1 y_1(x) + c_2 y_2(x) + c_3 y_3(x)D) y(x) = c_1 y_1(x) - c_2 y_2(x) + c_3 y_3(x)在球坐标系中,spherical harmonics Y_lm(θ, φ) 的定义式为:A) Y_lm(θ, φ) = (-1)^m * sqrt((2l + 1) / (4π)) * P_l^m(cos θ) e^(imφ)B) Y_lm(θ, φ) = (-1)^m * sqrt((2l + 1) / (4π)) * P_l^m(cos θ) e^(-imφ)C) Y_lm(θ, φ) = (-1)^m * sqrt((2l - 1) / (4π)) * P_l^m(cos θ) e^(imφ)D) Y_lm(θ, φ) = (-1)^m * sqrt((2l - 1) / (4π)) * P_l^m(cos θ) e^(-imφ)5 分在数学物理方法中,Bessel 函数的递归关系式为:A) J_n(x) = (x / 2) * (J_(n-1)(x) - J_(n+1)(x))B) J_n(x) = (x / 2) * (J_(n-1)(x) + J_(n+1)(x))C) J_n(x) = (2 / x) * (J_(n-1)(x) - J_(n+1)(x))D) J_n(x) = (2 / x) * (J_(n-1)(x) + J_(n+1)(x))5 分部分二:计算题(每题 20 分,共 60 分)证明 Legendre 方程的通解为 P_n(x) = (1 / 2^n n!) * d^n / dx^n (x^2 - 1)^n。
数学物理方法(4)--期末考试试卷(1)答案
w(z) = ck zk k =0
(2)系数递推公式。将 w(z) 代入方程,得:
� �
k (k - 1)ck zk-2 - ck zk+1 = 0
k =2
k =0
2c2 + [(k + 2)(k + 1)ck+2 - ck-1]zk = 0
k =1
c2 = 0,
ck +2
=
(k
+
-
4)L6 �5 �3 �2 c0
(b) 用 c1 表示 c3k+1
c3k +1
=
c3k -2 3k(3k + 1)
=
1 3k (3k+ Nhomakorabea1)(3k
-
c3k -5 2)(3k
-
3)
=
(3k
+ 1)3k(3k
-
1 2)(3k
-
3)L7
�6 �4 �3 c1
因 c2 = 0 ,故 c5 = c8 = L = 0
=
-d
'(x)
第 1 页(共 3 页)
得分 评阅人 三、计算题:(共 2 题,每题 10 分,共 20 分)
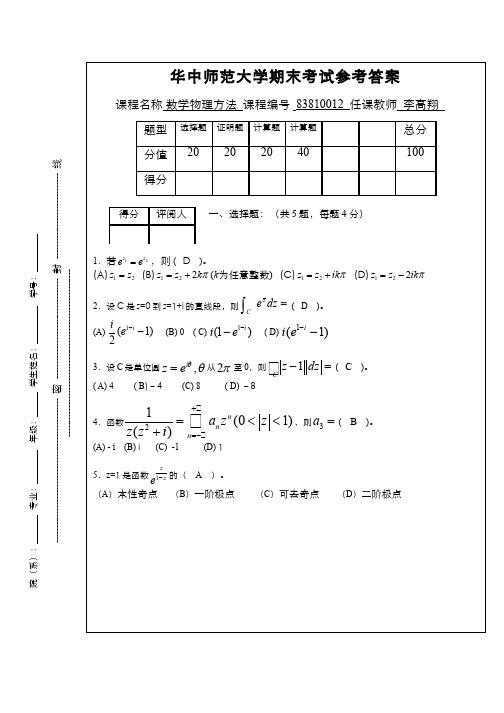
1.试用级数解法求解在 z0 = 0 邻域内 w''-zw = 0 的解,其初始条件为 w(0) = 1, w'(0) = 0 。 解:(1)解的形式。系数 p(z) = 0, q(z) = -z 在 z0 = 0 解析, z0 是方程的常点,所以解的形式为:
(1)
l=0
两边对 x 求导,得t(1 -
2xt
+
数学物理方法期末考试模拟题

数学物理方法期末考试复习题1.复数1z =-z =_________________________________ 2.复数1iz e+=的三角表示为z =_________________________________3.由方程10z e +=可解得z =____________________ 4.由方程3z i =可解得z =____________________ 5.计算ln(1)-=____________________ 6.计算3(1)i -=____________________7.解析函数()f z 的实部22(,)u x y x y =-,则其导函数()f z '=____________________ 8.解析函数()f z 的虚部(,)2v x y y xy =-+,则其导函数()f z '=____________________ 9.沿着折线1i +到2i +,再到24i +的曲线积分2421iiI z dz ++=⎰=_______________________10.沿1i +到24i +的直线积分2421iiI z dz ++=⎰=_______________________11.级数01(1)nn z ∞=-∑的收敛区域为____________________ 12.级数(1)nn z ∞=-∑的收敛区域为__________13.级数0!nn z n ∞=∑的收敛区域为____________________14.级数∑∞=-1)1(n nn z 的收敛区域为____________________15.判断奇点的类型:0z =是函数1()f z z z =+的 16.判断奇点的类型:0z =是函数sin ()zf z z =的17.判断奇点的类型:0z =是函数2sin ()zf z z=的18.判断奇点的类型:0z =是函数3cos 1)(z zz f -=的19.函数1()f z z z=+,在0,∞点的留数分别为Res[(),0]f z =_______;Res[(),]f z ∞=_____20.函数21()(1)f z z z =-,在0,1,∞点的留数分别为Res[(),0]f z =__________;Res[(),1]f z =__________;Res[(),]f z ∞=__________21.函数241()ze f z z -=,在0,∞点的留数分别为Res[(),0]f z =________;Res[(),]f z ∞=______22.以0z =为中心展开()21()1f z z =-为泰勒级数:___________________________23.以0z =为中心展开()21()1f z z =+为泰勒级数:___________________________24.以0z =为中心展开()zf z e =为泰勒级数:___________________________ 25.以0z =为中心展开()ln(1)f z z =+为泰勒级数:___________________________ 26.计算积分:=-⎰∞∞-dx x e x )1(2δ27.计算积分:⎰+∞∞-=dk e ikx π2128.已知π=Γ)21(,则=+Γ)21(n 29.已知1)1(=Γ,则=+Γ)1(n 30.11()l P x dx -=⎰31.11()()lk P x P x dx -=⎰32.2)(x x f =以{})(x P l 为基,展开为广义傅里叶级数的形式为 ______________ 33.3()f x x =以{})(x P l 为基,展开为广义傅里叶级数的形式为 ______________34.勒让德多项式的生成函数(,)t x ψ= 35.厄米多项式的生成函数(,)t q ψ= 36.贝塞尔函数的生成函数(,)t z ψ= 37.计算拉普拉斯变换:[]sin t t =____________________ 38.计算拉普拉斯变换:[]cos t t =____________________39.计算拉普拉斯变换:t te α-⎡⎤=⎣⎦____________________40.计算拉普拉斯变换:[]sin ()t ωτ-=____________________41.计算拉普拉斯变换:[]cos ()t ωτ-=____________________42.计算拉普拉斯逆变换:1222(1)(1)1p p ⎡⎤-⎢⎥=⎢⎥⎡⎤-+⎣⎦⎣⎦-_____________________43.计算拉普拉斯逆变换:121(2)(1)p p ⎡⎤=⎢⎥--⎣⎦-_____________________ 44.计算拉普拉斯卷积:sin t t ⊗=____________________45.计算拉普拉斯卷积:cos t t ⊗=____________________ 46.计算拉普拉斯卷积:sin sin t t ⊗=____________________ 47.计算拉普拉斯卷积:cos cos t t ⊗=____________________48.利用行波法解2(,0)(,0)()(,0)()tt xxt u a u x t u x x u x x ϕψ⎧=-∞≤≤+∞>⎪⎨==⎪⎩的解为(,)u x t =_____________________49.利用行波法解22(,0)(,0)sin (,0)tt xxt u a u x t u x x u x x ⎧=-∞≤≤+∞>⎪⎨==⎪⎩的解为(,)u x t =_____________________ 50.利用行波法解23(,0)(,0)(,0)tt xxt u a u x t u x xu x x⎧=-∞≤≤+∞>⎪⎨==⎪⎩的解为(,)u x t =_____________________二、 解答题1.设(,)4u x y xy y =--。
数学物理方法(10)--期末考试试卷(4)答案
k 2
k 0
� w( z )
2c2 +
ᆬ
[(k + 2)(k +1)ck+2 - ck-1]zk
0
k 1
将代入方程
c2 0c,3ckkk+23kk((ck33kkk--+-33-12c)1)k-()1k + 1)
即亦即
c3k
c3k -3 3k(3k -1)
1 3k (3k
-1)
代换,有
f1
t -
e- pt dt
0
f1
e- p + d
0
f1 e-p d
0
f2
第e- p d1
页F(1共p F23 p页 )
f (x) lim
n e -nx2
n
3. 试证明:是函数的一种表达式。
答: 函数的傅里叶变换:,又称为的像函数;
F -1 G
f
xGfx21
G eixd
-
函数的傅里叶逆变换:,又称为的像原函数。
专业:
院(系):
得分 评阅人 二、证明题:(共 3 题,每题 9 分,共 27 分)
1. 已知,试证明: ()
证明:将对 r 求导
ᆬ 1
1+ r2 - 2rx< 1)
(l +1)Pl+1(x) - (2l +l 1ᆬ)1xPl (x) + lPl-1(x) 0
ᆬ 1
1+ r2 - 2rx
ᆬ l0
Pl (x)rl
( x < 1)
数学物理方法期末试题(5年试题含答案)

………密………封………线………以………内………答………题………无………效……附:拉普拉斯方程02=∇u 在柱坐标系和球坐标系下的表达式 柱坐标系:2222222110u u u uzρρρρϕ∂∂∂∂+++=∂∂∂∂球坐标系:2222222111sin 0sin sin u u ur r r r r r θθθθθϕ∂∂∂∂∂⎛⎫⎛⎫++= ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭一、填空题36分(每空2分)1、 数量场2322u x z y z =+在点(2, 0, -1)处沿2423x xy z =-+l i j k 方向的方向导数是。
2、 矢量场()xyz x y z ==+A r r i +j k 在点(1, 3, 3)处的散度为 。
3、 面单连域内设有矢量场A ,若其散度0∇⋅A =,则称此矢量场为 。
4、 高斯公式Sd ⋅=⎰⎰ A S ;斯托克斯公式ld ⋅=⎰ A l 。
5、 将泛定方程和 结合在一起,就构成了一个定解问题。
只有初始条件,没有边界条件的定解问题称为 ;只有边界条件,没有初始条件的定解问题称为 ;既有边界条件,又有初始条件的定解问题称为 。
………密………封………线………以………内………答………题………无………效……6、 ()l P x 是l 次勒让德多项式,则11()()l l P x P x +-''-= ; m n =时,11()()mn P x P x dx -=⎰。
7、 已知()n J x 和()n N x 分别为n 阶贝塞尔函数和n 阶诺依曼函数(其中n 为整数),那么可知(1)()n H x = 。
(2)()n H x = 。
8、 定解问题2222000(0,0)|0,||0,|0x x ay y bu ux a y b x y u u V u u ====⎧∂∂+=<<<<⎪∂∂⎪⎪==⎨⎪==⎪⎪⎩的本征函数为 ,本征值为 。
数学物理方法期末考试试题

数学物理方法期末考试试题# 数学物理方法期末考试试题## 第一部分:选择题(每题2分,共20分)1. 以下哪个不是数学物理中的常用方法?A. 傅里叶变换B. 拉普拉斯变换C. 泰勒级数展开D. 牛顿迭代法2. 求解偏微分方程时,分离变量法的基本思想是什么?A. 将偏微分方程转化为常微分方程B. 将偏微分方程分解为几个独立的方程C. 将偏微分方程转化为线性方程D. 将偏微分方程转化为积分方程3. 在数学物理中,格林函数通常用于解决什么问题?A. 线性代数问题B. 非线性偏微分方程C. 边界值问题D. 初始值问题4. 以下哪个是求解波动方程的典型方法?A. 特征线法B. 有限差分法C. 有限元法D. 蒙特卡洛方法5. 拉普拉斯方程在数学物理中通常描述了什么类型的物理现象?A. 波动现象B. 热传导现象C. 流体动力学问题D. 电磁场问题## 第二部分:简答题(每题10分,共30分)6. 简述傅里叶变换在数学物理中的应用。
7. 解释什么是边界层理论,并说明它在流体力学中的重要性。
8. 描述格林函数在求解偏微分方程中的作用。
## 第三部分:计算题(每题25分,共50分)9. 给定函数 \( f(x) = x^2 - 4x + 3 \),使用泰勒级数展开在\( x = 1 \) 处展开 \( f(x) \) 并求出展开式。
10. 考虑一个无限长直导体,在 \( x \) 轴上,导体的电势 \( V(x) \) 满足泊松方程 \( \nabla^2 V = -\rho/\varepsilon_0 \),其中\( \rho \) 是电荷密度,\( \varepsilon_0 \) 是真空电容率。
假设\( \rho \) 是常数,求解 \( V(x) \)。
## 第四部分:论述题(共30分)11. 论述数学物理方法在解决实际物理问题中的应用,并给出至少两个具体的例子。
请注意,以上内容仅为示例,实际的数学物理方法期末考试试题可能会包含不同的问题和要求。
数学物理方法试题汇总

12届真题1. 求下列各小题(2*5=10分):(1)用几何图形表示0arg(1)4z π<-<; (2)给出序列(1/)sin 6n n z i n π=+的聚点; (3)在复数域中求解方程cos 4z =的解;(4)给出二阶偏微分方程的基本类型;(5)给出解析函数所满足的柯西-黎曼方程。
2.按给定路径计算下列积分(5*2=10分):(1)320Re izdz +⎰,积分路径为线段[0,3]和[3,3+2i]组成的折线;(2)11,==⎰积分路径由z=1出发的。
3.利用留数定理计算下列积分(5*2=10分):(1)241x dx x +∞-∞+⎰; (2)3||1zz e dz z =⎰。
4.求常微分方程20w z w ''-=在0z =邻域内的两个级数解(15分)。
5.求下列线性非奇次偏微分方程的通解:2222u u xy y x y∂∂-=-∂∂(15分)。
6.利用分离变量法求解:(20分)2222000(),|0, |0,0, 0.x x l t t u u x l x t x u u u u t ====⎧∂∂-=-⎪∂∂⎪⎪==⎨⎪∂⎪==∂⎪⎩7.用拉普拉斯变换方法求解半无解问题(20分)220, 0,0,(0,)1, lim (,) 0, (,0)|0, 0.x u u x t t x u t u x t t u x x κ→∞⎧∂∂-=>>⎪∂∂⎪⎪=>⎨⎪=>⎪⎪⎩有界,2005级一、填空(请写在答题纸上,每题6分,共计48分)1. 三维泊松方程是______________________________2. 边界为Γ的区域Ω上函数u 的第二类边界条件为___________________。
3. 极坐标下的二维拉普拉斯方程为__________________________。
4. 定解问题2002||0tt xx t t t u u x u x u ===-∞<<+∞⎧⎪⎨==⎪⎩, ,的解__________________________。
数学物理方法期末考试卷与解答

《数学物理方法》试卷(A 卷)参考答案姓名: 学号:题号 一 二 三 四 五 六 七八 总分 得分注:本试卷共一页,共八大题。
答案请做在答题纸上,交卷时,将试题纸与答题纸填好姓名与学号,必须同时交齐,否则考卷作废!可能用到的公式:1). (2l +1)xP l (x )=lP l −1(x )+(l +1)P l+1(x ), 2). P 0(x )=1, P 1(x )=x ;3))(~)]([00k k f x f eF xik −=;4))]([1])([x f F ikd f F x=∫∞−ξξ; 5).])1(1[2sin )(I 333n ln l xdx l n x l x −−=−=∫ππ一、 简答下列各题。
(12分,每题6分)1. 试在复平面上画出3)arg(0π<−<i z ,4Re 2<<z 点集的区域。
解:如图阴影部分为所求区域 (6分)2. 填空题:函数3)2)(1()(i z z z f +−=是单值的还是多值的?多值的(1分);若是多值,是几值?3值(2分);其支点是什么?1,-2i ,∞(3分)。
二、 (9分) 试指出函数3sin )(zzz z f −=的奇点(含ㆀ点)属于哪一类奇点? 解:22112033)12()1(])12()1([1sin )(−∞=+∞=∑∑+−=+−−=−=n n nn n n n n n z n z z z z z z f (3分) z=0为f (z )的可去奇点;(3分)z=∞为f (z )的本性奇点;(3分)三、 (9分) 已知解析函数f (z ) = u (x ,y ) + iv (x ,y )的虚部v (x,y ) = cos x sh y , 求f (z )= ? 解:由C-R 条件x y x v yy x u y y x v x y x u ∂∂−=∂∂∂∂=∂∂),(),(,),(),( (3分)得 u x (x,y ) = v y (x,y ) = cos x ch y u y (x,y ) = −v x (x,y ) = sin x sh y (3分)高数帮帮数帮高数帮高f (z ) = f (x +iy ) = u (x ,y ) + iv (x ,y ) = sin x ch y +i cos x sh y + c上式中令 x=z, y=0, 则 f (z ) = f (z+i0) = sinz + c (3分)四、 (10分) 求积分dz z e I Lz∫−=6)1(其中曲线L 为(a)圆周21=z ;(b)圆周2=z 解:(a) 6)1()(−=z e z f z 在圆周21=z 内解析,I = 0;(5分) (b) 在圆周2=z 内有一奇点,I = 2πiRes f (1)= 2π i !52)1()1()!16(166551lim e i z e z dx d z z π=−−−→(5分) 五、 (10分) 计算拉普拉斯变换?]2sin [=t t L (提示:要求书写计算过程)解:已知 42]2[sin ,][sin 222+=+=p t L p t L 也即ωωω(2分) 由象函数微分定理)3(4)(4p4)(4p ]2sin []2sin )[()2(4)(4p )42(]2sin )[()3(,)()1()]()[(2222222分分分+=+−−=−=−∴+−=+=−−=−p p t t L t t L p p dp d t t L p f dp d t f t L nnnn六、 (15分) 将f (x )= (35/8)x 4 + 5x 3−(30/8)x 2 +(10/3)x +1展开为以{ P l (x ) }基的广义付里叶级数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mathematical methods for physics
一、 单项选择题(每小题2分)
1.齐次边界条件0),(),0(==t u t u x x π的本征函数是_______。
A)Λ3,2,1 sin =n nx B) Λ,2,1,0 cos =n nx C)Λ2,1,0 )21sin(=+n x n D) Λ2,1,0 )2
1cos(=+n x n 2.描述无源空间静电势满足的方程是________。
A) 波动方程 B)热传导方程
C) Poisson 方程 D)Laplace 方程
3.半径为R 的圆形膜,边缘固定,其定解问题是⎪⎪⎪⎩
⎪⎪⎪⎨⎧====∇-∂∂===)(|
),(|0|0),(),(0t 02222ρψρϕρρρt t R u u u t u a t t u
其解的形式为∑∞
==100)()(),(m m
m k J t T t u ρρ,下列哪一个结论是错误的______。
A) )()()()(20222
t T k a t T dt
d t T m m m m -=满足方程 B )圆形膜固有振动模式是)sin(0t ak m
和)cos(0t ak m C )0m k 是零阶Bessel 函数的第m 个零点。
D ))()(00ρρm
m k J R =满足方程0)(2202=+'+''R k R R m ρρρ 4.)(5x P 是下列哪一个方程的解_________。
A )0202)1(2=+'-''-y y x y x
B )0252)1(2=+'-''-y y x y x
C )0302)1(2=+'-''-y y x y x
D )052)1(2=+'-''-y y x y x
5.根据整数阶Bessel 函数的递推公式,下列结论哪一个是正确的________。
A ))(2)()(120x J x J x J '=-
B ))()()(1
11x J x x J x xJ '=+ C ))(2)()(210x J x x J x J =
- D ))(2)()(120x J x
x J x J '=+ 二、 填空题(每题3分)
1. 定解问题⎪⎪⎪⎩
⎪⎪⎪⎨⎧====><<=-====0 ,00
,0)0,0( sin cos 0002t t t l x x x x xx tt u u u u t l x t l x A u a u ωπ用本征函数发展开求解时,关于T(t)满足的方程是:
2. Legendre 多项式)(x P l 的x 的值域是______________________。
Bessel 函数)(x J n 的x 的值域是______________________。
3. 一圆柱体内的定解问题为⎪⎪⎩⎪⎪⎨⎧===<=∆===)
( ),(0 ,0210ρρρρf u f u u a u h z z a
1)则定解问题关于ρ满足的方程是:_____________________________;
相应方程的解为___________________________;
2)关于z 满足的方程是_______________________________________;
4. 计算积分
⎰-11)(dx x xP l 5. 计算积分⎰a dx x xJ 0
0)( 三、 (10分)长为l 的弦,两端固定,初始位移为21x +,初始速度为4x ,写出此物理
问题的定解问题。
四、 (10分)定解问题⎪⎩⎪⎨⎧===><<=-===0
0 ,)0 ,0( ,000t l x x xx t u u t u t l x Du u ,若要使边界条件齐次化,,求其辅助函数,并写出相应的定解问题
五、 (10分)利用达朗贝尔公式求解一维无界波动问题
⎪⎩⎪⎨⎧==>+∞<<-∞=-==x u x u t x u u t t t xx tt sin ||)0,(040
0 六、 (15分)用分离变量法求解定解问题
计算积分⎰-+=1
11)()(dx x P x xP I l l 七、 (15分)有一半径为R 的薄圆盘,若圆盘的上下面绝热,圆盘边缘的温度分布为
ϕϕρρ2cos 2|),(==R u ,试求圆盘上稳定的温度分布),(ϕρu 。
八、 (15分)设有一半径为R 的球壳,其球壳的电位分布θ2cos |==R r u ,写出球外的
电位满足的定解问题,并求球外的电位分布参考公式
(1)柱坐标中Laplace算符的表达式
(2) Legendre多项式
(3) Legendre多项式的递推公式
(4) Legendre多项式的正交关系
(5)整数阶Bessel函数
(6) Bessel函数的递推关系。
