可降阶的高阶微分方程改一阶线性微分方程
合集下载
第三节 可降阶的高阶微分方程
例5
求方程 yy′′ − y′2 0 的通解 。 ＝
dp 解 令 p = y′ ，则 y′′ = p 。 dy dp yp − p2 = 0 。 于是， 于是，原方程化为 dy dy = 0 ，故此时有解 y = C 。 若 p = 0 ，则 dx dp dy = 。 若 p ≠ 0 ，则原方程化为 p y dy p = 0 对应于 C1 = 0 = p = C1 y 。 两边积分，得 两边积分， dx y = C2 eC1x。 运用分离变量法， 运用分离变量法，得此方程的通解为
2 2
（***）
此处取负号是因为物体运动的方向与y轴的正向相反. 在（***）中令 y=R，就得到物体到达地面时的速度为
2 gR(l − R) v=− l
最后求物体落到地面所需的时间. 由（***）式有
1 1 dy = v = −R 2g − , y l dt
分离变量，得
1 l y dt = − dy. R 2g l − y
1 y′′ = 1 + y ′2 a
取原点 O 到点 A 的距离为定值 a ，即 |OA|= a ,则初始条件为：
y x =0 = a, y′ x =0 = 0.
故初值问题为
′′ 1 y = 1 + y ′2 , a y x = 0 = a, y ′ x = 0 = 0
′′ 1 y = 1 + y ′2 , a y x = 0 = a, y ′ x = 0 = 0
令 y ′ = p,
y′′ = p′ 代入上方程，得
dx = a 1 + p2 dp
1 2 p′ = 1+ p . a
x ln( p + 1 + p ) = + C1 a
62可降阶的高阶微分方程改63一阶线性微分方程 共17页
解: 将方程变形可得
y 1 ya(11)
xlnx
lnx
于是 P(x) 1 , xlnx
Q(x)a(1 1 ) lnx
所以 y e P (x )d x [Q (x )e P (x )d x d x C ]
1接例2
e xl1 nxd x[a (1 1)exl1 nxd xd x C ]
dx x2 )
积分得 ln p l( n 1 x 2 ) ln C 1,即 pC 1(1x2)
利用 y x0 3, 得C13,于是有 y3(1x2)
两端再积分得 yx33xC2
利用 y x0 1, 得C21,因此所求特解为 yx33x1
机动 目录 上页 下页 返回 结束
用线性方程通解公式求解 .
设 P (y ) 2 ,Q (y ) y 2
于是 x e P (y )d y[Q (y )e P (y )d y d y C ]
3接例2
e2 d y[( y2)e 2 d yd y C ] e 2 y[y2e 2 yd y C ]
例3. 求解 yyy20.
解: 设 yp(y),则 y d p d p d y p d p dx d y d x d y
代入方程得 ypdpp2 0, 即 d p dy
dy
py
两端积分得 ln p ln y lC n 1,即 pC1y, y C 1 y (一阶线性齐次方程)
3 . y f(y,y ) 令 yp(y),则y p dp dy
机动 目录 上页 下页 返回 结束
例1. 求y解 e2xcox.s
解: y e 2 x cx o d x s C 1
12e2xsinxC1
一阶线性微分方程,可降阶的高阶微分方程
y = Ce ∫
− P( x)dx
y+ 1. 一阶线性齐次方程 − ∫ P( x )dx ′ P ( x ) y ≡ 0∫ P( x )dx 非齐次方程通解 C + Q( x)e dx 非齐次方程通解 y = e
可分离变量
∫
2.
一阶线性非 一阶线性非齐次方程
y′ + P( x) y = Q( x)
求解
1+ y ′ 2 (1) y′′ = ； 2y dy ′ dz dz dy dz 解：令 y ′ = z ，则 y ′′ = = = =z ，
dx
dx
dy dx
dy
dz 1+ z 2 2 zdz dy z = = ， ，即 2 y dy 2 y 1+ z
积分，得 ln(1+ z 2 )= ln y + lnC ， 1+ z 2 = C1 y ． 积分，
x=e ∫
=e ∫
− P ( y )dy
1 dy y
∫ P( y)dydy] ， [C + ∫ Q( y)e
3 −
[∫ y e
∫
1 dy y
故原方程的通解为 x = y + Cy ． 3
1 3 dy + C ] = y[ y + C ] ， 3 1 4
二 、 Bernoulli（伯努利）方程的解法 （ 伯努利）
(2)
( x 2 + y 2 + 2 x − 2 y )dx + 2( y − 1)dy = 0 ;
y′ + y y ln y = 2 ． x x
y y (2) y′ + ln y = 2 ． x x 1 1 1 y′ + ln y = 2 ， 解： y x x
14-15一阶微分方程及可降阶的高阶微分方程ppt课件
12
例 5．求方程 dy 4 y x y 的通解。
dx x
解：把方程 dy 4 y x y 改写为 dy 4 y x y ，
dx x
dx x
令 z y 或 y z2 ，则有 dy 2z dz ， dx dx
代入原方程，得 2z dz 4z2 zx ， dx x
即 dz 2z x ，这是线性方程。 dx x 2
1 ln(1 2
u2 )
ln
x
ln C1 ，
arctan u ln C1 x 1 u2 e ， arctanu C1 x 1 u2 ，
将u
y
代入，得原方程的通解：e
arctan
y x
C
x2 y2 。
x
6
（二）形如 y f (ax by) 的方程
令 u ax by ， y 1 (u ax) ， y 1 (u a) ，
， dy dx
( y )2 x， y 1
x
令 y u ，则 y ux ， dy u x du ，代入原方程得
x
dx
dx
u
x
du dx
u2 u1
，
dx x
u u
1
du ，
dx x
(1
1 )du u
，
ln x u ln u C1 ，ln xu u C1 ， xu eC1 eu ，
b
b
代入原方程得： u a bf (u) ，
即 du a bf (u)，这是可分离变量方程。 dx
7
例 3．求方程 y sin(x y) 的通解。
解：令 u x y ，则 y x u ， y 1 u ，
代入原方程得：1 u sin u ，即 du 1 sin u ，
第五节 可降阶的高阶微分方程
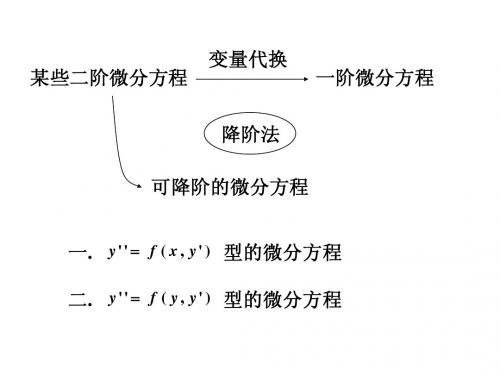
二、y′′ = f ( x, y′)型的微分方程 y′′ = f ( y, y′) 三、 y′′ = f ( y, y′) 型的微分方程
四、齐次方程 五、小结 思考题
定义：二阶及二阶以上的微分方程统称 为 高阶微分方程。一般形式为：
F ( x, y, y ', y ",L , y ( n ) ) = 0.
dy p= = ϕ ( x , C1 ) dx
通解为： 故方程的 通解为：y = ∫ ϕ ( x , C1 )dx + C 2
例 求微分方程 xy (5) + y ( 4) = 0的通解.
例 求微分方程 xy ′′ + y ' = 0的通解.
(1 + x 2 ) y ′′ = 2 xy ′ 满足初 例. 求微分方程 的特解. 始条件 y x = 0 = 1, y′ x = 0 = 3 的特解
二、y " = f ( x, y ')型的微分方程
特点： 特点： 右端不显含未知函数 y . 解法： 解法： 设 y′ = p 则 y′′ = dp = p′, dx . 方程变为 p′ = f（x，p） 关于x, 的 关于 p的
一阶微分方程，设其通解为 p = ϕ ( x , C1 ) 阶微分方程， 即
解： 设 y ′ = p , 代入方程并分离变量后 可得 dp 2x dx . = 2 p 1+ x 两端积分得 ln p = ln( 1 + x 2 ) + C 即 p = y ′ = C 1 (1 + x 2 ) (C 1 = ± e C )
由条件 y′
x=0
= 3，得C1 = 3
故 y ′ = 3(1 + x 2 )
可降阶的高阶微分方程
三、形如y″=f(y,y′)型的微分方程
【例4】
求微分方程yy″－y′2－y′=0的通解． 解方程不显含自变量x，设y′=p，则
，代入方程得
在y≠0,p≠0时，约去p并整理，得
这是关于p的一阶线性微分方程，利用公式解之得 p=C1y－1，即y′=C1y－1，再分离变量并两端积分，便得方程 的通解为
这是一阶方程，设其通解为
因y′=p(x)，于是
p=φ(x,C1)，
dydx=φ(x,C1)，
两端积分，得
y=∫φ(x,C1) dx+C2．
二、形如y″=f(x,y′)型的微分方程
【例2】
解方程xy″=y′lny′．
解设y′=p(x)，则
，方程化为
分离变量，得
为所求方程的通解．
二、形如y″=f(x,y′)型的微分方程
【例3】
三、形如y″=f(y,y′)型的微分方程
方程 y″=f(y,y′)（6-19）
中不显含自变量x．为了求出它的解，我们令y′=p，并利用复合函数 的求导法则把y″化为对y的导数，即
这样，方程（6-19）就成为
这是一个关于y,p变量的一阶微分方程．设它的通解为 y′=p=φ(y,C1)，
分离变量并积分，便得方程的通解为
可降阶的高阶 微分方程
一、形如y″=f(x)型的微分方程
对于微分方程
y″=f(x)，
其右端仅含自变量x，如分得
y′=∫f(x)dx+C1，
y=∫(∫f(x)dx)dx+C1x +C2． 以此类推，对于n阶微分方程，连续积分n次，便得含
有n个任意常数的通解．
一、形如y″=f(x)型的微分方程
【例1】
一阶微分方程解法
解法概述
01
一阶微分方程的解法主要包括分离变量法、常数变易法、积分因子法 等。
02
分离变量法适用于可以将方程改写为$frac{dy}{dx} = f(x)g(y)$形式的 方程。
03
常数变易法适用于形如$frac{dy}{dx} + P(x)y = Q(x)$的线性方程， 通过设定一个合适的常数变易，将方程转化为易于求解的形式。
06
可降阶的高阶微分方程解法
可降阶的高阶微分方程的概念
定义
可降阶的高阶微分方程是指可以通过适当的变换，将其化为较低阶的微分方程进行求解的一类高阶微 分方程。
分类
可降阶的高阶微分方程主要包括y''=f(x)型、y''=f(x,y')型和y''=f(y,y')型三种类型。
可降阶的高阶微分方程的解法
01
y''=f(x)型的解法
通过积分将二阶微分方程化为一阶微分方程进行求解。
02
y''=f(x,y')型的解法
通过适当的变量代换，将原方程化为关于新变量的一阶微分方程进行求
解。
03
y''=f(y,y')型的解法
令y'=p，将原方程化为关于y和p的一阶微分方程组进行求解。
可降阶的高阶微分方程的应用举例
常数变易法的步骤
第一步
观察原方程，确定需要变易的常数及其形式。
第二步
引入新的变量，将原方程中的常数替换为相应的函数，得到新方程。
第三步
求解新方程，得到通解或特解。
第四步
将通解或特解中的新变量还原为原方程的常数，得到原方程的解。
7-5 可降阶的高阶微分方程-精品文档
解
f( 二、 y x ,y ) 型微分方程
其特点为： 二阶方程中不显含未知 函数 y.
dp 令 p y， 则 y ， 解法： dx
原方程可化为一阶方程
dy ( x ,C ) ， 如果其通解为 p 1 即有 ( x , C ) ， 1 dx 上式两端积分，可得原 方程的通解为 ：
5 3 2 y d x d x d x d x d . 1 2 3 4 5
返回
三、 y f ( y ,y ) 型微分方程
其特点为：二阶方程中不显含自变 量x. dp dp dy dp 则 y p ， 解法：令 p y， dy dx dy dx
2 2 故原方程的通解为 ： C y 1 ( C x C ) . 1 1 2
返回2 例 Fra bibliotek 求方程 y y y 0 的通解 .
d ) (y y 0 , 解 将方程改写成 dx y dy Cdx , 故有 y y C ,即
2 两边积分得通解 y C x C . 1 2
函数 y，一阶线性非齐 解 此二阶方程不显含未知 dp 次微分方程 令 y p， 则y ， dx dp p dp 2 x, x 0 , 即 原方程可化为 x p dx dx x dx dx 从而p y e x xexdx C 1 1 2 1 2 C1 xdx C 1 x x 3 x 13 y x C ln C x . 故原方程的通解为 ： 1 2 9
y ln C cos x 上式两端再积分一次得 2 1 ln 由yx 2 得 C 2 1 2 4 ln cos x . 故所求特解为 ： y
可降阶高阶微分方程
n阶线性非奇次方程
y ( n ) + P1 ( x ) y ( n 1) + P2 ( x ) y ( n 2 ) + + Pn ( x ) y = 0
n阶线性奇次方程 下面以二阶方程为例,讨论高阶线性微分方程解的结构.
一. 二阶线性奇次方程解的结构 一般形式: y ′′ + P ( x ) y ′ + Q ( x ) y = 0, 显然, y = 0 是(2)的解. 讨论非平凡解: 定理1. 如果 y1 ( x), y2 ( x) 是(2)的两个解,则 y = C1 y1 ( x) + C2 y2 ( x) 也是(2)的解,其中 C1 ,C2 为任意常数. 证明: 由于 y1 ( x), y2 ( x)是(2)的两个解, 所以
∴C2 = 1
y = x3 + 3x + 1
三. y′′ = f ( y, y′) 型方程 如果方程不显含 x, dp = f ( y, p) 方程变为: p dy 解出这个以 y 为自变量的一阶方程的通解: 令 y′ = p , 则 y′′ =
dp dp dy dp = =p , dx dy dx dy
二. y′′ = f ( x, y′) 型方程 如果二阶方程不显含 y, 令 y′ = p ,则 y′′ = 方程变为: p′ = f ( x, p ) 解出这个一阶方程的通解: p = ( x, C1 ) 则原方程的通解为: 例:
dp = p′ dx
y = ∫ ( x, C1 ) dx + C2
的特解,则 y1 ( x) + y2 ( x) 是方程
y ′′ + P ( x ) y ′ + Q ( x ) y = f1 ( x ) + f 2 ( x ) ( 4)
可降阶的高阶微分方程
可降阶的高阶微分方程引言高阶微分方程是微积分中的一个重要概念，通常包含二阶及以上的导数。
然而，在某些情况下，我们可能希望将高阶微分方程降阶为一阶微分方程，这样可以更方便地求解和分析。
本文将讨论可降阶的高阶微分方程及其相关概念。
一阶可降阶微分方程一阶可降阶微分方程是指可以通过某种变换将其降为一阶微分方程的高阶微分方程。
例如，考虑一个二阶微分方程：d2y dx2+a(x)dydx+b(x)y=f(x)通过引入新的变量P(x)=dydx，我们可以将上述二阶微分方程转化为一个一阶可降阶微分方程：dPdx+a(x)P+b(x)y=f(x)这样，我们就成功地将高阶微分方程降为了一阶微分方程。
降阶方法降阶高阶微分方程的一般方法是引入新的变量，并通过适当选择这些变量的方式将其转化为一阶微分方程。
下面介绍几种常用的降阶方法。
1. 变量代换法变量代换法是一种常见的降阶方法，通过引入新的变量将高阶微分方程转化为一阶微分方程。
例如，对于一个三阶微分方程：d3y dx3+a(x)d2ydx2+b(x)dydx+c(x)y=f(x)我们可以引入新的变量P(x)=d 2ydx2和Q(x)=dydx，从而将该三阶微分方程转化为一个一阶微分方程：dPdx+a(x)P+b(x)Q+c(x)y=f(x)dQdx+b(x)P+c(x)Q=02. 微分幺正变换法微分幺正变换法是一种通过选择适当的变换矩阵将高阶微分方程转化为一阶微分方程的方法。
具体而言，通过选择一个幺正变换矩阵U(x)，我们可以将一个n阶微分方程转化为一个一阶微分方程：d dx [y1y2⋮y n]=U(x)[f1f2⋮f n]其中y i表示原始高阶微分方程的解，f i表示相应的一阶微分方程的解。
3. 特解代换法特解代换法是一种通过引入特解来降低高阶微分方程的阶数的方法。
具体而言，我们假设高阶微分方程的一个特解形式，并代入原方程求解。
将得到的特解代入原方程，我们可以得到一个低阶微分方程。
可降阶的高阶微分方程
y
( x3 6
ex
2x)dx
x4 24
ex
x2
C3.
再由y x0 1,得C3 2，所以
y x4 ex x2 2为所求的特解. 24
6.4.2 y(n) f ( x, y(n1) )型的微分方程
令 p y(n1)，则原方程化为
例6.40（略）
例6.41
求方程 y(5) 1 y(4) 0 的通解。 x
解 令y(4) p, 则y(5) p, 原方程可化为
p
1 x
p
0 .
p
C1e
(
1 x
)dx
C1 x .
y(4) .
y
C1xdx .
C1 2
x2
C2,
y
y ln x d x x ln x x C1，
y ( x ln x x C1)d x
x ln xdx (x C1)d x
x2
ln xd( 2 ) (x C1)d x
x2
x2 1
x2
ln x 2
2
dx x
例6.42 设函数y( x)在区间[0， ）上具有连续偏导数，
并且满足关系式y( x) 1 x 2 x ( x t) y(t) y(t)dt,求y(t). 0
解
x
x
y( x) 1 x 2x y(t)y(t)dt 2 ty(t)y(t)dt,
0
0
[
2 x2
e
3 x
dx
dx
C1]
可降阶的高阶微分方程
§10.3 可降阶的高阶微分方程
( n) y f ( x ) 型的微分方程 一.
二. y f ( x, y) 型的微分方程
三. y f ( y, y) 型的微分方程
教学目标
1. 掌握三种特殊高阶方程的求解方法.
机动
目录
上页
下页
返回
结束
从本节起，我们将讨论二阶及二阶以上的微分方程，即
y f ( x, y)
令 y p( x ), 则 y
dp dx
3.
y f ( y, y)
令 y p( y ),
dp 则 y p dy
16
机动 目录 上页 下页 返回 结束
2018/7/27
思考练习
1. 方程 y f ( y) 如何代换求解 ? 答: 令 y p( x ) 或 y p( y ) 均可. 一般说, 用前者方便些. 有时用后者方便 . 例如, y e
1 3 C1 ( x x ) C 2 3
以条件 y x0 1 ， y x0 3 代入得 C1 3 ， C2 1
故所求特解为 y x 3 3 x 1
19
机动 目录 上页 下页 返回 结束
则
p F ( x,C1 )
dy F ( x,C1 ) dx 这是个一阶微分方程，两端进行积分，便可得方程
(10.3.2)的通解为
y F ( x,C1 )dx C2
7
例2 求微分方程 xy y x 2 0 的通解. 解 由于方程中不显含未知函数 y ，是属于 y f ( x, y) 型. 设 y p, 则
y x 0 3 的特解.
解 令
p y 则原方程化为
( n) y f ( x ) 型的微分方程 一.
二. y f ( x, y) 型的微分方程
三. y f ( y, y) 型的微分方程
教学目标
1. 掌握三种特殊高阶方程的求解方法.
机动
目录
上页
下页
返回
结束
从本节起，我们将讨论二阶及二阶以上的微分方程，即
y f ( x, y)
令 y p( x ), 则 y
dp dx
3.
y f ( y, y)
令 y p( y ),
dp 则 y p dy
16
机动 目录 上页 下页 返回 结束
2018/7/27
思考练习
1. 方程 y f ( y) 如何代换求解 ? 答: 令 y p( x ) 或 y p( y ) 均可. 一般说, 用前者方便些. 有时用后者方便 . 例如, y e
1 3 C1 ( x x ) C 2 3
以条件 y x0 1 ， y x0 3 代入得 C1 3 ， C2 1
故所求特解为 y x 3 3 x 1
19
机动 目录 上页 下页 返回 结束
则
p F ( x,C1 )
dy F ( x,C1 ) dx 这是个一阶微分方程，两端进行积分，便可得方程
(10.3.2)的通解为
y F ( x,C1 )dx C2
7
例2 求微分方程 xy y x 2 0 的通解. 解 由于方程中不显含未知函数 y ，是属于 y f ( x, y) 型. 设 y p, 则
y x 0 3 的特解.
解 令
p y 则原方程化为
第十二章 微分方程习题课
它的特征方程 解得两个不同的实根
故齐次方程的通解为
r 2 3r 2 0
r1 1, r2 2
Y C1e x C2e2 x
x 由于 f ( x) 5 是Pm ( x)e 型(其中 Pm ( x) 5, 0 )，且 0
0 y * ae a ，求出 不是特征方程根，所以应设特解
y y 2 y (1 2 x)e x
y Y y C1e x C2e2 x xe x
【例5】求方程 y 3 y 2 y 5 满足初始条件 y(0) 1 , y(0) 2 的特解。
分析：此为二阶常系数非齐次线性微分方程，由解的结 构，先求出对应齐次的通解，再求出其本身的一个特解. 解：所给的方程是二阶常系数非齐次线性微分方程，
1．定义
y py qy 0 (2)二阶常系数线性非齐次微分方程: y py qy f ( x )
(1)二阶常系数线性齐次微分方程： 2．解的结构性质 (1)若 y1 和 y2 是齐次方程的解,则 C1 y1 C2 y2是齐次方程的解。 (2)若 y1 和 y2 是齐次方程的线性无关解,则 C1 y1 C2 y2 是齐次 方程的通解。
解题方法流程图
求 y py qy f ( x ) 通解 特征方程：r 2 pr q 0 Yes 有实根 No
Yes
r1 r2
No
r1,2 i
Y C1er1x C2er2 x
f ( x ) 的类型
Yes 混合型 No
Y (C1 C2 x)e r1 x
可降阶的高阶微分方程
解题方法流程图
No
Yes
y ( n) f ( x)
【精选】.一阶线性微分方程、可降阶二阶微分方程
所以
y 3(1 x2 )
再积分,得 y x2 3x C2
把初始条件 y x0 1 代入上式,得 C2 1
于是所求的特解为 y x2 3x 1
三、 y f y, y型的微分方程
y f y, y
右端不显
含自变量 x
解法 设y p( y),则y dp dp dy p dp
dx dy dx dy
y
1 4
e2x
cos
x
C1x
C2
二、 y f x, y 型的微分方程
y f x, y
右端不显
含未知数 y
解法 设y px, 则y dp p
dx 于是原方程变为
p f x, p
它是一个关于变量 x 、p 的一阶微分方程.解此一阶微分
方程,便得到原方程的通解.
例5-10 求微分方程 y 1 y 0的通解 x
二、 y f x, y型的微分方程 三、 y f y, y型的微分方程
一、 y f ( x) 型的微分方程
y f ( x)
右端仅含自
变量 x
解法 接连积分两次,便可得到方程的通解
例5-9 求微分方程 y e2x cos x的通解.
解 对所给方程连续积分两次,得
y
1 2
e2x
sin
x
C1
y
Ce
P( x)dx
dx
非齐次微分方程
dy dx
P(x)
y
Q(x)的通解
y C(x)e P(x)dx
一阶线性非齐次微分方程的通解中C(x)是个未定
式，下面我们确定C(x)。
非齐次方程通解形式 与齐次方程通解相比
C C(x)
非齐次微分方程 dy P(x) y Q(x) 的求解 dx
y 3(1 x2 )
再积分,得 y x2 3x C2
把初始条件 y x0 1 代入上式,得 C2 1
于是所求的特解为 y x2 3x 1
三、 y f y, y型的微分方程
y f y, y
右端不显
含自变量 x
解法 设y p( y),则y dp dp dy p dp
dx dy dx dy
y
1 4
e2x
cos
x
C1x
C2
二、 y f x, y 型的微分方程
y f x, y
右端不显
含未知数 y
解法 设y px, 则y dp p
dx 于是原方程变为
p f x, p
它是一个关于变量 x 、p 的一阶微分方程.解此一阶微分
方程,便得到原方程的通解.
例5-10 求微分方程 y 1 y 0的通解 x
二、 y f x, y型的微分方程 三、 y f y, y型的微分方程
一、 y f ( x) 型的微分方程
y f ( x)
右端仅含自
变量 x
解法 接连积分两次,便可得到方程的通解
例5-9 求微分方程 y e2x cos x的通解.
解 对所给方程连续积分两次,得
y
1 2
e2x
sin
x
C1
y
Ce
P( x)dx
dx
非齐次微分方程
dy dx
P(x)
y
Q(x)的通解
y C(x)e P(x)dx
一阶线性非齐次微分方程的通解中C(x)是个未定
式，下面我们确定C(x)。
非齐次方程通解形式 与齐次方程通解相比
C C(x)
非齐次微分方程 dy P(x) y Q(x) 的求解 dx
第六章 微分方程第三节 可降阶的高阶 微分方程
(t
2
故所求质点运动规律为
t
3
)
3T
-5-
第三节
可降阶的高阶微分方程
二、
y f ( x , y )
型的微分方程
原方程化为一阶方程
设 y p ( x ) ,
第 十 二 章 微 分 方 程
设其通解为 则得
p ( x , C1 ) y ( x , C1 )
再一次积分, 得原方程的通解
dp p
2 xdx (1 x )
2
2
ln | p | ln( 1 x ) ln | c | p c (1 x ) y c (1 x )
2 2
即
再次积分得通解
y cx
c 3
x c1
3
-7-
第三节
可降阶的高阶微分方程
例4
y 2 x y 2 x 3 求解 y x 0 1, y x 0 1
满足的方程 .
解:
在点 P(x, y) 处的切线倾角为 , 于是
y
S1
1 2
y cot
2
P(x, y)
S2
0
x
y
y( t ) d t
O
S2
S1
x x
y co t
- 16 -
第三节
可降阶的高阶微分方程
利用 两边对 x 求导, 得
第 定解条件为 十 二 令 y p ( y ), 章 微 分 方 程
y ( x , C1 ) d x C 2
-6-
第三节
可降阶的高阶微分方程
例3 求微分方程 ( 1 x 2 ) y 2 x y 的通解。 解 令p
2
故所求质点运动规律为
t
3
)
3T
-5-
第三节
可降阶的高阶微分方程
二、
y f ( x , y )
型的微分方程
原方程化为一阶方程
设 y p ( x ) ,
第 十 二 章 微 分 方 程
设其通解为 则得
p ( x , C1 ) y ( x , C1 )
再一次积分, 得原方程的通解
dp p
2 xdx (1 x )
2
2
ln | p | ln( 1 x ) ln | c | p c (1 x ) y c (1 x )
2 2
即
再次积分得通解
y cx
c 3
x c1
3
-7-
第三节
可降阶的高阶微分方程
例4
y 2 x y 2 x 3 求解 y x 0 1, y x 0 1
满足的方程 .
解:
在点 P(x, y) 处的切线倾角为 , 于是
y
S1
1 2
y cot
2
P(x, y)
S2
0
x
y
y( t ) d t
O
S2
S1
x x
y co t
- 16 -
第三节
可降阶的高阶微分方程
利用 两边对 x 求导, 得
第 定解条件为 十 二 令 y p ( y ), 章 微 分 方 程
y ( x , C1 ) d x C 2
-6-
第三节
可降阶的高阶微分方程
例3 求微分方程 ( 1 x 2 ) y 2 x y 的通解。 解 令p
降阶法求解微分方程
降阶法求解微分方程微分方程是数学中的重要概念，用来描述变量之间的关系和变化规律。
在求解微分方程的过程中，降阶法是一种常用且有效的方法。
本文将介绍降阶法的基本原理，并通过一个具体的例子来演示该方法的应用。
首先，降阶法是一种将高阶微分方程转化为一系列低阶微分方程的方法。
通过逐步降低微分方程的阶数，我们可以简化问题的复杂性，并更容易找到方程的解。
考虑一个简单的二阶线性微分方程：a(d^2y/dx^2)+b(dy/dx)+cy=0其中，a、b和c是常数，y是未知函数。
我们的目标是找到y关于x的解析表达式。
为了使用降阶法，我们引入一个新的变量v，令v=dy/dx。
这样，原始的二阶微分方程可以转化为一个一阶方程组：dv/dx=-b/a*v-c/a*ydy/dx=v现在，我们有两个关于v和y的一阶微分方程。
接下来，我们将对这个方程组进行求解。
首先，我们求解第一个微分方程dv/dx=-b/a*v-c/a*y。
可以将该方程转化为标准的一阶线性齐次微分方程形式：dv/dx+(b/a)*v+(c/a)*y=0该方程的解可以通过积分因子法求得。
假设积分因子为μ(x)，则乘以积分因子后，可以得到：(μ(x)*v)'+(b/a)*μ(x)*v+(c/a)*μ(x)*y=0通过选择适当的积分因子，使得方程中(b/a)*μ(x)等于μ'(x)，则上式可以化简为：(d/dx)(μ(x)*v)+(c/a)*μ(x)*y=0现在，我们可以通过积分的方式求解上式，得到：μ(x)*v+(c/a)*∫(μ(x)*y)dx=C1其中，C1是一个常数。
通过对上式两边关于x求导，我们可以得到：v=-(c/a)*y*∫μ(x)dx+C2其中，C2是另一个常数。
将上式代入第二个微分方程dy/dx=v，可以得到：dy/dx=-(c/a)*y*∫μ(x)dx+C2这是一个一阶线性非齐次微分方程，可以通过变量分离的方法进一步求解。
通过逐步求解这一系列的一阶微分方程，我们最终可以得到原始二阶微分方程的解析解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
化为 dx 2x y2 , dy
用线性方程通解公式求解 .
设 P( y) 2 , Q( y) y2
于是
x
e
P(
y
) dy
[
Q( y) e P( y)dydy C]
3接例2
e2dy [
(
y
2
)
e
2dy
dy
C
]
e2 y [ y2 e2 ydy C]
y2 y 1 Ce2 y . 2 24
(一阶线性齐次方程)
故所求通解为
机动 目录 上页 下页 返回 结束
例4. 求解
y ay2 0
y x0 0 ,
y x0 1
解: 令
则方程变为
积分得
1 p
ax
ቤተ መጻሕፍቲ ባይዱ
C1,
利用
p
x0 y
x0
1
得
C1
1
再解
dy dx
1 1 ax
,
并利用
y
x0
0,
定常数
C2
.
机动 目录 上页 下页 返回 结束
6.3 一阶线性微分方程
1 2
e2x
sin
x
C1
y
1 e2x 4
cos x
C1x C2
y
1 e2x 8
sin
x
C1 x 2
C2 x
C3
机动 目录 上页 下页 返回 结束
例2. 求解 解:
(1 x2 )y 2xy y x0 1, y x0 3
代入方程得
(1 x2 ) p 2x p 分离变量
积分得 ln p ln (1 x2 ) ln C1 , 利用 y x 0 3 , 得 C1 3,于是有 y 3(1 x2 )
积分得
即 y C(x 1)2
用常数变易法求特解. 令 y u (x) (x 1)2 , 则
y u (x 1)2 2u (x 1)
代入非齐次方程得 解得 故原方程通解为
u
2
(x
3
1) 2
C
3
机动 目录 上页 下页 返回 结束
例2. 求下列方程的通解 解: 将方程变形可得
于是
所以 y e P(x) dx[ Q(x) e P(x)dxdx C]
两端再积分得 y x3 3 x C2 利用 y x 0 1 , 得 C2 1, 因此所求特解为
y x3 3x 1
机动 目录 上页 下页 返回 结束
例3. 求解 解:
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
2. 解非齐次方程 dy P(x) y Q(x) dx
用常数变易法: 作变换 y(x) u(x) e P(x)d x , 则
ue P(x)d x P(x)u e P(x)d x P(x) u e P(x)d x Q(x)
即
两端积分得对应齐u 次 方Q程(x通) e解 P(x)ydx dCxeC P(x)dx
故原方程的通解
y
e
P(x)d
x
Q(
x)
e
P(
x)
d
x
dx
C
即
y Ce P(x)d x e P(x)d x Q(x) e P(x)d xdx
齐次方程通解
非齐次方程特解
机动 目录 上页 下页 返回 结束
例1. 解方程
解:
先解
dy 2y 0 , 即 dx x 1
dy 2dx y x 1
2.2 可降阶高阶微分方程
一、 二、 三、
型的微分方程 型的微分方程
型的微分方程
机动 目录 上页 下页 返回 结束
可降阶微分方程的解法 —— 降阶法 逐次积分
令 y p(x) , 令 y p(y) ,
机动 目录 上页 下页 返回 结束
例1.
解: y e2x cos x d x C1
一阶线性微分方程标准形式: dy P(x) y Q(x) dx
若 Q(x) 0, 称为齐次方程 ;
若 Q(x) 0, 称为非齐次方程 .
1. 解齐次方程 dy P(x) y 0 dx
分离变量
两边积分得 ln y P(x)dx ln C
故通解为
y C e P(x)dx
机动 目录 上页 下页 返回 结束
例3. 求一连续可导函数
使其满足下列方程:
令 u xt
解:
x
f (x) sin x 0 f (u)d u
f (x) f (x) cos x
则有
f (0) 0
利用公式可求出
f (x) 1 (cos x sin x ex ) 2
机动 目录 上页 下页 返回 结束
内容小结
1.可降阶微分方程解法 三种类型
1接例2
e
1 x ln
x
dx
[
a(1
1
)
e
x
1 ln
x
dx
dx
C
]
ln x
e
1 x ln
x
dx
[
a(1
1
)
e
x
1 ln
x
dx
dx
C
]
ln x
1 ln x
[
a(1
1 ln x
)
ln
xdx
C
]
1 [ax(ln x 2) C] ln x
2接例2
(2)
y
2x
1
y2
解： 调换自变量与因变量的地位 ,
2.一阶线性微分方程 齐次方程 非齐次方程 常数变易法
作业 P261 3(1)(7) .
用线性方程通解公式求解 .
设 P( y) 2 , Q( y) y2
于是
x
e
P(
y
) dy
[
Q( y) e P( y)dydy C]
3接例2
e2dy [
(
y
2
)
e
2dy
dy
C
]
e2 y [ y2 e2 ydy C]
y2 y 1 Ce2 y . 2 24
(一阶线性齐次方程)
故所求通解为
机动 目录 上页 下页 返回 结束
例4. 求解
y ay2 0
y x0 0 ,
y x0 1
解: 令
则方程变为
积分得
1 p
ax
ቤተ መጻሕፍቲ ባይዱ
C1,
利用
p
x0 y
x0
1
得
C1
1
再解
dy dx
1 1 ax
,
并利用
y
x0
0,
定常数
C2
.
机动 目录 上页 下页 返回 结束
6.3 一阶线性微分方程
1 2
e2x
sin
x
C1
y
1 e2x 4
cos x
C1x C2
y
1 e2x 8
sin
x
C1 x 2
C2 x
C3
机动 目录 上页 下页 返回 结束
例2. 求解 解:
(1 x2 )y 2xy y x0 1, y x0 3
代入方程得
(1 x2 ) p 2x p 分离变量
积分得 ln p ln (1 x2 ) ln C1 , 利用 y x 0 3 , 得 C1 3,于是有 y 3(1 x2 )
积分得
即 y C(x 1)2
用常数变易法求特解. 令 y u (x) (x 1)2 , 则
y u (x 1)2 2u (x 1)
代入非齐次方程得 解得 故原方程通解为
u
2
(x
3
1) 2
C
3
机动 目录 上页 下页 返回 结束
例2. 求下列方程的通解 解: 将方程变形可得
于是
所以 y e P(x) dx[ Q(x) e P(x)dxdx C]
两端再积分得 y x3 3 x C2 利用 y x 0 1 , 得 C2 1, 因此所求特解为
y x3 3x 1
机动 目录 上页 下页 返回 结束
例3. 求解 解:
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
2. 解非齐次方程 dy P(x) y Q(x) dx
用常数变易法: 作变换 y(x) u(x) e P(x)d x , 则
ue P(x)d x P(x)u e P(x)d x P(x) u e P(x)d x Q(x)
即
两端积分得对应齐u 次 方Q程(x通) e解 P(x)ydx dCxeC P(x)dx
故原方程的通解
y
e
P(x)d
x
Q(
x)
e
P(
x)
d
x
dx
C
即
y Ce P(x)d x e P(x)d x Q(x) e P(x)d xdx
齐次方程通解
非齐次方程特解
机动 目录 上页 下页 返回 结束
例1. 解方程
解:
先解
dy 2y 0 , 即 dx x 1
dy 2dx y x 1
2.2 可降阶高阶微分方程
一、 二、 三、
型的微分方程 型的微分方程
型的微分方程
机动 目录 上页 下页 返回 结束
可降阶微分方程的解法 —— 降阶法 逐次积分
令 y p(x) , 令 y p(y) ,
机动 目录 上页 下页 返回 结束
例1.
解: y e2x cos x d x C1
一阶线性微分方程标准形式: dy P(x) y Q(x) dx
若 Q(x) 0, 称为齐次方程 ;
若 Q(x) 0, 称为非齐次方程 .
1. 解齐次方程 dy P(x) y 0 dx
分离变量
两边积分得 ln y P(x)dx ln C
故通解为
y C e P(x)dx
机动 目录 上页 下页 返回 结束
例3. 求一连续可导函数
使其满足下列方程:
令 u xt
解:
x
f (x) sin x 0 f (u)d u
f (x) f (x) cos x
则有
f (0) 0
利用公式可求出
f (x) 1 (cos x sin x ex ) 2
机动 目录 上页 下页 返回 结束
内容小结
1.可降阶微分方程解法 三种类型
1接例2
e
1 x ln
x
dx
[
a(1
1
)
e
x
1 ln
x
dx
dx
C
]
ln x
e
1 x ln
x
dx
[
a(1
1
)
e
x
1 ln
x
dx
dx
C
]
ln x
1 ln x
[
a(1
1 ln x
)
ln
xdx
C
]
1 [ax(ln x 2) C] ln x
2接例2
(2)
y
2x
1
y2
解： 调换自变量与因变量的地位 ,
2.一阶线性微分方程 齐次方程 非齐次方程 常数变易法
作业 P261 3(1)(7) .