相似理论与模型试验例题集
初中数学相似6大模型问题(完整可编辑)
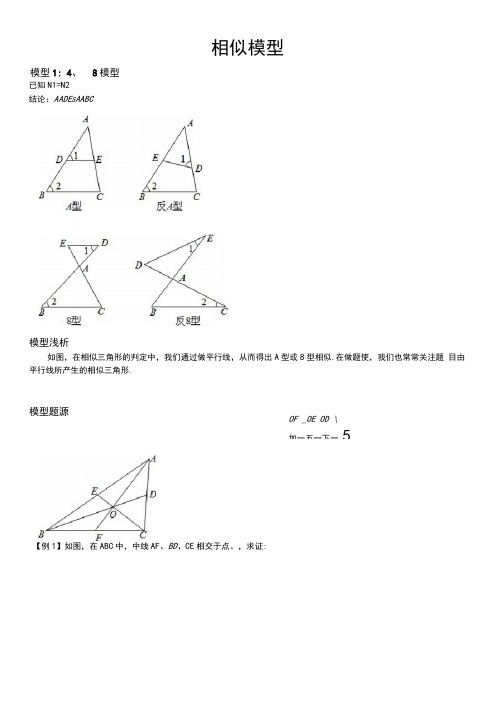
已知N1=N2 结论:AADE S AABC模型浅析如图,在相似三角形的判定中,我们通过做平行线,从而得出A 型或8型相似.在做题使,我们也常常关注题 目由平行线所产生的相似三角形.模型题源【例1】如图,在ABC 中,中线AF 、BD 、CE 相交于点。
,求证:模型1: 4、 8模型相似模型OF _OE OD \加一五一下一5DE 1证法一:如图①,连接。
£七是中点,,——=一.,DE//BCBC 2OF DF 1OF I•••△EODsacoB(8 模型).••& = &!=2.同理:—=1OC BC 2 OA 2• OF _OE _OD _1GF BF 1 证法二:如图②,过尸作"V/AC 交8。
于点G, ••加是中点,; ------ =——=-AD BC 2QF 1•;AD=CD,:.——=一・•:FG"AD, •二△G 。
/(8 模型)AD 2OF GF 1 lXi OE 1 OD 1 . OF OE OD 1 OAAD 2 OC2OB2 OAOCOB2【例2】如图,点从厂分别在菱形A8C 。
的边AB 、AO 上,且AE=O 凡BF 交DE 于点、G,延长斯交C 。
的延长AF 线于H,若——=2,DF••市一无一方一天图②求器的值.解答::四边形A8CQ是菱形,:.AB^=BC=CD=AD.设。
/=小则OF=AE=a, AF=EB=2a. 9:HD//AB, MHFDsABFAHD DF ■ —AB AF HFFB1=一,••HD = 1.5a, 2FHBH1=-93:.FH1= -BH 3■:HD”EB,:.△DGHs NGB,:-------- =GBHDEB\.5a2a_3=-9 4.BGHB4-7练习:1 .如图,D 、上分别是△ABC 的边AB 、8C 上的点,且DE 〃AC, AE,。
相交于点0,若S :: S^COA =1: 25.则 S/.BD E 与Szxc 的比是.DE 1解答:VDE//AC, AADOE^ACOA,又 S SOE : S^COA = 1: 25,; -------- -AC 52 .如图所示,在248CO 中,G 是8c 延长线上的一点,AG 与BD 交于点、E,与OC 交于点F,此图中的相似三 角形共有对.解::四边形ABCD 是平行四边形,,AD 〃BC, AB//CD,(1) AABD^ACDB : (2) AABE^AFDE ; (3) A AED ^A GEB :(4) AABG^AFCG^AFDA,可以组成3对相似三角形.,图形中一共有6对相似三角形.3.如图,在aABC 中,中线8。
(完整版)相似三角形经典模型总结及例题分类.doc
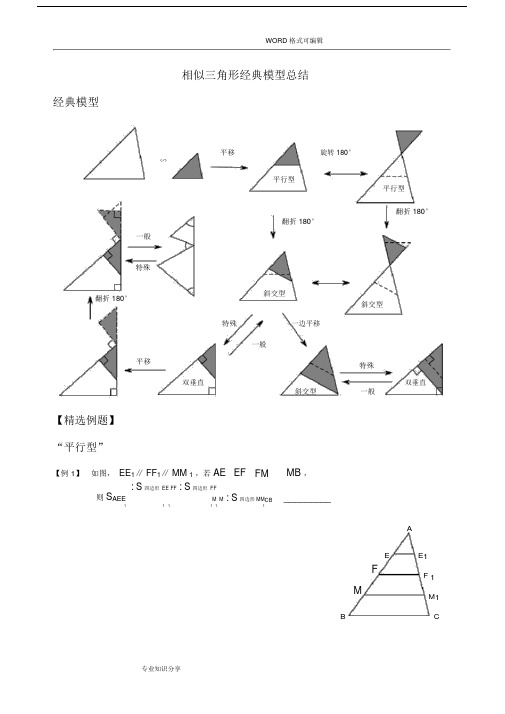
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB ,则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____A DE FMNB C【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H求证: PE PHPF PGG D CE PFA B H【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且AE2, BE、 CD相交于点 F ,求BF的值ECEF ADF EB C【例 5】已知:在ABC 中, AD 1AB,延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证:① DE EF ② AE 2CEADEB专业知识分享【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC求证:CEF 为等腰三角形ACDEB F【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:11 1 .c a bACEB F D【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论.CAEB F D【例 9】如图,四边形ABCD中,B D90M是AC上一点,ME AD于点EMF BC,,于点 F 求证:MFME 1AB CDDEMA CFB【例 10】如图,在ABC 中, D 是 AC 边的中点,过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证: AE BF BE CFAEDBC F 【例 11】如图,在线段AB 上,取一点 C ,以 AC , CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB, AE交 CD于点 P, BD交 CE于点Q,求证: CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中,求作一个正方形DEFG,使 D, E落在 BC边上, F , G分别落在AC , AB 边上,作法如下:ABC 两边上的正方形D'E'F 'G'如图,第一步:画一个有三个顶点落在第二步:连接 BF ' 并延长交 AC 于点 F第三步:过 F 点作 FE BC ,垂足为点 E第四步:过 F 点作 FG∥BC 交 AB 于点 G第五步:过 G 点作 GD BC ,垂足为点 D四边形 DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中,如果BC 6 3,ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理:E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况: B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C , E', F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD , AD ∥BC ,对角线AC 、 BD 互相垂直,则①证明: AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ,以点 O 为旋转中心,逆时针旋转度(090 ),问上面的结论是否成立,请说明理由DAOB C【例 15】(全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和 BEFG 均为正方形,求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图,ABC 中, D 在 AB 上,且 DE∥BC 交 AC 于 E , F 在 AD 上,且 AD2AF AB ,求证:AEF :ACDAFD EB C【例 17】如图,等边三角形ABC中,D,E分别在BC,AB上,且CE BE ,AD ,CE 相交于 M ,求证 : EAM : ECAAEMB DC AGF BE【例 18】如图,四边形ABCD 的对角线相交于点O ,BAC CDB ,求证:DAC CBDADOB C【例 19】如图,设ABBCCA,则 1 2 吗?AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中, AD , CE 分别为 BC , AB 边上的高,ABC 和BDE 的面积分别等于 18和 2 , DE 2,求 AC 边上的高AEB D C【例 21】如图,在等边ABC 的边 BC 上取点 D ,使BD 1,作CH AD,H为垂足,连结BH。
相似理论与模型试验例题集模型设计练习题

可得:
203 = 8000
⑨由准则
π9
=
J L4
可得:
(11)
J = J' L4 (L' )4
CJ Cl 4
=1
(12)
CJ = Cl4 = 204 = 160000
当高度按 Cl = 20 缩小后,J ' 和 ω' 用来求模
型梁的梁宽。如梁断面形状上所有的几何尺寸都
按 Cl 缩小后,A'、ω'、J '就自动满足了 π 7、π8、π 9
f [P、E、L、Ec、Rc、σ、y]=0 (1)
模型设计练习题三: 梁的力学特性模型试验
一、梁的尺寸和受力状况 如图1所示,试用模型试验的方法,求各跨度 中点的应力(不考虑重力)。
图1 梁的尺寸和受力状况示意图
1、列参数准则
根据图1已有参数和力学知识,影响应力的
参数有应力σ ⎡⎣N/cm2 ⎤⎦ ;变形 y[cm];转角[无因次]; 集中荷载 p[N ];连续荷载q[N / m];弯矩 M [N • m];梁的
①取 Cl = 5
时,模型管长
L' = l =10 = 2m 55
原型管直径
∅' = ∅ = 0.2 = 0.04 = 40mm C1 5
②试验中流水用与输水管中 和 相同的水,即
C μ=
μ μ'
=
1
Cρ =
ρ ρ'
=
1
③ 求模型中流速 ω ' 。从雷诺准则 Re = ωlρ 知,两现象相
μ
似其雷诺准则必相等,即
CP
=Cω2
=(
1 )2 = 5
1 25
桥梁模型试验相似理论及试验实例PPT课件

设:
跨度
原型
L
模型1 L/2
模型2 L/2
各物理参数(表中模型2为重度与原型一致对应):
面积
惯性矩
截面 模量
A
J
W
应力 集中力 F
弯矩 M
挠度 f
重度
A/4 J/16 W/8
F/4 M/8 f/2 2
A/4 J/16 W/8
F/4 M/16 f/4
第五章 桥梁模型试验
动力试验模型
动力试验模型除了要满足静力试验模型的三个要求外, 还要满足与动力有关的物体条件和运动条件(包括结构 的运动反应和产生的条件)的相似。
2023最新整理收集 do something
相似理论 桥梁静动力相似 桥梁模型试验实例
第五章 桥梁模型试验
概述
仿照原型(真实结构)并按照一定比例关系复制而 成的代表物,它具有原型的全部或部分特征。
通过对模型的试验,可以得到与原型相似的工作情 况,从而可以了解和研究原型的工作性能。
模型试验一般包括模型设计、制作、测试和分析等 内容,中心问题是如何设计模型。
关系式 1 1
1
说明
模型设计时的主要控制参数 模型设计时的主要控制参数
模型设计时的主要控制参数 施加动荷载时主要控制参数 施加动荷载时主要控制参数
第五章 桥梁模型试验
简支梁动力模型试验的相似
如前面静力模型动力相似,则需增加如下各参数:
跨度 弹性模量 时间 集中力荷载 加速度
原型
L
E
模型1
L/2
E
t
F
g
F/4
g
注意:时间的相似常数与几何常数之间的关系。
重度 2
相似模型练习题

相似模型练习题相似模型练习题是数学中一类常见的题型,用于考察学生对相似模型的理解和应用能力。
相似模型是指形状相似的两个或多个物体,在比例尺不变的情况下,对应部分的长度比保持不变。
以下是几个相似模型练习题,每个题目都附有解析和具体步骤。
题目一:已知圆A的半径是5,圆B的半径是8,求圆A和圆B面积的比值。
解析:圆A的面积为π * 5^2 = 25π圆B的面积为π * 8^2 = 64π所以圆A和圆B面积的比值为25π / 64π = 25 / 64 ≈ 0.39题目二:一辆汽车行驶了180公里,行驶时间是2小时。
求相似模型下,汽车行驶100公里所需要的时间。
解析:根据题意,汽车行驶180公里用时2小时,即速度为180 / 2 = 90公里/小时。
所以相似模型下,汽车行驶100公里所需要的时间为100 / 90 ≈ 1.11小时。
题目三:两根长度分别为12cm和16cm的木棍相似模型下的比例尺是1:2,求这两根木棍相似模型下的长度比。
解析:根据题意,相似模型下的比例尺是1:2,即长度比为1/2。
所以这两根木棍相似模型下的长度比为12 * 1/2 : 16 * 1/2 = 6 : 8 = 3 : 4。
题目四:已知两个相似三角形的边长比是3:5,其中一个三角形的周长是24cm,求另一个三角形的周长。
解析:根据题意,三角形的边长比为3:5。
假设其中一个三角形的周长是24cm,则另一个三角形的周长为24 * (5/3) = 40cm。
通过以上四个例子,我们可以发现相似模型练习题的基本思路是根据已知条件,运用相似模型的定义和性质进行推导和计算。
在解答过程中,要善于运用比例关系,注意单位的换算,严谨而准确地进行计算。
相似模型题目的难易程度有所不同,需要灵活运用所学知识进行求解。
相似模型在数学中具有广泛的应用,不仅可以用于求解长度、面积、体积等几何问题,还可以用于解决实际生活中的比例关系和缩放问题。
在学习相似模型的过程中,要加强对相似形状的观察和判断能力,培养准确运用比例关系和相似模型求解问题的能力。
中考相似模型大全(附20道绝妙好题)

中考相似模型大全(附20道绝妙好题)
“射影定理”
“一线三等角相似”
“手拉手相似模型”
两相似,共顶点,等顶角,则必有手拉手相似(口诀)
“对角互补相似模型”
“三平行模型”
证明方法:
“内接矩形相似模型”
“线束模型”
以下为中考超纲内容,仅供有兴趣的同学研究
看了这么多,来几道好题热热身吧!第一题:A字相似模型的构造
第二题:相似三角形的性质与判定
第三题:8字相似模型的构造
第四题:线束模型的构造
(此题如果学过四点共圆的同学应该可以秒杀)第五题:内接矩形相似模型的构造
第六题:三平行模型
第七题:反A模型的构造
第十、十一题:斜射影模型
第十二题:射影模型应用
第十三题:射影模型应用
第十四题:射影模型的构造
第十五题:三垂直模型的应用
第十六题:一线三等角模型的构造
第十七题:手拉手相似模型的构造(1)
第十八题:手拉手相似模型的构造(2)
第十九题:对角互补类旋转相似应用
第二十题:对角互补类旋转相似的构造
本篇推文从定内容到选题、排版、编辑,耗时近十个小时,希望能对大家有所帮助,如有错误辛苦指正,欢迎大家一起探讨!。
相似理论与模型试验例题集

1/2。也就是说,钢桥上对应点应力σ = 2σ '。
当模型长度仍为1m时,从(10)式可得:
CP
=
P P'
=
2(10)2
=
200
P' = P = 10*1000 = 50kg (0.05t )
200 200
(11)
此时,由于弹性模量之缩比CE ≠ 1 ,则带 来模型试验时加载减少,同时测得的应力亦小
d2 y' dl ' 2
= Kq'
l'
2
(2)
式中符号同(1)。
②写出单值条件的相似常数式:
CE
=
E E'
; CI
=
J⎫
J
'
⎪ ⎪
Cy
=
y y'
; Cl
=
l l'
⎪ ⎬ ⎪
Cq
=
q q'
⎪ ⎪ ⎭
③将(3)式代入(1)式得:
( ) ( ) CE E'CJ J '
Cyd2 y' Cl 2 dl ' 2
复合结构,要使模型和原型各组成部分应力变形严格
相似,必须要使加载变形前后结构模型与原型始终保
持几何相似,故有Cl= Cδ,即Cε=1,因此,上述应力 变形相似条件可写为:
Cp/ Cσ=1;CE Cε/ Cσ=1;Cv=1
(1)
为了使模型的破坏荷载和破坏形态与原结构完全
相似,不但要满足上述弹性状态下应力应变相似,而
f
⎛ ⎜
⎜⎜σ
⎜ ⎝
⎛ ⎜⎝
1
P 1 ⎞2 L ⎟⎠
,
相似三角形中常见基本模型及训练

万能解题模型1.(2019·遵义)如图,已知⊙O的半径为1,AB,AC是⊙O的两条弦,且AB=AC,延长BO交AC于点D,连接OA,OC.若AD2=AB·DC,则OD22.(2019·娄底)如图,点D 在以AB 为直径的⊙O 上,AD 平分∠BAC ,DC ⊥AC ,过点B 作⊙O 的切线交AD 的延长线于点E.求证:(1)直线CD 是⊙O 的切线; (2)CD·BE =AD·DE.证明:(1)连接OD. ∵AD 平分∠BAC , ∴∠CAD =∠BAD.∵OA =OD ,∴∠BAD =∠ADO. ∴∠CAD =∠ADO.∴AC ∥OD. ∵CD ⊥AC ,∴CD ⊥OD. 又∵OD 为⊙O 的半径, ∴直线CD 是⊙O 的切线. (2)连接BD.∵BE 是⊙O 的切线,AB 为⊙O 的直径, ∴∠ABE =∠BDE =90°.∵CD ⊥AC ,∴∠C =∠BDE =90°. ∴∠CAD =∠BAE =∠DBE.∴△ACD ∽△BDE.∴CD DE =ADBE.∴CD·BE =AD·DE.3.(2018·巴中)如图,⊙O的两弦AB,CD相交于点P,连接AC,BD,得S△ACP∶S△DBP=16∶9,则AC∶BD =4∶3.4.(2018·扬州)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE,AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP·MD=MA·ME;③2CB2=CP·CM.其中正确的是(A) A.①②③B.①C.①②D.②③相关结论:△ACD∽△ABC∽△CBD,CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.5.(2019·宜宾)如图,已知Rt △ABC 中,CD 是斜边AB 上的高,AC =4,BC =3,则AD =165.6.(2018·安顺)如图,点P 1,P 2,P 3,P 4均在坐标轴上,且P 1P 2⊥P 2P 3,P 2P 3⊥P 3P 4.若点P 1,P 2的坐标分别为(0,-1),(-2,0),则点P 4的坐标为(8,0).7.(2019·南充)如图,在△ABC 中,以AC 为直径的⊙O 交AB 于点D ,连接CD ,∠BCD =∠A. (1)求证:BC 是⊙O 的切线;(2)若BC =5,BD =3,求点O 到CD 的距离.解:(1)证明:∵AC 是⊙O 的直径, ∴∠ADC =90°.∴∠A +∠ACD =90°. ∵∠BCD =∠A ,∴∠ACD +∠BCD =90°. ∴∠ACB =90°.又∵OC 是⊙O 的半径, ∴BC 是⊙O 的切线.(2)过点O 作OH ⊥CD 于点H. ∵∠ACB =∠BDC =90°,∠B =∠B , ∴△ACB ∽△CDB. ∴BC BD =AB BC .∴53=AB 5. ∴AB =253.∴AD =163.∵OH ⊥CD ,∴CH =DH.∵AO =OC ,∴OH =12AD =83.∴点O 到CD 的距离是83.(1)如图1,△CAP ∽△PBD(此图又叫做“三垂图”); (2)如图2、图3,有以下结论: ①△CAP ∽△PBD ;②连接CD ,当点P 为AB 的中点时,△CAP ∽△PBD ∽△CPD.8.(2019·凉山州)如图,在正方形ABCD 中,AB =12,AE =14AB ,点P 在BC 上运动(不与B ,C 重合),过点P 作PQ ⊥EP ,交CD 于点Q ,则CQ 的最大值为4.9.如图,在边长为9的等边△ABC 中,BD =3,∠ADE =60°,求AE 的长.解:∵△ABC是边长为9的等边三角形,∴∠B=∠C=60°,AB=BC=AC=9.∴∠BAD+∠ADB=120°.∵∠ADE=60°,∴∠CDE+∠ADB=120°.∴∠BAD=∠CDE.∴△ABD∽△DCE.∴ABDC=BDCE,即99-3=3CE.∴CE=2.∴AE=9-2=7.【变式】点D,E分别变到CB,AC的延长线上.如图,△ABC是等边三角形,点D,E分别在CB,AC的延长线上,∠ADE=60°.求证:△ABD∽△DCE.证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∴∠ABD=∠DCE=120°.∵∠ABC=∠DAB+∠BDA,∠ADE=∠EDC+∠BDA,∠ABC=∠ADE=60°,∴∠DAB=∠EDC.∴△ABD∽△DCE.10.如图,在矩形纸片ABCD中,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E 重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)(2)如果AM=1,sin∠DMF=35,求AB的长.基本模型5三角形内接矩形模型解:(1)有三对相似三角形:△AMP ∽△BPQ ∽△CQD.(2)设AP =x ,由折叠的性质,得BP =AP =EP =x.∴AB =DC =2x.由△AMP ∽△BPQ ,得AM BP =APBQ ,∴BQ =x 2.由△AMP ∽△CQD ,得AP CD =AMCQ,∴CQ =2.AD =BC =BQ +CQ =x 2+2,MD =AD -AM =x 2+2-1=x 2+1.在Rt △FDM 中,sin ∠DMF =35,DF =DC =2x ,∴2x x 2+1=35. 解得x 1=3,x 2=13(不合题意,舍去).∴AB =2x =6.11.如图,已知正方形DEFG 的顶点D 、E 在△ABC 的边BC 上,顶点G 、F 分别在边AB 、AC 上.如果BC=4,△ABC 的面积是6,那么这个正方形的边长是 7.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) (2)
[ξ ] = [L];⎡⎣t0 −ty ⎤⎦ = [D]; [t0 −tD ] = [D]
式中 L—长度;T—时间; D—温度;Q—热量。
④把各物理量纲代入π项式,列出因次 (量纲)等价式(3)
[π] =[D]k [T]b ⎡⎣L2T−1⎤⎦c [L]d ⎡⎣QT−1L−1D−1⎤⎦e ⎡⎣QL−3⎤⎦f [L]g [D]h [D]i [ ] [ ] [ ] [ ] [ ] π = D T L Q k−e+h+i b−c−e 2c+d−e−3f +g e+f
相似理论与模拟实验例题
例1 静态应力模型 这是一个弹性模型,可求解静态应力问题。 a、 求导准则 平衡方程: ∂σ x + ∂τ yx + ∂τ zx + X = 0
∂x ∂y ∂z
∂τ xy + ∂σ y + ∂τ zy + Y = 0
∂x ∂y ∂z
∂τ xz + ∂τ yz + ∂σ z + Z = 0
Cl2 = 1 Cτ Ca
④将(3)式代入(5)式得
x2
( x ' )2
τ a =1
τ ' a'
经整理得 τ a = τ 'a' = π 。
( ) x2
x' 2
(5)
(1)式中有4个参数(n=4)。基本量
[L];[T];[D] (k=3),则准则数为n-k=4-3=1个。
导出之准则称傅里叶(J.Fourier)准则,记
型,故有:
CE= Cσ=Cp=CR=1 ;Cμ=1;Cρ=1
(2)
式中 CR为强度相似常数;
Cμ为钢筋配筋率相似常数;
Cρ为钢纤维体积率的相似常数。
在这种情况下,只要确定适当的几何相似常 数就可以了。
试验得到的模型强度就等于结构强度。
例3、一钢桥跨度10m,最大集中荷重为10t,现 用一个1m长,几何形状与钢桥相似之梁作试验, 求桥的应力。
复合结构,要使模型和原型各组成部分应力变形严格
相似,必须要使加载变形前后结构模型与原型始终保
持几何相似,故有Cl= Cδ,即Cε=1,因此,上述应力 变形相似条件可写为:
Cp/ Cσ=1;CE Cε/ Cσ=1;Cv=1
(1)
为了使模型的破坏荷载和破坏形态与原结构完全
相似,不但要满足上述弹性状态下应力应变相似,而
则可写出以下函数式
( ) ϕ⎡⎣t、τ、a、x、λ、δ、ξ、t0 −ty 、(t0 −tD)⎤⎦=0
②写出π项式
( ) ( ) π = tkτbacxdλeδ fξ g t0 −ty h t0 −tD i
③列出各参数的基本因次
[t] = [D];[τ ] = [T ]; [a] = ⎡⎣L2T −1⎤⎦ ;[x] = [L]; [λ ] = ⎡⎣QT L −1 −1D−1 ⎤⎦ ;[δ ] = ⎡⎣QL−3 ⎤⎦ ;
= P'
2
则
(7)
p
σ σ'
=
⎛
p' L ⎞2
⎜⎝ L ' ⎟⎠
即 Cσ
= CP Cl2
(8)
因
C得E:=
1, CE
CP
=
=
Cσ ,则Cσ
Cl2
=1
。代入(1)式
钢桥长10m,模型长1m,则Cl
= 10 1
=10
。
CP =
P P'
= Cl2
= 102
= 100
P' = P 100
(9)
原钢桥上集中荷载。则模型对应处应力荷载
模型试验相似指标为: 由几何方程得:Cε Cl /Cδ=1; 由边界方程得:Cp/Cσ=1; 由物理方程得:CECε/Cσ=1,Cv = 1 。 其中:Cl为几何相似常数;
Cp为荷载(面力)相似常数;
CE为弹性模量相似常数; Cδ为位移相似常数; Cε为应变相似常数; Cσ为应力相似常数; Cv为泊松比相似常数。 钢筋钢纤维高强混凝土结构是由三种材料组成的
解 假设应力σ 与荷载P,长度L和材料弹性模量E
有关。则可写出方程
f (σ , P, L, E ) = 0
将(1)式转换成准则方程
f
⎛ ⎜⎝
σ
K M2
, PK, LM , E
K M2
⎞ ⎟⎠
=
0
令:
LM = 1 PK = 1 即
M K
= =
1 L 1 P
⎫ ⎪⎪ ⎬ ⎪ ⎪⎭
(1) (2)
(3)
将(3)式代入(2)式得:
= 5×2 = 20
1 2
γ ' = 2γ ,故可在石膏中
这就是说,不是 cε 非取1不可,在小变形范围内
,可取cε ≤ 8
对于相似材料试验,如果:
Cl=20,Cr=1/2,CE=2,Cu=1
则有:Cε=CrCl/CE=5
Cδ= CεCl=5*20=100 但对C于x− =大1多0 数结构试验,采用严格相似,则
d2 y' dl ' 2
= Kq'
l'
2
(2)
式中符号同(1)。
②写出单值条件的相似常数式:
CE
=
E E'
; CI
=
J⎫
J
'
⎪ ⎪
Cy
=
y y'
; Cl
=
l l'
⎪ ⎬ ⎪
Cq
=
q q'
⎪ ⎪ ⎭
③将(3)式代入(1)式得:
( ) ( ) CE E'CJ J '
Cyd2 y' Cl 2 dl ' 2
= =
t t' ; a a'
Cτ ; Cl
=τ τ'
=x x'
⎫ ⎪⎪ ⎬ ⎪ ⎪⎭
③将(3)式代入(1)式得:
( ) Ct∂t'
Cτ ∂τ '
= Caa'
Ct∂2t ' Cl 2 ∂x'
2
即
( ) Cl2
Cτ Ca
∂t '
∂τ '
= a'
∂ 2t ' ∂x' 2
(3) (4)
比较(4)式和(2)式得:
cε =1,这时不考虑自重应力场,上部荷载采用施
加边界面力模拟。
例2 对钢筋钢纤维高强混凝土梁或柱的强度特性 (极限承载力)试验研究。
由于钢筋钢纤维高强混凝土结构的强度高,几何 尺寸大,不易进行原型的破坏性试验,可采用缩尺结 构模型。
根据试验目的,此类试验不但要搞清加载过程中 结构截面上的应力分布情况,而且还要测量模型的破 坏荷载。所以,模型设计不但要满足应力、变形的相 似条件,而且还要满足强度相似条件。根据相似理论 和弹性力学的基本方程,采用方程分析法,可推导出 其静力模型相似指标为:
X'
=0
对于平衡方程:
cσ cγ cL
(
∂σ ' x
∂x '
+
∂τ
' yx
∂y '
+
∂τ
' zx
∂z '
)
+
X'
=0
相似指标:ccγ σcL = 1
,相似准则π1=
σ γL
=
σ' γ ' L'
①
由几何方程: c ε .c L = 1 , л2= εL
②
cδ
δ
由物理方程: cε c E = 1
cσ
,л3=
CE=
E E'
=2
,由
cσ cγ cL
=1
得: cγ
=
cσ cL
=
2 = 1 =γ 20 10 γ '
即 γ ' = 10γ (石膏的混合料比岩石大10倍,很难,
找不到这种材料。)
为此:取cε ≠1而是 cε =5,cσ = cε .cE = 5 * 2 = 10
加铁则屑即cγ 可= c。cELcε
f
⎛ ⎜
⎜⎜σ
⎜ ⎝
⎛ ⎜⎝
1
P 1 ⎞2 L ⎟⎠
,
P
1 P
,L
1 L
,
E
⎛ ⎜⎝
1
P 1 ⎞2 L ⎟⎠
⎞ ⎟ ⎟ ⎟ ⎟ ⎠
=
0
f
⎛ σ L2
⎜ ⎝
P
,1,1,
E L2 P
⎞ ⎟ ⎠
=
0
(4)
由(4)式得到两个准则:
π1
=
σ L2
P
π2
=
EL2 P
①当试验模型的材料与钢桥材料相同(即E相同)
为:
F0
=
τa
x2
例6、求在半无限平面的不稳定导热的准则方程。
解: ①罗列参数,写出现象的函数式。
已知在半无限平面不稳定导热问题的影响参
数有:
温度 t ;时间 τ ;导温系数a ;
几何量 x ;导热系数 λ ;
结冰时单位体积潜热δ ;
冻结壁面位置ξ ;初始温度 t0;
冻结温度 tD ;冷源温度 t y 。
且还要满足以下强度相似条件:
强度相似条件: (a) 模型与原型的材料,在加载全过程中应 力应变曲线相似;
(b) 结构各部分材料的强度相似; (c) 结构破坏的强度准则相似。
显而易见,要完全满足上述相似条件,模型材料
