计算自由度和体系构造分析例题
结构工程师结构力学几何组成分析例题
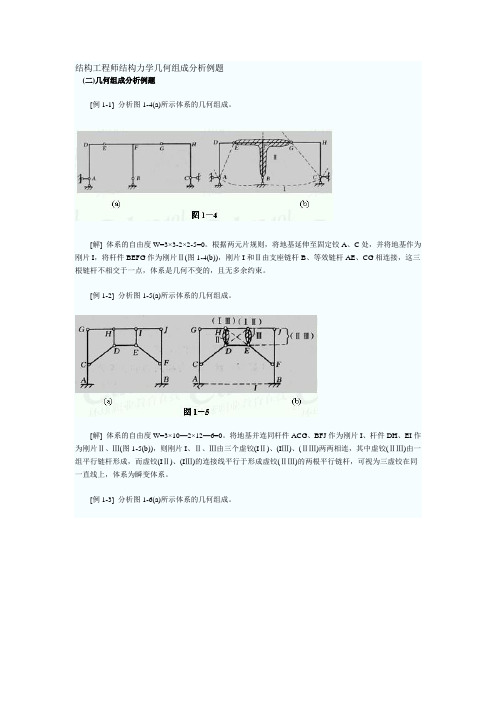
结构工程师结构力学几何组成分析例题(二)几何组成分析例题[例1-1] 分析图1-4(a)所示体系的几何组成。
[解] 体系的自由度W=3×3-2×2-5=0。
根据两元片规则,将地基延伸至固定铰A、C处,并将地基作为刚片I,将杆件BEFG作为刚片Ⅱ(图1-4(b)),刚片I和Ⅱ由支座链杆B、等效链杆AE、CG相连接,这三根链杆不相交于一点,体系是几何不变的,且无多余约束。
[例1-2] 分析图1-5(a)所示体系的几何组成。
[解] 体系的自由度W=3×10—2×12—6=0。
将地基并连同杆件ACG、BFJ作为刚片I、杆件DH、EI作为刚片Ⅱ、Ⅲ(图1-5(b)),则刚片I、Ⅱ、Ⅲ由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,其中虚铰(ⅡⅢ)由一组平行链杆形成,而虚铰(IⅡ)、(IⅢ)的连接线平行于形成虚铰(ⅡⅢ)的两根平行链杆,可视为三虚铰在同一直线上,体系为瞬变体系。
[例1-3] 分析图1-6(a)所示体系的几何组成。
[解] 体系的自由度W=3×8—2×10-4=0。
根据两元片规则,将地基延伸至固定铰A处,并将地基作为刚片I,将CEF作为等效刚片Ⅱ,DB杆作为刚片Ⅲ,这三个刚片由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,如图1-6(b)所示。
因形成无穷远处的两个虚铰(IⅢ)、(ⅡⅢ)的两组平行链杆不相互平行,故体系是无多余约束的几何不变体。
[例1-4] 分析图1-7(a)所示体系的几何组成。
[解] 体系的自由度W=3×9—2×12—3=0。
根据一元片规则,去除图1-7(a)所示体系的一元片,得图1-7(b)所示体系。
再将杆件AB、CE、DF分别作为刚片I、Ⅱ、ⅡⅢ,这三个刚片由三组平行链杆形成的三个无穷远处的虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,根据三刚片连接规则,体系为无多余约束的几何可变体系(无穷远处的三个点在一广义直线上)。
几何组成分析习题及答案.
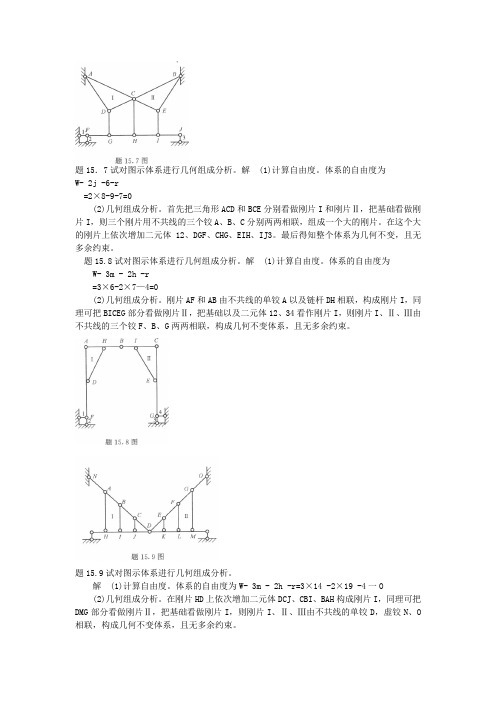
题15.7试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。
首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ,把基础看做刚片I,则三个刚片用不共线的三个铰A、B、C分别两两相联,组成一个大的刚片。
在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。
最后得知整个体系为几何不变,且无多余约束。
题15.8试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。
刚片AF和AB由不共线的单铰A以及链杆DH相联,构成刚片I,同理可把BICEG部分看做刚片Ⅱ,把基础以及二元体12、34看作刚片I,则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联,构成几何不变体系,且无多余约束。
题15.9试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。
在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I,同理可把DMG部分看做刚片Ⅱ,把基础看做刚片I,则刚片I、Ⅱ、Ⅲ由不共线的单铰D,虚铰N、O 相联,构成几何不变体系,且无多余约束。
题15.10试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。
由于AFG部分由基础简支,所以可只分析AFG部分。
可去掉二元体BAC只分析BFGC部分。
把三角形BDF、CEG分别看做附片I和I,刚片I和I由三根平行的链杆相联,因而整个体系为瞬变。
题15.11试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。
首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4,成一个大的刚片I。
机构的组成及其自由度的分析计算

一、机构的组成及其自由度的分析计算(共170题)1.组成机构的要素是和;构件是机构中的单元体。
2.具有、、等三个特征的构件组合体称为机器。
3.机器是由、、所组成的。
4.机器和机构的主要区别在于。
5.从机构结构观点来看,任何机构是由三部分组成。
6.运动副元素是指。
7.构件的自由度是指。
机构的自由度是指。
8.两构件之间以线接触所组成的平面运动副,称为副,它产生个约束,而保留个自由度。
9.机构中的运动副是指。
10.机构具有确定的相对运动条件是原动件数机构的自由度。
11.在平面机构中若引入一个高副将引入___个约束,而引入一个低副将引入____个约束,构件数、约束数与机构自由度的关系是12.平面运动副的最大约束数为,最小约束数为。
13.当两构件构成运动副后,仍需保证能产生一定的相对运动,故在平面机构中,每个运动副引入的约束至多为,至少为。
15.计算机机构自由度的目的是______________________________。
16.在平面机构中,具有两个约束的运动副是副,具有一个约束的运动副是副。
17.计算平面机构自由度的公式为F= ,应用此公式时应注意判断:(A) 铰链,(B) 自由度,(C) 约束。
18.机构中的复合铰链是指;局部自由度是指;虚约束是指。
19.划分机构的杆组时应先按的杆组级别考虑,机构的级别按杆组中的级别确定。
20.机构运动简图是的简单图形。
31.任何具有确定运动的机构都是由机架加原动件再加自由度为零的杆组组成的。
--------------()32.一种相同的机构组成不同的机器。
(A) 可以;(B) 不能33.机构中的构件是由一个或多个零件所组成,这些零件间产生任何相对运动。
(A) 可以;(B)不能34.有两个平面机构的自由度都等于1,现用一个带有两铰链的运动构件将它们串成一个平面机构,则其自由等于。
(A) 0;(B) 1;(C) 235.原动件的自由度应为。
(A) 1;(B) +1;(C) 036.基本杆组的自由度应为。
自由度计算例题

自由度计算例题在机械设计、力学分析以及各种工程领域中,自由度的计算是一项重要且基础的任务。
它帮助我们理解和预测物体或系统在特定条件下的运动可能性。
下面,我们通过几个具体的例题来深入探讨自由度的计算。
首先,来看一个简单的平面机构。
假设有一个平面四连杆机构,由四个杆件通过转动副连接而成。
我们要计算这个机构的自由度。
根据平面机构自由度的计算公式:F = 3n 2PL PH ,其中 F 表示自由度,n 表示活动构件的数目,PL 表示低副的数目,PH 表示高副的数目。
在这个四连杆机构中,活动构件的数目 n 为 3(因为机架不算活动构件),低副的数目 PL 为 4(四个转动副),高副数目 PH 为 0 。
将这些值代入公式,得到:F = 3×3 2×4 0 = 9 8 = 1 。
这意味着这个平面四连杆机构只有一个自由度,其运动是确定的。
再看一个稍微复杂一些的例子。
假设有一个平面凸轮机构,由一个凸轮和一个从动件组成,它们通过高副接触。
在这个例子中,活动构件的数目 n 为 2 ,低副的数目 PL 为 1(一个转动副或移动副),高副的数目 PH 为 1 。
代入公式可得:F = 3×2 2×1 1 = 6 2 1 = 3 。
这说明该平面凸轮机构有 3 个自由度。
接下来,考虑一个空间机构的例子。
假设有一个空间四连杆机构,由四个杆件通过球铰连接。
对于空间机构,自由度的计算公式为:F = 6n 5PL 6PH 。
这里,活动构件数目 n 为 3 ,低副数目 PL 为 4 (四个球铰相当于4 个低副),高副数目 PH 为 0 。
计算可得:F = 6×3 5×4 0 = 18 20 =-2 。
自由度为负数,这表明该机构的运动是受到约束的,无法自由运动。
再看一个包含复合铰链的例子。
假设有一个机构,其中三个杆件在同一处通过转动副连接。
在这种情况下,这个连接点处应视为两个复合铰链。
机构自由度题

F=3n-2Pl+P’=6-6+1=1
复合铰链
局部自由度
n=7
Pl=9
Ph=2
F=3n-2Pl-Ph=21-18-2=1
n=5, Pl=7
F=?
n=4, Pl=6
F=?
例:计算图示机构的自由度
局部自由度
则: n=7, PL=9, Ph=2,
F 3 n 2 P l Ph 37 29 2 1
虚约束
7
返回
例2:对图示机构进行结构分析。
解: 计算机构的自由度,
I处滚子为局部自由度,运动链HGF引入虚约束,应除去,
C处为复合铰链。 CG HD EF
n=8 ,PL = 11 ,Ph=1 则: F =3n-2PL-Ph =3×8-2×11-1 =1
19
去除局部自由度和虚约束后,进行高副低代。
20
机构为Ⅱ级机构
21
例3:对图示机构进行结构分析
试计算图示机构的自由 度;并分析下列2种 情况下组成机构的基 本杆组及机构的级别, 要求分别画出不同的 基本杆组。 • 1)当以构件2为原动 件时, • 2)当以构件5为原动 件时。
22
设计方案
主题:“幸福生活——今天和明天” 内容:“休闲娱乐机械和家庭用机械的设计和制作”。家庭 用机械指“对家庭或宿舍内物品进行清洁、整理、储存 和维护用机械”。休闲娱乐机械指“机械玩具或在家庭、 校园、社区内设置的健康益智的生活、娱乐机械” 要求:说明书A4纸5页以上
1. 名称,用途
2. 叙述工作原理,解决的关键技术问题
3. 机构简图,作品特色
4. 查找已有类似机构,说明背景,及类似机构原理。
2-2平面体系的计算自由度

§2 体系计算自由度
一、体系计算自由度公式
根据自由度和约束的概念,一个体系的计 算自由度在数值上等于组成体系的刚片或点具 有的总自由度与体系总约束的差。
计算自由度=组成体系的刚片或点具有的 总自由度-体系总约束数
yluo@
§2 体系计算自由度
一、体系计算自由度公式
1.一般体系的计算自由度公式
⑴ W>0,表明体系缺少足够的约束, 因此是几何可变的。
W=1
yluo@
W=1
§2 体系计算自由度
三、计算自由度与体系可变性
计算自由度W可用于判断体系所具有 的约束在数量上是否足够维持体系为几何 不变。
⑵ W=0,表明体系具有成为几何不变 所必需的最少约束数目。
几何 不变
yluo@
§2 体系计算自由度
例题2.7 试求图示体系的计算自由度。
体系为一般体系 刚片+约束
刚片数 m=7 单铰数 h=9 支座约束数 r=3 yluo@
W 3m (2h r )
3 7 (2 9 3) 0
§2 体系计算自由度
例题2.8 试求图示体系的计算自由度。 比较
例题2.5 试求图示体系的计算自由度。
把体系视为一般体系 刚片+约束
刚片数 m=17 单铰数 h=24 支座约束数 r=3 yluo@W 3m Fra bibliotek(2h r )
3 17 (2 24 3) 0
§2 体系计算自由度
例题2.5 试求图示体系的计算自由度。
按铰接链杆体系计算 点+约束
若不考虑体系与地基之间的支承关系, 而只研究体系自身的几何不变性时:
•W>3,表明体系缺少足够的约束,因此 是几何可变的。 •W=3,表明体系具有成为几何不变所必 需的最少约束数目。 •W<3,表明体系具有成为几何不变所必 需的约束外,尚有多余联系。
平面机构自由度计算例题及答案
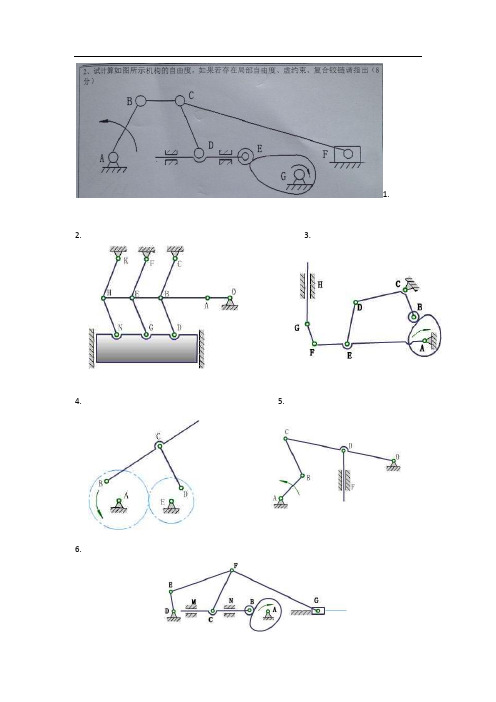
1.2. 3.4. 5.6.1.构件数n为7,低副p为9,高副pn为1,局部自由度为1,虚约束为0.E处为局部自由度,C处为复合铰链.F=3n-2p-pn=3*7-2*9-1=2(与原动件数目一致,运动确定)2. B处有复合铰链,有2个转动副。
无局部自由度。
B点左侧所有构件和运动副带入的约束为虚约束,属于与运动无关的对称部分。
n=5, PL=7, PH=0, F= 3n-2PL -PH=3×5-2×7-1×0=1。
运动链有确定运动,因为原动件数= 自由度数。
3.A处为复合铰链,因为有3个构件在此处组成成转动副,所以应算2个转动副。
B处为局部自由度,假设将滚子同构件CB固结。
无虚约束。
n=6, PL=8, PH=1, F= 3n-2PL -PH=3×6-2×8-1=1。
运动链有确定运动,因为原动件数= 自由度数。
4. 没有复合铰链、局部自由度、虚约束。
n=4, PL=5, PH=1, F= 3n-2PL -PH=3×4-2×5-1=1。
运动链有确定运动,因为原动件数= 自由度数。
5. 计算自由度:n=4, P L=6, P H=0, F= 3n-2P L -P H=3×4-2×6-1×0=0,运动链不能动。
修改参考方案如图所示。
6. F处为复合铰链,因为有3个构件在此处组成成转动副,所以应算2个转动副。
B处为局部自由度,假设将滚子同构件CB固结。
移动副M、N中有一个为虚约束,属于两构件在多处组成运动副。
n=7, PL=9, PH=1, F= 3n-2PL -PH=3×7-2×9-1=2。
运动链没有确定运动,因为原动件数< 自由度数。
结构力学自由度的计算例题及解析

1. 对于一个简单的平面桁架结构,若共有6个节点和10根构件,那么其自由度为多少?- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中,每个支座具有多少个约束?- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时,若结构有8个节点和12根构件,自由度公式为:自由度 = 3n - 2j,其中n是节点数,j是构件数。
该结构的自由度是多少?- A. 4- B. 6- C. 8- D. 104. 一个平面结构中,假设有4个节点,6根构件,所有构件都在一个平面上,计算其自由度时需考虑:- A. 3自由度每节点,减去2自由度每构件- B. 2自由度每节点,减去1自由度每构件- C. 2自由度每节点,减去2自由度每构件- D. 3自由度每节点,减去1自由度每构件5. 对于一个三维空间的桁架结构,若有10个节点和20根构件,其自由度计算应使用的公式是:- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中,如果节点数为5,构件数为8,计算其自由度时,正确的自由度为: - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构,其自由度为:- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点,8根构件,计算自由度时,如果框架是完全支撑的,结果是:- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构,其中有5个节点和12根构件,计算自由度时所用的公式为: - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7,构件数为10,且结构为刚性框架,计算其自由度时,结果为:- A. 5- B. 7- C. 9- D. 11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本规律运用
1、求体系的计算自由度W,并对其进行结构分析。
解:混合系:W = (3m + 2j)-(3g + 2h + b)
m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16
W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3
构造分析:在刚片FGHIJ的基础上增加二元体得到整个体系有多个三个多余约束的几何不变体系。
2、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)求解W 按照刚片系计算:
W = 3m - 2h - 3g - b
m=9 h=12 g=0 b=0
W = 3m - 2h - 3g - b =3×9-2×12=3
(2)构造分析。
如图所示三刚片连接。
三铰不共线组成几何不变体系且无多余约束。
3、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)计算W:W = (3m + 2j)-(3g + 2h + b)
m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16
W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3
(2)结构构造分析
如图示体系内部(先撤除支座及地基)由三个刚片Ⅰ、Ⅱ、Ⅲ 用三个瞬铰两两相连,且三个瞬铰在一直线上,为几何瞬变体系。
4、如图所示为三角形ABC及其他链杆所组成体系,试考察BC边上G铰不同位置与体系整体几何特性的关系,给出简要分析过程。
(a) (b)
(c) (d)
解:(1)观察图(a)所示体系,△BEG直接与大地固定铰支,可以将B点看做铰结点,则BE,BG为链杆,因此,与大地直接相连的约束多余三根支杆,所以将大地必须看做是一个刚片。
BG和CD与GC相连,BE和A支座与△AEF相连,通过“找对家”的思路可以找到如图所示三刚片。
G铰位于BC中间时,三虚铰共线,组成瞬变体系。
(2)G铰在B点时,如图(c)所示,B-C-D可以看做直接添加在大地上的二元体,可以与大地看做一个刚片,△AEF看做另一个刚片,两刚片之间通过共线的三根链杆相连,组成瞬变体系。
(3)G铰在C点时,如图(d)所示,△AEF和大地通过四根连杆相连,其中EF、EC、CF不共线,也不全交于一点。
因此体系是有一个多余约束的几何不变体系。
因此,G铰由B到C的过程中,提及的几何特性分别为瞬变、瞬变、有一个多余约束的几何不变体系。
5、试求图示体系的计算自由度,并进行几何构造分析。
(a) (b)
解:(1)计算W。
W = 3m - 2h - 3g–b
m=5 g=0 h=5 b=4
W = 3m - 2h - 3g–b=3×5-2×5-4=1>0 该体系缺少一个必要约束为几何可变。
(2)如图(b)所示,取刚片I,II,III,刚片I,III之间通过无穷远处的瞬铰O(1,3)相连,刚片II和III通过铰O(2,3)相连,如果没有铰A ,刚片I和II之
间会通过无穷远处的瞬铰相连,组成一个无多余约束的几何不变体系,因此,铰A使得该体系成为缺少一个必要约束的几何可变体系。
6、对图示体系作几何构造分析。
(浙江大学2011)
解:分析:本题上部体系与基础用三根不共点的链杆相连,通常先分析上部体系。
多次去掉二元体后得到678和56用一个铰相连,缺少一个约束,故上部为几何常变体系。
上部体系与基础用三根不共点的链杆相连组成几何常变体系。
7、对下列体系进行几何构造分析
7-17-27-3
7-47-57-6
7-7.7-8
7-97-10
解:
7-1 图中,刚片AB 、BE 、DC 由不共线的三个铰B 、D 、E 连接,组成一个大刚片,再和地基基础用不相交也不全平行的三链杆相连,组成没有多余约束的几何不变体系(5分)。
7-2 如图所示的三个刚片通过不在同一直线上的A 、B 、C 三个铰两两相连构成无多余约束的扩大刚
片,在此基础上依次增加二元体(1,2)、(3,4)、(5,6)、(7,8)组成无多余约束的几何不变体系。
(5分) Ⅰ
ⅡⅢ
43
12568
7A
B
C
7-3 如图所示的三个刚片通过同一直线上的A 、B 、C 三个铰两两相连构成了瞬变体系。
(5分) 7-4如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)
7-5如图依次拆除二元体(1,2)、(3,4)、剩下刚片Ⅰ和大地刚片Ⅱ通过一铰和不过该铰的链杆组成了几何不变体系,故原体系是无多余约束的几何不变体系。
(5分)
7-6 如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)
7-7如图刚片Ⅰ、Ⅱ、Ⅲ通过不共线的三铰两两相连组成了无多余约束的几何不变体系。
(5分)
7-8如图以铰接三角形ABC为基本刚片,并依次增加二元体(1,2)、(3,4)、(5,6)、(7,8)、(9,10)形成扩大刚片,其和大地刚片通过铰A和节点B处链杆组成了几何不变体系,11杆为多余约束,故原体系为含有1个多余约束的几何不变体系。
(5分)
7-9如图依次拆除二元体(1,2)、(3,4)、(5,6),刚片Ⅱ和大地刚片Ⅰ通过相交于同一点的三根链杆组成了瞬变体系。
(5分)
7-10如图依次拆除二元体(1,2)、(3,4)、(5,6)、(7,8)、(9,10)、(11,12)后只剩下大地刚片,故原体系是无多余约束的几何不变体系。
(5分)。
