信号与系统 §4.3 周期信号的频谱
合集下载
信号与系统第4章 周期信号的频域分析(3学时)
T0 /2
0
x(t )sin(n 0t )dt
四、信号对称性与傅里叶系数的关系
3、半波重迭信号
~ x (t ) ~ x (t T0 / 2)
~ x (t )
A t
T0
T0 / 2 0
T0 / 2
T0
特点： 只含有正弦与余弦的偶次谐波分量，而无奇次谐波分量。
四、信号对称性与傅里叶系数的关系
~ x (t )
2 1 -4 -3 -2 -1 1 2 3 4
~ x (t ) ~ x1 (t ) ~ x2 (t )
nπ nπt t~ x (t ) 1.5 Sa ( ) cos( ) 2 2 n 1
~ x1 (t )
2
x 1(t ) 2
1 2 3 4
-4 -3 -2 -1
三、周期信号的功率谱
一、周期信号频谱的概念
连续时间周期信号可以表示为虚指数信号之和，其 中Cn 为傅里叶系数 。
~ x (t )
n =
Cn e
jn0t
1 Cn T0
T0 t 0
t0
~ x (t )e jn 0t dt
问题1：不同信号的傅里叶级数形式是否相同？ 相同 问题2：不同信号的傅里叶级数不同表现在哪里？ 系数
例3 课本P129
例4 已知连续周期信号的频谱如图，试写出信号的 Fourier级数表示式。 Cn
3 2 1 1 3 4 3 2
9
6
0
3
6
9
n
解： 由图可知 C0 4
C 1 3
C2 1
C 3 2
~ x (t )
4.3 周期信号的频谱及特点
A、计算|Fn |和θn
4.3
周期信号的频谱及特点
2）、周期矩形脉冲的频谱
有一幅度为E，脉冲宽度为τ的周期矩 形脉冲，其周期为T，如图所示。求 频谱。 T τ
−
τ
2
τ
2
Fn =
1 T
∫
2
T − 2
f (t ) e
− jnΩt
E e− jnΩt = T − jnΩ
τ
2 −
τ
2
E 2 − jnΩt dt = dt τ e ∫ − T 2 nΩτ sin( ) Eτ sin nΩτ 2E 2 2 = = T nΩτ T nΩ
1）、定义
依据复傅立叶系数Fn随nΩ的变化关系所画的图称为 双边频谱图，简称双边谱； |Fn|~ nΩ为双边幅度谱，见图4.3-1（b）；其 以纵轴对称。 θn~ nΩ为双边相位谱。见图4.3-1（d）图。其 以原点对称。
第 第23 23-8 8页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
, n = 0,1,2,..., φ0 = 0.
Fn ~ nΩ
θ n ~ nΩ
周期信号的频谱是指周期信号中各次谐波幅值、相位随 频率的变化关系。
第 第23 23-3 3页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
4.3
A0 f (t ) = + 2
∞
周期信号的频谱及特点
ω1
T τ = = 2π Ω τ T
2π
见课本P131 页图4.3-4。
增多。
(b)、 τ 一定，T增大，谱线间隔 Ω 减小，频谱谱 线密度增大。谐波幅度减小：
4.3
周期信号的频谱及特点
2）、周期矩形脉冲的频谱
有一幅度为E，脉冲宽度为τ的周期矩 形脉冲，其周期为T，如图所示。求 频谱。 T τ
−
τ
2
τ
2
Fn =
1 T
∫
2
T − 2
f (t ) e
− jnΩt
E e− jnΩt = T − jnΩ
τ
2 −
τ
2
E 2 − jnΩt dt = dt τ e ∫ − T 2 nΩτ sin( ) Eτ sin nΩτ 2E 2 2 = = T nΩτ T nΩ
1）、定义
依据复傅立叶系数Fn随nΩ的变化关系所画的图称为 双边频谱图，简称双边谱； |Fn|~ nΩ为双边幅度谱，见图4.3-1（b）；其 以纵轴对称。 θn~ nΩ为双边相位谱。见图4.3-1（d）图。其 以原点对称。
第 第23 23-8 8页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
, n = 0,1,2,..., φ0 = 0.
Fn ~ nΩ
θ n ~ nΩ
周期信号的频谱是指周期信号中各次谐波幅值、相位随 频率的变化关系。
第 第23 23-3 3页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
4.3
A0 f (t ) = + 2
∞
周期信号的频谱及特点
ω1
T τ = = 2π Ω τ T
2π
见课本P131 页图4.3-4。
增多。
(b)、 τ 一定，T增大，谱线间隔 Ω 减小，频谱谱 线密度增大。谐波幅度减小：
周期信号的离散频谱
周期信号的离散频谱
目
CONTENCT
录
• 引言 • 周期信号的离散频谱特性 • 离散频谱的生成方法 • 离散频谱的应用 • 离散频谱与连续频谱的比较 • 总结与展望
01
引言
背景介绍
周期信号在现实世界中广泛存在，如交流电、机械振动等。为了 更好地理解和分析这些信号，需要研究其离散频谱。
离散频谱是周期信号的频率成分的集合，表示信号在不同频率上 的分布情况。
计算过程
傅立叶变换法需要将时间域信 号进行无穷积分，计算过程较 为复杂，需要较高的数学水平 。
应用范围
适用于周期信号和非周期信号 ，是信号处理领域中非常重要 的工具之一。
离散时间傅立叶变换法
定义ቤተ መጻሕፍቲ ባይዱ
离散时间傅立叶变换法是一种将离散时间序列转换为频域 信号的方法，通过将离散时间序列进行傅立叶变换，得到 离散频谱。
干扰抑制
在复杂电磁环境下，雷达系统可能受到各种干扰的影响，离散频谱分 析有助于识别和抑制这些干扰，提高雷达的抗干扰能力。
在图像处理中的应用
01
频域滤波
图像处理中，离散频谱分析用于频域滤波，通过改变图像信号在不同频
率段的权重实现图像的模糊、锐化、边缘检测等效果。
02
去噪与增强
离散频谱分析在图像去噪与增强方面具有广泛应用，通过滤除噪声成分
离散频谱的定义
01
离散频谱是指周期信号的频率成 分以离散的形式分布在频率轴上 。
02
与连续频谱相比，离散频谱的频 率分量是分离的，而不是连续分 布的。
02
周期信号的离散频谱特性
离散频谱的形状
正弦波形状
对于正弦波形状的离散频谱，其峰值出现在中心频 率处，随着频率的增加或减少，幅度逐渐减小。
目
CONTENCT
录
• 引言 • 周期信号的离散频谱特性 • 离散频谱的生成方法 • 离散频谱的应用 • 离散频谱与连续频谱的比较 • 总结与展望
01
引言
背景介绍
周期信号在现实世界中广泛存在，如交流电、机械振动等。为了 更好地理解和分析这些信号，需要研究其离散频谱。
离散频谱是周期信号的频率成分的集合，表示信号在不同频率上 的分布情况。
计算过程
傅立叶变换法需要将时间域信 号进行无穷积分，计算过程较 为复杂，需要较高的数学水平 。
应用范围
适用于周期信号和非周期信号 ，是信号处理领域中非常重要 的工具之一。
离散时间傅立叶变换法
定义ቤተ መጻሕፍቲ ባይዱ
离散时间傅立叶变换法是一种将离散时间序列转换为频域 信号的方法，通过将离散时间序列进行傅立叶变换，得到 离散频谱。
干扰抑制
在复杂电磁环境下，雷达系统可能受到各种干扰的影响，离散频谱分 析有助于识别和抑制这些干扰，提高雷达的抗干扰能力。
在图像处理中的应用
01
频域滤波
图像处理中，离散频谱分析用于频域滤波，通过改变图像信号在不同频
率段的权重实现图像的模糊、锐化、边缘检测等效果。
02
去噪与增强
离散频谱分析在图像去噪与增强方面具有广泛应用，通过滤除噪声成分
离散频谱的定义
01
离散频谱是指周期信号的频率成 分以离散的形式分布在频率轴上 。
02
与连续频谱相比，离散频谱的频 率分量是分离的，而不是连续分 布的。
02
周期信号的离散频谱特性
离散频谱的形状
正弦波形状
对于正弦波形状的离散频谱，其峰值出现在中心频 率处，随着频率的增加或减少，幅度逐渐减小。
信号与系统知识要点
《信号与系统》知识要点第一章 信号与系统1、 周期信号的判断 （1）连续信号思路：两个周期信号()x t 和()y t 的周期分别为1T 和2T ，如果1122T N T N =为有理数（不可约），则所其和信号()()x t y t +为周期信号，且周期为1T 和2T 的最小公倍数，即2112T N T N T ==。
（2）离散信号思路：离散余弦信号0cos n ω（或0sin n ω）不一定是周期的，当 ①2πω为整数时，周期02N πω=；②122N N πω=为有理数（不可约）时，周期1N N =； ③2πω为无理数时，为非周期序列注意：和信号周期的判断同连续信号的情况。
2、能量信号与功率信号的判断 （1）定义连续信号 离散信号信号能量：2|()|k E f k ∞=-∞=∑信号功率： def2221lim ()d T T T P f t t T →∞-=⎰ /22/21lim|()|N N k N P f k N →∞=-=∑⎰∞∞-=t t f E d )(2def（2）判断方法能量信号： P=0E <∞， 功率信号： P E=<∞∞， （3）一般规律①一般周期信号为功率信号；②时限信号(仅在有限时间区间不为零的非周期信号)为能量信号；③还有一些非周期信号，也是非能量信号。
例如：ε(t )是功率信号； t ε(t )3、典型信号① 指数信号： ()at f t Ke =，a ∈R② 正弦信号： ()sin()f t K t ωθ=+tt4、信号的基本运算 1) 两信号的相加和相乘 2) 信号的时间变化 a) 反转: ()()f t f t →- b) 平移: 0()()f t f t t →± c)尺度变换: ()()f t f at →3) 信号的微分和积分注意：带跳变点的分段信号的导数，必含有冲激函数，其跳变幅度就是冲激函数的强度。
正跳变对应着正冲激；负跳变对应着负冲激。
《信号与系统》教与学第四章
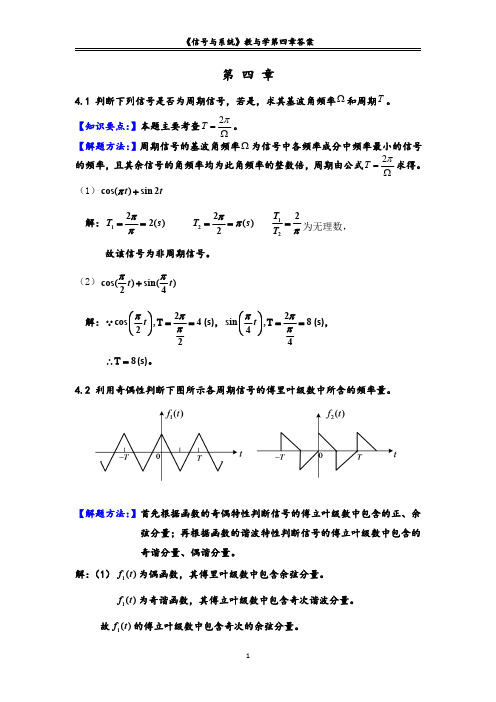
j n e 3
j n
e3
1 n
sin
n 3
,
n
0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示，求其三角函数表达式。
【知识要点：】本题主要考查周期信号的频谱概念，单边谱与双边谱的关系。
（3）计算信号的功率。
【知识要点：】本题主要考查周期信号的频谱概念应用；帕斯瓦尔功率等式应用。
T
2
；
f
t
A0 2
n1
An
cos
nt n
；P
Fn 2 。
n
【解题方法：】利用已知条件观察求出 ，并带入公式计算求出各次谐波分量；
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱；最后利用帕斯瓦尔功率等式计算信号的功率。
解：（1）
x
t
16 cos
20
t
4
6
cos
30
t
6
4
cos
40
t
3
10 (rad/s) ，
T
2
2 10
1 (s) ， 5
周期信号所含谐波次数为二次，三次，四次；
求得。
（1） cos( t ) sin 2t
解： T1
《信与系统》教与学
4.14
利用能量等式
f
2 (t )dt
1 2
2
F ( j) d ，计算
sin t
2t
2
dt
。
【解题方法：】先利用门函数常用对和对称性求出 sin(2t) 的傅里叶变换， t
4.11 如下图所示信号， f1 (t ) 的傅立叶变换 F1 ( j ) 已知，求信号 f 2 (t ) 的傅立叶 变换 F2 ( j ) 。
解：
f2 (t ) f1 (t t0 ) f1(t t0 ) f1(t ) F1( j)
f1(t t0 ) F1( j)e jt0
9
《信号与系统》教与学第四章答案
解： T1
2
2(s )
T2
2 2
(s)
故该信号为非周期信号。
（2）
cos(
t)
sin(
t)
2
4
T1 T2
2
为无理数，
解： cos
2
t
,
2
4
(s)，
sin
4
t
,
2
8
(s)，
2
4
8 (s)。
4.2 利用奇偶性判断下图所示各周期信号的傅里叶级数中所含的频率量。
【解题方法：】首先根据函数的奇偶特性判断信号的傅立叶级数中包含的正、余 弦分量；再根据函数的谐波特性判断信号的傅立叶级数中包含的 奇谐分量、偶谐分量。
df (t) ( j ) F ( j ) dt
jt
df (t) dt
d( j) F(
d
j)
jF
(j)
j
dF ( j ) d
4t
df (t dt
信号与系统 -第四章 傅里叶变换和系统的频域分析
A2cos(2 t+ 2)称为二次谐波，它的频率是基波的2倍； 一般而言，Ancos(n t+ n)称为n次谐波。
第4-13页
■
信号与系统电子教案
4.2 傅里叶级
例1：将图示方波信号f(t)展开为数傅里叶级数。
f (t)
1
T T 0 T T 3T
t
2 1 2
2
解：f (t)为T 3, 2 / T 2 / 3的周期信号，傅里叶系数为
号空间找到若干个相互正交的信号作为基本信号，使 得 信号空间中任意信号均可表示成它们的线性组合。
第4-5页
■
信号与系统电子教案
y C2v
y
0
A
x C1v x
4.1 信号分解为正交函 数
y C2vy
0 C3v
zz
A C1vx x
第4-6页
■
信号与系统电子教案
4.1 信号分解为正交函
二、信号正交与正交函数数集
第四章 傅里叶变换和系统的频域分析
傅里叶简介
法国数学家、物理学家。1768年3月21日生 于 欧塞尔，1830年5月16日卒于巴黎。
1807年向巴黎科学院呈交《热的传播》论文，推导出著 名
的热传导方程，并在求解该方程时发现解函数可以由三角函数 构成的级数形式表示，从而提出任一函数都可以展成三角函数 的无穷级数。
■
信号与系统电子教案
4.2 傅里叶级
A0
2
1 An
n1
e j n jn t
1数
2 An n1
e j n jn
t
令A0=A0
。
如三维空间中，以矢量 vx=（2，0，0）、vy=（0 ，2，0）、vz=（0，0，2) 所组成的集合就是一个 正交矢量集。
信号与系统分析基础----周期信号的频谱周期信号的频谱分析——傅里叶级数
n1t
sin
m1t
0
2
T 2 T 2
cos n1t
cos m1t
T , 2 0,
mn mn
T 2 T 2
sin n1t
sin m1t
T , 2 0,
mn mn
3
2．级数形式
周期信号
f t ,周期为T1
, 基波角频率为1
2
T1
在满足狄氏条件时，可展成:
f (t) a0 an cos n1t bn sin n1t
§3.2 周期信号的频谱分析——傅里叶级数
1
主要内容
•三角函数形式的傅氏级数 • 指数函数形式的傅氏级数 •两种傅氏级数的关系 • 频谱图
2
一．三角函数形式的傅里叶级数
1.三角函数集
cosn1t , sin n1 t是一个完备的正交函数集
由积分可知
t在一个周期内，n=0,1,....
T
2 T
cos
周期信号可分解为直流，基波（1）和各次谐波 （n1 : 基波角频率的整数倍）的线性组合．
cn ~ 关系曲线称为幅度频谱图 n ~ 关系曲线称为相位频谱图
可画出频谱图
周期信号频谱具有离散性，谐波性，收敛性
9
二．指数函数形式的傅里叶级数
1．复指数正交函数集 e jn1t n 0,1,2
2．级数形式 f (t ) F (n1 ) e jn1t
f
2
(
t
)dt
t2 t1
f 2 (t )
f
1
(t
)dt
0
若在区间(t1,t2)内，复变函数集 {gr (t)}(r 1,2,...,n)
满足关系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理意义。为什么引入负频率？ f(t)是实函数，分解成虚指数，必须有共轭对ejnΩt和
e-jnΩt，才能保证f(t)的实函数的性质不变。
▲
■
第3页
二、周期信号频谱的特点
举例：有一幅度为1，脉冲宽
f(t) 1
度为的周期矩形脉冲，其周
0
期为T，如图所示。求频谱。
-T
Fn
1 T
T
2 T
2
f (t) e d jnt t
(3)离散谱（谐波性）
（4)第一个零点坐标：2π T
当ω nΩ时取值 （5）Fn是复函数（此
处
令 n n＝ 2π
为实函2数），幅度/相位
Fn 0，相位为 0，Fn 0, 相位为π 。 ▲
■
第5页
周期信号频谱的特点
(1)周期信号的频谱具有谐波(离散)性。谱线位置是基频 Ω的整数倍；(2)一般具有收敛性。总趋势减小。
1 T
2
e
jnt
dt
2
2
2
1 e jnt T jn
2
2
2
sin(
n
2
)
T n
T
sin n
2
n
2
令Sa(x)=sin(x)/x (取样函数）
…
T
t
▲
■
第4页
Fn
Sa( n ) Sa( n )
T 2TT
, n = 0 ,±1，±2，…
图中T 5
Fn
T
2π
O 2
(1)包络线形状：抽样函数 (2)其最大值在 n 0处，为 。
§4.3 周期信号的频谱
• 信号频谱的概念 • 周期信号频谱的特点
■
第1页
一、信号频谱的概念
从广义上说，信号的某种特征量随信号频率变
化的关系，称为信号的频谱，所画出的图形称为信 号的频谱图。
周期信号的频谱是指周期信号中各次谐波幅值、 相位随频率的变化关系，即
将An~ω和n~ω的关系分别画在以ω为横轴的平
谱线的结构与波形参数的关系 ➢T一定，变小，此时（谱线间隔）不变。两零点之 间的谱线数目：1/=（2/）/(2/T)=T/ 增多。
➢ 一定，T增大，间隔减小，频谱变密。幅度减小。
如果周期T无限增长（这时就成为非周期信号），
那么，谱线间隔将趋近于零，周期信号的离散频谱就过
渡到非周期信号的连续频谱。各频率分量的幅度也趋近
于无穷小。
总结▲■来自第6页面上得到的两个图，分别称为振幅频谱图和相位频 谱图。因为n≥0，所以称这种频谱为单边谱。
也可画|Fn|~ω和n~ω的关系，称为双边谱。若Fn
为实数，也可直接画Fn 。
▲
■
第2页
频谱概念演示
T
f (t)
1
O T /2 T
t
1
方波
既是奇函数又是奇谐函数
例1
例2
只含奇次谐波,且为正弦波.
对于双边频谱，负频率，只有数学意义，而无物
e-jnΩt，才能保证f(t)的实函数的性质不变。
▲
■
第3页
二、周期信号频谱的特点
举例：有一幅度为1，脉冲宽
f(t) 1
度为的周期矩形脉冲，其周
0
期为T，如图所示。求频谱。
-T
Fn
1 T
T
2 T
2
f (t) e d jnt t
(3)离散谱（谐波性）
（4)第一个零点坐标：2π T
当ω nΩ时取值 （5）Fn是复函数（此
处
令 n n＝ 2π
为实函2数），幅度/相位
Fn 0，相位为 0，Fn 0, 相位为π 。 ▲
■
第5页
周期信号频谱的特点
(1)周期信号的频谱具有谐波(离散)性。谱线位置是基频 Ω的整数倍；(2)一般具有收敛性。总趋势减小。
1 T
2
e
jnt
dt
2
2
2
1 e jnt T jn
2
2
2
sin(
n
2
)
T n
T
sin n
2
n
2
令Sa(x)=sin(x)/x (取样函数）
…
T
t
▲
■
第4页
Fn
Sa( n ) Sa( n )
T 2TT
, n = 0 ,±1，±2，…
图中T 5
Fn
T
2π
O 2
(1)包络线形状：抽样函数 (2)其最大值在 n 0处，为 。
§4.3 周期信号的频谱
• 信号频谱的概念 • 周期信号频谱的特点
■
第1页
一、信号频谱的概念
从广义上说，信号的某种特征量随信号频率变
化的关系，称为信号的频谱，所画出的图形称为信 号的频谱图。
周期信号的频谱是指周期信号中各次谐波幅值、 相位随频率的变化关系，即
将An~ω和n~ω的关系分别画在以ω为横轴的平
谱线的结构与波形参数的关系 ➢T一定，变小，此时（谱线间隔）不变。两零点之 间的谱线数目：1/=（2/）/(2/T)=T/ 增多。
➢ 一定，T增大，间隔减小，频谱变密。幅度减小。
如果周期T无限增长（这时就成为非周期信号），
那么，谱线间隔将趋近于零，周期信号的离散频谱就过
渡到非周期信号的连续频谱。各频率分量的幅度也趋近
于无穷小。
总结▲■来自第6页面上得到的两个图，分别称为振幅频谱图和相位频 谱图。因为n≥0，所以称这种频谱为单边谱。
也可画|Fn|~ω和n~ω的关系，称为双边谱。若Fn
为实数，也可直接画Fn 。
▲
■
第2页
频谱概念演示
T
f (t)
1
O T /2 T
t
1
方波
既是奇函数又是奇谐函数
例1
例2
只含奇次谐波,且为正弦波.
对于双边频谱，负频率，只有数学意义，而无物