2019版高考数学一轮总复习第六章数列题组训练36等比数列理

合集下载

2019版高考数学一轮复习题组训练第6章第3讲等比数列及其前n项和(含最新模拟题) Word版含答案

第三讲等比数列及其前项和题组等比数列及其前项和.[新课标全国Ⅱ分][文]已知等比数列{}满足(),则() ...[新课标全国Ⅰ分][文]设首项为,公比为的等比数列{}的前项和为,则().[江苏分][文]等比数列{}的各项均为实数,其前项和为.已知,则..[新课标全国Ⅰ分][文]在数列{}中为{}的前项和.若,则..[广东分][文]设数列{}是首项为,公比为的等比数列,则..[全国卷Ⅲ分]已知数列{}的前项和λ,其中λ≠.(Ⅰ)证明{}是等比数列,并求其通项公式;(Ⅱ)若,求λ..[北京分][文]已知等差数列{}满足.(Ⅰ)求{}的通项公式;(Ⅱ)设等比数列{}满足.问与数列{}的第几项相等?题组等比数列的性质及应用.[重庆分]对任意等比数列{},下列说法一定正确的是() 成等比数列成等比数列成等比数列成等比数列.[全国卷Ⅰ分]设等比数列{}满足,则…的最大值为..[广东分][文]若三个正数成等比数列,其中,则..[广东分]若等比数列{}的各项均为正数,且,则… ..[天津分][文]已知{}是等比数列,前项和为(∈*),且.(Ⅰ)求{}的通项公式;(Ⅱ)若对任意的∈*是和的等差中项,求数列{()}的前项和.组基础题.[河北衡水中学二调]设正项等比数列{}的前项和为,且<,若,则() 或.[益阳市、湘潭市高三调研]已知等比数列{}中,则的值为().[洛阳市尖子生高三第一次联考]在等比数列{}中是方程的根,则的值为() . 或.[吉林省部分学校高三仿真考试][数学文化题]《张丘建算经》中“今有马行转迟,次日减半,疾七日,行七百里.问日行几何?”意思是:“现有一匹马行走的速度逐渐变慢,每天走的里数是前一天的一半,连续行走天,共走了里路,问每天走的里数为多少?”则该匹马第一天走的里数为(). . . ..[广州市高三调研测试]在各项都为正数的等比数列{}中,若,则的最小值为..[惠州市一调]已知等比数列{}的公比为正数,且,则..[昆明市高三适应性检测]数列{}满足.()证明{}是等比数列,并求数列{}的通项公式;()已知符号函数()设·(),求数列{}的前项和.组提升题.[石家庄市重点高中摸底考试]已知等比数列{}的前项和为,若,则数列{}的前项和为() ()×()×()×()×。

2019-2020学年高中新创新一轮复习理数通用版：第六章数列Word版含解析.doc

第八早第一节数列的概念与简单表示本节主要包括2个知识点： 1.数列的通项公式; 2.数列的性质.突破点(一)数列的通项公式抓牢双基自学区［基本知识］1. 数列的定义按照一定顺序排列的一列数称为数列•数列中的每一个数叫做这个数列的项，数列中的每一项都和它的序号有关，排在第一位的数称为这个数列的第一项(通常也叫做首项).2. 数列的通项公式如果数列｛a n｝的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式.3. 数列的递推公式如果已知数列｛a n｝的第一项(或前几项)，且任何一项a n与它的前一项a n-1(或前几项)间的关系可以用一个式子来表示，即a n= f(a n-i)(或a n= f(a n-1, a n-2)等)，那么这个式子叫做数列｛a n｝的递推公式.4. S n与a n的关系S1, n = 1,已知数列｛a n｝的前n项和为S n，则a n = ■o这个关系式对任意数列均S n —Sn-1 n> 2,成立.［基本能力］1. 判断题(1) 所有数列的第n项都能使用公式表达.()(2) 根据数列的前几项归纳出数列的通项公式可能不止一个. ()1⑶若已知数列｛a n｝的递推公式为a n+1 = _ 1,且a2= 1,则可以写出数列｛a n｝的任何一2a n —I项.()⑷如果数列｛a n｝的前n项和为S n,则对？n € N*，都有a+1 = S“+1—S n.( )答案：(1)X (2)V (3) V (4) x2. 填空题(1)已知数列｛a n｝的前4项为1,3,7,15，则数列｛a n｝的一个通项公式为________ .答案：a n= 2n—1(n € N*)⑵已知数列｛a n｝中，a i= 1, a n+i = 2at 3，贝卩逓=_____________ .1答案：15⑶已知S n是数列｛a n｝的前n项和，且S n =『+ 1 ,则数列gn｝的通项公式是答案：a n=‘，n= 1，2n—1, n> 2研透高考*讲练区［全析考法］给出数列的前几项求通项时，需要注意观察数列中各项与其序号之间的关系，在所给数列的前几项中，先看看哪些部分是变化的，哪些是不变的，再探索各项中变化部分与序号间的关系.［例1］ (1)(2018江西鹰潭一中期中)数列1, —4,9,—16,25,…的一个通项公式是()A. a n = n2B. a = (—1)n n2C. a n = (—1)n"n2D. a n = (—1)n(n + 1)2(2)(2018山•西太原五中调考)把1,3,6,10,15,…，这些数叫做三角形数，这是因为这些数目的圆点可以排成一个正三角形(如图所示).1 361015则第7个三角形数是()A. 27B. 28C. 29D. 30［解析］⑴法一：该数列中第n项的绝对值是n2，正负交替的符号是(—1)n+ S故选C. 法二：将n= 2代入各选项，排除A, B, D,故选C.(2)观察三角形数的增长规律，可以发现每一项比它的前一项多的点数正好是该项的序号，即a n= a n-1+ n(n>2).所以根据这个规律计算可知，第7个三角形数是a y= a&+ 7=+ 6+ 7 = 15+ 6+ 7 = 28.故选 B.［答案］(1)C (2)B［方法技巧］由数列的前几项求通项公式的思路方法(1)分式形式的数列，分别求分子、分母的通项，较复杂的还要考虑分子、分母的关系.⑵若第n项和第n + 1项正负交错，那么符号用(―1)n或(-1)n+1或(-1)n—1来调控.(3)对于较复杂数列的通项公式，其项与序号之间的关系不容易发现，这就需要将数列各项的结构形式加以变形，可使用添项、通分、分割等方法，将数列的各项分解成若干个常见数列对应项的“和” “差” “积” “商”后再进行归纳.［提醒］根据数列的前几项写出数列的一个通项公式利用了不完全归纳法，其蕴含着“从特殊到一般”的思想，由不完全归纳得出的结果是不可靠的，要注意代值检验.S i, n= 1,数列｛a n｝的前n项和S n与通项a n的关系为a n= * 通过纽带：a n= S nS n- S n-1, n > 2,-S n-1(n> 2),根据题目已知条件，消掉a n或S n,再利用特殊形式(累乘或累加)或通过构造成等差数列或者等比数列求解.[例2]已知数列｛a n｝的前n项和为S n.(1) 若S n= (—1) •，求a5+ a6 及a n；(2) 若S n= 3 +2n + 1，求a n.[解](1)a5+ a6= S6― S4= (― 6)—( ― 4) =—2,当n = 1 时，a1= S1= 1;当n > 2 时，a n= S n - S n-1= (—1)n 1 n- (—1)n (n —1)=(—1)n+1 [n + (n—1)]=(—1)n+1 (2n —1),又a1也适合此式，所以a n = (—1)n+1 (2n—1).(2)因为当n= 1 时，a1 = S1 = 6；当n>2 时，a n= S n—S n-1= (3n+ 2n+ 1) —[3n—1+ 2(n—1) + 1] = 2 3n—1+ 2,由于a1不适合此式，所以a n =’6, n= 1,2 3n—1+ 2, n > 2.［方法技巧］已知S n求a n的三个步骤(1) 先利用a1 = S1求出a1.(2) 用n —1替换S n中的n得到一个新的关系，禾U用a n = S n—S n—1(n>2)便可求出当n >2 时a n的表达式.⑶对n= 1时的结果进行检验，看是否符合n > 2时a n的表达式，如果符合，则可以把数列的通项公式合写；如果不符合，则应该分n= 1与n> 2两段来写.［例3］ (1)在数列｛a n 1n +1 n n .⑵在数列｛a n ｝中，a 1= 1, a n = 专a n - 1(n > 2)，求数列｛a n ｝的通项公式.⑶在数列｛a n ｝中a i = 1, a n +1 = 3a “+ 2，求数列仙｝的通项公式. ⑷已知数列｛a n ｝中，a 1= 1, a n +1 = o~+；,求数列｛a n ｝的通项公式. ［解］(1)因为 a n +1 - a = 3n + 2, 所以 a “ — a “—1= 3n — 1(n 》2), 所以 a n = (a n — a n —1)+ (a n — 1 — a*-2)+ …+ (a 2— a“ + a 1 =」_2 当 n = 1 时，a 1= 2 = 1x (3 x 1+ 1)，符合上式, 所以 a n = |n 2+ 2.n — 1⑵因为 a n = —Ja n -1(n A 2), n — 21所以 a n —1= 口a n —2’ …，a 2=丹由累乘法可得a n = a 1 2 2 - - - 1= 7= J (n > 2).又a 1= 1符合上式」a n = n (3)因为 a n +1= 3a n + 2,所以 a n +1 + 1= 3(a n + 1),所以 a + 1 = 3,所以数列｛a n + 1｝为等比数列，公比 q = 3.又 a 1+ 1 = 2,所以 a n + 1= 2 3n —1,所以a n = 2 3n —1 — 1.丄=1+2，即丄L —1=2, a n +1 a n 2 a n +1a n 21又 a 1= 1，则-=1,是以1为首项，2为公差的等差数列. .1 1 1 n . 1a n =a ；+(n —1) x 2=2+2~+1(n € N *). n +1［方法技巧］典型的递推数列及处理方法n > 2).a n +1 + 12a n(4) a n +1=a n +2,a1 = 1 ,…a n 工 0 ,a n +1a n［全练题点］1.［考点一］（2018湖南衡阳二十六中期中）在数列1,1,2,3,5,8, x,21,34,55，…冲，x 的值为12C . 13和，所以x = 5+ 8= 13，故选C.5 7 92.［考点一］数列1,— 5, 15，— 24，…的一个通项公式是（n +12n — 1a n = (—1)n +n(n € N )n -1 2n + 1*a n = (— 1)(n€ N )n +1 2n — 1跖=(―1)齐亦(n €N )14解析：选C 观察所给数列的项，发现从第3项起，每一项都是与它相邻的前两项的B . a n = (-1)n —1 2n +1** N )解析：选D所给数列各项可写成:3—5 71 X 3，2 X 4，3 X5戈，…，通过对比各选项，可知选D.3.［考点二］（2018黑龙江双鸭山一中期末）已知数列｛a n ｝的前n 项和为S n ,若S n = 2a n ~ 4, n € N ,贝V a n =()A . 2n +1解析：选A 因为S n = 2a n — 4，所以n >2时，有S n —1= 2a n —1 — 4,两式相减可得 S n —a nS n -1= 2a n — 2a n -1, 即卩 a n = 2a n — 2a n-1，整理得 a n = 2a n -1,即亠匚=2(n > 2).因为 S 1 = a ja n —1=2a1—4，所以a1= 4,所以a“= 2n+14.［考点三］(2018 •东潍坊期中)在数列｛a n ｝中，a i = 2, a *+1= O n + In 1 +半，则a n =()A . 2+ In nB . 2+ (n — 1)ln nC . 2+ nln nD . 1 + n + In n解析：选 A 法一：由已知得 a n +1— a n = In’ + * = In"：1,而 a n = (a n — a n — 1)+ (a n -1n n — 1 2+ a n -2) + …+ (a 2 — a 1)+ a 1, n >2,所以 a n = In - + In - + …+ In; + 2= n — 1 n — 2 12• + 2= In n + 2, n > 2.当 n = 1 时，a 1 = 2 = In 1+ 2.故选 A.1法——:由 O n = O n -1 + In 1 + n 1 = O n -1 + In1 = O n -1 + In n — In(n — 1)(n 》2)，可知 O n—In n = O n -1 — In(n — 1)(n >2).令 b n = O n — In n ,则数列｛b n ｝是以 b 1= O 1— In 1 = 2 为首项的常数列，故b n = 2，所以2= O n — In n ,所以O n = 2 + In n .故选A.突破点(——)数列的性质抓牢双基自学区［基本知识］数列的分类分类标准类型满足条件按项数分类有穷数列项数有限无穷数列项数无限按项与项间的大小关系分类递增数列On + 1〉O n其中n € N *递减数列 O n ： 1V O n常数列 On + 1= O n按其他标准分类有界数列存在正数 M ，使|O n |W M摆动数列从第二项起，有些项大于它的前一项，有些项小于它的前一项［基本能力］X — 1 、r*(1)已知函数f(x) ，设O n = f(n)(n € N ),则｛O n ｝是 ______数列(填“递增”或“递减”).答案：递增⑵数列｛O n ｝的通项公式为O n =— n 2 + 9n ，则该数列第 _________项最大.In答案：4或5⑶现定义a n = 5n + ［1>，其中n € N ,则｛a “｝是 _________ 数列(填“递增”或“递减”).答案：递增⑷对于数列｛a n ｝, “a n + i >|a n |(n = 1,2,…)”是“ ｛a n ｝为递增数列”的 ___________ 条件. 答案：充分不必要研透高考・讲练区［全析考法］(1)数列的单调性与函数的单调性有所不同，其自变量的取值是不连续的，只能取正整数，所以在求数列中的最大 (小)项时，应注意数列中的项可以是相同的，故不应漏掉等号.(2)数列是自变量不连续的函数，不能对数列直接求导判断单调性•要先写出数列对应的函数，对函数进行求导，再将函数的单调性对应到数列中去.(2 \［例1］ (1)已知数列｛a n ｝的通项公式为a n = n 3 n ，则数列仙｝中的最大项为()D . （- 3,+° ）［解析］(1)法一(作差比较法):当 n<2 时，a n +1— a n >0，即 a n +1>a n ；当 n = 2 时，a *+1 — a * = 0，即 a *+1= a *; 当 n>2 时，a n +1 一 a n <0，即 a n +1<a n .所以 a 1<a 2= a 3, a 3>a 4>a 5> …〉a n ,所以数列｛a n ｝中的最大项为a 2或a 3,且a 2= a 3= 2X 2 2= §.故选A.64 C.64125D. 243(2)已知数列｛a n ｝的通项公式为值范围是( )a n = 2n 2+ tn + 1,若｛a n ｝是单调递增数列，则实数 t 的取 A"8 B . A . （一 6 ,+m）B . （一 °°, 一6）C .（一°,一 3） a n +1 — a n = （n + 1） 2”1-nf =亍 3"，法二(作商比较法):a n +1令丁>1，解得n<2 ;a n令—<1，解得n>2.a n 又 a n >0，故 a 1<a 2=a3, a 3>a 4>a 5>…>a n ,所以数列｛a n ｝中的最大项为a 2或a 3,且a 2= a 3= 2X 3 2= §.故选A. (2)法一：因为｛a n ｝是单调递增数列，所以对于任意的n € N *，都有a n + 1>a n , 即 2(n + 1)2+ t(n + 1) + 1>2n 2+ tn + 1, 化简得t>— 4n — 2,所以t> — 4n — 2对于任意的n € N *都成立，因为一4n — 2W — 6，所以t> — 6.故选 A. 法二：设f(n) = 2n 2+ tn + 1,其图象的对称轴为 n = — 4，要使｛a n ｝是递增数列,1+ 2< 2 ，即卩 t> — 6.故选 A.［答案］(1)A (2)A［方法技巧］1.判断数列单调性的两种方法 (1) 作差比较法a n +1 — a n >0?数列｛a n ｝是单调递增数列；a n +1 — a n <0?数列｛a n ｝是单调递减数列; a n = 0?数列｛a n ｝是常数列.(2) 作商比较法a n +1①a >1 ?数列｛a n ｝是单调递增数列;②a <1 ?数列｛a n ｝是单调递减数列; a n+1③ 4= 1 ?数列｛a n ｝是常数列a n +1丄i'2冷+1n +12 n!!)a n + 1 —a n >0 时a n _ 1W a n ,(1) 利用不等式组、(n > 2)找到数列的最大项;|a n ，a n + 1 a n _ 1》a n ,(2) 利用不等式组’孑(n > 2)找到数列的最小项.a n Wa n +1数列的周期性与函数的周期性相类似. 求解数列的周期问题时，通常是求出数列的前 n项观察规律•确定出数列的一个周期，然后再解决相应的问题.［例 2］ (1)(2018 黄冈质检)已知数列｛X n ｝满足 X n +2=|X n + 1一 X n |(n € N ),若 X 1 = 1 , X 2 = a(a W 1 , a M 0),且X n + 3= X n 对于任意的正整数 n 均成立，则数列｛X n ｝的前2 017项和S 2 017 =( )A . 672B . 673C . 1 342D . 1 3454 *⑵(2018广•东四校联考)数列｛a n ｝满足 a 1= 2, an+1=(n € N )，贝U a 2 018=(1 — a n)A . - 2B . - 1C . 21 D. 1［解析］(1) •/ X 1= 1, X 2= a(a W 1, a M 0),「. X 3= |x ?— xf = |a - 1|= 1- a ,「. X 1+ x ?+ X 3=1+ a + (1 - a)= 2,又X n + 3= X n 对于任意的正整数 n 均成立，.••数列｛X n ｝的周期为3,所以数列｛X n ｝的前 2 017 项和 S 2 017= S 672X 3 + 1 = 672X 2+ 1 = 1 345.故选 D.1-=2,…，可知此数列有周期性，周期 T = 3, 即卩a n +3= a n ,则a 2 018= a 672x 3+ 2= a 2 = 1 -1 -1.故选B.［答案］(1)D (2)B ［方法技巧］周期数列的常见形式与解题方法(1)周期数列的常见形式1 * 1 1 1(2)数列｛a n｝满足a1 = 2, a n+1= 1 —a(n € N),「. a2 = ^—2 =- 1, a3= 1 ——1= 2a4n + 2L n—70>0,解得 * — 10或n>7.又因为n € N , 解析：选B 由数列1的前n 项的乘积1 ••n + 2 n +1 n + 22 >36 ,得 n 2+ 3n所以n 的最小值为8，故选B.3.［考点一］已知函数f(x)=， 3 — ax + 2, 2X 2-9 x+11a , x>2x < 2,(a>0，且a ^ 1),若数列｛a n ｝满足a n =f(n)(n € N ),且｛a n ｝是递增数列，则实数 a 的取值范围是(A . (0,1) C . (2,3)D . (1,3) 3 — a>0,解析：选C 因为｛a n ｝是递增数列，所以a>1,［(3 - a )x 2+ 2<a 2,解得2<a<3，所以实数a 的取值范围是(2,3).4.［考点二］(2018辽宁重点中学协作体联考)在数列｛a n ｝中，a 1= 1,第+勺―a n = si① 利用三角函数的周期性，即所给递推关系中含有三角函数； ② 相邻多项之间的递推关系，如后一项是前两项的差；③ 相邻两项的递推关系，等式中一侧含有分式，又较难变形构造出特殊数列. (2)解决此类题目的一般方法根据给出的关系式求出数列的若干项，通过观察归纳出数列的周期，进而求有关项的值或者前n 项的和.［全练题点］1.［考点二］(2018安徽名校联盟考前模拟)在数列｛a n ｝中，若对任意的n € N *均有a “ + a “+1+ a n + 2为定值，且a 1 = 2, a g = 3, a g8 = 4,则数列｛a n ｝的前100项的和S 1oo =()A. 132 D . 99解析：选B 因为对任意的n € N 均有a n + a n +1 + a n + 2为定值，所以a n + a n +1 + a n +2= a n+1+an + 2+ a n + 3,所以a n + 3= a n ,所以数列｛a n ｝是周期数列，且周期为3.故a 2= a 98= 4,a3 =a 9= 3, a 100= a 1 = 2,所以 S 1QQ = 33(a 1 + a 2+ a 3)+ a 100= 299.故选 B ・积大于36,则n 的最小值为( )10B . 299C . 682.［考点一］(2018 •东枣庄第八中学阶段性检测 )已知数列，欲使它的前n 项的乘记S n为数列｛a n｝的前n 项和，贝V S2 018 =( )A. 0B. 2 018C. 1 010D. 1 009解析：选 C 由a1= 1 及a n+1—a n= sin®；1)n,得a“+1= a“+ sin(nn,所以a?= a j3 n4 n5 n6 n+ sin n= 1, a3= a2+ sinq = 0, a4= a3 + sinq = 0, a5= a4 + sin^ = 1, a6= a5+ sinq = 1,7 n 8 na?= a6+ siny = 0, a8 = a?+ siny = 0,…，可见数列｛a n｝为周期数列，周期T = 4,所以S2 018=504(a1 + a2 + a3 + a4)+ a1 + a2= 1 010.［全国卷5年真题集中演练一一明规律］1 . (2015全国卷n )设S n是数列｛a n｝的前n项和，且a1=—1 , a n+ 1= S n S n + 1,贝V S n =解析：1 1• a n+ 1 —S n+ 1 — 5 , a n + 1 —S n S n+ 1,…S n+ 1 —S n —S n S n+1. - S n^ 0，• • a ——，即宀—右=—1.又1=—1, S是首项为—1，公差为—1的等差数列.S n+1 S n S1 Qn』1—1)X (—1)=—n，二S n=—=n1答案：一1n1 戸,2. （2014全国卷n ）数列｛a n｝满足a n+1= , a8= 2,则引= ______________.1 —a n1 11 1解析：将a8= 2代入a n+1= ，可求得a7= 1；再将a7=;代入a n+1= ，可求得1 —a n2 2 1 —a n1a6=—1;再将a6=—1代入a“+1= ，可求得a5= 2;由此可以推出数列｛a n｝是一个周期1 —a n数列，且周期为3,所以a1 = a7= 2.答案：12 1 …,3. （2013全国卷I ）若数列｛a n｝的前n项和S n = "a n + §，则｛a n｝的通项公式是a n =解析：当n= 1 时，由已知S n= ：a n+3，=—1+ (n得a1=尹勺+3，即卩a1=1；2 1当n >2时，由已知得到 S n -!= -a n -1 + 3,3 3 所以 a n = S n — S n -1 = §a n + § — -a n -l +所以a n = — 2a n -1,所以数列｛a n ｝为以1为首项，以—2为公比的等比数列,答案：(—2)n —124. （2016全国卷川）已知各项都为正数的数列｛a n ｝满足a 1= 1, a — （2a n +1 — 1）a n —2a n +1的等差数列，故 —=1+ (n — 1) x 1 =人+ £即a n 2 2 2a n a n -1= a n-1+ (— 1)n (n >2, n € N )，则二的a 5值是（）=0. (1) 求 a 2, a s ；⑵求｛a n ｝的通项公式.1 1解：(1)由题意可得 a 2= §, a 3= 4. (2) 由 a iJ—(2an + 1—1)an — 2a n + 1= 0 得2a n +1(a n + 1) = a n (a n +1).a n +1 = 1 a n 21故｛a n ｝是首项为1,公比为1的等比数列，因此1 a n = 2n _1.因此｛a n ｝的各项都为正数，所以［课时达标检测1［小题对点练一一点点落实］对点练（一）数列的通项公式2a* 11.在数列｛a n ｝中，a 1= 1, a n +1 = a +；（n € N ）,则4是这个数列的（）A .第6项B .第C .第8项D .第解析：选B 由a n +1 ==—+ - a n +2 a n +1 a n «_1 1即数列「一是以-=1为首项, a n 」 - a 1所以a n =(—2)n — 12 2 1 a n =市，由市=4，解得° = 7,故选B.+ 1,即a “+1 — a “= n + 1,用累加法可得 a n = a 1+ n ~ 12n + 2 = ,••• 115 A运15 3 3B — C. 一 D - B . 8 4 D . 8解析：选 C 由已知得 a 2= 1 + (— 1)2 = 2,.•.2a 3= 2 + (— 1)彳,a 3=?, — ?a 4= ?+ (— 1)°, a 4=3,. 3a 5=3+(-1)5,. a 5=3,. 2=2X2=3 3. （2018河南郑州一中考前冲刺）数列｛a n ｝满足：a 1= 1，且对任意的 m , n € N ,都有 a m +n = a m + a “+ mn ,则 1 +1 +1 +…+a 1 a 2 a 3a JL -=() 2 017 A A2 018 2 018 2 019 C 4 034 C .2 018 4 036 2 019 解析：选D •/a 1= 1,且对任意的m , n € N *都有 a m + n = a m + a n + mn ,「. a “+1 = a “+ n2〉土 , 丄 + - + 1 +^ + 丄 n n +1 a 1 a 2 a 3 a 2 018 _ 1 1 1 =2J —2+ 2—3 it 1 1 '、= 4 036 故选 2 018 2 019 厂 2 019，故选D. 4. （2018甘肃天水检测）已知数列｛a n ｝的前n 项和为S n , a 1= 1,Sn = 2a n +1,则S n =（）C. 3 n -1D . 2n -1解析：选 D 因为 a n + 1= S n + 1— S n ，所以 S n = 2a *+ 1= 2(S n + 1— S n ),所以S n + 1 S n 33,,所以数列｛S n ｝是以S 1= a 1= 1为首项，3为公比的等比数列，所以 S n = 2 n -1.故选D. 5. （2018兰州模拟）在数列1,2, 7, 10, 13，…中2 19是这个数列的第项. 解析：数列 3 X 4 + 1,…, 76,二 n = 26, 1,2, 7, 10 , 13,…，即数列 1, 3 X 1+ 1, 3 X 2+ 1, 3 X 3+ 1 , .该数列的通项公式为 a n =/3 n — 1 + 1 = 3n — 2, . 3n — 2= 2 19 = 故2 19是这个数列的第26项. a 3 = 答案：26 6. （2018河北冀州中学期中）已知数列｛a n ｝满足a 1= 1,且a “= n （a “+1 — a“（n € N ）,则 ,a n =解析：由a n = n(a n +1 — aj ，可得a n na n + 1 n +1 ,则 a n = _a ^an _j a n_2a n — 1 a n — 2 an — 3^•1=七X 冗a 1n — 1 n — 2a n n n + 11 3n 2 2x x …x — x 1 = n(n > 2),「. a 3= 3. T a i = 1 满足 a n = n ,「. a n = n. n _ 3 1答案：3 n7. (2018福建晋江季延中学月考 )已知数列｛a n ｝满足a i + 2a —+ 3a 3+-+ na “= n + 1(n € N ),则数列｛a n ｝的通项公式为 _________________ .已知a 1 + 2a 2+ 3a 3+・・・ + na n = n + 1,将n = 1代入，得 a 1= 2;当n > 2时，将n 1a p + 2a 2+ 3a 3+…+ (n _ 1)a n _ 1= n ，两式相减得 na n = (n + 1)_ n = 1,「. a “= n n = 1, n > 2.2, n = 1, a n = 1 1一，n > 2 n对点练(二)数列的性质—9n _ 9n + 2 *1.已知数列｛a n ｝的通项公式为a n = 9n 2_ 4 (n € N ).则下列说法正确的是 ()A .这个数列的第10项为名3 1是该数列中的项D .数列｛a n ｝是单调递减数列得9n = 300此方程无正整数解，故卷不是该数列中的项.因为a n =貯=呼亍3*1=1_ 3^，又n € N ,所以数列｛a n ｝是单调递增数列，所以：＜ a “v1，所以数列中的各项都在区间4，1内，故选项 C 正确，选项D 不正确，故选 C.11 | a2. (2018湖北黄冈中学期中)已知数列｛a n ｝中，a 1 = 1, a “+1="，贝V a 2。

2019届高考数学人教A版理科第一轮复习课件：第六章+数列+6.4

-3-
知识梳理
双基自测
1 2 3
(5)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
常见的裂项公式:①
1 1 ② =2 (2��-1)(2��+1) 1 1 ③ = ��(��+1)(��+2) 2 1 1 ④ = �� ( �� + �� + ��+��
�� -1 ��-1 ��+1
(5)已知等差数列{an}的公差为 d,则有�� = �� - �� . �� +1 �� +1
(× (2)√ ) (1) (3)√ (4)√ (5)× (6)√
.
关闭
��+1
��(��+1) , 2 1 2 1 1 ∴�� = ��(��+1)=2 �� - ��+1 . �� 1 1 1 1 1 1 1 ∴Sn=2 1- + - + - + … + 2 2 3 3 4 �� +1 1 2�� = 2 1 = . 2�� +1 ��+1
∵an=1+2+3+…+n=
关闭
-9解析
答案
知识梳理
双基自测
1 2 3 4 5
5.(2017全国Ⅱ,理15)等差数列{an}的前n项和为Sn,a3=3,S4=10,则 . ��1 + 2�� = 3, 4×3 设等差数列的首项为 a1,公差为 d,由题意可知解 4 ��1 + �� = 10, 2 �� = 1, 得 1 �� = 1. �� (�� -1) �� (1+�� ) 所以 Sn=na1+ d= .

(江苏专版)2019版高考数学一轮复习第六章数列 6.3 等比数列课件.pptx

=(2n+1)bn+1,
令cn= bn ,则cn=2n .1
an
2n
因此Tn=c1+c2+…+cn= 3
2
+ 5 + 7 +…2+n 1+
22 23
2n1
所以 1
2
Tn=
3 22
+
5 23
+7
24
+…+2n 1+
2n
2n, 1
2n1
2n, 1
2n
两式相减得 1
2
Tn=3
2
+1
2
1-
22
,
1 2n1
故b3=5,公比q= b4 =2. 由b3=b1·22,即5=bb31·22,
解得b1= 5 .
4
所以{bn}是以 5 为首项,2为公比的等比数列,其通项公式为bn=5
4
4
3.
9
·2n-1=5·2n-
5 (1 2n )
(2)证明:数列{bn}的前n项和Sn= 4 =5·2n-2-
1 2
,即5Sn+
1 q
3
拓展延伸等差数列与等比数列的关系: (1)若{an}是正项等比数列,则{logaan}(a>0且a≠1)是以logaa1为首项,logaq 为公差的等差数列(q是{an}的公比). (2)若{an}是等差数列,则{ba}n (b≠0)是以 b为a1 首项,bd为公比的等比数列 (d是{an}的公差).
2.解题时适当利用性质转化条件,可简化运算. 3.挖掘隐含条件,发现等差(或等比)关系,使解题目的明确.
例3 (2017山东文,19,12分)已知{an}是各项均为正数的等比数列,且a1+

2019届高考数学人教B理一轮复习讲义：第六章数列第3

第3节等比数列及其前n 项和最新考纲 1.理解等比数列的概念，掌握等比数列的通项公式与前n 项和公式；2.能在具体的问题情境中识别数列的等比关系，并能用有关知识解决相应的问题；3.了解等比数列与指数函数的关系.知识梳理1.等比数列的概念(1)如果一个数列从第2项起，每一项与它的前一项的比都等于同一个非零常数，那么这个数列叫做等比数列.数学语言表达式：a na n －1＝q (n ≥2，q 为非零常数).(2)如果三个数x ，G ，y 组成等比数列，则G 叫做x 和y 的等比中项. 2. 等比数列的通项公式及前n 项和公式(1)若等比数列{a n }的首项为a 1，公比是q ，则其通项公式为a n ＝a 1q n －1；通项公式的推广：a n ＝a m q n －m .(2)等比数列的前n 项和公式：当q ＝1时，S n ＝na 1；当q ≠1时，S n ＝a 1（1－q n ）1－q ＝a 1－a n q 1－q .3.等比数列的性质已知{a n }是等比数列，S n 是数列{a n }的前n 项和.(1)若k ＋l ＝m ＋n (k ，l ，m ，n ∈N +)，则有a k ·a l ＝a m ·a n . (2)相隔等距离的项组成的数列仍是等比数列，即a k ， a k ＋m ，a k ＋2m ，…仍是等比数列，公比为q m .(3)当q ≠－1，或q ＝－1且n 为奇数时，S n ，S 2n －S n ，S 3n －S 2n ，…仍成等比数列，其公比为q n .[常用结论与微点提醒]1.若数列{a n }为等比数列，则数列{c ·a n }(c ≠0)，{|a n |}，{a 2n }，⎩⎨⎧⎭⎬⎫1an 也是等比数列. 2.由a n ＋1＝qa n ，q ≠0，并不能立即断言{a n }为等比数列，还要验证a 1≠0.3.在运用等比数列的前n 项和公式时，必须注意对q ＝1与q ≠1分类讨论，防止因忽略q ＝1这一特殊情形而导致解题失误.诊断自测1.思考辨析(在括号内打“√”或“×”)(1)等比数列公比q 是一个常数，它可以是任意实数.( ) (2)三个数a ，b ，c 成等比数列的充要条件是b 2＝ac .( )(3)数列{a n }的通项公式是a n ＝a n，则其前n 项和为S n ＝a （1－a n）1－a.( )(4)数列{a n }为等比数列，则S 4，S 8－S 4，S 12－S 8成等比数列.( ) 解析 (1)在等比数列中，q ≠0.(2)若a ＝0，b ＝0，c ＝0满足b 2＝ac ，但a ，b ，c 不成等比数列. (3)当a ＝1时，S n ＝na .(4)若a 1＝1，q ＝－1，则S 4＝0，S 8－S 4＝0，S 12－S 8＝0，不成等比数列. 答案 (1)× (2)× (3)× (4)×2.(教材习题改编)已知{a n }是等比数列，a 2＝2，a 5＝14，则公比q 等于( ) A.－12B.－2C.2D.12解析由题意知q 3＝a 5a 2＝18，即q ＝12. 答案 D3.(2018·湖北省七市联考)公比不为1的等比数列{a n }满足a 5a 6＋a 4a 7＝18，若a 1a m ＝9，则m 的值为( ) A.8B.9C.10D.11解析由题意得，2a 5a 6＝18，a 5a 6＝9，∴a 1a m ＝a 5a 6＝9， ∴m ＝10. 答案 C4.(2015·全国Ⅰ卷)在数列{a n }中，a 1＝2，a n ＋1＝2a n ，S n 为{a n }的前n 项和.若S n ＝126，则n ＝________.解析由a n ＋1＝2a n ，知数列{a n }是以a 1＝2为首项，公比q ＝2的等比数列，由S n ＝2（1－2n ）1－2＝126，解得n ＝6.答案 65.(2017·北京卷)若等差数列{a n }和等比数列{b n }满足a 1＝b 1＝－1，a 4＝b 4＝8，则a 2b 2＝________.解析 {a n }为等差数列，a 1＝－1，a 4＝8＝a 1＋3d ＝－1＋3d ，∴d ＝3，∴a 2＝a 1＋d ＝－1＋3＝2.{b n }为等比数列，b 1＝－1，b 4＝8＝b 1·q 3＝－q 3，∴q ＝－2， ∴b 2＝b 1·q ＝2，则a 2b 2＝22＝1.答案 1考点一等比数列基本量的运算【例1】 (1)(2017·全国Ⅲ卷)设等比数列{a n }满足a 1＋a 2＝－1，a 1－a 3＝－3，则a 4＝________.(2)(2017·江苏卷)等比数列{a n }的各项均为实数，其前n 项和为S n ，已知S 3＝74，S 6＝634，则a 8＝________.解析 (1)由{a n }为等比数列，设公比为q . 由⎩⎨⎧a 1＋a 2＝－1，a 1－a 3＝－3，得⎩⎨⎧a 1＋a 1q ＝－1，①a 1－a 1q 2＝－3，② 显然q ≠1，a 1≠0，②①得1－q ＝3，即q ＝－2，代入①式可得a 1＝1，所以a 4＝a 1q 3＝1×(－2)3＝－8.(2)设数列{a n }首项为a 1，公比为q (q ≠1)，则⎩⎪⎨⎪⎧S 3＝a 1（1－q 3）1－q ＝74，S 6＝a 1（1－q 6）1－q ＝634，解得⎩⎪⎨⎪⎧a 1＝14，q ＝2，所以a 8＝a 1q 7＝14×27＝32. 答案 (1)－8 (2)32规律方法 1.等比数列基本量的运算是等比数列中的一类基本问题，等比数列中有五个量a 1，n ，q ，a n ，S n ，一般可以“知三求二”，通过列方程(组)便可迎刃而解.2.等比数列的前n 项和公式涉及对公比q 的分类讨论，当q ＝1时，{a n }的前n 项和S n ＝na 1；当q ≠1时，{a n }的前n 项和S n ＝a 1（1－q n ）1－q ＝a 1－a n q1－q.【训练1】 (1)(2018·烟台调研)设公比为q (q >0)的等比数列{a n }的前n 项和为S n ，若S 2＝3a 2＋2，S 4＝3a 4＋2，则a 1＝( ) A.－2 B.－1 C.12D.23(2)(2016·全国Ⅰ卷)设等比数列满足a 1＋a 3＝10，a 2＋a 4＝5，则a 1a 2…a n 的最大值为________.解析 (1)由S 2＝3a 2＋2，S 4＝3a 4＋2得a 3＋a 4＝3a 4－3a 2，即q ＋q 2＝3q 2－3，解得q ＝－1(舍)或q ＝32，将q ＝32代入S 2＝3a 2＋2，得a 1＋32a 1＝3×32a 1＋2，解得a 1＝－1，故选B.(2)设等比数列{a n }的公比为q ，∴⎩⎨⎧a 1＋a 3＝10，a 2＋a 4＝5⇒⎩⎨⎧a 1＋a 1q 2＝10，a 1q ＋a 1q 3＝5，解得⎩⎪⎨⎪⎧a 1＝8，q ＝12， ∴a 1a 2…a n ＝a n 1q 1＋2＋…＋(n －1)＝2－n 22＋7n2.记t ＝－n 22＋7n 2＝－12(n 2－7n )，结合n ∈N +，可知n ＝3或4时，t 有最大值6.又y ＝2t 为增函数.所以a 1a 2…a n 的最大值为64. 答案 (1)B (2)64考点二等比数列的性质及应用【例2】 (1)(教材习题原题)等比数列{a n }的各项均为正数，且a 5a 6＋a 4a 7＝18，则log 3a 1＋log 3a 2＋…＋log 3a 10＝( ) A.12B.10C.8D.2＋log 35(2)(2018·云南11校调研)已知数列{a n }是等比数列，S n 为其前n 项和，若a 1＋a 2＋a 3＝4，a 4＋a 5＋a 6＝8，则S 12＝( ) A.40B.60C.32D.50解析 (1)由等比数列的性质知a 5a 6＝a 4a 7，又a 5a 6＋a 4a 7＝18，所以a 5a 6＝9，则原式＝log 3(a 1a 2…a 10)＝log 3(a 5a 6)5＝10.(2)数列S 3，S 6－S 3，S 9－S 6，S 12－S 9是等比数列，即数列4，8，S 9－S 6，S 12－S 9是首项为4，公比为2的等比数列，则S 9－S 6＝a 7＋a 8＋a 9＝16，S 12－S 9＝a 10＋a 11＋a 12＝32，因此S 12＝4＋8＋16＋32＝60. 答案 (1)B (2)B规律方法 1.在解决等比数列的有关问题时，要注意挖掘隐含条件，利用性质，特别是性质“若m ＋n ＝p ＋q ，则a m ·a n ＝a p ·a q ”，可以减少运算量，提高解题速度.2.在应用相应性质解题时，要注意性质成立的前提条件，有时需要进行适当变形.此外，解题时注意设而不求思想的运用.【训练2】 (1)(2018·西安八校联考)已知数列{a n }是等比数列，数列{b n }是等差数列，若a 1·a 6·a 11＝－33，b 1＋b 6＋b 11＝7π，则tan b 3＋b 91－a 4·a 8的值是( )A.－ 3B.－1C.－33D. 3(2)(一题多解)设等比数列{a n }的前n 项和为S n ，若S 6S 3＝3，则S 9S 6＝________. 解析 (1)依题意得，a 36＝(－3)3，a 6＝－3，3b 6＝7π，b 6＝7π3，b 3＋b 91－a 4·a 8＝2b 61－a 26＝－7π3，故tan b 3＋b 91－a 4·a 8＝tan ⎝⎛⎭⎪⎫－7π3＝－tan π3＝－ 3. (2)法一由等比数列的性质S 3，S 6－S 3，S 9－S 6仍成等比数列，由已知得S 6＝3S 3， ∴S 6－S 3S 3＝S 9－S 6S 6－S 3，即S 9－S 6＝4S 3，S 9＝7S 3，∴S 9S 6＝73.法二因为{a n }为等比数列，由S 6S 3＝3，设S 6＝3a ，S 3＝a ，所以S 3，S 6－S 3，S 9－S 6为等比数列，即a ，2a ，S 9－S 6成等比数列，所以S 9－S 6＝4a ，解得S 9＝7a ，所以S 9S 6＝7a 3a ＝73.答案 (1)A (2)73考点三等比数列的判定与证明【例3】 (2016·全国Ⅲ卷)已知数列{a n }的前n 项和S n ＝1＋λa n ，其中λ≠0. (1)证明{a n }是等比数列，并求其通项公式； (2)若S 5＝3132，求λ.(1)证明由题意得a 1＝S 1＝1＋λa 1，故λ≠1，a 1＝11－λ，a 1≠0.由S n ＝1＋λa n ，S n ＋1＝1＋λa n ＋1，得a n ＋1＝λa n ＋1－λa n ，即a n ＋1(λ－1)＝λa n ，由a 1≠0，λ≠0得a n ≠0，所以a n ＋1a n ＝λλ－1.因此{a n }是首项为11－λ，公比为λλ－1的等比数列，于是a n ＝11－λ⎝ ⎛⎭⎪⎫λλ－1n －1. (2)解由(1)得S n ＝1－⎝⎛⎭⎪⎫λλ－1n. 由S 5＝3132，得1－⎝⎛⎭⎪⎫λλ－15＝3132，即⎝ ⎛⎭⎪⎫λλ－15＝132. 解得λ＝－1.规律方法证明一个数列为等比数列常用定义法与等比中项法，其他方法只用于选择题、填空题中的判定；若证明某数列不是等比数列，则只要证明存在连续三项不成等比数列即可.【训练3】 (2017·安徽江南十校联考)已知S n 是数列{a n }的前n 项和，且满足S n －2a n ＝n －4.(1)证明：{S n －n ＋2}为等比数列； (2)求数列{S n }的前n 项和T n . (1)证明因为a n ＝S n －S n －1(n ≥2)，所以S n －2(S n －S n －1)＝n －4(n ≥2)，则S n ＝2S n －1－n ＋4(n ≥2)，所以S n －n ＋2＝2[S n －1－(n －1)＋2](n ≥2)，又由题意知a 1－2a 1＝－3，所以a 1＝3，则S 1－1＋2＝4，所以{S n －n ＋2}是首项为4，公比为2等比数列. (2)解由(1)知S n －n ＋2＝2n ＋1，所以S n ＝2n ＋1＋n －2，于是T n ＝(22＋23＋…＋2n ＋1)＋(1＋2＋…＋n )－2n ＝4（1－2n ）1－2＋n （n ＋1）2－2n ＝2n ＋3＋n 2－3n －82.基础巩固题组 (建议用时：40分钟)一、选择题1.已知{a n }，{b n }都是等比数列，那么( ) A.{a n ＋b n }，{a n ·b n }都一定是等比数列B.{a n ＋b n }一定是等比数列，但{a n ·b n }不一定是等比数列C.{a n ＋b n }不一定是等比数列，但{a n ·b n }一定是等比数列D.{a n ＋b n }，{a n ·b n }都不一定是等比数列解析两个等比数列的积仍是一个等比数列. 答案 C2.(2018·青岛模拟)在单调递减的等比数列{a n }中，若a 3＝1，a 2＋a 4＝52，则a 1＝( ) A.2B.4C. 2D.2 2解析在等比数列{a n }中，a 2a 4＝a 23＝1，又a 2＋a 4＝52，数列{a n }为递减数列，所以a 2＝2，a 4＝12，所以q 2＝a 4a 2＝14，所以q ＝12，a 1＝a 2q ＝4.答案 B3.(2017·全国Ⅱ卷)我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯( ) A.1盏B.3盏C.5盏D.9盏解析设塔的顶层的灯数为a 1，七层塔的总灯数为S 7，公比为q ，则依题意S 7＝381，公比q ＝2.∴a 1（1－27）1－2＝381，解得a 1＝3.答案 B4.设等比数列{a n }中，前n 项和为S n ，已知S 3＝8，S 6＝7，则a 7＋a 8＋a 9等于( ) A.18B.－18C.578D.558解析因为a 7＋a 8＋a 9＝S 9－S 6，且公比不等于－1，在等比数列中，S 3，S 6－S 3，S 9－S 6也成等比数列，即8，－1，S 9－S 6成等比数列，则8(S 9－S 6)＝(－1)2，S 9－S 6＝18，即a 7＋a 8＋a 9＝18. 答案 A5.(2018·昆明诊断)在等比数列{a n }中，若a 3，a 7是方程x 2＋4x ＋2＝0的两根，则a 5的值是( ) A.－2B.－ 2C.± 2D. 2解析根据根与系数之间的关系得a 3＋a 7＝－4， a 3a 7＝2，由a 3＋a 7＝－4<0，a 3a 7>0，所以a 3<0，a 7<0，即a 5<0，由a 3a 7＝a 25，得a 5＝－a 3a 7＝－ 2. 答案 B 二、填空题6.(2018·河南百校联盟联考改编)若等比数列{a n }的前n 项和为S n ，a 5＝40，且S 6＋3a 7＝S 8，则a 2等于________.解析由S 6＋3a 7＝S 8，得2a 7＝a 8，则公比q 为2，所以a 2＝a 523＝4023＝5. 答案 57.已知数列{a n }的前n 项和为S n ，且满足a n ＋S n ＝1(n ∈N +)，则通项a n ＝________. 解析 ∵a n ＋S n ＝1，①∴a 1＝12，a n －1＋S n －1＝1(n ≥2)，②由①－②，得a n －a n －1＋a n ＝0，即a n a n －1＝12(n ≥2)，∴数列{a n }是首项为12，公比为12的等比数列，则a n ＝12×⎝ ⎛⎭⎪⎫12n －1＝12n .答案 12n8.(2018·成都诊断)已知数列{a n }中，a 1＝2，且a 2n ＋1a n ＝4(a n ＋1－a n )(n ∈N +)，则其前9项的和S 9＝________.解析由a 2n ＋1a n＝4(a n ＋1－a n )得，a 2n ＋1－4a n ＋1a n ＋4a 2n ＝0，∴(a n ＋1－2a n )2＝0，a n ＋1a n ＝2，∴数列{a n }是首项a 1＝2，公比为2的等比数列，∴S 9＝2（1－29）1－2＝1 022.答案 1 022 三、解答题9.(2017·全国Ⅰ卷)记S n 为等比数列{a n }的前n 项和.已知S 2＝2，S 3＝－6. (1)求{a n }的通项公式；(2)求S n ，并判断S n ＋1，S n ，S n ＋2是否成等差数列. 解 (1)设{a n }的公比为q ，由题设可得 ⎩⎨⎧a 1（1＋q ）＝2，a 1（1＋q ＋q 2）＝－6，解得⎩⎨⎧q ＝－2，a 1＝－2. 故{a n }的通项公式为a n ＝(－2)n .(2)由(1)得S n ＝a 1（1－q n ）1－q ＝－2[1－（－2）n ]1－（－2）＝23[(－2)n －1]，则S n ＋1＝23[(－2)n ＋1－1]，S n ＋2＝23[(－2)n ＋2－1]，所以S n ＋1＋S n ＋2＝23[(－2)n ＋1－1]＋23[(－2)n ＋2－1]＝23[2(－2)n －2]＝43[(－2)n －1]＝2S n ，∴S n ＋1，S n ，S n ＋2成等差数列.10.(2018·惠州调研)已知数列{a n }中，点(a n ，a n ＋1)在直线y ＝x ＋2上，且首项a 1＝1.(1)求数列{a n }的通项公式；(2)数列{a n }的前n 项和为S n ，等比数列{b n }中，b 1＝a 1，b 2＝a 2，数列{b n }的前n 项和为T n ，请写出适合条件T n ≤S n 的所有n 的值. 解 (1)根据已知a 1＝1，a n ＋1＝a n ＋2，即a n ＋1－a n ＝2＝d ，所以数列{a n }是一个等差数列，a n ＝a 1＋(n －1)d ＝2n －1. (2)数列{a n }的前n 项和S n ＝n 2.等比数列{b n }中，b 1＝a 1＝1，b 2＝a 2＝3，所以q ＝3，b n ＝3n －1.数列{b n }的前n 项和T n ＝1－3n 1－3＝3n －12.T n ≤S n 即3n －12≤n 2，又n ∈N +，所以n ＝1或2.能力提升题组 (建议用时：20分钟)11.数列{a n }中，已知对任意n ∈N +，a 1＋a 2＋a 3＋…＋a n ＝3n －1，则a 21＋a 22＋a 23＋…＋a 2n 等于( ) A.(3n －1)2 B.12(9n －1) C.9n －1D.14(3n －1)解析 ∵a 1＋a 2＋…＋a n ＝3n －1，n ∈N +，n ≥2时，a 1＋a 2＋…＋a n －1＝3n －1－1， ∴当n ≥2时，a n ＝3n －3n －1＝2·3n －1，又n ＝1时，a 1＝2适合上式，∴a n ＝2·3n －1，故数列{a 2n }是首项为4，公比为9的等比数列. 因此a 21＋a 22＋…＋a 2n ＝4（1－9n）1－9＝12(9n－1).答案 B12.(2018·东北三省三校联考)各项均为正数的数列{a n }和{b n }满足：a n ，b n ，a n ＋1成等差数列，b n ，a n ＋1，b n ＋1成等比数列，且a 1＝1，a 2＝3，则数列{a n }的通项公式为________.解析由题意知2b n ＝a n ＋a n ＋1，a 2n ＋1＝b n ·b n ＋1，∴a n ＋1＝b n b n ＋1，当n ≥2时，2b n ＝b n －1b n ＋b n b n ＋1，∵b n >0，∴2b n ＝b n －1＋b n ＋1，∴{b n }成等差数列，由a 1＝1，a 2＝3，得b 1＝2，b 2＝92，∴b 1＝2，b 2＝322，∴公差d ＝22，∴b n ＝n ＋122，∴b n ＝（n ＋1）22， ∴a n ＝b n －1b n ＝n （n ＋1）2. 答案 a n ＝n （n ＋1）213.(2017·合肥模拟)设{a n }是公比为q 的等比数列.(1)推导{a n }的前n 项和公式；(2)设q ≠1，证明数列{a n ＋1}不是等比数列. 解 (1)设{a n }的前n 项和为S n ，当q ＝1时，S n ＝a 1＋a 1＋…＋a 1＝na 1；当q ≠1时，S n ＝a 1＋a 1q ＋a 1q 2＋…＋a 1q n －1，① qS n ＝a 1q ＋a 1q 2＋…＋a 1q n, ②①－②得，(1－q )S n ＝a 1－a 1q n ，∴S n ＝a 1（1－q n）1－q ，∴S n ＝⎩⎨⎧na 1，q ＝1，a 1（1－q n ）1－q ，q ≠1. (2)假设{a n ＋1}是等比数列，则对任意的k ∈N +， (a k ＋1＋1)2＝(a k ＋1)(a k ＋2＋1)，a 2k ＋1＋2a k ＋1＋1＝a k a k ＋2＋a k ＋a k ＋2＋1，a 21q 2k ＋2a 1q k ＝a 1qk －1·a 1q k ＋1＋a 1q k －1＋a 1q k ＋1， ∵a 1≠0，∴2q k ＝q k －1＋q k ＋1.∵q≠0，∴q2－2q＋1＝0，∴q＝1，这与已知矛盾. 故数列{a n＋1}不是等比数列.。

2019-2020年高考数学一轮总复习第六章数列题组训练36等比数列理

2019-2020年高考数学一轮总复习第六章数列题组训练36等比数列理1．在等比数列{a n }中，a 1＝12，q ＝12，a n ＝132，则项数n 为( )A ．3B ．4C ．5D ．6答案 C2．如果－1，a ，b ，c ，－9成等比数列，那么( ) A ．b ＝3，ac ＝9 B ．b ＝－3，ac ＝9 C ．b ＝3，ac ＝－9 D ．b ＝－3，ac ＝－9答案 B3．在等比数列{a n }中，若公比q ＝2，S 4＝1，则S 8的值为( ) A ．15 B ．17 C ．19 D ．21答案 B4．(2018·安徽芜湖五联考)在等比数列{a n }中，a 3＝7，前3项之和S 3＝21，则公比q 的值为( ) A ．1 B ．－12C ．1或－12D ．－1或12答案 C解析根据已知条件得⎩⎪⎨⎪⎧a 1q 2＝7，①a 1＋a 1q ＋a 1q 2＝21，②②÷①得1＋q ＋q2q 2＝3. 整理得2q 2－q －1＝0，解得q ＝1或q ＝－12.5．(2018·江西新余一中调研卷)已知等比数列{a n }中，a 2＝2，a 6＝8，则a 3a 4a 5＝( ) A ．±64 B ．64 C ．32 D ．16答案 B解析因为a 2＝2，a 6＝8，所以由等比数列的性质可知a 2a 6＝a 42＝16，而a 2，a 4，a 6同号，所以a 4＝4，所以a 3a 4a 5＝a 43＝64，故选B.6．(2018·保定一中模拟)若项数为2m(m∈N *)的等比数列的中间两项正好是方程x 2＋px ＋q＝0的两个根，则此数列的各项积是( ) A ．p mB ．p 2mC ．q mD ．q 2m答案 C解析由题意得a m a m ＋1＝q ，所以由等比数列的性质得此数列各项积为(a m a m ＋1)m＝q m. 7．(2018·广西南宁联考)已知在等比数列{a n }中，a 3＝2，a 4a 6＝16，则a 9－a 11a 5－a 7＝( )A ．2B ．4C ．8D ．16答案 B解析因为数列{a n }是等比数列，a 3＝2，所以a 4a 6＝a 3q ·a 3q 3＝4q 4＝16，所以q 2＝2.所以a 9－a 11a 5－a 7＝a 3q 6－a 3q 8a 3q 2－a 3q 4＝（q 2）3－（q 2）4q 2－（q 2）2＝q 4＝4.故选B. 8．数列{a n }的前n 项和为S n ＝4n＋b(b 是常数，n ∈N *)，若这个数列是等比数列，则b 等于( ) A ．－1 B ．0 C ．1 D ．4答案 A解析等比数列{a n }中，q ≠1时，S n ＝a 1·（q n－1）q －1＝a 1q －1·q n －a 1q －1＝A·q n －A ，∴b ＝－1.9．设等比数列{a n }的前n 项和为S n ，若S 1＝13a 2－13，S 2＝13a 3－13，则公比q ＝( )A ．1B ．4C ．4或0D ．8答案 B解析 ∵S 1＝13a 2－13，S 2＝13a 3－13，∴⎩⎪⎨⎪⎧a 1＝13a 1q －13，a 1＋a 1q ＝13a 1q 2－13，解得⎩⎪⎨⎪⎧a 1＝1，q ＝4或⎩⎪⎨⎪⎧a 1＝－13，q ＝0，(舍去) 故所求的公比q ＝4.10．在14与78之间插入n 个数组成等比数列，若各项总和为778，则此数列的项数( )A ．4B ．5C ．6D ．7答案 B解析 ∵q≠1(14≠78)，∴S n ＝a 1－a n q 1－q ，∴778＝14－78q1－q .解得q ＝－12，78＝14×(－12)n ＋2－1，∴n ＝3.故该数列共5项．11．(2017·名师原创)《张丘建算经》中“今有马行转迟，次日减半，疾七日，行七百里．问日行几何？”意思是：“现有一匹马行走的速度逐渐变慢，每天走的里数是前一天的一半，连续行走7天，共走了700里路，问每天走的里数为多少？”则该匹马第一天走的里数为( ) A.128127 B.44 800127 C.700127 D.17532答案 B解析由题意知每日所走的路程成等比数列{a n }，且公比q ＝12，S 7＝700，由等比数列的求和公式得a 1（1－127）1－12＝700，解得a 1＝44 800127，故选B.12．(2018·云南省高三调研考试)已知数列{a n }是等比数列，S n 为其前n 项和，若a 1＋a 2＋a 3＝4，a 4＋a 5＋a 6＝8，则S 12＝( ) A ．40 B ．60 C ．32 D ．50答案 B解析由等比数列的性质可知，数列S 3，S 6－S 3，S 9－S 6，S 12－S 9是等比数列，即数列4，8，S 9－S 6，S 12－S 9是等比数列，因此S 12＝4＋8＋16＋32＝60，故选B.13．(2018·广东惠州一中月考)已知数列{a n }是等比数列，且a 2＝2，a 5＝14，则a 1a 2＋a 2a 3＋…＋a n a n ＋1＝( ) A ．16(1－4－n) B ．16(1－2－n) C.323(1－4－n) D.323(1－2－n) 答案 C解析因为等比数列{a n }中，a 2＝2，a 5＝14，所以a 5a 2＝q 3＝18，所以q ＝12.由等比数列的性质，易知数列{a n a n ＋1}为等比数列，其首项为a 1a 2＝8，公比为q 2＝14，所以要求的a 1a 2＋a 2a 3＋…＋a n a n ＋1为数列{a n a n ＋1}的前n 项和．由等比数列的前n 项和公式得a 1a 2＋a 2a 3＋…＋a n a n ＋1＝8（1－14n ）1－14＝323(1－4－n)，故选C. 14．等比数列{a n }的前n 项和为S n ，若S 3＋3S 2＝0，则公比q ＝________．答案－2解析由S 3＋3S 2＝0，即a 1＋a 2＋a 3＋3(a 1＋a 2)＝0，即4a 1＋4a 2＋a 3＝0，即4a 1＋4a 1q ＋a 1q 2＝0，即q 2＋4q ＋4＝0，所以q ＝－2.15．在等比数列{a n }中，若a 1＝12，a 4＝－4，则公比q ＝________；|a 1|＋|a 2|＋…＋|a n |＝________．答案－2，2n －1－12解析设等比数列{a n }的公比为q ，则a 4＝a 1q 3，代入数据解得q 3＝－8，所以q ＝－2；等比数列{|a n |}的公比为|q|＝2，则|a n |＝12×2n －1，所以|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝12(1＋2＋22＋…＋2n －1)＝12(2n －1)＝2n －1－12. 16．一正项等比数列前11项的几何平均数为32，从这11项中抽去一项后所余下的10项的几何平均数为32，那么抽去的这一项是第________项．答案 6解析由于数列的前11项的几何平均数为32，所以该数列的前11项之积为3211＝255. 当抽去一项后所剩下的10项之积为3210＝250， ∴抽去的一项为255÷250＝25.又因a 1·a 11＝a 2·a 10＝a 3·a 9＝a 4·a 8＝a 5·a 7＝a 62，所以a 1·a 2·…·a 11＝a 611.故有a 611＝255，即a 6＝25.∴抽出的应是第6项．17．已知{a n }是等比数列，S n 是其前n 项和，a 1，a 7，a 4成等差数列，求证：2S 3，S 6，S 12－S 6成等比数列．答案略证明由已知得2a 1q 6＝a 1＋a 1q 3，即2q 6－q 3－1＝0，得q 3＝1或q 3＝－12.当q 3＝1即q ＝1，{a n }为常数列，S 62S 3＝S 12－S 6S 6命题成立．当q 3＝－12时，S 62S 3＝1－q 62（1－q 3）＝14. S 12－S 6S 6＝1－q 121－q 6－1＝14.∴命题成立． 18．(2018·四川成都一诊)已知数列{a n }满足a 1＝－2，a n ＋1＝2a n ＋4. (1)证明数列{a n ＋4}是等比数列； (2)求数列{|a n |}的前n 项和S n . 答案 (1)略 (2)S n ＝2n ＋1－4n ＋2解析 (1)∵a 1＝－2，∴a 1＋4＝2.∵a n ＋1＝2a n ＋4，∴a n ＋1＋4＝2a n ＋8＝2(a n ＋4)，∴a n ＋1＋4a n ＋4＝2，∴{a n ＋4}是以2为首项，2为公比的等比数列． (2)由(1)可知a n ＋4＝2n，∴a n ＝2n－4. 当n ＝1时，a 1＝－2<0，∴S 1＝|a 1|＝2；当n≥2时，a n ≥0，∴S n ＝－a 1＋a 2＋…＋a n ＝2＋(22－4)＋…＋(2n－4)＝2＋22＋ (2)－4(n －1)＝2（1－2n）1－2－4(n －1)＝2n ＋1－4n ＋2.又当n ＝1时，上式也满足． ∴S n ＝2n ＋1－4n ＋2.1．(2018·衡水中学调研)等比数列{a n }的前n 项和为S n ，已知a 2a 5＝2a 3，且a 4与2a 7的等差中项为54，则S 5＝( )A ．29B ．31C ．33D ．36答案 B解析方法一：设等比数列{a n }的首项为a 1，公比为q ，由题意知⎩⎪⎨⎪⎧a 1q ·a 1q 4＝2a 1q 2，a 1q 3＋2a 1q 6＝2×54，解得⎩⎪⎨⎪⎧q ＝12，a 1＝16，所以S 5＝16×[1－（12）5]1－12＝31，故选B. 方法二：由a 2a 5＝2a 3，得a 4＝2.又a 4＋2a 7＝2×54，所以a 7＝14，所以q ＝12，所以a 1＝16，所以S 5＝16×[1－（12）5]1－12＝31，故选B.2．(2018·延边质检)已知a 1，a 2，a 3，a 4依次成等比数列，且公比q 不为1.将此数列删去一个数后得到的数列(按原来的顺序)是等差数列，则正数q 的值是( ) A.1＋52B.±1＋52 C.±1＋32D.－1＋32答案 B解析因为公比q 不为1，所以删去的数不是a 1，a 4.①若删去a 2，则由2a 3＝a 1＋a 4得2a 1q2＝a 1＋a 1q 3，又a 1≠0，所以2q 2＝1＋q 3，整理得q 2(q －1)＝(q －1)(q ＋1)．又q≠1，所以q 2＝q ＋1，又q>0，得q ＝1＋52；②若删去a 3，则由2a 2＝a 1＋a 4得2a 1q ＝a 1＋a 1q 3，又a 1≠0，所以2q ＝1＋q 3，整理得q(q ＋1)(q －1)＝q －1.又q≠1，则可得q(q ＋1)＝1，又q>0，得q ＝－1＋52.综上所述，q ＝±1＋52，故选B.3．(2017·沧州七校联考)设等比数列{a n }的前n 项和为S n ，若S 6S 3＝3，则S 9S 6＝( )A ．2 B.73 C.83 D ．3答案 B解析方法一：由S 6S 3＝3知该等比数列的公比q≠－1，则S 3，S 6－S 3，S 9－S 6仍成等比数列，于是由S 6＝3S 3，可推出S 9－S 6＝4S 3，S 9＝7S 3，∴S 9S 6＝73.方法二：设数列{a n }的公比为q ，则S 6S 3＝（1＋q 3）S 3S 3＝1＋q 3＝3，所以q 3＝2，于是S 9S 6＝（1＋q 3＋q 6）S 3（1＋q 3）S 3＝1＋2＋41＋2＝73. 4．(2015·浙江)已知{a n }是等差数列，公差d 不为零．若a 2，a 3，a 7成等比数列，且2a 1＋a 2＝1，则a 1＝________，d ＝________．答案 23；－1解析 ∵a 2，a 3，a 7成等比数列，∴a 32＝a 2a 7，即(a 1＋2d)2＝(a 1＋d)·(a 1＋6d)，解得d ＝－32a 1①，∵2a 1＋a 2＝1，∴3a 1＋d ＝1②，由①②可得a 1＝23，d ＝－1. 5．在等比数列{a n }中，若a 7＋a 8＋a 9＋a 10＝158，a 8·a 9＝－98，则1a 7＋1a 8＋1a 9＋1a 10＝________．答案－53解析 ∵1a 7＋1a 10＝a 7＋a 10a 7a 10，1a 8＋1a 9＝a 8＋a 9a 8a 9，而a 8a 9＝a 7a 10，∴1a 7＋1a 8＋1a 9＋1a 10＝a 7＋a 8＋a 9＋a 10a 7a 10＝－15898＝－53.6．(2017·广州综合测试)已知数列{c n }，其中c n ＝2n＋3n，且数列{c n ＋1－pc n }为等比数列，则常数p ＝________．答案 2或3解析由数列{c n ＋1－pc n }为等比数列，得(c 3－pc 2)2＝(c 2－pc 1)(c 4－pc 3)，即(35－13p)2＝(13－5p)(97－35p)．解得p ＝2或p ＝3.。

2019版高考数学理科课标A版一轮复习习题：第六章数列

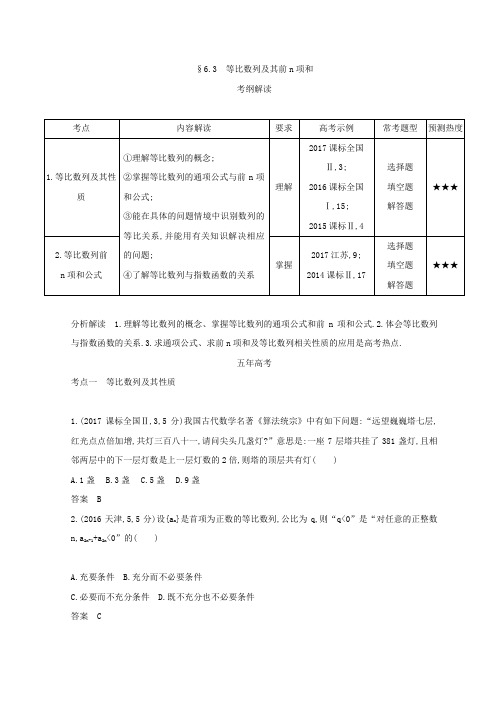
§6.3等比数列及其前n项和考纲解读分析解读 1.理解等比数列的概念、掌握等比数列的通项公式和前n项和公式.2.体会等比数列与指数函数的关系.3.求通项公式、求前n项和及等比数列相关性质的应用是高考热点.五年高考考点一等比数列及其性质1.(2017课标全国Ⅱ,3,5分)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )A.1盏B.3盏C.5盏D.9盏答案 B2.(2016天津,5,5分)设{a n}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n-1+a2n<0”的( )A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件答案 C3.(2015课标Ⅱ,4,5分)已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7=( )A.21B.42C.63D.84答案 B4.(2017北京,10,5分)若等差数列{a n}和等比数列{b n}满足a1=b1=-1,a4=b4=8,则= .答案 15.(2016课标全国Ⅰ,15,5分)设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为.答案646.(2015湖南,14,5分)设S n为等比数列{a n}的前n项和.若a1=1,且3S1,2S2,S3成等差数列,则a n= .答案3n-1教师用书专用(7—13)7.(2013江西,3,5分)等比数列x,3x+3,6x+6,…的第四项等于( )A.-24B.0C.12D.24答案 A8.(2013福建,9,5分)已知等比数列{a n}的公比为q,记b n=a m(n-1)+1+a m(n-1)+2+…+a m(n-1)+m,c n=a m(n-1)+1·a m(n-1)+2·…·a m(n-1)+m(m,n∈N*),则以下结论一定正确的是( )A.数列{b n}为等差数列,公差为q mB.数列{b n}为等比数列,公比为q2mC.数列{c n}为等比数列,公比为D.数列{c n}为等比数列,公比为答案 C9.(2014广东,13,5分)若等比数列{a n}的各项均为正数,且a10a11+a9a12=2e5,则ln a1+ln a2+…+ln a20= .答案5010.(2014天津,11,5分)设{a n}是首项为a1,公差为-1的等差数列,S n为其前n项和.若S1,S2,S4成等比数列,则a1的值为.答案-11.(2014江苏,7,5分)在各项均为正数的等比数列{a n}中,若a2=1,a8=a6+2a4,则a6的值是.答案 412.(2014安徽,12,5分)数列{a n}是等差数列,若a1+1,a3+3,a5+5构成公比为q的等比数列,则q= .答案 113.(2013江苏,14,5分)在正项等比数列{a n}中,a5=,a6+a7=3.则满足a1+a2+…+a n>a1a2…a n的最大正整数n的值为.答案12考点二等比数列前n项和公式1.(2013课标全国Ⅱ,3,5分)等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1=( )A. B.-C. D.-答案 C2.(2017江苏,9,5分)等比数列{a n}的各项均为实数,其前n项和为S n.已知S3=,S6=,则a8= .答案323.(2015安徽,14,5分)已知数列{a n}是递增的等比数列,a1+a4=9,a2a3=8,则数列{a n}的前n项和等于.答案2n-14.(2016四川,19,12分)已知数列{a n}的首项为1,S n为数列{a n}的前n项和,S n+1=qS n+1,其中q>0,n∈N*.(1)若2a2,a3,a2+2成等差数列,求数列{a n}的通项公式;(2)设双曲线x2-=1的离心率为e n,且e2=,证明:e1+e2+…+e n>.解析(1)由已知,S n+1=qS n+1,S n+2=qS n+1+1,两式相减得到a n+2=qa n+1,n≥1.又由S2=qS1+1得到a2=qa1,故a n+1=qa n对所有n≥1都成立.所以,数列{a n}是首项为1,公比为q的等比数列.从而a n=q n-1.由2a2,a3,a2+2成等差数列,可得2a3=3a2+2,即2q2=3q+2,则(2q+1)(q-2)=0,由已知,q>0,故q=2.所以a n=2n-1(n∈N*).(2)由(1)可知,a n=q n-1.所以双曲线x2-=1的离心率e n==.由e2==,解得q=.因为1+q2(k-1)>q2(k-1),所以>q k-1(k∈N*).于是e1+e2+…+e n>1+q+…+q n-1=,故e1+e2+…+e n>.疑难突破由(1)可得e n=,因为不等式左边是e1+e2+…+e n,直接求和不行,利用放缩法得e n=>=q n-1,从而得e1+e2+…+e n>q0+q1+…+q n-1,化简即可.评析本题涉及的知识点比较多,由递推思想推出数列{a n}是等比数列,由等差中项求出q,由放缩法证明不等式成立.综合性较强.5.(2014课标Ⅱ,17,12分)已知数列{a n}满足a1=1,a n+1=3a n+1.(1)证明是等比数列,并求{a n}的通项公式;(2)证明++…+<.解析(1)由a n+1=3a n+1得a n+1+=3.又a1+=,所以是首项为,公比为3的等比数列.a n+=,因此{a n}的通项公式为a n=.(2)由(1)知=.因为当n≥1时,3n-1≥2×3n-1,所以≤.于是++…+≤1++…+=<.所以++…+<.教师用书专用(6—11)6.(2013北京,10,5分)若等比数列{a n}满足a2+a4=20,a3+a5=40,则公比q= ;前n项和S n= .答案2;2n+1-27.(2013辽宁,14,5分)已知等比数列{a n}是递增数列,S n是{a n}的前n项和.若a1,a3是方程x2-5x+4=0的两个根,则S6= .答案638.(2015山东,18,12分)设数列{a n}的前n项和为S n.已知2S n=3n+3.(1)求{a n}的通项公式;(2)若数列{b n}满足a n b n=log3a n,求{b n}的前n项和T n.解析(1)因为2S n=3n+3,所以2a1=3+3,故a1=3,当n>1时,2S n-1=3n-1+3,此时2a n=2S n-2S n-1=3n-3n-1=2×3n-1,即a n=3n-1,所以a n=(2)因为a n b n=log3a n,所以b1=,当n>1时,b n=31-n log33n-1=(n-1)·31-n.所以T1=b1=;当n>1时,T n=b1+b2+b3+…+b n=+[1×3-1+2×3-2+…+(n-1)×31-n],所以3T n=1+[1×30+2×3-1+…+(n-1)×32-n],两式相减,得2T n=+(30+3-1+3-2+…+32-n)-(n-1)×31-n=+-(n-1)×31-n=-,所以T n=-.经检验,n=1时也适合.综上可得T n=-.9.(2015江苏,20,16分)设a1,a2,a3,a4是各项为正数且公差为d(d≠0)的等差数列.(1)证明:,,,依次构成等比数列;(2)是否存在a1,d,使得a1,,,依次构成等比数列?并说明理由;(3)是否存在a1,d及正整数n,k,使得,,,依次构成等比数列?并说明理由.解析(1)证明:因为==2d(n=1,2,3)是同一个常数,所以,,,依次构成等比数列. (2)令a1+d=a,则a1,a2,a3,a4分别为a-d,a,a+d,a+2d(a>d,a>-2d,d≠0).假设存在a1,d,使得a1,,,依次构成等比数列,则a4=(a-d)(a+d)3,且(a+d)6=a2(a+2d)4.令t=,则1=(1-t)(1+t)3,且(1+t)6=(1+2t)4,化简得t3+2t2-2=0(*),且t2=t+1.将t2=t+1代入(*)式,得t(t+1)+2(t+1)-2=t2+3t=t+1+3t=4t+1=0,则t=-.显然t=-不是上面方程的解,矛盾,所以假设不成立,因此不存在a1,d,使得a1,,,依次构成等比数列.(3)假设存在a1,d及正整数n,k,使得,,,依次构成等比数列,则(a1+2d)n+2k=(a1+d)2(n+k),且(a1+d)n+k(a1+3d)n+3k=(a1+2d)2(n+2k).分别在两个等式的两边同除以及,并令t=,则(1+2t)n+2k=(1+t)2(n+k),且(1+t)n+k(1+3t)n+3k=(1+2t)2(n+2k).将上述两个等式两边取对数,得(n+2k)ln(1+2t)=2(n+k)·ln(1+t),且(n+k)ln(1+t)+(n+3k)ln(1+3t)=2(n+2k)ln(1+2t).化简得2k[ln(1+2t)-ln(1+t)]=n[2ln(1+t)-ln(1+2t)],且3k[ln(1+3t)-ln(1+t)]=n[3ln(1+t)-ln(1+3t)].再将这两式相除,化简得ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t)=4ln(1+3t)ln(1+t)(**).令g(t)=4ln(1+3t)ln(1+t)-ln(1+3t)ln(1+2t)-3ln(1+2t)·ln(1+t),则g'(t)=.令φ(t)=(1+3t)2ln(1+3t)-3(1+2t)2ln(1+2t)+3(1+t)2·ln(1+t),则φ'(t)=6[(1+3t)ln(1+3t)-2(1+2t)ln(1+2t)+(1+t)·ln(1+t)].令φ1(t)=φ'(t),则φ'1(t)=6[3ln(1+3t)-4ln(1+2t)+ln(1+t)].令φ2(t)=φ'1(t),则φ'2(t)=>0.由g(0)=φ(0)=φ1(0)=φ2(0)=0,φ'2(t)>0,知φ2(t),φ1(t),φ(t),g(t)在和(0,+∞)上均单调.故g(t)只有唯一零点t=0,即方程(**)只有唯一解t=0,故假设不成立.所以不存在a1,d及正整数n,k,使得,,,依次构成等比数列.10.(2013天津,19,14分)已知首项为的等比数列{a n}不是．．递减数列,其前n项和为S n(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.(1)求数列{a n}的通项公式;(2)设T n=S n-(n∈N*),求数列{T n}的最大项的值与最小项的值.解析(1)设等比数列{a n}的公比为q,因为S3+a3,S5+a5,S4+a4成等差数列,所以S5+a5-S3-a3=S4+a4-S5-a5,即4a5=a3,于是q2==.又{a n}不是递减数列且a1=,所以q=-.故等比数列{a n}的通项公式为a n=×=(-1)n-1·.(2)由(1)得S n=1-=当n为正奇数时,S n随n的增大而减小,所以1<S n≤S1=,故0<S n-≤S1-=-=.当n为正偶数时,S n随n的增大而增大,所以=S2≤S n<1,故0>S n-≥S2-=-=-.综上,对于n∈N*,总有-≤S n-≤.所以数列{T n}最大项的值为,最小项的值为-.11.(2013湖北,18,12分)已知等比数列{a n}满足:|a2-a3|=10,a1a2a3=125.(1)求数列{a n}的通项公式;(2)是否存在正整数m,使得++…+≥1?若存在,求m的最小值;若不存在,说明理由.解析(1)设等比数列{a n}的公比为q,则由已知可得解得或故a n=·3n-1,或a n=-5·(-1)n-1.(2)若a n=·3n-1,则=·,故是首项为,公比为的等比数列,从而==·<<1.若a n=(-5)·(-1)n-1,则=-(-1)n-1,故是首项为-,公比为-1的等比数列,从而=故<1.综上,对任何正整数m,总有<1.故不存在正整数m,使得++…+≥1成立.三年模拟A组2016—2018年模拟·基础题组考点一等比数列及其性质1.(2018广东广雅中学、东华中学、河南名校第一次联考,7)已知公比不为1的等比数列{a n}的前n项和为S n,a1a2a3a4a5=,且a2,a4,a3成等差数列,则S5=( )A. B. C. D.答案 D2.(2018云南玉溪模拟,7)等比数列{a n}中,a1=512,公比q=-,记Πn=a1×a2×…×a n(即Πn表示数列{a n}的前n项之积),Π8,Π9,Π10,Π11中,值为正数的个数是( )A.1B.2C.3D.4答案 B3.(2017福建4月模拟,6)已知递增的等比数列{a n}的公比为q,其前n项和S n<0,则( )A.a1<0,0<q<1B.a1<0,q>1C.a1>0,0<q<1D.a1>0,q>1答案 A4.(2016福建厦门一中期中,4)已知数列{a n}为等比数列,且a1a13+2=4π,则tan(a2a12)的值为( )A. B.-C.±D.-答案 A考点二等比数列前n项和公式5.(2017河北衡水中学高三上学期第三次调研,4)等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=( )A.29B.31C.33D.36答案 B6.(2018江西新余第一中学四模,14)等比数列{a n}的前n项和为S n,S n=b(-2)n-1-a,则= .答案-7.(2017江西吉安一中期中,15)已知正项等比数列{a n}满足log2a n+2-log2a n=2,且a3=8,则数列{a n}的前n项和S n= .答案2n+1-2B组2016—2018年模拟·提升题组(满分:50分时间:40分钟)一、选择题(每小题5分,共20分)1.(2018湖北荆州一模,9)已知数列{a n}是公差不为0的等差数列,且a1,a3,a7为等比数列{b n}的连续三项,则的值为( )A. B.4 C.2 D.答案 A2.(2017河南洛阳期中,11)已知数列S n为等比数列{a n}的前n项和,S8=2,S24=14,则S2 016=( )A.2252-2B.2253-2C.21 008-2D.22 016-2答案 B3.(2017江西南昌摸底考试,11)设等比数列{a n}的公比为q,其前n项之积为T n,并且满足条件:a1>1,a2 016a2 017>1,<0,给出下列结论:(1)0<q<1;(2)a2 016a2 018-1>0;(3)T2 016是数列{T n}中的最大项;(4)使T n>1成立的最大自然数等于4 031,其中正确的结论为( )A.(2)(3)B.(1)(3)C.(1)(4)D.(2)(4)答案 B4.(2016江西名校学术联盟调研三,7)已知等比数列{a n}的各项都为正数,其前n项和为S n,且a1+a7=9,a4=2,则S8=( )A.15(1+)B.15C.15(-1)或15D.15(1+)或15答案 D二、填空题(每小题5分,共15分)5.(2018广东广州第一次调研,14)在各项都为正数的等比数列{a n}中,若a2 018=,则+的最小值为.答案 46.(2018湖北黄石第三中学阶段性检测,15)下表给出一个“三角形数阵”:,,,,,,……已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为a i-j,则(1)a8-3= ;(2)前20行中这个数共出现了次.答案(1) (2)47.(2017江西仿真模拟,16)已知数列{a n}的前n项和为S n,且满足:a1=1,a2=2,S n+1=a n+2-a n+1(n∈N*),若不等式λS n>a n恒成立,则实数λ的取值范围是.答案λ>1三、解答题(共15分)8.(2017湖南郴州第一次教学质量检测,19)已知数列{a n}的首项a1=1,且a n+1=(n∈N*).(1)证明:数列是等比数列;(2)若b n=-,求数列{b n}的前n项和S n.解析(1)证明:∵a n+1=,∴==+,∴-=.又a1=1,∴-=,∴数列是以为首项,为公比的等比数列.(2)由(1)知,-=·=,即=+.∴b n=-=.于是S n=+++…+,①S n=++…++,②①-②得,S n=++…+-=-=1--,则S n=2--=2-,∴数列{b n}的前n项和S n=2-.C组2016—2018年模拟·方法题组方法1 等比数列基本运算的解题技巧1.(2017福建漳州八校2月联考,3)等比数列{a n}的前n项和为S n,若S3=2,S6=18,则等于( )A.-3B.5C.-31D.33答案 D2.(2017山西运城康杰中学模拟(2),7)已知{a n}是各项均为正数的等比数列(公比q>1),b n=log2a n,b1+b2+b3=3,b1b2b3=-3,则a n=( )A.22n-3B.25-2nC.22n-5D.22n-3或25-2n答案 A方法2 等比数列的判定与证明3.(2016河南洛阳期中模拟,5)下列结论正确的是( )A.若数列{a n}的前n项和S n=n2+n+1,则{a n}为等差数列B.若数列{a n}的前n项和S n=2n-2,则{a n}为等比数列C.非零实数a,b,c不全相等,若a,b,c成等差数列,则,,也可能构成等差数列D.非零实数a,b,c不全相等,若a,b,c成等比数列,则,,一定构成等比数列答案 D4.(2018湖北八校第一次联考,17)已知数列{a n}满足a1=1,a2=4,a n+2=4a n+1-4a n.(1)求证:{a n+1-2a n}为等比数列;(2)求数列{a n}的通项公式.解析(1)证明:由a n+2=4a n+1-4a n得a n+2-2a n+1=2a n+1-4a n=2(a n+1-2a n),∴=2,又a2-2a1=2≠0,∴{a n+1-2a n}是等比数列.(2)由(1)可得a n+1-2a n=2n-1(a2-2a1)=2n,∴-=,∴是首项为,公差为的等差数列,∴=,∴a n=n·2n-1.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

题组训练36 等比数列
1．在等比数列{a n }中，a 1＝12，q ＝12，a n ＝1
32，则项数n 为( )
A ．3
B ．4
C ．5
D ．6
答案 C
2．如果－1，a ，b ，c ，－9成等比数列，那么( ) A ．b ＝3，ac ＝9 B ．b ＝－3，ac ＝9 C ．b ＝3，ac ＝－9 D ．b ＝－3，ac ＝－9
答案 B
3．在等比数列{a n }中，若公比q ＝2，S 4＝1，则S 8的值为( ) A ．15 B ．17 C ．19 D ．21
答案 B
4．(2018·安徽芜湖五联考)在等比数列{a n }中，a 3＝7，前3项之和S 3＝21，则公比q 的值为( ) A ．1 B ．－1
2
C ．1或－1
2
D ．－1或1
2
答案 C
解析根据已知条件得⎩
⎪⎨⎪⎧a1q2＝7，①a1＋a1q ＋a1q2＝21，②②÷①得1＋q ＋q2
q2＝3.
整理得2q 2
－q －1＝0，解得q ＝1或q ＝－12
.
5．(2018·江西新余一中调研卷)已知等比数列{a n }中，a 2＝2，a 6＝8，则a 3a 4a 5＝( ) A ．±64 B ．64 C ．32 D ．16
答案 B
解析因为a 2＝2，a 6＝8，所以由等比数列的性质可知a 2a 6＝a 42
＝16，而a 2，a 4，a 6同号，所以a 4＝4，所以a 3a 4a 5＝a 43
＝64，故选B.
6．(2018·保定一中模拟)若项数为2m(m∈N *
)的等比数列的中间两项正好是方程x 2
＋px ＋q ＝0的两个根，则此数列的各项积是( ) A ．p m
B ．p 2m
C ．q m
D ．q 2m
答案 C
解析由题意得a m a m ＋1＝q ，所以由等比数列的性质得此数列各项积为(a m a m ＋1)m ＝q m
. 7．(2018·广西南宁联考)已知在等比数列{a n }中，a 3＝2，a 4a 6＝16，则a9－a11
a5－a7＝( )
A ．2
B ．4
C ．8
D ．16
答案 B
解析因为数列{a n }是等比数列，a 3＝2，所以a 4a 6＝a 3q ·a 3q 3
＝4q 4
＝16，所以q 2
＝2.所以a9－a11a5－a7＝a3q6－a3q8a3q2－a3q4＝（q2）3－（q2）4q2－（q2）2
＝q 4
＝4.故选B.
8．数列{a n }的前n 项和为S n ＝4n
＋b(b 是常数，n ∈N *
)，若这个数列是等比数列，则b 等于( ) A ．－1 B ．0 C ．1 D ．4
答案 A
解析等比数列{a n }中，q ≠1时，S n ＝a1·（qn －1）q －1＝a1q －1·q n －a1q －1＝A·q n －A ，∴b ＝
－1.
9．设等比数列{a n }的前n 项和为S n ，若S 1＝13a 2－13，S 2＝13a 3－1
3，则公比q ＝( )
A ．1
B ．4
C ．4或0
D ．8
答案 B
解析 ∵S 1
＝13a 2
－13，S 2
＝13a 3
－13，∴⎩⎪⎨⎪⎧a1＝13a1q －1
3，a1＋a1q ＝13a1q2－13
，解得⎩⎪⎨⎪⎧a1＝1，q ＝4或⎩⎪⎨⎪⎧a1＝－13，q ＝0，(舍
去)
故所求的公比q ＝4.
10．在14与78之间插入n 个数组成等比数列，若各项总和为77
8，则此数列的项数( )
A ．4
B ．5
C ．6
D ．7
答案 B。

2019版高考数学一轮总复习第六章数列题组训练36等比数列理

推荐2019届高三数学(理 新课标)一轮复习课件第六章 数列6.3

2019版高考数学一轮复习题组训练第6章 第3讲 等比数列及其前n项和(含最新模拟题) Word版含答案

2019-2020学年高中新创新一轮复习理数通用版：第六章数列Word版含解析.doc

2019届高考数学人教A版理科第一轮复习课件：第六章+数列+6.4

(江苏专版)2019版高考数学一轮复习 第六章 数列 6.3 等比数列课件.pptx

2019届高考数学人教B理一轮复习讲义：第六章 数列 第3

2019-2020年高考数学一轮总复习第六章数列题组训练36等比数列理

2019版高考数学理科课标A版一轮复习习题：第六章 数列

推荐2019届高三数学(理新课标)一轮复习课件第六章数列6.3

2019版高考数学一轮复习题组训练第6章第3讲等比数列及其前n项和(含最新模拟题) Word版含答案

(江苏专版)2019版高考数学一轮复习第六章数列 6.3 等比数列课件.pptx

2019届高考数学人教B理一轮复习讲义：第六章数列第3

2019版高考数学理科课标A版一轮复习习题：第六章数列