德尔菲法预测案例
德尔菲法案例分析
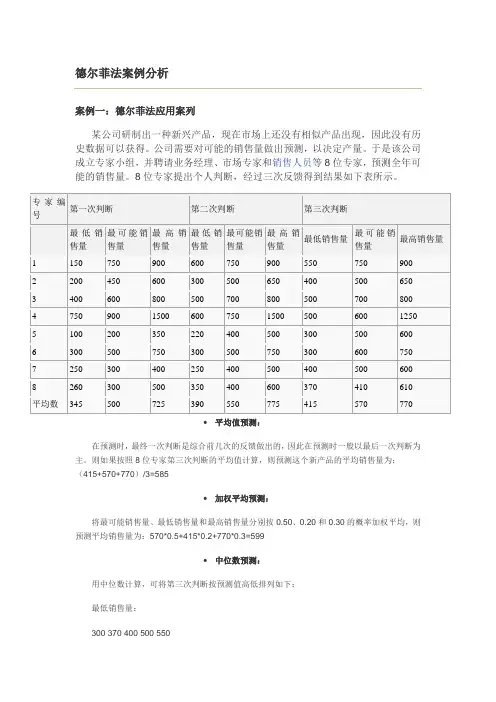
德尔菲法案例分析案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
•平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585•加权平均预测：将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：570*0.5+415*0.2+770*0.3=599•中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
将可最能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：600*0.5+400*0.2+750*0.3=695德尔菲法德尔菲法/得尔飞法(Delphi Method)目录[隐藏]• 1 德尔菲法的简介o 1.1 德尔菲法的起源演变o 1.2 德尔菲法的典型特征• 2 德尔菲法的特征• 3 德尔菲法的具体实施步骤o 3.1 德尔菲法实施注意事项• 4 德尔菲法的应用• 5 德尔菲法的优缺点• 6 德尔菲法与其他决策法相比较•7 德尔菲法案例分析o7.1 案例一：德尔菲法应用案列[1]o7.2 案例二：德尔菲法在企业人力资源预测中的运用[2]•8 相关条目•9 参考文献[编辑]德尔菲法的简介德尔菲法是在20世纪40年代由O．赫尔姆和N．达尔克首创，经过T．J．戈尔登和兰德公司进一步发展而成的。
德尔菲法
德尔菲法的简介德尔菲法是在20世纪40年代由O．赫尔姆和N．达尔克首创，经过T．J．戈尔登和兰德公司进一步发展而成的。
德尔菲这一名称起源于古希腊有关太阳神阿波罗的神话。
传说中阿波罗具有预见未来的能力。
因此，这种预测方法被命名为德尔菲法。
1946年，兰德公司首次用这种方法用来进行预测，后来该方法被迅速广泛采用。
德尔菲法也称专家调查法，是一种采用通讯方式分别将所需解决的问题单独发送到各个专家手中，征询意见，然后回收汇总全部专家的意见，并整理出综合意见。
随后将该综合意见和预测问题再分别反馈给专家，再次征询意见，各专家依据综合意见修改自己原有的意见，然后再汇总。
这样多次反复，逐步取得比较一致的预测结果的决策方法。
德尔菲法依据系统的程序，采用匿名发表意见的方式，即专家之间不得互相讨论，不发生横向联系，只能与调查人员发生关系，通过多轮次调查专家对问卷所提问题的看法，经过反复征询、归纳、修改，最后汇总成专家基本一致的看法，作为预测的结果。
这种方法具有广泛的代表性，较为可靠。
德尔菲法的起源演变起源德尔菲法是在20世纪40年代由赫尔默(Helmer)和戈登(Gordon)首创，1946年，美国兰德公司为避免集体讨论存在的屈从于权威或盲目服从多数的缺陷，首次用这种方法用来进行定性预测，后来该方法被迅速广泛采用。
20世纪中期，当美国政府执意发动朝鲜战争的时候，兰德公司又提交了一份预测报告，预告这场战争必败。
政府完全没有采纳，结果一败涂地。
从此以后，德尔菲法得到广泛认可。
德尔菲是古希腊地名。
相传太阳神阿波罗(Apollo)在德尔菲杀死了一条巨蟒，成了德尔菲主人。
在德尔菲有座阿波罗神殿，是一个预卜未来的神谕之地，于是人们就借用此名，作为这种方法的名字。
演变德尔菲法最初产生于科技领域，后来逐渐被应用于任何领域的预测，如军事预测、人口预测、医疗保健预测、经营和需求预测、教育预测等。
此外，还用来进行评价、决策、管理沟通和规划工作。
德尔菲法预测案例
德尔菲法预测北京现代11月销量
加权平均法： 将第3次专家意见的最可能数、最低数和最高数按 0.5、 0.2、0.3进行加权平均，则预测销售数量为 (7.1125*0.2+7.3625*0.5+7.7125*0.3)/(0.2+0.5+0.3)=7.4175（万辆）
第 最低数
7.0 7.2 7.3 6.8 6.9 7.3 7.2 7.2 7.1125
三
次 最可能数 7.3 7.5 7.5 7.0 7.3 7.6 7.4 7.3 7.3625
最高数
7.7 7.7 7.8 7.5 7.5 7.8 7.9 7.8 7.7125
单位：万辆
德尔菲法预测北京现代11月销量
德尔菲法预测北京现代11月销量
将第二轮专家意见进行汇总，下发各位专家， 进行第三轮征求专家意见，结果如下: 专家号 1 2 3 4 5 6 7 8 最低数 7.0 7.2 7.3 6.8 6.9 7.3 7.2 7.2 最可能数 7.3 7.5 7.5 7.0 7.3 7.6 7.4 7.3 最高数 7.7 7.7 7.8 7.5 7.5 7.8 7.9 7.8
销量（万辆） 6.3 3.7 6.2 5.7 5.6 5.4 4.8 6.0 7.3 5.9 6.8 6.5
德尔菲法预测北京现代汽车11月销量
选择专家团队 从各相关领域选择8名专家，组成专家小组
德尔菲法预测北京现代11月销量
制作调查咨询表，下发各位专家进 行第一轮专家意见征求，结果如下:
专家号 1 2 3 4 5 6 7 8 最低数 6.5 7.2 6.9 5.9 7.4 7.7 7.0 7.5 最可能数 7.0 7.6 7.5 6.5 7.8 8.2 7.3 7.9 最高数 7.8 8.2 7.9 7.4 8.2 8.5 7.7 8.1
德尔菲法案例分析
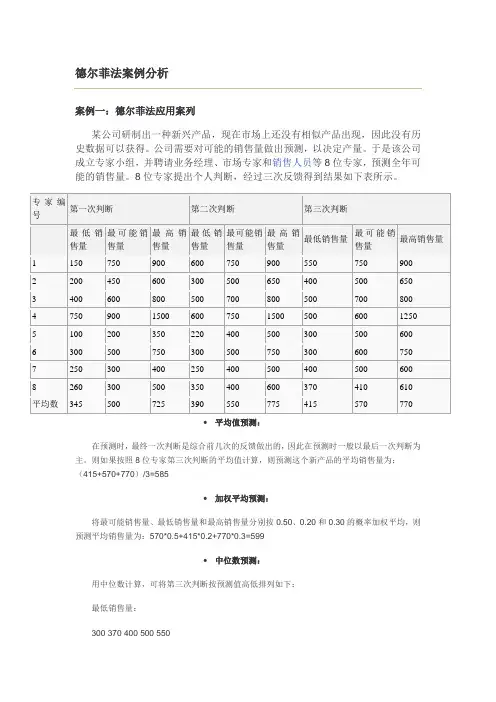
德尔菲法案例分析案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
专家编号第一次判断第二次判断第三次判断最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量1 150 750 900 600 750 900 550 750 9002 200 450 600 300 500 650 400 500 6503 400 600 800 500 700 800 500 700 8004 750 900 1500 600 750 1500 500 600 12505 100 200 350 220 400 500 300 500 6006 300 500 750 300 500 750 300 600 7507 250 300 400 250 400 500 400 500 6008 260 300 500 350 400 600 370 410 610 平均数345 500 725 390 550 775 415 570 770∙平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585∙加权平均预测：将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：570*0.5+415*0.2+770*0.3=599∙中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
德尔菲法案例
德尔菲法案例[1]案例一:德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
专家第一次判断第二次判断第三次判断编号最低销最可能最高销最低销最可能最高销最低销最可能最高销售量销售量售量售量销售量售量售量销售量售量 1 150 750 900 600 750 900 550 750 900 2 200 450 600 300 500 650 400 500 650 3 400 600 800 500 700 800 500 700 800 4 750 900 1500 600 750 1500 500 600 1250 5 100 200 350 220 400 500 300 500 600 6 300 500 750 300 500 750 300 600 750 7 250 300 400 250 400 500 400 500 600 8 260 300 500 350 400 600 370 410 610 平均数 345 500 725 390 550 775 415 570 770,,, 平均值预测:在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为:(415+570+770)/3=585, 加权平均预测:将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为:570*0.5+415*0.2+770*0.3=599, 中位数预测:用中位数计算，可将第三次判断按预测值高低排列如下:最低销售量:300 370 400 500 550最可能销售量:410 500 600 700 750最高销售量:600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
德尔菲法案例
德尔菲法案例[1]案例一:德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
专家第一次判断第二次判断第三次判断编号最低销最可能最高销最低销最可能最高销最低销最可能最高销售量销售量售量售量销售量售量售量销售量售量 1 150 750 900 600 750 900 550 750 900 2 200 450 600 300 500 650 400 500 650 3 400 600 800 500 700 800 500 700 800 4 750 900 1500 600 750 1500 500 600 1250 5 100 200 350 220 400 500 300 500 600 6 300 500 750 300 500 750 300 600 750 7 250 300 400 250 400 500 400 500 600 8 260 300 500 350 400 600 370 410 610 平均数 345 500 725 390 550 775 415 570 770,,, 平均值预测:在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为:(415+570+770)/3=585, 加权平均预测:将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为:570*0.5+415*0.2+770*0.3=599, 中位数预测:用中位数计算，可将第三次判断按预测值高低排列如下:最低销售量:300 370 400 500 550最可能销售量:410 500 600 700 750最高销售量:600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
德尔菲法案例
德尔菲法案例德尔菲法是一种专家咨询技术，它通过专家群体的意见征询和反馈，以达成一致意见或者解决问题的方法。
德尔菲法的应用范围非常广泛，可以用于决策、预测、评估、规划等方面。
下面我们通过一个案例来了解一下德尔菲法的具体应用。
某公司在新产品研发过程中，需要对市场需求进行预测，以确定产品的定位和推广策略。
在这种情况下，德尔菲法可以被用来进行市场需求的预测。
首先，确定参与德尔菲法的专家群体，他们可以包括市场营销专家、行业资深人士、消费者代表等。
然后，制定调查问卷，征求专家们对市场需求的看法和预测。
问卷内容可以包括市场趋势、消费者偏好、竞争对手动向等方面的问题。
专家们可以根据自己的经验和知识，对这些问题进行评估和预测。
接着，收集专家们的意见和反馈，进行数据分析和整合。
在这个过程中，可以采用统计学方法对专家们的意见进行加权平均，以得出市场需求的预测结果。
最后，将预测结果反馈给公司管理层，作为决策的参考依据。
通过德尔菲法的应用，公司可以得到专家们对市场需求的多方面意见和预测，避免了单一意见的片面性和盲目性。
同时，德尔菲法还能够保护专家的隐私，避免了个别专家在讨论中被其他专家所影响。
此外，德尔菲法还可以通过多轮问卷调查，逐步减少专家们的意见差异，最终达成一致意见。
因此，德尔菲法在市场需求预测中具有较高的可靠性和准确性。
除了市场需求预测，德尔菲法还可以应用于其他领域。
比如在医疗领域，可以用于制定诊疗方案和医疗政策的制定；在教育领域，可以用于评估教学质量和学生表现等方面。
总之，德尔菲法作为一种专家咨询技术，具有广泛的应用前景和重要的决策意义。
综上所述，德尔菲法作为一种专家意见征询和反馈的方法，在市场需求预测和其他领域的决策中具有重要的应用价值。
通过德尔菲法，可以充分发挥专家的意见和经验，提高决策的科学性和准确性，为企业的发展和社会的进步提供有力支持。
希望本文的案例分析能够帮助大家更好地理解德尔菲法的应用和意义。
德尔菲法的案例分析
德尔菲法的案例分析案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
•平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585•加权平均预测：将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：570*0.5+415*0.2+770*0.3=599•中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
将可最能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：600*0.5+400*0.2+750*0.3=695德尔菲法德尔菲法/得尔飞法(Delphi Method)• 3 德尔菲法的具体实施步骤o 3.1 德尔菲法实施注意事项• 4 德尔菲法的应用• 5 德尔菲法的优缺点• 6 德尔菲法与其他决策法相比较•7 德尔菲法案例分析o7.1 案例一：德尔菲法应用案列[1]o7.2 案例二：德尔菲法在企业人力资源预测中的运用[2]•8 相关条目•9 参考文献[编辑]德尔菲法的简介德尔菲法是在20世纪40年代由O．赫尔姆和N．达尔克首创，经过T．J．戈尔登和兰德公司进一步发展而成的。
德尔菲这一名称起源于古希腊有关太阳神阿波罗的神话。
德尔菲法的案例分析
德尔菲法的案例分析德尔菲法是一种专家参与的集体决策方法，旨在收集和汇总专家的意见来达成一致的决策。
它被广泛应用于各种领域，例如政策制定、技术评估和风险分析。
以下是一个关于使用德尔菲法的案例分析。
背景：公司计划推出一款新产品，但在进行市场投放之前，需要进行一系列的评估和决策。
该产品的成功与否将直接影响公司的利润和声誉。
为了确保决策的科学性和准确性，公司决定使用德尔菲法来收集专家的意见并达成共识。
目标：通过德尔菲法评估产品的潜在市场需求和竞争力，并确定推出该产品的最佳时机。
步骤：1.确定专家组：为了确保评估的权威性和可靠性，公司首先确定了一个由行业内相关领域的专家组成的小组。
这些专家在市场调研、产品开发和竞争分析方面具有丰富的经验和知识。
2.编制问卷：公司设计了一份问卷，涵盖了关于产品特性、目标市场、竞争对手和推广策略等方面的问题。
问卷采用开放性、封闭性和量化问题的组合形式，以便专家们提供全面和具体的意见。
3.第一轮调查：公司向专家组发放了问卷，并要求他们根据自己的专业经验和了解回答问题。
这些专家独立进行调查，并提供他们对每个问题的意见和建议。
4.整理和汇总数据：公司收集和整理了专家们的回答，并将其整合成汇总报告。
该报告提供了每个问题的平均意见、标准差和意见分布的图表，以及一些关键观点的摘要。
5.第二轮调查：6.整理和汇总第二轮调查结果：公司再次收集和整理专家们的回答，并将其整合成第二轮调查汇总报告。
该报告与第一轮调查汇总报告进行比较，以检测意见的收敛和差异的变化。
7.达成共识：公司组织一次专家会议，讨论第二轮调查的结果，并尝试达成共识。
在会议上，专家们可以相互交流意见、分享观点，并通过讨论来消除存在的分歧。
最终，经过深入讨论和权衡，专家们将根据综合考虑做出决策。
8.制定决策方案：公司将专家共识的决策方案转化为实际的行动计划。
它们可能包括产品开发、市场营销策略和推广活动等方面的计划。
优势和局限性：-集思广益：通过收集和整合专家的意见，可以充分利用专家的知识和经验，避免个体决策的局限性。
德尔菲法案例分析
德尔菲法案例分析案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
专家编号第一次判断第二次判断第三次判断最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量1 150 750 900 600 750 900 550 750 9002 200 450 600 300 500 650 400 500 6503 400 600 800 500 700 800 500 700 8004 750 900 1500 600 750 1500 500 600 12505 100 200 350 220 400 500 300 500 6006 300 500 750 300 500 750 300 600 7507 250 300 400 250 400 500 400 500 6008 260 300 500 350 400 600 370 410 610 平均数345 500 725 390 550 775 415 570 770∙平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585∙加权平均预测：将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：570*0.5+415*0.2+770*0.3=599∙中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
德尔菲法介绍及案例
1、概念
是一种匿名式的、轮番征询专家意见的， 最终得出预测结果的一种集体经验判断法。
2、预测程序
评
（1）准备阶段
价 误
• 明确预测主题和预测目的
差
• 准备背景材料
• 选择专家 ：广泛性 --- 内部业务人员 1/3 ，与本部
门、本企业有业务联系、关系密切的行业专家1/3 ， 社会上有影响的专家1/3 ；自愿性 ； 人数适度 。
3、对德尔菲法的评价 • 匿名性 • 反馈性 • 趋同性 4、案例分析 • [ 案例 ]：采用德尔菲法对浙江省1990年手扶拖拉机市场需求变化趋势
进行预测。
浙江省1990年手扶拖拉机市场需求变化趋势预测
1． 确定预测主题
根据历年农机产品的销售实绩，手扶拖拉机是该公司的拳头产品，因此，按照“ABC分析 法”的原理，把手扶拖拉机作为主要预测对象。
2． 选择专家
对1990年手扶拖拉机需求趋势做出预测，这要求预测参与者必须要有丰富的业务经验，掌 握大量的市场信息，同时要有一定的表达能力。另一方面，为了取得比较全面的信息，确 定以全省87个地区、县农机公司的业务经理组成预测专家小组。
3． 准备背景材料
为了使专家在预测过程中能全面了解有关手扶拖拉机的历史和现状，使预测更加准确，预 测组织者准备了有关的北京材料，主要有：
（1）1980---1989年全省手扶拖拉机历史销量和逐年的增长率，本把各年的销量用表格和曲 线图两种形式直观表达出来，使预测者一目了然。
（2）根据组织者掌握的信息，列出了1990年对手扶拖拉机的销售有利的影响因素（四个方 面）和不利的影响因素（五个方面）。
设计调查表
根据预测对象的要求设计咨询表。因预测主题比较单一，调查表较为简单，如表1所示：
德尔菲法分析案例
•预测主题：中美贸易战对能源供给影响 •预测目的：得到一个较为有效的关于中美贸易战中能源需求的预测结果
2． 选择专家
对中美贸易战中能源需求的趋势变化做出预测，这要求预测参与者必须要有丰富的业务经验，掌握大量的市场信息，同时 要有一定的表达能力。 另一方面，为了取得比较全面的信息，以广泛性（内部业务人员 1/3，与本部门、本企业有业务联系、关系密切的行业专 家1/3 ，社会上有影响的专家1/3）、自愿性和人数适度性的原则进行专家的选择，选取了中石油、中石化等能源企业（包 括国企和非国企）专家、经济学专家教授、能源行业专家教授三类共87位专家进行预测调查。
3． 准备背景材料
为了使专家在预测过程中能全面了解有关中美贸易战中能源需求的背景和现状，使预测更加准确，预测组织者准备了有关 的背景材料，主要有： （1）贸易战时间线梳理 （2）贸易战背景 （3）贸易战原因 （4）贸易战影响
设计调查表
根据预测对象的要求设计咨询表。因 预测主题比较单一，调查表较为简单， 如表1所示：
• 因此，在油气供给方面，美国的出口供应将显著 下降，中国油气使用将由于关税的加增而转向其
他国家进口。
• 美国曾是中国光伏产品的第二大出口国。随着美国不断对中国 光伏产品发起调查和增加关税，美国市场对中国光伏行业的地 位逐年下降。根据中国光伏行业协会的统计数据，2018年至今， 中国光伏产品对美国的直接出口几乎为0。 去年中旬美国对中 国进口产品的增税清单上，就涉及到光伏逆变器、附带微型逆 变器的太阳能电池板，但中国光伏逆变器的主要海外市场并不 是美国，并且通过海外设厂，也可以绕过美国的关税壁垒。本 次贸易摩擦升级，我国对原产于美国的太阳能电池、逆变器以 及变压器等光伏产品确定征收25%的关税，对贸易战发起反击。
德尔菲法案例分析
德尔菲法案例分析案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
•平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585•加权平均预测：将最可能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：570*0.5+415*0.2+770*0.3=599•中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
将可最能销售量、最低销售量和最高销售量分别按0.50、0.20和0.30的概率加权平均，则预测平均销售量为：600*0.5+400*0.2+750*0.3=695德尔菲法德尔菲法/得尔飞法(Delphi Method)目录[隐藏]•1德尔菲法的简介o 1.1德尔菲法的起源演变o 1.2德尔菲法的典型特征•2德尔菲法的特征•3德尔菲法的具体实施步骤o 3.1德尔菲法实施注意事项•4德尔菲法的应用•5德尔菲法的优缺点•6德尔菲法与其他决策法相比较•7德尔菲法案例分析o7.1案例一：德尔菲法应用案列[1]o7.2案例二：德尔菲法在企业人力资源预测中的运用[2]•8相关条目•9参考文献[编辑]德尔菲法的简介德尔菲法是在20世纪40年代由O．赫尔姆和N．达尔克首创，经过T．J．戈尔登和兰德公司进一步发展而成的。
德尔菲法案例
德尔菲法案例德尔菲法案例：某公司计划开发一个新产品，他们决定采用德尔菲法来评估市场需求和产品可行性。
公司邀请了一组行业专家参与讨论和决策，并利用德尔菲法来达成一致意见。
首先，公司将问题提交给专家小组，询问他们对市场需求和产品的看法。
问题是“这个新产品有多大的市场需求？产品是否具备可行性？”每个专家都独立回答这个问题，并给出一个评分，10分表示非常高的市场需求和可行性，1分表示非常低的市场需求和可行性。
然后，公司主持一个讨论会，专家可以交流意见和观点，并重新评估自己的答案。
如果有两个以上的答案出现差异较大的情况，公司会要求专家重新评估并解释他们的理由。
此后，公司会收集所有专家的答案和评分，并计算每个问题的平均值。
如果平均值很接近，说明专家们对问题达成了一致意见。
如果平均值有较大的差异，公司会继续进行第二轮讨论，直到达成一致意见或者无法达成一致为止。
最终，公司会根据专家的意见和评分来决定是否继续开发这个新产品。
如果市场需求和可行性评分较高，公司就会投入资源和时间来开发这个产品。
如果市场需求和可行性评分较低，公司可能会重新考虑或者放弃开发这个产品。
通过德尔菲法，公司能够借助专家的意见和经验来评估市场需求和产品可行性，减少了决策风险和不确定性。
专家们的评分和意见提供了决策依据，让公司能够做出更明智的决策。
同时，通过多轮讨论和解释，专家们在讨论过程中也可以相互学习和分享知识，提高了整个团队的专业水平和决策能力。
总之，德尔菲法能够帮助公司利用专家的智慧来评估市场需求和产品可行性，促进团队合作和决策的一致性。
这个方法具有广泛的应用领域，不仅适用于市场调研和产品开发，还可用于战略规划、风险评估等方面。
德尔菲法介绍及案例
德尔菲法介绍及案例德尔菲法是一种专家群体决策方法，它通过循环迭代的方式，通过专家意见的匿名交流和整合，达到达成共识的目的。
该方法被广泛用于众多领域，如技术预测、决策支持、战略规划等。
下面将通过引入一个案例来详细介绍德尔菲法。
案例：公司市场营销策略规划公司为了制定市场营销策略，决定采用德尔菲法来征集专家意见，以确定适合公司的策略方向。
参与的专家包括公司内外的市场专家、营销顾问等人士，共计10名。
第一轮在第一轮中，公司向专家们发放调查问卷，要求专家根据自己的经验和见解回答一些关键问题，如当前市场趋势、目标市场的细分、竞争对手的策略等。
专家们在问卷中匿名回答问题，并在最后对市场中的关键因素按重要性进行打分。
第二轮在第一轮结束后，公司的决策者进行数据的整理和分析，将结果汇总后形成一个反馈报告。
报告中反映了专家们在第一轮中的回答结果和权重，同时也给出了专家间意见的差异性和一致性。
在第二轮中，公司将专家们的个人回答结果反馈给他们，并附上第一轮调查结果的汇总报告。
专家可以根据汇总结果来进行再次的个人思考，并重新给出自己的回答。
第三轮在第二轮结束后，公司再次进行数据的整理和分析，形成一个新的反馈报告。
报告中反映了专家们在第二轮中的回答结果和权重，并与第一轮的结果进行对比。
报告还给出了专家间意见的变化情况，并展示了达成共识的程度。
在第三轮中，公司将专家们的个人回答结果反馈给他们，并附上第二轮调查结果的汇总报告。
专家可以根据汇总结果来进行再次的个人思考，并重新给出自己的回答。
继续迭代直至共识达成按照需要，公司可以继续进行多轮的德尔菲法调查，直至达成共识为止。
迭代的过程可以帮助专家们逐渐减小意见的差异，形成相对较为一致的结论。
当专家们在两轮之间的回答差异很小且共识程度较高时，公司可以认为达到了一个可行的市场营销策略。
总结通过德尔菲法，公司针对市场营销策略的制定，借助专家群体的智慧和经验，最终达成了尽可能一致的共识。
德尔菲法以匿名交流和迭代的方式，削弱了主观偏见和个人影响，保证了决策的客观性和科学性。
德尔菲法运用的典型案例
德尔菲法运用的典型案例
嘿，你知道德尔菲法不？这可是个超厉害的决策工具呢！就好比你在迷雾中找路，德尔菲法就像那盏明灯，给你指引方向呀！
给你举个例子吧，比如说有个公司要决定下一款产品的设计方案。
他们就找了一群专家，这些专家呢，各自发表自己的想法和建议，就像八仙过海，各显神通一样。
然后呢，把这些意见汇总起来，去掉那些不靠谱的，留下精华的部分。
接着，再把这些精华反馈给专家们，让他们再思考、再讨论。
哎呀，是不是有点像在雕琢一块美玉呀！
再比如，城市要规划建设一个新的公园。
这可不是随随便便就能决定的事情哦！这时候德尔菲法就大显身手啦！找来规划师、建筑师、居民代表等等，大家一起出谋划策。
每个人都像小蜜蜂一样，贡献着自己的智慧。
一次又一次的循环，让公园的规划越来越完美。
还有呢，在预测未来市场趋势的时候，德尔菲法也能发挥巨大作用哦！就好像预测天气一样，虽然不能百分百准确，但能给到一个大概的方向呀！专家们根据自己的经验和知识，给出对未来的预判。
然后再不断调整、修正，多有意思啊！
德尔菲法可不简单呢，它就像一个魔法盒子，里面装着无数的智慧和可能性。
它能让不同的人、不同的想法汇聚在一起，碰撞出奇妙的火花。
它能让决策变得更加明智、更加合理。
总之，德尔菲法真的是太有用啦！谁用谁知道呀！你说是不是呢？。
德尔菲法案例分析
案例一：德尔菲法应用案列某公司研制出一种新兴产品，现在市场上还没有相似产品出现，因此没有历史数据可以获得。
公司需要对可能的销售量做出预测，以决定产量。
于是该公司成立专家小组，并聘请业务经理、市场专家和销售人员等8位专家，预测全年可能的销售量。
8位专家提出个人判断，经过三次反馈得到结果如下表所示。
专家编号第一次判断第二次判断第三次判断最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量最低销售量最可能销售量最高销售量1150750900600750900550750900 2200450600300500650400500650 3400600800500700800500700800 4750900150060075015005006001250 5100200350220400500300500600 6300500750300500750300600750 7250300400250400500400500600 8260300500350400600370410610 平均数345500725390550775415570770平均值预测：在预测时，最终一次判断是综合前几次的反馈做出的，因此在预测时一般以最后一次判断为主。
则如果按照8位专家第三次判断的平均值计算，则预测这个新产品的平均销售量为：（415+570+770）/3=585加权平均预测：将最可能销售量、最低销售量和最高销售量分别按、和的概率加权平均，则预测平均销售量为：570*+415*+770*=599中位数预测：用中位数计算，可将第三次判断按预测值高低排列如下：最低销售量：300 370 400 500 550最可能销售量：410 500 600 700 750最高销售量：600 610 650 750 800 900 1250最高销售量的中位数为第四项的数字，即750。
将可最能销售量、最低销售量和最高销售量分别按、和的概率加权平均，则预测平均销售量为：600*+400*+750*=695德尔菲法德尔菲法/得尔飞法(Delphi Method)目录[隐藏]1德尔菲法的简介o德尔菲法的起源演变o德尔菲法的典型特征2德尔菲法的特征3德尔菲法的具体实施步骤o德尔菲法实施注意事项4德尔菲法的应用5德尔菲法的优缺点6德尔菲法与其他决策法相比较7德尔菲法案例分析o案例一：德尔菲法应用案列[1]o案例二：德尔菲法在企业人力资源预测中的运用[2]8相关条目9参考文献[编辑]德尔菲法的简介德尔菲法是在20世纪40年代由O．赫尔姆和N．达尔克首创，经过T．J．戈尔登和兰德公司进一步发展而成的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【德尔菲法预测案例】：某空调机厂对某种型号的空调机投放市场后的年销售量进行预测，聘请9位专家应用德尔菲法，进行四轮的征询、反馈、修改汇总后得到如下数据：
从表可以看出专家的第一轮意见汇总得出的中位数为27，极差为31。
数据表明，专家的意见相当分散。
专家根据反馈意见，大多数人修改了自己的意见并向中位数靠拢，因此，第二轮意见汇总后极差变小。
但第四轮征询时，每位专家都不再修改自己的意见了，于是得出最终的预测值，可以认为年销售量将达到26万台，但极差达22万台。