四年级奥数长方形的面积
四年级奥数详解答案 第6讲 面积的计算

四年级奥数详解答案 第6讲第六讲 面积的计算一、知识概要1. 面积:面积是围成的平面图形的大小。
2. 各种图形的计算公式1. 三角形 面积=底×高÷2 用字母表示为:S=ah ÷2(注:高,就是从三角形的顶点向它的对边所做的那条垂线段)}是特殊的平行四边形为:用字母表示边长边长面积正方形为:用字母表示宽长面积长方形2a S . 3.ab S .2=⨯==⨯= 4. 平行四边形 面积=底×高 用字母表示为:S=ah5. 梯形 面积=(上底+下底)×高÷2 用字母表示为:S=2h b)a ⨯+( {注: 解梯形应用题常用到梯形的中位线。
中位线就两腰的中立的连线。
中位线等于两底边之和的一半,即,中位线=(a+b)÷2}}二、典型题目精讲1. 用同样大小的长方形纸片摆成下图,已知每张小纸片的宽是4厘米,阴影部分的面积是多少平方厘米?分析:(如图)5个长方形的长等于3个长十3个宽即5a=3a+3b,则2a=3b,a=3×4÷2=6(cm) 图中阴影部分是三个相等的小正方形,其一个正方形的边长为长-宽,即6-4=2(cm),这样,全部阴影部分面积就是(2×2×3)cm 2了。
解:①3×4÷2=6(cm)②6-4=2(cm)③2×2×3=12(cm 2)答:阴影部分的面积是12 cm 2。
2. 下图是一个边长为20厘米的正方形和一个长方形的组合图形,求阴影部分的面积。
分析:作二条辅助线,交于正点使EF=20cm ,EG=10 cm(如图)则阴影面积=上、下两个长方形面积之和-∆ABC 的面积-∆ADE 的面积解:①S ∆ABC=(20+10+4)×14÷2=238(cm 2) ②S ∆ADE=(20+10)×(20+14)÷2=510(cm 2) ③34×14+30×20=1076(cm 2) ④1076-(238+510)=328(cm 2)答:阴影部分的面积等于328cm2。
四年级奥数几何知识(面积的计算)

四年级奥数几何知识(面积的计算)小升初奥数:四年级奥数几何知识(面积的计算)1、人民路小学操场长90米,宽45米,改造后,长增加10米,宽增加5米。
现在操场面积比原来增加多少平方米?(思路导航)用操场现在的面积减去操场原来的面积,就得到增加的面积,操场现在的面积是:〔90+10〕&215;〔45+5〕=5000〔平方米〕,操场原来的面积是:90&215;45=4050〔平方米〕。
所以现在比原来增加5000-4050=950平方米。
〔90+10〕&215;〔45+5〕-〔90&215;45〕=950〔平方米〕练习〔1〕有一块长方形的木板,长22分米,宽8分米,如果长和宽分别减少10分米,3分米,面积比原来减少多少平方分米?练习〔2〕一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?2、一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米,如果长不变,宽减少3米,那么它的面积减少36平方米,这个长方形原来的面积是多少平方米?(思路导航)由:“宽不变,长增加6米,那么它的面积增加54平方米〞可知它的宽是54&247;6=9〔米〕;又由“长不变,宽减少3米,那么它的面积减少了36平方米〞,可知它的长为:36&247;3=12〔米〕,所以,这个长方形的面积是12&215;9=108〔平方米〕。
〔36&247;3〕&215;〔54&247;9〕=108〔平方米〕练习〔1〕一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米,如果长不变,宽增加4米,那么它的面积增加60平方米,这个长方形原来的面积是多少平方米?练习〔2〕一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米,如果长不变,宽增加3米,那么它的面积增加48平方米,这个长方形的面积原来是多少平方米?练习〔3〕一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米,求这个长方形原来的面积。
奥数四年级—长方形和正方形面积

2×2=4
52-4=48 48÷2=24 24÷2=12
12×4
练 5、如图,是由9个小长方形组成的,按图中 习 编号,第1,2,3,4,5号的面积分别是1平
方米,2平方米,3平方米,4平方米,5平方 米,那么,第6号长方形和面积是多少呢?
图形不规则,已知条件也很少!
3
2021/8/14
拆分
例2、如图,是由6个相同的等腰三角形拼成的图形, 求这个图形的面积是多少?(单位:米)
拆 开
4×4 =16(平方米) 16÷2=8 (平方米) 16+8=24 (平方米)
4
2021/8/14
分块
例3、如图,已知大正方形的边长比小正方形的边长 多4,大正方形的面积比小正方形的面积多96。求大 小正方形面积各是多少? (单位:厘米)
长方形和正方形(面积)
上节我们学了长方形、正方形的周长的计算,
本节我们学习,如何将复杂的图形变成我们熟
悉的长方形和正方形, 计算面积。
长方形面积=长×宽 正方形面积=边长×边长
方法有:减法、拆分、分块、分段、等技巧, 使大家在解题中能顺利地找到突破口,化难为易, 化繁为简。
1
2021/8/14
减法
场平均分成四块(如图6),每一块的面积 是多少?
100-4=96
80-4=76
76×96=7296 7296÷4=1824
12
2021/8/14
练 3、如图,是由12个相等的等腰直角三角形 习 拼成的,这个图形的面积是多少?
2×2=4 4×6=24
13
2021/8/14
练 4、如图,已知大正方形的面积比小正方形 习 多52平方分米,大正方形比小正方形的边长
小学四年级奥数思维问题之图形面积

图形面积问题教学目标:①知识与技能目标:借助所学知识计算组合图形的面积②过程与方法目标:通过对数量关系地分析,让学生在解决问题过程中掌握一些解决问题的基本策略③情感态度与价值观目标:感受所学知识与现实生活的紧密联系教学重点:图形面积公式的运用教学难点:组合图形的面积计算[知识引领与方法]1.细心观察,把握图形特点,合理的进行切拼,从而使问题得以顺利解答2.从整体上观察图形的特征,掌握图形本质,结合必要的分析,推理和计算,使隐蔽的数量关系明朗化[例题精选及训练]【例1】一块长方形铁板,长18分米,宽15分米。
若长和宽分别减少3分米,面积比原来的减少多少平方分米?练习:1.人民路小学操场长90米,宽45米,改造后,长和宽分别增加10米。
现在操场面积比原来增加了多少平方米?2.有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米和3分米,木板的面积比原来减少多少平方分米?3.一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?【例2】一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
问这个长方形原来的面积是多少平方米?练习:1.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2.一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
问这个长方形原来的面积是多少平方米?3.一个长方形花圃,如果它的长减少5米,或它的宽减少6米,那么它的面积都减少60平方米。
求这个长方形花圃原来的面积。
【例3】下图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场,那么这个养鸡场的占地面积是多少平方米?练习:1.右图是某个养鸡专业户用一段长13米的篱笆围成一个长形的养鸡场,则养鸡场的占地面积有多大?2.用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?【例4】街心花园中一个正方形的花坛四周有一条1米宽的水泥路,如果水泥路的总面积是12平方米,那么中间花坛的面积是多少平方米?练习:1.有一个正方形的水池,如右图阴影部分所示,在它的周围修了一个宽8米的花池,花池的面积是480平方米,求水池的边长。
四年级奥数思维训练第28讲 长方形面积(二)
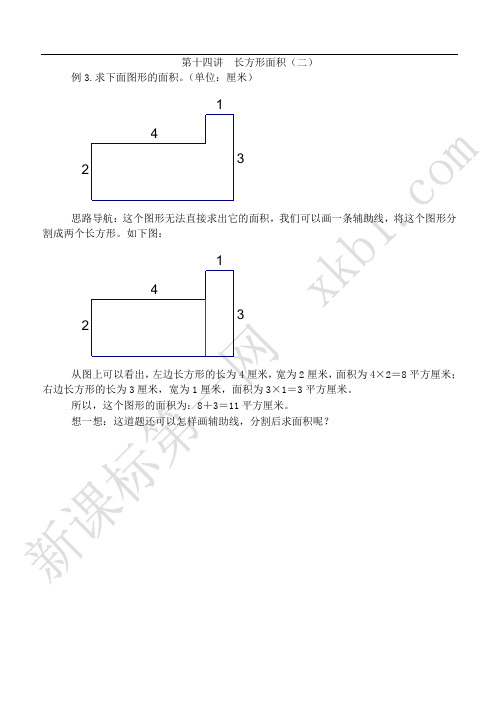
所以,这个图形的面积为:8+3=11平方厘米。
想一想:这道题还可以怎样辅助线,分割后求面积呢?
练习十四
1.运动场有一个正方形的游泳池,在游泳池四周粘上瓷砖,瓷砖总长400米,求游泳池的面积是多少平方米。
2.在公园里有两个花圃,它们的周长相等。其中长方形花圃长40米,宽20米,求另一个正方形花圃的面积。
第十四讲长方形面积(二)
例3.求下面图形的面积。(单位:厘米)
思路导航:这个图形无法直接求出它的面积,我们可以画一条辅助线,将这个图形分割成两个长方形。如下图:
从图上可以看出,左边长方形的长为4厘米,宽为2厘米,面积为4×2=8平方厘米;右边长方形的长为3厘米,宽为1厘米,面积为3×1=3平方厘米。
四年级奥数题及答案-养鸡场最大面积多大?

四年级奥数题及答案-养鸡场最大面积多大?1.用60米长的篱笆围成一个长方形养鸡场,其中一面利用墙,求这个养鸡场的面积最大是()米。
考点:长方形、正方形的面积.分析:设养鸡场宽为x米,则长为(60-2x)米,再通过枚举法由长方形的面积公式S=ab,即可求出面积.解答:解:设养鸡场宽为x米,则长为(60-2x)米,根据题意宽为1米时,长是58米,面积是58×1=58(平方米),宽是2米时,长是56米,面积是56×2=112(平方米),宽是3米时,长是54米,面积是54×3=162(平方米),宽是4米时,长是52米,面积是52×4=208(平方米),宽是5米时,长是50米,面积是50×5=250(平方米),宽是6米时,长是48米,面积是48×6=288(平方米),宽是7米时,长是46米,面积是46×7=322(平方米),宽是8米时,长是44米,面积是44×8=352(平方米),宽是9米时,长是42米,面积是42×9=378(平方米),宽是10米时,长是40米,面积是40×10=400(平方米),宽是11米时,长是38米,面积是38×11=418(平方米),宽是12米时,长是36米,面积是36×12=432(平方米),宽是13米时,长是34米,面积是34×13=442(平方米),宽是14米时,长是32米,面积是32×14=448(平方米),宽是15米时,长是30米,面积是30×15=450(平方米),宽是16米时,长是28米,面积是28×16=448(平方米),由此看出当宽是15米时,长是30米,面积最大,为30×15=450(平方米),答:这个养鸡场的面积最大是450平方米。
故答案为:450平方米。
点评:根据长方形的面积公式,利用枚举法,得出如何围才能够使面积最大。
四年级奥数周长与面积易错题

四年级奥数周长与面积易错题【最新版】目录一、四年级奥数周长与面积的易错题二、常见的周长与面积计算公式三、如何避免在计算中出现错误四、提高奥数解题能力的方法正文一、四年级奥数周长与面积的易错题在四年级的奥数题中,周长与面积的计算问题是一个重要的考点,同时也是一个易错点。
很多学生在做这类题目时,容易因为对公式的理解不透彻,或者在计算过程中出现粗心大意而导致错误。
例如,在计算长方形的面积时,学生可能会忘记将长和宽相乘,或者在计算周长时忘记将长和宽都考虑到。
二、常见的周长与面积计算公式在解决周长与面积问题时,我们需要掌握一些基本的公式。
1.长方形的周长:C = (a + b) × 2,其中 a 和 b 分别表示长方形的长和宽。
2.长方形的面积:S = a × b,其中 a 和 b 分别表示长方形的长和宽。
3.正方形的周长:C = 4a,其中 a 表示正方形的边长。
4.正方形的面积:S = a × a,其中 a 表示正方形的边长。
三、如何避免在计算中出现错误为了避免在计算周长与面积问题时出现错误,我们可以采取以下方法:1.仔细阅读题目,理解题意,确定需要求解的是周长还是面积。
2.在计算过程中,注意使用正确的公式,并按照公式的步骤逐步计算。
3.在计算完成后,进行验算,确保计算结果正确。
4.做题时,要保持细心和耐心,避免因为粗心大意而犯错。
四、提高奥数解题能力的方法要想提高奥数解题能力,我们需要从以下几个方面入手:1.加强基础知识的学习,掌握基本的数学概念和公式。
2.多做练习题,通过做题来提高自己的解题能力。
3.在做题时,注意分析题目,找到题目中的关键信息,并灵活运用公式。
4.在解题过程中,遇到困难时,不要轻易放弃,要勇于挑战自己,多尝试不同的解题方法。
总之,四年级的奥数周长与面积问题虽然难度不大,但是容易出错。
四年级奥数面积求解

关于图形面积求解主讲:姬老师我们要学会观察、分析,通过添加辅助线或者割补的方法,运用一些平移、分解、合并等方法,将不规则的图形转化为我们已学过的基本图形来求解。
在直接运用面积公式求解受阻时,我们往往会采用移位、合并、分解、转化等解题技巧。
所以,同学们拥有敏锐的观察力和灵活的思维在解题过程中就显得相当的重要。
例1.一张长方形纸片,在长边上剪下10cm,宽边上剪下5cm,余下的部分正好是一个正方形。
已知正方形的面积比原长方形纸片面积少140C㎡,求原长方形纸片的面积。
例2,在一个正方形的小花园的周围,环绕着宽为5m的水池,水池的面积是300㎡,问小花园的面积是多少㎡?例3,一块菜地长16m,宽8m,菜地中间留了宽2m的路,把菜地平均分成4块,问每一块地的面积是多少?例4,正方形的内部套着一个长方形,正方形的边长是15cm,长方形的4个角的顶点,恰好分别把正方形的4条边分成2段,其中长的一段是短的2倍。
那么,这个长方形的面积是多少?课堂练习1.四边形面积:下图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE的面积是?四边形AFDC的面积=三角形AFD+三角形ADC=(1/2×FD×AF)+(1/2×AC×CD)=1/2(FE+ED)×AF+1/2(AB+BC)×CD= (1/2×FE×AF+1/2×ED×AF)+(1/2×AB×CD+1/2×BC×CD)。
所以阴影面积=四边形AFDC-三角形AFE-三角形BCD=(1/2×FE×AF+1/2×ED×AF)+(1/2×AB×CD+1/2×BC×CD)-1/2×FE×AF-1/2×BC×CD=1/2×ED×AF+1/2×AB×CD=1/2×8×7+1/2×3×12=28+18=46。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10、如果正方形A的周长是正的多少倍?
11、将一个长方形的长增加1厘米,宽增加3厘米,就变成了一个正方形,面积增加33平方厘米,原来的长方形面积是多少平方厘米?
12、如图,正方形与阴影长方形的边分别平行,正方形边长为10,阴影长方形的面积为6,那么图中四边形ABCD的面积是多少?
2、如图,大小两个正方形对应边的距离均为2厘米,如果两个正方形之间部分的面积是40平方厘米,那么小正方形的面积是多少平方厘米?
第2题
3、把一个长26厘米,宽14厘米的长方形分成5块,两个长方形能完全重合,两个正方形也能完全重合,求小正方形的面积是多少?
第3题
4、每边长是10厘米的正方形纸片,正中间挖去了一个正方形的洞,成为宽度为1厘米的方框,把五个这样的方框放在桌面上(如图),问桌面上这些方框盖住的面积是多少平方厘米?
4、如图,大小两个正方形部分重合,重合部分的面积是2平方厘米,阴影部分的面积是多少平方厘米?
第3题
第4题
5、一个正方形,如果边长增加1厘米,那么面积增加17平方厘米,这个正方形原来面积是多少平方厘米?
6、现代养鸡场是一个长方形,其中一条边利用原来的旧墙,其余三面打砖墙,砖墙总长60米,若长是宽的2倍,求其面积;若长与宽相等,其面积是多少?
7、如图,阴影部分的面积是多少?
第7题
8、有一个长方形长为8厘米,宽为3厘米,把它的长和宽分别增加2厘米,那么这个长方形面积增加了多少平方厘米?
9、如图,是一个边长为4的正方形,我们称它为第一个正方形,依次连结四条边的中点,得到第二个正方形,继续这样下去,得到第三个、第四个、第五个正方形,那么第一个正方形至第五个正方形的面积是多少?
7、一个长方形的宽增加4厘米,就成了一个正方形,这样面积增加了48平方厘米,求原来长方形的面积。
8、计划修一个正方形的花坛,并在花坛的周围铺宽2米的草坪,草坪的面积是40平方米,那么修建花坛、草坪共需占地多少平方米?
[能力拓展平台]
1、有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,小正方形的面积是多少平方厘米?
第4题
[全讲综合练习]
1、一个长方形的周长为72厘米,长比宽的2倍少3厘米,那么这个长方形的长是多少厘米?宽是多少厘米?面积是多少平方厘米?
2、长方形是由5个一样的正方形拼成的,总面积是245平方厘米,那么这个长方形的周长是多少厘米?
3、一个长方的面积为44平方厘米,靠一边裁出一个面积为16平方厘米的正方形,如图,那么原长方形的长是多少厘米?剩下的小长方形的面积是多少平方厘米?周长是多少厘米?
(单位:米)第3题第4题
4、如图,已知正方形ABCD的边长为6分米,长方形BCEF和长方形AGHD的面积分别为24平方分米和20平方分米,求阴影部分的面积?
5、一个正方形,如果边长增加2厘米,它的面积增加16平方厘米,求原正方形的面积。
6、一个长方形,如果宽增加2厘米,或长增加3厘米,它们的面积都增加120平方厘米,原来长方形的面积是多少?
长方形的面积
[同步巩固演练]
1、两个相同的长方形,长7厘米,宽3厘米,按下图的样子重叠在一起,这个图形的周长是多少厘米?面积是多少平方厘米?
第1题
2、用长36厘米的一根铁丝围成一个正方形,它的面积是多少?用这根铁丝围成一个长12厘米的长方形,它的面积是多少?
3、如图,有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是草坪,草坪的面积是多少平方米?
