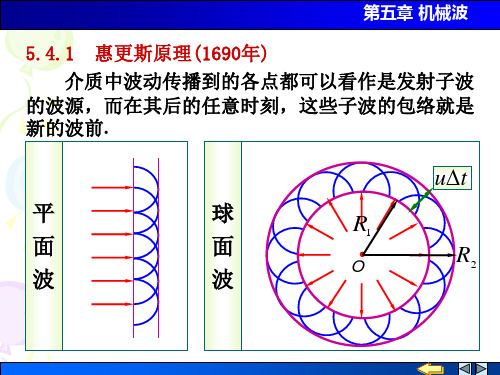
6.3 惠更斯原理和波的叠加原理
合集下载
波的叠加,惠更斯原理,多普勒效应
2 3 解： 3 ( r1 r2 ) 2
2
为 的奇数倍，
合振幅最小，
P
Q
R
3 / 2
| A1 A 2 |
14
四、驻波
1.驻波的产生
有两列相干波，它们不仅频率相同、位相差恒 定、振动方向相同，而且振幅也相等。当它们在同 一直线上沿相反方向传播时，在它们迭加的区域内 就会形成一种特殊的波。这种波称为驻波。
11
干涉相消
I1I 2
当两相干波源为同相波源 时，有： 1 2
此时相干条件写为：
r1 r2 k ,
r1 r2 ( 2 k 1)
2 ,
( 2 1 )
2
( r2 r1 )
称 为 波 程 差
k 0 ,1, 2 , 3 ,... 干涉相长
水波通过狭缝后的衍射图象。
3
2 .波的反射与折射
当波传播到两种介质的分界 面时，一部分反射形成反射波， 另一部分进入介质形成折射波。 （1）反射定律
1
u1
n
c u
i i'
n1 n2
①.入射线、反射线和界面的法 线在同一平面上；
4
②.反射角等于入射角。 i ' i （2）折射定律 ①.入射线、折射线和界面的法线在同一平面上； n2 sin i u1 1 ②. n 21 sin r u 2 2 n1
当一列波遇到障碍时产生的反射波与入射波叠 加可产生驻波。
驻波的特点：媒质中各质点都作稳定的振动。波形 并没有传播。
15
2.驻波的表达式
设有两列相干波，分别沿X轴 正、负方向传播，选初相位 均为零的表达式为： 入射波
波的反射与折射和惠更斯原理
5.5 波的叠加 干涉和驻波
一、波的叠加原理 介质中几列 波同时传播，每一列波不会因为其他波的 存在而改变各自的特点——独立性原理；在波列相遇的 区域，介质每一点的振移是各波列单独存在时该点振移 的矢量和。
Hale Waihona Puke 你可以区分出不同的乐器！二、驻波（波的干涉）
两列波
t x 1 ( x , t ) A cos 2 ( ) T
M N
i
i'
AN MD u t
容易算出
A B C D
i i
AN MD u2 u1
MD u1 t
（n1）
（n2）
i1
M A B iC D
AN u2 t
2
i1
MD AD sini1 AN AD sini2
i2
N
c u1 n1
c u2 n2
n1 sini1 n2 sini2
被介质吸收 3、介质对高频的能量吸收大 大振幅波 ，色散与非线性效应相抵消时形成孤波 （定域性——小范围、稳定性——不变形） +（完整性——两孤波相遇后分开各自继续传播） 流体中的旋涡；超导体中的磁通量子；激光自聚 焦；神经系统中的信号……都是 孤子
孤 子
三、有半波损失时的反射波
1 u1 2 u2
x 设另一简谐波为 ( x , t ) A cos[2 ( t ) ] 法1 (0, t ) A cos( t ) 法2 从旋转矢量图上可见 3 5 O 点任何时刻反相，则 或 4 4 (t ) ( t ) 4 3 5 A(0,0) 得 或
vs
s
u
vD
惠更斯原理
波在弹性介质中运动时,任一点 的振动, 波在弹性介质中运动时,任一点P 的振动,将会 引起邻近质点的振动。就此特征而言， 引起邻近质点的振动。就此特征而言，振动着的 P 点与波源相比，除了在时间上有延迟外， 点与波源相比，除了在时间上有延迟外，并无其他 区别。因此， 可视为一个新的波源。 区别。因此，P 可视为一个新的波源。1678年，惠 年 更斯总结出了以其名字命名的惠更斯原理： 更斯总结出了以其名字命名的惠更斯原理： 惠更斯原理 介质中任一波面上的各点， 介质中任一波面上的各点，都可 看成是产生球面子波的波源； 看成是产生球面子波的波源；在其后 的任一时刻， 的任一时刻，这些子波的包络面构成 新的波面。 新的波面。
惠更斯 荷兰
惠更斯原理
S2
新波阵面
S1
原波阵面 t+∆t 时刻
u∆t
t 时刻
障碍物的小孔成为新的波源
t 时刻波面 t +∆t 时刻波面
· · · · ·
波传播方向
t + ∆t t· · · · · · ·
· · · · · · ·
u∆t ∆
平面波 球面波
· a· ·
·
波的衍射
当波在传播过程中遇到障碍物时， 当波在传播过程中遇到障碍物时，其传播方向绕过障 碍物发生偏折的现象，称为波的衍射 波的衍射。 碍物发生偏折的现象，称为波的衍射。
波在窄缝的衍射效应
波的反射和折射
反射与折射也是波的特征，当波传播到两种介 反射与折射也是波的特征， 质的分界面时，波的一部分在界面返回，形成反射 质的分界面时，波的一部分在界面返回，形成反射 另一部分进入另一种介质形成折射波 折射波。 波，另一部分进入另一种介质形成折射波。 折 射 定 律 的 推 导
惠更斯 荷兰
惠更斯原理
S2
新波阵面
S1
原波阵面 t+∆t 时刻
u∆t
t 时刻
障碍物的小孔成为新的波源
t 时刻波面 t +∆t 时刻波面
· · · · ·
波传播方向
t + ∆t t· · · · · · ·
· · · · · · ·
u∆t ∆
平面波 球面波
· a· ·
·
波的衍射
当波在传播过程中遇到障碍物时， 当波在传播过程中遇到障碍物时，其传播方向绕过障 碍物发生偏折的现象，称为波的衍射 波的衍射。 碍物发生偏折的现象，称为波的衍射。
波在窄缝的衍射效应
波的反射和折射
反射与折射也是波的特征，当波传播到两种介 反射与折射也是波的特征， 质的分界面时，波的一部分在界面返回，形成反射 质的分界面时，波的一部分在界面返回，形成反射 另一部分进入另一种介质形成折射波 折射波。 波，另一部分进入另一种介质形成折射波。 折 射 定 律 的 推 导
波的特性知识点及练习(干涉、衍射等)
波的特有现象——波的反射、波的折射、波的叠加原理〔独立传播原理〕、波的衍射、波的干预、多普勒效应一.波面和波线、波前波面：同一时刻，介质中处于波峰或波谷的质点所构成的面叫做波面．〔振动相位相同的各点组成的曲面。
〕波线：用来表示波的传播方向的跟各个波面垂直的线叫做波线．波前：某一时刻波动所到达最前方的各点所连成的曲面。
二.惠更斯原理荷兰物理学家 惠 更 斯1.惠更斯原理：介质中任一波面上的各点，都可以看作发射子波的波源，而后任意时刻，这些子波在波前进方向的包络面便是新的波面。
2.三、波的特性：波的反射、波的折射、波的叠加原理〔独立传播原理〕、波的衍射、波的干预、多普勒效应〔一〕.波的反射1.波遇到障碍物会返回来继续传播，这种现象叫做波的反射．•反射定律：入射线、法线、反射线在同一平面内，入射线与反射线分居法线两侧，反射角等于入射角。
•入射角〔i 〕和反射角〔i ’〕：入射波的波线与平面法线的夹角i 叫做入射角．反射波的波线与平面法线的夹角i ’ 叫做反射角． · 平面波· · · ·u t 波传播方向•反射波的波长、频率、波速都跟入射波相同．•波遇到两种介质界面时，总存在反射〔二〕、波的折射1.波的折射：波从一种介质进入另一种介质时，波的传播方向发生了改变的现象叫做波的折射．2.折射规律：(1).折射角〔r 〕：折射波的波线与两介质界面法线的夹角r 叫做折射角．2.折射定律：入射线、法线、折射线在同一平面内，入射线与折射线分居法线两侧．入射角的正弦跟折射角的正弦之比等于波在第一种介质中的速度跟波在第二种介质中的速度之比：•当入射速度大于折射速度时，折射角折向法线.•当入射速度小于折射速度时，折射角折离法线.•当垂直界面入射时，传播方向不改变，属折射中的特例．•在波的折射中，波的频率不改变，波速和波长都发生改变．•波发生折射的原因：是波在不同介质中的速度不同．由惠更斯原理，A 、B 为同一波面上的两点，A 、B 点会发射子波，经⊿t 后， B 点发射的子波到达界面处D 点， A 点的到达C 点，21sin sin v v r i〔三〕波的叠加原理〔独立传播原理〕在两列波相遇的区域里，每个质点都将参与两列波引起的振动，其位移是两列波分别引起位移的矢量和．相遇后仍保持原来的运动状态．波在相遇区域里，互不干扰，有独立性．两列波叠加时，假设两列波振动方向相同，则振动加强，振幅增大；假设两列波振动方向相反，则振动减弱，振幅减小。
惠更斯原理 波的叠加和干涉
(1)振幅 2 A cos 2π x 随 x 而异,与时间无关
cos 2π x
1 2 π x 2k k 0,1,2,
2
0 2 π x (2k 1) k 0,1,2,
2
第五章 机械波
a 当 cos 2π x 0 时 A 0 为波节
x (2k 1) ( 的奇数倍)
44
(k 0,1,2， )
vO
vsB
AO
B
第五章 机械波
解 (1)已知 u 330 m s-1, vsA 0, vsB 60 m s-1
' u v0
u vs
' 330 30 500 454.5 Hz
330
vO
vsB
AO
B
第五章 机械波
(2) 观察者听到来自B 的频率
330 30 500 461.5 Hz
解 如图，飞机在4s内经过的距离为AB
AB vst h(cot cot )
vAC vs cos vBC vs cos
A
vs
B
h
第五章 机械波
1
u
u
vAC
0
u
u
vs cos
0
2
u
u vBC
0
u
u
vs cos
0
cos 1 0 u 0.275 cos 0 2 u 0.413
dWp
(y )2 x
节
x
波
腹
x
dWk
(y )2 t
A B C 平衡位置时
第五章 机械波
驻波的能量 驻波的能量在相邻的波腹和波节 间往复变化，在相邻的波节间发生动 能和势能间的转换，动能主要集中在 波腹，势能主要集中在波节，但无能 量的定向传播.
cos 2π x
1 2 π x 2k k 0,1,2,
2
0 2 π x (2k 1) k 0,1,2,
2
第五章 机械波
a 当 cos 2π x 0 时 A 0 为波节
x (2k 1) ( 的奇数倍)
44
(k 0,1,2， )
vO
vsB
AO
B
第五章 机械波
解 (1)已知 u 330 m s-1, vsA 0, vsB 60 m s-1
' u v0
u vs
' 330 30 500 454.5 Hz
330
vO
vsB
AO
B
第五章 机械波
(2) 观察者听到来自B 的频率
330 30 500 461.5 Hz
解 如图，飞机在4s内经过的距离为AB
AB vst h(cot cot )
vAC vs cos vBC vs cos
A
vs
B
h
第五章 机械波
1
u
u
vAC
0
u
u
vs cos
0
2
u
u vBC
0
u
u
vs cos
0
cos 1 0 u 0.275 cos 0 2 u 0.413
dWp
(y )2 x
节
x
波
腹
x
dWk
(y )2 t
A B C 平衡位置时
第五章 机械波
驻波的能量 驻波的能量在相邻的波腹和波节 间往复变化，在相邻的波节间发生动 能和势能间的转换，动能主要集中在 波腹，势能主要集中在波节，但无能 量的定向传播.
6.1-6.3 机械波的概念、波的能量与传播、惠更斯原理和波的叠加原理
（二）、纵波和横波
横波——振动方向与传播方向垂直，如电磁波 纵波——振动方向与传播方向相同，如声波，弹簧波
传播方向 传播 / 2
t 3T / 4
t T
t 5T / 4
如绳波为横波。
2.纵波
各质点振动方向与波的 传播方向平行。 传播方向
纵波是靠介质疏密部变化传播的，如声波， 弹簧波为纵波。
作业P151：
6.8、6.10、 6.12
6.2 波的能量与传播
在波动过程中，振源的能量通过弹性介质传播出 去，介质中各质点在平衡位置附近振动，介质中各部 分具有动能，同时介质因形变而具有势能。
波不仅是振动状态的传播，而且也是伴随着 振动能量的传播
一、波的能量和能量密度
有一平面简谐波
x y A cos[ ( t ) 0 ] u
解：①设振源方程为
y A cos(t )
由图可知
y
0.02m
t=0
0.8m
a
b
0.5m P
u
0.8
o
T / u 16s
x/m
2 / T / 8
A 0.02 m
t = 0 时，o点处的质 点向 y 轴负向运动， 由旋转矢量法可知
y
0.02m
a
b
0.5m P
质量为 dm dV
在x处取一体积元 dV ,
质点的振动速度
y x A sin[ (t ) 0 ] t u
体积元内媒质质点动能为 1 x 1 2 2 2 2 dEk dm A sin [ ( t ) 0 ]dV 2 u 2 可以证明体积元内媒质质点的弹性势能与动能相同即 1 2 2 x 2 dE p A sin [ ( t ) 0 ]dV 2 u 体积元内媒质质点的总能量为：
8-惠更斯原理+波的叠加+波的干涉
1. 波的传播的独立性 2. 波的叠加原理 当几列波在介质中某点处相遇时,该处质点 的振动是各列波单独存在时的振动的合成。
14
二、波的干涉 1. 相干条件: 两波源 频率相同 振动方向相同
相差恒定
15
频率相同、振动
方向平行、相位 相同或相位差恒 定的两列波相遇 时，使某些地方
振动始终加强，
而使另一些地方 振动始终减弱的 现象，称为波的 干涉现象.
3
一、波的衍射 1. 衍射现象: 波传播过程中当遇到障碍物时，能绕过 障碍物的边缘而传播的现象。 2. 衍射产生条件: 衍射物（障碍物 ＞＞λ, 衍射不明显
或缝）的线度d
～λ，衍射明显
声波 (20－2×104 Hz) 对围墙衍射明显； “ 隔墙有耳 ”， “闻其声而不见其人”。
4
(若广播电台、电视台都在山前侧) 障 碍 物
18
合振动: y y1 y2 A cos( t )
r2 r1 [ ( t ) 2 ] [ ( t ) 1 ] u u
r2 r1 (2 1 ) 2 u 2 (2 1 ) (r2 r1 ) 注意顺序！ 2 2 合振幅 A A1 A2 2 A1 A2 cos
无线电广播 电报通讯 无线电广播 调频广播、 9 电视与导航
1.0×10 2 ～ 1.5×10 3
1.5K～6M
短波
甚高频 6M～30M 超高频 30M～0.3G
超短波 （米波）
衍射产生条件:
衍射物（障碍物 或缝）的线度d ＞＞λ, 衍射不明显 ～λ，衍射明显
障 碍 物
听广播比看电视更容易！
10
二、惠更斯原理 1. 衍射现象：
5-4 惠更斯原理 波的叠加和干涉
波的叠加和干涉
大学物理学 （第3版）
二
波的叠加原理
各列波在相遇前和相遇后都保持原来的特性(频 率、波长、振动方向、传播方向等)不变，与各波单 独传播时一样.
在相遇处各质点的振动是各列波在该处激起的 振动的合成.
第5章 机械波
5–4 惠更斯原理
波的叠加和干涉
大学物理学 （第3版）
三
波的干涉
两列波若频率相同、
振动方向相同、在
相遇点的位相相同 或位相差恒定，则 在合成波场中会出 现某些点的振动始
终加强，另一些点
的振动始终减弱(或 完全抵消)，这种现 象称为波的干涉.
第5章 机械波
5–4 惠更斯原理
波的叠加和干涉
大学物理学 （第3版）
水波的干涉现象
第5章 机械波
5–4 惠更斯原理
波的叠加和干涉
大学物理学 （第3版）
'
2
2x
'
u 340 2125 Hz 2x 2 0.08
第5章 机械波
u
5–4 惠更斯原理
波的叠加和干涉
大学物理学 （第3版）
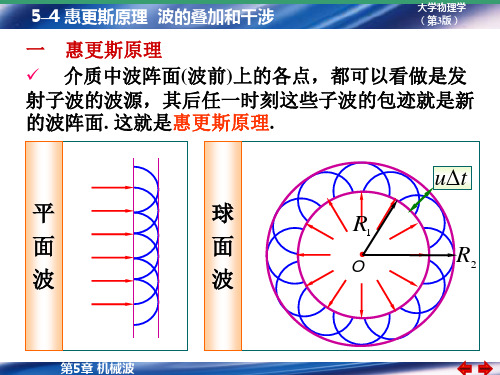
一
惠更斯原理 介质中波阵面(波前)上的各点，都可以看做是发 射子波的波源，其后任一时刻这些子波的包迹就是新 的波阵面. 这就是惠更斯原理.
ut
平 面 波 球 面 波
R1
O
R2
第5章 机械波
5–4 惠更斯原理
波的叠加和干涉
大学物理学 （第3版）
k
k 0,1,2,
干涉加强
A A1 A2
3)
(k 1 2)
A A1 A2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r2 r1
p
具有恒定的相位差 振动方向相同
满足相干条件的波源称为相干波源。
设有两个相干波源S1和S2 发出的简谐波在空间p点相遇。
S2 S1
r2 r1
p
y10 A10 cos( t 10 )
y20 A20 cos( t 20 )
传播到p点引起的振动分别为： 2 y1 A1 cos( t 10 r1 )
A2 A12 A22 2 A1 A2 cos
I I1 I 2 2 I1 I 2 cos
相长干涉的条件：
（ 20 10） 2
A Amax A1 A2
r2 r1
2k
k 0 ,1,2 ,3 ,...
I I max I1 I 2 2 I1 I 2
在p点的振动为同 方向同频率振动 的合成。
2 y2 A2 cos( t 20 r2 )
合成振动为：
y y1 y2 A cos( t 0 )
y A 10
2r1 2r2 A1 cos( 10 ) A2 sin( 20 ) 2 2 A2 A1 A2 2 A1 A2 cos
2x
2 ( 30 x )
( 2k 1) k 0,1,2,...
相干相消的点需满足： 30 2 x k 因为： u 4m
x 15 k 2 k 0,1,2,...
O
x
X B
A
30 x 30m
x 1,3,5,7,9,......25,27,29m
M
sin i n2 sin n1
AB u2 t AB3 sin A1 介质1 i B3 sin i u1 c n1 A B1 B2 N sin u2 c n2 B 介质2
二、波的叠加 波传播的独立性原理或波的叠加原理： 各列波在相遇前和相遇后都保持原来的特性 （频率、波长、振动方向、传播方向等）不便， 与各波单独传播时一样，而在相遇处各质点的振 动则是各列波在该处激起的振动的合成。 能分辨不同的声音正是这个原因
r2 r1 (2k 1) , 2 称为波程差
k 0,1,2,3,... 相长干涉
k 0,1,2,3,... 相消干涉
波的非相干叠加
I I1 I 2
例题 位于A、B两点的两个波源，振幅相等，频 率都是100赫兹，相位差为，其A、B相距30米， 波速为400米/秒，求:A、B连线之间因相干干涉而 静止的各点的位置。 解：如图所示，取A点为坐标原点，A、B联线为X轴， 取A点的振动方程 : x X
yB A cos(t 0)
在X轴上B点发出的行波方程：
yB A cos[t 0
2 ( 30 x )
]
因为两波同频率，同振幅，同方向振动，所以相干 为静止的点满足：
2x 2 (30 x ) (2k 1)
k 0,1,2,...
相消干涉的条件：
( 20 10 )
2
( r2 r1 ) ( 2k 1 )
k 0 ,1,2 ,3 ,...
A Amin | A1 A2 |
I I min I1 I 2 2 I1 I 2
当两相干波源为同相波源时，相干条件写为
r2 r1 k ,
6.3 惠更斯原理 波的叠加和干涉
一、惠更斯原理 惠更斯原理： 介质中波阵面（波前） 上的各点，都可以看作 为发射子波的波源，其 后一时刻这些子波的包 迹便是新的波阵面。
t时刻波面 t+t时刻波面波的传播方向 t时刻波面
· · · ·
t+t时刻波面
t + t
· ·· · · · t · · · · ·· · ·
2r1
) A2 sin( 20
2r2
)
由于波的强度正比于振幅，所以合振动的强度为：
I I1 I 2 2 I1 I 2 cos
其中： ( 20 10 )
2
( r2 r1 )
对空间不同的位置，都有恒定的，因而合强 度在空间形成稳定的分布，即有干涉现象。
说明： 振动的叠加仅发生在单一质点上 波的叠加发生在两波相遇范围内的许多质点上
三、波的干涉 两列波若频率相同、振动方向相同、在相遇点的 位相相同或位相差恒定，则合成波场中会出现某些点
的振动始终加强，另一点的振动始终减弱（或完全抵
消），这种现象称为波的干涉。 相干条件 两波源具有相同的频率
S2 S1
波传播方向
u t
平面波 如你家在大山后 ,听广播和看电 视哪个更容易 ? (若广播台、电 视台都在山前侧)
球面波
*应用惠更斯原理证明波的反射和折射定律
A3
B
AA3 B3 ABB3
A3 AB3 BB3 A
M
i i A B1 B2 B3
A2
A3
A1
A2
N
i i
A3 B3 u1t AB3 sin i
O
yA A cos(t )
在X轴上A点发出的行波方程：
A
30 x 30m
B
yA A cos(t
B点的振动方程 :
2x
yB A cos(t 0)
)
2x yA A cos(t )
B点的振动方程 :
O
x
30 x 30m
X B
A