轴对称讲义(全)(完整资料)
轴对称(知识讲座)

§12.1 轴对称§12.1.1 轴对称〔一〕教学目标1.在生活实例中认识轴对称图.2.分析轴对称图形,理解轴对称的概念.教学重点轴对称图形的概念.教学难点能够识别轴对称图形并找出它的对称轴.教学过程Ⅰ.创设情境,引入新课我们生活在一个充满对称的世界中,许多建筑物都设计成对称形,艺术作品的创作往往也从对称角度考虑,自然界的许多动植物也按对称形生长,中国的方块字中些也具有对称性……对称给我们带来多少美的感受!初步掌握对称的奥秒,不仅可以帮助我们发现一些图形的特征,还可以使我们感受到自然界的美与和谐.轴对称是对称中重要的一种,从这节课开始,我们来学习第十四章:轴对称.今天我们来研究第一节,认识什么是轴对称图形,什么是对称轴.Ⅱ.导入新课出示课本的图片,观察它们都有些什么共同特征.这些图形都是对称的.这些图形从中间分开后,左右两局部能够完全重合.小结:对称现象无处不在,从自然景观到分子结构,从建筑物到艺术作品,•甚至日常生活用品,人们都可以找到对称的例子.现在同学们就从我们生活周围的事物中来找一些具有对称特征的例子.我们的黑板、课桌、椅子等.我们的身体,还有飞机、汽车、枫叶等都是对称的.如课本的图14.1.2,把一张纸对折,剪出一个图案〔折痕处不要完全剪断〕,•再翻开这张对折的纸,就剪出了美丽的窗花.观察得到的窗花和图14.1.1中的图形,你能发现它们有什么共同的特点吗?窗花可以沿折痕对折,使折痕两旁的局部完全重合.不仅窗花可以沿一条直线对折,使直线两旁重合,上面图14.1.1中的图形也可以沿一条直线对折,使直线两旁的局部重合.结论:如果一个图形沿一直线折叠,直线两旁的局部能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线〔成轴〕•对称.了解了轴对称图形及其对称轴的概念后,我们来做一做.取一张质地较硬的纸,将纸对折,并用小刀在纸的中央随意刻出一个图案,•将纸翻开后铺平,你得到两个成轴对称的图案了吗?与同伴进行交流.结论:位于折痕两侧的图案是对称的,它们可以互相重合.由此可以得到轴对称图形的特征:一个图形沿一条直线折叠后,折痕两侧的图形完全重合.接下来我们来探讨一个有关对称轴的问题.有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。
《轴对称》 讲义

《轴对称》讲义一、轴对称的定义如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,这条直线就是它的对称轴。
例如,等腰三角形、正方形、圆形都是轴对称图形。
生活中也有许多轴对称的例子,比如飞机的外形、蝴蝶的翅膀、建筑物的对称设计等等。
二、轴对称的性质1、对称轴是任何一对对应点所连线段的垂直平分线。
2、对应线段、对应角相等。
3、成轴对称的两个图形全等。
三、轴对称图形的判定一个图形如果能找到一条直线,使得沿此直线折叠后,直线两侧的部分能够完全重合,那么这个图形就是轴对称图形。
四、常见的轴对称图形1、线段线段是轴对称图形,它的对称轴是线段的垂直平分线和它本身所在的直线。
2、角角是轴对称图形,它的对称轴是角平分线所在的直线。
3、等腰三角形等腰三角形是轴对称图形,它的对称轴是底边的高线(或顶角平分线或底边的中线)所在的直线。
4、等边三角形等边三角形有三条对称轴,分别是三条边的高线所在的直线。
5、矩形矩形是轴对称图形,它有两条对称轴,分别是对边中点所连的直线。
6、菱形菱形是轴对称图形,它的两条对角线所在的直线就是对称轴。
7、正方形正方形有四条对称轴,分别是两条对角线所在的直线和对边中点所连的直线。
8、圆圆是轴对称图形,它有无数条对称轴,经过圆心的任意一条直线都是它的对称轴。
五、作轴对称图形1、作一个图形关于某条直线对称的图形(1)确定关键点:找出原图形中的关键点,如顶点、交点等。
(2)作垂线:过关键点作对称轴的垂线。
(3)量距离:在垂线上量取与关键点到对称轴距离相等的点。
(4)依次连接:依次连接对称点,得到对称图形。
2、用坐标表示轴对称(1)点(x,y)关于 x 轴对称的点的坐标为(x,y)。
(2)点(x,y)关于 y 轴对称的点的坐标为(x,y)。
六、轴对称的应用1、在建筑设计中的应用许多著名的建筑都采用了轴对称的设计,如中国的故宫、印度的泰姬陵等。
这种设计不仅美观,还能使建筑物在结构上更加稳固。
轴对称课件(60张PPT)

轴对称在解直角三角形中应用
在解直角三角形时,可以利用轴对称的 性质来构造全等或相似的直角三角形,
从而简化计算过程。
例如,如果一个直角三角形关于某条直 线对称,那么它的两个锐角相等,同时 它的两条直角边也相等。这样我们就可 以通过已知的一边和一角来求解其他未
知量。
另外,如果两个直角三角形关于某条直 线对称,那么它们一定是相似的。这样 我们就可以通过已知的相似比来求解未
知量。
05
绘制和分析轴对称图形方 法技巧
使用直尺和圆规绘制轴对称图形
确定对称轴
在平面上选择一条直线作为对 称轴。
找到对称点
使用直尺和圆规,按照轴对称 的定义,找到该点关于对称轴 的对称点。
选择一个点
在对称轴的一侧选择一个点。
绘制图形
连接原点和对称点,即可得到轴对 称图形的一部分。重复以上步骤,
可以得到完整的轴对称图形。
动物
一些动物的身体结构也具 有轴对称性,如蝴蝶的翅 膀、蜻蜓的复眼等。
晶体
晶体结构中的原子排列往 往呈现出轴对称性,如雪 花、钻石等。
科技产品中的轴对称设计
电子产品
手机、平板电脑等电子产品的外观设 计中,常采用轴对称元素,实现简洁、 时尚的视觉效果。
汽车设计
航空航天
飞机、火箭等航空航天器的设计中也 广泛应用轴对称性,以确保飞行稳定 性和安全性。
典型例题解析
解析
根据轴对称性质,我们知道 △ABC≌△A'B'C',所以 ∠BAC=∠B'A'C'。
例题2
已知点P(2,3)关于x轴对称的点为P', 求点P'的坐标。
解析
由于点P关于x轴对称,所以点P'的 横坐标不变,纵坐标取反。因此, 点P'的坐标为(2,-3)。
《轴对称完整》课件

对轴对称的未来展望
轴对称作为数学中的一个基础概念,仍有很大的研究和发展空间。随着数学和其 他学科的发展,轴对称的应用范围也将不断扩大。我们鼓励学生们在未来的学习 和研究中继续关注轴对称,探索它的更多应用和价值。
在《轴对称完整》ppt课件的最后,我们总结了轴对称的基本原理、方法和应用 ,并提出了进一步探索的问题和方向。我们希望学生们能够带着这些问题和思考 ,继续深入探索轴对称的奥秘,为未来的研究和应用打下坚实的基础。
轴对称是数学中的一个重要概念,它描述了一个图形通过某个直线折叠后与自身重合的性质。在《轴对称完整 》ppt课件中,我们深入探讨了轴对称的定义、性质和分类,帮助学生们更好地理解这一概念。
轴对称在几何学中有着广泛的应用,它不仅在平面几何中出现,还涉及到立体几何、解析几何等多个领域。通 过对轴对称的深入理解,学生们可以更好地掌握几何学的基本原理和方法。
05
轴对称的实践应用
在设计中的应用
对称美学的运用
设计作品中,轴对称的运用可以创造出平衡、和谐的感觉。例如,在服装设计中,设计师可以通过轴对称的裁 剪方式,使服装看起来更加优雅、庄重。
产品设计的指导
在产品设计中,轴对称的原理可以帮助设计师更好地布局产品的各个部分,使其更加符合人机工程学,提高使 用体验。
04
轴对称的意义
美学的意义
美学欣赏
轴对称的形状、图案和结 构常常被视为具有美感, 可以给人带来视觉上的享 受和满足感。
艺术创作
艺术家们经常利用轴对称 的原理来创作美丽的艺术 品,如建筑设计、绘画和 雕塑等。
平衡与和谐
轴对称能够给人带来平衡 和和谐的感觉,使整体效 果更加协调和完整。
科学的意义
自然界中的轴对称
轴对称讲义(全)

轴对称【知识重点】1、轴对称图形:假如沿某条直线对折,对折的两部分是完整重合的,这样的图形为轴对称图形。
这条直线叫做这个图形的对称轴。
2、轴对称:把一个图形沿着某一条直线翻折过去,假如它能够与另一个图形重合,说这两个图形为轴对称。
这条直线叫做这个图形的对称轴。
3、对称点:翻折后(图形重合时)能够相互重合的点。
4、垂直均分线(中垂线):垂直而且均分一条线段的直线。
结论 1:线段垂直均分线上的点到这条线段两个端点的距离相等。
结论 2:假如一个图形对于某一条直线对称,那么连结对称点的线段的垂直均分线就是该图形的对称轴。
【典型例题】例 1. 在以下十个汉字中,哪几个是轴对称图形?他们各有几条对称轴?上下目天田土吕林显王例 2. 如图,以下图案是我国几家银行的标记,此中轴对称图形有()A.1 个B.2个C.3 个D.4个例 3. 以下图形中是轴对称图形的有()①矩形;②菱形;③平行四边形;④四边形;⑤等腰梯形;⑥直角梯形;⑦三角形;⑧等边三角形;⑨等腰三角形;⑩ 正六边形A. 5 个个个 D.8 个例 3. 判断题②两个图形对于某直线对称,对称点必定在直线的两旁。
()③两个对称图形对应点连线的垂直均分线,就是他们的对称轴()④平面上两个完整同样的图形必定对于某直线对称()例 4. 如图, l1、 l 2交于 A 点, P、 Q 的地点以下图,试确立M 点,使它到l 1、 l 2的距离相等,且到P、Q 两点的距离也相等。
l 1PAl2Q例 5. 已知如图1,MN 垂直均分线段 AB,CD垂足分别为E、F,求证:AC=BD,∠ ACD=∠BDC.例 6. 已知:在△ ABC中,AB=AC,D是 AB 的中点,且 DE⊥ AB, △ BCE周长为 8,且 AC- BC=2, 求 AB,BC的长。
例 7. 如图,将一张长方形纸片 ABCD 沿 EF折叠后, D′ E 与 BC 的交点为 G,点 D、C 分别落在点 D′、 C′的地点上,若∠ EFG=55°,求∠ 1,∠ 2 的度数.绘图形的对称轴【知识重点】1. 随意两点总对于某一条直线对称,故画这两点的对称轴的方法是_____________2.对于复杂图形的对称轴的画法:可先找出轴对称图形或成轴对称的两个图形的随意一组对称点;再连结对称点;而后画出_________则这条 ________画轴对称图形【知识重点】1、对于某些图形,先画出图形中的一些特别点(如线段端点)的对称点,连结这些对称点,就能够获得原图形的轴对称图形;2、平面直角坐标系中对于X 轴和 Y 轴对称的图形的做法:先找出一些特别点的对称点坐标,连结对称点,即可获得;3、角均分线和垂直均分线的做法。
初二数学讲义(轴对称)(详细答案)

初二数学讲义(轴对称)知识梳理1、轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
2、轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
3、轴对称图形与轴对称的区别与联系:(1)区别:轴对称图形讨论的是“一个图形与一条直线的对称关系”;轴对称讨论的是“两个图形与一条直线的对称关系”。
(2)联系:把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称;把轴对称的“两个图形看作一个整体”便是轴对称图形。
4、轴对称的性质:(1)成轴对称的两个图形全等。
(2)对称轴与连结“对应点的线段”垂直。
(3)对应点到对称轴的距离相等。
(4)对应点的连线互相平行。
5、线段的垂直平分线:(1)定义:经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
(2)性质:线段垂直平分线上的点与线段两端点的距离相等。
(3)判定:与线段两端点距离相等的点在线段的垂直平分线上。
6、等腰三角形:(1)定义:有两条边相等的三角形,叫做等腰三角形。
底角只能是锐角。
(2)性质:①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线”,只有一条。
②“等边对等角”:等腰三角形的两个底角相等。
③三线合一:顶角平分线、底边上的中线和地边上的高相互重合。
(3)判定方法:①定义法:有两条边相等的三角形是等腰三角形。
②判定(“等角对等边”):有两个角相等的三角形是等腰三角形。
7、等边三角形:(1)定义:三条边都相等的三角形,叫做等边三角形。
说明:等边三角形就是腰和底相等的等腰三角形,因此,等边三角形是特殊的等腰三角形。
(2)性质:①等边三角形是轴对称图形,其对称轴是“三边的垂直平分线”,有三条。
②三条边上的中线、高线及三个内角平分线都相交于一点。
③等边三角形的三个内角都等于60°。
(3)判定方法:①定义法:三条边都相等的三角形是等边三角形。
轴对称课外讲义

第一部分轴对称轴对称一.概念与要点:1.轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
这时,我们也说这个图形关于这条直线(成轴)对称。
2.轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
3.轴对称和轴对称图形的区别和联系:区别:①轴对称图形说的是一个具有特殊形状的图形;轴对称说的是两个图形的一种特殊位置关系。
②轴对称是对两个图形说的,而轴对称图形是对一个图形说的。
联系:①都沿某条直线对折,图形重合。
②如把两个成轴对称的图形看成一个整体,那么它就是一个轴对称图形;反过来,把轴对称图形的两部分分别看作两个图形,那么这两个图形成轴对称。
4.线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
5. 轴对称的性质:(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
(2)关于某条直线成轴对称的两个图形是全等图形。
(3)轴对称图形的性质:(轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
)6. 线段的垂直平分线的性质及判定(1)线段垂直平分线上的点与这条线段两个端点的距离相等。
如图①,若PC是线段AB的垂直平分线(AC=BC,PC⊥AB),则PA=PB(2)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
如图②,若PA=PB,则点P在线段AB的垂直平分线上。
(A )(B )(C)(D )二.规律与结论1. 轴对称图形的特征:一个图形沿一条直线折叠后,折痕两侧的图形完全重合. 2.轴对称的特征:成轴对称的两个图形全等.如果把一个轴对称图形沿对称轴分成两个图形,这两个图形全等,并且也是成轴对称的. 3.线段垂直平分线的实质:线段垂直平分线上的点与这条线段两个端点的距离相等;反过来,与这条线段两个端点距离相等的点都在它的垂直平分线上.所以线段的垂直平分线可以看成是与线段两端点距离相等的所有点的集合.4.成轴对称的两个图形,对应线段的延长线如果相交,交点一定在对称轴上;对应线段的延长线如果不相交,也就是对应线段所在的直线平行,•那么它们也与对称轴平行.5. 画已知图形关于某直线的对称图形:①对称轴是对应点连线的垂直平分线,②若对应线段或延长线相交,则交点一定在对称轴上。
轴对称--完整版课件
BC=10cm,那么△BCD的周长是
_______cm.
26cm
A
E D
B
C
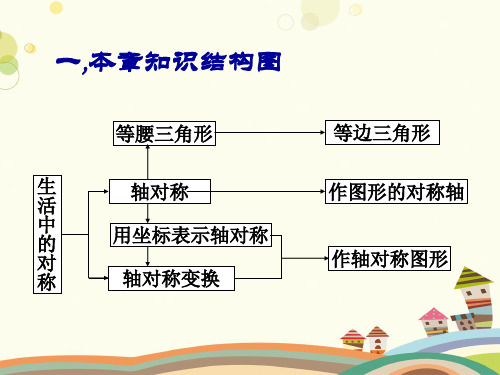
一,本章知识结构图
等腰三角形
等边三角形
生 活
轴对称
作图形的对称轴
中 的
用坐标表示轴对称
对
作轴对称图形
称
轴对称变换
轴对称的性质
•对应点所连的线段的中垂线就是 对称轴 •对应线段相等,对应角相等
轴对称变换
准确做图形对称轴的方法
因为对称轴垂直平分每对对应点所连接 的线段,所以只要找一对对应点,用圆规 作出对应点所连线段的垂直平分线即可。
8、已知,如图: AB=AC AD=DC=BC
则∠A=
Байду номын сангаас
360
A
D
B
C
9.在△ABC中,AB=AC,DE 为AB的垂直 A 平分线,D为垂足,交AC与E,若AB=8cm, △ABC的周长为21cm,求△BCE的周长.
D E
10.如图∠ ABC=70°, ∠ A=50°
B
C
AB的垂直平分线交AC于D,则∠DBC=___.
A
E
B
D
C
11 如图, ∠ABC、∠ACB的平分线相 交于F,过F作DE//BC交AB于D,交AC于E, 若AB=9cm, AC=8cm,则△ADE的周长是 多少? A
AB=AD+DB=AD+DF D F E AC=AE+EC=AE+EF
B
C
13、如图,在△ABC中,AB=AC=16cm,
AB的垂直平分线交AC于D,如果
利用轴对称变换作图1
作出三角形关于直线L对称的图形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴对称
【知识要点】
1、轴对称图形:如果沿某条直线对折,对折的两部分是完全重合的,这样的图形为轴对称图形。
这条直线叫做这个图形的对称轴。
2、轴对称:把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,说这两个图形为轴对称。
这条直线叫做这个图形的对称轴。
3、对称点:翻折后(图形重合时)能够互相重合的点。
4、垂直平分线(中垂线):垂直并且平分一条线段的直线。
结论1:线段垂直平分线上的点到这条线段两个端点的距离相等。
结论2:如果一个图形关于某一条直线对称,那么连接对称点的线段的垂直平分线就是该图形的对称轴。
【典型例题】
例 1. 在下列十个汉字中,哪几个是轴对称图形?他们各有几条对称轴?
上下目天田土吕林显王
例 2. 如图,下列图案是我国几家银行的标志,其中轴对称图形有()
A.1个
B.2个C.3 个
例 3. 下列图形中是轴对称图形的有()
①矩形;②菱形;③平行四边形;④四边形;⑤等腰梯形;⑥直角梯形;⑦三角形;⑧等边三角形;⑨等腰三角形;⑩ 正六边形
A. 5 个
B.6个
C.7个
D.8 个
例 3. 判断题
D.4个
①两个关于某直线对称的图形是一模一样的。
②两个图形关于某直线对称,对称点一定在直线的两旁。
()
③两个对称图形对应点连线的垂直平分线,就是他们的对称轴()
④平面上两个完全相同的图形一定关于某直线对称()
例 4. 如图,l1、l2交于A点,P、Q 的位置如图所示,试确定
例 5. 已知如图1,MN 垂直平分线段AB,CD垂足分别为E、F,求证:AC=BD,∠ACD=∠ BDC.
例 6. 已知:在△ ABC中,AB=AC,D是AB的中点,且DE⊥ AB, △ BCE周长为8,且AC-BC=2,
求AB,BC 的长。
例7. 如图,将一张长方形纸片ABCD沿EF折叠后,D′E与BC的交点为G,点D、C 分别落在点D′、C′的位置上,若∠ EFG=55°,求∠ 1,∠2 的度数.
M 点,使它到l1、l2的距离相等,且到P、Q 两点的距离也相等。
l2
知识要点】
1. 任意两点总关于某一条直线对称,故画这两点的对称轴的方法是______________
2. 对于复杂图形的对称轴的画法:可先找出轴对称图形或成轴对称的两个图形的任意一组
对称点;再连结对称点;然后画出_________ 则这条_______
画轴对称图形
【知识要点】
1、对于某些图形,先画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形;
2、平面直角坐标系中关于X 轴和Y轴对称的图形的做法:先找出一些特殊点的对称点坐标,连接对称点,即可得到;
3、角平分线和垂直平分线的做法。
典型例题】
例 3. 看以下两个图形是否是轴对称图形?你能否画出它的对称轴?
画图形的对称轴
例 1. 找出下列轴对称图形的所有对称轴,并把它画出
来.
例
4
.如图,连结B、B′的线段的垂直平分线是否还是你在上图中画的对称轴?
例 5. 印制一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:先将
一张整版的纸,对折一次为 4 页,再对折一次为8 页,连续对折三次为16 页,⋯⋯;然后再排页码.如果想设计一本16 页码的毕业纪念册,请你按图1,图2,图3(图中的1,16 表示页码)的方法折叠,在图中填上按这种折叠方法得到的各页在该面相应位置上的页码.
例 6. 如图,∠ AOB 内一点P,试分别画出
点
例8. 下图中,直线L 是一个轴对称图形的对称轴,画出这个图形关于直线L 对称的另一半.
P关于OA和OB的对称点P1和P2
例7. 画出下列图形关于直
线
例9. 如图是台球桌面矩形网格示意图,图中的四个角各有一个入球孔,如果一个球按图中所示的方向被击出(球可以多次反射),那么该球最后将落入的球袋是()
A.1号袋B.2号袋C.3 号袋D.4号袋
等腰三角形
【知识要点】
1、等腰三角形的两个底角相等;
2、等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”);
3、等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等
(简写成“等角对等边” )。
4、等边三角形:
①等边三角形的三个内角都相等,并且每一个角都等于60 °;②三个角都相等的三角形
是等边三角形;
③有一个角是60°的等腰三角形是等边三角形。
5、在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
【典型例题】
例 1. 若等腰三角形的底边长为10cm,则腰长x的取值范围是.
例 2. 若等腰三角形的一个角为40°,则另两个角为__________________ 。
例 3. 等腰三角形一腰上的高与底边的夹角为45°,则这个三角形是()
A.锐角三角形
B.钝角三角形
C.等边三角形
D.等腰直角三角形
例 4. 设α是等腰三角形的一个底角,则α的取值范围是()
A. 0<α<90°
B. α<90°
C. 0<α≤ 90°
D. 0≤α<90°
例 5. 若等腰三角形的一个外角为120 °,一边长为2cm,则另外两边长为
例 6. △ABC中,∠ ACB=90°,∠ B=60°,AB+BC=6cm,则BC=。
