北师大版数学必修4课时作业：24二倍角的三角函数(一)含解析

合集下载

【精准解析】高中数学北师大必修4一课三测：3.3 二倍角的三角函数+Word版含解析byde

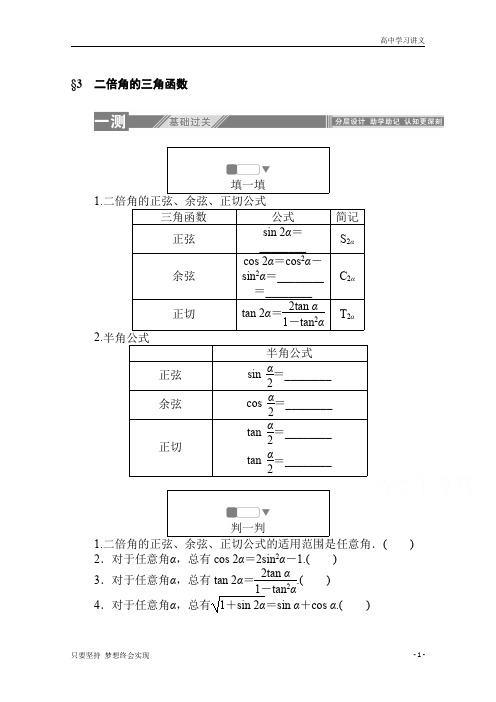
＝1＋cos
2α－π 2
＝1＋sin
2α＝2.
2
2
3
答案：D
4．解析：设等腰三角形的顶角为α，底角为β，则 cos α＝ 7 .又β 25
＝π－α，所以 cos β＝cos 22
π－α 22
＝sin
α＝ 2
1－275＝3，故选 B. 25
答案：B
sin x
5．解析：f(x)＝1＋cocssoinxs22xx＝cossin2xx＋cossinx2x＝sin
的值．
高中学习讲义
基础达标
一、选择题
1．计算 2sin2105°－1 的结果等于( )
A．－ 3 B．－1
2
2
C.1
D. 3
2
2
2．下列各式中，值为 3的是( ) 2
A．2sin 15°cos 15° B．cos215°－sin215°
C．2sin215°－1
D．sin215°＋cos215°
3．已知
A.12
B.
2 2
C. 3 D. 3
3
2
3．已知 cos α＝45，α∈
3π，2π 2
，则 sin
α2等于(
)
A．－
10 10
B.
10 10
C. 3 3 D．－3
10
5
4．已知 cos α＝－35，且 180°<α<270°，则 tan α2＝________.
知识点一 1.若 sin α＝13，则 cos 2α＝(
8．sin 15°＝± 1－cos 30°.( ) 2
想一想
1.二倍角公式有哪些变形？
提示：(1)倍角公式的逆用

北师大版数学必修4课时作业：25二倍角的三角函数(二)含解析

A. B.
C．－ D．－
解析：因为α∈ ，
所以cosα<sinα，(cosα－sinα)2＝1－sin2α，
所以cosα－sinα＝－ .
答案：C
3．若sin(α＋β)cosβ－cos(α＋β)sinβ＝0，则sin(α＋2β)＋sin(α－2β)＝()
A．1 B．－1
C．0 D．±1
解析：因为sin(α＋β)cosβ－cos(α＋β)·sinβ＝sin(α＋β－β)＝sinα＝0，
＝sin[(α＋β)－α]＝sinβ，
两边同除以sinα得－2cos(α＋β)＝ .
|
11．已知sinα＋cosα＝，则2cos2 －1＝()
A. B.
C．－ D．－
解析：∵sinα＋cosα＝，平方可得1＋sin2α＝，可得sin2α＝－ .
2cos2 －1＝cos ＝sin2α＝－ .
答案：C
答案：D
5．化简 2＋2sin2 得()
A．2＋sinαB．2＋ sin
C．2 D．2＋ sin
解析：原式＝1＋2sin cos ＋1－cos ＝2＋sinα－cos ＝2＋sinα－sinα＝2.
答案：C
二、填空题(每小题5分，共15分)
6．已知sin －cos ＝，则cos2θ＝________.
所以sin(α＋2β)＋sin(α－2β)＝2sinαcos2β＝0.
答案：C
4．若θ∈ ，sin2θ＝，则sinθ＝()
A. B.
C. D.
解析：因为θ∈ ，所以2θ∈ ，
所以cos2θ≤0，
所以cos2θ＝－
＝－＝－ .
又cos2θ＝1－2sin2θ，
所以sin2θ＝＝＝，

高中数学必修四北师大版二倍角的三角函数课时作业含答案

二倍角的三角函数课时作业北师大版必修4一、选择题1．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos2θ的值为( )A ．－45B ．－35C ．35D ．45[答案] B[解析] 由题意知tan θ＝2，且θ为第一或第三象限角，故cos2θ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ ＝1－221＋22＝－35. 2．已知等腰三角形底角的余弦值为23，则顶角的正弦值是( )A ．259B ．459C ．－459D ．－259[答案] B[解析] 设等腰三角形的底角为α，则cos α＝23，∴sin α＝53，设顶角为β，则sin β＝sin(180°－2α) ＝sin2α＝2sin αcos α＝2×53×23＝459. 3．设α∈(π，2π)，则1－cos π＋α2等于( )A ．sin α2B ．cos α2C ．－sin α2D ．－cos α2[答案] D[解析] ∵α∈(π，2π)，则α2∈(π2，π)，∴1－cos π＋α2＝1＋cos α2＝cos2α2＝－cos α2. 4．若tan θ＋1tan θ＝4，则sin2θ＝( )A ．15B ．14C ．13D ．12[答案] D[解析] ∵tan θ＋1tan θ＝4，∴sin θcos θ＋cos θsin θ＝4. ∴sin 2θ＋cos 2θcos θsin θ＝4，即2sin2θ＝4.∴sin2θ＝12.5．若θ∈[π4，π2]，sin2θ＝378，则sin θ＝( )A ．35 B ．45 C ．74D ．34[答案] D[解析] 本题考查了三角的恒等变形以及倍半角公式．由θ∈[π4，π2]可得2θ∈[π2，π]，cos2θ＝－1－sin 22θ＝－18，sin θ＝1－cos2θ2＝34. 6．函数y ＝2cos 2⎝ ⎛⎭⎪⎫x －π4－1是( )A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C ．最小正周期为π2的奇函数D ．最小正周期为π2的偶函数[答案] A[解析] 考查倍角公式和三角函数的性质．因为y ＝2cos 2⎝ ⎛⎭⎪⎫x －π4－1＝cos ⎝ ⎛⎭⎪⎫2x －π2＝sin2x 为奇函数，T ＝2π2＝π，所以选A ．二、填空题7．若sin ⎝ ⎛⎭⎪⎫π2＋θ＝35，则cos2θ＝______.[答案] －725[解析] 本题主要考查诱导公式及二倍角公式的灵活运用． ∵sin ⎝ ⎛⎭⎪⎫π2＋θ＝cos θ＝35， ∴cos2θ＝2cos 2θ－1＝2×⎝ ⎛⎭⎪⎫352－1＝－725.8．若cos2θ＝23，则sin 4θ＋cos 4θ的值为________． [答案]1118[解析] 因为sin 4θ＋cos 4θ＝(sin 2θ＋cos 2θ)2－2sin 2θ·cos 2θ＝1－12sin 22θ，又因为cos2θ＝23，所以sin 22θ＝1－cos 22θ＝1－29＝79，所以sin 4θ＋cos 4θ＝1－12×79＝1－718＝1118. 三、解答题9．已知sin(x ＋π4)sin(π4－x )＝16，x ∈(π2，π)，求sin4x ，cos4x ，tan4x 的值．[解析] ∵sin(x ＋π4)sin(π4－x )＝sin(π4＋x )cos[π2－(π4－x )]＝sin(x ＋π4)cos(π4＋x ) ＝12sin(2x ＋π2)＝12cos2x ＝16， ∴cos2x ＝13.。

2021年高中数学北师大版必修4学案： 3.3 二倍角的三角函数(含解析)

§3 二倍角的三角函数Q 情景引入ing jing yin ru如图甲所示，已知弓弦的长度AB ＝2a ，弓箭的长度MN ＝2b (其中MA ＝MB ，MN ⊥AB )．假设拉满弓时，箭头和箭尾到A ，B 的连线的距离相等(如图乙所示)，设∠AMN ＝α，你能用a ，b 表示∠AMB 的正切值，即tan 2α的值吗？tan 2α与tan α之间存在怎样的关系呢？现在我们来学习二倍角与半角公式的知识．X 新知导学in zhi dao xue1．二倍角的正弦、余弦、正切公式(1)在和角公式S α＋β，C α＋β，T α＋β中，当α＝β时就可得到二倍角的三角函数公式S 2α，C 2α，T 2α.sin 2α＝__2sin αcos α__，cos 2α＝__cos 2α－sin 2α__，tan 2α＝__2tan α1－tan 2α__.(2)余弦函数的二倍角公式有三种形式，即cos 2α＝__cos 2α－sin 2α__＝__2cos 2α－1__＝__1－2sin 2α__，由此可得变形公式sin 2α＝__1－cos2α2__，cos 2α＝__1＋cos2α2__，它的双向应用分别起到缩角升幂和扩角降幂的作用．2．半角公式 (1)sin α2＝__±1－cos α2__. (2)cos α2＝__±1＋cos α2__. (3)tan α2＝__±1－cos α1＋cos α__＝__sin α1＋cos α__＝__1－cos αsin α__.在这些公式中，根号前面的符号由α2所在象限相应的三角函数值的符号确定，如果α2所在象限无法确定，则应保留根号前面的正、负两个符号．[知识点拨]1.倍角的含义：对于“二倍角”应该有广义的理解，如2α是α的二倍角，4α是2α的二倍角，8α是4α的二倍角，α是α2的二倍角……这里的蓄含着换元思想．这就是说，“倍”是相对而言的，是描述两个数量之间的关系的．2．二倍角公式的逆用、变形用 (1)逆用形式：2sin αcos α＝sin 2α；sin αcos α＝12sin 2α；cos α＝sin2α2sin α；cos 2α－sin 2α＝2cos 2α－1＝1－2sin2α＝cos 2α；2tan α1－tan 2α＝tan 2α.(2)变形用形式：1±sin 2α＝sin 2α＋cos 2α±2sin αcos α＝(sin α±cos α)2； 1＋cos 2α＝2cos 2α； 1－cos 2α＝2sin 2α；cos 2α＝1＋cos2α2； sin 2α＝1－cos2α2.Y 预习自测u xi zi ce1．已知sin α＝35，cos α＝45，则sin 2α等于( D )A ．75B ．125C ．1225D ．2425[解析] sin 2α＝2sin αcos α＝2425. 2．(2018·全国卷Ⅲ)若sin α＝13，则cos 2α＝( C )A ．89B ．79C ．－79D ．－89[解析] cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫132＝79. 3．若tan α＝12，则tan 2α＝( A )A ．43B ．34C ．15D ．－43[解析]tan 2α＝2tanα1－tan2α＝11－14＝43.4．cos 2π8－sin2π8＝__22__.[解析]由二倍角公式，得cos 2π8－sin 2π8＝cos (2×π8)＝22.H互动探究解疑u dong tan jiu jie yi命题方向1⇨二倍角公式的正用典例1已知sin α＋cos α＝13，且0<α<π，求sin 2α，cos 2α，tan 2α的值．[思路分析]sinα＋cosα＝13→sin2α→cos2α→tan2α[解析]∵sin α＋cos α＝13∴sin 2α＋cos 2α＋2sin α·cos α＝19，∴sin 2α＝－89且sin αcos α＝－49<0.∵0<α<π，sin α>0，∴cos α<0，∴sin α－cos α>0，∴sin α－cos α＝1－sin2α＝173，∴cos 2α＝cos 2α－sin 2α＝(sin α＋cos α)(cos α－sin α)＝13×(－173)＝－179，∴tan 2α＝sin2αcos2α＝81717.『规律总结』对于给值求值问题，即由给出的某些角的三角函数值，求另外一些角的三角函数值，关键在于“变角”使“目标角”变成“已知角”，另外角的范围应根据所给条件进一步缩小，避免出现增解．〔跟踪练习1〕已知sin α＝513，α∈(π2，π)，求sin 2α、cos 2α、tan 2α的值．[解析]∵sin α＝513，α∈(π2，π)，∴cos α＝－1－sin2α＝－1－(513)2＝－1213，∴sin 2α＝2sin αcos α＝2×513×(－1213)＝－120169，cos 2α＝cos 2α－sin 2α＝(－1213)2－(513)2＝119169，tan 2α＝sin2αcos2α＝(－120169)÷119169＝－120119.命题方向2 ⇨二倍角公式的逆用典例2 求下列各三角函数式的值：(1)cos 72°cos 36°； (2)1sin50°＋3cos50°. [思路分析] 对于(1)题，72°＝2×36°，应想办法“凑”成二倍角形式；对于(2)题，须先通分，分子引入辅助角后适合两角和的正弦公式，分母恰好也适合二倍角的正弦公式，约分后即可得值．[解析] (1)原式＝cos 36°·cos 72° ＝2sin36°·cos36°·cos72°2sin36°＝12sin144°2sin36°＝14. (2)原式＝cos50°＋3sin50°sin50°·cos50°＝2sin (50°＋30°)12sin100°＝4sin80°sin100°＝4.『规律总结』 (1)“给角求值”：一般所给出的角都是非特殊角，从表面来看是很难的，但仔细观察，非特殊角与特殊角总有一定的关系．解题时，要利用观察得到的关系，结合倍角公式转化为特殊角并且消除非特殊角的三角函数而得解．(2)当公式出现2sin αcos α时，要逆用公式，然后再寻找关系解决．〔跟踪练习2〕求下列各式的值： (1)sinπ12cos π12；(2)1－2sin 2390°；(3)2tan330°1－tan 2330°； (4)1sin10°－3cos10°；(5)cos 20°cos 40°cos 80°. [思路分析] 观察角的特点→寻求角的联系→选择公式→化简求值 [解析] (1)原式＝2sin π12cos π122＝sinπ62＝14.(2)原式＝cos (2×390°)＝cos 780°＝cos (2×360°＋60°)＝cos 60°＝12.(3)原式＝tan (2×330°)＝tan 660°＝tan (720°－60°) ＝－tan 60°＝－ 3. (4)原式＝cos10°－3sin10°sin10°cos10°＝2(12cos10°－32sin10°)sin10°cos10°＝4(sin30°cos10°－cos30°sin10°)2sin10°cos10°＝4sin20°sin20°＝4. (5)原式＝2sin20°·cos20°·cos40°·cos80°2sin20°＝2sin40°·cos40°·cos80°4sin20°＝2sin80°·sin80°8sin20°＝sin160°8sin20°＝18.命题方向3 ⇨半角公式的应用典例3 已知sin α2－cos α2＝－55，450°<α<540°，求tan α2的值．[思路分析] 要求tan α2的值，结合条件，可以联立sin 2α2＋cos 2α2＝1，求得sin α2，cos α2，从而获解．但这种方法需要解方程，联想到有理形式的半角正切公式，可以有以下解法．[解析] 由题意得⎝⎛⎭⎫sin α2－cos α22＝15，即1－sin α＝15，得sin α＝45.而450°<α<540°， ∴cos α＝－35，∴tan α2＝1－cos αsin α＝1－⎝⎛⎭⎫－3545＝2.『规律总结』利用半角公式求tan α2的值时，为避免讨论，一般尽量采用半角正切公式的有理式tan α2＝sin α1＋cos α＝1－cos αsin α，利用半角公式求sin α2，cos α2的值时，要注意根号前面的符号由角α2所在象限相应的三角函数值的符号来确定．〔跟踪练习3〕已知|cos θ|＝35，且5π2<θ<3π，求sin θ2，cos θ2，tan θ2的值．[分析] 本题主要考查半角公式，先由角的范围去掉绝对值符号，再由半角公式即得． [解析] ∵|cos θ|＝35，5π2<θ<3π，∴cos θ＝－35，5π4<θ2<3π2.由cos θ＝1－2sin 2θ2，有sin θ2＝－1－cos θ2＝－1＋352＝－255. 又cos θ＝2cos 2θ2－1，有cos θ2＝－1＋cos θ2＝－55， ∴tan θ2＝sinθ2cos θ2＝2.X 学科核心素养ue ke he xin su yang二倍角公式的变形应用典例4 (1)化简：21＋sin8＋2＋2cos8；(2)设α∈(3π2，2π)，化简：12＋1212＋12cos2α. [思路分析] (1)1＋sin 8＝sin 24＋2sin 4cos 4＋cos 24＝(sin 4＋cos 4)2,2(1＋cos 8)＝4cos 24.(2)连续运用公式：1＋cos 2α＝2cos 2α. [解析] (1)原式＝21＋2sin4cos4＋4cos 24＝2|sin 4＋cos 4|＋2|cos 4|.因为4∈(π，3π2)，所以sin 4<0，cos 4<0.故原式＝－2(sin 4＋cos 4)－2cos 4＝－2sin 4－4cos 4＝－2(sin 4＋2cos 4)． (2)因为α∈(3π2，2π)，所以cos α>0，cos α2<0.故原式＝12＋12cos 2α＝12＋12cos α ＝cos 2α2＝|cos α2|＝－cos α2.『规律总结』二倍角公式的变形应用(1)公式的逆用、变形用十分重要．特别是1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α形式相似极易出错．应用时要加强“目标意识”．(2)公式变形的主要形式有1±sin 2α＝sin 2α＋cos 2α±2sin αcos α＝(sin α±cos α)2,1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α，cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2.〔跟踪练习4〕化简cos 2(θ＋15°)＋sin 2(θ－15°)＋sin (θ＋180°)·cos (θ－180°)．[解析] 原式＝1＋cos (2θ＋30°)2＋1－cos (2θ－30°)2＋12sin 2θ＝1＋12[cos (2θ＋30°)－cos (2θ－30°)]＋12sin 2θ＝1＋12(cos 2θcos 30°－sin 2θsin 30°－cos 2θcos 30°－sin 2θsin 30°)＋12sin 2θ＝1＋(－sin 2θsin 30°)＋12sin 2θ＝1.Y 易混易错警示i hun yi cuo jing shi典例5 已知θ是第二象限角，化简1＋sin θ＋1－sin θ.[错解] 原式＝1＋2sin θ2cos θ2＋1－2sin θ2cos θ2＝(sin θ2＋cos θ2)2＋(sin θ2－cos θ2)2＝sin θ2＋cos θ2＋sin θ2－cos θ2＝2sin θ2. [错因分析] 在去根号时，对sin θ2±cos θ2的符号未加以讨论，导致化简错误．[正解] 原式＝1＋2sin θ2cos θ2＋1－2sin θ2cos θ2＝(sin θ2＋cos θ2)2＋(sin θ2－cos θ2)2＝|sin θ2＋cos θ2|＋|sin θ2－cos θ2|.因为θ是第二象限角，即2k π＋π2<θ<2k π＋π，k ∈Z ，所以k π＋π4<θ2<k π＋π2，k ∈Z ，所以原式＝⎩⎨⎧2sin θ2(2k π＋π4<θ2<2k π＋π2，k ∈Z )，－2sin θ2(2k π＋5π4<θ2<2k π＋3π2，k ∈Z ).『规律总结』盲目地运用公式化简函数的解析式，而忽略定义域，是解决与三角函数有关问题的易错点，要想正确求解，需要掌握倍角、分角的终边所在象限的确定方法，这在第一章中已经详细介绍，此处不再赘述．〔跟踪练习5〕若 (1－cos θ1＋cos θ－1＋cos θ1－cos θ)sin θ2cosθ2(sin θ2－cos θ2)(sin θ2＋cos θ2)＝1，则θ的取值范围是__(2k π，2k π＋π2)∪(2k π＋π2，2k π＋π)，k ∈Z .__[解析] 化简，原式左边＝((1－cos θ)21－cos 2θ－(1＋cos θ)21－cos 2θ)12sin θ－cos θ＝(1－cos θ|sin θ|－1＋cos θ|sin θ|)sin θ－2cos θ＝－2cos θ|sin θ|·sin θ－2cos θ＝sin θ|sin θ|. 由题意知sin θ>0且cos θ≠0，解得θ的取值范围是(2k π，2k π＋π2)∪(2k π＋π2，2k π＋π)，k∈Z .K 课堂达标验收e tan g da biao yan shou1．cos 2π8－12的值为( D )A ．1B ．12C ．22D ．24[解析] 原式＝1＋cosπ42－12＝12＋24－12＝24.2．(cos π12－sin π12)(cos π12＋sin π12)＝( D ) A ．－32B ．－12C ．12D ．32[解析] 原式＝cos 2π12－sin 2π12＝cos π6＝32.3．(2018·全国卷Ⅲ)函数f ()x ＝tan x1＋tan 2x的最小正周期为( C )A ．π4B ．π2C ．πD ．2π[解析] f (x )＝sin x cos x 1＋sin 2x cos 2x ＝sin x cos x cos 2x ＋sin 2x＝sin x cos x ＝12sin 2x ，所以f (x )的最小正周期为T ＝2π2＝π.4．已知tan (π4＋α)＝2，则tan 2α＝__34__.[解析] ∵tan (π4＋α)＝1＋tan α1－tan α＝2，∴tan α＝13.∴tan 2α＝2tan α1－tan 2α＝34.5．利用倍角公式求下列各式的值． (1)2sinπ12cos π12；(2)1－2sin 2750°； (3)2tan150°1－tan 2150°；(4)cos π12cos 5π12； (5)1sin10°－3cos10°. [解析] (1)原式＝sin ⎝⎛⎭⎫2×π12＝sin π6＝12. (2)原式＝cos (2×750°)＝cos 1500°＝cos (60°＋4×360°)＝cos 60°＝12.(3)原式＝tan (2×150°)＝tan 300°＝tan (360°－60°)＝－tan 60°＝－ 3. (4)原式＝cosπ12cos ⎝⎛⎭⎫π2－π12＝cos π12sin π12＝12·⎝⎛⎭⎫2sin π12cos π12＝12sin π6＝12×12＝14. (5)原式＝cos10°－3sin10°sin10°cos10°＝2⎝⎛⎭⎫12cos10°－32sin10°sin10°cos10°＝4(sin30°cos10°－cos30°sin10°)2sin10°cos10°＝4sin (30°－10°)sin (2×10°)＝4sin20°sin20°＝4.。

高中(北师大版)数学必修4(45分钟课时作业与单元测试卷)：26二倍角的三角函数1含解析

9. 的值是__________．
答案：
解析：原式＝＝＝＝ .
三、解答题：(共35分，11＋12＋12)
10．已知sin －2cos ＝0.
(1)求tanx的值；
(2)求的值．
解析：(1)由sin －2cos ＝0，⇒tan ＝2，
∴tanx＝＝＝－ .
(2)原式＝＝，由(1)知cosx－sinx≠0，
26二倍角的三角函数1
时间：45分钟满分：80分
班级________姓名________分数________
一、选择题：(每小题5分，共5×6＝30分)
1．计算1－2sin222.5°的结果等于()
A. B.
C. D.
答案：B
解析：1－2sin222.5°＝cos45°＝ .
2．设sin ＝，则sin2θ＝()
A．30°或270°B．45°
C．60°D．30°
答案：D
解析：因为cos2α＝1－2sin2α，故由题意，知2sin2α＋sinα－1＝0，即(sinα＋1)(2sinα－1)＝0.因为α为锐角，所以sinα＝，所以α＝30°.故选D.
6．锐角三角形的内角A、B满足tanA－＝tanB，则有()
二、填空题：(每小题5分，共5×3＝15分)
7．sin22.5°cos202.5°＝________.
答案：－
解析：sin22.5°cos202.5°＝sin22.5°·(－cos22.5°)＝－ sin45°＝－ .
8．cos cos π的值是__________．
答案：
解析：原式＝ ·2sin cos cos ＝ ·2sin cos2x＋2sinx的最小值和最大值分别为()

高中数学必修四北师大版二倍角的三角函数(一) 课时提升作业含答案

关闭Word文档返回原板块。

课时提升作业二十六二倍角的三角函数(一)一、选择题(每小题5分，共25分)1.sin15°sin105°=( )A. B.- C. D.-【解析】选A.sin15°sin105°=³2sin15°sin(90°+15°)=³2sin15°cos15°=sin30°=.2.(2016²全国卷Ⅲ)若tanθ=-，则cos2θ=( )A.-B.-C.D.【解题指南】选择合适的运算公式，尽量避免讨论.【解析】选D.因为cos2θ=cos2θ-sin2θ==，又tanθ=-，所以代入上式可得cos2θ=.3.已知sin2α=，则cos2=( )A. B. C. D.【解析】选B.因为sin2α=，所以cos2====.4.(2016²阜阳高一检测)已知cos=，且sinθ<0，则tanθ的值为( )A.-B.±C.-D.【解析】选C.已知cos=，且sinθ<0，所以cosθ=2cos2-1=2×-1=，故sinθ=-=-，所以tanθ==-.5.(2016²景德镇高一检测)若tanθ+=4，则sin2θ=( )A. B. C. D.【解析】选D.因为tanθ+=4，所以+=4.所以=4，即=4.所以sin2θ=.二、填空题(每小题5分，共15分)6.已知<α<π，3sin2α=2cosα，则cos(α-π)=________. 【解析】因为<α<π，3sin2α=2cosα，所以sinα=，cosα=-.所以cos(α-π)=-cosα=-=.答案：7.cos=，那么sin2x=________.【解析】因为cos=，所以sin2x=cos=cos=2cos2-1=2×-1=-.答案：-8.已知AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=4DB，设∠COD=θ，则cos2θ=________.【解题指南】利用圆的性质求出cosθ，再用二倍角公式求cos2θ. 【解析】如图，因为AD=4DB，所以OC+OD=4(OC-OD)，即3OC=5OD，所以cos2θ=2cos2θ-1=2×-1=2×-1=-.答案：-三、解答题(每小题10分，共20分)。

数学北师大版必修4知识导航：3.3二倍角的三角函数含

§2 二倍角的三角函数知识梳理1.倍角公式（1）公式：sin2α=2sinαcosα；（S 2α）cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;（C 2α） tan2α=αα2tan 1tan 2-.（T 2α）（2）公式的理解①成立的条件：在公式S 2α、C 2α中，角α可以为任意角，T 2α则只有当α≠kπ+2π及α≠2πk +4π（k ∈Z ）时才成立.②倍角公式不仅限于2α是α的二倍形式，其他如4α是2α的二倍、2α是4α的二倍、3α是23α的二倍等等都是适用的.要熟悉多种形式的两个角的倍数关系，才能熟练地应用好二倍角公式，这是灵活运用公式的关键. ③cos2α的变形：cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α， cos 2α=22cos 1α+，sin 2α=22cos 1α-；（这两个公式称为降幂公式） 1+cos2α=2cos 2α，1-cos2α=2sin 2α.（这两个公式称为升幂公式）2.半角公式（1）公式：sin2α=±2cos 1α-；cos 2α=±2cos 1α+； tan2α=±ααααααcos 1sin sin cos 1cos 1cos 1+=-=+-. （2）公式的理解关于半角正切公式：tan2α=ααsin cos 1-不带有根号，而且分母为单项式，运用起来特别方便，但要注意它与以下两个公式：tan2α=±ααcos 1cos 1+-和tan 2α=ααcos 1sin +的使用范围不完全相同，后两个公式只要α≠(2k+1)π（k ∈Z ），而第一个公式除α≠(2k+1)π（k ∈Z ）之外，还必须有α≠2kπ（k ∈Z ）.当然，这三个公式可以互化，在使用时要根据题目中式子的特征灵活选用.知识导学①要学好本节，有必要复习两角和的正弦、余弦、正切公式；②学好本节的小窍门：在公式的选择运用上，审题是关键，找准题目的突破口，选择适当的方法，定能事半功倍；③选择二倍角余弦公式形式的策略：1加余弦想余弦；1减余弦想正弦；幂升一次角减半；幂降一次角翻番. 解释如下：难疑突破1.求半角的正切值常用什么方法？剖析：难点是半角的正切值公式有三种形式，到底选择哪个来处理问题，突破的路径是靠平时经验的积累.根据经验有，处理半角的正切问题有三条途径：第一种方法是用tan2α=±ααcos 1cos 1+-来处理；第二种方法是用tan2α=ααsin cos 1-来处理；第三种方法是用tan 2α=ααcos 1sin +来处理.例如：已知cosα=33，α为第四象限的角，求tan 2α的值.解法一：（用tan2α=±ααcos 1cos 1+-来处理）∵α为第四象限的角，∴2α是第二或第四象限的角. ∴tan2α<0. ∴tan 2α=ααcos 1cos 1+-=32331331--=+-- =262)26(21348212-=--=--. 解法二：（用tan2α=ααsin cos 1-来处理）∵α为第四象限的角，∴sinα<0. ∴sinα=36311cos12-=--=--α. ∴tan 2α=ααsin cos 1-=26236331-=--. 解法三：（用tan2α=ααcos 1sin +） ∵α为第四象限的角，∴sinα<0. ∴sinα=36311cos12-=--=--α. ∴tan 2α=ααcos 1sin +=26233633136-=--=--. 比较上述三种解法可知：在求半角的正切tan2α时，用tan 2α=±ααcos 1cos 1+-来处理，要由α所在的象限确定2α所在的象限，再用三角函数值的符号取舍根号前的双重符号；而用tan 2α=ααsin cos 1-或tan 2α=ααsin cos 1+来处理，可以避免这些问题.尤其是tan 2α=ααsin cos 1+，分母是单项式，容易计算.因此常用tan 2α=ααsin cos 1+求半角的正切值.2.为什么说1+sinα和1-sinα是完全平方的形式？剖析：疑点是对此结论总是产生质疑.其突破的方法是学会推导.要明确这个问题，先从完全平方公式来分析.(a+b)2=a 2+2ab+b 2；(a-b)2=a 2-2ab+b 2，由此看一个式子是完全平方的形式，必须有a 2+2ab+b 2或a 2-2ab+b 2的形式特点.1±sinα要具备这种形式特点，需要进行恒等变形.观察到完全平方的式子中有a 2和b 2，联想1±sinα中的1能变形为平方和的形式，即变形的方向是1=a 2＋b 2，sinα=2ab.由同角三角函数基本关系式和二倍角的正弦公式得1±sinα=sin 22α+cos 22α±2sin 2αcos 2α=(sin 2α±cos 2α)2.这个结论应用很广泛.。

2020-2021学年北师大版高中数学必修4《二倍角的三角函数》精品课时练习及解析

（新课标）最新北师大版高中数学必修四§3 二倍角的三角函数(一)课时目标1．会从两角和的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式．2．能熟练运用二倍角的公式进行简单的恒等变换，并能灵活地将公式变形运用．1．倍角公式(1)S 2α：sin 2α＝2sin αcos α，sinα2cos α2＝12sin α； (2)C 2α：cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α；(3)T 2α：tan 2α＝2tan α1－tan 2α． 2．倍角公式常用变形 (1)sin 2α2sin α＝__________，sin 2α2cos α＝__________； (2)(sin α±cos α)2＝______________； (3)sin 2α＝__________________，cos 2α＝________________________________________________________________________．一、选择题1．计算1－2sin 222．5°的结果等于( )A ．12B ．22C ．33D ．322．函数y ＝2cos 2(x －π4)－1是( )A ．最小正周期为π的奇函数B ．最小正周期为π2的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π2的偶函数3．若sin(π6－α)＝13，则cos(2π3＋2α)的值为( )A ．－13B ．－79C ．13D ．794．若1－tan θ2＋tan θ＝1，则cos 2θ1＋sin 2θ的值为( )A ．3B ．－3C ．－2D ．－125．如果|cos θ|＝15，5π2<θ<3π，则sin θ2的值是( )A ．－105B ．105C ．－155D ．1556．已知角α在第一象限且cos α＝35，则1＋2cos (2α－π4)sin (α＋π2)等于( )A ．25B ．75C ．145D ．－25二、填空题7．3－sin 70°2－cos 210°的值是________． 8．函数f(x)＝cos x －sin 2x －cos 2x ＋74的最大值是______．9．已知tanθ2＝3，则1－cos θ＋sin θ1＋cos θ＋sin θ＝______． 10．已知sin 22α＋sin 2αcos α－cos 2α＝1，α∈(0，π2)，则α＝________．三、解答题11．求证：3－4cos 2A ＋cos 4A 3＋4cos 2A ＋cos 4A ＝tan 4A ．12．若cos ⎝ ⎛⎭⎪⎫π4－x ＝－45，5π4<x<7π4，求sin 2x －2sin 2x1＋tan x 的值．能力提升13．求值：cos 20°cos 40°cos 80°．14．求值：tan 70°·cos 10°·(3tan 20°－1)．1．对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍；α3是α6的二倍；α2n ＝2·α2n ＋1 (n ∈N *)．2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛，二倍角的常用形式： ①1＋cos 2α＝2cos 2α，②cos 2α＝1＋cos 2α2，③1－cos 2α＝2sin 2α，④sin 2α＝1－cos 2α2．§3 二倍角的三角函数(一) 答案知识梳理2．(1)cos α sin α (2)1±sin 2α (3)1－cos 2α2 1＋cos 2α2作业设计1．B 2．A3．B [cos(2π3＋2α)＝－cos(π3－2α)＝－cos[2(π6－α)]＝－[1－2sin 2(π6－α)]＝2sin 2(π6－α)－1＝－79．]4．A [∵1－tan θ2＋tan θ＝1，∴tan θ＝－12．∴cos 2θ1＋sin 2θ＝cos 2θ－sin 2θ(sin θ＋cos θ)2＝cos θ－sin θcos θ＋sin θ＝1－tan θ1＋tan θ＝1－⎝ ⎛⎭⎪⎫－121＋⎝ ⎛⎭⎪⎫－12＝3．] 5．C [∵5π2<θ<3π，|cos θ|＝15，∴cos θ<0，cos θ＝－15．∵5π4<θ2<32π，∴sin θ2<0．由sin2θ2＝1－cos θ2＝35， ∴sinθ2＝－155．] 6．C [∵cos α＝35且α在第一象限，∴sin α＝45．∴cos 2α＝cos 2α－sin 2α＝－725，sin 2α＝2sin αcos α＝2425，原式＝1＋2(cos 2αcos π4＋sin 2αsin π4)cos α＝1＋cos 2α＋sin 2αcos α＝145．]7．2 解析3－sin 70°2－cos 210°＝3－sin 70°2－1＋cos 20°2＝2(3－cos 20°)3－cos 20°＝2．8．2解析 f(x)＝cos x －(1－cos 2x)－(2cos 2x －1)＋74＝－cos 2x ＋cos x ＋74＝－⎝ ⎛⎭⎪⎫cos x －122＋2．∴当cos x ＝12时，f(x)max ＝2．9．3解析 1－cos θ＋sin θ1＋cos θ＋sin θ＝2sin2θ2＋2sin θ2cos θ22cos 2θ2＋2sin θ2cosθ2＝2sin θ2⎝⎛⎭⎪⎫sin θ2＋cos θ22cos θ2⎝⎛⎭⎪⎫cos θ2＋sin θ2＝tanθ2＝3． 10．π6解析 ∵sin 22α＋sin 2αcos α－(cos 2α＋1)＝0．∴4sin 2αcos 2α＋2sin αcos 2α－2cos 2α＝0．∵α∈(0，π2)．∴2cos 2α>0．∴2sin 2α＋sin α－1＝0．∴sin α＝12(sin α＝－1舍)．∴α＝π6．11．证明 ∵左边＝3－4cos 2A ＋2cos 22A －13＋4cos 2A ＋2cos 22A －1＝⎝ ⎛⎭⎪⎫1－cos 2A 1＋cos 2A 2＝⎝ ⎛⎭⎪⎫2sin 2A 2cos 2A 2＝(tan 2A)2 ＝tan 4A ＝右边．∴3－4cos 2A ＋cos 4A 3＋4cos 2A ＋cos 4A＝tan 4A ． 12．解 sin 2x －2sin 2x 1＋tan x ＝2sin x (cos x －sin x )cos xcos x ＋sin x＝sin 2x (cos x －sin x )cos x ＋sin x＝sin 2x 1－tan x 1＋tan x ＝sin 2xtan ⎝ ⎛⎭⎪⎫π4－x＝cos ⎝ ⎛⎭⎪⎫π2－2x tan ⎝ ⎛⎭⎪⎫π4－x ＝⎣⎢⎡⎦⎥⎤2cos 2⎝ ⎛⎭⎪⎫π4－x －1tan ⎝ ⎛⎭⎪⎫π4－x ，∵5π4<x<7π4， ∴－3π2<π4－x<－π．又∵cos ⎝ ⎛⎭⎪⎫π4－x ＝－45，∴sin ⎝ ⎛⎭⎪⎫π4－x ＝35，tan ⎝ ⎛⎭⎪⎫π4－x ＝－34．∴原式＝⎝ ⎛⎭⎪⎫2×1625－1×⎝ ⎛⎭⎪⎫－34＝－21100．13．解原式＝2sin 20°·cos 20°·cos 40°·cos 80°2sin 20°＝2sin 40°·cos 40°·cos 80°4sin 20°＝2sin 80°·cos 80°8sin 20°＝sin 160°8sin 20°＝18．14．解原式＝sin 70°cos 70°·cos 10°⎝ ⎛⎭⎪⎫3sin 20°cos 20°－1 ＝sin 70°cos 70°·cos 10°·⎝ ⎛⎭⎪⎫3sin 20°－cos 20°cos 20°＝cos 20°sin 20°·cos 10°·2⎝ ⎛⎭⎪⎫32sin 20°－12cos 20°cos 20°＝2cos 10°·sin (－10°)sin 20°＝－sin 20°sin 20°＝－1．。

2022-2021学年高一数学北师大版必修4学案：3.3 二倍角的三角函数(一) Word版含答案

明目标、知重点 1.会从两角和的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式.2.能娴熟运用二倍角的公式进行简洁的恒等变形，并能机敏地将公式变形运用．1．倍角公式(1)S 2α：sin 2α＝2sin_αcos_α，sin α2cos α2＝12sin α；(2)C 2α：cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； (3)T 2α：tan 2α＝2tan α1－tan 2α.2．倍角公式常用变形(1)sin 2α2sin α＝cos_α，sin 2α2cos α＝sin_α； (2)(sin α±cos α)2＝1±sin_2α； (3)sin 2α＝1－cos 2α2，cos 2α＝1＋cos 2α2.[情境导学] 利用我们已经学习的公式，能否将2sin 20°cos 20°进一步化简呢？明显，利用我们已经学习的两角和与差的正弦、余弦、正切公式已不能对2sin 20°cos 20°做进一步的化简，这就使得我们有必要进一步扩展三角函数公式的“阵营”，以便于我们解决类似的问题．探究点一二倍角公式的推导思考1 二倍角的正弦、余弦、正切公式就是用α的三角函数表示2α的三角函数的公式．依据前面学过的两角和与差的正弦、余弦、正切公式．你能推导出二倍角的正弦、余弦、正切公式吗？试一试？答 sin 2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α； cos 2α＝cos(α＋α)＝cos αcos α－sin αsin α ＝cos 2α－sin 2α；tan 2α＝tan(α＋α)＝2tan α1－tan 2α.思考2 依据同角三角函数的基本关系式sin 2α＋cos 2α＝1，你能否只用sin α或cos α表示cos 2α？答 ∵cos 2α＝cos 2α－sin 2α＝cos 2α－(1－cos 2α) ＝2cos 2α－1；或cos 2α＝cos 2α－sin 2α＝(1－sin 2α)－sin 2α＝1－2sin 2α.探究点二余弦的二倍角公式的变形及应用思考余弦的二倍角公式是否有其他变形？答二倍角的余弦公式cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α变形较多，应用机敏．其中sin 2α＝1－cos 2α2，cos 2α＝1＋cos 2α2称作降幂公式，1－cos α2＝sin 2α2，1＋cos α2＝cos 2α2称作升幂公式．这些公式在统一角或函数名时格外有用．练习1：函数f (x )＝3sin x cos x ＋cos 2x －12的最小正周期是________．答案 π 解析 ∵f (x )＝32sin 2x ＋12(2cos 2x －1) ＝32sin 2x ＋12cos 2x ＝sin ⎝⎛⎭⎫2x ＋π6， ∴T ＝2π2＝π.练习2：函数f (x )＝cos 2x ＋4sin x 的值域是________．答案 [－5,3]解析 f (x )＝cos 2x ＋4sin x ＝1－2sin 2x ＋4sin x ＝－2sin 2x ＋4sin x ＋1＝－2(sin x －1)2＋3.当sin x ＝1时，f (x )max ＝3；当sin x ＝－1时，f (x )min ＝－5.例1 已知sin 2α＝513，π4<α<π2，求sin 4α，cos 4α，tan 4α的值．解由π4<α<π2，得π2<2α<π.又由于sin 2α＝513，cos 2α＝－1－sin 22α＝－1－⎝⎛⎭⎫5132＝－1213. 于是sin 4α＝2sin 2αcos 2α＝2×513×⎝⎛⎭⎫－1213＝－120169； cos 4α＝1－2sin 22α＝1－2×⎝⎛⎭⎫5132＝119169； tan 4α＝sin 4αcos 4α＝－120169119169＝－120119.反思与感悟解答此类题目一方面要留意角的倍数关系；另一方面要留意函数名称的转化方法，利用同角三角函数关系及诱导公式解决问题是常用方法．跟踪训练1 求下列各式的值． (1)sin π8sin 3π8；(2)cos 215°－cos 275°；(3)2cos 25π12－1；(4)tan 30°1－tan 230°. 解 (1)∵sin 3π8＝sin(π2－π8)＝cos π8，∴sin π8sin 3π8＝sin π8cos π8＝12·2sin π8cos π8＝12sin π4＝24. (2)∵cos 275°＝cos 2(90°－15°)＝sin 215°， ∴cos 215°－cos 275°＝cos 215°－sin 215° ＝cos 30°＝32.(3)2cos 25π12－1＝cos 5π6＝－32. (4)tan 30°1－tan 230°＝12×2tan 30°1－tan 230° ＝12tan 60°＝32. 例2 求证：3－4cos 2A ＋cos 4A 3＋4cos 2A ＋cos 4A ＝tan 4A .证明 ∵左边＝3－4cos 2A ＋2cos 22A －13＋4cos 2A ＋2cos 22A －1＝⎝ ⎛⎭⎪⎫1－cos 2A 1＋cos 2A 2＝⎝⎛⎭⎫2sin 2A 2cos 2A 2＝(tan 2A )2＝tan 4A ＝右边， ∴3－4cos 2A ＋cos 4A3＋4cos 2A ＋cos 4A＝tan 4A .反思与感悟利用倍角公式证明三角恒等式，关键是找到左、右两边式子中角间的倍角关系，先用倍角公式统一角，再用同角三角函数基本关系式等完成证明．跟踪训练2 化简：1＋sin 2θ－cos 2θ1＋sin 2θ＋cos 2θ.解方法一原式＝(1－cos 2θ)＋sin 2θ(1＋cos 2θ)＋sin 2θ＝2sin 2θ＋2sin θcos θ2cos 2θ＋2sin θcos θ＝2sin θ(sin θ＋cos θ)2cos θ(cos θ＋sin θ)＝tan θ.方法二原式＝(sin θ＋cos θ)2－(cos 2θ－sin 2θ)(sin θ＋cos θ)2＋(cos 2θ－sin 2θ)＝(sin θ＋cos θ)[(sin θ＋cos θ)－(cos θ－sin θ)](sin θ＋cos θ)[(sin θ＋cos θ)＋(cos θ－sin θ)]＝2sin θ2cos θ＝tan θ. 例3 在△ABC 中，cos A ＝45，tan B ＝2，求tan(2A ＋2B )的值．解方法一在△ABC 中，由cos A ＝45，0<A <π，得sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫452＝35.所以tan A ＝sin A cos A ＝35×54＝34，tan 2A ＝2tan A 1－tan 2A ＝2×341－⎝⎛⎭⎫342＝247，又tan B ＝2，所以tan 2B ＝2tan B 1－tan 2B ＝2×21－22＝－43.于是tan(2A ＋2B )＝tan 2A ＋tan 2B1－tan 2A tan 2B＝247－431－247×⎝⎛⎭⎫－43＝44117.方法二在△ABC 中，由cos A ＝45，0<A <π，得sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫452＝35.所以tan A ＝sin A cos A ＝35×54＝34.又tan B ＝2，所以tan(A ＋B )＝tan A ＋tan B1－tan A tan B＝34＋21－34×2＝－112.于是tan(2A ＋2B )＝tan [2(A ＋B )]＝2tan (A ＋B )1－tan 2(A ＋B )＝2×⎝⎛⎭⎫－1121－⎝⎛⎭⎫－1122 ＝44117. 反思与感悟解题时首先要分析已知条件和结论中各种角之间的相互关系，并依据这种关系来选择公式，“凑角法”是解决此类三角问题的常用技巧．跟踪训练3 已知sin ⎝⎛⎭⎫π4－x ＝513，0<x <π4，求cos 2xcos ⎝⎛⎭⎫π4＋x 的值．解原式＝sin ⎝⎛⎭⎫π2＋2x cos ⎝⎛⎭⎫π4＋x＝2sin ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x . ∵sin ⎝⎛⎭⎫π4－x ＝cos ⎝⎛⎭⎫π4＋x ＝513，且0<x <π4，∴π4＋x ∈⎝⎛⎭⎫π4，π2， ∴sin ⎝⎛⎭⎫π4＋x ＝1－cos 2⎝⎛⎭⎫π4＋x ＝1213，∴原式＝2×1213＝2413.1．cos 275°＋cos 215°＋cos 75°cos 15°的值等于( ) A.62B.32C.54 D ．1＋34答案 C解析原式＝sin 215°＋cos 215°＋12sin 30°＝1＋14＝54.2．sin 4π12－cos 4π12等于( ) A ．－12B ．－32C.12D.32答案 B解析原式＝⎝⎛⎭⎫sin 2π12＋cos 2π12·⎝⎛⎭⎫sin 2π12－cos 2π12 ＝－⎝⎛⎭⎫cos 2π12－sin 2π12 ＝－cos π6＝－32.3.tan 7.5°1－tan 27.5°＝________.答案 1－32解析原式＝12·2tan 7.5°1－tan 27.5°＝12·tan 15°＝12tan(60°－45°)＝12×3－11＋3＝1－32. 4．设sin 2α＝－sin α，α∈⎝⎛⎭⎫π2，π，则tan 2α的值是________．答案3解析 ∵sin 2α＝－sin α，∴sin α(2cos α＋1)＝0，又α∈⎝⎛⎭⎫π2，π，∴sin α≠0,2cos α＋1＝0 即cos α＝－12，sin α＝32，tan α＝－3，∴tan 2α＝2tan α1－tan 2α＝－231－(－3)2＝ 3.[呈重点、现规律]1．对“二倍角”应当有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍；α3是α6的二倍；α2n ＝2·α2n ＋1(n ∈N＋)．2．二倍角的余弦公式的运用在二倍角公式中，二倍角的余弦公式最为机敏多样，应用广泛．二倍角的常用形式：①1＋cos 2α＝2cos 2α，②cos 2α＝1＋cos 2α2，③1－cos 2α＝2sin 2α，④sin 2α＝1－cos 2α2.一、基础过关1．若sin α2＝33，则cos α等于( )A ．－23B ．－13C.13D.23答案 C解析 cos α＝1－2sin 2α2＝1－2×⎝⎛⎭⎫332＝13.2．已知sin α＋cos α＝13，则sin 2α等于( )A.12 B ．－12C.89 D ．－89答案 D解析 ∵sin α＋cos α＝13，∴1＋2sin αcos α＝19，∴sin 2α＝－89.3．若sin(π6－α)＝13，则cos(2π3＋2α)的值为( )A ．－13B ．－79C.13D.79 答案 B解析 cos(2π3＋2α)＝－cos(π3－2α)＝－cos[2(π6－α)]＝－[1－2sin 2(π6－α)]＝2sin 2(π6－α)－1＝－79.4．若1－tan θ2＋tan θ＝1，则cos 2θ1＋sin 2θ的值为( )A ．3B ．－3C ．－2D ．－12答案 A解析 ∵1－tan θ2＋tan θ＝1，∴tan θ＝－12.∴cos 2θ1＋sin 2θ＝cos 2θ－sin 2θ(sin θ＋cos θ)2＝cos θ－sin θcos θ＋sin θ＝1－tan θ1＋tan θ＝1－⎝⎛⎭⎫－121＋⎝⎛⎭⎫－12＝3.5．已知等腰三角形底角的正弦值为53，则顶角的正弦值是( )A.459B.259C ．－459D ．－259答案 A解析设底角为θ，则θ∈⎝⎛⎭⎫0，π2，顶角为180°－2θ. ∵sin θ＝53，∴cos θ＝1－sin 2θ＝23.∴sin(180°－2θ)＝sin 2θ＝2sin θcos θ ＝2×53×23＝459. 6．2sin 222.5°－1＝________. 答案－22解析原式＝－cos 45°＝－22. 7．已知α∈⎝⎛⎭⎫π2，π，sin α＝55. (1)求sin ⎝⎛⎭⎫π4＋α的值； (2)求cos ⎝⎛⎭⎫5π6－2α的值．解 (1)由于α∈⎝⎛⎭⎫π2，π，sin α＝55，所以cos α＝－1－sin 2α＝－255.故sin ⎝⎛⎭⎫π4＋α＝sin π4cos α＋cos π4sin α ＝22×⎝⎛⎭⎫－255＋22×55＝－1010. (2)由(1)知sin 2α＝2sin αcos α ＝2×55×⎝⎛⎭⎫－255＝－45， cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫552＝35，所以cos ⎝⎛⎭⎫5π6－2α＝cos 5π6cos 2α＋sin 5π6sin 2α ＝⎝⎛⎭⎫－32×35＋12×⎝⎛⎭⎫－45＝－4＋3310. 二、力气提升8．4cos 50°－tan 40°等于( ) A. 2 B.2＋32C. 3 D ．22－1答案 C解析 4cos 50°－tan 40°＝4sin 40°cos 40°－sin 40°cos 40°＝2sin 80°－sin 40°cos 40°＝2sin (50°＋30°)－sin 40°cos 40°＝3sin 50°＋cos 50°－sin 40°cos 40°＝3sin 50°cos 40°＝ 3.9．函数y ＝sin 2x ＋23sin 2x 的最小正周期T 为________．答案 π解析 ∵y ＝sin 2x ＋3(1－cos 2x ) ＝2sin ⎝⎛⎭⎫2x －π3＋3，∴T ＝π. 10．已知tan θ2＝3，则1－cos θ＋sin θ1＋cos θ＋sin θ＝______.答案 3解析 1－cos θ＋sin θ1＋cos θ＋sin θ＝2sin 2θ2＋2sin θ2cos θ22cos 2θ2＋2sin θ2cos θ2＝2sin θ2⎝⎛⎭⎫sin θ2＋cos θ22cos θ2⎝⎛⎭⎫cos θ2＋sin θ2＝tan θ2＝3.11．(1)已知π<α<32π，化简1＋sin α1＋cos α－1－cos α＋1－sin α1＋cos α＋1－cos α；(2)化简：sin 50°(1＋3tan 10°)．解 (1)∵π<α<32π，∴π2<α2<34π，∴1＋cos α＝2|cos α2|＝－2cos α2，1－cos α＝2|sin α2|＝2sin α2.∴1＋sin α1＋cos α－1－cos α＋1－sin α1＋cos α＋1－cos α＝1＋sin α－2(cos α2＋sin α2)＋1－sin α2(sin α2－cos α2)＝(cos α2＋sin α2)2－2(cos α2＋sin α2)＋(sin α2－cos α2)22(sin α2－cos α2)＝－2cos α2.(2)原式＝sin 50°cos 10°＋3sin 10°cos 10°＝2sin 50°sin (10°＋30°)cos 10°＝2sin 50°sin 40°cos 10°＝2sin 40°cos 40°cos 10°＝sin 80°cos 10°＝1.12．求值：(1)sin 6°sin 42°sin 66°sin 78°； (2)sin 50°(1＋3tan 10°)－cos 20°cos 80°1－cos 20°.解 (1)原式＝sin 6°cos 48°cos 24°cos 12° ＝sin 6°cos 6°cos 12°cos 24°cos 48°cos 6°＝sin 96°16cos 6°＝cos 6°16cos 6°＝116.(2)∵sin 50°(1＋3tan 10°) ＝sin 50°·cos 10°＋3sin 10°cos 10°＝sin 50°·2sin 40°cos 10°＝1，cos 80°1－cos 20°＝sin 10°2sin 210°＝2sin 210°，∴sin 50°(1＋3tan 10°)－cos 20°cos 80°1－cos 20°＝1－cos 20°2sin 210°＝ 2.三、探究与拓展13．已知向量a ＝⎝⎛⎭⎫cos x ，－12，b ＝(3sin x ，cos 2x )，x ∈R ，设函数f (x )＝a ·b . (1)求f (x )的最小正周期；(2)求f (x )在⎣⎡⎦⎤0，π2上的最大值和最小值．解 (1)∵f (x )＝a ·b ＝3sin x cos x －12cos 2x＝32sin 2x －12cos 2x ＝sin ⎝⎛⎭⎫2x －π6. ∴f (x )的最小正周期为T ＝2π2＝π.(2)∵x ∈⎣⎡⎦⎤0，π2， ∴2x －π6∈⎣⎡⎦⎤－π6，5π6， ∴sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－12，1，故当2x －π6＝π2即x ＝π3时，f (x )max ＝1；当2x －π6＝－π6即x ＝0时，f (x )min ＝－12.。

高中数学北师大版必修4学案3.3 二倍角的三角函数 Word版含解析

§二倍角的三角函数
．掌握倍角公式与半角公式及公式的推导方法．(重点)
．能利用倍角公式与半角公式进行三角函数的求值、化简、证明．(重点) ．能利用倍角公式与半角公式解决一些简单的实际问题．(难点)
[基础·初探]
教材整理二倍角公式与半角公式
阅读教材～练习以上部分，完成下列问题．
．二倍角公式
．半角公式
()＝±α))；
()＝±α))；
()＝±α＋α))＝α＋α)＝α α).
判断(正确的打“√”，错误的打“×”)
()对任意α∈，总有α＝α.( )
()对任意α∈，总有α＝－α.( )
()对任意α∈，总有α＝α－α).( )
() °′ °′＝.( )
【解析】() α＝αα，所以()错．
() α＝α－，所以()错．
()α≠＋(∈)时，有α＝α－α)，所以()错．
() °′ °′＝× °′ °′＝°＝，所以()对．
【答案】()×()×()×()√
[质疑·手记]
预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问：
解惑：
疑问：
解惑：
疑问：
解惑：
[小组合作型]
已知α＝，α为第四象限的角，求的值．
【精彩点拨】根据条件求出α，然后求出α，利用半角公式求. 【自主解答】∵α为第四象限的角，α＝，
∴α＝－＝－.
∴α＝α α)＝－.
∵α为第四象限角，
∴是第二或第四象限的角，
∴<.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2tanθ ＝tan2θ 1－tan2θ 2cos2α－1 π 2sin －α 4 π · cos2 －α π 4 cos －α 4
(2)原式＝
2cos2α－1 ＝ π π 2sin －αcos －α 4 4 ＝ cos2α cos2α ＝ π cos2α sin －2α 2
1 ∴sinα＋cosα≠0，cosα＝－， 4 ∴原式＝ 2 ＝－ 2. 4cosα
|能力提升|(20 分钟，40 分) π 2 11．已知 sin2α＝，则 cos2α＋4＝( 3
)
A. C.
1 6 1 2
B. D.
1 3 2 3
2 π 1－ 1＋cos2α＋2 3 1 π 2 1－sin2α 解析：∵sin2α＝，∴cos2α＋4＝＝＝＝ . 3 2 2 2 6 答案：A π 12．若 0<θ< ，则化简 1＋sinθ－ 1－sinθ的结果是________． 2 解析：原式＝＝ θ θ θ θ sin2 ＋cos2 ＋2sin cos － 2 2 2 2 θ θ 2 sin2－cos2 θ θ θ θ sin2 ＋cos2 －2sin cos 2 2 2 2
2
)
1 3 6 1 cos θ＋sinθcosθ 1＋tanθ 解析：cos2θ＋ sin2θ＝＝＝ .故选 B. 2 2 2 ＝ 2 cos θ＋sin θ 1＋tan θ 1 5 1＋ 9 1＋答案：B 1 5．(2016· 定西高三月考)已知 α∈(0，π)，且 sinα＋cosα＝，则 cos2α 的 2 值为( A．± ) 7 4 7 4 B. 7 4 3 4
θ θ2 sin2＋cos2 －
θ θ θ θ ＝sin2＋cos2－sin2－cos2. π π θ 因为 θ∈0，2，所以 ∈0，4. 2 θ θ 所以 cos >sin >0， 2 2 θ θ θ θ θ 所以原式＝sin ＋cos －cos ＋sin ＝2sin . 2 2 2 2 2 答案：2sin θ 2
C．－
D．－
1 解析：因为 sinα＋cosα＝，α∈(0，π)， 2 1 所以 1＋2sinαcosα＝， 4 3 所以 sin2α＝－，且 sinα>0，cosα<0， 4 所以 cosα－sinα＝－ 1－2sinαcosα＝－ 7 ， 2 7 .故选 C. 4
所以 cos2α＝(cosα－sinα)(cosα＋sinα)＝－答案：C 二、填空题(每小题 5 分，共 15 分)
＝1 π sinα＋4 15 10．已知 α 为第二象限角，且 sinα＝，求的值． 4 sin2α＋cos2α＋1 2 sinα＋cosα 2 2sinα＋cosα 解析：原式＝ . 2 ＝ 2sinαcosα＋2cos α 4cosαsinα＋cosα ∵α 为第二象限角，且 sinα＝ 15 ， 4
π 8．已知 tanx＝2，则 tan2x－4＝________. 解析：∵tanx＝2， ∴tan2x＝ 2tanx 4 2 ＝－ . 1－tan x 3
π π tan2x－4＝tan2x－2 π sin2x－2 ＝ π cos2x－2 ＝－cos2x 1 3 ＝－＝ . sin2x tan2x 4 3 4
答案：
三、解答题(每小题 10 分，共 20 分) 9．化简：(1) 1 1 －； 1－tanθ 1＋tanθ
2cos2α－1 (2) . π 2π － α ＋ α 2tan4 sin 4 解析：(1)原式＝＝ 1＋tanθ－1－tanθ 1－tan2θ
6．(cos75° －sin75° )(cos75° ＋sin75° )＝________.
解析：(cos75° －sin75° )(cos75° ＋sin75° )＝cos275° －sin275° ＝cos150° ＝－sin60° ＝－答案：－ 3 . 2 3 2
θ θ 2 3 7．已知 sin ＋cos ＝，那么 sinθ＝________，cos2θ＝________. 2 2 3 θ θ 2 3 解析：∵sin ＋cos ＝， 2 2 3 θ θ 4 ∴sin2＋cos22＝， 3 1 θ θ 4 即 1＋2sin cos ＝，∴sinθ＝， 2 2 3 3 1 7 ∴cos2θ＝1－2sin2θ＝1－2× 2＝ . 3 9 答案： 1 3 7 9
C. 2
D. 3
1 解析：由 cos2α＝1－2sin2α，得到 sin2α＋cos2α＝1－sin2α＝，则 sin2α 4
π 3 3 π π ＝，又 α∈0，2，所以 sinα＝，则 α＝，所以 tanα＝tan ＝ 3.故选 D. 4 2 3 3 答案：D 1 1 4．已知 tanθ＝，则 cos2θ＋ sin2θ 的值为( 3 2 A．－ C．－ 6 5 4 5 B. D. 6 5 4 5
课时作业 24
二倍角的三角函数(一)
ห้องสมุดไป่ตู้
|基础巩固|(25 分钟，60 分) 一、选择题(每小题 5 分，共 25 分) π 3 1．(2016· 海淀区模拟)已知 sin4－x＝，则 sin2x 的值为( 5 A. C. 19 25 14 25 B. D. 16 25 7 25 2 3 (cosx－sinx)＝， 2 5 )
解析：由已知得
1 9 两边平方得 (1－sin2x)＝， 2 25 解得 sin2x＝答案：D 2．函数 y＝1－2cos2x 的最小正周期是( A. π 4 π B. 2 ) 7 .故选 D. 25
C．π D．2π 解析：y＝1－2cos2x＝－cos2x，其最小正周期是 T＝答案：C π 1 3．(2016· 赣州期中)若 α∈0，2，且 sin2α＋cos2α＝，则 tanα 的值等于 4 ( ) A. 2 2 B. 3 3 2π ＝π.故选 C. 2