固体物理学中两种边界条件的对比
边界条件的类型

边界条件的类型一、边界条件的类型嘿,小伙伴们!今天咱们来唠唠边界条件的类型这个事儿哈。
那啥是边界条件呢?简单来说,就是在解决一些物理、数学或者工程问题的时候,在研究区域的边界上所需要满足的一些条件啦。
咱先说说第一类边界条件,这也叫狄利克雷边界条件哦。
想象一下,就像是在一个大的区域里面,边界上的值是给定好的。
比如说,在研究热传导问题的时候,在物体的边界上,温度是已经知道的数值,这个数值就像是一个固定的标准,不管里面怎么变,边界上就是这个数,是不是很神奇呢?接着呢,就是第二类边界条件啦,也被称为诺伊曼边界条件。
这个条件就有点不同咯,它规定的不是边界上的值,而是边界上值的变化率。
就好比在流体流动的问题里,在边界上流体的流速的变化率是给定的。
这就像是在一个游戏里,不是告诉你边界上的具体状态,而是告诉你这个状态的变化速度呢。
还有第三类边界条件,这可就更有趣了。
它是前两种边界条件的一种混合形式呢。
比如说在一些热交换的问题里,边界上的热量交换既和边界上的温度有关,也和温度的变化率有关。
这就像是把两个规则混合起来玩一个更复杂的游戏。
然后呢,还有周期性边界条件。
这个在研究一些具有周期性结构的问题里特别有用。
比如说晶体结构,它的边界就像是循环的一样,一边的边界和另一边的边界在某种意义上是一样的。
就像一个无限循环的图案,这边的边界和那边的边界就像双胞胎一样有着相同的性质。
最后呀,还有混合边界条件。
这个就比较复杂啦,它是把好几种不同的规则组合在一起,根据具体的问题来设定边界上的各种条件。
就像是一个超级复杂的拼图,每一块都有自己的规则,但是组合起来就能解决那些特别难搞的问题。
哈哈,边界条件的类型是不是很有趣呢?它们就像是一把把钥匙,能帮我们打开解决各种问题的大门哦。
固体物理学中两种边界条件的比较

固体物理学中两种边界条件的比较在固体物理学中,通常使用两种边界条件:周期性边界条件和固定边界条件。
它们分别适用于不同的情况,下面是它们的比较:
1. 周期性边界条件
周期性边界条件是指,在模拟一个固体体系时,将系统的一侧与相反侧相连,形成一个环形结构。
这样,当粒子在一侧移动到另一侧时,它们就会出现在相反的一侧。
周期性边界条件的优点在于,它可以有效地减少边界效应的影响,从而更好地模拟整个固体体系的行为。
2. 固定边界条件
固定边界条件是指,在模拟一个固体体系时,将固体的边界固定在一个位置,不允许粒子从边界处穿过。
这样做的优点在于,可以更加准确地模拟固体表面的行为,比如表面的强度和形变。
固定边界条件也可以用于研究材料界面的性质,比如界面的能量和扩散性等。
总的来说,选择使用哪种边界条件应该根据具体的模拟目的和所研究的固体体系的性质来决定。
如果需要更好地模拟整个固体体系的行为,那么应该选择周期性边界条件;如果需要更加准确地模拟固体表面的行为,那么应该选择固定边界条件。
1/ 1。
固体物理学中两种边界条件的比较

固体物理学中两种边界条件的比较固体物理学中,边界条件是解决问题时必须考虑的重要因素之一。
边界条件可以分为两种类型:第一类边界条件和第二类边界条件。
这两种边界条件在固体物理学中有着不同的应用和作用。
本文将对这两种边界条件进行比较分析。
一、第一类边界条件第一类边界条件也称为Dirichlet边界条件,是指在固体物理学中,给定边界上的物理量的具体数值。
这种边界条件要求在给定的边界上,物理量的数值是已知的。
例如,在热传导问题中,可以给定固体表面的温度;在弹性问题中,可以给定固体表面的位移或受力。
第一类边界条件的应用范围非常广泛。
它可以用来描述固体物体与外界的相互作用,以及固体物体内部的变化情况。
通过给定边界上的物理量,我们可以计算出整个固体物体中的物理量的分布情况。
这种边界条件的优点在于,它能够直接给出问题的具体解,使得问题的求解变得相对简单。
然而,第一类边界条件也存在一些限制。
由于它要求在边界上给定物理量的具体数值,因此在实际应用中可能会受到一些限制。
例如,在实验中很难直接测量固体表面的温度或位移,这就给确定边界条件带来了一定的困难。
二、第二类边界条件第二类边界条件也称为Neumann边界条件,是指在固体物理学中,给定边界上的物理量的变化率。
与第一类边界条件不同,第二类边界条件要求在给定的边界上,物理量的变化率是已知的。
例如,在热传导问题中,可以给定固体表面的热流密度;在弹性问题中,可以给定固体表面的应力或应变。
第二类边界条件的应用范围也非常广泛。
它可以用来描述固体物体内部的物理量的变化情况,以及固体物体与外界的相互作用。
通过给定边界上的物理量的变化率,我们可以计算出整个固体物体中的物理量的分布情况。
与第一类边界条件相比,第二类边界条件的优点在于,它不需要直接给出问题的具体解,而是给出了物理量的变化率,使得问题的求解更加灵活。
然而,第二类边界条件也存在一些限制。
由于它要求在边界上给定物理量的变化率,因此在实际应用中可能会受到一些限制。
固体物理补充习题

23. 设有某种简单立方晶体,熔点为 800C,由熔点结晶后,晶粒大小为 L=1 m 的立方体,晶格常数 a = 410 –10 m。求结晶后每个晶粒中的空位数,已 知空位的形成能为 1 eV。若晶体在高温形成的空位,降到室温后聚集到一 个晶面上,形成一个空位园片,以致引起晶体内部的崩塌,结果将转变为何
,
其中 m 为电子质量。
29. 在低温下,金属钾摩尔热容量的实验结果可表为
C = ( 2.08T+2.57T3 ) ×10 –3 J/mol.K ,
试求: (1)钾的 Debye 温度 D ; (2)Fermi 温度 TF; (3)在 Fermi 面上一摩尔金属的电子能态密度 N(EF0)。
30. 已知 Cu 的电子密度为 n = 8.45×1022 cm –3,Debye 温度 D = 315 K。
21. 若晶体中原子的总数为 N,间隙位置的总数为 N’,形成一个 Frenkel 缺陷 所需的能量为 uf 。在一定的温度下,平衡时晶体中有 nf 个 Frenkel 缺陷,
试由 N’ 。
= 0 导出平衡时 Frenkel 缺陷数目的表达式,设 nf = N,
22. 已知 1100C 时,碳在Fe 中的扩散系数 D=6.7×10 –7 cm2/s。若保持表 面处碳的浓度不变,要得到 d = 1 mm 厚的渗碳层(碳的浓度为表面处的一 半),问在此温度下需要扩散多长时间?(erf(0.500) = 0.52050, erf(0.477) = 0.50005)
2. 格常数为 a 的简单二维密排晶格的基矢可以表为
(1)求出其倒格子基矢 和 , 证明倒格子仍为二维密排格子;
(2)求出其倒格子原胞的面积 b 。
3. 由 N 个原子(或离子)所组成的晶体的体积 V 可以写为 V=Nv = Nr3,其 中 v 为平均一个原子(或离子)所占的体积,r 为最近邻原子(或离子)间 的距离, 是依赖于晶体结构的常数,试求下列各种晶体结构的 值:
三类边界条件推导
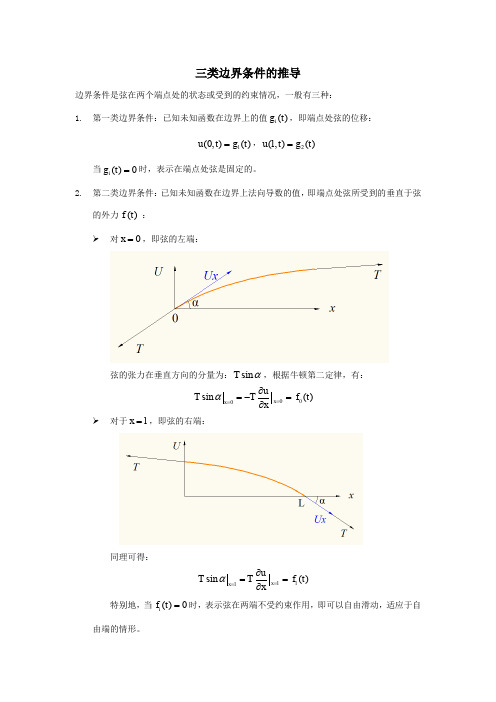
边界条件是弦在两个端点处的状态或受到的约束情况,一般有三种: 1. 第一类边界条件:已知未知函数在边界上的值 gi (t ) ,即端点处弦的位移:
u(0, t ) g1 (t ) , u(l , t ) g2 (t )
当 gi (t ) 0 时,表示在端点处弦是固定的。 2. 第二类边界条件: 已知未知函数在边界上法向导数的值, 即端点处弦所受到的垂直于弦 的外力 f (t ) : 对 x 0 ,即弦的左端:
弦的张力在垂直方向的分量为: T sin ,根据牛顿第二定律,有:
T sin x0 T
对于 x l ,即弦的右端:
u x
x 0
f 0 (t )
同理可得:
T sin xl T
u x
x l
fl (t )
特别地,当 fi (t ) 0 时,表示弦在两端不受约束作用,即可以自由滑动,适应于自 由端的情形。
x l
ku
x l
fl (t)
(
u u) x
x l
v(t )
对于外力 fi (t ) 0 的特殊情况,即 v(t ) 0 ,边界条件在弦的两端可统一简化为:
(
u u) x
x a
0 (a 0, a l )
3. 第三类边界条件: 又称混合边界条件, 它给出了未知函数和它的法线方向上的导数的线 性组合在边界上的值。 对弦的一维振动问题,即已知端点处弦的位移(引起弹性支撑的力)和所受的垂直于弦 线的外力。 对 x 0 ,即弦的左端:
弦对支撑外力的垂直分量为: T
u ,由胡克定律知: x u T x 0 ku x 0 f 0 (t) x
《固体物理学》房晓勇主编教材-思考题解答参考03第三章_晶体振动和晶体的热学性质

第三章晶体振动和晶体的热学性质3.1相距为某一常数(不是晶格常数)倍数的两个原子,其最大振幅是否相同?解答:(王矜奉3.1.1,中南大学3.1.1)以同种原子构成的一维双原子分子链为例, 相距为不是晶格常数倍数的两个同种原子, 设一个原子的振幅A, 另一个原子振幅B, 由《固体物理学》第79页公式,可得两原子振幅之比(1)其中m原子的质量. 由《固体物理学》式(3-16)和式(3-17)两式可得声学波和光学波的频率分别为, (2). (3)将(2)(3)两式分别代入(1)式, 得声学波和光学波的振幅之比分别为, (4). (5)由于=,则由(4)(5)两式可得,1B A=. 即对于同种原子构成的一维双原子分子链, 相距为不是晶格常数倍数的两个原子, 不论是声学波还是光学波, 其最大振幅是相同的.3.2 试说明格波和弹性波有何不同?解答:晶格中各个原子间的振动相互关系3.3 为什么要引入玻恩-卡门条件?解答:(王矜奉3.1.2,中南大学3.1.2)(1)方便于求解原子运动方程.由《固体物理学》式(3-4)可知, 除了原子链两端的两个原子外, 其它任一个原子的运动都与相邻的两个原子的运动相关. 即除了原子链两端的两个原子外, 其它原子的运动方程构成了个联立方程组. 但原子链两端的两个原子只有一个相邻原子, 其运动方程仅与一个相邻原子的运动相关, 运动方程与其它原子的运动方程迥然不同. 与其它原子的运动方程不同的这两个方程, 给整个联立方程组的求解带来了很大的困难.(2)与实验结果吻合得较好.对于原子的自由运动, 边界上的原子与其它原子一样, 无时无刻不在运动. 对于有N 个原子构成的的原子链, 硬性假定的边界条件是不符合事实的. 其实不论什么边界条件都与事实不符. 但为了求解近似解, 必须选取一个边界条件. 晶格振动谱的实验测定是对晶格振动理论的最有力验证(《固体物理学》§3.1与§3.6). 玻恩卡门条件是晶格振动理论的前提条件. 实验测得的振动谱与理论相符的事实说明, 玻恩卡门周期性边界条件是目前较好的一个边界条件.3.4 试说明在布里渊区的边界上()/q π=a ,一维单原子晶格的振动解n x 不代表行波而代表驻波。
固体物理学习笔记

固体物理学习笔记固体物理学是研究固体物质的物理性质、微观结构、构成物质的各种粒子的运动形态及其相互关系的科学。
它是物理学中内容极丰富、应用极广泛的分支学科。
固体物理学是研究固体的性质、它的微观结构及其各种内部运动,以及这种微观结构和内部运动同固体的宏观性质的关系的学科。
固体的内部结构和运动形式很复杂,这方面的研究是从晶体开始的,因为晶体的内部结构简单,而且具有明显的规律性,较易研究。
以后进一步研究一切处于凝聚状态的物体的内部结构、内部运动以及它们和宏观物理性质的关系。
这类研究统称为凝聚态物理学。
固体通常指在承受切应力时具有一定程度刚性的物质,包括晶体和非晶态固体。
简单地说,固体物理学的基本问题有:固体是由什么原子组成?它们是怎样排列和结合的?这种结构是如何形成的?在特定的固体中,电子和原子取什么样的具体的运动形态?它的宏观性质和内部的微观运动形态有什么联系?各种固体有哪些可能的应用?探索设计和制备新的固体,研究其特性,开发其应用。
新的实验条件和技术日新月异,为固体物理不断开拓出新的研究领域。
极低温、超高压、强磁场等极端条件、超高真空技术、表面能谱术、材料制备的新技术、同步辐射技术、核物理技术、激光技术、光散射效应、各种粒子束技术、电子显微术、穆斯堡尔效应、正电子湮没技术、磁共振技术等现代化实验手段,使固体物理性质的研究不断向深度和广度发展。
由于固体物理本身是微电子技术、光电子学技术、能源技术、材料科学等技术学科的基础,也由于固体物理学科内在的因素,固体物理的研究论文已占物理学中研究论文三分之一以上。
同时,固体物理学的成就和实验手段对化学物理、催化学科、生命科学、地学等的影响日益增长,正在形成新的交叉领域。
固体物理对于技术的发展有很多重要的应用,晶体管发明以后,集成电路技术迅速发展,电子学技术、计算技术以至整个信息产业也随之迅速发展。
其经济影响和社会影响是革命性的。
这种影响甚至在日常生活中也处处可见。
数学物理方法三类边界条件

数学物理方法三类边界条件
在数学物理中,常常会遇到需要考虑边界条件的问题。
根据不同的情况,可以将数学物理方法中的边界条件分为三类,第一类边界条件、第二类边界条件和第三类边界条件。
1. 第一类边界条件(Dirichlet边界条件):
第一类边界条件是指在边界上给定了物理量的具体值。
例如,在一个热传导问题中,可以给定边界上的温度值。
在一个波动方程中,可以给定边界上的振幅值。
这类边界条件可以用数学上的等式或函数来表示。
2. 第二类边界条件(Neumann边界条件):
第二类边界条件是指在边界上给定了物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度(即温度梯度)。
在一个波动方程中,可以给定边界上的振幅的导数。
这类边界条件可以用数学上的导数来表示。
3. 第三类边界条件(Robin边界条件):
第三类边界条件是指在边界上给定了物理量的线性组合,其中既包括物理量的值,也包括物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度和温度的线性组合。
这类边界条件可以用数学上的线性组合来表示。
需要注意的是,以上分类只是一种常见的方式,具体问题中的边界条件可能会有其他形式。
此外,边界条件的选择和应用也取决于所研究的具体物理问题和数学模型。
在实际问题中,根据边界条件的具体形式,可以选择合适的数学方法和技巧来求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
固体物理学中两种边界条件的对比
固体物理学中,边界条件是指在研究固体物理问题时,需要考虑物体表面与外界的相互作用所产生的影响。
常见的边界条件有两种:自由边界条件和固定边界条件。
自由边界条件是指物体表面的自由度不受限制,即表面可以自由振动,不受外界限制。
这种边界条件在研究固体物理问题时比较常见,例如在研究固体中的声波传播时,需要考虑自由边界条件。
自由边界条件的数学表达式为:
$$\frac{\partial u}{\partial n}=0$$
其中,$u$表示位移,$n$表示法向量。
固定边界条件是指物体表面的自由度受到限制,即表面不能自由振动,必须保持固定。
这种边界条件在研究固体物理问题时也比较常见,例如在研究固体中的热传导时,需要考虑固定边界条件。
固定边界条件的数学表达式为:
$$u=0$$
其中,$u$表示位移。
两种边界条件的主要区别在于,自由边界条件要求物体表面可以自由振动,而固定边界条件要求物体表面必须保持固定。
在实际应用中,需要根据具体问题来选择适合的边界条件。
