阵列天线方向图函数实验
阵列天线方向图的初步研究

通信信号处理实验报告——阵列天线方向图的初步研究 11级通信(研) 刘晓娟一、实验原理:1、智能天线的基本概念:智能天线是一种阵列天线,它通过调节各阵元信号的加权幅度和相位来改变阵列的方向图形状,即自适应或以预制方式控制波束幅度、指向和零点位置,使波束总是指向期望方向,而零点指向干扰方向,实现波束随着用户走,从而提高天线的增益,节省发射功率。
智能天线系统主要由①天线阵列部分;②模/数或数/模转换部分;③波束形成网络部分组成。
本次实验着重讨论天线阵列部分。
2、智能天线的工作原理:智能天线的基本思想是:天线以多个高增益的动态窄波束分别跟踪多个期望信号,来自窄波束以外的信号被抑制。
3、方向图的概念:以入射角为横坐标,对应的智能天线输出增益为纵坐标所作的图称为方向图,智能天线的方向图有主瓣、副瓣等,相比其他天线的方向图,智能天线通常有较窄的主瓣,较灵活的主、副瓣大小、位置关系,和较大的天线增益。
与固定天线相比最大的区别是:不同的全职通常对应不同的方向图,我们可以通过改变权值来选择合适的方向图,即天线模式。
方向图一般分为两类:一类是静态方向图,即不考虑信号的方向,由阵列的输出直接相加得到;另一类是带指向的方向,这类方向图需要考虑信号的指向,通过控制加权相位来实现。
二、实验目的:1、设计一个均匀线阵,给出λ(波长),N (天线个数),d (阵元间距),画出方向图曲线,计算3dB 带宽。
2、通过控制变量法讨论λ,N ,d 对方向图曲线的影响。
3、分析旁瓣相对主瓣衰减的程度(即幅度比)。
三、实验内容:1、公式推导与整理:权矢量12(,,......)T N ωωωω=,本实验旨在讨论静态方向图,所以此处选择ω=(1,1,......1)T 。
信号源矢量(1)()[1,,...]j j N T a e e ββθ---=,2sin dπβθλ=,幅度方向图函数()()HF a θωθ==(1)1sin2sin 2Nj n n N eβββ--==∑=sin(sin /)sin(sin /)n d n d πθλπθλ。
在室外测试场中阵列天线方向图的测试方法

在室外测试场中阵列天线方向图的测试方法郝延刚;李淑华【摘要】On the basis of the commonly used antenna pattern measurement method, is the size of a large array antenna taken into consideration, and designed a set of array antenna pattern testing method in an outdoor test field. According to this method, the array antenna pattern of a particular model of aircraft is firstly tested. Then the radiation pattern of the pitch surface is measured and compared with the theoretical simulation results thus proving the accuracy of the experimental program. Finally, the experimental error is analyzed.%在常用天线方向图测量方法的基础上,考虑大型阵列天线尺寸大的特殊性,并且结合实际测量条件,设计出一套在室外测试场中阵列天线方向图的测试方法.按照此方法,对某型号飞机的阵列天线方向图进行测试.测得其俯仰面辐射方向图后与理论仿真结果对比,论证实验方案的准确性,并对实验误差进行分析.【期刊名称】《科学技术与工程》【年(卷),期】2012(012)029【总页数】4页(P7745-7748)【关键词】阵列天线;方向图;室外测试场【作者】郝延刚;李淑华【作者单位】海军航空工程学院青岛分院,青岛266041;海军航空工程学院青岛分院,青岛266041【正文语种】中文【中图分类】TN820.1阵列天线具有较强的方向性和较高的增益,并且能够实现方向图扫描等优点。
在室外测试场中阵列天线方向图的测试方法

络分析仪能接收记 录被测天线在各个方位角 所接
收 到 的相 对信 号 电平 , 器 动态 范 围不 小 于 5 B 仪 0d 。 在 系统规 定 频 率 范 围 内校 准 检 验 仪 器 和 仪 表 。 主
关键词
阵列天线
方 向图
室外测试场 文献标志码 A
中图法分类号
T 80 1 N 2. ;
阵列天 线具 有 较 强 的方 向性 和 较 高 的 增 益 , 并
状态[ 。
且能够实现方 向图扫描等优点 。随着无线通 信 的
迅 猛发 展 , 阵列 天 线 越来 越 多 地 被 应 用 其 中。 阵列
天线可 以实现单 个 天 线所 无 法 实 现 的复 杂 功 能 , 具 有 更大 的灵 活性 和 更 高 的信 号 容 量 , 能显 著 提 高 系
本 文 以某 型 号 飞 机 的 雷 达 阵 列 天 线 为测 试 目 标, 对其 辐 射特性 和端 口特 性 进行 测 试 。该 天 线 以
件 为 : 1 辅 助 天 线 和被 测 天线 之 问 的距 离 应 满 足 () 最小 测 试距 离。 ( ) 2 气候 条件 和 机 械应 力 等应 符 合
天 线产 品规范 的规定 。( ) 避 免 或设 法 减少 外 界 3应
统 自带 源天线 ( 元 为半 波 振 子 的 1×3行 阵 ) 网 阵 ,
21 0 2年 6月 7日收到, 6月 2 51 3修改 第一作 者简介 : 郝延 刚 ( 97 ) 男 , 1 8 一 , 黑龙江齐 齐 哈尔人 , 硕士研 究 牛, 研究方 向 : 军用 飞行器天线设计 。
度为 5I, 度 为 2i, I宽 T 重量 约 为 30k 。 由于室 内 n 0 g 测试场 受 空 问 大 小 的 限 制 , 且 该 天 线 由于 尺 寸 并
天线线列阵方向图
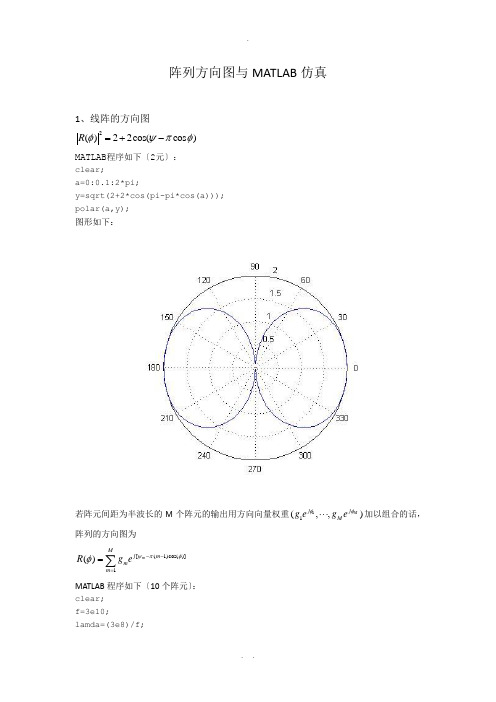
阵列方向图与MATLAB 仿真1、线阵的方向图2()22cos(cos )R φψπφ=+-MATLAB 程序如下〔2元〕:clear;a=0:0.1:2*pi;y=sqrt(2+2*cos(pi-pi*cos(a)));polar(a,y); 图形如下:若阵元间距为半波长的M 个阵元的输出用方向向量权重11(,,)M j j M g eg e φφ⋅⋅⋅加以组合的话,阵列的方向图为 [(1)cos()]1()m Mj m m m R g e ψπφφ--==∑MATLAB 程序如下〔10个阵元〕:clear;f=3e10;lamda=(3e8)/f;beta=2.*pi/lamda;n=10;t=0:0.01:2*pi;d=lamda/4;W=beta.*d.*cos(t);z1=((n/2).*W)-n/2*beta* d;z2=((1/2).*W)-1/2*beta* d;F1=sin(z1)./(n.*sin(z2));iK1=abs(F1) ;polar(t,K1);方向图如下:2、圆阵方向图程序如下:clc;clear all;close all;M = 16; % 行阵元数k = 0.8090; % k = r/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值m = [0 : M-1];w = exp(-j*2*pi*k*cos(2*pi*m'/M-DOA_theta*pi/180)*cos(DOA_fi*pi/180));% w = exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)+sin(2*pi*m'/M)*si n(DOA_fi*pi/180))); % 竖直放置% w = chebwin(M, 20) .* w; % 行加切比雪夫权% 绘制水平面放置的均匀圆阵的方向图theta = linspace(0,180,360);fi = linspace(0,90,180);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)a = exp(-j*2*pi*k*cos(2*pi*m'/M-theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180));%a=exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)+sin(2*pi*m'/ M)*sin(fi(i_fi)*pi/180))); % 竖直放置Y(i_theta,i_fi) = w'*a;endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);% Y = (Y+20) .* ((Y+20)>0) - 20; % 切图Z = Y + 20;Z = Z .* (Z > 0);Y = Z - 20;figure; mesh(fi, theta, Y); view([66, 33]);title('水平放置时的均匀圆阵方向图');% title('竖面放置时的均匀圆阵方向图'); % 竖直放置axis([0 90 0 180 -20 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角/(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:3、平面阵方向图:clc;clear all;close all;Row_N = 16; % 行阵元数Col_N = 16; % 列阵元数k = 0.5; % k = d/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值Row_n = [0 : Row_N-1]; Col_n = [0 : Col_N-1];W_Row = exp(-j*2*pi*k*Row_n'*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); % W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_fi*pi/180)); % 竖直放置W_Row = chebwin(Row_N, 20) .* W_Row; % 行加切比雪夫权W_Col = chebwin(Col_N, 30) .* W_Col; % 列加切比雪夫权W = kron(W_Row, W_Col); % 合成的权值N*N x 1% 绘制水平面放置的平面阵的方向图theta = linspace(0,180,180);fi = linspace(0,90,90);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)row_temp = exp(-j*2*pi*k*Row_n'*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 行导向矢量N x 1col_temp = exp(-j*2*pi*k*Col_n'*sin(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 列导向矢量N x 1% col_temp = exp(-j*2*pi*k*Col_n'*sin(fi(i_fi)*pi/180)); % 竖直放置Y(i_theta,i_fi) = W'*kron(row_temp, col_temp); % 合成的导向矢量N*N x 1 endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);Y = (Y+60) .* ((Y+60)>0) - 60; % 切图% Z = Y + 60;% Z = Z .* (Z > 0);% Y = Z - 60;figure; mesh(fi, theta, Y); view([66, 33]);title('水平面放置时的面阵方向图');axis([0 90 0 180 -60 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:4、CAPON方法波束形成MATLAB程序如下〔阵元16,信号源3,快拍数1024〕:clear alli=sqrt(-1);j=i;M=16;%均匀线阵列数目P=3;%信号源数目f0=10;f1=50;f2=100;%信号频率nn=1024;%快拍数angle1=-15;angle2=15;angle3=30;%the signal angleth=[angle1;angle2;angle3]';SN1=10;SN2=10;SN3=10;%信噪比sn=[SN1;SN2;SN3];degrad=pi/180;tt=0:.001:1024;x0=exp(-j*2*pi*f0*tt);%3个信号x0、x1、x2x1=exp(-j*2*pi*f1*tt); %x2=exp(-j*2*pi*f2*tt); %t=1:nn;S=[x0(t);x1(t);x2(t)];nr=randn(M,nn);ni=randn(M,nn);u=nr+j*ni;%复高斯白噪声Ps=S*S'./nn;%信号能量ps=diag(Ps);refp=2*10.^(sn/10);tmp=sqrt(refp./ps);S2=diag(tmp)*S;%加入噪声tmp=-j*pi*sin(th*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A=exp(a2);X=A*S2+.1*u;%接收到的信号Rxx=X*X'./nn;%相关矩阵invRxx=inv(Rxx);%搜寻信号th2=[-90:90]';tmp=-j*pi*sin(th2'*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A2=exp(a2);den=A2'*invRxx*A2;doa=1./den;semilogy(th2,doa,'r');title('spectrum'); xlabel('angle'); ylabel('spectrum'); axis([-90 90 1e1 1e5]); grid;。
圆形阵列天线方向图的分布函数优化方法

向的 方向 图与期 望的 窗 函数 近似 。 关 键词 : 圆形 阵列 ; 线方 向 图; 天 分布 函数 ; 系数 优化 权
中图分 类号 :N 5 T 9
文 献标 识码 : A
第5 0卷 第 7 期
21 00年 7 月
Hale Waihona Puke 电讯 技 术 Tee o lc mmu iain En ie rn nc to gn e g i
Vo . 0 No. 15 7
J1 01 u .2 0
文章 编 号 :0 1 9 X(00 0 0 9 — 6 10 —83 2 1 }7— 0 1 0
ZHAO n c u , HI Wa —h n S 2
( .L itr D l ai fc r 5 at y Pnzo 190 C ia2 Sho o l t nc 1P A M la e gtnO ief 7Fc r,eghu6 13 , hn ; . ol f e r i iy e o o1 o c E co E g er g U i r t o l t n c n eadT cnl yo hn ,hnd 10 4 C ia ni e n , nv sy f e r i S i c n eh o g f ia C egu60 5 , hn ) ni e i E co c e o C
圆 形 阵 列 天 线 方 向图 的 分 布 函 数 优 化 方 法
赵 万春 师 , 君2
(. 1 中国人 民解放军驻 17厂军事代表室 , 5 四川 彭州 6 13 ; . 190 2 电子科技大学 电子工程学院 , 成都 605 ) 104
阵列天线方向图的MATLAB实现

阵列天线方向图的MATLAB 实现课程名称:MATLAB程序设计与应用任课教师:周金柱班级:04091202姓名:黄文平学号:04091158成绩:阵列天线方向图的MATLAB 实现摘要:天线的方向性是指电磁场辐射在空间的分布规律,文章以阵列天线的方向性因子F(θ,φ)为主要研究对象来分析均匀和非均匀直线阵天线的方向性。
讨论了阵列天线方向图中主射方向和主瓣宽度随各参数变化的特点,借助M ATLAB绘制出天线方向性因子的二维和三维方向图,展示天线辐射场在空间的分布规律,表现辐射方向图的特点。
关键词:阵列天线;;方向图;MATLAB前言:天线是发射和接收电磁波的重要的无线电设备,没有天线也就没有无线电通信。
不同用途的天线要求其有不同的方向性,阵列天线以其较强的方向性和较高的增益在工程实际中被广泛应用。
因此,对阵列天线方向性分析在天线理论研究中占有重要地位。
阵列天线方向性主要由方向性因子F(θ,φ)表征,但F(θ,φ)在远区场是一组复杂的函数,如果对它的认识和分析仅停留在公式中各参数的讨论上,很难理解阵列天线辐射场的空间分布规律[ 1 ]。
MATLAB以其卓越的数值计算能力和强大的绘图功能,近年来被广泛应用在天线的分析和设计中。
借助MATLAB可以绘制出阵列天线的二维和三维方向图,直观地从方向图中看出主射方向和主瓣宽度随各参数的变化情况,加深对阵列天线辐射场分布规律的理解。
1 均匀直线阵方向图分析若天线阵中各个单元天线的类型和取向均相同,且以相等的间隔d 排列在一条直线上。
且各单元天线的电流振幅均为I,相位依次滞后同一数值琢,那么,这种天线阵称为均匀直线式天线阵,如图1 所示[ 2 ]:均匀直线阵归一化阵因子为[ 3 ]:Fn(θ,φ)是一个周期函数,所以除§= 0 时是阵因子的主瓣最大值外,§= ±2 mπ(m=1,2,...)都是主瓣最大值,这些重复的主瓣称为栅瓣,在实际应用中,通常希望出现一个主瓣,为避免出现栅瓣,必须把g限制在- 2π<§<2π范围内[ 4 ],其中k=λ/2π,即波数,n 表示阵元数目。
阵列天线方向图综合算法研究
入有关数据库进行检索,可以 采用影印、缩印 或扫描等复制手段保存和汇编本学位论文。 同 时本人保证, 毕业后结合学位论文研究课题再撰写的文章一律注明 作者单位为西北工业
大学 。 保密论文待解密 后适用 本声 明。
西北工业大学硕士学位论文
摘 要
摘 要
随 着高速计算机技术的 发展, 优化算法因 智能 其鲁棒性强、 适合多目 且 标,
对目 标函数无可微性要求等特点, 在天线设计领域得到了越来越广泛的应用。 本 文主要研究分析了两种智能优化方法- 遗传算法和粒子群算法, 以及这两种算 法在阵列天线方向图综合中的应用。 遗传算法是一种模拟自 然界生物进化规律的迭代算法, 通过选择、 复制、 交 叉和变异等算子进行进化操作, 逐步靠近最优解. 本文对遗传算法的原理和特点
eo tnTe t tn b i d uh cn, itg c sn ad vli . bssuo iotn t g sei r lan, sg uo h e o i s e h l a o e tg e c i r i n l p o m ti . t o d r tiio G ip s t . em ns e u tgTe r a ca crt f s e e Te et c r t an h h y n h aes e c A r n d h l ' u n e e r a pt e pa o le aa a e a ot id e c t m x u m l d a h e i a ry n a pmz t r ue a m m i n s f r n n r i e o u d n r t e d h e i se l cnot ba s p, a ip vd loe ec ot . i l ea otl e h ewt n r e r - d Gnt Agrh de n v d r h m e a i m o ec h a e i l im T i ip vd n i Agr m ao d ds n t cngr l h m r e G ec ot i l u t eg ptr r ofu b s o e t l i s s o i ae e i a e h s e n at n, li rus u a e ofu b aa a e a c hs n nas u tn l aot tr r ngr l ry n w i a e i ao e t b m s p t e i a e n n h h an c r t to t alst a e ti i tt t m t d us its ei w sihb te rg n n c e t e o d cs d h ppr w c e s i o a h h h i e n a s a e v d a e s i
相控阵天线方向图推导及仿真
相控阵天线方向推导及仿真1、推导线阵天线方向图公式一个接收线阵,由等间距为d 的N 个各向同性单元组成,那么在θ方向,相邻单元接收信号的相位差为Ф=2πdλsinθ,线阵排列情况如图1所示。
图1 线阵排列示意图因为天线辐射方向图可以由天线上各种各样电流源辐射的单独贡献进行矢量叠加而得出,故各单元电压和为:E a =sin (ωt )+sin (ωt +ϕ)+sin (ωt +2ϕ)+⋯+sin[ωt +(N −1)ϕ]将等式两边同时乘以2sin(ϕ2),根据积化和差、和差化积等相关数学公式,可得到如下公式:2sin (ϕ2)E a =cos (ωt −ϕ2)−cos (ωt +ϕ2)+cos (ωt +ϕ2)−cos (ωt −32ϕ)+⋯+cos (ωt +2N −32ϕ)−cos(ωt +2N −12ϕ)整理得,2sin (ϕ2)E a =cos (ωt −ϕ2)−cos (ωt +2N−12ϕ)=2sin(ωt +N −12ϕ)sin(N2ϕ) 最终得到场强方向图,E a =sin[ωt +(N −1)ϕ2⁄]sin(Nϕ2⁄)sin(ϕ2⁄)平方归一化后,得到辐射方向图(阵列因子):|G a (θ)|=sin 2[Nπ(dλ)sinθ]N 2sin 2[π(dλ)sinθ]上式中,当(dλ)sinθ=0,±1,±2,···±n 时|G a (θ)|取得相等的最大值,但是我们只期望看到(dλ)sinθ=0的情况,取其他值产生的栅瓣是我们所不想见到的,为避免这种情况,特令d <λ。
前面的公式中认定主瓣指向为0°,当主瓣指向θ0方向时,则各向同性单元线阵的归一化辐射方向图为:G (θ)=sin 2[Nπ(dλ)(sinθ−sinθ0)]N 2sin 2[π(d λ)(sinθ−sinθ0)]此时,由于−2≤sin (θ)−sin (θ0)≤2,故防止产生栅瓣的条件为d <λ2⁄。
阵列天线方向图函数实验
阵列天线方向图函数实验一、 实验目的1. 设计一个均匀线阵,给定d N d ,,,λθ画出方向图)(θF 函数图;2. 改变参数后,画出方向图)(θF 函数图,观察方向图)(θF 的变化并加以分析;3. 分析方向图)(θF 主瓣的衰减情况以及主瓣对第一旁瓣的衰减情况,确定dB3衰减对应的θ;二、 实验原理阵列输出的绝对值与来波方向之间的关系称为天线的方向图。
方向图一般有两类:一类是阵列输出的直接相加(不考虑信号及其来向),即静态方向图;另一类是带指向的方向图(考虑信号指向),当然信号的指向是通过控制加权的相位来实现的。
对于某一确定的M 元空间阵列,在忽略噪声的条件下,第k 个阵元的复振幅为),2,1(0M k e g x k j k Λ==-ωτ (2.1)式中:0g 为来波的复振幅,k τ为第k 个阵元与参考点之间的延迟。
设第k 个阵元的权值为k w ,那么所有阵元加权的输出得到的阵列的输出为),2,1(010M k e g w Y k j Mk k Λ==-=∑ωτ (2.2)对上式取绝对值并归一化后可得到空间阵列的方向图{}00max )(Y Y F =θ (2.3)如果),2,1(1M k w k Λ==式(2.3)即为静态方向图)(θF 。
下面考虑均匀线阵方向图。
假设均匀线阵的间距为d ,且以最左边的阵元为参考点(最左边的阵元位于原点),另假设信号入射方位角为θ,其中方位角表示与线阵法线方向的夹角,与参考点的波程差为θθτsin )1(1)sin (11d k cx ck -== (2.4)则阵列的输出为βθλπωτ)1(10sin )1(210100--=--=-=∑∑∑===k j Mk k d k jMk k j Mk k e g w eg w eg w Y k(2.5)式中:λθπβ/sin 2d =,λ为入射信号的波长。
当式(2.5)中),2,1(1M k w k Λ==时,式(2.5)可以进一步简化为)2/sin()2/sin(2)(00βββM M e Mg Y k M j == (2.6)可得均匀线阵的静态方向图,即)2/sin()2/sin()(0ββθM M F =(2.7)当式(2.5)中),2,1(,/sin 2,)1(M k d e w d d k j k d Λ===-λθπββ时,式(2.6)可简化为]2/)sin[(]2/)(sin[2)()1(00d d M j M M e Mg Y d ββββββ--=-= (2.7)于是可得到指向为d θ的阵列方向图,即]2/)sin[(]2/)(sin[)(d d M M F ββββθ--=(2.8)三、 实验过程1. 指向0=d θ静态方向图函数的实验1.1均匀线阵阵元个数N 对方向图函数)(θF 的影响sita=-pi/2:0.01:pi/2; lamda=0.03; d=lamda/2; n1=10; sita_d=0beta=2*pi*d*sin(sita)/lamda; beta_d=2*pi*d*sin(sita_d)/lamda; z11=(n1/2)*(beta-beta_d); z21=(1/2)*(beta-beta_d); f1=sin(z11)./(n1*sin(z21)); F1=abs(f1); figure(1);plot(sita,F1,'b'); hold on ; n2=20;beta=2*pi*d*sin(sita)/lamda;z12=(n2/2)*beta;z22=(1/2)*beta;f2=sin(z12)./(n2*sin(z22));F2=abs(f2);plot(sita,F2,'r');hold on;n3=30;beta=2*pi*d*sin(sita)/lamda;z13=(n3/2)*beta;z23=(1/2)*beta;f3=sin(z13)./(n3*sin(z23));F3=abs(f3);plot(sita,F3,'k')hold off;grid on;xlabel('theta/radian');ylabel('amplitude');title('¾ùÔÈÏßÕóÕóÔª¸öÊý¶Ô·½Ïòͼº¯Êý µÄÓ°Ïì'); legend('n1=10','n2=20','n3=30');分析:随着阵元数的增加,波束宽度变窄,分辨力提高。
实验二: 利用仿真软件研究直线式天线阵的最大辐射方向
电磁场与电磁兼容实验报告学号:姓名:院系:专业:教师:实验二:研究性教学利用仿真软件研究直线式天线阵的最大辐射方向实验时间:实验地点:一、实验目的学会使用仿真软件绘制直线式天线阵的最大辐射方向图,研究直线式天线阵的最大辐射方向。
二、实验原理和内容1、均匀直线式天线阵由N个相同的振子平行地以相等的间距排列在与各振子轴相垂直的一条直线上,各个振子上的电流振幅相等,而相位则以均匀的比例递增或递减,这种天线阵就称为均匀直线式天线阵。
2、方向性相乘原理天线阵的方向性函数为单个振子的方向性函数与阵因子的乘积。
方向性图也可以相乘。
均匀直线式天线阵的方向性:在赤道面内均匀直线式天线阵的方向性取决于阵因子3、最大辐射方向三、实验过程(使用Matlab仿真软件绘制阵因子图像)1、根据题目要求的频率fre=300MHz,根据公式lbd=c(波速)/fre求出波长lbd,根据公式k=2*pi/lbd求出波数k。
2、阵元数N=8,间距d为lbd/4,根据我的学号15212155,确定最大辐射方向为sita=pi/3,从而确定相位差为kesai=k*d*cos(sita)。
3、定义fai=k*d*cos(a)+kesai,它的物理意义是在与阵轴夹角为a的方向上远区观察处第(i+1)个阵元产生的场超前于第i个阵元产生的场的相位值。
4、将以上所有量代入阵因子表达式f=sin((fai)*(N/2))./(sin((fai)*(1/2))*N)中计算即可。
四、实验数据和结果902701800最大辐射方向60度的8元端射式阵因子H 面-0.4-0.500.5最大辐射方向60度的8元端射式阵因子三维图1、方向性图2、Matlab源程序:a=linspace(0,2*pi);b=linspace(0,pi);fre=300*10^6 %频率lbd=(3*10^8)/fre %波长k=2*pi/lbd %波数N=8 %阵元数d=lbd/4 %间距sita=pi/3 %最大辐射方向kesai=k*d*cos(sita) %相位差fai=k*d*cos(a)+kesaif=sin((fai)*(N/2))./(sin((fai)*(1/2))*N);figure (1)polar(a,-f);title('最大辐射方向60度的8元端射式阵因子H面'); y1=(f.*sin(a))'*cos(b);z1=(f.*sin(a))'*sin(b);x1=(f.*cos(a))'*ones(size(b));figure (2)surf(x1,y1,z1);axis equaltitle('最大辐射方向60度的8元端射式阵因子三维图');3. 在方向性图中确定主瓣宽度估算天线增益=pi/62700最大辐射方向60度的8元端射式阵因子H 面90270最大辐射方向60度的16元端射式阵因子H 面270最大辐射方向60度的32元端射式阵因子H 面用MATLAB 计算:G=10*log10(1/(sin(0.707*(pi/6))))解得:= 4.42五、 实验总结1、改变每幅天线馈电电流的相位可以控制最大增益的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阵列天线方向图函数实验一、 实验目的1. 设计一个均匀线阵,给定d N d ,,,λθ画出方向图)(θF 函数图;2. 改变参数后,画出方向图)(θF 函数图,观察方向图)(θF 的变化并加以分析;3. 分析方向图)(θF 主瓣的衰减情况以及主瓣对第一旁瓣的衰减情况,确定dB3衰减对应的θ;二、 实验原理阵列输出的绝对值与来波方向之间的关系称为天线的方向图。
方向图一般有两类:一类是阵列输出的直接相加(不考虑信号及其来向),即静态方向图;另一类是带指向的方向图(考虑信号指向),当然信号的指向是通过控制加权的相位来实现的。
对于某一确定的M 元空间阵列,在忽略噪声的条件下,第k 个阵元的复振幅为),2,1(0M k e g x k j k ==-ωτ (2.1)式中:0g 为来波的复振幅,k τ为第k 个阵元与参考点之间的延迟。
设第k 个阵元的权值为k w ,那么所有阵元加权的输出得到的阵列的输出为),2,1(010M k e g w Y k j M k k ==-=∑ωτ (2.2)对上式取绝对值并归一化后可得到空间阵列的方向图 {}00max )(Y Y F =θ (2.3)如果),2,1(1M k w k ==式(2.3)即为静态方向图)(θF 。
下面考虑均匀线阵方向图。
假设均匀线阵的间距为d ,且以最左边的阵元为参考点(最左边的阵元位于原点),另假设信号入射方位角为θ,其中方位角表示与线阵法线方向的夹角,与参考点的波程差为θθτsin )1(1)sin (11d k cx c k -== (2.4) 则阵列的输出为βθλπωτ)1(10sin )1(210100--=--=-=∑∑∑===k j Mk k d k j M k k j M k k e g w e g w eg w Y k (2.5) 式中:λθπβ/sin 2d =,λ为入射信号的波长。
当式(2.5)中),2,1(1M k w k ==时,式(2.5)可以进一步简化为)2/sin()2/sin(2)(00βββM M e Mg Y k M j == (2.6) 可得均匀线阵的静态方向图,即)2/sin()2/sin()(0ββθM M F = (2.7) 当式(2.5)中),2,1(,/sin 2,)1(M k d e w d d k j k d ===-λθπββ时,式(2.6)可简化为]2/)sin[(]2/)(sin[2)()1(00d d M j M M e Mg Y d ββββββ--=-= (2.7) 于是可得到指向为d θ的阵列方向图,即]2/)sin[(]2/)(sin[)(d d M M F ββββθ--= (2.8) 三、 实验过程1. 指向0=d θ静态方向图函数的实验1.1均匀线阵阵元个数N 对方向图函数)(θF 的影响sita=-pi/2:0.01:pi/2;lamda=0.03;d=lamda/2;n1=10;sita_d=0beta=2*pi*d*sin(sita)/lamda;beta_d=2*pi*d*sin(sita_d)/lamda;z11=(n1/2)*(beta-beta_d);z21=(1/2)*(beta-beta_d);f1=sin(z11)./(n1*sin(z21));F1=abs(f1);figure(1);plot(sita,F1,'b');hold on ;n2=20;beta=2*pi*d*sin(sita)/lamda;z12=(n2/2)*beta;z22=(1/2)*beta;f2=sin(z12)./(n2*sin(z22));F2=abs(f2);plot(sita,F2,'r');hold on;n3=30;beta=2*pi*d*sin(sita)/lamda;z13=(n3/2)*beta;z23=(1/2)*beta;f3=sin(z13)./(n3*sin(z23));F3=abs(f3);plot(sita,F3,'k')hold off;grid on;xlabel('theta/radian');ylabel('amplitude');title('¾ùÔÈÏßÕóÕóÔª¸öÊý¶Ô·½Ïòͼº¯Êý µÄÓ°Ïì'); legend('n1=10','n2=20','n3=30');分析:随着阵元数的增加,波束宽度变窄,分辨力提高。
1.2均匀线阵间距d对方向图函数)F的影响(sita=-pi/2:0.01:pi/2;lamda=0.03;d1=0.5*lamda;n1=10;sita_d=0;beta=2*pi*d1*sin(sita)/lamda;beta_d=2*pi*d1*sin(sita_d)/lamda;z11=(n1/2)*(beta-beta_d);z21=(1/2)*(beta-beta_d);f1=sin(z11)./(n1*sin(z21));F1=abs(f1);figure(1);plot(sita,F1,'b');hold on;d2=0.9*lamda;beta=2*pi*d2*sin(sita)/lamda;beta_d=2*pi*d2*sin(sita_d)/lamda;z12=(n2/2)*(beta-beta_d);z22=(1/2)*(beta-beta_d);f2=sin(z12)./(n2*sin(z22));F2=abs(f2);plot(sita,F2,'r');hold on ;d3=0.25*lamda;beta=2*pi*d3*sin(sita)/lamda;beta_d=2*pi*d3*sin(sita_d)/lamda;z13=(n3/2)*(beta-beta_d);z23=(1/2)*(beta-beta_d);f3=sin(z13)./(n3*sin(z23));F3=abs(f3);plot(sita,F3,'k')hold off ;grid on ;xlabel('theta/radian');ylabel('amplitude');title('¾ùÔÈÏßÕó¼ä¾à¶Ô·½Ïòͼº¯ÊýµÄÓ°Ïì');legend('d1=0.5*lamda','d2=0.9*lamda','d3=0.25*lamda');分析:当阵元间距2/λ>d 时,会出现栅瓣,导致空间模糊。
1.3入射信号波长λ对方向图函数)(θF 的影响sita=-pi/2:0.01:pi/2;d=0.06lamda1=0.06;n1=10;sita_d=0;beta=2*pi*d1*sin(sita)/lamda1;beta_d=2*pi*d*sin(sita_d)/lamda1;z11=(n1/2)*(beta-beta_d);z21=(1/2)*(beta-beta_d);f1=sin(z11)./(n1*sin(z21));F1=abs(f1);figure(1);plot(sita,F1,'b');hold on ;lamda2=0.12;beta=2*pi*d*sin(sita)/lamda2;beta_d=2*pi*d*sin(sita_d)/lamda2;z12=(n2/2)*(beta-beta_d);z22=(1/2)*(beta-beta_d);f2=sin(z12)./(n1*sin(z22));F2=abs(f2);plot(sita,F2,'r');hold on ;lamda3=0.24;beta=2*pi*d*sin(sita)/lamda3;beta_d=2*pi*d*sin(sita_d)/lamda3;z13=(n3/2)*(beta-beta_d);z23=(1/2)*(beta-beta_d);f3=sin(z13)./(n1*sin(z23));F3=abs(f3);plot(sita,F3,'k')hold off;grid on;xlabel('theta/radian');ylabel('amplitude');title('ÈëÉäÐźŲ¨³¤¶Ô·½Ïòͼº¯ÊýµÄÓ°Ïì');legend('lamda1=0.06','lamda2=0.12','lamda3=0.24');分析:不同的入射波长会改变阵列方向图函数的幅值大小,波长越长,幅值越大。
2.分析静态方向图函数的主瓣对第一旁瓣的衰减情况,确定dB3衰减对应的θ;sita=-pi/2:0.01:pi/2;d=0.06lamda=0.12;n1=10;sita_d=0;beta=2*pi*d1*sin(sita)/lamda1;beta_d=2*pi*d*sin(sita_d)/lamda1;z11=(n1/2)*(beta-beta_d);z21=(1/2)*(beta-beta_d);f1=sin(z11)./(n1*sin(z21));F1=abs(f1);figure(1);plot(sita,F1,'b');hold onplot(sita,0.5,'r');hold offgrid on;xlabel('theta/radian');ylabel('amplitude');title('Ö÷°êË¥¼õ·ÖÎö¼°Ë¥¼õ´ø¿íµÄÈ·¶¨n=10,d=0.06,lamda=0.12');分析:通过对坐标轴的细化,可以看出确定dB3衰减对应的θ宽度为28.7度,第一旁瓣对主瓣的衰减为24%左右,衰减较迅速。
