八年级数学一次函数和反比例函数
反比例函数与一次函数

反比例函数与一次函数1.函数自变量的取值范围自变量的取值范围必须使含有自变量的表达式都有意义.①当表达式的分母不含有自变量时,自变量取全体实数.例如y=2x+13中的x.②当表达式的分母中含有自变量时,自变量取值要使分母不为零.例如y=x+2x﹣1.③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.2.函数的图象函数的图象定义:对于一个函数,如果把自变量与函数的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象.注意:①函数图形上的任意点(x,y)都满足其函数的解析式;②满足解析式的任意一对x、y的值,所对应的点一定在函数图象上;③判断点P(x,y)是否在函数图象上的方法是:将点P(x,y)的x、y的值代入函数的解析式,若能满足函数的解析式,这个点就在函数的图象上;如果不满足函数的解析式,这个点就不在函数的图象上.3.函数的表示方法函数的三种表示方法:____、____、____.其特点分别是:列表法能具体地反映自变量与函数的数值对应关系,在实际生活中应用非常广泛;解析式法准确地反映了函数与自变量之间的对应规律,根据它可以由自变量的取值求出相应的函数值,反之亦然;图象法直观地反映函数值随自变量的变化而变化的规律.注意:①它们分别从数和形的角度反映了函数的本质;②它们之间可以互相转化.4.反比例函数的性质反比例函数的性质:(1)反比例函数y=xk(k≠0)的图象是____;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.注意:反比例函数的图象与坐标轴没有交点.5.反比例函数图象上点的坐标特征反比例函数y=xk(k为常数,k≠0)的图象是双曲线,①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.6.待定系数法求反比例函数解析式用待定系数法求反比例函数的解析式要注意:(1)设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.7.反比例函数的应用(1)利用反比例函数解决实际问题:①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.(2)跨学科的反比例函数应用题要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.(3)反比例函数中的图表信息题正确的认识图象,找到关键的点,运用好数形结合的思想.8.反比例函数综合题(1)应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能力和从实际问题向数学问题转化的能力.在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识.(2)数形结合类综合题利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.9.一次函数的图象(1)一次函数的图象的画法:经过两点(0,b)、(﹣bk,0)或(1,k+b)作直线y=kx+b.注意:①使用两点法画一次函数的图象,不一定就选择上面的两点,而要根据具体情况,所选取的点的横、纵坐标尽量取整数,以便于描点准确.②一次函数的图象是与坐标轴不平行的一条直线(正比例函数是过原点的直线),但直线不一定是一次函数的图象.如x=a,y=b 分别是与y 轴,x 轴平行的直线,就不是一次函数的图象.(2)一次函数图象之间的位置关系:直线y=kx+b,可以看做由直线y=kx 平移|b|个单位而得到.当b>0时,向上平移;b<0时,向下平移.注意:①如果两条直线平行,则其比例系数相等;反之亦然;②将直线平移,其规律是:________;③两条直线相交,其交点都适合这两条直线.10.一次函数图象与系数的关系由于y=kx+b 与y 轴交于(0,b),当b>0时,(0,b)在y 轴的正半轴上,直线与y 轴交于正半轴;当b<0时,(0,b)在y 轴的负半轴,直线与y 轴交于负半轴.①k>0,b>0⇔y=kx+b 的图象在一、二、三象限;②k>0,b<0⇔y=kx+b 的图象在一、三、四象限;③k<0,b>0⇔y=kx+b 的图象在一、二、四象限;④k<0,b<0⇔y=kx+b 的图象在二、三、四象限.11.两条直线相交或平行问题直线y=kx+b,(k≠0,且k,b 为常数),当k 相同,且b 不相等,图象平行;当k 不同,且b 相等,图象相交;当k,b 都相同时,两条线段重合.(1)两条直线的交点问题两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.(2)两条直线的平行问题若两条直线是平行的关系,那么他们的自变量系数相同,即k 值相同.例如:若直线y 1=k 1x+b 1与直线y 2=k 2x+b 2平行,那么k 1=k 2.12.一次函数的应用1、分段函数问题分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.2、函数的多变量问题解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数.3、概括整合(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用.(2)理清题意是采用分段函数解决问题的关键.13.一次函数综合题(1)一次函数与几何图形的面积问题首先要根据题意画出草图,结合图形分析其中的几何图形,再求出面积.(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x的取值范围,进而利用一次函数的增减性在前面范围内的前提下求出最值.(3)用函数图象解决实际问题从已知函数图象中获取信息,求出函数值、函数表达式,并解答相应的问题.14.反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.(2)判断正比例函数y=k1x和反比例函数y=在同一直角坐标系中的交点个数可总结为:①当k1与k2同号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有2个交点;②当k1与k2异号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有0个交点.1.函数自变量的取值范围;分式有意义的条件;二次根式有意义的条件.【例1】(2014•成都双流中学期末)在函数中,自变量x的取值范围是()A.x<B.x≠﹣C.x≠D.x>练1.(2014春•湘潭中学质检)下列函数中,自变量x的取值范围是x≥3的是()A.y=B.y=C.y=x﹣3D.y=2.待定系数法求反比例函数解析式;反比例函数的性质.【例2】(2014•山西中考一模)如果反比例函数的图象经过点(﹣2,﹣3),那么k的值为()A.B.C.﹣6D.6练2.已知反比例函数y=的图象经过点P(﹣1,2),则这个函数的图象位于()A.第二,三象限B.第一,三象限C.第三,四象限D.第二,四象限3.反比例函数图象上点的坐标特征.【例3】(2014•河北博野县一模)点M (﹣2,3)在曲线y=上,则下列点一定在该曲线上的是()A.(2,3)B.(﹣2,﹣3)C.(3,﹣2)D.(3,2)练3.已知点P(m,n)在某反比例函数的图象上,则此图象上还有点()A.(0,0)B.(﹣m,﹣n)C.(m,﹣n)D.(﹣m,n)4.一次函数的图象.【例4】(2014•秋•宜昌校级月考)关于x 的一次函数y=kx+k 2+1的图象可能正确的是()A.B.C.D.练4.已知函数y=kx+b 的图象如图,则y=2kx+b 的图象可能是()A.B.C.D.5.反比例函数与一次函数的交点问题.【例5】(2014•东营中学期中)如图所示,反比例函数y 1与正比例函数y 2的图象的一个交点坐标是A(2,1),若y 2>y 1>0,则x 的取值范围在数轴上表示为()A.B.C.D.练5.如图,反比例函数y=的图象与直线y=x+m 在第一象限交于点P(6,2),A、B 为直线上的两点,点A 的坐标为2,点B 的横坐标为3.D、C 为反比例函数图象上的两点,且AD、BC 平行于y 轴.(1)直接写出k,m 的值;(2)求梯形ABCD 的面积.1.若一次函数y=kx+b(k≠0)的函数值y随x的增大而增大,则()A.k<0B.k>0C.b<0D.b>02.如果函数y=ax+b(a<0,b<0)和y=kx(k>0)的图象交于点P,那么点P应该位于()A.第一象限B.第二象限C.第三象限D.第四象限3.小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图象大致是()A.B.C.D.4.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:则m与v之间的关系最接近于下列各关系式中的()m1234v0.01 2.98.0315.1A.v=2m﹣2B.v=m2﹣1C.v=3m﹣3D.v=m+15.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度为y(cm)与燃烧时间x(小时)的函数关系用图象表示为下图中的()A.B.C.D.6.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应()A.不小于4.8ΩB.不大于4.8ΩC.不小于14ΩD.不大于14Ω__________________________________________________________________________________________________________________________________________________________________1.矩形面积为4,它的长y与宽x之间的函数关系用图象大致可表示为()A.B.C.D.2.为了预防“HINI”流感,某校对教室进行药熏消毒,药品燃烧时,室内每立方米的含药量与时间成正比;燃烧后,室内每立方米含药量与时间成反比,则消毒过程中室内每立方米含药量y与时间t的函数关系图象大致为()A.B.C.D.3.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应()A.不小于4.8ΩB.不大于4.8ΩC.不小于14ΩD.不大于14Ω4.设从茂名到北京所需的时间是t,平均速度为v,则下面刻画v与t的函数关系的图象是()A.B.C.D.)与它的体积v(m3)5.根据物理学家波义耳1662年的研究结果:在温度不变的情况下,气球内气体的压强p(pa 的乘积是一个常数k,即pv=k(k为常数,k>0),下列图象能正确反映p与v之间函数关系的是()A.B.C.D.6.如图,一次函数y=kx+b的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.(1)试确定上述反比例函数和一次函数的表达式;(2)求△AOB的面积.7.某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?8.为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:(1)求药物燃烧时y与x的函数关系式;(2)求药物燃烧后y与x的函数关系式;(3)当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经多长时间学生才可以返回教室?。
八年级数学一次函数和反比例函数

[单选,A1型题]关于99mTc-MDP骨显像,显像剂被脏器或组织摄取的机制是()A.化学吸附B.细胞吞噬C.选择性浓聚D.选择性排泄E.通透弥散 [单选]在感光丝网制版法中,耐印力最高的方法是()。A.直接法B.间接法C.直间法 [单选]在仪表专业中,现场压力变送器常常用符号PIT表示,其中I表示()。A、电流B、压力C、电压D、带指示功能 [单选,A2型题,A1/A2型题]下面与颅脑MRI技术无关的项是()A.检查病人是否有禁忌物品B.线圈用头部正交线圈C.脑梗死、颅内出血和脑的先天畸形等一般只需做平扫D.相位编码方向:横断位取前后向E.血管性病变常做平扫加血管成像 [判断题]搬运装卸润滑脂,应尽可能轻拿轻放,避免过重地碰摔,包装桶损坏、密封不严、混入外界杂质或渗入雨水会使脂变质,运输中要盖好盖,做好防雨措施。()A.正确B.错误 [单选,A2型题,A1/A2型题]下列哪味是治疗梅毒的药物()A.马钱子B.黄连C.轻粉D.硼砂E.蛇床子 [单选]税收地方性法规的效力高于()。A.税收行政法规B.税收授权立法C.税收地方政府规章D.税收部门规章 [单选]信息处理的步骤不包括()。A.信息筛选B.信息交流C.信息存储D.信息使用 [单选,A1型题]学龄前期的保健要点不包括()A.平衡膳食B.定期检查儿童的视力、听力和牙齿C.开展健康教育D.促进思维发展E.预防意外事故 [填空题]如果需要在吊起的()、()以及汽缸盖下面进行清理结合面、涂抹涂料等工作时,应使用专用(),由检修工作负责人()后方可进行。 [单选]Aluminumlifeboatsaresubjecttodamagebyelectrolyticcorrosion(thealuminumbeingeatenaway).Inworkingaroundboatsofaluminumyoumustbeverycareful().A.tokeeptheboatscoveredatalltimesB.nottoleavesteelorirontoolslyinginorneartheseboatsC.tokeepanelectricchargeonth [单选,A1型题]指出有关甲沟炎的错误描述()。A.甲沟炎可因剪指甲过深引起B.非嵌甲引起的甲沟炎也可拔甲治疗C.甲沟炎不会引起指骨骨髓炎D.脓液可蔓延至对侧E.可形成甲根部环形脓肿 [单选]急性盆腔炎的主要症状()A.下腹疼痛难忍,伴高热不退B.腹胀,恶心呕吐C.尿频尿急D.白带增多E.下腹一侧撕裂样痛 [单选]()是指一个测验的结果与被测验者行为的公认标准之间的相关程度。A.信度B.效度C.难度D.标准化 [单选]排水沟沿道路布置时,纵坡至少不得小于()。A.0.2%B.0.4%C.0.6%D.0.8% [单选]在劳动争议调解中,贯彻"三方原则"体现了()的社会救济机制的特点。A.权利B.义务C.责任D.利益 [单选,A2型题,A1/A2型题]下列哪项叙述是错误的()A.皇甫谧著《针灸甲乙经》B.杨继洲著《针灸大成》C.徐凤著《针灸大全》D.高武著《十四经发挥》E.李时珍著《奇经八脉考》 [单选]以下治疗甲状腺危象的方案中,最完善的是()A.抗甲状腺药物、强心药、镇静剂、抗生素B.抗甲状腺药物、强心药、镇静剂、β受体阻滞剂C.大剂量抗甲状腺药物、糖皮质激素、镇静剂D.大剂量丙硫氧嘧啶、大量复方碘溶液、糖皮质激素、β受体阻滞剂E.大剂量复方碘溶液、糖 [单选]一般情况下,下列关于外部融资需求的表述正确的是()。A.敏感负债总额越大,外部融资需求越大B.销售净利率越大,外部融资需求越大C.股利支付率越高,外部融资需求越大D.股利支付率越低,外部融资需求越大 [单选]下列()不是保安押运人员的基本素质要求。A.遵纪守法B.特立独行C.严于律己D.团结协作 [填空题]人类学家从非洲、亚洲、欧洲发现古人类化石,得出人类起源于人猿,从猿到人的科学结论,并以三大洲的人型体质特征将人类化分为:()、()、()。 [名词解释]CoD值 [单选,A2型题,A1/A2型题]导致腱反射亢进的病损部位为()。A.脊神经后根B.脊髓前角C.脊髓后索D.锥体束E.锥体外系 [单选,A1型题]共同参与型的医患关系模式最适合于()。A.急性病人B.绝症病人C.慢性病人D.重症病人E.精神病人 [单选]根据支付结算法律制度的规定,下列票据欺诈行为中,属于伪造票据的是()。A.假冒出票人在票据上签章B.涂改票据号码C.对票据金额进行挖补篡改D.修改票据密押 [单选]捻转补泻法中的补法是()。A.捻转角度大,频率慢,用力轻B.捻转角度小,频率快,用力重C.捻转角度大,频率快,用力重D.捻转角度小,频率慢,用力轻E.捻转角度小,频率慢,用力重 [单选]驾驶厂内机动车,应当依法取得()A、操作上岗证B、驾驶证C、企业内部通行证 [问答题,案例分析题]B企业拟在A市郊区原A市卷烟厂厂址处(现该厂已经关闭)新建屠宰量为120万头猪/年的项目(仅屠宰,无肉类加工),该厂址紧临长江干流,A市现有正在营运的日处理规模为3万t的城市污水处理厂,距离B企业1.5km。污水处理厂尾水最终排入长江干流(长江干流在A市段 [多选]对于安装工程施工图预算,可采用()编制单位工程施工图预算。ABCD [单选]皮肤表皮分为5层,其中最外层是()A.棘层B.基底层C.角质层D.透明层E.颗粒层 [单选]工程造价的确定要根据不同的建设阶段,分次进行。这种计价特点被称为()。A.单件性计价B.分部组合计价C.多次性计价D.按构成计价 [问答题,简答题]在电气化区段清除危石、危树时,应有那些部门人员配合? [单选,A2型题,A1/A2型题]《医疗机构从业人员行为规范》适用于那些人员?()A.医疗机构的医生、护士、药剂、医技人员B.医疗机构的医护及后勤人员C.医疗机构的管理、财务、后勤等人员D.药学技术人员E.医疗机构内所有从业人员 [多选]关节镜手术的禁忌证有()。A.早中期类风湿关节炎B.有出血性疾患,出血倾向得到控制后C.关节局部皮肤感染D.类风湿关节炎或骨关节炎患者关节间隙严重狭窄者E.色素绒毛结节性滑膜炎病变侵犯软骨下骨者 [单选]不能转入“本年利润”账户借方的是()账户。A、生产成本B、主营业务成本C、管理费用D、财务费用 [问答题,简答题]GMP的中文名称是? [多选]按风机排出气体压力高低,风机可分为()。A.送风机B.通风机C.鼓风机D.压缩机 [单选]水力清淤时,应该注意()。A、在用水季节施行B、按先下游后上游,分阶段进行C、引入含沙量较少的清水D、关闭一切闸门 [单选]类风湿关节炎最早的关节症状是()。A.关节疼痛B.关节畸形C.梭形肿大D.皮肤发红E.关节强直 [填空题]电子商务系统是由()、()、()、()和()五介部份组成。
【中考数学复习】一次函数与反比例函数知识
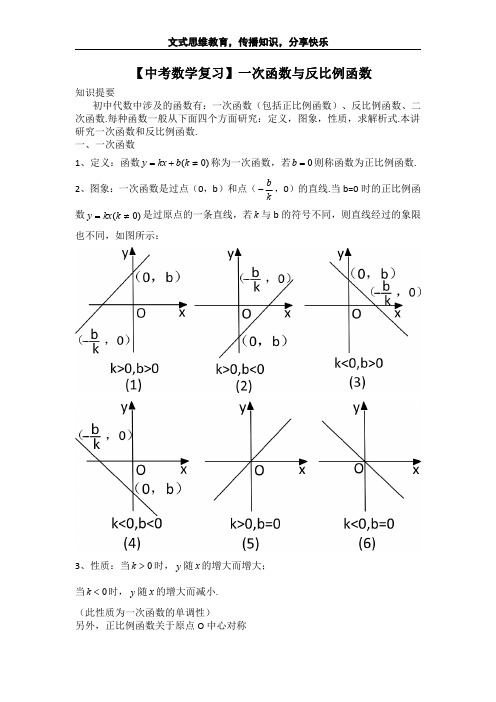
【中考数学复习】一次函数与反比例函数知识提要初中代数中涉及的函数有:一次函数(包括正比例函数)、反比例函数、二次函数.每种函数一般从下面四个方面研究:定义,图象,性质,求解析式.本讲研究一次函数和反比例函数.一、一次函数1、定义:函数)0(≠+=k b kx y 称为一次函数,若0=b 则称函数为正比例函数.2、图象:一次函数是过点(0,b )和点(kb -,0)的直线.当b=0时的正比例函数)0(≠=k kx y 是过原点的一条直线,若k 与b 的符号不同,则直线经过的象限也不同,如图所示:3、性质:当0>k 时,y 随x 的增大而增大;当0<k 时,y 随x 的增大而减小.(此性质为一次函数的单调性)另外,正比例函数关于原点O 中心对称4、求解析式:求一次函数的解析式,一般需要两个条件,求出表达式b kx y +=中的k 及b 的值,常用待定系数法来求一次函数.而正比例函数的解析式只需要一个条件.二、反比例函数1、定义:形如)0(≠=k x k y 形式称为反比例函数,定义域为0≠x 的所有实数.2、图象:反比例图象为双曲线,如图所示:3、性质:反比例函数x k y =在0>k 且0>x 时,函数值y 随x 的增大而减小;在0>k 且0<x 时,函数值y 随x 的增大而减小.即:当0>k 时,反比例函数x k y =分布在一、三象限,在每个象限内,y 随x 的增大而减小,如图(1)所示.当0<k 时,反比例函数xk y =分布在二、四象限,在每个象限内,y 随x 的增大而增大,如图(2)所示.反比例函数x k y =图象上的点关于原点O 成中心对称的.当0>k 时,函数的图象关于直线x y =成轴对称;当0<k 时,函数的图象关于直线x y -=成轴对称.4、求解析式:反比例函数的解析式,只需要一个条件,求出xk y =)0(≠k 中的k 即可.在解决有关一次函数及反比例函数的问题时,常运用数形结合及分类讨论的思想方法.待定系数法是研究函数表达式的基本方法,同时紧密结合图象寻求思路,是处理这类问题的重要方法.例1、已知正比例函数x y =和)0(>=a ax y 的图象与反比例函数xky =(k>0)的图象在第一象限内分别相交于A 、B 两点,过A 、B 作x 轴的垂线,垂足分别为C 、D ,设△AOC 和△BOD 的面积分别为1S 、2S ,则1S 与2S 的大小关系怎样?例2、两个反比例函数x y 3=,x y 6=在第一象限内的图象如图所示,点1P ,2P ,3P ,…2005P 在反比例函数x y 6=图象上,它们的横坐标分别是1x ,2x ,3x ,…2005x ,纵坐标分别是1,3,5,…,共2005个连续奇数,过点1P ,2P ,3P ,…2005P 分别作y 轴的平行线,与xy 3=的图象交点依次是)(111y x Q ,,)(222y x Q ,,)(333y x Q ,,…)(200520052005y x Q ,,则_________2005=y .例3、平面直角坐标系内有A (2,-1)、B (3,3)两点,点P 是y 轴上一动点,求P 到A 、B 距离之和最小时的坐标.例4、已知一次函数的图象经过点(2,2),它与两坐标轴所围成的三角形的面积等于1,求这个一次函数的解析式.例5、已知A (-2,0)、B (4,0),点P 在直线221+=x y 上,若△PAB 是直角三角形,求点P 的坐标.例6、已知两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供两个方面的信息,如图所示,请根据图中提供的信息,求:(1)第2年全县生产甲鱼的只数及甲鱼池的个数;(2)到第6年,这个县的甲鱼养殖规模比第1年是扩大了还是缩小了,请说明理由.例7、如图,已知C 、D 是双曲线xm y =在第一象限内的分支上的两点,直线CD 分别交x 轴、y 轴于A 、B 两点,设C 、D 的坐标分别是(11y x ,)、(22y x ,),连接OC 、OD.(1)求证:111y m y OC y +<<;(2)若α=∠=∠AOD BOC ,31tan =α,10=OC ,求直线CD 的解析式.(3)在(2)的条件下,双曲线是否存在一点P ,使POD POC S S ∆∆=?若存在,求出P 点坐标;若不存在,请说明理由.例8、有一个附有进、出水管的容器,每单位时间进、出的水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水又出水,得到时间x (分)与水量y (升)之间的关系如图所示,若20分钟后只放水不进水,求多长时间能将水放完?例9、为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y (毫克)与时间x (分钟)成正比例,药物燃烧后,y 与x 成反比例(如图),观测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息解答下列问题:(1)药物燃烧时,y 关于x 的函数关系式为__________,自变量x 的取值范围是___________;药物燃烧后y 关于x 的函数关系式为____________.(2)研究表明,当空气中的每立方米含药量低于1.6毫克时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室.(3)研究表示,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?例10、某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表所示:家电名称空调器彩电冰箱工时/个213141产值/千元432问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)练习1、已知0≠abc 并且p b a c a c b c b a =+=+=+而直线p px y +=一定通过()A 第一、二象限B 第二、三象限C 第三、四象限D 第一、四象限2、函数kx y =和)0(<=k x k y 在同一坐标系中的图象是()3、一次函数b kx y +=过点)(11y x ,和)(22y x ,,且0>k ,b<0,当210x x <<时,有()A 21y b y >>B 21y b y <<C b y y <<<210D 012<<<y b y 4、若点(-2,1y ),(1,2y ),(2,3y )在反比例函数x y 21=的图象上,则下列结论正确的是()A 123y y y >>B 312y y y >>C 132y y y >>D 321y y y >>5、反比例函数x k y =的图象是轴对称图形,它的一条对称轴是下列正比例函数图象中的()A kxy -=B x k y =C x k k y =D kxy =6、一个一次函数图象与直线49545+=x y 平行,与x 轴、y 轴的交点分别为A 、B ,并且过点(-1,-25),则在线段AB 上(包括端点A 、B ),横、纵坐标都是整数的点有()A 4个B 5个C 6个D 7个7、如图,正比例函数x y 3=的图象与反比例函数xk y =(0>k )的图象交于点A ,若取k 为1,2,3,…,20,对应的Rt △AOB 的面积分别为1S ,2S ,…20S ,则__________2021=+++S S S .8、不论k 为何值,解析式0)11()3()12(=--+--k y k x k 表示函数的图象都经过一定点,则这个定点是_________.9、如图所示,直线l 和双曲线x k y =(0>k )交于A 、B 两点,P 是线段AB 上的点(不与A 、B 重合),过点A 、B 、P 分别向x轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、OP.设△AOC 的面积为1S ,△BOD 的面积为2S ,△POE 的面积为3S ,则321S S S 、、的大小关系是______________.10、甲、乙两车出发后再同一条公路行驶,行驶路程与时间的关系如图所示,那么可以知道:(1)出发行驶在前面的车是_________,此时两车相隔_________;(2)两车的速度分别为甲:___________千米/小时,乙:_________千米/小时,经过___________小时,快车追上慢车;(3)甲、乙两车均行驶600千米时各用的时间分别是:甲用_________小时,乙用__________小时.11、如图,函数221+-=x y 的图象交y 轴于M ,交x 轴于N ,MN 上两点A ,B 在x 轴上射影分别为11B A 、,若411>+OB OA ,则A OA 1∆的面积1S 与B OB 1∆的面积2S 的大小关系是_____________.12、已知非负数x 、y 、z 满足323=++z y x ,433=++z y x ,则z y x w 423+-=的最大值为_________,最小值为__________.13、在直角坐标系中,有四个点:A (-8,3),B (-4,5),C (0,n ),D (m ,0),当四边形ABCD 的周长最短时,求nm 的值.14、设直线1)1(=++y k kx (k 是自然数)与两坐标轴所围成的图形的面积为1S ,2S ,…,2000S .求200021S S S +++ 的值.15、如图(1),已知直线m x y +-=21与反比例函数xk y =的图象在第一象限内交于A 、B 两点(点A 在点B 的左侧),分别于x 、y 轴交于C 、D ,AE ⊥x 轴于E.(1)若OE·CE=12,求k 的值;(2)如图(2),作BF ⊥y 轴于F ,求证:EF ∥CD ;(3)在(1)(2)的条件下,5=EF ,52=AB ,P 是x 轴正半轴上一点,且△PAB 是以P 为直角顶点的等腰直角三角形,求P 点的坐标.(1)(2)16、已知直线62+-=-k y x 和143+=+k y x ,若它们的交点在第四象限内.(1)求k 的取值范围;(2)若k 为非负整数,点A 的坐标为(2,0),点P 在直线62+-=-k y x 上,求使△PAO 为等腰三角形的点P 的坐标.17、A 市、B 市和C 市分别有某种机器10台、10台和8台,现决定把这些机器支援给D 市18台,E 市10台.已知从A 市调运一台机器到D 市、E 市的运费分别为200元和800元,从B 市调运一台机器到D 市、E 市的运费分别为300元和700元,从C 市调运一台机器到D 市、E 市的运费分别为400元和500元.(1)设从A 市、B 市各调x 台到D 市,当28台机器全部调运完毕后,求总运费w (元)关于x (台)的函数式,并求w 的最大值和最小值;(2)设从A 市调x 台到D 市,从B 市调y 台到D 市,当28台机器全部调运完毕后,用x ,y 表示总运费w (元),并求w 的最大值和最小值.18、直线133+-=x y 与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作等腰直角三角形ABC ,其中∠BAC=90°.如果第二象限内有一点P (a ,21),使△ABP 的面积和△ABC 的面积相等,求a 的值.文式思维教育,传播知识,分享快乐19、如图,在直角坐标系中,点1O 的坐标为(1,0),⊙1O 与x 轴交于原点O 和点A ,又点B 、C 的坐标分别为(-1,0),(0,b ),且30<<b ,直线l 是过B 、C 点的直线.(1)当点C 在线段OC 上移动时,过点1O 作l D O 直线⊥1,交l 于D ,若a S S CBO BOC=∆∆1,试求b a 与的函数关系式及a 的取值范围.20、某仓储系统有20条输入传送带、20条输出传送带.某日,控制室的电脑显示,每条输入传送带每小时进库的货物流量如图(a ),每条输出传送带每小时出库的货物流量如图(b ),而该日仓库中原有货物8吨,在0时至5时,仓库中货物存量变化情况如图(c ),则在0时至2时有多少条输入传送带在工作?在4至5时有多少条输入传送带和输出传送带在工作?。
八年级反比例函数和一次函数综合题型含答案解析

反比例函数与一次函数综合一.选择题(共12小题)1.已知反比例函数的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,M n,则= _________ .2.如图,正比例函数y=kx(k>0)与反比例函数y=的图象相交于A、C两点,过A作x轴的垂线,交x轴于点B,连接BC.若△ABC的面积为S,则()3.如图,已知点A是一次函数的图象与反比例函数的图象在第一象限的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且OA=OC,△AOB的面积为,则AC的长为()4.已知直线y1=x,,的图象如图所示,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为()5.如图,直线y=+3与双曲线y=(x>0)相交于B,D两点,交x轴于C点,若点D是BC的中点,则k=()6.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的个数有()A.2B.3C.4D.57.函数的图象如图所示,则结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③当x=1时,BC=3;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是()A.①③④B.①②③C.②③④D.①②③④8.如图,已知一次函数y=x+1的图象与反比例函数y=的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x 轴于B,△AOB的面积为1,则AC的长为()9.正比例函数y=x与反比例函数的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD 的面积为()10.如图,直线AB交y轴于点C,与双曲线(k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),Q为线段BC上的点(不与B、C重合),过点A、P、Q分别向x轴作垂线,垂足分别为D、E、F,连接OA、OP、OQ,设△AOD的面积为S1、△POE的面积为S2、△QOF的面积为S3,则有()11.如图,点A是直线y=﹣x+5和双曲线在第一象限的一个交点,过A作∠OAB=∠AOX交x轴于B点,AC⊥x 轴,垂足为C,则△ABC的周长为()12.如图,函数y=x与y=的图象交于A、B两点,过点A作AC垂直于y轴,垂足为C,则△BOC的面积为()二.解答题(共18小题)13.如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C.(1)分别求反比例函数和一次函数的解析式(关系式);(2)连接OA,求△AOC的面积.14.如图,一次函数y=x+1与反比例函数的图象相交于点A(2,3)和点B.(1)求反比例函数的解析式;(2)求点B的坐标;(3)过点B作BC⊥x轴于C,求S△ABC.15.如图,直线y=x与双曲线y=相交于A、B两点,BC⊥x轴于点C(﹣4,0).(1)求A、B两点的坐标及双曲线的解析式;(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.16.如图,已知反比例函数(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC 的面积为1,且tan∠AOC=2.(1)求出反比例函数与一次函数的解析式;(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?17.如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.18.如图,已知函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.(1)求一次函数的解析式;(2)将一次函数y=kx+b的图象沿x轴负方向平移a(a>0)个单位长度得到新图象,求这个新图象与函数的图象只有一个交点M时a的值及交点M的坐标.19.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于M(﹣2,1),N(1,t)两点.(1)求k、t的值.(2)求一次函数的解析式.(3)在x轴上取点A(2,0),求△AMN的面积.20.如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.21.已知一次函数y=kx+b的图象与反比例函数的图象相交于A,B两点,其中A点的横坐标与B点的纵坐标都是2,如图:(1)求这个一次函数的解析式;(2)求△AOB的面积;(3)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请在坐标轴相应位置上用P1,P2,P3…标出符合条件的点P;(尺规作图完成)若不存在,请说明理由.22.如图,反比例函数y=的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,﹣1).(1)求反比例函数与一次函数的函数关系式;(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;(3)连接AO、BO,求△ABO的面积;(4)在反比例函数的图象上找点P,使得点A,O,P构成等腰三角形,直接写出两个满足条件的点P的坐标.23.如图,已知反比例函数的图象经过点,过点A作AB⊥x轴于点B,且△AOB的面积为.(1)求k和m的值;(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点C,求|AO|:|AC|的值;(3)若D为坐标轴上一点,使△AOD是以AO为一腰的等腰三角形,请写出所有满足条件的D点的坐标.24.阅读下面材料,然后解答问题:在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.(1)求a、b、k的值及点C的坐标;(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.25.(如图,已知反比例函数(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).(1)求一次函数的关系式;(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=(O为坐标原点),求反比例函数的关系式;(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.26.如图.已知A、B两点的坐标分别为A(0,),B(2,0).直线AB与反比例函数的图象交于点C和点D(﹣1,a).(1)求直线AB和反比例函数的解析式.(2)求∠ACO的度数.(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少时,OC′⊥AB,并求此时线段AB’的长.27.如图,在平面直角坐标系中,点O为原点,反比例函数y=的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.(1)求反比例函数的关系式;(2)直接写出菱形OABC的面积.28.如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.(1)求k的值;(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、NA′BC.设线段MC′、NA′分别与函数(x >0)的图象交于点E、F,求线段EF所在直线的解析式.29.如图所示,直线y=kx+6与函数y=(x>0,m>0)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点,且与x轴、y轴分别交于D、C两点.又AE⊥x轴于E,BF⊥x轴于F.已知△COD的面积是△AOB面积的倍.(1)求y1﹣y2的值.(2)求k与m之间的函数关系式,并画出该函数图象的草图.(3)是否存在实数k和m,使梯形AEFB的面积为6?若存在,求出k和m的值;若不存在,请说明理由.30.●探究:(1)在图中,已知线段AB,CD,其中点分别为E,F.①若A(﹣1,0),B(3,0),则E点坐标为_________ ;②若C(﹣2,2),D(﹣2,﹣1),则F点坐标为_________ ;(2)在图中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d 的代数式表示),并给出求解过程.●归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y)时,x= _________ ,y= _________ .(不必证明)●运用:在图中,一次函数y=x﹣2与反比例函数的图象交点为A,B.①求出交点A,B的坐标;②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标.八年级反比例函数与一次函数综合参考答案与试题解析一.选择题(共12小题)1.(2012•江)已知反比例函数的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,M n,则= .2.(2000•天津)如图,正比例函数y=kx(k>0)与反比例函数y=的图象相交于A、C两点,过A作x轴的垂线,交x轴于点B,连接BC.若△ABC的面积为S,则()3.如图,已知点A是一次函数的图象与反比例函数的图象在第一象限的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且OA=OC,△AOB的面积为,则AC的长为()4.已知直线y1=x,,的图象如图所示,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为()5.如图,直线y=+3与双曲线y=(x>0)相交于B,D两点,交x轴于C点,若点D是BC的中点,则k=()∴x1=2×4﹣6=2,由③2k=x1x2=8,那么k=4.故选D.点评:此题主要考查了一次函数与反比例函数的交点坐标问题,同时也利用了中点坐标的公式,其中利用方程组和待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.6.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的个数有()A.2B.3C.4D.57.函数的图象如图所示,则结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③当x=1时,BC=3;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是()8.如图,已知一次函数y=x+1的图象与反比例函数y=的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x 轴于B,△AOB的面积为1,则AC的长为()9.正比例函数y=x与反比例函数的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D(如图),则四边形ABCD 的面积为()10.如图,直线AB交y轴于点C,与双曲线(k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),Q为线段BC上的点(不与B、C重合),过点A、P、Q分别向x轴作垂线,垂足分别为D、E、F,连接OA、OP、OQ,设△AOD的面积为S1、△POE的面积为S2、△QOF的面积为S3,则有()11.如图,点A是直线y=﹣x+5和双曲线在第一象限的一个交点,过A作∠OAB=∠AOX交x轴于B点,AC⊥x 轴,垂足为C,则△ABC的周长为()12.如图,函数y=x与y=的图象交于A、B两点,过点A作AC垂直于y轴,垂足为C,则△BOC的面积为()二.解答题(共18小题)13.(2012•)如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C.(1)分别求反比例函数和一次函数的解析式(关系式);(2)连接OA,求△AOC的面积.14.(2012•)如图,一次函数y=x+1与反比例函数的图象相交于点A(2,3)和点B.(1)求反比例函数的解析式;(2)求点B的坐标;(3)过点B作BC⊥x轴于C,求S△ABC.15.(2012•贵港)如图,直线y=x与双曲线y=相交于A、B两点,BC⊥x轴于点C(﹣4,0).(1)求A、B两点的坐标及双曲线的解析式;(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.16.(2011•)如图,已知反比例函数(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.(1)求出反比例函数与一次函数的解析式;(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?17.(2011•)如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.18.(2011•)如图,已知函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.(1)求一次函数的解析式;(2)将一次函数y=kx+b的图象沿x轴负方向平移a(a>0)个单位长度得到新图象,求这个新图象与函数的图象只有一个交点M时a的值及交点M的坐标.19.(2010•)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于M(﹣2,1),N(1,t)两点.(1)求k、t的值.(2)求一次函数的解析式.(3)在x轴上取点A(2,0),求△AMN的面积.20.(2009•达州)如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.21.已知一次函数y=kx+b的图象与反比例函数的图象相交于A,B两点,其中A点的横坐标与B点的纵坐标都是2,如图:(1)求这个一次函数的解析式;(2)求△AOB的面积;(3)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请在坐标轴相应位置上用P1,P2,P3…标出符合条件的点P;(尺规作图完成)若不存在,请说明理由.点评:此题主要考查了一次函数、反比例函数、待定系数法以及等腰三角形的性质等,难易程度适中.22.如图,反比例函数y=的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,﹣1).(1)求反比例函数与一次函数的函数关系式;(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;(3)连接AO、BO,求△ABO的面积;(4)在反比例函数的图象上找点P,使得点A,O,P构成等腰三角形,直接写出两个满足条件的点P的坐标.考点:反比例函数与一次函数的交点问题.专题:待定系数法.分析:(1)根据待定系数法就可以求出函数的解析式;(2)观察图象可得出一次函数的值大于反比例函数的值时,x的取值围;(3)先求出一次函数与x轴的交点坐标,再利用分割法将三角形的面积分为△BOC和△AOC的面积之和进行求解;23.如图,已知反比例函数的图象经过点,过点A作AB⊥x轴于点B,且△AOB的面积为.(1)求k和m的值;(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点C,求|AO|:|AC|的值;(3)若D为坐标轴上一点,使△AOD是以AO为一腰的等腰三角形,请写出所有满足条件的D点的坐标.24.(2012•)阅读下面材料,然后解答问题:在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.(1)求a、b、k的值及点C的坐标;(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.25.(2011•)如图,已知反比例函数(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).(1)求一次函数的关系式;(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=(O为坐标原点),求反比例函数的关系式;(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.26.(2011•)如图.已知A、B两点的坐标分别为A(0,),B(2,0).直线AB与反比例函数的图象交于点C和点D(﹣1,a).(1)求直线AB和反比例函数的解析式.(2)求∠ACO的度数.(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少时,OC′⊥AB,并求此时线段AB’的长.。
反比例函数与一次函数交点线段相等

反比例函数与一次函数交点线段相等是一个重要的数学问题,它涉及到两种不同类型的函数之间的关系,对于理解两种函数的特性和性质有着重要的指导作用。
本文将从反比例函数和一次函数的定义、性质以及它们的交点线段等长度三个方面展开论述,以期为读者提供全面、深入的理论解释和具体实例分析,帮助读者更好地理解这一数学问题。
一、反比例函数和一次函数的定义和性质反比例函数是指函数的定义域为实数集,值域为非零实数集,并且函数的图像在直角坐标系中呈现出双曲线的函数。
一次函数是指形式为y=kx+b的函数,其中k和b为常数,且k不为零,其图像在直角坐标系中呈现出直线的函数。
从函数的定义和性质上来看,反比例函数和一次函数是两种截然不同的函数类型,反比例函数的图像是双曲线,而一次函数的图像是直线。
二、反比例函数和一次函数的交点反比例函数与一次函数的交点是指当两种函数的图像在直角坐标系中相交时的交点,这个交点的横纵坐标就是两种函数的自变量和因变量相等的值。
具体来说,当反比例函数y=k/x和一次函数y=kx+b相交时,就产生了交点。
三、反比例函数与一次函数交点线段相等反比例函数与一次函数交点线段相等,意味着从两种函数的交点开始,到两条函数的横坐标值相等时,所对应的纵坐标的长度是相等的。
这个性质是从函数的定义和性质以及它们的交点出发所得出的。
针对这一数学问题,可以通过具体的例子来进一步说明。
假设反比例函数为y=1/x,一次函数为y=2x+3,求它们的交点线段相等。
我们来求两种函数的交点。
当y=1/x和y=2x+3相交时,即1/x=2x+3,求解得到x=-1和x=1。
将x代入y=1/x和y=2x+3中,得到两个交点为(-1,-1)和(1,5)。
接下来,根据交点线段相等的定义,计算两条函数的横坐标值相等时,纵坐标的长度。
当x=1时,反比例函数的纵坐标为1,一次函数的纵坐标为5;当x=-1时,反比例函数的纵坐标为-1,一次函数的纵坐标为1。
可以看出,从两种函数的交点开始,到它们的横坐标值相等时,所对应的纵坐标的长度是相等的。
一次函数和反比例函数

一次函数和反比例函数一次函数和反比例函数是数学中常见的两种函数类型。
它们在数学、工程、经济等领域中都有广泛的应用。
本文将详细介绍一次函数和反比例函数的概念、性质、图像和应用。
一、一次函数一次函数又称为一次方程,是指形如y=ax+b的函数,其中a和b是常数,x和y分别表示自变量和因变量。
一次函数的图像是一条直线,其中a称为直线斜率,表示直线倾斜的程度,b称为截距,表示直线与y轴的交点。
1. 性质(1)斜率为零的直线是水平直线,斜率为正的直线是向上倾斜的直线,斜率为负的直线是向下倾斜的直线。
(2)当x取不同的值时,y的变化量与x的变化量成正比例关系。
(3)直线的截距表示当x为0时,直线与y轴的交点的纵坐标。
2.图像一次函数的图像是一条直线,其斜率和截距决定了直线的位置和形状。
可以通过画出两个点来确定一条直线,但也可以通过斜率和截距来快速绘制出直线。
如果一次函数的斜率为2,截距为1,则可以画出通过点(0,1)和(1,3)的直线。
3.应用一次函数在很多领域中都有广泛的应用。
斜率表示了物体运动的速率和变化率,截距表示了与x轴的位移,因此一次函数可以被用来描述运动、重力、天体物理等等。
二、反比例函数反比例函数是指形如y=k/x的函数,其中k是常数,x和y分别表示自变量和因变量。
当x趋近于0时,y趋近于无限大;当x趋近于无限大时,y趋近于0。
反比例函数的图像是一条无限接近x和y轴的双曲线。
(1)当x趋近于0时,y趋近于无限大;当x趋近于正无穷大时,y趋近于0。
(2)反比例函数的图像是一条双曲线,其两条渐进线是x轴和y轴。
(3)当x增大时,y减小,反之亦然。
反比例函数在很多领域中都有广泛的应用。
它可以被用来计算电路中的电流和电压、计算物体的加速度、分析经济学中的消费和产量关系等等。
反比例函数的性质和图像使得其在工程、经济等领域中具有很大的实用价值。
在实际应用中,一次函数和反比例函数经常被用来描述各种现象和过程。
一次函数 反比例函数 求一次函数解析式
一、引言一次函数和反比例函数是数学中常见的两种函数类型,它们在实际生活中有着广泛的应用。
本文将分别介绍一次函数和反比例函数,并重点讨论如何求解一次函数的解析式。
二、一次函数的定义和特点1. 一次函数的定义一次函数又称为线性函数,其一般形式可以写作y = ax + b,其中a和b为常数,且a≠0。
2. 一次函数的特点一次函数的图像是一条直线,其斜率为a,常数项为b。
直线的斜率决定了直线的倾斜程度,而常数项决定了直线与y轴的交点。
三、求解一次函数的解析式1. 已知斜率和截距的情况当已知一次函数的斜率和截距时,求解其解析式非常简单。
只需要将已知的斜率和截距代入到一次函数的一般形式中即可得到解析式。
以y = 2x + 3为例,斜率为2,截距为3,因此解析式为y = 2x + 3。
2. 已知两个点的情况当已知一次函数上的两个点时,可以通过求解直线的斜率和截距来得到解析式。
首先根据已知两个点的坐标(x₁, y₁)和(x₂, y₂),可以求得直线的斜率a=(y₂-y₁)/(x₂-x₁)。
然后可以取其中一个点代入斜率和一次函数的一般形式中,解出常数项b。
以两点(-1, 1)和(2, 4)为例,斜率为(4-1)/(2-(-1))=1,带入(-1, 1)可以得到方程组1 = -2 + b,解得b=3,结合斜率a=1,得到解析式为y = x + 3。
3. 已知斜率和直线上一点的情况当已知一次函数的斜率和直线上的一个点时,可以通过斜率和直线上的点来求解解析式。
首先将斜率和给定点代入到一次函数的一般形式中,得到方程y = ax + b。
以斜率为2和点(3, 7)为例,将斜率和点的坐标代入,得到方程7 =2*3 + b,解得b=1,因此解析式为y = 2x + 1。
四、反比例函数的定义和特点1. 反比例函数的定义反比例函数又称为一次函数的倒数函数,其一般形式可以写作y = k/x,其中k为比例系数,且k≠0。
2. 反比例函数的特点反比例函数的图像是一条以原点为中心的双曲线,其横轴为渐近线。
八年级数学一次函数和反比例函数(PPT)5-3
y=3x-2
1
x 0 2/3 y -2 0
-1 o
1
x
-1
-2
-3
教学教程
一、给出问题 1.一次函数(y=kx+b,k≠0)
(1)k、b的符号对图象的影响是怎样的?
(2)如何求一次函数的图象与坐标轴的交点坐标?
(3)如何画一次函数的图象? (4)若两条直线互相平行,A的值是否会相同?
(5)会用待定系数法求一次函数的解析式吗?
(6)一次函数的性质如何表述?
长,家庭教师和家长,店员和店主)。 【宾服】ī〈书〉动服从;归附。 【宾服】ī?〈方〉动佩服:你说的那个理,俺不~。 【宾馆】ī名招待来宾住宿的地 方。现指较大而设施好的旅馆。 【宾客】ī名客人(总称):迎接八方~。 【宾朋】ī名宾客;朋友:~满座。 【宾语】ī名动词的一种连带成分,一般在动词 后边,用来回答“谁?”或“什么?”例如“我找; / 笔趣阁;厂长”的“厂长”,“他开拖拉机”的“拖拉机”,“接受批评” 的“批评”,“他说他不知道”的“他不知道”。有时候一个动词可以带两个宾语,如“教我们化学”的“我们”和“化学”。 【宾至如归】īī客人到了这 里就像回到自己的家一样,形容旅馆、饭馆等招待周到。 【宾主】ī名客人和主人:~双方进行了友好的会谈。 【彬】ī①[彬彬](īī)〈书〉形文雅的样 子:~有礼|文质~。②(ī)名姓。 【傧】(儐)ī[傧相](ī)名①古代称接引宾客的人,也指赞礼的人。②举行婚礼时陪伴新郎新娘的人:男~|女~。 【斌】ī同“彬”。 【滨】(濱)ī①水边;近水的地方:海~|湖~|湘江之~。②靠近(水边):~海|~江。③(ī)名姓。 【缤】(繽)ī[缤纷](ī) 〈书〉形繁多而凌乱:五彩~|落英(花)~。 【槟】(檳、梹)ī[槟子](ī?)名①槟子树,花红的一种,果实比苹果小,红色,熟后转紫红,味酸甜带 涩。②这种植物的果实。 【镔】(鑌)ī[镔铁](ī)名精炼的铁。 【濒】(瀕)ī①紧靠(水边):~湖|东~大海。②临近;接近:~危|~行。 【濒绝】 ī动濒临灭绝或绝迹:~物种。 【濒临】ī动紧接;临近:我国~太平洋|精神~崩溃的边缘。 【濒死】ī动临近死亡:从~状态下抢救过来。 【濒危】ī动接 近危险的境地,指人病重将死或物种临近灭绝:病人~|~动物。 【濒于】ī动临近;接近(用于坏的遭遇):~危境|~绝望|~破产。 【豳】ī古地名, 在今陕西彬县、旬邑一带。也作邠。 【摈】(擯)〈书〉抛弃;排除:~诸门外|~而不用。 【摈斥】动排斥:~异己。 【摈除】动排除;抛弃:~陈规
一次函数与反比例函数交点取值范围
一、题目一次函数与反比例函数交点取值范围二、概述在数学中,一次函数和反比例函数是两种常见的函数类型。
它们在图像上有着不同的特点,而当这两种函数相交时,交点的取值范围则是一个有意义的数学问题。
本文将通过分析一次函数与反比例函数的交点,探讨其取值范围。
三、一次函数与反比例函数简介1. 一次函数一次函数是指具有形如f(x) = ax + b的函数,其中a和b是常数且a 不等于0。
一次函数的图像是一条直线,斜率为a,截距为b。
2. 反比例函数反比例函数是指具有形如f(x) = k/x的函数,其中k是常数且k不等于0。
反比例函数的图像是一条开口向下的抛物线。
四、一次函数与反比例函数的交点一次函数和反比例函数的交点是指它们在坐标平面上的图像相交的点。
具体来说就是通过求解方程f(x) = g(x),其中f(x)是一次函数,g(x)是反比例函数。
五、求解交点的一般步骤1. 设定f(x) = ax + b和g(x) = k/x。
2. 通过解方程f(x) = g(x),得到交点的x坐标。
3. 将得到的x坐标带入f(x)或g(x)中,求得交点的y坐标。
六、交点的取值范围一次函数和反比例函数的交点的取值范围可以通过以下步骤来确定:1. 确定一次函数和反比例函数的交点的x坐标的取值范围(1) 一次函数的定义域是全部实数,即一次函数的x可以取任意实数。
(2) 反比例函数的定义域是x不等于0的实数,即反比例函数的x不能为0。
2. 求解交点的x坐标(1) 通过解方程f(x) = g(x),得到交点的x坐标。
(2) 讨论方程f(x) = g(x)的解的情况,即交点的x坐标。
3. 确定交点的y坐标的取值范围(1) 将得到的x坐标带入f(x)或g(x)中,求得交点的y坐标。
(2) 结合一次函数和反比例函数在x坐标取值范围的情况,确定交点的y坐标的取值范围。
七、总结一次函数与反比例函数的交点取值范围是一个有趣且具有挑战性的数学问题。
通过本文的分析,我们对这一问题有了一定的了解。
反比例函数和一次函数
反比例函数和一次函数
反比例函数和一次函数是数学中两种基本的函数类型。
反比例函数指的是当一个变量增加时,另一个变量会以相反的比例减小的函数。
一次函数则指的是一个变量的增加会导致另一个变量的相应增加的函数。
这两种函数在数学中都有广泛的应用。
反比例函数的一般形式为y=k/x,其中k为常数。
这里的x和y 都表示实数。
这个函数在x=0处不存在,因为x不能为零,但是当x趋于0时,y会趋于无穷大或无穷小。
这个函数的图像通常是一个双曲线。
一次函数的一般形式为y=kx+b,其中k和b都是常数。
这个函数在x=0处的值为b,而斜率k则表示了y随x变化的速率。
这个函数的图像通常是一条直线。
反比例函数和一次函数都可以被用来描述各种自然现象,例如物体的运动、电流的变化等等。
它们也都可以被用来解决各种实际问题,例如经济学中的成本和收益问题、物理学中的速度和加速度问题等等。
总之,反比例函数和一次函数是数学中常见的两种函数类型,它们都有广泛的应用,并且在解决实际问题中都扮演着重要的角色。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
பைடு நூலகம் k7怎么作弊
[问答题,简答题]使用维护过程中遇到难于解决的问题或出现异常情况如何和厂家取得联系? [判断题]稠化剂加在基础油中从而形成半固体润滑脂。()A.正确B.错误 [判断题]ABS中的制动压力调节器主要有液压式、气压式和空气液压加力式。A.正确B.错误 [单选,A1型题]治热毒上炎致口舌生疮、咽喉肿痛、目赤肿痛,宜选()A.白矾B.炉甘石C.硼砂D.雄黄E.硫黄 [单选]¥15409.02,写成中文人民币大写应为()。A.人民币壹万伍仟肆佰零玖元贰分B.人民币壹万伍仟肆佰零玖元零贰分C.人民币壹万伍仟肆佰零玖元零角贰分D.人民币壹万伍仟肆佰零玖元零贰分整 [多选]下列关于着作权主体的说法中,正确的有()。A.招标文件属于单位作品,着作权完全归单位所有B.单位作品的作者是单位,而职务作品的作者是个人C.一般情况下,职务作品的着作权由作者享有D.职务作品的作者可以许可第三人使用该作品E.委托作品的着作权属于委托人。 [单选,A1型题]某眼屈光度为-3.00D,在完全矫正屈光不正后,其近点距离为5cm,则其调节幅度为()。A.20DB.23DC.17DD.8DE.5D [单选]男,65岁,有高血压、糖尿病多年。一天前发现左侧上、下肢活动受限,吐字不清,神志清楚。无明显头痛、呕吐,检查发现左侧上、下肢肌力3级,左半身痛觉减退,头颅CT未见异常,临床上考虑可能性最大的疾病是()A.脑出血B.脑栓塞C.短暂性脑缺血发作D.蛛网膜下腔出血E.脑血栓 [单选]如图A_2所示,闭合铁心中磁通量一定时,其励磁电流的大小()。A. [单选,A4型题,A3/A4型题]男,32岁,进食后上腹饱胀不适,伴返酸、烧心、嗳气、食欲不振,临床诊断为慢性胃炎。该病治疗中不正确的是()。A.避免饮酒B.胃酸高者使用抑酸剂C.胃酸低者使用胃黏膜保护剂D.抗Hp治疗E.以上都不是 [填空题]开水蒸气阀门时,开阀前应先打开排凝阀,将设备或管道内的()排净,关闭排凝阀后再由()到()逐渐把蒸汽阀打开,以防止蒸汽遇水造成水锤现象,产生震动而损坏设备和管道。 [配伍题]内容同住院病历,但重点更突出、更简要的是()</br>病人住院期间的全部病情经过应记录在()A.会诊记录B.入院记录C.病程记录D.出院记录E.死亡记录 [单选]教育信息资源的开发和利用是()的基本内容是教育信息化建设取得实效的关键。A.教育信息化B.信息化建设C.电子商务D.专业技术 [填空题]()是指地基稳定具有足够安全度的承载力,它相当于地基极限承载力除以一个安全系数k,且要验算地基变形不超过允许变形值。 [填空题]电子商务规划的可行性分析主要包括:()和()。 [单选,A1型题]大多数肾损伤采取的治疗方法是()A.肾切除术B.部分肾切除术C.肾周引流术D.非手术治疗E.肾修补术 [单选]船政学堂中的()是负责教授造船工艺的。A、左学堂B、右学堂C、前学堂D、后学堂 [单选]论文得不到公认,就是不科学的:()A、对B、不全对C、错 [单选]患者女性,40岁,风心病二尖瓣狭窄并关闭不全,发热5周,间断口服抗生素治疗,镜下血尿1周,结膜下可见数个出血点,疑诊亚急性细菌性心内膜炎,最可能的致病菌是()A.金黄色葡萄球菌B.草绿色链球菌C.肠球菌D.真菌E.衣原体 [问答题,简答题]简述伤口换药。 [单选]关于安氏Ⅱ类错?,下列说法不正确的是()A.安氏Ⅱ类错?是一个单纯的错类型B.安氏Ⅱ类错?中大多数上颌骨位正常C.在上颌骨位置异常者中,上颌后明显多于上颌前突D.上牙弓后缩多于上牙弓前突E.安氏Ⅱ类错?中约60%患者下颌后缩 [单选,A型题]下列哪种肠梗阻一般多为绞窄性梗阻()A.肠套叠B.蛔虫性肠梗阻C.胆石性肠梗阻D.粘连性肠梗阻E.麻痹性肠梗阻 [单选,A1型题]拔毒化腐生肌药多含砷、汞、铅等元素,多具剧烈毒性或强大刺激性,下列哪项使用方法是错误的()A.严格控制剂量和用法B.既可外用,也可内服C.根据患者的体质及病情确定用法D.部分中药不宜用于头面及黏膜上E.外用不可过量或持续服用 [单选]建筑内部因采用大量可燃材料装修、使用可燃家具,将()。(易)A、延长轰燃出现的时间B、增加火灾荷载C、降低耐火等级D、影响防火间距 [单选,A2型题,A1/A2型题]下列哪项不属于泄卫透表法的范围?()A.疏风散热法B.解表清暑法C.清热泻火法D.宣表化湿法E.疏卫润燥法 [填空题]历史数据采集可以用不同的存储()间隔。 [单选]()型车的结构形式为整体承载结构。A.C61、C63、C6a、C64、C16、K13B.P64、G70C.N17、X6A、X6B、X2H、X2KD.C16、K13、X2K [单选]Inmarsat通信系统中,移动站的工作波段为()。A.L波段B.C波段C.S波段D.X波段 [单选]在企业有盈利,需要追加外部投资的情况下,下列有关外部融资需求的表述正确的是()。A.销售增加,必然引起外部融资需求的增加B.销售净利率与外部融资需求成正比关系C.股利支付率与外部融资需求成正比关系D.资产周转率的提高必然引起外部融资额增加 [单选]有关纤维支气管镜检,下列哪项不正确()A.术前应禁食4~6小时B.术前应作X线胸片检查C.术前均应做肺通气功能检查及血气分析D.术前半小时注射阿托品及鲁米那E.术后应禁食2小时 [单选]热处理基础工艺代号中,第四位数字代表()。A.加热方法B.工艺类型C.附加工艺代号 [判断题]个人对外贸易经营者办理对外贸易购付汇、收结汇可通过任何外汇结算账户进行。A.正确B.错误 [单选]不属于仓库的主要作业的是货品的()A.入库作业B.在库管理C.包装作业D.出库作业 [单选]以下哪种肺癌副癌综合征的说法是不正确的()A.重症肌无力B.库欣综合征C.中叶综合征D.感觉性神经病E.类癌综合征 [单选]下列哪种情况下,测深辨位可得出比较准确的结果()。A.计划航线与等深线平行,等深线稀疏B.计划航线与等深线垂直,等深线稀疏C.计划航线与等深线平行,等深线密集D.计划航线与等深线垂直,等深线密集 [单选]某建设项目的总投资为5600万元,年平均利润总额为1200万元,则该建设项目的总投资收益率为()。A.23.43%B.21.43%C.17.65%D.18.46% [单选,A型题]尿常规红细胞(++),腹部平片阴性。造影见右肾上极肾盏有充盈缺损,周边肾盂肾盏无异常,CT显示病变肾盏内有一较高密度影,应考虑为()A.肾肿瘤B.肾结石C.肾囊肿D.肾盏憩室E.肾盏痉挛 [单选,A2型题,A1/A2型题]下列微生物哪种属于原核细胞型微生物()A.病毒B.螺旋体C.真菌D.噬菌体E.以上都不是 [单选]下列各项业务中,可以确认收入的是。A.企业销售的商品在质量、品种、规格等方面不符合合同或协议的要求,又未根据正常的保证条款予以弥补B.企业尚未完成售出商品的安装或检验工作,且安装或检验工作是销售合同和协议的重要组成部分C.销售合同和协议中规定了买方由于特殊原因 [单选]高分子烃蜡一般存在于()和润滑油馏分中。A、汽油B、柴油C、煤油D、石脑油
