第二章流体静力学-静压强及其特性
合集下载
工程流体力学2

§2-1 流体静压强及其特性
静压强:当流体处于平衡或者相对平衡状态时, 作用在流体单位面积上的力。
p lim Fn
A 0
A
pn
特性一:
流体静压强的作用方向沿着
作用面的内法线方向。
静止流体对容器的作用一定垂直于固体壁面。
§2-1 流体静压强及其特性
特性二:
静止流体中的任一点上,来自任意方向上的静压强都是相等的。
三、流体静压强的测量和液柱式测压计
常见的测压仪器有:液柱式测压计;金属式压强计(利用
金属的变形来测量压强);电测式仪表(将压强变化转化
为电信号的变化)等。
液柱式测压计的测量原理是以流体静力学基本方程 为依据的。
§2-3 重力场中流体的平衡
1、测压管
p pa
p p a gh
p pa
计。通常采用双U形管或三U形管测压计。
§2-3 重力场中流体的平衡
3. U形管差压计 用于测量两个容器或管 道流体中不同位置两点 的压强差。
p p A p B 2 gh 1 gh 2 1 gh 1 2 1 gh
§2-3 重力场中流体的平衡
§2-3 重力场中流体的平衡
水头:单位重量流体所具有的能量用液柱高度来表示。 静水头:位置水头和压强水头之和。
方程的几何意义:
在重力作用下,静止的不可压缩流体中各点的静水头都相等。
§2-3 重力场中流体的平衡
有自由液面的静压强公式: p0 p z z h g g
p p 0 gh
h 为任意点在自由液面下的深
度,即淹深。
流体内部的静压强包含两部分:
第二章流体静力学

A、9:1:10:2 B、相同 C、与形状有关
流体力学
pA pB 2 gh2 3 gh3 1gh1
倾斜式测压计(微压计)
通常用来测量气体压强
pAm 2 gl sin 1 gh1
倾斜管放大了测量距 离,提高了测量精度
流体力学
l h
1
sin
作业:P.63~65 23 26 2 10 2 13
流体力学
小结1
作等压面 被测点 相界面 等高的两点必须在连 通的同一种液体中 沿液柱向上,压强减小 沿液柱向下,压强增大
流体力学
U型管测压计2
U型管测压计特点 测量范围较大 可测量气体压强
pAm 2 gh2 1gh1 2 gh2 可测量真空压强 指示液不能与被测液体掺混
流体力学
差压计
流体力学
x
y
z
j
p y
x
y
z
k
p z
x
y
z
i
p x
j
p y
k
p z
x
y
z
p
x
y
z
流体力学
压强梯度
2.2 静止流体平衡微分方程
静止流体受力平衡
f xyz pxyz 0
静止流体平衡方程-欧拉平衡方程
流体静压强的特性
垂直于作用面,指向流体内部
大小与作用面方位无关,只是作 用点位置的函数
绝对压强、计示压强小结2
液柱式测压计
各种测压计的优缺点 指示液的选取 几个概念 相对静止、等压面
流体力学
pA pB 2 gh2 3 gh3 1gh1
倾斜式测压计(微压计)
通常用来测量气体压强
pAm 2 gl sin 1 gh1
倾斜管放大了测量距 离,提高了测量精度
流体力学
l h
1
sin
作业:P.63~65 23 26 2 10 2 13
流体力学
小结1
作等压面 被测点 相界面 等高的两点必须在连 通的同一种液体中 沿液柱向上,压强减小 沿液柱向下,压强增大
流体力学
U型管测压计2
U型管测压计特点 测量范围较大 可测量气体压强
pAm 2 gh2 1gh1 2 gh2 可测量真空压强 指示液不能与被测液体掺混
流体力学
差压计
流体力学
x
y
z
j
p y
x
y
z
k
p z
x
y
z
i
p x
j
p y
k
p z
x
y
z
p
x
y
z
流体力学
压强梯度
2.2 静止流体平衡微分方程
静止流体受力平衡
f xyz pxyz 0
静止流体平衡方程-欧拉平衡方程
流体静压强的特性
垂直于作用面,指向流体内部
大小与作用面方位无关,只是作 用点位置的函数
绝对压强、计示压强小结2
液柱式测压计
各种测压计的优缺点 指示液的选取 几个概念 相对静止、等压面
工程流体力学 第二章 流体静力学201012

Y = ω 2 r sin α = ω 2 y Z = −g
z ω
1.等压面方程 1.等压面方程
dp = ω 2 xdx + ω 2 ydy − gdz = 0
⇓ 积分
ω 2 x2
2 +
p0
o
m
h z
zs y
ω 2 y2
2
− gz = C
ω 2r 2
2
− gz = C
等压面是一簇绕z轴的旋转抛物面。 等压面是一簇绕z轴的旋转抛物面。 自由液面: 自由液面: x=0 z=0 C=0
z g p0
2
⇒
dp = ρ(Xdx +Ydy + Zdz)
dp = −ρgdz
p2
p1
1
⇒
dp dz + =0 ρg
z1
z2
积分得: 积分得:
p z+ =C ρg
o
p p z1 + 1 = z2 + 2 ρg ρg
基准面
x
2.物理意义 2.物理意义
z+ p =C ρg
总 势 能
3.几何意义 3.几何意义
o y
αr
y x ω2y ω2r
⇓
zs =
ω 2r 2
2g
x
ω2x
二、等角速旋转容器中液体的相对平衡
2. 静压强分布规律
dp = ρ (ω 2 xdx + ω 2 ydy − gdz )
z ω
⇓ 积分
p = ρ(
ω 2x2
2
+
ω 2 y2
2
− gz ) + C
p = ρg (
ω 2r 2
z ω
1.等压面方程 1.等压面方程
dp = ω 2 xdx + ω 2 ydy − gdz = 0
⇓ 积分
ω 2 x2
2 +
p0
o
m
h z
zs y
ω 2 y2
2
− gz = C
ω 2r 2
2
− gz = C
等压面是一簇绕z轴的旋转抛物面。 等压面是一簇绕z轴的旋转抛物面。 自由液面: 自由液面: x=0 z=0 C=0
z g p0
2
⇒
dp = ρ(Xdx +Ydy + Zdz)
dp = −ρgdz
p2
p1
1
⇒
dp dz + =0 ρg
z1
z2
积分得: 积分得:
p z+ =C ρg
o
p p z1 + 1 = z2 + 2 ρg ρg
基准面
x
2.物理意义 2.物理意义
z+ p =C ρg
总 势 能
3.几何意义 3.几何意义
o y
αr
y x ω2y ω2r
⇓
zs =
ω 2r 2
2g
x
ω2x
二、等角速旋转容器中液体的相对平衡
2. 静压强分布规律
dp = ρ (ω 2 xdx + ω 2 ydy − gdz )
z ω
⇓ 积分
p = ρ(
ω 2x2
2
+
ω 2 y2
2
− gz ) + C
p = ρg (
ω 2r 2
流体力学第二章流体静力学

第二章 流体静力学
❖ 流体静力学研究流体的平衡规律,由平衡条 件求静压强分布规律,并求静水总压力。
❖静止是一个相对概念,指流体相对于地球无 运动的绝对平衡和流体相对于地球运动但质点 之间、质点与容器之间无运动的相对平衡。
❖流体质点之间没有相对运动,意味着粘性将 不起作用,所以流体静力学的讨论不须区分流 体是实际流体或理想流体。
pA mhm a
p1左 pA a p1右 mh
2.5.3水银压差计
即使在连通的 静止流体区域中 任何一点的压强 都不知道,也可 利用流体的平衡 规律,知道其中 任何二点的压 差,这就是比压 计的测量原理。
p1左 pA ( z A hm ) p1右 pB mhm zB
面,自由表面上压强为大气压,则液面
以下 h 处的相对压强为 γh ,所以在
液体指定以后,高度也可度量压强,称 为 液 柱 高 , 例 如 : ××m(H2O) , ××mm(Hg) 等。特别地,将水柱高称 为水头。
p=0 h
ph
98 kN/m2=一个工程大气压=10 m(H2O)=736 mm(Hg)
任意形状平面上的静水总压力大 小,等于受压面面积与其形心点 压强的乘积。
2.静水总压力的方向垂直并指 向受压面
3.总压力P的作用点
根据合力矩定理,对x轴
PyD ydP
yy sin dA sin y2dA
p
1 2
p x
dx
dydz
p
1 2
p x
dx
dydz
X
dxdydz
0
化简得:
X 1 p 0
x
Y,z方向可得:
Y Z
1
1
p y p
0
❖ 流体静力学研究流体的平衡规律,由平衡条 件求静压强分布规律,并求静水总压力。
❖静止是一个相对概念,指流体相对于地球无 运动的绝对平衡和流体相对于地球运动但质点 之间、质点与容器之间无运动的相对平衡。
❖流体质点之间没有相对运动,意味着粘性将 不起作用,所以流体静力学的讨论不须区分流 体是实际流体或理想流体。
pA mhm a
p1左 pA a p1右 mh
2.5.3水银压差计
即使在连通的 静止流体区域中 任何一点的压强 都不知道,也可 利用流体的平衡 规律,知道其中 任何二点的压 差,这就是比压 计的测量原理。
p1左 pA ( z A hm ) p1右 pB mhm zB
面,自由表面上压强为大气压,则液面
以下 h 处的相对压强为 γh ,所以在
液体指定以后,高度也可度量压强,称 为 液 柱 高 , 例 如 : ××m(H2O) , ××mm(Hg) 等。特别地,将水柱高称 为水头。
p=0 h
ph
98 kN/m2=一个工程大气压=10 m(H2O)=736 mm(Hg)
任意形状平面上的静水总压力大 小,等于受压面面积与其形心点 压强的乘积。
2.静水总压力的方向垂直并指 向受压面
3.总压力P的作用点
根据合力矩定理,对x轴
PyD ydP
yy sin dA sin y2dA
p
1 2
p x
dx
dydz
p
1 2
p x
dx
dydz
X
dxdydz
0
化简得:
X 1 p 0
x
Y,z方向可得:
Y Z
1
1
p y p
0
流体静力学

p pa g (h h)
其表压力为
p g g (h h)
单管杯式测压计
p g g (h h)
根据体积平衡的原理
h
D 2
4
h
d 2
4
d2 h 2 h D pg d2 gh(1 ) 2 D
单管杯式测压计
P1 P2 P3
P4 P5
因为:
p A p1 1 gh 1
p3 p4 2 gh2 pB p5 3 gh3
所以:
p A pB ( 1h1 2 h2 3 h3 ) g
另一种方法:
根据“从一边开始,找等压面,向上减,向下加”的原则进行。
解:此处的等压面有两个,1—2—3和4—5。
1 1 p x dydz pn dAn cos( n x) dxdydzX 0 2 6
因为: dAn cos( n x)
把PX,Pn和Fx 的各式代入得:
p x p n dx X 0 3 p x pn 略去高阶无穷小量,得到:
或:
A
Py
Pn
dz
Px o dy Pz dx x
设其中心点压力为p。进行受力分析。 以x方向为例:
p
表面力----作用于此六面体上的静压强
p dx x 2
z
dy p dz dx x
p
p dx x 2
在x轴方向上作用在微六面体上的压力共为: o
p dx p dx p p dydz p dydz dxdydz y x 2 x 2 x
Px
o dy
dx
因为 :微元四面体处于平衡状态, 故:作用在其上的一切力在任意 轴上投影的总和等于零。 y 对于直角坐标系,则:
第二章 流体静力学

工程实际:堤坝、闸门、桥墩 研究目标:合力的大小、方向、作用点 计算方法:解析法和图解法
h
h
一、解析法
如图所示,静止液体中有一倾斜放置的平面MN,试求作用 在该平面上的总压力。
1)粗线MN代表其侧视图,正面投影为绕其对称轴转90 度 2)平面MN的延伸面与自由液面的交角为;
3)坐标系:ox轴为平面MN的延伸面与自由液面的交线;
二、欧拉平衡微分方程的全微分形式
p X
x ×dx
p Y
y
×dy
p Z
z
×dz
p dx p dy p dz ( Xdx Ydy Zdz)
x y z
p p(x, y, z) dp p dx p dy p dz x y z
通常作用在流体上的单位 质量力是已知的,利用上 式便可求得流体静压强的 分布规律。
yD
sin Iox
P
sin Iox hc A
sin Iox yc sin A
I ox yc A
引入平行移轴公式 Iox Ic Ayc2
yD
I ox yc A
Ic yc2 A yc A
yc
Ic yc A
由此可知,压力中心D必位于受压面形心c之下。
说明:
工程中常见的受压平面多具有轴对称性(对称轴与
当流体存在真空时,工程习惯上用真空度(负压)表示。
真空
pv pabs pa
道 路
三者关系
当p>pa 时,绝对压强=表压强+当地大气压 当p<pa 时,绝对压强=当地大气压-真空度
p 表压强
p>pa 真空度
当地大气压 pa
绝对压强
p<pa
绝对真空 p=0
h
h
一、解析法
如图所示,静止液体中有一倾斜放置的平面MN,试求作用 在该平面上的总压力。
1)粗线MN代表其侧视图,正面投影为绕其对称轴转90 度 2)平面MN的延伸面与自由液面的交角为;
3)坐标系:ox轴为平面MN的延伸面与自由液面的交线;
二、欧拉平衡微分方程的全微分形式
p X
x ×dx
p Y
y
×dy
p Z
z
×dz
p dx p dy p dz ( Xdx Ydy Zdz)
x y z
p p(x, y, z) dp p dx p dy p dz x y z
通常作用在流体上的单位 质量力是已知的,利用上 式便可求得流体静压强的 分布规律。
yD
sin Iox
P
sin Iox hc A
sin Iox yc sin A
I ox yc A
引入平行移轴公式 Iox Ic Ayc2
yD
I ox yc A
Ic yc2 A yc A
yc
Ic yc A
由此可知,压力中心D必位于受压面形心c之下。
说明:
工程中常见的受压平面多具有轴对称性(对称轴与
当流体存在真空时,工程习惯上用真空度(负压)表示。
真空
pv pabs pa
道 路
三者关系
当p>pa 时,绝对压强=表压强+当地大气压 当p<pa 时,绝对压强=当地大气压-真空度
p 表压强
p>pa 真空度
当地大气压 pa
绝对压强
p<pa
绝对真空 p=0
流体静力学

a. 测压管:利用液柱高度表达压强的原理制成的简
单的测量装置。
pA hA
pAlsin
b. U型水银测压计
p 0 水 h m 银 水 h 1 h 2
pAp0水 h1
c. 组合水银测压计
p
h1 a
空 气
h2
a h3
b
p水银 gh3 水银 gh2
gh1
b
水银
d. U型管压差计
pBpA水银 h
方程: d p(X dYxd Z y)dz
令 dp=0 得
Xd Y xd Z yd 0 z
等压面性质:
(1)等压面就是等势面。 dpdU
(2)作用在静止流体中任一点的质量力必然垂直于 通过该点的等压面。
证明:沿等压面移动无穷小距离dL=idx+jdy+kdz, 则单位质量 力做的功应为Xdx+Ydy+Zdz,显然它等于零,所以,质量 力与等压面相垂直。
对于不可压缩流体,γ=const,积分(2)式得:
pzC
(3)
代入边界条件:z=0时,p=p0
则 C= p0
pp0 z
令 -z=h 则
pp0 h
(4) (5)
——静力学基本方程
适用条件:静止、不可压缩流体。
二、静力学基本方程式的意义 由(3)式: z p C (6)
1、几何意义
z 位置水头
p 压强水头 该点压强的液柱高度
Ah1h2Bh2h
e. 组合式U形管压差计
p 1 p 2H h g h 2 h 1
2、金属测压计 原理:弹性元件在压强作用下产生弹性变形。 分类:弹簧管式(a)、薄膜式(b)压力表。
3.电测式压力计
流体力学-流体静力学
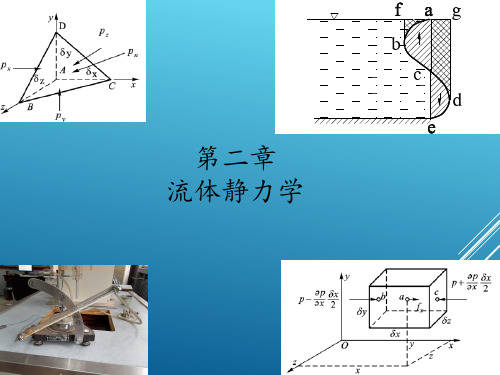
边长 δx、δy、δz 静压强 px、py、pz和pn
密度 ρ
单位质量力的投影
fx 、fy、 fz
力在x方向的平衡方程为:
px
1 yz
2
pn
ABCD
cos pn ,
x
fx
1 xyz
6
0
px
1 yz
2
pn
ABCD
cospn, x
fx
1 xyz
6
0
由于
ABCD
cos pn ,
x
1 2
yz
px
pn
fx
特例二
边界条件 z 0 r R 时
得
C
pa
2R2
2
p pa
p
pa
g
2
R2 r2 2g
z
等角速旋转容器中液体的相对平衡
2.5静止液体作用在固体壁面上的总压力
意义:油箱、油罐及各种压力容器的设计等。往往以计示压强进行计算。
一、液体作用在平面上的总压力(大小、方向) 研究对象:如图
微元总压力 dFP ghdA gy sindA
求: H ?
已知:d1 45cm, d2 30cm, F1 3197N, F2 4945.5N,
13600kg / m3, pe 9810pa.
求: h ?
2.4 液体的相对平衡
1.水平直线等加速运动容器中液体的相对平衡
静压强的分布规律 f x 0 f y a f z g
代入压强差公式 dp ady gdz
fx
x
fy
y
f grad
f z z
代入:
d
p
f xdx
f y dy
密度 ρ
单位质量力的投影
fx 、fy、 fz
力在x方向的平衡方程为:
px
1 yz
2
pn
ABCD
cos pn ,
x
fx
1 xyz
6
0
px
1 yz
2
pn
ABCD
cospn, x
fx
1 xyz
6
0
由于
ABCD
cos pn ,
x
1 2
yz
px
pn
fx
特例二
边界条件 z 0 r R 时
得
C
pa
2R2
2
p pa
p
pa
g
2
R2 r2 2g
z
等角速旋转容器中液体的相对平衡
2.5静止液体作用在固体壁面上的总压力
意义:油箱、油罐及各种压力容器的设计等。往往以计示压强进行计算。
一、液体作用在平面上的总压力(大小、方向) 研究对象:如图
微元总压力 dFP ghdA gy sindA
求: H ?
已知:d1 45cm, d2 30cm, F1 3197N, F2 4945.5N,
13600kg / m3, pe 9810pa.
求: h ?
2.4 液体的相对平衡
1.水平直线等加速运动容器中液体的相对平衡
静压强的分布规律 f x 0 f y a f z g
代入压强差公式 dp ady gdz
fx
x
fy
y
f grad
f z z
代入:
d
p
f xdx
f y dy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论课教案教案编号
编写教师编写日期年8月26 日审核教师审核日期年月日教学班级
教学日期2014年月日
课程名称流体力学泵与风机
课题:第二章流体静力学
2-1流体静压强及其特性
教学目标:1.流体静压强的定义;
2.流体静压强的特性。
教学重点:流体静压强的两个特性;
教学难点:两个特性的的理论推导。
教学方法:讲授法、练习法
其它说明:
时间分配教学组织1分钟小结与作业5分钟引入新课4分钟分钟讲解新课80分钟分钟
课后记事
教学内容
教学方法 [复习引入]
高中物理所学压强,水中物体压强分布。
[讲解新课]
第二章 流体静力学 §2-1流体静压强及其特性
一、流体静压强的定义
流体的静压力是作用在某一面积上的总压力;流体的静压强则是作用在某一面积上的平均压强或某一点压强。
二、流体静压强的特性
1.静压强的垂向性
流体不能承受拉力;且具有易流动性,静止时不能承受切向力,故静压强方向与作用面的内法线方向重合。
流体静压强的方向只能是垂直指向作用面。
2. 静压强的各向等值性
作用于静止流体同一点压强的大小各向相等,与作用面的方位无关。
说明:
1) 静止流体中不同点的压强一般是不等的,同一点的各向静压强大小相等。
2) 运动状态下的实际流体,流体层间若有相对运动,则由于粘性会产生切应力,这时同一点上各向法应力不再相等。
[小结与作业]
1.流体静压强的两个特性;
2.作业:简述流体静压强的两个特性。
讲授 讲授
A P
A P p A d d lim
0=
∆∆=→∆。
